第一篇第四章电阻率测深法
《电阻率测深法》课件
THANKS
感谢观看
电阻率测深法的数学模型
电阻率测深法的基本公式
基于电场理论和电路原理，通过测量不同电极间距下的电阻值，推 算出地下岩层的电阻率分布。
数据处理方法
对实测数据进行整理、滤波、反演等处理，提取地下地质信息。
深度推断方法
根据地下岩层的电导率差异，结合已知的地球物理参数和地质资料 ，推断地下不同深度岩层的分布和性质。
电流
02
电荷的定向移动形成电流，单位时间内通过导体横截面的电荷
量称为电流强度，简称电流。
电压
03
电场中任意两点间的电位差称为电压。
电阻率测深法的物理基础
电阻
表示物质导电性能的物理量，与导体的长度 、截面积、材料性质和温度有关。
电导率
电阻率的倒数，表示物质导电能力的物理量 。
电场强度
电场中某点的电场力与单位电荷量的比值， 表示电场强弱的物理量。
局限性
精度问题
由于受到地形、土壤湿度等多种因素的 影响，电阻率测深法的精度有时可能不
够高。
复杂地形的影响
在复杂地形地区，电阻率测深法的结 果可能受到地形起伏的影响，需要进
行校正。
深度限制
该方法的探测深度受到电极间距的限 制，对于深层地下结构的探测可能存 在困难。
数据处理难度
电阻率测深法得到的数据量较大，需 要专业的软件和人员进行处理和分析 。
数据处理
对采集的数据进行预处理，包括数据筛选、异常值剔除、数据格式转换等，为后续解释和反演提供准确的基础数 据。
结果解释与反演
结果解释
根据测量结果，结合地质资料和相关 理论，对测量结果进行解释，识别地 下地质体的分布、性质和规模。
反演计算
环境与工程物探：电阻率测深法
电测深法
（一）电测深法概述
前述的电剖面法是在测量过程中保持AB不变，使整 个或部分装置沿测线移动，逐点观测，以了解某一深 度范围内不同电性体沿水平方向的分布。
而电测深法是在同一点上逐次扩大供电电极距，使探 测深度逐渐增大，以此来得到观测点处沿垂直方向上 由浅到深的ρs变化情况。
一、电测深法的原理 什么是电测深法：
这8种类型分别为：HK、HA、KH、KA、AA、AK、 QQ、QH。
例如:HK（ρ1>ρ2<ρ3>ρ4） HA（ρ1>ρ2<ρ3<ρ4）
ρ1 ρ2 ρ3 ρ4
HA HK
h1 h2 h3 h4→∞
地电断面的电性层很多（例如：大于三层）时， 每增加一层，则表示电测深曲线类型的字母就 增加一个。如“五层”则用“三个字母”来表 示，例如：HKH、HKQ等。
2、装置形式及视电阻率公式
A
M
N
B
O
通常采用对称四级装置
AO=BO; MO=NO
s
k
U MN I
k AM AN
MN
k—随电极距的逐次扩大而改变。
3、电测深曲线 视电阻率ρs随着供电极距（AB/2）变化的曲线，称为 电测深曲线。
电测深曲线的特点： （1）每个电测深点均可以得到一条电测深曲线 （2）该曲线通常以AB/2为横坐标，以ρs为纵坐标，绘 制在模数为6.25cm的双对数坐标纸上。
ρ 1
> ρ2 >
ρ 3
3、多层断面的电测深曲线类型
由四层电性层组成的地电断面，按相邻各层电 阻率的组合关系，其电测深曲线有8种不同的 类型
每种电测深曲线的类型由两个字母表示。第一 个字母表示断面中的前三层（即第一、二、三 层）所对应的电测深曲线类型，第二个字母表 示断面中的后三层（即第二、三、四层）所对 应的电测深曲线类型。
《电阻率测深法》课件
实例分析和应用
地下水资源勘探
电阻率测深法可以用于寻找地下水层的分布，以 指导地下水资源的合理利用。
矿产资源勘探
根据地下矿石和围岩的电阻率差异，可以寻找矿 产资源的存在和分布。
地质工程调查
通过测量地下岩土的电阻率，可以了解地质体的 性质和稳定性，为地质工程设计提供参考。
环境工程监测
通过监测地下水体和土壤的电阻率变化，可以评 估环境工程的效果和影响。
《电阻率测深法》PPT课 件
欢迎来到《电阻率测深法》的世界！在这个课件中，我们将介绍电阻率测深 法的原理、仪器和设备，以及实验步骤和数据分析。让我们共同踏上这场有 趣而富有收获的深度探索之旅吧！
电阻率测深法的介绍
电阻率测深法是一种用于探测地下物质的电阻率分布的地球物理方法。通过测量地下电流和电位差，可以推断 地下岩石、土壤和水体的电阻特性。
控制与数据采集系统
负责控制电流和记录电位差， 以及实时数据采集和分析。
实验步骤
1
准备工作
选择测量地点、安装和连接电极、配置
电流注入
2
仪器。
通过电流电极注入一定大小的电流。
3
电位差测量
记录不同位置的电位差数据。
数据采集与分析
4
将释。
5
结果解读
根据数据分析结果解读地下物质的电阻 率分布。
影响测量结果的因素
1 地下介质类型
不同类型的地下介质具有 不同的电阻率特征，影响 测量结果的准确性。
2 温度和湿度
地下温度和湿度的变化会 影响地下物质的电阻率。
3 电极接触性能
电极与地下介质的接触情 况直接影响测量结果的稳 定性。
数据分析与解释
通过对采集到的电流和电位差数据进行分析，可以得出地下物质的电阻率分布图。结合地质信息和其他地球物 理方法的结果，可以进行更准确的地下结构解释。
对称四极电阻率测深
电阻率影像剖面法是兼具垂直与侧向解析 能力的一种探测方式。其现场勘测配置与地震 反射法类似，系沿着一个既定的测线配置电极， 除能达到如垂直测深的“测深”目的之外，由 于沿测线方向的测点较密，因此容易反应出地 层侧向的变化情形。因属于二维的观测方式， 若再配合二维资料处理，可以克服因地形所造 成的影响。
双极排列法pole-pole Array是將傳統 四極法中的其中兩電極（一個電流 極Ｂ；及一個電位極Ｎ）固定放置 於遠處（一般應超過測深的七倍距 離），施測時僅需移動另外的電流 極Ａ與電位極Ｍ，具有降低更換電 極數目，達到節省測勘時間的目的， 並在有限範圍內，可獲得最大的探 測深度。應用在地電阻影像剖面法 探測上時，在測線上每間隔相同距 離預先插一根電極棒，並透過預先 設定的電極切換規則，以程式化由 儀器自動控制電流極與電位極的切 換。施測的次序是：先不移動測線 上的電流極位置，僅移動電位極至 與電流極達預先設定的距離；然後 將電流極往前移動一電極棒，重複 移動電位極，直至電流極移至倒數 第二電極棒為止，達到掃描地層結 構之目的。
• 电阻率法在地表配置四根电极，其中
两根供电电极（Ａ与Ｂ）以低頻之交
替直流电通入地下，兩根测量电极（：
Ｍ与Ｎ）测量因电流分佈所造成的电
位差V。电位差V与通入地下的电流
強度I、电极间相对位置及地层的电
阻率有关。若测得电流強度Ｉ、电位
差Ｖ及电极之相对位置计算出相对均
匀半空间地层的电阻率ρa：
ρa＝Ｋ（Ｖ／Ｉ） 式中Ｋ称装置系数（或几何因子）， 与电极排列位置有关。 ρa 称视电阻 率，通常不代表地层之真电阻率 ，
电法勘探
电阻率勘探原理
地層由於組成材料及膠結等狀 況之不同，因而表現出不同的導電 特性，一般以電阻率代表物質的導 電性質，不同地層岩性及不同含水 狀況會對應不同的電阻率（或稱為 地電阻譜）；地電阻譜提供我們一 個構想，即若能藉由儀器測量及分 析技術瞭解地下地層的電阻率，則 輔以適當地質資訊，可以用來瞭解 地下地層的岩性分佈情形，進而解 釋地質構造、礦產分佈、地下水資 源、及地下水污染等。由於地電阻 法花費少且工期短，因此適用於工 程地質、探礦、地下水調查、海水 入侵調查與地熱測勘等多方面。
电法勘探原理与方法
电法勘探原理与方法教案刘国兴2003．5总学时64，讲授54学时，实验10绪论：（1学时）绪论中讲5个方面的问题1.对电法勘探所属学科及具体定义。
2.电法勘探所利用的电学性质及参数。
3.电法勘探找矿的基本原理。
在此主要解释如何利用地球物理（电场）的变化，来表达找矿及解决其它地质问题的原理。
4.电法勘探的应用。
1)应用条件2)应用领域3)解决地质问题的特点4)电法勘探在勘探地球物理中所处的位置第一章电阻率法本章为电法勘探的常用成熟的方法，在地质勘察工作中发挥着重要作用，是学习电法勘探的重点之一。
本章计划用27学时，其中理论教学21学时，实验教学6学时。
§1.1 电阻率法基础本节计划用7学时，其中讲授5学时，实验2学时。
本节主要讲述如下五个问题一、矿石的导电性（1学时）讲以下3个问题：1)岩，矿石导电性参数电阻率的定义及特性。
2)天然岩，矿石的电阻率矿物的电阻率及变化范围，岩石电阻率的变化范围。
3)影响岩，矿石电阻率的因素。
I.与组成的矿物成分及结构有关。
II.与所含水分有关。
III.与温度有关。
二稳定电流场的基本性质。
主要回顾场论中有关稳定电流场的一些知识，给出稳定电流场的微分欧姆定律公式电流的连续性（克希霍夫定律）；稳定电流场是势场三个基本性质。
三均匀介质中的点源电场及视电阻率的测定主要讲述三个内容：1)导出位场微分方程（拉氏方程）及的位函数的解析解法。
2)点电流源电场空间分布规律。
3)均匀大地电阻率的测定方法。
电法勘探中测量介质电阻率的方法由此问题引出，开始建立电法勘探中“装量”这一词的概念，本节重点：稳定电流场的求法及空间分布；均匀大地电阻率的公式的导出及测定方法。
以上内容两学时四非均匀介质中的电场及视电阻率（1学时）阐述4个问题1)什么是非均匀介质中的电场？特点，交代出低阻体吸引电流，高阻体排斥电流的概念2)非均匀电场的实质：积累电荷的过程。
3)什么是视电阻率？如何定义？4)视电阻率微分公式。
4-2电与电磁法原理第四章02电测深法
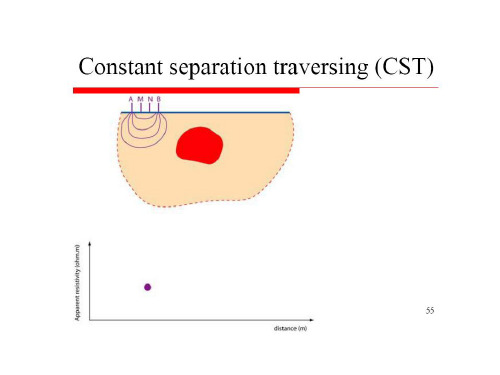
水平地层的纵向电导和横向电阻
对于多层水平地层，当电流平行层面流动时，所 有地层表现的总电阻为各层电阻的并联，而电流 垂直层面流动时，总电阻为各层电阻的串联。 下面从地层中切出一个m层总厚度为，底面为 一米乘一米的柱体来分析。当电流平行层面流动 时，第i层沿层面的纵向电导为Si。柱体总的纵向 电导S为各层电导并联的结果：
U1
0
I 1 2 B 1 ( mr ) dm 2
J ( mr ) dm 0
• 式中：J０（ｍｒ)为零阶第一类贝赛尔函数； B１（ｍ）为积分变量m的函数。
• 对于层数确定的水平地层，根据地层界 面上电位和电流密度法向分量连续的边 界条件，可具体求出B1（m）的表示式。 • 例如，最简单的二层水平地层，利用ρ １ 和ρ 2 岩层分界面的相应边界条件可具体 求出
• • • •
③ 二层电测深曲线的性质 A、首支 B、中段 C、尾支
• (2)三层水平地层的电测深曲线 • ①三层电测深曲线的类型 • 三层水平地电断面，依照相邻地层电阻 率的相对关系，划分为如下四种类型： • H、A、Q、K
• ②三层量板 • 三层水平地层的断面参数ρ １、ｈ１、 • ρ ２、ｈ２、ρ ３给定后，由(6.1-63) 式可以计算出相应的三层电测深理论曲 线。 • 我国交通部第四铁路工程局和交通部科 学院曾经计算了约2000条理论曲线。
2 mh i 2 mh i
) )
(6.1-66)
Tn ( m ) n
• 电阻率转换函数递推公式(6.1-66)的导出， 免去应用边界条件解方程组求系数B１(m) 的计算，开辟了正演计算层状大地电测深 曲线的新领域。
用双曲函数表达：
• 可以由此推出向下递推的公式如下：
第一篇第四章电阻率测深法
笨，没有学问无颜见爹娘 ……” • “太阳当空照，花儿对我笑，小鸟说早早早……”
4
§1.4.1 多层水平地层面点电流源的 电场及表达式
一、多层水平地层地面点 电流源的电场
0
（1.4.5）
（1.4.4）式为零阶贝塞方程，其解便为零阶贝塞尔
函数 J0 (mr) 和 Y0 (mr) ；而（1.4.5）式的解为 emz 和 emz 。 由于 Y0(mr) 在 Z 轴上（即 r=0）变为无限大，这与电 位极限条件不符，故应舍掉，于是（1.4.1）式的通
解便为：
7
U (r, z)
…………………………
0
[
An
1
(m)e
mH
n1
Bn1(m)emHn1 ]J0 (mr)dm
0
An
(m)e mH n1
J0
(mr)dm
1
n1
0
[
Ai
(m)e
mH
n1
Bn1(m)emHn1 ]J0 (mr)mdm
1
n
0
An
(m)emHn1
J
0
(mr)mdm
12
从而得到
(e2mH1
1)B1(m)
1
K e2mh1 12
K e2m(h1 h2 ) 23
K12
K
e2mh2
23
1 1
K
K12
K
e2mh2
23
（1.4.19）
17
将其写为双曲线函数形式，用数学归纳法可得到 n
电阻率测深法技术规程
电阻率测深法技术规程电阻率测深法技术规程中华人民共和国地质矿产行业标准Dz/T 0072一93电阻率测深法技术规程1993一05一18发布1994一01一01实施中华人民共和国地质矿产部发布中华人民共和国地质矿产行业标准DZ/T 0072一93电阻率测深法技术规程主题内容与适用范围本标准规定了电阻率测深法(以下简称电测深法)工作的基本要求和技术规则。
本标准适用于能源、金属、非金属矿产地质找矿中的电测深法工作，其中的技术规则也适应水文、工程、环境、灾害地质勘察中的电测深法工作。
引用标准DZ/T 0069 地球物理勘查图图式图例及用色标准3 总则11 电测深法是以地下岩(矿)石的电性差异为基础，人工建立地下稳定直流电场或脉动电场，通过逐次加大供电(或发送)与测量(或接收)电极极距，观测与研究同一测点下垂直方向不同深度范围岩(矿)层电阻率的变化规律.以查明矿产资源或解决与深度有关的各类地质问题的一组直流电法勘查方法。
3.2 电测深法的装置形式3.2.2 三极装释3.2-2. 1 单侧三极装胃3.2. 3 偶极装置3,2.3.1 轴向偶极装置装置符号<- AB M N->装置简图装置系数K值计算公式(5),(6):3.2.4 五极纵轴装置装置符号3. 3 电测深法的应用条件3.3.1 电测深法的应用，必须同时满足下列地球物理前提: a. 勘查对象与其围岩或其他地质体之间应存在较明显的电阻率差异;b. 勘查对象产生的电阻率异常能从干扰背景中分辨出来。
13.2 遇下列条件，一般不宜设计电测深工作或不设计提交定量解释成果的工作。
a. 接地严重困难;b. 地电断面中存在强烈的电性屏蔽层;c. 地下经常存在无法克服的强大的工业游散电流;d. 地形影响难以改正。
工作设计工作任务1 电测深法的具体任务应在任务书中明确规定，其内容包括:a. 项目名称、工作地区及范围;b 工作目的、勘查对象;c. 实物工作量及技术经济指标;d. 提交成果资料的内容及期限。
电阻率测深法技术规程
出发英语作文600字成长性Embarking on the Journey of Growth.In the symphony of life, growth is an indispensable melody that harmonizes the ebb and flow of existence. It is a perpetual journey, fraught with both triumphs and setbacks, but each step we take along its path enriches our lives beyond measure. As we embark on this transformative expedition, we encounter a myriad of opportunities that shape our character, expand our horizons, and inspire us to reach our full potential.Embracing Challenges as Stepping Stones.Like a ship braving the tempestuous seas, growth often requires us to navigate through uncharted waters and confront formidable challenges. These trials may initially test our resilience, but if we approach them with determination and an unwavering belief in ourselves, they become stepping stones that propel us forward. It isthrough adversity that we develop our fortitude, learn from our mistakes, and discover hidden strengths within ourselves.Seeking Knowledge and Wisdom.The pursuit of knowledge is an integral aspect of personal growth. By immersing ourselves in books, attending workshops, and engaging in intellectual discussions, we expand our understanding of the world and develop new perspectives. Wisdom, on the other hand, is the ability to apply our knowledge with discernment and compassion. It is through experience and reflection that we cultivate wisdom, and it empowers us to make informed decisions and navigate life's complexities with greater clarity.Nurturing Relationships and Connections.Our relationships with others play a vital role in our growth. Surrounding ourselves with supportive and inspiring individuals creates a fertile environment for personal development. By sharing ideas, offering encouragement, andchallenging each other's perspectives, we foster a sense of community and accountability. True growth occurs when weare open to learning from others and allowing theirinfluence to shape us.Exploring New Interests and Passions.Venturing beyond our comfort zones and exploring new interests and passions is essential for personal growth. Whether it's trying a different hobby, learning a new skill, or traveling to unfamiliar destinations, exposing ourselves to new experiences broadens our horizons and helps us discover hidden talents and passions. It ignites our curiosity, sparks our imagination, and enriches our lives with newfound meaning.Embracing a Growth Mindset.At the heart of personal growth lies the concept of a growth mindset. Unlike a fixed mindset, which perceives intelligence and abilities as unchangeable traits, a growth mindset embraces the belief that we can improve ourabilities through hard work and perseverance. It empowers us to view challenges as opportunities for learning and motivates us to constantly strive for self-improvement.Reflection and Self-Assessment.Regular reflection and self-assessment are essentialfor personal growth. By taking the time to introspect on our thoughts, actions, and experiences, we gain valuable insights into our strengths and weaknesses. This process enables us to identify areas for improvement, set realistic goals, and adjust our course as needed. It is through self-reflection that we cultivate self-awareness and embark on a conscious path of growth.Embracing Change and Adaptability.In the ever-evolving tapestry of life, change is an inevitable constant. To thrive in the face of change, we must cultivate adaptability and a willingness to embrace the unknown. By developing the ability to learn quickly, adjust our perspectives, and respond to new situations withcreativity and resilience, we equip ourselves to navigate the complexities of a dynamic world and emerge stronger on the other side.Conclusion.Embarking on the journey of growth is a lifelong commitment that requires dedication, perseverance, and a unwavering belief in ourselves. By embracing challenges, seeking knowledge and wisdom, nurturing relationships, exploring new interests, embracing a growth mindset, engaging in self-reflection, and embracing change, we unlock the transformative power within us. Each step we take on this path brings us closer to our full potential and empowers us to live a life of purpose, meaning, and fulfillment.。
三、电阻率测深法
图4-57是云南某地用电测深法寻找古河道
ρ s（Ω·m）
Ⅰ-Ⅰ′剖面 ZK125 地柱 电测 质状 曲线 15
10 35 30 20 20 30
ZK40 地柱 电测 质状 曲线
古河道的上方，ρs 曲线 出现明显的K型；在古 河道两侧，ρs 曲线为平 直的低值“一”字型。 图（a）为I-Iˊ剖面上的 等ρs 断面图，可看出， 高阻异常（ρs =20～ 35Ω·m）反映了古河道 的砂砾石层。图（c） 是电极距AB/2=15m时 ρs 等值线平面图，图中 高阻异常带大致反映了 古河道的平面位置（阴 影线带）。
• 当采用电测深法时，其曲线特征如下： • 当基岩岩性比较单一，外界影响和旁侧影响 大体一致时，电测深曲线一般呈G型反映，其 中曲线低阻部分反映近地表的浮土或基岩风 化壳，而高阻部分则是完整基岩的反映。 • 图4-61为某灰岩地区实测电测深曲线。该区覆 盖层薄，水位较浅，基岩相对完整，电测深 曲线为G型。
1—AB/2=1000米 2—AB/2=3000米
3.等AB/2视电阻率平面图
• 选择一定的AB/2，并在各测深点测深曲 线上查出它所对应的s 值，将它标在测 深点之旁，然后将s值相同的点用曲线 连接起来即得到等AB/2视电阻率平面图。 • 此图能反映出相同的勘探深度视电阻率 在测区平面上的变化情况。 • 取大小不同的AB/2即可反映出不同深度 平面上视电阻率的变化。
结论：
• 通过上述分析可以看出，改变电极距的 目的就是改变电场作用的空间范围，达 到对测点下面不同深度岩层研究的目的。 这就是电测深法的物理实质。
（二）地电断面与电测深曲线类型
• 地电断面是按岩层的电性不同来划分的 界面。 • 而地质断面是根据岩性的不同来确定界 面的。
第四章第二节电阻率法-文档资料
一、电阻率剖面法 电阻率剖面法简称电剖面法。它包含多种变 种方法，在这些方法中，测量电极均沿测线方向 逐点进行测量，以探测地下一定深度内地电断面 沿水平方向的变化。由于变种方法较多，因此适 应各种地电条件的能力较强，应用范围较广。它 不仅能有效寻找金属矿和非金属矿，还可进行地 质填图，解决地质构造等问题，并且在水文地质 和工程地质调查中，也获得了广泛应用。
7.野外作业技术 （1）测站布置 ①测站是野外作业中枢。剖面测量时，测站位置应 尽量靠近观测地段的中心，以便控制测区较大的 面积。通常选择在视野开阔，地势平坦，通行方 便，避风干燥处。测站应远离高压输电线和变压 器，以避免电磁感应与电源漏电影响；测站应采 取防潮（如地面上应铺上塑料布其上放好仪器）、 防雨、防晒（撑伞）措施；把自测站引出的供电 及测量导线绑在牢固的木桩上，以免放线时拖倒 仪器及其附件。当用发电机作电源时，需要进行 发电机试车以观察空载和负载条件下的运转情况； 当用干电池作电源时，应按规定方式接好干电池。
2.测区范围、测网与比例尺 测区范围应包括整个被探测对象可能存在的 地段，应保证探测结果轮廓完整，其周围应包括 一定面积的“正常”地段。同时要照顾到测区边 界整齐规则。如果测区边缘发现异常时，应根据 需要扩大测区，将异常追索完整。 测线方向应垂直或尽量垂直被探测地质体的 主要走向。当发现的异常走向与测线交角小于 90°过多时，应垂直异常走向布置补充工作。
4.野外观测记录要求 （1）基本观测及技术要求 基本观测又称原始观测，其观测结果是原始 资料的重要组成部分。对电阻率法基本观测的技 术要求： ①供电电压不宜低于15V，以免因低压供电电极极 化缓慢致使供电电流不稳；同时供电电压低将造 成极化电压所占比例增大，影响观测精度。
②在观测进程中，应将供电电流的变化控制在±2% 以内，当电流以不稳（在±3%范围内变化）时， 应采取“IU -I”的读数方式和短暂供电的办法观 测，并应以I的平均值参与视电阻率计算。当外界 U -I”的方式 干扰使 U观测时间较长时，应以“ 读数。中间梯度装置每经5~10个测点测定电流一 次，其间电流变化不允许大于2%，若大于2%， 以后应逐点测量电流。 ③对于单个测回（指对测点完成一次 U 和I的连续测 定过程），应采用短暂而相同的观测时间，以避 免观测过程中电极极化引起电流变化以及某些地 质体的激电效应给观测结果带来影响。
第四章 电阻率测深法
0
[
Ai
1
(m)e
mHi
Bi1(m)emHi ]J0 (mr)mdm
…………………………
0
[
An
1
(
m)e
mH
n1
Bn1(m)emHn1 ]J0 (mr)dm
0
An
(m)e mH n1
J0
(mr)dm
1
n1
0
[
Ai
(m)e
mH n1
Bn1(m)emHn1 ]J0 (mr)mdm
1
第四章 电阻率测深法
电剖面法是将极距保持固定沿一定测线观测，以 了解在某一深度范围内地质情况沿水平方向的变化。 而电阻率测深法（简称电测深）则是在同一测点上逐 次扩大电极距，使探测深度逐渐加大，这样便可得到 观测点处沿垂直方向由浅到深的视电阻率变化情况。 电测深也可像电剖面法那样使用不同的装置，如三极 电测深，对称四极电测深、偶极电测深等。本章主要 讨论用得最广的对称四极电测深，它是以测点为中心， AB 极距对称于测点向两旁按一定倍数增加，MN 分段 固定（另一种方法是 MN 与 AB 间保持固定比例，随 AB 的增关而增大），对每一 AB 极距均可测出一 s 值， 对每一测点的电测深结果，
U (r, z)
[ A(m)emz
0
B(m)emz ]J0 (mr)dm
式中 Am 和 B(m) 为待定的积分变量 m 的函数。
（1.4.6）
现先确定第一层电位的具体形式，由于当
R
r2
z2
0 时，电位与半无限介质相同，即U
1I 2
1
R，
因此，在第一层中电位表达式为
U1(r,
z)
3电阻率法(3) 电阻率测深法
Taiyuan University of technology
式中y为观测点距离连线的以下水平距离；z为深度;I为供电电流强
度。透入给定深度z以下的相对电流强度为
Taiyuan University of technology
Taiyuan University of technology
（1）ρs表达式与电阻率转换函数
由
j MN EMN 2r 2 U s MN j0 j0 I r
Z=0: 由
1 I U1 (r ,0) 2
1 2B(m)J
0
0
(rm)dm
J 0 (m r) J1 (m r) (m r)
Taiyuan University of technology
Taiyuan University of technology
利用衔接条件求取2（n－1）个待定函数 ，由 于电测深研究位于地面上的电位分布，即仅需 要给定层数n后的 B1（m）式。如
n=2
其中
n=3
其中
Taiyuan University of technology
二.视电阻率函数、电阻率转换函数 及其递推关系
Taiyuan University of technology
§1.4电阻率测深法
通过在测点上固定MN，逐次改变供电极距，以 扩大人工外电流场的有效作用空间，观测到主要以 地下垂向电阻率分布为特征的变化情况，分析 的电阻率测深曲线，达到探测地下垂向地 体分布的目的。
AB s ~ 2
该方法基于地表水平、地下水平成层、层内介 质导电性均匀各向同性的地电模型。
它是目前正演理论和反演理论最完善的电法勘 探方法。
Taiyuan University of technology
煤田勘查领域中电阻率测深法应用
煤田勘查领域中电阻率测深法应用电阻率测深法是煤田勘探中常用的勘探方法之一。
该方法是通过测量岩石或土壤的电阻率分布，来推断其下面的地层情况，为煤田开发提供数据和依据。
电阻率测深法可以应用于煤田的地质研究、勘探评价和资源储量预测等方面。
它可以通过对煤层内部结构、厚度和含煤层位等信息的探测，为煤田勘探提供较为准确的物理学依据。
一般来说，电阻率测深法是通过将接地电极和电流源电极放置在地面上，并通过一定频率的交流电流注入地下，再利用电阻率仪器测量地下岩石或土壤的电阻率值。
通过对电阻率测量值的分析，我们可以推断出地下不同类型的岩石和土壤层的情况。
在煤田勘探中，电阻率测深法可以自动记录和绘制地下岩石或土壤的电阻率剖面图和地形图，提供全面和准确的地下地貌图像信息。
而且该方法也不受地形、水体和植被等因素的干扰，具有很大的优势和应用前景。
在煤田勘探中，电阻率测深法主要应用在以下几个方面。
一、煤层勘探评价。
电阻率测深法可以对煤层下部岩层的厚度、性质及构造等进行研究，并可以确定煤层的搭合和岩性。
在煤炭选择性采矿和合理布置工作面方面，该方法都具有不可替代的作用。
二、资源储量预测。
通过电阻率测深法对煤层厚度、分布、质量、含煤层位及受地质构造和改造的影响等进行深入研究，可以有效地预测煤田的资源储量和合理开采方案，改善煤田的开发生产效益。
三、煤层水文勘探。
水文勘探是煤层地下水文特征的研究和分析，电阻率测深法可以帮助我们研究煤层内的水文特征，如地下水含量、水流速度、水压力等，从而为煤层开发的工程设计和水文地质环境管理等提供依据。
四、煤层地质构造研究。
电阻率测深法还可以用于研究煤层地质构造。
煤层地质构造对煤的分布和数量有着重要影响，了解地质构造状况可以更好地指导煤田勘测和开采。
电阻率测深法能够帮助我们在地下区域不可见的地质构造状况下进行研究，减少了成本和人力资源浪费，提高了工作效率。
综上所述，电阻率测深法在煤田勘探中的应用是非常重要的。
第三讲：电测深法
A j A在MN中点O处产生的电流密度： MN
ＡＢ两个点电源在Ｏ处产生的电流密度 翻倍。
j 均匀半空间Ｏ点处电流密度：
AB
o
视电阻率的微分形式
s
r AB 2
AB jMN s AB MN jo
I 2 r
MN 1
1
h1
1
h1
h1 AB lg s lg lg 2 1
复 习 ： 几 个 基 本 问 题
横向电阻、总横向电阻
当电流垂直岩柱体底面 流过时，测得的电阻称横
向电阻（T）
T h
岩柱体由多个厚度和电 性不同的岩层组成时，总 横向电阻为：
T T1 T2 Tn hi i
i 1
n
复 习 ： 几 个 基 本 问 题
纵向电导、总纵向电导
证这一中间层的纵向电导 S2 变，曲线形态不发生变化。
2
h2
h2 2 定， 较小的情况下ρs曲线中段 h1
不
红色：h1=10,h2=2,h3=∞;ρ1=150, 蓝色：h1=10,h2=1,h3=∞;ρ1=150, 玫红：h1=10,h2=2,h3=∞;ρ1=150, 绿色：h1=10,h2=1,h3=∞;ρ1=150,
ρ2=400, ρ2=800, ρ2=800, ρ2=400,
ρ3=20 ρ3=20 （虚线） ρ3=20 ρ3=20
其它参数不变， h2不是很大时： ρ2 增大时（枚红色曲线）视电阻率曲线 极大值升高；相反，只减小ρ2 时，视电 阻率曲线的极大值降低。 h2 减小时（绿色曲线）视电阻率曲线极 大值降低；相反，只增大h2 时，视电阻 率曲线的极大值升高。
2.1.3电阻率测深法
高密度电阻率成像法的概念
高密度电阻率成像法（Electrical Resistivity Tomography 简称 “ERT”）是通过测定介质的电阻率差异以达到对介质进行勘察 的地球物理方法,其优势：方便快捷，数据量大，可进行无损的 自动监测，近年来被广泛应用于地下水研究领域
1.3.1 对称四极测深装置
一、对称四极测深极距的选择
•
AB为供电电极，MN为测量电极，它们都对称于装置 中心O。地面的测点和装置的O点重合 。 • 选择供电极距时，要求最小的极距应能反映第一层电 阻率，最大的极距则能满足勘探深度要求，并保证测 深曲线尾支的完整，可解释最后一个电性层。为使曲 线光滑，以保证解释精度，各供电电极距在对数的 AB/2轴上应均匀分布。
1 18 32 43 51 56
图3 高密度电阻率成像法勘测地面测量数据采集方法和原理
1、高密度电阻率方法在地下空洞探测实例
图4 d是总剖面的照片，e是电阻率反演结果，与剖面对应的b和c（放大图）是 先前发现的墓穴，位置a（放大图）是先前没有注意到的另一个墓穴。采用温 纳装置，电极距为1米。
2 、高密度电法在阳煤集团规划水泥厂地基勘 察中的应用
log (AB/2)
1.3.1对称四极测深装置
二、对称四极测深法测量 • 若是剖面性测量，则除 画各电测深点单支电阻 率测深曲线外，还需要 画视电阻率拟断面图， 即在单对数坐标纸上， 横轴算术坐标取测点位 置，纵轴对数坐标取 AB/2，然后把各测深点 不同极距的视电阻率值 填入图中相应位置，画 出等值线图
1.3 电测深法
• 电测深法的全称为“电阻率垂向测深法”，它是研究 垂向地质构造的重要地球物理方法。 • 对地面上某一测点进行电测深法测量的实质是用改变 供电电极的办法来控制不同的勘探深度，由浅入深， 可了解该测点地下介质垂向上电阻率的变化。
电阻率测深法 PPT
§1.4电阻率测深法
通过在测点上固定MN，逐次改变供电极距，以
扩大人工外电流场的有效作用空间，观测到主要以
地下垂向电阻率分布为特征的变化情况，分析
s
~
AB 2
的电阻率测深曲线，达到探测地下垂向地
体分布的目的。
该方法基于地表水平、地下水平成层、层内介 质导电性均匀各向同性的地电模型。
它是目前正演理论和反演理论最完善的电法勘 探方法。
J 0 (mr )
k 0
1k
1
k ! k
1
mr 2
2k
lim
mr 0
Y0
(mr
)
:
2 ln mr c
2
Z (z) E(m)emz F (m)emz
通解
考虑到
Y0 (mr )
mr0
(ln
2
mr 2
c)
U
[
0
A(m)emz
B(m)emz
]J 0
(mr
)dm
U1
U0
U
ห้องสมุดไป่ตู้
c1 R
一.水平层状地电条件下的点电流场
1. 边值问题
鉴于点源场对水平层状介质 的轴对称性，引入柱坐标系的电 位为U（r,z）,场源A点以外的边 值问题为：
2U1 r 2
1 r
U1 r
2U1 z 2
2I ( p
A)
U 0 1 z2 r 2
U1 Z
Z 0
0
U1
I1 C1 2 R z2 r2 0 R
n=2
其中
n=3 其中
二.视电阻率函数、电阻率转换函数 及其递推关系
（1）ρs表达式与电阻率转换函数
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
令 则
T1 ( m) 1[1 2 B ( m)]
s (r ) r
2
0
T1 ( m ) J 1 ( mr ) mdm
T1 ( m ) 便定义为电阻率转换函数， B(m) 称为核函数。
电阻率转换函数或核函数只与各层电阻率及厚度有关， 与 r 无关，因而是表征地电断面性质的函数。 为了求 T1 ( m ) ，可直接解线性方程组（1.4.11）式，但 更有用处的是它的双曲线函数表示法和递推公式。
d 2 R ( r ) 1 dR ( r ) d 2 Z ( z ) 2 dr r dr dz 2 整理得 R (r ) Z ( z)
用分离变量法求上式的解，设 U (r , z ) R (r ) Z ( z )
（1.4.3）
上式左边为仅含 r 的函数，右边为仅含 z 的函数。要 它们相等，只有都等于一个常数 m2 才有可能。故由 （1.4.3）得到二个常微方程：
应用韦伯—莱布尼兹积分
0
e mz B1 ( m )( e mz e mz ) J 0 ( mr ) dm
将第一层的电位公式写为：
U1 [
0
1 I mz e B1 ( m)(e mz e mz )]J 0 (mr )dm 2
（1.4.8） （1.4.9）
T1 ( m )
cth 1th
mh1 th 1
cth
1
cth 2 th
[ mh2 ] th 1
cth
1
cth n 1th ( mhn
（1.4.20） 式中
2 2 , 3 3 , , n n 2 , n 1 2 n 1 n 1
0
Un
An ( m )e mz J 0 ( mr ) dm
B2 (m) , Bn 1 (m) ，共有 2( n 1) 个。根据在各个界面上
电位连续和电流密度法向分量连续这两组边界条件，可 列出：
0
1 I mH [ e B1 ( m )(e mH e mH )] J 0 ( mr ) dm 2
1
1
1
（1.4.12）
1 1 2 1 2 2
K12 e 2 mh K 23 e 2 m ( h h ) 1 I B1(3) ( m ) 2 1-K12 e 2 mh K 23 e 2 m ( h h ) K12 K 23 e 2 mh
二、电阻率转换函数
一）电阻率转换函数的定义 在对电测深曲线进行量论分析及在电测深资料电子 计算机解释中，常用电阻率转换函数，其内容是：在地面 上， z 0 ，可由（1.4.8）式得到电位表达式：
（二）电阻率转换函数的双曲函数表示法 根据定义，将（1.4.12）和(1.4.13)代入到（1.4.15） 及 （1.4.17） 式中， 便得到二层和三层情况的 T1( 2) ( m ) 和 T (m)
(3) 1
T1(2) ( m ) 1
T1(3) ( m ) 1
1 K12 e 2 mh1 1 K12 e 2 mh1
U1 ( r , 0)
0
令 则
1 I [ 2 B1 ( m)]J 0 ( mr ) dm 2 1 I B1 (m) B (m) 2
1 I 2
（1.4.14） （1.4.15） （1.1.14）´
U 1 ( r , 0)
0
[1 2 B ( m)]J 0 ( mr ) dm
2 n
图 1.4.1 多层水平地层
引用圆柱坐标系，将原点设在 A 点，z 轴垂直向 下，由于问题的解对 Z 轴有对称性，与 无关，故电 位分布满足下面形式的拉普拉斯方程。
2U r
2
1 U r r
2U Z
2
0
（1.4.1）
（1.4.2） R（r）为仅含自变量 r 的待定函数，Z(z)是仅含自变 量 z 的待定函数。将（1.4.2）式代入（1.4.1）式，经
mz
m2 Z ( z) 0
mz
U ( r , z ) [ A( m ) e mz B ( m )e mz ] J 0 ( mr ) dm
0
（1.4.6）
式中 A m 和 B(m) 为待定的积分变量 m 的函数。
现先确定第一层电位的具体形式，由于当
R r z
第四章 电阻率测深法
电剖面法是将极距保持固定沿一定测线观测，以 了解在某一深度范围内地质情况沿水平方向的变化。 而电阻率测深法（简称电测深）则是在同一测点上逐 次扩大电极距，使探测深度逐渐加大，这样便可得到 观测点处沿垂直方向由浅到深的视电阻率变化情况。 电测深也可像电剖面法那样使用不同的装置，如三极 电测深，对称四极电测深、偶极电测深等。本章主要 讨论用得最广的对称四极电测深，它是以测点为中心， AB 极距对称于测点向两旁按一定倍数增加，MN 分段 固定（另一种方法是 MN 与 AB 间保持固定比例，随 AB 的增关而增大） ，对每一 AB 极距均可测出一 s 值， 对每一测点的电测深结果，
d 2 R (r ) dr 2 1 dR ( r ) r dr m 2 R (r ) 0
（1.4.4）
d 2 Z (z) dz 2
（1.4.5） （1.4.4）式为零阶贝塞方程，其解便为零阶贝塞尔 函数 J 0 (mr ) 和 Y0 (mr ) ；而（1.4.5）式的解为 e 和 e 。 由于 Y0 (mr ) 在 Z 轴上（即 r=0）变为无限大，这与电 位极限条件不符，故应舍掉，于是（1.4.1）式的通 解便为：
（1.4.18）
1 K12 e 2 mh1 K 23 e 2 m ( h1 h2 ) K12 K 23 e 2 mh2 1 K12 e 2 mh1 K 23 e 2 m ( h1 h2 ) K12 K 23 e 2 mh2
（1.4.19）
将其写为双曲线函数形式， 用数学归纳法可得到 n 层介质情况 T1 ( m ) 的双曲函数表达式：
1
1 I -2mH e 2
解上列线性方程组便可求出各系数。由于电测深工作地 面上进行，矿只研究地表面（ z 0 ）的电位分布，即仅 需求出 B1 ( m ) 。例如，通过解（1.4.11）式求得两层和三 B1( 2) ( m ) 和 B ( m ) 为 层情况的
(3) 1
1 I K12 e 2 mh B1(2) ( m ) 2 1-K12 e 2 mh
2 2
0 时， 电位与半无限介质相同， U 即
1 I 1 2 R
，
因此，在第一层中电位表达式为
1 I 1 U1 (r , z ) [ A1 (m)e mz B1 (m)e mz ]J 0 (mr )dm （1.4.7） 0 2 R
地面上任意一点的电流密度法向分量等于零
第二层以下到第 n 1 层的电位为
U i [ Ai ( m ) e mz Bi ( m ) e mz ]J 0 ( mr ) dm
0
i 2,, n 1
当 z 时，电位应等于零，故 Bn ( m) 0 ，在此第 n 层 中的电位为： （1.4.10） 在（1.4.8）～（1.4.10）式中的系 A2 ( m ) 和
1 1 1
1
0
[ A2 ( m )e mH1 B2 e mH1 ] J 0 ( mr ) dm
1 1 1
1
0
[
1 I mH e B1 ( m )(e mH e mH )] j0 ( mr ) mdm 2
1
2
Байду номын сангаас
0
[ A2 ( m )e mH1 B2 ( m ) mH1 ] J 0 ( mr ) mdm
将上式对 r 微分，并代入 MN 0 时的 s 表达式
s ( r ) 2 r
2
E I
2 r 2 I
(
U 1 r
)
便得
s ( r ) 1 r 2 [1 2 B ( m )] J 1 ( mr ) mdm
0
（1.4.16） （1.4.17） （1.4.16）´
n 1
1
0
[ Ai ( m )e mH n1 Bn 1 ( m )e mH n1 ]J 0 ( mr ) mdm
n
0
An ( m )e mH n1 J 0 ( mr ) mdm
从而得到
I 2 (1 e 2 mH1 1) B1 ( m ) 1e 2 mH1 A2 ( m ) 1 B2 ( m ) 1 2 e -2mH1 2 2 mH i 2 mH i e Ai ( m ) Bi (m)-e Ai 1 ( m ) Bi ( m ) 0 2 mH 1 2 mH 1 i 1e Ai ( m ) i 1 Bi (m )+ i e Ai 1 ( m ) i Bi 1 ( m ) 0 （1.4.11） 2 mH n 1 2 mH n 1 e An 1 ( m ) Bn 1 (m )-e An ( m ) 0 2 mH n 1 2 mH n 1 ne An 1 ( m ) n 1 Bn 1 (m )+ n 1e An ( m ) 0 (e 2 mH1 1) B1 ( m ) e 2 mH1 A2 ( m ) B2 ( m )
„„„„„„„„„„