Mrbayes学习
系统发育分析
系统发育分析实习四: 系统发育分析-PHYLIP, MEGA, MrBayes实习⽬的1. 学会使⽤PHYLIP,MEGA和MrBayes构建进化树2. 学会分析建树结果,体会各种⽅法差异实习内容:⼀、PHYLIPPHYLIP⽹址: /doc/d40e7fe51711cc7931b716b1.html /PHYLIP.htmlPHYLIP是⼀个免费的系统发育树构建软件,它的功能⽐较全⾯,可⽤距离法、最⼤简约法和最⼤似然法分别进⾏建树,还可以对进化树可靠性进⾏检验。
PHYLIP没有多序列⽐对功能,所以先要⽤其它序列⽐对软件完成序列⽐对,并保存为phy格式后,才可提交给PHYLIP 进⾏分析。
1.1 ⽐对序列的准备1.将教学材料⾥demo sequence.zip⽂件解压到D盘根⽬录下,分别⽤其中的mRNA和protein序列学习进化树构建。
⾸先我们⽤实习2学过的多序列⽐对软件对序列进⾏⽐对。
这⾥以CLUSTAX为例来说明。
强烈建议:将你的所有同源核酸(或蛋⽩质)序列存到⼀个⽂本⽂档⾥,将”>”之后那⾏只保留物种名称,或物种名称_蛋⽩(或基因)名称,⽅便后⾯分析⽐较。
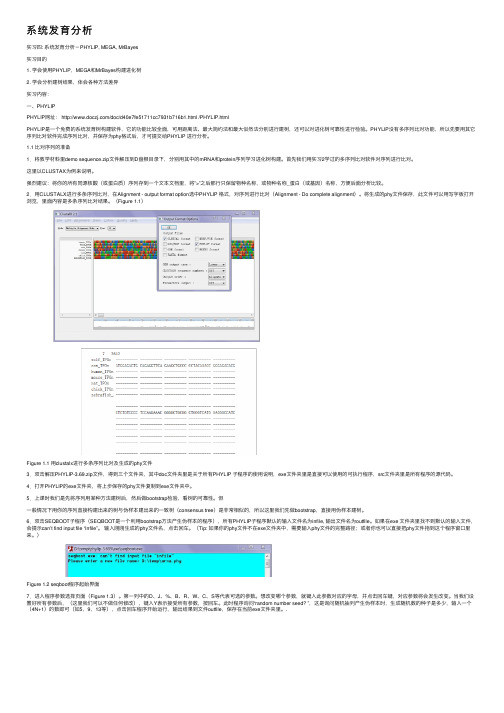
2.⽤CLUSTALX进⾏多条序列⽐对,在Alignment - output format option选中PHYLIP 格式,对序列进⾏⽐对(Alignment - Do complete alignment)。
将⽣成的phy⽂件保存,此⽂件可以⽤写字板打开浏览,⾥⾯内容是多条序列⽐对结果。
(Figure 1.1)Figure 1.1 ⽤clustalx进⾏多条序列⽐对及⽣成的phy⽂件3.双击解压PHYLIP-3.69.zip⽂件,得到三个⽂件夹,其中doc⽂件夹⾥是关于所有PHYLIP ⼦程序的使⽤说明,exe⽂件夹⾥是直接可以使⽤的可执⾏程序,src⽂件夹⾥是所有程序的源代码。
4.打开PHYLIP的exe⽂件夹,将上步保存的phy⽂件复制到exe⽂件夹中。
bayes 分类器设置实验总结

bayes 分类器设置实验总结Bayes 分类器设置实验总结在机器学习领域中,分类算法是一个常见的任务之一。
Bayes 分类器是一种基于概率统计的分类算法,它基于贝叶斯定理对样本进行分类。
在本次实验中,我们将对Bayes 分类器的设置进行实验,并总结实验结果。
一、实验目的Bayes 分类器是一种简单但有效的分类算法,通过实验设置我们的目的是验证Bayes 分类器在不同参数下的分类效果,并探索如何对其进行优化。
我们希望通过实验的设计和分析,能够决定最佳的参数设置,并对Bayes 分类器的性能有更深入的了解。
二、数据集选择在进行实验之前,我们需要选择一个合适的数据集作为实验对象。
数据集应具备以下特点:1. 包含有标签的样本数据:由于Bayes 分类器是一种监督学习算法,我们需要有样本的标签信息来进行分类。
2. 具备多类别分类的情况:我们希望能够测试Bayes 分类器在多类别分类问题上的表现,以便更全面地评估其性能。
三、实验设置1. 数据预处理:根据所选数据集的特点,我们需要对数据进行适当的预处理。
可能的预处理步骤包括特征选择、特征缩放、处理缺失值等。
2. 分类器参数设置:Bayes 分类器的性能会受到不同参数的影响,我们希望通过实验找到最佳的参数设置。
例如,在朴素贝叶斯分类器中,我们可以选择不同的先验概率分布,或者使用不同的平滑技术来处理零概率问题。
3. 评价指标选择:为了评估分类器的性能,我们需要选择合适的评价指标。
常见的评价指标包括准确率、召回率、精确率和F1 分数等。
四、实验结果在实验完成后,我们将根据所选的评价指标对实验结果进行分析和总结。
我们可以比较不同参数设置下的分类器性能,并选择最佳的参数设置。
此外,我们还可以考虑其他因素对分类器性能的影响,如数据预处理方法和样本量等。
五、实验总结在本次实验中,我们通过对Bayes 分类器的设置进行实验,得到了一些有价值的结果和经验。
根据实验结果,我们可以总结以下几点:1. 参数设置的重要性:Bayes 分类器的性能受到参数设置的影响。
MrBayes操作指南

MrBayes操作指南MrBayes教程传统的系统进化学研究⼀般采⽤的要么是表型的数据,要么是化⽯的证据。
化⽯的证据依赖于考古学的发现,⽽表型数据往往极难量化,所以往往会得到许多极具争议的结论。
如今,现代分⼦⽣物学尤其是测序技术的发展为重建进化史提供了⼤量的数据,如多态性数据(如SNPs或微卫星)、基因序列、蛋⽩序列等等。
常规的做法⼀般都是利⽤某⼀个或者⼏个基因来构建物种树(species tree),但是⼀个基因的进化史能不能完全代表所有被研究物种的进化史呢?这是⾮常值得讨论的问题,但这不是我们本次实验的重点,在这⾥就不多赘述了。
所以,我们这⾥所指的进化树如⾮特别说明,指的都是基因树(gene tree)。
经典的研究系统进化的⽅法主要有距离法、最⼤简约法(maximum parsimony,MP)、最⼤似然法(maximum likelihood,ML)等等。
这些⽅法各有各的优点,也分别有其局限性,例如距离法胜在简单快速、容易理解,但是其模糊化了状态变量,将其简化为距离,也就不可避免的丧失了许多序列本⾝所提供的信息。
⽽最⼤简约法虽然⽤的是原始数据,但也只是原始数据的⼀⼩部分。
特别是在信息位点⽐较⼩的情况下,其计算能⼒还不如距离法。
相对来说,最⼤似然法虽然考虑问题更加全⾯,但带来的另⼀个结果是其计算量⼤⼤增加,因此常常需要采⽤启发式(heuristic)⽅法推断模型参数,重建进化模型。
本实验利⽤的是贝叶斯⽅法来重建基因进化史。
1.贝叶斯⽅法概述不可免俗的,我们还是要来看看贝叶斯模型,并分别对模型内部的⼀系列内容⼀⼀进⾏简单的介绍。
Bayes模型将模型参数视作随机变量(r.v.),并在不考虑序列的同时为参数假设先验分布(prior distribution)。
所谓先验分布,是对参数分布的初始化估计。
根据Bayes定理,可以不断对参数进⾏改进:f(θ|D)=f(D|θ)f(θ)f(D)(1) 其中f(θ|D)为后验概率分布(posterior probability distribution),⽽f(θ)是先验概率分布(prior probability distribution),⽽f(D|θ)为似然值。
Mrbayes 3.2 编译并行

How to download and compile the most recent version of MrBayes 3.2 (Mac and Unix) from the MrBayes svn repository on SourceForge1. If a Mac, open Terminal (located in Applications/Utilities). Then check that you have gcc installed by typing$ which gccThis should result in the directory location of your current copy of gcc, if you have one installed. If not, install one from the Developer Tools CD that came with your computer. Most Unix systems will already have gcc installed.2. Type (on one line):svn co https:///svnroot/mrbayes/trunk/src mrbayesYou should now get a number of files downloaded to your directory, in a folder named ”mrbayes”.3. Change to the mrbayes directory by typing:$ cd mrbayes4. Create the Makefile, which contains the instructions for the compiler (the ”make” command), by typing:$ ./configure5. Now compile the program by typing:$ makeIt will take a few minutes for the compiler to assemble the binary version of the program.6. Run the program by typing:$ ./mbYou may want to put the executable in your path. Consult a Unix savvy person on how to do this.Compiling and running the MPI version of MrBayes1. Download the source code and shift to the ”mrbayes” directory as described above.2. In step 4, use the following command to create the Makefile instead:$ ./configure --enable-mpi=yes3. Now compile the program by typing$ makeIt will take a few minutes for the compiler to assemble the binary version of the program. If the first entry on each line printed during the compilation step is ”mpicc”, you are compiling the parallel version. If it is ”gcc”, something went wrong during the configure step and you are compiling the serial version instead.If you have already compiled the serial version of the program in the same directory, you first need to remove the compiled objects by running$ make cleanThen you run the ”make” command as above. Note that the compiled program is going to be called ”mb” both for the serial and the parallel version, so the compilation of the parallel version will overwrite the serial version unless you rename or move the latter executable first.4. Run the parallel version of the program using the command$ mpirun -np 2 ./mbwhere 2 is the number of available processors or processor cores. The MrBayes header should say that you are running the parallel version and it should also give the number of processors (cores) available.5. In practical use, it is often convenient to run the MPI version of MrBayes in batch mode. For instance, you can prepare a Nexus batch file ”batch.nex”, which contains a MrBayes block. To use such a file and have the screen output written to the log file”log.txt”, use the command:$ mpirun -np 2 ./mb batch.nex > log.txt &You can now look into the end of the log file every now and then to see what the run is doing currently using$ tail log.txtIf you wish to continuously follow what is being printed to the log file, you can use$ tail -f log.txtThere are many other ways of running the MPI version of MrBayes. Clusters often come with special instructions on how to run mpi programs; they typically involve launching the MrBayes MPI runs through an appropriate script. Consult your supercomputer support for instructions.。
bayes法

Bayes法概述Bayes法,也称为贝叶斯法或贝叶斯统计学,是以英国数学家Thomas Bayes命名的一种统计学方法。
Bayes法基于贝叶斯定理,通过利用相关先验概率和观测数据的条件概率,推断出后验概率分布。
Bayes法在各个领域都有广泛的应用,包括机器学习、人工智能、自然语言处理等。
贝叶斯定理贝叶斯定理是Bayes法的核心基础。
贝叶斯定理是一种用于更新概率估计的公式,它表达了在观测到新信息后如何更新先验概率。
贝叶斯定理的数学表达如下:P(A|B) = P(B|A) * P(A) / P(B)其中,P(A|B)表示在B发生的条件下A发生的概率,P(B|A)表示在A发生的条件下B发生的概率,P(A)和P(B)分别表示A和B的先验概率。
贝叶斯分类器贝叶斯分类器是Bayes法在机器学习领域的一个重要应用。
贝叶斯分类器基于贝叶斯定理,通过计算给定特征条件下每个类别的后验概率,来预测未知实例的类别。
贝叶斯分类器在文本分类、垃圾邮件过滤、情感分析等任务中有广泛的应用。
贝叶斯分类器的基本原理是先计算每个类别的先验概率,然后计算给定特征条件下每个类别的似然概率,最后通过贝叶斯定理计算后验概率,选择具有最高后验概率的类别作为预测结果。
贝叶斯分类器在计算后验概率时,通常假设特征之间是独立的,这称为朴素贝叶斯分类器。
贝叶斯网络贝叶斯网络是一种用于建模不同变量之间条件依赖关系的图模型。
贝叶斯网络由有向无环图表示,其中节点表示变量,边表示变量之间的依赖关系。
贝叶斯网络可以用于推断变量之间的概率分布,根据已知的变量值,推断未知变量的概率分布。
贝叶斯网络常用于处理不确定性的推理问题,包括诊断、预测、决策等。
贝叶斯网络还可用于发现变量之间的因果关系和生成概率模型。
贝叶斯网络在医学诊断、图像处理、金融风险分析等领域有广泛的应用。
贝叶斯优化贝叶斯优化是一种优化算法,用于解决黑盒函数的最优化问题。
贝叶斯优化通过不断探索和利用函数在搜索空间中的信息,逐步优化目标函数的值。
贝叶斯深度主动深度学习讲解

VA E - A C G A N 损 失 函 数 • 这个模型框架的损失函数由VAE和ACGAN两部分构成:
l ቤተ መጻሕፍቲ ባይዱ lVAE lACGAN
• lVAE 由重构损失lrec 和先验正则化损失 lprior 相加构成
• ACGAN网络损失函数:
• 算法过程:
试验结果:
ACGAN和VAE-ACGAN产 生的样本信息量值:
t
p^tc log 1 T
t
p^tc 1 T
c,t
pc ^t log pc^t
T 表示交互的次数, P^t
p
^
t 1
,....,
p^t c
soft max
f
X ; t
函数 f 代表着在第 t 次迭代时用 t 表示的后验概率 p | D。
二 数据扩充
Variational Auto-Encoder(VAE)网络
ACGAN网络结构示意:
• 扩充数据样本 X ',y* 中 X·由VAE-ACGAN网络生成,其包含一个编码器和
解码器。
X ' gex*
• 编码器和解码器都是由两个深度卷积网络构成。
为了定量描述生成样本和真实样本之间的相似性,作者计算了两者特征向 量之间的范数。
|| X' X* ||
三 生成样本信息量验证过程
• 抽出的 x * 是属于样本池 Dpool 的点。
• 由抽样策略函数可知 x*是一个局部最大值所以:
x (x*, M ) 0
经过多次迭代以后 || X' X* || 已经满足
x (x*, M ) 0 (x, M ) (x*, M ) x (x*, M )T (x x*) (x*, M )
bayse定律

bayse定律贝叶斯定律的形式可以表示为:P(A|B) = P(B|A) * P(A) / P(B),其中P(A|B)表示在事件B发生的条件下,事件A发生的概率;P(B|A)表示在事件A发生的条件下,事件B发生的概率;P(A)表示事件A发生的概率;P(B)表示事件B发生的概率。
在贝叶斯定律中,事件A被称为“先验概率”,即在没有任何其他信息的情况下,事件A发生的概率;事件B被称为“后验概率”,即在得到观测数据后,事件B发生的概率。
贝叶斯定律的核心是通过后验概率来更新先验概率,从而得到更加准确的概率估计。
贝叶斯定律在各个领域都有着广泛的应用,尤其在机器学习和人工智能领域中占据着重要的地位。
贝叶斯定律可以被用来构建分类模型、推断模型参数、处理缺失数据等任务,从而提高模型的准确性和鲁棒性。
在机器学习中,贝叶斯定律通常被用来构建朴素贝叶斯分类器(Naive Bayes Classifier)。
朴素贝叶斯分类器是一种简单且高效的分类算法,通过基于特征条件独立性的假设,利用贝叶斯定律计算出每个类别的后验概率,从而实现对未知样本的分类。
除了在机器学习领域,贝叶斯定律还被广泛应用于自然语言处理、图像识别、医学诊断、金融风控等领域。
通过利用贝叶斯定律来处理不确定性信息和结构化数据,可以更好地理解数据之间的关联性,从而做出更加准确的预测和决策。
尽管贝叶斯定律在实际应用中取得了显著的成就,但是也存在一些局限性和挑战。
其中最主要的挑战是如何选择先验概率的分布,这在某些情况下可能会导致后验概率的偏差。
此外,贝叶斯定律在处理大规模数据和高维数据时也会面临计算复杂度的问题。
总的来说,贝叶斯定律是一种强大的工具,能够有效地处理不确定性信息和推断问题。
随着数据科学领域的不断发展,贝叶斯定律将继续发挥着重要的作用,为解决实际问题提供理论支持和方法指导。
贝叶斯网络的参数学习方法(六)

贝叶斯网络是一种概率图模型,它以有向无环图的形式表示随机变量之间的依赖关系。
贝叶斯网络的参数学习是指在已知数据集的情况下,通过对数据进行学习,来估计贝叶斯网络中的概率分布参数。
本文将从贝叶斯网络的参数学习方法入手,介绍常见的参数学习算法及其应用。
1. 极大似然估计法极大似然估计法是最简单的参数学习方法之一。
对于贝叶斯网络中的每个节点,我们可以根据观测到的数据来估计其条件概率分布。
以一个简单的例子来说明,假设有两个随机变量X和Y,它们之间存在依赖关系。
对于X和Y的联合分布P(X,Y),我们可以通过观测到的数据样本来估计条件概率P(X|Y)。
假设我们观测到了n组(Xi,Yi)的数据样本,那么P(X|Y)的估计值可以通过计算在给定Y的条件下X的分布来得到。
具体地,P(X|Y)的估计值可以通过统计每个Y取值对应的X的分布来得到。
极大似然估计法简单直观,但是在数据较少或者存在稀疏数据时容易出现过拟合问题。
2. 贝叶斯估计法贝叶斯估计法是对极大似然估计法的改进。
在贝叶斯估计法中,我们引入了先验概率分布来对参数进行估计。
通过引入先验概率分布,我们可以在一定程度上减小对观测数据的过拟合。
对于贝叶斯网络中的每个节点,我们可以通过最大后验估计来估计其条件概率分布参数。
具体地,我们可以通过观测到的数据样本来更新先验概率分布,得到后验概率分布,然后再根据后验概率分布得到条件概率分布参数的估计值。
贝叶斯估计法在参数学习中更加稳健,尤其在数据较少的情况下表现更好。
3. EM算法EM算法是一种常见的参数学习算法,它在贝叶斯网络中也有广泛的应用。
EM 算法通过迭代的方式来估计模型参数。
在每一次迭代中,EM算法分两步进行:E步(Expectation step)和M步(Maximization step)。
在E步中,我们计算隐变量的期望值,然后在M步中,基于这些期望值来更新模型参数。
EM算法在处理存在隐变量的情况下具有很好的效果,所以在贝叶斯网络中也有着广泛的应用。
