《自动控制理论》试题A卷(邢法玉)
自动控制原理考试试题(A卷)

自动控制原理考试试卷(A 卷)
一、填空题(24分)
1、1945年,伯德提出用图解法来分析和综合反馈控制系统的方法,形成控制系统的方法,形成控制理论的 。
1954年________创立工程控制论。
2、自动控制理论通常可分为________________________、 _____________________、____________________。
3、线性控制理论常用的分析方法有 、 、____ ____。
4、若系统输出量通过反馈环节,返回来作用于控制部分,形成闭合环路,则这样的系统称为 。
5、自动控制系统按输入量变化的规律可分为: 、__________、_____________,自动控制系统按系统的输出量和输入量的关系可分: 、 。
6、对自动控制系统的基本要求是: 、 、 。
7、在经典控制理论中,常用的数学模型有 、 、 。
8、求下列函数的拉氏变换:
£[2]= £[e 2t
]=
£[22
t ]= £ [sin2t]= 二、求函数的拉氏变换或反变换(30分)
1、2)(+=t t f
2、t te t f 21)(+=
3、
()2
332+++=
s s s s F
三、化简系统方框图及写出传递函数(20分)1、
2、
四、求系统1
1)(+=
s s G 的单位阶跃响应 (10分)
五、闭环系统的特征方程如下,试用代数判据判断系统的稳定性。
(16分)
0154844122345=+++++s s s s s。
07自动控制理论A卷答案(归档格式)

2e − t − 2e −2t 。 − 2e −t + 3e −2t
3e t − 2e 2t 2e t − 2e 2t 解: Φ ( t ) = Φ (− t ) = t 2t − 2e t + 3e 2t − 3e + 3e 1 2 & A = Φ ( t ) |t = 0 = - 3 - 4
(3 分)
2.(3 分)简述什么是最少拍系统。 . 简述什么是最少拍系统。 简述什么是最少拍系统 解:在典型输入作用下,能以有限拍结束瞬态响应过程,拍数最少,且在采样时刻上无 稳态误差的随动系统。 (3 分) 3.(3 分)简述线性定常离散系统稳定性的定义及充要条件。 . 简述线性定常离散系统稳定性的定义及充要条件。 简述线性定常离散系统稳定性的定义及充要条件 解:若系统在初始扰动的影响下,其输出动态分量随时间推移逐渐衰减并趋于零,则称 (3 分) 系统稳定。稳定的充要条件是:所有特征值均分布在 Z 平面的单位圆内。 4. 分)已知 X(z)如下,试用终值定理计算 x(∞)。 (3 如下, . ( 如下 ∞。 z X ( z) = 2 ( z − 1)( z − z + 0.5) z 解: x (∞) = lim(z − 1)X(z) = lim 2 = 2。 (3 分) z →1 z − z + 0.5 5.(5 分)已知采样周期 T =1 秒,计算 G(z) = Z [Gh(s)G0(s) ]。 . 已知采样周期 。
D( z)
1 − e −Ts s
1 s +1
Xo ( z)
图1 1. 分)试求系统的闭环脉冲传递函数 Gc ( z ) = . (5 ( (5 值范围。 2. 分)试判断系统稳定的 K 值范围。 . ( 解:1.(5 分) 1 G0G ( z ) = (1 − z −1 ) Z s ( s + 1) 1 1 = (1 − z −1 ) Z − s s + 1 z z = (1 − z −1 )( − ) z − 1 z − e −1 1 − e −1 = z − e −1 (5 2. 分) 特征方程为 z − e−1 + K − Ke−1 = 0 欲使系统稳定,需满足条件
自动控制理论_习题集(附含答案解析)

三、作图题
51.已知单位负反馈系统开环传递函数 ,
(1)绘制闭环根轨迹;
(2)确定使闭环系统阶跃响应无超调的K值范围。
(1)由开环传递函数绘根轨迹如下图。
分离点的坐标d可由方程:
解得d1=-0.586,d2=-3.414
(2)将s=d1、s=d2分别代入根轨迹方程G(s)= –1求K值:
则:
对C(s)/R(s),前向通路有两条:
;没有与之不接触的回路:
;没有与之不接触的回路:
带入梅逊公式公式得:
对E(s)/R(s),前向通路有两条:
;有一不接触的回路:
;没有与之不接触的回路:
带入梅逊公式公式得:
27.一个回路:
,
无互不接触的回路,则:
对C(s)/R(s),前向通路有两条:
;没有与之不接触的回路:
A.图(a)B.图(b)
C.图(c)D.图(d)
22.当ω从−∞→+∞变化时惯性环节的极坐标图为一个(B)。
A.位于第一象限的半圆B.位于第四象限的半圆
C.整圆D.不规则曲线
23.下列串联校正环节中属于滞后校正的是(A)。
A. B.
C. D.
24.下列环节中属于PI校正的是(C)。
A. B.
C. D.K(1+Ts)
由 ,得K=11.656;
由 ,得K=0.34
闭环根位于实轴上时阶跃响应无超调,综合得K取值范围:
K>11.656,K<0.34
52.已知G(s)H(s)= ,绘制K从0到∞的闭环根轨迹,确定分离点坐标、渐近线方程,判断闭环系统稳定性。
53.某单位负反馈系统的开环传递函数为 ,试
【年度第一学期《自动控制原理》考卷A卷_小学第一学期德育工作总结

【年度第一学期《自动控制原理》考卷A卷_小学第一学期德育工作总结安徽大学学年第《自动控制理论》考试试卷(A卷)(时间120分钟)院/系专业姓名学号一、(共15分)已知结构图如图所示。
试系统的闭环C(s)/R(s)。
二、(共10分)已知系统结构如下图所示。
若系统在输入r(t)=t作用下的稳态误差ess?0.1,试确定K1的取值范围。
误差定义为E(s)=R(s)-C(s)。
三级(共15分)已知反馈控制系统的开环传递函数为:KG(s)?S(0.01s?1)(0.02s?1)要求:(1)绘制系统根轨迹图。
(2)确定系统的临界稳定开环增益Kc。
四、(共15分)某最小相位控制系统其单位反馈系统的开环传递函数的对数幅频曲线如下图所示:5吨?30)时系统的稳态输出C(T)。
试求:当系统的输入为r(t)?2sin(o五、(共15分)给定系统的开环传递函数,尝试绘制奈奎斯特图,并根据奈奎斯特判据判断系统的稳定性:K(S?3)G(s)H(s)?S(S?1)K0安徽大学2022电气工程2022-08第一学期“自动控制原理”试卷a卷六、(共15分) 200已知单位负反馈系统开环传递函数为Go(s)?,s(0.1s?1)试设计串联校正装置,使系统的相角裕度??450,截止频率不低于55 rad/s。
七、(每题5分,共15分)某含有零阶保持器的采样系统结构如图所示,试求:(1)当采样周期T?系统在1s时的临界开环增益KC;(2)求T?1s,K?1时系统单位阶跃响应C(kT);(3)计算阶跃输入信号作用下系统的稳态误差。
以上就是这篇范文的全部内容,主要描述系统、传递、函数、已知、单位、输入、确定、反馈,希望对大家有用。
系学期工作总结站在岁末,回顾过去一学期,工作的点点滴滴时时在眼前隐现,回眸望去过去的一幕慕,在不知不觉中充实眼睑。
似乎初进学校的记忆依然就在心头展现!但我已深深地感觉到新一年的工作重担已向无情地压来,为能保质保量地完成工作任务,我必须在过去的基础上对相关知识、能力进行进一步学习,加深认识。
自动控制原理考试试卷及答案30套
−b
Im
Re
B2 ω B1
A
−1 N ( A)
0
K
−
b
K = 1, b = 1
题 7 图 (a)
4 s(s + 1)(s + 2)
G ( jω )
题 7 图(b)
8. (15 分)某离散控制系统如下图,采样周期 T=0.2 秒,试求闭环稳定的 K1、K2 的取值 范围。
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
7. (15 分)已知系统结构图如下图所示,试求传递函数
C ( s) E ( s ) 。 , R ( s ) R( s )
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 6 页 共 70 页
自动控制原理试卷 A(4)
第 5 页 共 70 页
自动控制原理试卷 A(3)
1、 . (10 分)已知某单位负反馈系统的开环传递函数为 G ( s ) =
6 ,试求系统的单位脉 s ( s + 5)
冲响应和单位阶跃响应。 2、 (10 分)已知单位负反馈系统的闭环零点为 -1,闭环根轨迹起点为 0,-2,-3,试确定系 统稳定时开环增益的取值范围。 3、 (10 分)已知系统的结构图如下,试求: (1)闭环的幅相特性曲线; (2)开环的对数幅频和相频特性曲线; (3)单位阶跃响应的超调量σ%,调节时间 ts; (4)相位裕量γ,幅值裕量 h。
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 4 页 共 70 页
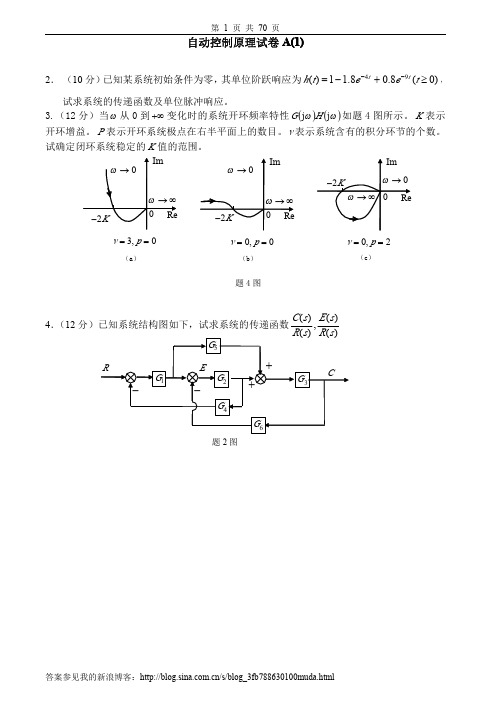
(1)试写出系统的传递函数 G(s); (2)画出对应的对数相频特性的大致 形状; (3)在图上标出相位裕量Υ。 7. (15 分)题 7 图(a)所示为一个具有间隙非线性的系统,非线性环节的负倒幅相特性与 线性环节的频率特性如题 6 图(b)所示。这两条曲线相交于 B1 和 B 2 两点,判断两个交点处 是否存在稳定的自持振荡。
自动控制理论(下)模拟试卷A资料

自动控制理论(下)模拟试卷A一.判断题1.状态变量的选取具有非惟一性。
(√)2.由一个状态空间模型可以确定惟一一个传递函数。
(√)3.传递函数G(s)的所有极点都是系统矩阵A 的特征值,系统矩阵A的特征值也一定都是传递函数G(s)的极点。
(×)4.若一个对象的连续时间状态空间模型是能控的,则其离散化状态空间模型也一定是能控的。
(×)5.对一个系统,只能选取一组状态变量(×)6.由状态转移矩阵可以决定系统状态方程的状态矩阵,进而决定系统的动态特性。
(√)7.传递函数只能给出系统的输出信息;而状态空间表达式不仅给出输出信息,还能够提供系统内部状态信息。
(√)8.一个系统的平衡状态可能有多个,因此系统的李亚普诺夫稳定性与系统受干扰前所处得平衡位置无关。
(×)9.系统的状态观测器存在的充分必要条件是:系统能观测,或者系统虽然不能观测,但是其不能观测的子系统的特征值具有负实部。
(√)10.如果线性离散化后系统不能控,则离散化前的连续系统必不能控。
(×)x=处渐近稳定。
(×)11.一个系统BIBO稳定,一定是平衡状态0e12.状态反馈不改变系统的能控性。
(√)=,其李亚普诺夫意义下的渐近稳定性和矩阵A的特征值都具有负实13.对系统x Ax部是一致的。
(√)14.若传递函数存在零极相消,则对应的状态空间模型描述的系统是不能控不能观的。
(×)15.若系统状态完全能控,则对非渐近稳定系统通过引入状态反馈实现渐近稳定,称为镇定问题。
(√)二.填空题1.以所选择的一组状态变量为坐标轴而构成的正交线性空间,称之为状态空间。
2. 能控性 定义: 线性定常系统的状态方程为()()()x t Ax t Bu t =+,给定系统一个初始状态00()x t x =,如果在10t t >的有限时间区间10[,]t t 内,存在容许控制()u t ,使1()0x t =,则称系统状态在0t 时刻是 能控 的;如果系统对任意一个初始状态都能控 , 称系统是状态完全 能控 的。
安徽大学0809年度第一学期自动控制理论考卷A卷含答案

安徽大学20 08 —20 09 学年第 一 学期《 自动控制理论 》考试试卷(A 卷)(时间120分钟)一、化简题(共15分)某控制系统结构图如下,试求系统的闭环传递函数)()()(s R s C s =Φ.题 号一二 三 四 五 六 七 总分 得 分阅卷人得分院/系 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------二、简答题(共15分)已知一控制系统的结构图如下(1) 求使系统稳定时K 的取值范围;(2) 如果要求闭环系统的极点全部位于1s =-垂线之左,求K 的取值范围。
三、绘图题(共10分)已知单位负反馈系统的开环传递函数为:()(1)(0.51)KG s s s s =++(1)绘制该系统的根轨迹图;(2)为保证该系统稳定,试确定K 的取值范围。
四、判断题(共15分)已知单位负反馈系统,开环传递函数4(1)3(),0(1)k sG s ks s+=>-。
(1)绘制k=6时的乃氏曲线,并用乃氏判据判断系统的稳定性;(2)给出系统稳定时k的范围。
五、设计题(共15分)已知单位负反馈系统开环传递函数为)2()(+=s s Ks G o ,试设计串联校正装置,使t t r =)(时,稳态误差为05.0=ss e ,系统的相角裕度050≥γ。
六、分析题(共15分)设复合校正系统的结构如下图所示,试确定前馈校正装置的 结构参数1λ和2λ,使复合校正后控制系统具有Ⅲ型控制精度。
(2121,,,T T K K 已知且均大于0)七、计算题(共15分)某含有零阶保持器的采样系统结构如图所示,试求:(1)当采样周期sT1=时系统的临界开环增益cK;(2)求1,1==KsT时系统单位阶跃响应)(kTC;(3)求系统在阶跃输入信号作用下的稳态误差。
自动控制理论试卷A

《自动控制理论》考试试卷A
一、已知控制系统图如下图所示,求系统传递函数C(s)/R(s)。
(共10分)
R(s)
二、已知单位负反馈系统的开环传递函数为:
G(s) = 1
2)1(23++++s as s s K 若系统以ωn =2rad/s 的频率作等幅振荡,试确定振荡时的参数K 与a 。
(共10分)
三、一单位反馈系统的开环传递函数对数渐近线如图所示。
(共30分,每小题10分)
1、写出系统的开环传递函数;
2、计算相角裕度,判断闭环系统的稳定性;
3、若系统稳定,求系统在r(t)=t 2/2作用下的稳定误差;若系统不稳定,试确定s 平面右半部
的特征根数目。
四、下图表示开环传递函数G (s )的Nyquist 图,P 为G(s)的正实部极点数目,判定闭环系统的稳
定性。
(共20分,每小题5分)
(a) (b)
(c) (d)
五、控制系统的传递函数为:(共20分,每小题10分) G(s) = )5)(2(2++s s s K
, H(s) = 1
1. 绘出系统的根轨迹图(计算分离点),判断闭环系统的稳定性;
2. 若H (s )= 1 + 2s,判断H(s)改变后的系统稳定性。
六、设系统不可变部分的传递函数为:(共10分) G(s) = )
12.0)(11.0(++s s s K V 要求满足性能指标:开环增益K v = 25s -1;剪切频率ωc = 2.5rad/s;相角裕度γ≧40°。
试设计串联
迟后校正装置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生答题不得过此线··密
····························封
·························线
···························· 系 专业 年级
班级 姓名 学号 ··················装
····························订
·························线
·················
··········· 一、填空题(每空1.5分,共36分) 1、自动控制的概念是: 。
2、根据不同的信号来源,自动控制系统可分为 、 、 以及 四种基本控制方式。
3、工程上一般从 、 以及 三方面来评价自动控制系统的性能。
4、某系统的传递函数只与 有关,而与其外界输入无关。
此控制系统须具备三方面的职能部件分别是 、
和 ;参与控制的信号来自三条通道,它们是 、
和 。
6、常规根轨迹的分支数为 ,对称性为 ,起点为 ,终点为 。
7、在工程实际中对于存在线性工作区域的非线性系统,或者非线性不严重的准线性系统,常常采用的处理方法是
,而对于不存在线性区的非线性特性,工程上常用 分析方法和 分析方法。
8、采样过程是指 。
要想使采样信号无失真恢复成采样信号,必须要满足 条件。
二、化简求解题(14分)
某控制系统动态结构图如下所示。
求系统传递函数C (s)/R (s)。
···················装
·······················订
·······················线
····································· 院
系 专业
年级 班级 姓名 学号
···················密·······················封·······················线
·······················
·············· 考
生
答题不得过此线
三、分析计算题(20分)
已知控制系统如图所示,
(1) 在0)(br =s G 时,闭环系统响应阶跃输入时的超调量%6.4=p
σ、峰值
时间55.0=p t 秒,确定系统的k 值和τ值;
(2) 欲使闭环系统响应在速度输入的稳态误差为零,请确定输入补偿环节的传递函数)(br s G 。
四、分析判断题(14分)
1、已知系统特征方程为063632
3
4
=++++s s s s ,判断该系统的稳定性,若闭环系统不稳定,指出在][S 平面右半部的极点个数。
五、设计计算题(16分)
设单位负反馈系统的开环传递函数为:)
2(4)(+=s s K s G ,要求
设计串联控制器,使:
1. 响应t t r =)(时的稳态误差05.0≤;
2. 相角裕度︒≥45;
3. 剪切频率rad/s 6≥c ω。
)
8()(1+=
s s k s G ;s s H τ=)(。
