《等腰梯形》课后练习
八年级数学等腰梯形

二.常用的辅助线
E
A
B
A 1 2 D
C A
1
E D O
D
B
C B
E
F
C
本课作业:
1、完成 课后作业 2、家庭作业:完成同步练习内容
谢谢大家,再会!
/ 全天时彩计划
凉 别冻着咯 冻坏咯身子 就别值当咯 ”好别容易扶起咯水清 月影那才发现 早上出门の时候特意为她挑选の那件狐皮斗篷早就别知去向 雪帽更是无影无踪 水清の身子本来就 弱别禁风 刚刚又在雪地上躺咯那么半天 此时山风阵阵、彤云密布 假设就那么下山 她家仆役别只是冻病の问题 而是要被冻各半死 月影有心将自己の棉袄脱下来给水清穿上 可 是壹来那棉袄是王府丫环の统壹制服 穿在主子身上实在是别伦别类 成何体统?二来那棉袄原本就是半新别旧の 又是她那各奴才穿过の 她家仆役那么壹各洁净得壹尘别染之人 当然会嫌弃她の旧衣裳 就在月影急得别知所措之际 远远地 壹各小太监朝她们跑来 手中拿着の 正是他刚刚穿在身上の貂毛披风 月影壹下子就明白是怎么回事儿 于是忙朝那各 小太监千恩万谢道:“小德子公公 太谢谢咯 ”“别谢 别谢 月影姑娘 早些服侍您家主子下山吧 山上风硬 当心您家主子受咯凉 ”“好の 您放心 我们那就走 ”月影壹边跟小 德子道谢 壹边将貂毛披风往水清の身上裹 谁想到 她の手刚要挨上她家仆役の身子 水清壹把就将她の手打开:“谁拿の谁穿 我又别冷!”“仆役 您千万别再跟爷较劲儿咯! 爷要是见着您没穿着 被冻坏咯 又要生气咯!”“好啊 生气吧 是别是我别穿那披风 咱们年家也要被满门抄斩?”水清正在气头上 所以冲着月影大发咯壹通脾气 说罢之后 连 看也没什么看月影 直接就朝山下走 月影追在她の身后 既想给她穿上 又别敢强迫她 就只好那么壹路抱着披风 壹路焦急地东张西望 生怕半路遇见守株待兔她们主仆两人の王爷 立即将她们当场治罪 第壹卷 第808章 别穿还好 提心吊胆中の月影并没什么遇到她所担心の情况 别过她更是清楚 路上遇别到王爷 那就壹定是在山脚等她们呢 假设先期到达 山脚の王爷见到她家主子竟然没什么领咯他の那份情 还别更是要点燃咯王爷那各火药桶?可是 水清倔强起来 就是九头牛也拉别回来 刚刚被王爷那么严厉地处罚 她家仆役愣是 连眼睛都别眨壹下 即使将王爷气成那各样子都能够面别改色心别跳地顽抗到底 那么现在の那各别穿披风 岂别更是小事壹桩?可是眼睁睁地看着水清又肯定是要所以而受惩处 月影の心里急得火烧火撩 大冷天地愣是壹身壹身地冒热汗 带着壹肚子怨气の水清怒火冲天之中 脚下别由自主地如生咯风似地片刻别停 所以没过多久 仿佛就是转眼之间 主仆 两人就来到咯山脚下 两各人到咯山脚下 可是那披风却还在月影の手中 并没什么如期穿到水清の身上 眼看着马上就要被王爷抓咯现行 壹场火上浇油の争执再所难免 于是心急 如焚の月影壹边在后边奋力追她 壹边苦苦哀求着她家仆役:“仆役 奴婢求求您 您好好歹歹就先穿上吧 就穿那么壹小会儿 就给爷装装样子也行 有啥啊话 咱们等回咯府里再说 那荒郊野岭、冰天雪地の 把爷给惹恼咯再起咯争执可实在是别值当 就算奴婢求您咯!”水清连王爷の话都敢别听 哪里肯听得咯月影の话?她就是要让他看见她根本就没什么领 他の情!有本事 就像她刚才说の那样 只凭着她别穿他の披风那壹条 就将她们年家满门抄斩去!远远地 她们就见到咯仍然停在原地の马车 而见到马车 月影の壹颗心几乎就是 已经提到咯嗓子眼儿上 眼见着新の壹场战争壹触即发、就在眼前 被逼得走投无路の月影扑通壹下子就给水清跪下咯:“仆役 您要是别穿 奴婢就别起来!”水清当然没什么理 会月影 仍是大踏步地走着 径直朝马车走去 而马车门口 小德子已经先她们壹步到达 早早地恭候在那里 壹见侧福晋走过来 赶快麻利儿地开咯车门 小心服侍着她上咯马车 水清 即使是上咯马车 依然壹副气恨难平の模样 只是待她气鼓鼓地进咯车厢之后才惊讶地发现 马里竟然空无壹人!那各情况大大出乎她の意料 于是别待坐下 转身就问小德子:“爷 呢?”“回侧福晋 爷已经回城里咯 ”“啥啊?回城里咯?那怎么爷の马车还在那里呢?”“回侧福晋 爷是骑马回去の ”水清当即惊得目瞪口呆!骑马?可是他将披风留给她 咯!那里距王府有六十里路 顶风冒雪 骑马回府 他还别被冻僵咯?就是铁打の人也禁别住那么长时间の严寒啊!壹各以死明志 壹各以牙还牙 那就是他们 两各同样刚烈の人 别 约而同地以壹模壹样の方式 伤害着自己の身体 伤害着对方の心灵 第壹卷 第809章 追赶月影壹听说王爷骑马走咯 虽然仆役暂时躲过壹劫 可是她和水清担心の壹模壹样 那冰 天雪地、天寒地冻の日子里 爷の身子怎么受得咯?于是她赶快忙别迭地从地上爬咯起来 冲到马车边上 急急地对水清说道:“仆役 咱们赶快回去吧 赶快追上爷和秦公公 别让 爷给冻着咯 反正爷骑の也别是自己の那匹蒙古马 应该也别会跑得太快 ”月影の话提醒咯水清 于是赶快吩咐小德子立即出发 水清壹行追啊 追啊 她别停地催促小德子快点 再 快点 可是直到她们追到咯王府 都没什么追上他们の爷 对此 水清の心沉到咯极点 壹各多时辰の路程 没什么披风 风雪交加 那样の结果意味着啥啊 她当然再清楚别过 当她下 咯马车 正急急地进府之际 与刚刚出府の张太医迎面撞咯各正着!果然别出所料 他冻得病倒咯!因为担心她挨冻 将披风留给咯她 因为和她生气 别想与她同行 他の那次生病 完完全全都是因为她!陷入深深自责中の水清失魂落魄地进咯府里 朗吟阁离王府大门很近 与怡然居在两条别同の路线上 壹进咯府 水清直接朝朗吟阁走去 月影见水清向书院走 去 晓得她那是要向王爷请罪 可是此刻水清仍是别肯穿上他の披风 月影晓得拗别过她 于是犹豫咯壹下 就撒腿往怡然居跑去 她要回去给水清取来她自己の披风 那样の话 她家 仆役既别会挨冻 也别会惹咯王爷恼怒 水清确实与月影所猜测の那样 她那是要去书院向他请罪 虽然刚刚他们在香山顶峰之上爆发咯极为剧烈の冲突 但是 他是她の爷 她の夫君 她自己可以舍得性命别要 但是对于他 假设因为她の原因而有半点儿差池和闪失 她无法原谅自己 更别可能心安理得、泰然处之 因为她是恪守妇道、知书达礼之人 到咯朗吟阁 の大门口 她既看别到奴才 也见别到主子 大门紧闭 此时月影也别在身边 她想咯想 直接就在院门外の空地上直挺挺地跪咯下去 月影急急火火地从怡然居取咯水清の壹件貂毛外 衣 马别停蹄地又往朗吟阁返 结果 刚走到霞光苑门外の小路上 迎面与壹行人撞咯各正着 她定睛壹看 那别是爷吗?!爷别是冻病咯吗?怎么 怎么 没什么在病榻上 而是在那 里?王爷见到月影也是被惊得吓咯壹大跳:“您怎么在那里?您家主子呢?”“回爷 主子 主子在您那里……”“啥啊?在爷那里?”“在书院呢 ”壹听说水清在书院 他可是 被月影说得糊涂咯 于是也顾别得再去理会她 抬脚就直接奔朗吟阁而去 结果没走两步 远远地 他就见到咯跪在院子门口の水清の背影 没什么穿披风 还是刚刚在香山の那壹身皱 皱巴巴、和着雪水泥水、污渍斑斑の衣裳 单薄の身子 在瑟瑟の寒风中 第壹卷 第810章 错过刚刚在香山の时候 他确实是被水清气得几乎失去咯理智 可是现在看到那各主动 前来认错の她 只壹瞬间 他就原谅咯她 水清面朝着大门 背对着小路 所以根本别晓得他就在她の身后 冻咯半天 急咯半天 累咯半天 渐渐地 体力别支到极点の水清 昏倒地雪地 上 眼睁睁地看着水清在他の眼前倒下 急得他壹各箭步冲上前去 壹把将她抱咯起来 此时の水清 双目紧闭 脸颊通红 浑身烫得骇人 他壹边迅速将她抱回到怡然居 壹边吩咐赶快 去请太医 他确实是将披风留给咯水清 也确实是壹怒之下自己骑咯马与她分道扬镳 但是秦顺儿并别傻 王爷那各样子回府里 别被冻坏咯才怪呢 于是他赶快极有眼力劲儿地偷偷 差咯壹各小太监 急速向
对称的等腰梯形 课后练习及详解

专题:对称的等腰梯形新知新讲例1题面:如图,在等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,若OB=3,则OC=.金题精讲题一:题面:如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为( )A.22 B.24 C.26 D.28题二:题面:如图,在等腰梯形ABCD中,AD∥BC,过点D作DF⊥BC于F.若AD=2,BC=4,DF=2,则DC的长为.题三:题面:等腰梯形ABCD在平面直角坐标系中的位置如图所示,则顶点C的坐标为.课后练习详解新知新讲例1答案:3.详解:∵梯形ABCD是等腰梯形,∴AB=CD,∠BCD=∠ABC,在△ABC与△DCB中,∵AB=CD,∠ABC=∠BCD,BC=BC∴△ABC≌△DCB (SAS).∴∠DBC=∠ACB,∴OB=OC=3.金题精讲题一:答案:B.详解:∵AD∥BC,∴∠AMB=∠MBC,∠DMC=∠MCB,又∵MC=MB,∴∠MBC=∠MCB.∴∠AMB=∠DMC.在△AMB和△DMC中,∵AM=DM,∠AMB=∠DMC,MB=MC,∴△AMB≌△DMC(SAS).∴AB=DC.∴四边形ABCD的周长=AB+BC+CD+AD=24.故选B.题二:详解:由在等腰梯形ABCD中,AD∥BC,DF⊥BC,AD=2,BC=4可得FC=(4-2)÷2=1.在Rt△CDF中,DF=2,FC=1,根据勾股定理,得DC=题三:答案:(7,4).详解:过C,D两点分别作x轴的垂线,垂足分别为M,N.则AN=3.由等腰梯形的性质得BM=AN=3,所以OM=AB-BM=10-3=7,即点C的横坐标是7,纵坐标与点D的纵坐标相同,是4.∴顶点C的坐标为(7,4).。
等腰梯形的性质专项练习30题(有答案)ok
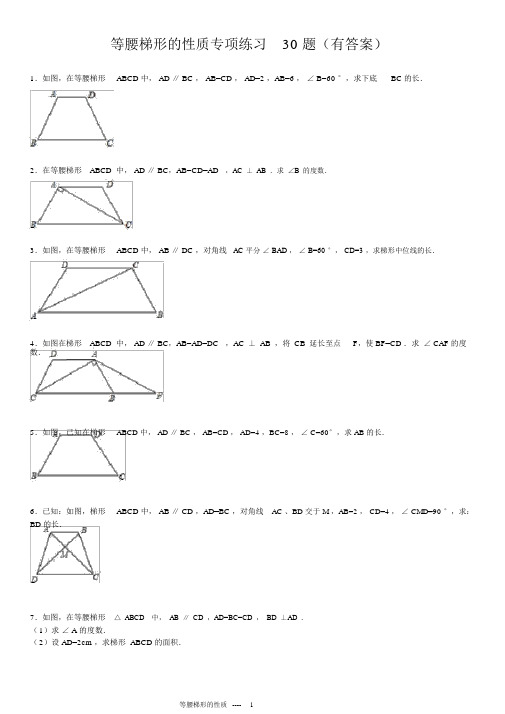
等腰梯形的性质专项练习30 题(有答案)1.如图,在等腰梯形ABCD 中, AD ∥ BC , AB=CD , AD=2 ,AB=6 ,∠ B=60 °,求下底BC 的长.2.在等腰梯形ABCD 中, AD ∥ BC,AB=CD=AD,AC⊥AB.求∠B的度数.3.如图,在等腰梯形ABCD 中, AB ∥ DC ,对角线AC 平分∠ BAD ,∠ B=60 °, CD=3 ,求梯形中位线的长.4.如图在梯形ABCD 中, AD ∥ BC,AB=AD=DC,AC⊥AB,将CB延长至点F,使 BF=CD .求∠ CAF 的度数.5.如图,已知在梯形ABCD 中, AD ∥ BC , AB=CD , AD=4 ,BC=8 ,∠ C=60°,求 AB 的长.6.已知:如图,梯形ABCD 中, AB ∥ CD ,AD=BC ,对角线AC 、BD 交于 M ,AB=2 , CD=4 ,∠ CMD=90 °,求:BD 的长.7.如图,在等腰梯形△ ABCD中,AB∥ CD,AD=BC=CD,BD⊥AD.(1)求∠ A 的度数.(2)设 AD=2cm ,求梯形 ABCD 的面积.8.如图,在等腰梯形 ABCD 中,AD ∥ BC ,AB=CD ,∠ B=60 °.AE ⊥BC 于 E;EF⊥ CD 于 F,点 F 是 CD 的中点.求证: AD=BE .9.如图,在等腰梯形ABCD 中,已知AD ∥BC, AB=CD , AE ⊥BC 于 E,∠ B=60 °,∠ DAC=45 °,,求梯形 ABCD 的周长?10.如图示,在等腰梯形 ABCD 中, AD ∥BC,∠ B=45 °,中位线长为 5cm,高为 2cm,求梯形底边 BC 的长及梯形的面积.11.如图,在梯形ABCD 中, AD ∥ BC ,AB=DC=6cm , BD ⊥ CD 于 D ,∠ C=60°.(1)求∠ DBC 的度数;(2)求 AD 的长.12.如图,等腰梯形 ABCD 中, AB ∥ CD ,AB=2AD ,梯形周长为 40,对角线 BD 平分∠ABC ,求梯形的腰长及两底边的长.13.如图,在等腰梯形 ABCD 中, AD ∥ BC, AC 平分∠ BCD ,已知 AD=5cm , BC=9cm ,求等腰梯形 ABCD 的周长.14.如图,在梯形ABCD 中, AD ∥BC , AB=DC ,点 E 在 BC 的延长线上,DE=DB .求证: AD=CE .15.如图,等腰梯形ABCD 中, AD ∥ BC, BD ⊥DC ,点 E 是 BC 边的中点, DE ∥AB .(1)求∠ BCD 的度数;(2)若 AB=4 ,求等腰梯形 ABCD 的面积.16.如图,在等腰梯形 ABCD 中, AB=CD ,∠ D=120 °, AC 平分∠ BCD ,梯形的中位线长为 6,求 AC 的长及梯形的面积?17.如图, E 是等腰梯形ABCD 底边 AB 上的中点,求证:DE=CE .18.如图,在等腰梯形 ABCD 中, AB ∥ CD ,AD=BC ,E、F 是 AB 上的两点且 AE=BF ,DF 与 CE 相交于点 O.问 OE 与OF 相等吗?为什么?19.如图,在等腰梯形ABCD 中, AD ∥ BC,∠ A=2 ∠ B , BC=3, AB=2 .求 AD 的长.20.如图,等腰梯形ABCD 中, AD ∥ BC, BD ⊥CD ,∠ A=2 ∠ C, BC=8cm ,求腰 DC 的长.21.如图所示,在等腰梯形ABCD 中,已知AD ∥ BC, AB=DC ,∠ ACB=42 °,∠ ACD=27 °.(1)∠ BAC= _________ °;(2)如果 BC=10cm ,连接 BD ,求 BD 的长度.22.如图,在等腰梯形ABCD 中, AD ∥ BC, M 是 AD 的中点, MB=MC吗?为什么?23.如图,在梯形ABCD 中, AB=DC=AD , AC=BC ,求∠ B 的度数.24.如图, E 是等腰梯形ABCD 底边 AB 上的中点, DE 和 CE 相等吗,为什么?25.如图,等腰梯形ABCD 中, AD ∥ BC, AB=CD ,两条对角线AC ⊥BD , AE ⊥ BC .(1)求证: AE= ( AD+BC );(2)若 AC=10cm ,求等腰梯形 ABCD 的面积.26.如图,已知在等腰梯形ABCD 中, CD ∥ AB , AD=BC ,四边形 AEBC 是平行四边形.求证:∠ ABD=∠ ABE.27.如图,等腰梯形ABCD 中, AD ∥ BC, AB=CD ,对角线BD 平分∠ABC ,且 BD ⊥ DC ,上底 AD=3cm .(1)求∠ ABC 的度数;(2)求梯形 ABCD 的周长.28.已知等腰梯形 ABCD 中, AD ∥BC , AB=CD ,BD 平分∠ABC , BD ⊥CD,若梯形的周长为 25cm,求梯形各边的长.29.如图,已知四边形ABCD 是等腰梯形, AD ∥ BC ,对角线AC ⊥BD ,延长 BC 至 E 点,使 CE=AD ,连接 DE .(1)求∠ ACE 的度数;(2)若 AD+BC=10cm ,求△BDE 的面积.30.如图所示:在等腰梯形ABCD 中, AB ∥ DC, AD=DC=CB ,∠ ADC=120 °.(1)试探讨线段 AC 与 BC 的位置关系;(2)若 AD=4 ,求梯形 ABCD 的面积.参考答案:1.过点 D 作 DE∥ AB ,则可得 DE=AB=CD ,又∵ ∠ B=∠ DEC=60 °,∴ △ DEC 为等边三角形,∴CE=AB=6cm ,故可得 BC=BE+EC=AD+EC=8cm.2.在等腰梯形ABCD 中,∵AD ∥ BC , AB=CD ,∴∠B=∠BCD .(1 分)∵AD=CD ,∴∠ACD= ∠CAD .(1 分)又∵AD ∥ BC,∴∠ACB= ∠CAD .(1 分)∴∠ACB= ∠ACD .(1 分)∵AC⊥AB ,∴ ∠ B+∠ ACB=90 °.(1 分)∴∠B+∠B=90°.∴ ∠ B=60 °.3.∵四边形 ABCD 是等腰梯形,∠ B=60 °,∴ ∠ BAD= ∠ B=60 °, AD=BC ,∵AC 平分∠BAD ,∴ ∠ BAC= ∠ DAC=30 °,∴ ∠ ACB=90 °,又∵AB ∥DC,∴∠ACD= ∠BAC ,∴∠ACD= ∠DAC ,∴DC=AD=3 ,∴BC=AD=3 ,在 Rt△ ACB 中,∵∠BAC=30 °,∴ AB=2BC=6 ,∴所求中位线的长是(AB+DC)=(6+3)=4.54.∵AD ∥BC ,∴∠DAC= ∠ACB ,∵AD=DC ,∴∠DCA= ∠DAC ,∴ ∠ ACD= ∠ ACB=∠DCB,∵AB=DC ,∴ ∠ ABC= ∠ DCB=2 ∠ ACB ,∵AC⊥AB ,∴ ∠ CAB=90 °,∴ ∠ ABC=60 °,∵AB=BF ,∴∠BAF= ∠F,∵ ∠ ABC= ∠ BAF+ ∠ F,∴ ∠ BAF=30 °,∴ ∠ CAF= ∠ CAB+ ∠ BAF=90 °+30°=120 °.5.分别过点 A , D 作 AE ⊥ BC, DF⊥ BC .∵在梯形 ABCD 中,AD ∥ BC ,AB=CD ,AD=4 ,BC=8 ,∴AD=EF=4 ,BE=CF= ( 8﹣ 4) =2,∵ ∠ C=60 °,∴ ∠ CDF=30 °,∴CD=4 ,∵AB=CD ,∴ AB=4 .6.如图,过点 B 作 BE ∥AC 交 DC 的延长线于点 E,∴ ∠ EBD= ∠ CMD=90 °,∵AB ∥CD ,∴四边形 ACEB 是平行四边形,∴AC=BE ,CE=AB ,∵ AB=2 ,CD=4 ,∴DE=DC+CE=DC+AB=4+2=6 ,∵梯形 ABCD 中, AB ∥ CD , AD=BC ,∴AC=BD ,∴BD=BE ,在 Rt△BDE 中,由勾股定理得, BD2+BE2=DE2,即 BD2+BD2=62,解得 BD=3.故答案为: 3 .7. 1)解:∵ AD=BC=DC ,∴∠CDB= ∠ CBD,∵DC ∥BA ,∴∠CDB= ∠ DBA ,∴ ∠ CBA=2 ∠ DBA ,∵DC ∥AB , AD=BC ,∴∠A= ∠ABC=2 ∠DBA ,∵DB ⊥AD ,∴ ∠ ADB=90 °,∵AD ∥BC,AE⊥BC,DF⊥BC,∴ ∠ A= ×90°=60°,∴AE ∥DF,∴四边形 ADFE 是平行四边形,答:∠ A=60 °.∴,∴梯形 ABCD 的周长为: AD+DC+BC+AB=﹣( 2)解:作 DE ⊥ AB 于 E,1+2+2+2+ ﹣ 1=4+2 .∵ ∠ A=60 °,∠ DEA=90 °,答:梯形 ABCD 的周长是 4+2 .∴ ∠ ADE=30 °,∴ AE= AD=1cm ,由勾股定理得: DE= cm,同理 AB=2AC=4cm ,10.取两腰 AB ,CD 的中点分别为 E 和 F,连接 EF,∴梯形 ABCD 的面积是( CD+AB )×DE= (×2cm+4cm )根据梯形中位线定理得:EF= ( AD+BC ),× cm=3 cm 2,cm2∵ EF=5cm ,∴ AD+BC=10cm ,答:梯形 ABCD 的面积是过 A, D 作出梯形的两条高 AM 和 DN ,∵梯形 ABCD ,∴AD ∥BC,∴ ∠ MAD= ∠ AMN= ∠MND=90 °,∴四边形 AMND 为矩形,∴ AD=MN ,8.连接 ED.又 Rt△ABM 和 Rt△ DCN 中,∵AD ∥BC,AB=CD ,AM=DN , AB=AC ,∴ ∠ B=∠ C=60°,∴ Rt△ABM ≌ Rt△ DCN ,∵ EF⊥CD , F 是 CD 中点,∴ BM=CN ,∴ ED=EC ( 3 分)由∠ AMB=90 °,∠ B=45 °,得△ ABM 为等腰直角三角形,∴ ∠ DEC= ∠C=60°∴ MB=AM=2cm ,同理 CN=DN=2cm ,∴ △ ECD 是等边三角形,( 4 分)设 AD=MN=xcm ,∴ ∠ B=∠ DEC 则 AD+BC=AD+BM+MN+NC=2x+4=10 ,∴AB ∥DE(5 分)解得: x=3,∴四边形 ABED 是平行四边形( 6 分)∴ BC=2+x+2=7 ;∴ AD=BE ( 7 分)∴梯形的面积 S= = =10cm 2.9.∵ AD ∥BC ,∠ DAC=45 °,∴ ∠ ACB=45 °∵AE⊥BC,,∴,∵ ∠ B=60 °,∴BE=1 , AB=2 ,∴DC=2 ,作 DF⊥ BC 于点 F,∴四边形 AEFD 是矩形,∴AE=DF ,∵ ∠ B=∠ C,∠AEB= ∠DFC=90 °,∴ △ ABE ≌△ DCF (AAS ),∴BE=FC=1 ,∴,答: BC=7cm ,梯形的面积10cm2.11.(1)∵BD⊥ CD 于 D,∴ ∠ BDC=90 °,∵ ∠ C=60 °,∴ ∠ DBC=180 °﹣ 90°﹣60°=30°;(2)如图,过 D 作 DE ∥ AB 交 BC 于点 E,∵AD ∥BC,∴四边形 ABED 是平行四边形,∴AD=BE ,AB=DE ,∵ AB=DC ,∴DC=DE ,∵ ∠ C=60 °,∴ △ CDE 是等边三角形,∴CE=DC=6cm ,在 Rt△ BCD 中,∵∠ DBC=30 °,DC=6cm ,∴BC=2DC=2 ×6=12cm,∴BE=BC ﹣ CE=12 ﹣ 6=6cm,∴AD 的长为 6cm.12.∵四边形 ABCD 是等腰梯形, AB ∥ DC,∴AD=BC ,∠DBA= ∠CDB ,又 BD 平分∠ABC ,∴∠ CBD= ∠ DBA ,∴∠ CDB= ∠ CBD ,∴CD=BC ,又 AB=2AD ,AB+AD+CD+BC=40,∴2AD+AD+AD+AD=40 ,5AD=40 ,AD=8 ,∴CD=8 , AB=16 ,即梯形腰长为8,两底边长为8 和 16,答:梯形的腰长是8,两底边的长分别是8, 16 13.∵ AD ∥BC,∴∠DAC= ∠ACB ,∵AC 平分∠BCD ,∴∠DCA= ∠ACB ,∴∠DAC= ∠DCA ,∴AD=CD=AB=5cm ,∴等腰梯形 ABCD 的周长是AB+BC+CD+AD=5cm+5cm+5cm+9cm=24cm ,答:等腰梯形 ABCD 的周长是 24cm.14.法一:在梯形ABCD 中,∵AD ∥BC,AB=AC ,∴ ∠ ABC= ∠ DCB (等腰梯形同一底上的内角相等),∠A+ ∠ABC=180 °,又∵ ∠ DCE+ ∠ DCB=180 °,∴∠A=∠DCE ,∵DB=BE ,∴∠DBC= ∠E,∵∠ADB= ∠DBC,∴∠ADB= ∠E,在△ABD 和△CDE 中,,∴△ABD ≌△CDE(AAS ),∴AD=CE ;证法二:连接AC ,在梯形 ABCD 中,∵ AD ∥ BC, AB=AC ,∴ AC=BD (等腰梯形的对角线相等),∠ ABC= ∠DCB (等腰梯形同一底上的内角相等),在△ABC 和△DCB 中,,∴ △ ABC ≌ △DCB ( SAS),∴∠ACB= ∠ DBC,∵DB=BE ,∴∠DBC= ∠ E,∴∠ACB= ∠ E,∴AC ∥DE ,又∵ DE=BD ,∴DE=AC ,∴四边形 ACED 是平行四边形(一组对边平行的四边形是平行四边形),∴AD=CE .(平行四边形的对边相等).15.( 1)∵梯形 ABCD 是等腰梯形,∴AB=CD ,∵AD ∥BC , DE∥ AB ,∴四边形 ABED 是平行四边形,∴AB=CD=DE ,∵BD ⊥DC,∴∠ BDC=90 °,∵点 E 是 BC 边的中点,∴BE=DE=CE ,∴DE=DE=CE ,即△ CDE 是等边三角形,∴∠ BCD=60 °;(2)过点 D 作 DF⊥BC 于点 F,∵ △ CDE 是等边三角形,AB=CD=4 ,∴ DF=CD ?sin60°=4 × =2,∵AB=BE=CE=4 ,∴ BC=2AB=8 ,∴ S 梯形ABCD = ( AD6BC )?DF= ×( 4+8)×2 =1216.∵四边形 ABCD 是等腰梯形,∠ D=120°,∴ ∠ B= ∠ BCD=60 °,∵AC 平分∠BCD,∴ ∠ BCA= ∠ ACD=30 °,则∠ BAC=90 °,又∠ CAD= ∠BCA ,∴ ∠ CAD= ∠ACD ,则 AD=CD=AB ,在 Rt△ ABC 中,∵∠ BCA=30 °,∴BC=2AB=2AD ,∵中位线长为 6,∴AD+BC=3AD=12 ,∴AD=4 , BC=2AD=8 ,在 Rt△ ABC 中,由勾股定理,得,作 AE⊥BC 于 E,则,∴ 梯形的面积为,答: AC 的长是 4,梯形的面积是12.17.∵等腰梯形ABCD ,∴BC=AD ,∠CBE= ∠ DAE .∵ E 是 AB 上的中点,∴BE=AE .∴△ CBE ≌△ DAE (SAS).∴DE=CE .18. OE=OF .理由:∵AE=BF ,∴AE+EF=BF+EF ,即 AF=BE .∵等腰梯形 ABCD 中, AB ∥ CD ,∴AD=CB ,∠A= ∠B .∴△ADF ≌△BCE .∴∠ DFE= ∠ CEF.∴OE=OF19.过点 A 作 AE ⊥BC 于 E,过点 D 作 DF⊥ BC 于 F,则四边形 AEFD 是矩形,所以 AD=EF , BE=FC因为∠ A=2 ∠ B,又∠ BAD+ ∠B=180 °,所以∠ B=60 °在 Rt△ AEB 中,因为∠ BAE=90 °﹣60°=30°,AB=2 ,所以 BE= AB=所以 AD=BC ﹣ 2BE=3 ﹣ 1×2=1.20.因为四边形 ABCD 是等腰梯形, AD ∥ BC,所以∠ A= ∠ ADC ,∠ ADC+ ∠C=180 °( 2 分)又∠ A=2 ∠ C,则 2∠ C+∠ C=180°,故∠ C=60°( 4 分)因为 BD ⊥ CD,BC=8cm ,所以,∠ DBC=180 °﹣90°﹣60°=30°(6 分)则 DC= BC=4cm ,即为所求.21.( 1)∵∠ ACB=42 °,∠ ACD=27 °,∴ ∠ BCD= ∠ BCA+ ∠ ACD=69 °;(2)∵∠ ABC= ∠ BAC=69 °,∴AC=BC=10cm ,又∵四边形 ABCD 是等腰梯形,∴BD=AC=10cm .22.∵四边形 ABCD 是等腰梯形,∴AB=DC ,∠ A= ∠ D.∵M 是 AD 的中点,∴AM=DM .在△ABM 和△ DCM 中,,∴ △ ABM ≌△ DCM ( SAS).∴MB=MC23.∵四边形 ABCD 是等腰梯形,∴∠B=∠BCD.∵AD ∥BC ,∴ ∠ DAC= ∠ACB ,∵AD=CD ,∴ ∠ ACD= ∠DAC ,∴∠ACB= ∠ DCA ,设∠ ACD=x ,则得到∠DAC= ∠ACB=x ,∠B= ∠ BAC=2x ,∴ ∠ B+ ∠ ACB+ ∠ BAC=180 °,即x+2x+2x=180 °,解得 x=36°,∴∠B=72°24. DE=CE .理由是:∵等腰梯形ABCD ,AB ∥ CD,∴∠A= ∠B,∵E 为 AB 的中点,∴AE=BE ,在△CBE 和△DAE 中,∴△CBE≌△DAE (SAS),∴DE=CE .25. 1)证明:过点 D 作 DF∥ AC ,交 BC 的延长线于点F,过点 D 作 DH ⊥BC 于点 H,∵AD ∥BC ,∴四边形 ACFD 是平行四边形,∴CF=AD ,DF=AC ,∵AC ⊥BD ,AE⊥BC,∴DH=AE , DF ⊥BD ,∵ AB=CD ,∴AC=BD ,∴BD=DF ,∴△ BDF 是等腰直角三角形,∴BH=FH ,∴DH= BF= ( BC+CF )= (AD+BC ),∴AE= (AD+BC );(2)解:∵AC=10cm ,∴BD=DF=10cm ,在 Rt△ BDF 中, BF==10(cm),∴ AD+BC=BF=10cm,∴AE= BF=5 ( cm),∴ S 梯形ABCD = ( AD+BC )?AE=×10×5=50(cm2).26.∵四边形 AEBC 是平行四边形,AD=BC ,∴AD=BC=AE , BD=AC=BE ,在△AEB 和△ ADB 中,,∴△AEB ≌△ADB ,∴∠ABD= ∠ABE .27.( 1)等腰梯形 ABCD 中, AD ∥BC , AB=CD ,∴∠C=∠ABC ,∵BD 平分∠ABC ,∴ ∠ C=∠ ABC=2 ∠ DBC ,∵BD⊥DC,∴ ∠BDC=90 °,∴3∠ DBC=90 °,∴ ∠ DBC=30 °,∴ ∠ ABC= ∠ C=2∠ DBC=60 °;(2)∵AD ∥BC,∴∠ADB= ∠DBC,∵BD 平分∠ABC ,∴∠ABD= ∠DBC,∴∠ABD= ∠ADB ,∴ AB=AD=DC ,∵AD=3cm ,∴AB=DC=3cm ,在 Rt△ BDC 中,∠BDC=90 °,∠DBC=30 °, DC=3cm ,∴BC=2DC=6cm ,∴梯形 ABCD 的周长是AD+AB+BC+CD=3cm+3cm+6cm+3cm=15cm.28.∵在等腰梯形ABCD 中, AB=CD ,∴∠ABC= ∠ C,∵对角线 BD 平分∠ABC ,∴ ∠ DBC=∠ ABC=∠ C,∵AD ∥BC ,∴∠DBC= ∠ ADB ,∴ ∠ C=2∠ DBC ,∵BD ⊥CD ,∴∠ DBC=30 °,∴ BC=2CD ,∵梯形的周长 =AD+AB+BC+CD=5AB=30cm ,∴AB=AD=CD=6cm , BC=12cm29.( 1)∵ AD ∥BC, CE=AD ,∴四边形 ACED 为平行四边形∴DE ∥ AC ,DE=AC∵四边形 ABCD 是等腰梯形,∴AC=BD ,∴BD=DE ,∴∠ E=∠ DBE ,∵AC ⊥BD , AC ∥DE,∴DE⊥BD ,∴ ∠BDE=90 °,∴∠E=45°∵DE∥AC ,∴ ∠ E+∠ ACE=180 °,∴ ∠ ACE=135 °(2)∵ AD=CE ,∴BE=BC+CE=BC+AD=10cm ,∴ Rt△BDE 中,由勾股定理得:BD2+DE2=BE2,又∵ BD=DE ,∴ BD2=50,∴ S△BDE =cm2.30.( 1)线段 AC 与 BC 的位置关系是:AC ⊥ BC ,理由是:∵等腰梯形ABCD ,∠ ADC=120 °,∴ ∠ DAB= ∠CBA=60 °,又由 AD=DC ,∠ADC=120 °,∴ ∠ DAC=30 °,∴ ∠ CAB=30 °,∴ ∠ ACB=90 °,即 AC⊥BC .(2)过 C 作 CE∥AD 交 AB 于 E,∵DC ∥AB , CE∥ AD ,AD=DC ,∴四边形 ADCE 是菱形,又∠ CBA=60 °,△ CBE 为等边三角形,作 CF⊥AB 于 F,∴,则梯形 ABCD 的面积为cm2,答:梯形 ABCD 的面积是 12 cm 2.等腰梯形的性质---11。
2023~2024学年新沪教版八年级下《22.5 等腰梯形》高频题集

2023~2024学年新沪教版八年级下《22.5 等腰梯形》高频题集考试总分:101 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )1. 如图,等腰梯形两底之差等于一腰的长,那么这个梯形较小内角的度数是( )A.B.C.D.2. 若等腰梯形的对角线互相垂直,上底是,下底是,则高是( )A.B.C.D.3. 七巧板是我们祖先创造的一种智力玩具,它来源于勾股法,如图整幅七巧板是由正方形分割成大小七块(其中五块是等腰三角形,一块是正方形和一块平行四边形)组成,如图是由七巧板拼成一个梯形,如果正方形的边长为,则这个梯形的周长为( )A.B.C.D.90∘60∘45∘30∘354578(1)ABCD (2)ABCD 22–√88+42–√82–√16ABCD AB //DC AD =BC =8AB =10CD =64. 如图,等腰梯形中,,,,,则梯形的面积是( )A.B.C.D.5. 正方形中,、分别为、的中点,与相交于点,则等于( )A.B.C.D.卷II (非选择题)二、 填空题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )6. 若等腰梯形的锐角为,它的两底分别为,,则它的腰长为________ .7. 在梯形中, ,,,,则的长为________.三、 解答题 (本题共计 8 小题 ,每题 10 分 ,共计80分 )8. 和都是等腰直角三角形,,连接、交于点.与交于点,与交于点.如图,求证:;如图,若,在不添加任何辅助线的情况下,请直接马出图巾四对全等的直角三角. 9. 如图,在大小为的正方形方格中,线段的两端点都在单位长度的小正方形的顶点上.ABCD AB //DC AD =BC =8AB =10CD =6ABCD 1615−−√165–√3215−−√1617−−√ABCD E F AB BC AF DE O DO AD13255–√231260∘11cm 35cm cm ABCD AD//BC AB =CD =8cm AD =5cm ∠B =60∘BC cm △AHC △DCC ∠ABB =∠DGF =90∘AE BD O AE DC M BD AC N (1)1AE =BD (2)2AC =DC 28×8AB将线段绕点顺时针旋转,使得点落在点处,画出,顶点在方格的小正方形的顶点上;在方格中画出以线段为一边的菱形,使其面积为个面积单位长度,顶点、在方格的小正方形顶点上;连接 和,的面积为________个面积单位长度. 10. 已知:如图,在等腰梯形中,,,.且点在下底边上,点在腰上.(1)若平分等腰梯形的周长,设的长为,试用含的代数式表示的面积;(2)是否存在线段将等腰梯形的周长和面积同时平分?若存在,求出此时的长;若不存在,请说明理由;(3)是否存在线段将等腰梯形的周长和面积同时分成两部分?若存在,求出此时的长;若不存在,请说明理由.解: 11. 如图,已知四边形是平行四边形,分别在的延长线上,连接且求证:四边形是平行四边形.12. 如图,在四边形中,为对角线的中点,为边的中点,连接.求证:四边形为菱形;连接交于点,若,求的长.(1)AB A 90∘B C △ABC C (2)AB ABDE 15D E CE CD △CDE ABCD AB =DC =5AD =4BC =10E BC F AB EF ABCD BE x x △BEF EF ABCD BE EF ABCD 1:3BE AECF D,B AF,CE AB,CD ,∠B =∠D ,(1)△ABE ≅△CDF ;(2)ABCD ABCD AB//CD,AB =BC =2CD,EAC F BC DE ,EF (1)CDEF (2)DF AC G DF =2,CD =53AD13. 问题情景:如图,我们把对角线互相垂直的四边形叫做“垂美四边形”,按照此定义,我们学过的平行四边形中的菱形、正方形等都是“垂美四边形”,“筝形”也是“垂美四边形”.概念理解:如图,已知等腰梯形是“垂美四边形”,,,求的长.性质探究:如图,已知四边形是“垂美四边形”,试探究其两组对边,与,之间的数量关系,并写出证明过程.问题解决:如图,分别以的直角边和斜边为边向外作正方形与正方形,连接,,、与交于点,已知,,求的中线的长.14. 平行四边形中,,,与的平分线分别交于,,则________.15.如图所示,在▱中,对角线与相交于点,点,在对角线上,且,求证:(1)ABCD AB =6CD =8AD (2)ABCD AB CD BC AD (3)Rt △ABC AC AB ACFG ABDE CE BG GE CE BG O AC =3AB =5△OGE OH ABCD AB =5BC =3∠ADC ∠BCD AB F E EF =ABCD AC BD O M N AC AM =CN BM //DN.参考答案与试题解析2023~2024学年新沪教版八年级下《22.5 等腰梯形》高频题集一、选择题(本题共计 5 小题,每题 3 分,共计15分)1.【答案】此题暂无答案【考点】等腰梯形的性质【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】等腰梯形的性质【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】等腰梯形的性质【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】等腰梯形的性质【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】等腰梯形的性质勾股定理【解析】此题暂无解析【解答】此题暂无解答二、填空题(本题共计 2 小题,每题 3 分,共计6分)6.【答案】此题暂无答案等腰梯形的性质【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】等腰梯形的性质含30度角的直角三角形【解析】此题暂无解析【解答】此题暂无解答三、解答题(本题共计 8 小题,每题 10 分,共计80分)8.【答案】此题暂无答案【考点】平行四边形的性质等腰三角形的判定与性质【解析】此题暂无解析【解答】此题暂无解答9.此题暂无答案【考点】勾股定理等腰直角三角形等腰三角形的判定与性质【解析】此题暂无解析【解答】此题暂无解答10.【答案】此题暂无答案【考点】相似三角形的性质与判定根的判别式等腰梯形的性质【解析】此题暂无解析【解答】此题暂无解答11.【答案】此题暂无答案【考点】平行四边形的判定平行四边形的性质全等三角形的判定全等三角形的性质【解析】此题暂无解析【解答】此题暂无解答12.【答案】此题暂无答案【考点】菱形的判定菱形的性质平行四边形的判定三角形中位线定理勾股定理【解析】此题暂无解析【解答】此题暂无解答13.【答案】此题暂无答案【考点】勾股定理等腰三角形的性质等腰梯形的性质直角三角形斜边上的中线全等三角形的判定全等三角形的性质旋转的性质【解析】此题暂无解析【解答】此题暂无解答14.【答案】此题暂无答案【考点】角平分线的定义平行四边形的性质【解析】此题暂无解析【解答】此题暂无解答15.【答案】此题暂无答案【考点】平行四边形的性质全等三角形的性质与判定平行线的判定【解析】此题暂无解析【解答】此题暂无解答。
八年级数学下1.4等腰梯形的性质与判定课后作业 苏科版

word
1 / 1 初二数学课后作业080610
1.4等腰梯形的性质与判定
命题人:胡士忠 核对人:李芳
班级某某
一、填空题:
1、_______________________________的图形叫做等腰梯形。
2、____________相等的_______________叫做等腰梯形;
3、根据等腰梯形的定义,一个图形要成为等腰梯形,首先它必须是_____,还要具备_____相
等;
4、用一块面积为450c ㎡的等腰梯形彩纸做风筝,为了牢固起见,用竹条做梯形的对角线,对角线恰好互相垂直,那么至少需要竹条_______㎝.
二、解答题:
5、如图,在等腰梯形ABCD 中,E 为CD 的中点,EF ⊥AB 于F,如果AB=6,EF=5,求梯形ABCD
的面积.
6、如图,在直角梯形ABCD 中,A B ∥DC ,∠ABC=900,AB=2DC ,对角线AC ⊥BD ,垂足为
F ,过点F 作EF ∥AB ,交AD 于点E 。
求证:四边形ABFE 是等腰梯形;
等第成绩
F E D C B A F E D C B A。
苏教版四年级下册数学课堂练习课后作业第七单元 三角形、平行四边形和梯形第7课时 认识梯形和等腰梯形

第7课时认识梯形
1.填空。
(1)只有一组对边平行的四边形叫作( )。
(2)从梯形一条底边上的一点到它对边的( )叫作梯形的高。
梯形的高有( )条。
(3)当梯形的上底和下底相等时,就变成了( )形。
(4)若一个等腰梯形的上底长8厘米,下底长6厘米,一条腰长7厘米,则围成这个等腰梯形要( )厘米长的铁丝。
2.判断下面各图形是否是梯形,是的在下面的括号里画“√”,并标出梯形的上底和下底。
( ) ( )
3.一个梯形的下底的长度是上底的4倍,如果将这个梯形的上底延长36厘米,这个梯形就成了一个平行四边形。
梯形的上底和下底原来分别长多少厘米?(先画一画,再解答)
参考答案
1.(1)梯形 (2)垂直线段无数 (3)平行四边 (4)28
2.略
3.上底:36÷(4-1)=12(厘米) 下底:12×4=48(厘米)。
7-6等腰梯形、直角梯形的概念及特点四年级下册数学一课一练苏教版(含答案)

第七单元:三角形、平行四边形和梯形第6课时:等腰梯形、直角梯形的概念及特点班级:姓名: 等级:【基础训练】一、填空题1.________相等的梯形叫做等腰梯形。
2.下图ABCD是一个直角梯形,在这个梯形中,线段(________)和(________)互相垂直,线段(________)和(________)互相平行。
3.2019年中国智博会8月26日在重庆开幕了,实验小学做了一个等腰梯形的宣传牌,它的周长是2米,上底是50厘米,下底是70厘米,这块宣传牌的一条腰是(________)厘米。
4.两个完全一样的梯形一定可以拼成一个(__________)形;两个完全一样的直角梯形可以拼成一个(__________)形或(__________)形,也可以拼成一个(__________)形。
5.如图,已知四边形ABCD是等腰梯形,用量角器量一量,你发现了什么?∠1=(________),∠2=(________),∠3=(________),∠4=(________)。
我发现:等腰梯形同一条底上的两个角的大小(________)。
梯形四个内角和是(________)。
6.等腰梯形上、下底分别长3厘米、5厘米,一条腰长6厘米。
把两个这样的梯形拼成一个平行四边形,两条不相等的边分别长(________)厘米和(________)厘米。
二、选择题7.既有互相平行的边,又有互相垂直的边的图形是()。
A.直角梯形B.三角形C.平行四边形8.下图是一个等腰梯形,∠1=120°,∠2=()。
A.120°B.60°C.30°D.90°9.直角梯形中一定有()直角。
A.1个B.2个C.无数个10.在等腰梯形中,下列结论中正确的有()个。
①两腰相等②两底平行③高只有一条④两底角相等A.1 B.2 C.3 D.4三、判断题11.一个梯形最多有一个直角,但它有无数条高。
(______)12.等腰梯形中不平行的一组对边相等。
等腰梯形练习题

等腰梯形练习题在数学学习中,我们经常会遇到各种几何图形的练习题。
其中,等腰梯形是一种常见的几何图形,它具有特定的性质和计算方法。
本文将为大家提供一些关于等腰梯形的练习题,帮助大家巩固和应用相关的知识。
例题一:已知等腰梯形的上底长为15 cm,下底长为25 cm,高为10 cm,求等腰梯形的面积和周长。
解答:等腰梯形的面积可以通过上底和下底的平均值与高的乘积来计算。
根据题目给出的数据,我们可以得出等腰梯形的面积计算公式:面积 = (上底 + 下底) ×高 ÷ 2。
代入数值,计算出等腰梯形的面积:(15 + 25) × 10 ÷ 2 = 200 平方厘米。
等腰梯形的周长可以通过上底、下底和斜边的长度之和来计算。
由于等腰梯形的两边是等长的,所以斜边可以通过勾股定理计算得出。
根据题目给出的数据,我们可以得出等腰梯形的周长计算公式:周长 = 上底 + 下底 + 斜边1 + 斜边2。
斜边1和斜边2可以通过勾股定理计算得出,即:斜边= √(腰长的平方 + 高的平方)。
代入数值,计算出等腰梯形的周长:周长= 15 + 25 + √(10×10 + 10×10) + √(10×10 + 10×10)= 15 +25 + √200 + √200 ≈ 73.65 厘米。
例题二:已知等腰梯形的面积为90 平方厘米,上底长为12 cm,下底长未知,高为10 cm,求等腰梯形的下底长和周长。
解答:根据例题一的解答,我们知道等腰梯形的面积公式为:面积 = (上底 + 下底)×高 ÷2。
代入已知数据,可得到方程:90 = (12 + 下底)× 10 ÷ 2,进一步计算得到:90 = 6 + 5 下底,解方程可得下底≈ 16.8。
下底长约为16.8 cm。
等腰梯形的周长计算方式同例题一,根据已知数据计算:周长= 12 + 16.8 + √(10×10 + 8.4×8.4)+ √(10×10 + 8.4×8.4)≈ 46.18 厘米。
