二向应力状态分析
应力状态概述二向和三向应力状态的实例二向

2.作应力圆 主应力为 1 , 3 ,并可 确定主平面的法线。
材料力学
第七章
应力和应变分析
3.分析 纯剪切应力状态的两个主应力绝对值相等, 但一为拉应力,另一为压应力。由于铸铁抗拉强度较 低,圆截面铸铁构件扭转时构件将沿倾角为 45º 的螺旋面因拉伸而发生断裂破坏。
材料力学
第七章
2 2
x y
xy
n
材料力学
y a xy
y On D( x , ) a a
a
第七章
n
应力和应变分析
二、应力圆的画法
建立应力坐标系,如下图所 示,(注意选好比例尺) 在坐标系内画出点A( x, xy)和B(y,yx)
x
C O
2a
AB与a 轴的交点C便是圆 A( x , xy) 心。
150°
第七章
应力和应变分析
x y 2 2 1 x y ( ) xy 2 2 2
解法2—解析法:分析——建立坐标系如图
95
60°
y 45MP a yx 25 3MP a xy
25 3
x ?
y O x
60 95MPa 60 25 3MPa
材料力学
第七章
应力和应变分析
应力表示——单元体:
①dx、dy、dz(微小的正六面体) ②单元体某斜截面上的应力就代表了构件内 对应点同方位截面上的应力。
B P
dz
dx
dy
A
C
பைடு நூலகம்
B
D
C
B、C——单向受力,τ =0 A——纯剪切, σ =0
D
D——既有 σ ,又有τ
二向应力状态下的应力分析(应力圆)

x
-s y )2
2
+
t
2 x
当斜截面随方位角 a 变化时, 其上的应力 σα , τ α 在
s - t 直角坐标系内的轨迹是一个圆 ,圆心位于横坐标轴
(
s
轴
)上,离原点的距离为
sx
+sy
2
半径为
此圆习惯上称为应力圆 , 或称为莫尔圆。
s
(
x
2
s
y
)2
+
t
2 x
(sa
-sx
+s
2
y )2
+ ta2
A1 s
α o 确定后, s1 对应的主平面方位即确定。
tg(-2a 0 )
=
B1D1 CB1
=
2t x (s x -s
y)
再根据应力圆判断α0的
合理范围
由此可定出主应力s1 所 o 在平面的位置。由于A1A2 为 应力圆的直径, 则s2 所在的另 一主平面与s1 所在的主平面 垂直 。
t
σ2
A2 B2
σy
t
o
B2
sy
D2
sx
量取 OB2=sy , B2D2= ty ,
得D2 点
(b)
D1
B1 s
连接D1D2两点的直线与 s 轴相交于C 点, 以C为 圆心, CD1或CD2为半径 作圆
σy τy
σx
σx
τx
τx
τy
σy
t
(b)
D1
o
B2
B1
C
s
sy
D2
sx
t
该圆的圆心 C 点到 坐标
第七章应力状态及应变状态分析

第七章 应力状态及应变状态分析第一节 概 述在第一章中将应力定义为内力的集度或单位面积的内力值。
应力又分正应力σ和剪应力τ两种。
前面各章的知识表明,受力杆件中任一点的应力是随截面位置及点的位置的不同而不同,如7-1(a )中a 、b 两点分别在两个截面上,其应力是不同的。
同一截面上的各点,如图7-1(b )中b 、c 两点的应力一般情况下也是不同的。
同一点不同方向的应力也是不同的。
过一点各个方向上的应力情况称为该点的应力状态....,应力状态分析就是要研究杆件中某一点(特别是危险点)各个方向上的应力之间的关系,确定该点处的最大正应力和最大剪应力,为强度计算提供重要依据。
研究应力状态的方法是过杆件中的任一点取出一个微小的六面体——单元..体.。
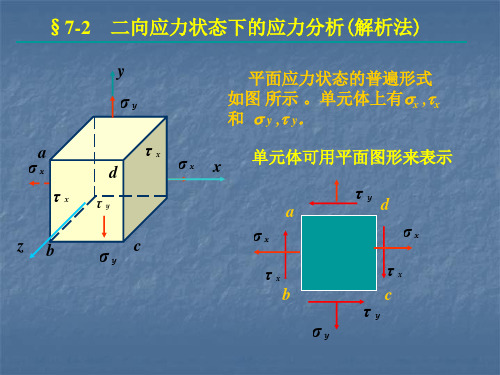
如图7-1(a )中过a 点取出的单元体放大如图7-2所示。
单元体三个方向的边长很小且趋于零,则该单元体代表一点,即a 点,互相平行的平面上的正应力相等,剪应力也相等。
杆件在任意荷载作用下,从中所取出的单元体表面上一般既有正应为又有剪应力,如图7-2所示。
当图7-2所示的单元体各面上的,0,0,0,0,0,0======zy zx yx yz xz xy ττττττ 即六个面上均没有剪应力作用时,这种面叫做特殊平面,并定义为主平面...。
该主(a)(b)图7-1各点的应力情况平面上作用的正应力称为主应力...,用,,,321σσσ表示(,321σσσ≥≥),如图7-3所示。
各面均为主平面的单元体,称为主单元体....。
三个主应力中若有两个等于零一个不等于零,该单元体称为单向应力状态......,如图7-4(a );三个主应力中有一个等于零,两个不等于零,该单元体称为二向应...力状态...,如图7-4(b );三个主应力均不等于零,该单元体称为三向应力状态......,如7-3。
单向应力状态和二向应力状态属平面应力状态,三向应力状态属空间应力状.....态.。
材料力学第18讲 Chapter7-2第七章 应力状态(应力圆)

x
y
2
R cos[180o
(2
20 )]
xy
x
2
y
R cos(2
20 )
O
xy
x
y
2
R(cos 2
cos 20
sin 2
sin 20 )
x
y
2
x
2
y
cos 2
xy
sin
2
D
A ( x , xy )
y R 2 20
E
C
x
B ( y , xy )
13
单元体与应力圆的对应关系
y y
y
10
a
64103 110103 3.206107 1012
219.6MPa
200
b
64103 100103 3.206107 1012
199.6MPa
10
c
64103 0 3.206107 1012
0.0MPa
120
10
c z
b a y
30
(Fs 160kN; M 64kN m)
xy
(3)以C 为圆心,AC为半径画圆
—应力圆或莫尔圆
O
xy
y
y
xy x
Ox
A ( x , xy )
y C
B ( y , xy )
x
10
3、单元体公式与应力圆的关系
以上由单元体公式
应力圆(原变换)
下面寻求由应力圆
单元体公式(逆变换)
只有这样,应力圆才能与公式等价 换句话,单元体与应力圆是否有一一对应关系?
x
x
x
0
y 1
二向应力状态分析—图解法

x
2
y
x
2
y
cos 2
x
sin
2
x
2
y
sin
2
x
cos 2
1、 莫尔圆的概念
(
x
y 2
)2
2
(x
y )2 2
2 x
(
x
y 2
)2
2
(x
y 2
)2
2x
当斜截面随方位角 变化时, 其上的应力 , 在 - 直角坐标系内的轨迹是一个圆 。
圆心的坐标为(the coordinates of MOHR circle’s center)
y
xm
900
t
450
k
D
y
xm
900
t
450
k
D
y
3
τ max
x
τ max
k
450
1
解: 从圆筒表面 k 点处取出单元体, 其各面上的应力分量如图 所示
可求得
y 1 max 80MPa
x 3 max 80MPa
z 0
k点处的线应变 x , y 为
y
x
1 E
(x
y )
1 E
(max
z
x
二、纯剪的本构关系
xy
xy
G
i 0 ( i x,y,z ) yz zx 0
y
xy
z
x
三、复杂状态下的本构关系
y
依叠加原理,得
y
z
z
x
xy
x
x
x
E
y
E
《材料力学 第2版》_顾晓勤第09章第2节 二向应力状态分析
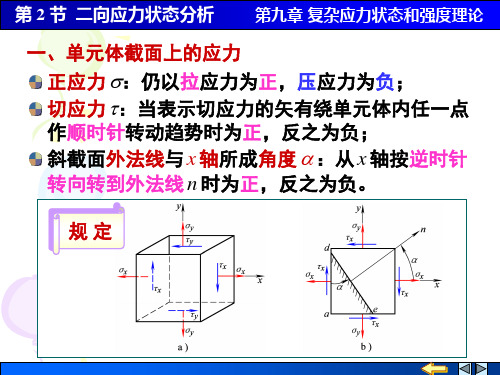
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
最大主应力和最小主应力的计算式
max m in
x
y
2
x
2
y
2
2 x
确定 max 和 min 所在平面的方法
1)若x>y,则所求的两个角度0 和 90º+0 中, 绝对值较小的一个确定max 所在的平面;
2)若x <y,则所求的两个角度0 和 90º+0 中, 绝对值较小的一个确定min 所在的平面;
2
及
2sin cos sin 2 对以上二式进行整理得到:
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
利用上述两式可以求得 de 斜截面上的正应力和切
设 de 斜截面面积为 dA,则 ae 面的面积为 dAsin , ad面的面积为 dAcos 。取 t 和 n 为参考轴,建立棱
柱体 ade 的受力平衡方程如下:
dA ( xdAcos ) sin ( xdAcos ) cos ( ydAsin ) cos ( ydAsin ) sin 0
y
2
2 x
105 MPa
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
0
1 2
arctan(
2 x x
一般二向应力状态下求解主应力方法

一般二向应力状态下求解主应力方法1.引言二向应力状态是指材料在受力情况下同时受到两个不同方向的应力作用。
在工程实践中,很多材料都会出现二向应力状态,因此如何准确求解在这种情况下的主应力是非常重要的。
本文将介绍一般二向应力状态下求解主应力的方法。
2.二向应力状态的概念在材料受力的情况下,如果同时存在两个不同方向的应力作用,就形成了二向应力状态。
一般来说,二向应力状态可以分为各向同性的和各向异性的两种情况。
各向同性是指材料在各个方向上的性能均相同,而各向异性则是指材料在不同方向上的性能存在差异。
在工程实践中,需要根据具体情况来判断材料的二向应力状态,以便正确求解主应力。
3.一般二向应力状态下求解主应力方法一般二向应力状态下求解主应力的方法可以分为数学方法和实验方法两种。
3.1 数学方法数学方法是通过数学推导和计算来求解主应力的方法。
在一般二向应力状态下,可以采用坐标变换的方法将二向应力状态转化为主应力状态。
具体步骤如下:(1)确定材料受力情况并获取二向应力状态的数值;(2)根据材料的各向同性或各向异性特点,选择合适的坐标系,进行坐标变换;(3)利用坐标变换后的应力矩阵,通过数学运算求解出主应力的数值。
3.2 实验方法实验方法是通过实验手段来求解主应力的方法。
在一般二向应力状态下,可以采用应变片法或光栅法来进行主应力的实验测量。
具体步骤如下:(1)利用应变片或光栅在材料表面进行应力测量;(2)根据实验测量结果,计算出主应力的数值。
4.应用举例为了更好地理解一般二向应力状态下求解主应力的方法,我们可以举一个具体的应用例子。
某种材料同时受到水平和垂直方向的应力作用,需要求解主应力。
可以采用数学方法进行坐标变换,将二向应力状态转化为主应力状态,再通过数学计算求解主应力的数值。
5.总结一般二向应力状态下求解主应力是工程实践中的重要课题。
通过数学方法和实验方法的结合,可以准确求解出材料在二向应力状态下的主应力,为工程设计和材料应用提供重要依据。
二向应力
(a)当 (a)当σx>σy时,
− 2τ xy 2α0 = arctg σ −σ y x
此时, 2α = 2α0 +180° 得到 σmin (主应力) 主应力)
σmin
σx +σ y = − 2
σx −σ y 2
2 +τ xy
f
t
t
由
∑n = 0
即
可得
σα dA − (σxdAcosα)cosα + (τ xdAcosα)sin α −
(σ ydAsin α)sin α + (τ ydAsin α) cosα = 0
σα = σ x cos2 α +σ y sin 2 α − 2τ x sin α cosα
1 cos2 α = (1+ cos 2α) 2 1 2 sin α = (1− cos 2α) 2
α1 = ±45°
具体是正负可由力的合成定理直接判断. 具体是正负可由力的合成定理直接判断.
(1)最小主应力及作用平面 由
σx +σy σx −σy σα = cos 2α −τ xy sin2α + 2 2
作三角变换得
σx +σ y σα = + 2
当
σx −σ y 2
二、主应力和主平面 主平面: 主平面 一点处剪应力等于零的平面称为主平面 主应力: 主应力 主平面上的正应力称为主应力 说明: 一点处必定存在这样的一个单元体, 说明 一点处必定存在这样的一个单元体 三个相互垂直 的面均为主平面, 三个互相垂直的主应力分别记为 σ1 ,σ2 , σ3 的面均为主平面 且规定按代数值大小的顺序来排列 即 且规定按代数值大小的顺序来排列, 值大小的顺序来排列
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、应力圆方程
( x - a) + y R
2 2
2
圆心坐标: 半径:
任一点坐标:
x
+ 2
y
,0
2 + x
x - y 2
2
,
上述方程所表示的圆——应力圆或莫尔圆
二.应力圆的画法:
1.设 , 轴,选取应力比例尺。 2.以 x , x 为坐标,得D点,
y
, y 得E点。
3.连DE交
轴于C点,C点即为应力圆的圆心。
4.以CD或CE为半径画圆。即得应力圆。 5.以CD为基准线,沿反时针方向另取角度 2 ,得一射线,与 圆交于G点 , 6.按比例尺量出 , 值,即为单元体 斜面上的正应力和剪 应力 ,
x
xy
q
x'y'
x´
x'
dA
yx
F
x
0
F
y
0
y
平面应力状态的解析法
F
x
x
0
y´
x ' dA - (dA cos q ) cosq + xy (dA cos q ) sin q + yx (dA sin q ) cos q - (dA sin q ) sin q 0
3
4点
1 100MPa
2 0
3 0
2 0
3 -8.6MPa
自受力构件内取一单元体,其上承受应力如图示, 试求此点的主应力及主平面. 3
.
a
x
a
y
ad面,db面是该点的主 平面.
x
d
c
60 0
60 0
b
b
x -
1
F
x
0
3
y
yx
y
平面应力状态的解析法
化简得到以下两个方程:
x' x cos 2 q + y sin 2 q - xy sin q cos q - yx sin q cos q
x ' y ' x sin q cosq - y sin q cos q + xy cos 2 q - yx sin 2 q
- sin 2
max
x - y sin 2 + x cos 2 2
45 max -
0
cos 2
铸铁圆试样扭转试验时,正是沿着 最大拉应力作用面(即45o螺旋面) 断开的。因此,可以认为这种脆性破 坏是由最大拉应力引起的。
45
x y
0
x + y x - y y 2 x sin 2 dA - x dA cos cos + x dA+ sin +cosdA sin - cos - y dA sin sin cos
利用三角恒等式,整理得
x'
x + y
2 +
x - y
2
cos 2q - xy sin 2q
x' y'
x - y
2
sin 2q + xy cos 2q
平面应力状态的解析法
应力变换的实质——同一点的应力
状态可以有各种各样的描述方式:
y
y
yx
y'
xy
y'x'
x' y'
x'
y''
x
x
y'
x'
yp
x''
xp
x-y坐标系
x´-y´坐标系
xp-yp坐标系
a
a
x x
y
b
n
F
n
0
F 0
c y
x
x
y
2
1 + cos 2 cos 2 1 - cos 2 2 sin 2
2
y
c
三.验证 , 的正确性
由应力圆可得:
y yx x xy
y
G1' ,E
D(x, xy) 2 2 CL A
n
x x xy
B1 O 2
B
A1 1
y
yx
D’ (y, yx)
G2 "
EL CE sin2 + 2
y
x
D
c
o
A
(y ,y)
d
a (x ,x)
点面对应——应力圆上某一点的坐标值对应着单元 体某一方向面上的正应力和切应力; 转向对应——半径旋转方向与斜截面法线旋转方向 一致; 二倍角对应——半径转过的角度是斜截面旋转角度 的两倍。
点面对应
y
A a
y
x
x
c
转向对应、二倍角对应
3
1
2
3
4
h
2
3
Fs
4
1点
2、计算各点主应力
My 10 103 50 1 100MPa 4 Iz 500 10
2点 (处于纯剪状态)
max
bh 3 500cm 4 Iz 12
1 2 0 3 -100MPa
3点 (一般平面状态)
3 Fs 3 120 103 30MPa 2 A 2 60 100
0
+ -45 max
0
45 0
0
例题4: 图示一矩形截面简支梁,在跨中有集中力作用。已
知:P=100KN,L=2m,b=200mm,h=600mm,=400。求:离左支座 L/4处截面上C点在400斜截面上的应力。
P
h/4
b
h 解: P L
MC 2 4
25KN m
低碳钢拉伸时,其上任意一点都是单向应力状态。
x
x + y x - y + cos 2 - x sin 2 2 2 x x y + cos 2
x - y sin 2 + x cos 2 2
x
2 sin 2
2
2
45
y
y
min
max
x
x
0
max
min
G1' ,E
2 20 CF A D(x, xy) A1 1
B1 O 2
B
D’ (y, yx) G " 2 从应力圆中还可看出:应力圆上对应于G1G2两点,剪应力最大, 由此可得到,最大、最小剪应力分别为:
1 30MPa
* z
2 0
3 -30MPa
My 10 103 25 50MPa 4 3 500 10 Iz 1 58.6MPa
Fs S 120 10 60 25 37.5 22.5MPa I zb 500 104 60
§8.2.1 二向应力状态分析——解析法
平面应力状态的解析法
• 确定任意方向面上的应力 • 应用平衡的方法
正负号规则 平衡原理的应用— 微元局部的平衡方程 应力变换及其实质
平面应力状态的解析法
正 负 号 规 则
x
正 应 力
x
x
拉为正
x
压为负
平面应力状态的解析法
正负号规则
x'y'
CEsin 2 cos 2 + cos 2 sin 2 CA sin 2 + DA cos 2
yx y y n
CD cos 2 sin 2 + CD sin 2 cos 2
G1' ,E
D(x, xy)
1.04 MPa(压应力)
0.469 MPa
C
C
C
§8-2-3 平面应力状态下的最大应力,主应力
y y
y
G1' ,E
D(x,xy) 2 20 CF A
B1 O 2
B
A1 1
D’ (y, yx)
G2 "
- 2 x DF DA tg - 2 0 tg 2 0 CF x - y CA
扭 转
弯 曲
已知矩形截面梁,某截面上的剪力Q=120kN及弯矩 M=10kNm.绘出表示1、2、3、4点应力状态的单元体,并 求出各点的主应力。b=60mm,h=100mm.
b
M
1
1、画各点应力状态图 13
z
25mm
x + y
2
1 2
x
2 - y + 4 x 2
1
y
+
x - y
2
cos 2 - x sin 2
y yx y n
G1' ,G
D(x, xy) 2 2 CL A
x
xy
x x
xy
B1 O 2
B
A1 1
y
yx
D’ (y, yx)
G2 "
