北京市中考真题
北京市2023年中考语文现代文阅读真题及答案

北京市2023年中考语文现代文阅读真题(2)根据材料二的文字内容和表1的信息,在文中横线处补写一句话。
下列选项恰当的一项是A.医疗服务领域文明指数位列第一B.公共交通领域文明指数排名第三C.两个一级指标的文明指数将近90D.九大公共生活领域文明指数均有提升(3)从上述三则材料可以看出,提高首都公共文明建设水平需要从①、②、③三个方面系统设计,整体推进。
【答案】【分析】这是关于首都精神文明建设的非连续性文本阅读题。
第一题考查内容理解与评析。
第二题考查衔接与排序。
第三题考查内容理解与概括。
【解答】(1)ABD.正确;C.有误,根据“在‘公共交通’的下一级指标中,‘文明交通践行’由上年的72.61提升至90.25。
在‘文明交通践行’各指标中,‘驾车时会在斑马线前礼让行人’数值最高,为92.43,表明驾驶员已具有良好的礼让意识”可知,“驾驶员已具有良好的礼让意识”是“文明交通践行”各指标中的一项,因此,该项说法有误。
故选:C。
(2)根据下文“据报道,在‘公共交通’的下一级指标中,‘文明交通践行’由上年的72.61提升至90.25。
在‘文明交通践行’各指标中,‘驾车时会在斑马线前礼让行人’数值最高,为92.43,表明驾驶员已具有良好的礼让意识”可知,该段主要内容是说明公共交通领域文明指数排名提升的情况。
故选:B。
(3)根据材料三“正式发布《北京市文明行为促进工作发展报告》白皮书”可知,应从制度建设方面进行系统设计;根据材料一“从2005年开始,首都精神文明建设委员会办公室每年要对北京市民的公共行为文明程度进行问卷调查和现场观测。
在获取大量第一手资料的基础上,经过综合分析和论证,确定北京市民公共行为文明指数”可知,应采取措施落实制度;根据“提升北京市民公共行为文明指数,要求市民不仅在某一个方面提升文明素质,而且在所有的公共生活领域全面提升文明素质;不仅要求某一部分群体提升文明素质,而且要求全体市民共同提升公共文明素质”可知,还需从全民共建方面进行系统设计。
精品解析:2023年北京市中考地理真题(解析版)

A.地球运动B.地球形状C.海陆变迁D.海陆分布
【答案】1. B 2. A
【解析】
【1题详解】
图中①为清明节,踏青郊游,亲近自然。②为端午节,吃粽子,赛龙舟。③为中秋节,赏月亮,吃月饼。④为春节,辞旧迎新,贴春联,守岁,拜年。综上所述,B正确,ACD错误,故选B。
长江三角洲地区对长江流域乃至全国具有辐射带动作用。图为长江三角洲地区简图。读图,完成下面小题。
11.长江三角洲地区( )
A.地处长江下游地区,濒临南海B.依托长江干流,联系京津冀地区
C.地处江海交汇之地,港口众多D.依托京杭运河,联系粤港澳地区
12.该地区的沪宁杭工业基地( )
A.矿产资源丰富,以重工业为主B.以首都为核心,科研力量雄厚
【4题详解】
读沿MN绘制的地形剖面示意图,M处为陆地,海拔较高,N处为海洋,海拔低,排除CD;MN穿越山峰,海拔高于500米,排除B,故选A。
【点睛】等高线闭合,且数值从中心向四周逐渐降低的为山峰;等高线向海拔较低处凸出的为山脊,也叫分水岭;等高线向海拔较高处凸出的为山谷,发育河流;等高线重合的为陡崖,适合攀岩运动;位于两个山顶之间,地势较为低洼,是鞍部。等高线密集,坡度陡,攀爬难度大;等高线稀疏,坡度平缓,攀爬难度小。
8.长城主要分布在( )
A.北方地区和南方地区B.南方地区和青藏地区
C.西北地区和北方地区D.西北地区和青藏地区
9.在长城上可能看到的自然景观有( )
①沙漠②草原③大海④椰林
A.①②③B.①②④C.①③④D.②③④
10.我国正在规划建设长城国家文化公园,这有助于( )
①恢复长城的军事防御功能②维护长城沿线地区生态环境
2023年北京市中考地理真题(原卷版和解析版)

2023年北京市初中学业水平考试地理试卷第一部分本部分共25题,每题1分,共25分。
在每题列出的四个选项中,选出最符合题目要求的一项。
传统节日是传承中华优秀传统文化的重要载体。
图为我国某地四大传统节日景观及习俗简笔画。
读图,完成下面小题。
1.图中景观及习俗,与传统节日对应正确的是()A.①——春节B.——②端午节C.——③清明节D.——④中秋节2.图中自然景观差异的形成,主要是由于()A.地球运动B.地球形状C.海陆变迁D.海陆分布等高线地形图是认识地表高低起伏的地理工具。
图为某地等高线地形图。
读图,完成下面小题。
3.图中()A.①地海拔为300米B.②地地处山谷C.在③地可东眺大海D.④地坡度最大4.沿MN绘制的地形剖面示意图是()A. B.C. D.分析降水量分布状况是认识区域差异的重要内容。
图为中国年降水量分布和国地降水量柱状图。
读图,完成下面小题。
5.我国年降水量()A.随纬度升高而逐渐增加B.沿北纬40°线自东向西递增C.沿东经120°线自北向南递减D.自东南沿海向西北内陆递减6.四地中()A.甲地降水季节变化最大B.乙地雨季最长C.丙地7月降水量最大D.丁地年降水量最大7.乙地为()A.乌鲁木齐B.北京C.武汉D.广州长城是我国现存规模最大的文化遗产。
图为我国长城分布示意图。
读图,完成下面小题。
8.长城主要分布在()A.北方地区和南方地区B.南方地区和青藏地区C.西北地区和北方地区D.西北地区和青藏地区9.在长城上可能看到的自然景观有()①沙漠②草原③大海④椰林A.①②③B.①②④C.①③④D.②③④10.我国正在规划建设长城国家文化公园,这有助于()①恢复长城的军事防御功能②维护长城沿线地区生态环境③保护长城沿线的文化遗址④了解我国多民族交融的历史A.①②③B.①②④C.①③④D.②③④长江三角洲地区对长江流域乃至全国具有辐射带动作用。
图为长江三角洲地区简图。
读图,完成下面小题。
2023年北京市中考数学真题(含答案解析)
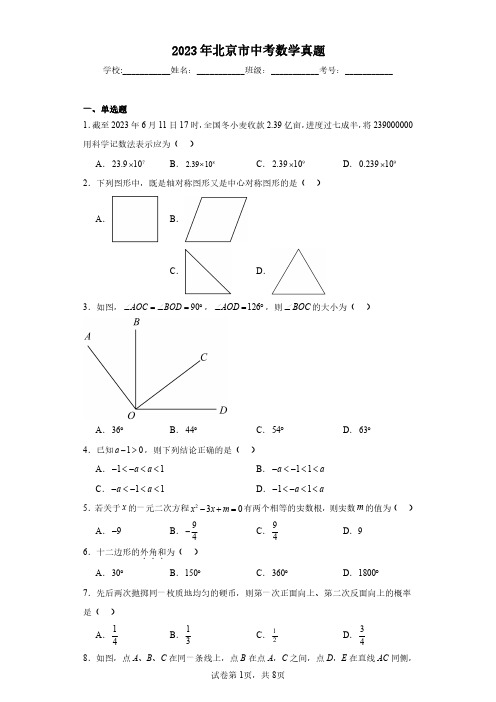
2023年北京市中考数学真题学校:___________姓名:___________班级:___________考号:___________.....如图,90AOC ∠=∠=︒,126AOD ∠=,则BOC ∠的大小为(A .36︒B .44︒54︒4.已知10a ->,则下列结论正确的是(A .11a a -<-<<11a a -<-<<C .11a a -<-<<11a a-<-<<5.若关于x 的一元二次方程23x x m -+=有两个相等的实数根,A .9-B .94-946.十二边形的外角和...为()A .30︒B .150︒360︒7.先后两次抛掷同一枚质地均匀的硬币,则第一次正面向上、第二次反面向上的概率是()A .14B .138.如图,点A 、B 、C 在同一条线上,点上述结论中,所有正确结论的序号是(A .①②B .①③二、填空题9.若代数式52x -有意义,则实数10.分解因式:23x y y -=11.方程31512x x=+的解为12.在平面直角坐标系xOy 中,若函数则m 的值为.13.某厂生产了1000只灯泡.为了解这灯泡进行检测,获得了它们的使用寿命(单位:小时)使用寿命1000x <1000x ≤<灯泡只数510根据以上数据,估计这1000只灯泡中使用寿命不小于只.14.如图,直线AD ,BC 交于点O 的值为.15.如图,OA 是O 的半径,BC 是 交OC 的延长线于点E .若45AOC ∠=︒16.学校组织学生参加木艺艺术品加工劳动实践活动.A ,B ,C ,D ,E ,F ,G 七道工序,加工要求如下:①工序C ,D 须在工序A 完成后进行,工序在工序C ,D 都完成后进行;②一道工序只能由一名学生完成,此工序完成后该学生才能进行其他工序;③各道工序所需时间如下表所示:工序A B C D E 所需时间/分钟99797在不考虑其他因素的前提下,若由一名学生单独完成此木艺艺术品的加工,则需要分钟;若由两名学生合作完成此木艺艺术品的加工,则最少需要三、解答题17.计算:114sin602123-⎛⎫︒++-- ⎪⎝⎭18.解不等式组:23535x x x x+⎧>⎪⎨⎪-<+⎩.19.已知210x y +-=,求代数式x(1)求证:四边形AECF 是矩形;(2)AE BE =,2AB =,1tan 2ACB ∠=21.对联是中华传统文化的瑰宝,对联装裱后,如图所示,上、下空白处分别称为天头和地头,左、右空白处统称为边.一般情况下,天头长与地头长的比是的宽相等,均为天头长与地头长的和的宽为27cm .若要求装裱后的长是装裱后的宽的自《启功法书》)22.在平面直角坐标系xOy 中,函数y kx =+与过点()0,4且平行于x 轴的线交于点C .(1)求该函数的解析式及点C 的坐标;(2)当3x <时,对于x 的每一个值,函数23y =小于4,直接写出n 的值.23.某校舞蹈队共16名学生,测量并获取了所有学生的身高(单位:如下:a .16名学生的身高:(1)求证DB 平分ADC ∠,并求BAD ∠(2)过点C 作CF AD ∥交AB 的延长线于点25.某小组研究了清洗某种含污物品的节约用水策略.部分内容如下.每次清洗1个单位质量的该种含污物品,清洗前的清洁度均为度为0.990方案一:采用一次清洗的方式.结果:当用水量为19个单位质量时,清洗后测得的清洁度为结果:结合实验数据,利用所画的函数图象可以推断,当第一次用水量约为位质量(精确到个位)时,总用水量最小.根据以上实验数据和结果,解决下列问题:(1)当采用两次清洗的方式并使总用水量最小时,与采用一次清洗的方式相比、可节水约______个单位质量(结果保留小数点后一位)(2)当采用两次清洗的方式时,若第一次用水量为围.参考答案:【详解】如图,所有结果有4种,满足要求的结果有1种,故概率为【点睛】本题考查概率的计算,运用树状图或列表工具是解题的关键.【分析】如图,过D 作DF AE ⊥于F ,则四边形,可得a b c +<,进而可判断①的正误;由a =,AE BC b ==,ABE CDB ∠=∠,∴DF AC a b ==+,∵DF DE <,∴a b c +<,①正确,故符合要求;∵EAB BCD ≌△△,∴BE BD =,CD AB a ==,AE =∵90CBD CDB ∠+∠=︒,∴90∠+∠=︒CBD ABE ,EBD ∠=∴BDE △是等腰直角三角形,由勾股定理得,22BE AB AE =+∵AB AE BE +>,【点睛】本题考查了一次函数的图象和性质,特征,利用数形结合的思想是解题的关键.23.(1)166m =,165n =;(2)甲组(3)170,172【分析】(1)根据中位数和众数的定义求解即可;(2)计算每一组的方差,根据方差越小数据越稳定进行判断即可;(3)根据要求,身高的平均数尽可能大且方差小于【详解】(1)解:将这组数据按照从小到大的顺序排列为:165,166,166,167,168,168,170出现次数最多的数是165,出现了3次,即众数由图象可得,当第一次用水量约为4个单位质量(精确到个位)时,总用水量最小;(1)当采用两次清洗的方式并使总用水量最小时,用水量为19-7.7=11.3,即可节水约11.3个单位质量;(2)由图可得,当第一次用水量为6个单位质量,总用水量超过的清洁度能达到0.990,第一次用水量为6个单位质量,总用水量为7.5故答案为:<.【点睛】本题考查了函数图象,根据数据描绘函数图象、26.(1)32t =(2)12t ≤【分析】(1)根据二次函数的性质求得对称轴即可求解;(2)根据题意可得()11,x y 离对称轴更近,1x 右侧,根据对称性求得1213222x x +<<,进而根据【详解】(1)解:∵对于11x =,22x =有1y =∴抛物线的对称轴为直线12322x x x +==,∵抛物线的对称轴为x t =.【点睛】本题考查了等腰三角形的判定和性质,旋转的性质,三角形外角的性质,三角形中位线定理以及全等三角形的判定和性质等知识,题的关键.28.(1)1C ,2C ;2OC =(2)2313t ≤≤或2633t ≤≤.a、若12C B与O相切,AC经过点O,①当S 位于点()0,3M 时,MP 为O 的切线,作PJ OM ⊥∵()0,3M ,O 的半径为1,且MP 为O 的切线,∴OP MP ⊥,。
北京市2024年中考英语真题(含答案)

北京市2024年中考英语真题姓名:__________班级:__________考号:__________题号一二三四五总分评分一、单项填空,从下面各题所给的A、B、C、D四个选项中,选择可以填入空白处的最佳选项。
(每题0.5分,共6分)1.Animals are our good friends.We should learn to protect____in our daily lives.A.her B.them C.him D.it2.I helped my parents clean the house every day____the last summer holiday.A.after B.at C.during D.on3.—Excuse me.How____l get to Ditan Park?-—Go along this road,and you can't miss it.A.can B.must C.may D.need4.Jack enjoys playing basketball,which makes him____than before.A.active B.more activeC.most active D.the most active5.—____do you go to the English corner to practise spoken English?—I go to the English corner three times a week.A.How much B.How long C.How often D.How soon 6.Swimming is good for health,____it is dangerous to swim alone in the river.A.or B.and C.but D.so7.一John,what's your older sister doing?—She____Beijing Opera in the club.A.learns B.learned C.is learning D.was learning8.Many tourists in Hainan____the launch of Tianzhou-7on January17,2024.A.watch B.watched C.are watching D.will watch9.If you join us for the hiking trip next weekend,you____beautiful views and get unforgettable memories. A.enjoy B.enjoyed C.have enjoyed D.will enjoy10.Our teacher____math in this school since2021.A.teaches B.taught C.has taught D.will teach11.Too much water____every day in our lives.We should take action to save water.A.wastes B.wasted C.is wasted D.was wasted12.—Lucy,could you tell me____with your family during the winter holiday this year?—Sure.We travelled to the Great Wall.A.where you will travel B.where you travelledC.where will you travel D.where did you travel二、完形填空(每题1分,共8分)阅读下面的短文,掌握其大意,然后从短文后各题所给的A、B、C、D四个选项中,选择最佳选项。
2023年北京市中考数学真题答案

参考答案第一部分 选择题一、选择题(共16分,每题2分)第1—8题均有四个选项,符合题意的选项只有一个.1. 【答案】B【分析】用科学记数法表示绝对值较大的数时,一般形式为10n a ⨯,其中110a ≤<,n 为整数,且n 比原来的整数位数少1,据此判断即可.【详解】解:8239000000 2.3910=⨯,故选:B .【点睛】本题考查了科学记数法的表示方法,用科学记数法表示绝对值较大的数时,一般形式为10n a ⨯,其中110a ≤<,n 为整数,且n 比原来的整数位数少1,解题的关键是要正确确定a 和n 的值. 2. 【答案】A【分析】根据轴对称图形,中心对称图形的定义进行判断即可.【详解】解:A 既是轴对称图形又是中心对称图形,故符合要求;B 不是轴对称图形,是中心对称图形,故不符合要求;C 是轴对称图形,不是中心对称图形,故不符合要求;D 是轴对称图形,不是中心对称图形,故不符合要求;故选:A .【点睛】本题考查了轴对称图形,中心对称图形,解题的关键在于熟练掌握:在平面内,把一个图形绕着某个点旋转180︒,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形叫做轴对称图形.3. 【答案】C【分析】由90AOC BOD ∠=∠=︒,126AOD ∠︒=,可求出COD ∠的度数,再根据角与角之间的关系求解.【详解】∵=90AOC ∠︒,126AOD ∠︒=,∴36COD AOD AOC ∠=∠−∠=︒,∵90BOD ∠=︒,∴903654BOC BOD COD ∠=∠−∠=︒−︒=︒.故选:C .【点睛】本题考查的知识点是角的计算,注意此题的解题技巧:两个直角相加和AOD ∠相比,多加了BOC ∠.4. 【答案】B【分析】由10a −>可得1a >,则0a >,根据不等式的性质求解即可.【详解】解:10a −>得1a >,则0a >,∴1a −<−,∴11a a −<−<<,故选:B .【点睛】本题考查了不等式的性质,注意:当不等式两边同时乘以一个负数,则不等式的符号需要改变. 5. 【答案】C【分析】根据一元二次方程有两个相等的实数根,可得Δ0=,进而即可求解.【详解】解:∵关于x 的一元二次方程230x x m −+=有两个相等的实数根,∴24940b ac m ∆=−=−=. 解得:94m =. 故选:C .【点睛】本题考查了一元二次方程20ax bx c ++= (0a a b c ≠,,,为常数)的根的判别式24b ac ∆=−,理解根的判别式对应的根的三种情况是解题的关键.当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程没有实数根.6. 【答案】C【分析】根据多边形的外角和为360°进行解答即可.【详解】解:∵多边形的外角和为360°∴十二边形的外角和是360°.故选:C .【点睛】本题考查多边形的内角和与外角和的求法,掌握多边形的外角和为360°是解题的关键.7. 【答案】A【分析】整个实验分两步完成,每步有两个等可能结果,用列表法或树状图工具辅助处理.【详解】如图,所有结果有4种,满足要求的结果有1种,故概率为14. 故选:A 【点睛】本题考查概率的计算,运用树状图或列表工具是解题的关键.8. 【答案】D【分析】如图,过D 作DF AE ⊥于F ,则四边形ACDF 是矩形,则DF AC a b ==+,由DF DE <,可得a b c +<,进而可判断①的正误;由EAB BCD ≌△△,可得BE BD =,CD AB a ==,AE BC b ==,ABE CDB ∠=∠,则90EBD ∠=︒,BDE △是等腰直角三角形,由勾股定理得,BE ==,由AB AE BE +>,可得a b +>,进而可判断②的正误;由勾股定理得222DE BD BE =+,即()2222c a b=+,则)c a b =<+,进而可判断③的正误. 【详解】解:如图,过D 作DF AE ⊥于F ,则四边形ACDF 是矩形,∴DF AC a b ==+,∵DF DE <,∴a b c +<,①正确,故符合要求;∵EAB BCD ≌△△,∴BE BD =,CD AB a ==,AE BC b ==,ABE CDB ∠=∠,∵90CBD CDB ∠+∠=︒,∴90∠+∠=︒CBD ABE ,90EBD ∠=︒,∴BDE △是等腰直角三角形,由勾股定理得,BE ==, ∵AB AE BE +>,∴a b +>,②正确,故符合要求;由勾股定理得222DE BD BE =+,即()2222c a b=+,∴)c a b =<+,③正确,故符合要求;故选:D .【点睛】本题考查了矩形的判定与性质,全等三角形的性质,勾股定理,等腰三角形的判定,不等式的性质,三角形的三边关系等知识.解题的关键在于对知识的熟练掌握与灵活运用.第二部分 非选择题二、填空题(共16分,每题2分)9. 【答案】2x ≠【分析】根据分式有意义的条件列不等式求解即可. 【详解】解:若代数式52x −有意义,则20x −≠, 解得:2x ≠,故答案为:2x ≠.【点睛】本题考查了分式有意义的条件,熟知分式有意义,分母不为零是解题的关键.10. 【答案】()()y x y x y +−【详解】试题分析:原式提公因式得:y (x 2-y 2)=()()y x y x y +−考点:分解因式点评:本题难度中等,主要考查学生对多项式提公因式分解因式等知识点的掌握.需要运用平方差公式. 11. 【答案】1x =【分析】方程两边同时乘以()251x x +化为整式方程,解整式方程即可,最后要检验.【详解】解:方程两边同时乘以()251x x +,得651x x =+,解得:1x =,经检验,1x =是原方程的解,故答案为:1x =.【点睛】本题考查了解分式方程,熟练掌握解分式方程的步骤是解题的关键.12. 【答案】3【分析】先把点A 坐标代入求出反比例函数解析式,再把点B 代入即可求出m 的值. 【详解】解:∵函数()0k y k x=≠的图象经过点()3,2A −和(),2B m − ∴把点()3,2A −代入得326k =−⨯=−, ∴反比例函数解析式为6y x−=, 把点(),2B m −代入得:62m −−=, 解得:3m =,故答案为:3.【点睛】本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征,熟知反比例函数图象上的点的坐标一定满足函数解析式是解题的关键.13. 【答案】460【分析】用1000乘以抽查的灯泡中使用寿命不小于2200小时的灯泡所占的比例即可.【详解】解:估计这1000只灯泡中使用寿命不小于2200小时的灯泡的数量为176100046050+⨯=(只),故答案为:460.【点睛】本题考查了用样本估计总体,用样本估计总体时,样本容量越大,样本对总体的估计也就越精确.14. 【答案】32【分析】由平行线分线段成比例可得,21BO AO OE OF ==,12OE OF EC FD ==,得出2BO OE =,2EC OE =,从而2322BE OE OE EC OE +==. 【详解】AB EF CD , 2AO =,1OF =, 21BO AO OE OF ∴==, 2BO OE ∴=,12OE OF EC FD ==, 2EC OE ∴=,2322BE OE OE EC OE +∴==; 故答案为:32. 【点睛】本题考查了平行线分线段成比例的知识点,根据平行线分线段成比例找出线段之间的关系是解决本题的关键.15.【分析】根据OA BC ⊥,得出90ODC ∠=︒,112DC BC ==,根据等腰直角三角形的性质得出OC ==,即OA OC ==,根据90OAE ∠=︒,45AOC ∠=︒,得出AOE △为等腰直角三角形,即可得出AE OA ==【详解】解:∵OA BC ⊥,∴90ODC ∠=︒,112DC BC ==. ∵45AOC ∠=︒,∴ODC 为等腰直角三角形,∴OC ==∴OA OC == ∵AE 是O 的切线,∴90OAE ∠=︒,∵45AOC ∠=︒,∴AOE △为等腰直角三角形,∴AE OA ==.【点睛】本题主要考查了垂径定理,等腰直角三角形的判定和性质,切线的性质,解题的关键是熟练掌握垂径定理,得出112DC BC ==. 16. 【答案】 ①. 53 ②. 28【分析】将所有工序需要的时间相加即可得出由一名学生单独完成需要的时间;假设这两名学生为甲、乙,根据加工要求可知甲学生做工序A ,乙学生同时做工序B ;然后甲学生做工序D ,乙学生同时做工序C ,乙学生工序C 完成后接着做工序G ;最后甲学生做工序E ,乙学生同时做工序F ,然后可得答案.【详解】解:由题意得:9979710253++++++=(分钟),即由一名学生单独完成此木艺艺术品的加工,需要53分钟;假设这两名学生为甲、乙,∵工序C ,D 须在工序A 完成后进行,工序E 须在工序B ,D 都完成后进行,且工序A ,B 都需要9分钟完成,∴甲学生做工序A ,乙学生同时做工序B ,需要9分钟,然后甲学生做工序D ,乙学生同时做工序C ,乙学生工序C 完成后接着做工序G ,需要9分钟, 最后甲学生做工序E ,乙学生同时做工序F ,需要10分钟,∴若由两名学生合作完成此木艺艺术品的加工,最少需要991028++=(分钟),故答案为:53,28;【点睛】本题考查了逻辑推理与时间统筹,根据加工要求得出加工顺序是解题的关键.三、解答题(共68分,第17—19题,每题5分,第20—21题,每题6分,第22—23题,每题5分,第24题6分,第25题5分,第26题6分;第27—28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 【答案】5【分析】代入特殊角三角函数值,利用负整数指数幂,绝对值和二次根式的性质化简,然后计算即可.【详解】解:原式432=+−32=++−5=.【点睛】本题考查了实数的混合运算,牢记特殊角三角函数值,熟练掌握负整数指数幂,绝对值和二次根式的性质是解题的关键.18. 【答案】12x <<【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集. 【详解】23535x x x x +⎧>⎪⎨⎪−<+⎩①②解不等式①得:1x >解不等式②得:2x <∴不等式的解集为:12x <<【点睛】本题考查了解一元一次不等式组,正确掌握一元一次不等式解集确定方法是解题的关键. 19. 【答案】2【分析】先将分式进行化简,再将210x y +−=变形整体代入化简好的分式计算即可.【详解】解:原式()()222222x y x yx y =+++=, 由210x y +−=可得21x y +=,将21x y +=代入原式可得,原式221==. 【点睛】本题考查了分式的化简求值,注意整体代入思想的应用.20. 【答案】(1)见解析 (2)【分析】(1)利用平行四边形的性质求出AF EC =,证明四边形AECF 是平行四边形,然后根据对角线相等的平行四边形是矩形得出结论;(2)证明ABE 是等腰直角三角形,可得AE BE ==,然后再解直角三角形求出EC 即可. 【小问1详解】证明:∵四边形ABCD 是平行四边形,∴AD BC =,AD BC ∥,∵BE DF =,∴AF EC =,∴四边形AECF 是平行四边形,∵AC EF =,∴平行四边形AECF 是矩形;【小问2详解】解:由(1)知四边形AECF 是矩形,∴90AEC AEB ∠=∠=︒,∵AE BE =,2AB =,∴ABE 是等腰直角三角形,∴2AE BE AB === 又∵1tan 2AE ACB EC ∠==,∴12EC =,∴EC =∴BC BE EC =+=+=.【点睛】本题考查了平行四边形的判定和性质,矩形的判定和性质以及解直角三角形,熟练掌握相关判定定理和性质定理是解题的关键.21.【答案】边的宽为4cm ,天头长为24cm【分析】设天头长为cm x ,则地头长为2cm 3x ,边的宽为121cm cm 1036x x x ⎛⎫+= ⎪⎝⎭,再分别表示础装裱后的长和宽,根据装裱后的长是装裱后的宽的4倍列方程求解即可.【详解】解:设天头长为cm x ,由题意天头长与地头长的比是6:4,可知地头长为2cm 3x , 边的宽为121cm cm 1036x x x ⎛⎫+= ⎪⎝⎭, 装裱后的长为cm cm 2510010033x x x ⎛⎫⎛⎫+++ ⎪⎝⎭⎝⎭=⎪, 装裱后的宽为cm cm 1112727663x x x =⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭, 由题意可得:5110027433x x ⎛⎫+=+⨯ ⎪⎝⎭ 解得24x =, ∴146x =, 答:边的宽为4cm ,天头长为24cm .【点睛】本题考查了一元一次方程的应用,题中的数量关系较为复杂,需要合理设未知数,找准数量关系.22. 【答案】(1)1y x =+,()3,4C ;(2)2n =.【分析】(1)利用待定系数法可求出函数解析式,由题意知点C 的纵坐标为4,代入函数解析式求出点C 的横坐标即可;(2)根据函数图象得出当23y x n =+过点()3,4时满足题意,代入()3,4求出n 的值即可. 【小问1详解】 解:把点()0,1A ,()1,2B 代入()0y kx b k =+≠得:12b k b =⎧⎨+=⎩,解得:11k b =⎧⎨=⎩, ∴该函数的解析式为1y x =+,由题意知点C 的纵坐标为4,当14y x =+=时,解得:3x =,∴()3,4C ;【小问2详解】解:由(1)知:当3x =时,14y x =+=,因为当3x <时,函数23y x n =+的值大于函数1y x =+的值且小于4, 所以如图所示,当23y x n =+过点()3,4时满足题意, 代入()3,4得:2433n =⨯+, 解得:2n =.【点睛】本题考查了一次函数的图象和性质,待定系数法的应用,一次函数图象上点的坐标特征,利用数形结合的思想是解题的关键.23. 【答案】(1)166m =,165n =;(2)甲组 (3)170, 172【分析】(1)根据中位数和众数的定义求解即可;(2)计算每一组的方差,根据方差越小数据越稳定进行判断即可;(3)根据要求,身高的平均数尽可能大且方差小于329,结合其余学生的身高即可做出选择. 【小问1详解】解:将这组数据按照从小到大的顺序排列为:161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,175,出现次数最多的数是165,出现了3次,即众数165n =,16个数据中的第8和第9个数据分别是166,166, ∴中位数1661661662m +==, ∴166m =,165n =;【小问2详解】 解:甲组身高的平均数为()1162165165166166164.85++++=, 甲组身高的方差为()()()()()222221162164.8165164.8165164.8166164.8166164.8 2.165⎡⎤−+−+−+−+−=⎣⎦ 乙组身高的平均数为()1161162164165175165.45++++=, 乙组身高的方差为()()()()()222221161165.4162165.4164165.4165165.4175165.425.045⎡⎤−+−+−+−+−=⎣⎦, ∵25.04 2.16>∴舞台呈现效果更好的是甲组,故答案为:甲组;【小问3详解】解:168,168,172的平均数为)1116933168168172=++ ∵所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于329, ∴数据的差别较小,数据才稳定,可供选择的有:170, 172,且选择170, 172时,平均数会增大,故答案为:170, 172. 【点睛】本题考查了平均数、众数、中位数和方差,熟记方差的计算公式以及方差的意义:方差越小数据越稳定是解题的关键.24. 【答案】(1)见解析,90BAD ∠=︒(2)4【分析】(1)根据已知得出AB BC =,则ADB CDB ∠=∠,即可证明DB 平分ADC ∠,进而根据BD 平分ABC ∠,得出AD CD =,推出BAD BCD =,得出BD 是直径,进而可得90BAD ∠=︒;(2)根据(1)的结论结合已知条件得出,90F ∠=︒,ADC △是等边三角形,进而得出1302CDB ADC ∠=∠=︒,由BD 是直径,根据含30度角的直角三角形的性质可得12BC BD =,在Rt BFC △中,根据含30度角的直角三角形的性质求得BC 的长,进而即可求解.【小问1详解】解:∵BAC ADB ∠=∠∴AB BC =,∴ADB CDB ∠=∠,即DB 平分ADC ∠.∵BD 平分ABC ∠,∴ABD CBD ∠=∠,∴AD CD =,∴AB AD BC CD +=+,即BAD BCD =,∴BD 是直径,∴90BAD ∠=︒;【小问2详解】解:∵90BAD ∠=︒,CF AD ∥,∴180F BAD ∠+∠=︒,则90F ∠=︒.∵AD CD =,∴AD DC =.∵AC AD =,∴AC AD CD ==,∴ADC △是等边三角形,则60ADC ∠=︒.∵BD 平分ADC ∠, ∴1302CDB ADC ∠=∠=︒. ∵BD 是直径, ∴90BCD ∠=︒,则12BC BD =. ∵四边形ABCD 是圆内接四边形,∴180ADC ABC ∠+∠=︒,则120ABC ∠=︒,∴60FBC ∠=︒,∴906030FCB ∠=︒−︒=︒, ∴12FB BC =. ∵2BF =,∴4BC =,∴28BD BC ==.∵BD 是直径, ∴此圆半径的长为142BD =. 【点睛】本题考查了弧与圆周角的关系,等弧所对的圆周角相等,直径所对的圆周角是直角,含30度角的直角三角形的性质,等边三角形的性质与判定,圆内接四边形对角互补,熟练掌握以上知识是解题的关键.25. 【答案】(Ⅰ)见解析;(Ⅱ)见解析,4;(1)11.3;(2)<【分析】(Ⅰ)直接在表格中标记即可;(Ⅱ)根据表格中数据描点连线即可做出函数图象,再结合函数图象找到最低点,可得第一次用水量约为4个单位质量时,总用水量最小;(1)根据表格可得,用两次清洗的方式并使总用水量最小时,用水量为7.7个单位质量,计算即可; (2)根据表格可得当第一次用水量为6个单位质量,总用水量超过8个单位质量,则清洗后的清洁度能达到0.990,若总用水量为7.5个单位质量,则清洁度达不到0.990.【详解】(Ⅰ)表格如下:由图象可得,当第一次用水量约为4个单位质量(精确到个位)时,总用水量最小;(1)当采用两次清洗的方式并使总用水量最小时,用水量为7.7个单位质量,19-7.7=11.3,即可节水约11.3个单位质量;(2)由图可得,当第一次用水量为6个单位质量,总用水量超过8个单位质量,则清洗后的清洁度能达到0.990,第一次用水量为6个单位质量,总用水量为7.5个单位质量,则清洗后的清洁度0.990C <,故答案为:<.【点睛】本题考查了函数图象,根据数据描绘函数图象、从函数图象获取信息是解题的关键.26. 【答案】(1)32t =(2)12t ≤ 【分析】(1)根据二次函数的性质求得对称轴即可求解;(2)根据题意可得()11,x y 离对称轴更近,12x x <,则()11,x y 与()22,x y 的中点在对称轴的右侧,根据对称性求得1213222x x +<<,进而根据122x x t +>,即可求解. 【小问1详解】解:∵对于11x =,22x =有12y y =, ∴抛物线的对称轴为直线12322x x x +==, ∵抛物线的对称轴为x t =. ∴32t =; 【小问2详解】解:∵当101x <<,212x <<, ∴1213222x x +<<,12x x <, ∵12y y <,0a >,∴()11,x y 离对称轴更近,12x x <,则()11,x y 与()22,x y 的中点在对称轴的右侧, ∴122x x t +>, 即12t ≤. 【点睛】本题考查了二次函数的性质,熟练掌握二次函数的对称性是解题的关键.27. 【答案】(1)见解析 (2)90AEF ∠=︒,证明见解析【分析】(1)由旋转的性质得DM DE =,2MDE α∠=,利用三角形外角的性质求出C DEC α∠=∠=,可得DE DC =,等量代换得到DM DC =即可;(2)延长FE 到H 使FE EH =,连接CH ,AH ,可得DE 是FCH 的中位线,然后求出B ACH ∠∠=,设DM DE m ==,CD n =,求出2BF m CH ==,证明()SAS ABF ACH ≅,得到AF AH =,再根据等腰三角形三线合一证明AE FH ⊥即可.【小问1详解】证明:由旋转的性质得:DM DE =,2MDE α∠=,∵C α∠=,∴D DEC M E C α∠−∠∠==,∴C DEC ∠=∠,∴DE DC =,∴DM DC =,即D 是MC 的中点;【小问2详解】90AEF ∠=︒;证明:如图2,延长FE 到H 使FE EH =,连接CH ,AH ,∵DF DC =,∴DE 是FCH 的中位线,∴DE CH ∥,2CH DE =,由旋转的性质得:DM DE =,2MDE α∠=,∴2FCH α∠=,∵B C α∠=∠=,∴ACH α∠=,ABC 是等腰三角形,∴B ACH ∠∠=,AB AC =,设DM DE m ==,CD n =,则2CH m =,CM m n =+,∴DF CD n ==,∴FM DF DM n m =−=−,∵AM BC ⊥,∴BM CM m n ==+,∴()2BF BM FM m n n m m =−=+−−=,∴CH BF =,在ABF △和ACH 中,AB AC B ACH BF CH =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABF ACH ≅,∴AF AH =,∵FE EH =,∴AE FH ⊥,即90AEF ∠=︒.【点睛】本题考查了等腰三角形的判定和性质,旋转的性质,三角形外角的性质,三角形中位线定理以及全等三角形的判定和性质等知识,作出合适的辅助线,构造出全等三角形是解题的关键.28. 【答案】(1)1C ,2C ;OC=(2)13t ≤≤或3t ≤≤ 【分析】(1)根据题目中关联点的定义并分情况讨论计算即可;(2)根据()0,3M ,,05N ⎛⎫ ⎪ ⎪⎝⎭两点来求最值情况,S 共有2种情况,分别位于点M 和经过点O 的MN 的垂直平分线上,运用相似三角形计算即可.【小问1详解】解:①由关联点的定义可知,若直线CA CB ,中一经过点O ,另一条是O 的切线,则称点C 是弦AB 的“关联点”,∵点()1,0A −,1,22B ⎛⎫− ⎪ ⎪⎝⎭,()11,1C −,20()C ,(3C , ∴直线2AC 经过点O ,且2BC 与O 相切,∴2C 是弦1AB 的“关联点”,又∵()11,1C −和()1,0A −横坐标相等,与122B ⎛− ⎝⎭都位于直线y x =−上, ∴1AC 与O 相切,11B C 经过点O ,∴1C 是弦1AB 的“关联点”.②∵()1,0A −,222B ⎛− ⎝⎭,设()C a b ,,如下图所示,共有两种情况,a 、若12C B 与O 相切,AC 经过点O ,则12C B 、1AC 所在直线为: 0y x y ⎧=⎪⎨=⎪⎩,解得:)1C 0,∴1OC =,b 、若2AC 与O 相切,22C B 经过点O , 则22C B 、2AC 所在直线为:1x y x =−⎧⎨=−⎩, 解得:()211C −,,∴2OC =,综上,OC =【小问2详解】解:∵线段MN 上一点S ,存在O 的弦PQ ,使得点S 是弦PQ 的“关联点”,又∵弦PQ 随着S 的变动在一定范围内变动,且()0,3M ,N ⎫⎪⎪⎝⎭,OM ON >, ∴S 共有2种情况,分别位于点M 和经过点O 的MN 的垂直平分线上,如图所示,①当S 位于点()0,3M 时,MP 为O 的切线,作PJ OM ⊥,∵()0,3M ,O 的半径为1,且MP 为O 的切线,∴OP MP ⊥,∵PJ OM ⊥,∴MPO POJ ∽, ∴OP OM OJ OP =,即13OJ=, 解得13OJ =,∴根据勾股定理得,3PJ ==,123Q J =根据勾股定理,13PQ ==,同理,23PQ ==,∴当S 位于点()0,3M 时,1PQ 的临界值为3和3. ②当S 位于经过点O 的MN 的垂直平分线上即点K 时,∵点()0,3M ,5N ⎛⎫ ⎪ ⎪⎝⎭,∴5MN ==, ∴2OK OM ON MN =⨯÷=,又∵O 的半径为1,∴30OKZ ∠=︒,∴三角形OPQ 为等边三角形,∴在此情况下,1PQ =,PQ =∴当S 位于经过点O 的MN 的垂直平分线上即点K 时,1PQ 的临界值为1∴在两种情况下,PQ 的最小值在13t ≤≤内,最大值在3t ≤≤综上所述,t 的取值范围为13t ≤≤或3t ≤≤ 【点睛】本题主要考查最值问题,题目较为新颖,要灵活运用知识点,明确新概念时解答此题的关键.。
2024年北京市中考真题数学试卷含答案解析

2024年北京市中考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .【答案】B【分析】本题考查了中心对称图形与轴对称图形,根据轴对称图形和中心对称图形的定义进行逐一判断即可,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转180︒,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.掌握中心对称图形与轴对称图形的判断是解题的关键.【详解】解:A 、是中心对称图形,但不是轴对称图形,故不符合题意;B 、既是轴对称图形,也是中心对称图形,故符合题意;C 、不是轴对称图形,也不是中心对称图形,故不符合题意;D 、是轴对称图形,但不是中心对称图形,故不符合题意;故选:B .2.如图,直线AB 和CD 相交于点O ,OE OC ⊥,若58AOC ∠=︒,则EOB ∠的大小为( )A .29︒B .32︒C .45︒D .58︒【答案】B【分析】本题考查了垂直的定义,平角的定义,熟练掌握知识点,是解题的关键.根据OE OC ⊥得到90COE ∠=︒,再由平角180AOB ∠=︒即可求解.【详解】解:∵OE OC ⊥,∴90COE ∠=︒,∵180AOC COE BOE ∠+∠+∠=︒,58AOC ∠=︒,∴180905832EOB ∠=︒-︒-=︒,故选:B .3.实数a ,b 在数轴上的对应点的位置如图所示,下列结论中正确的是( )A .1b >-B .2b >C .0a b +>D .0ab >4.若关于x 的一元二次方程240x x c -+=有两个相等的实数根,则实数c 的值为( )A .16-B .4-C .4D .16【答案】C【分析】根据方程的根的判别式()22Δ44410b ac c =-=--⨯⨯=即可.本题考查了根的判别式,熟练掌握根的判别式是解题的关键.【详解】∵方程240x x c -+=,1,4,a b c c ==-=,∴()22Δ44410b ac c =-=--⨯⨯=,∴416c =,解得4c =.故选C .5.不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别.从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )A .34B .12C .13D .14共有4种等可能的结果,其中两次都取到白色小球的结果有∴两次都取到白色小球的概率为故选:D .6.为助力数字经济发展,北京积极推进多个公共算力中心的建设.北京数字经济算力中心日前已部署上架和调试的设备的算力为17410⨯Flops (Flops 是计算机系统算力的一种度量单位),整体投产后,累计实现的算力将是日前已部署上架和调试的设备的算力的5倍,达到m Flops ,则m 的值为( )A .16810⨯B .17210⨯C .17510⨯D .18210⨯【答案】D【分析】用移动小数点的方法确定a 值,根据整数位数减一原则确定n 值,最后写成10n a ⨯的形式即可.本题考查了科学记数法表示大数,熟练掌握把小数点点在左边第一个非零数字的后面确定a ,运用整数位数减去1确定n 值是解题的关键.【详解】17184105210m =⨯⨯=⨯,故选D .7.下面是“作一个角使其等于AOB ∠”的尺规作图方法.(1)如图,以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ;(2)作射线O A '',以点O '为圆心,OC 长为半径画弧,交O A ''于点C ';以点C '为圆心,CD长为半径画弧,两弧交于点D ¢;(3)过点D ¢作射线O B '',则A O B AOB '''∠=∠.上述方法通过判定C O D COD '''△≌△得到A O B AOB '''∠=∠,其中判定C O D COD '''△≌△的依据是( )A .三边分别相等的两个三角形全等B .两边及其夹角分别相等的两个三角形全等C .两角及其夹边分别相等的两个三角形全等D .两角分别相等且其中一组等角的对边相等的两个三角形全等【答案】A【分析】根据基本作图中,同圆半径相等,判定三角形全等的依据是边边边原理,解答即可.本题考查了作一个角等于已知角的基本作图,熟练掌握作图的依据是边边边原理是解题的关键.【详解】根据基本作图中,同圆半径相等,判定三角形全等的依据是边边边原理,故选A.8.如图,在菱形ABCD 中,60BAD ∠=︒,O 为对角线的交点.将菱形ABCD 绕点O 逆时针旋转90︒得到菱形A B C D '''',两个菱形的公共点为E ,F ,G ,H .对八边形BFB GDHD E ''给出下面四个结论:①该八边形各边长都相等;②该八边形各内角都相等;③点O 到该八边形各顶点的距离都相等;④点O 到该八边形各边所在直线的距离都相等。
北京市中考:《数学》2023年考试真题与参考答案

金属屋面构造做法
作为一种常见的建筑材料,金属屋面建造在建筑工程中起着重要的作用。
金属屋面的构造做法与其他屋顶材料有许多不同之处,特别是在雨水排放、保温隔热和防腐蚀等方面,所以建造时需要认真考虑这些问题。
下面我们就来详细了解一下金属屋面的构造做法。
首先,金属屋面有许多不同材质可供选择,例如镀锌铁皮、彩钢板、铝合金、铜等,需要根据实际情况进行选择。
其次,金属屋面的构造分为上下两部分,即屋面瓦和桁架支撑。
屋面瓦是将金属材料切割和折弯成预先设计好的形状制成的,一般采用滚压成型机进行生产。
桁架支撑是屋面的骨架,由木材或钢材制成,负责整个屋顶的支撑和稳定。
桁架支撑的高度和间距应根据建筑设计图纸中的规定进行调整。
同时,桁架需要加入抗风设备以确保建筑的安全性。
在屋面瓦的安装过程中,需要注意以下几点:
1.确保屋面平整:给予桁架支撑稳定才能确保屋面平整。
2.防水设计:在屋面的连接处,应使用专业的防水带进行包裹,以阻止雨水渗入建筑内部。
3.屋面的排水设计:屋面的坡度应符合标准,防止积水。
同时需设计好雨水排放口。
4.接口处理:金属屋面的接口处理特别重要,避免隐蔽问题。
5.抗风设计:常规的金属屋面需要在桁架中加入抗风设备,以便在强风或风暴中确保安全。
最后,需要注意的是,金属屋面建造的过程需要认真审查建筑设计图纸,以确保屋面的结构符合国家安全标准,在施工过程中严格遵守安全操作规程。
这些有关金属屋面的构造做法,无论是建筑工程还是自己的小屋,都有着重要的意义。
做好以上方面的工作,才能让屋面建造更安全、稳定和美观。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0) 的左侧) ,与 y 轴交于点 C ,点 B 的坐标为 (3, ,将直线 y kx 沿 y 轴向上平移 3 个单位
长度后恰好经过 B,C 两点. (1)求直线 BC 及抛物线的解析式; (2)设抛物线的顶点为 D ,点 P 在抛物线的对称轴上,且 APD ACB ,求点 P 的坐 标; y (3)连结 CD ,求 OCA 与 OCD 两角和的度数. 解: (1) 4 3 2 1 (2) -2 -1 O -1 -2 1 2 3 4 x
考 生 须 知:
第Ⅰ卷(机读卷
考 生 须 知:
共 32 分)
1.第Ⅰ卷从第 1 页到第 2 页,共 2 页,共一道大题,8 道小题. 2.考生须将所选选项按要求填涂在答题卡上,在试卷上作答无效.
一、选择题(共 8 道小题,每小题 4 分,共 32 分) 下列各题均有四个选项,其中只有一个是符合题意的.用铅笔把“机读答题卡”上对应题 .. 目答案的相应字母处涂黑. 1. 6 的绝对值等于( ) A. 6 B.
1 中,自变量 x 的取值范围是 2x 1
3 2
. A D B E C ,
10.分解因式: a ab
.
11.如图,在 △ ABC 中, D,E 分别是 AB,AC 的中点, 若 DE 2cm ,则 BC cm.
b2 b5 b8 b11 , 3 , 3 , 4 , ( ab 0 ) 其中第 7 个式子是 12. 一组按规律排列的式子: „ , a a a a
A
G
A
G
B
E C BF 图1
C
B
E C B F 图2
C
(1)若把三角形纸片 ABC 放在等边三角形网格中(图中每个小三角形都是边长为 1 的等 边三角形) ,点 A,B,C,D 恰好落在网格图中的格点上.如图 2 所示,请直接写出此时重 ABC 的面积; 叠三角形 (2)实验探究:设 AD 的长为 m ,若重叠三角形 AB C 存在.试用含 m 的代数式表示重 叠三角形 AB C 的面积, 并写出 m 的取值范围 (直接写出结果, 备用图供实验, 探究使用) . A A
y kx 3 y
M 1 O 1 x
2
17. (本小题满分 5 分) 已知 x 3 y 0 ,求 解:
2x y ( x y ) 的值. x 2 xy y 2
2
四、解答题(共 2 道小题,共 10 分) 18. (本小题满分 5 分)
如图,在梯形 ABCD 中, AD ∥ BC , AB AC , B 45 , AD 2 , BC 4 2 ,
(2)
六、解答题(共 2 道小题,共 9 分) 21. (本小题满分 5 分)列方程或方程组解应用题: 京津城际铁路将于 2008 年 8 月 1 日开通运营,预计高速列车在北京、天津间单程直达运行 时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了 6 分钟, 由天津返回北京的行驶时间与预计时间相同. 如果这次试车时, 由天津返回北京比去天津时 平均每小时多行驶 40 千米,那么这次试车时由北京到天津的平均速度是每小时多少千米? 解:
)
A.5 B.6 C.7 D.8 6.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有北京奥运会的会徽、吉祥 物(福娃) 、火炬和奖牌等四种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向 下放在桌子上,从中随机抽取一张,抽出的卡片正面图案恰好是吉祥物(福娃)的概率是 ( )
A.
2008 年北京市高级中等学校招生考试 数 学 试 卷
1.本试卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷共 2 页,第Ⅱ卷共 8 页.全卷共九 道大题,25 道小题. 2.本试卷满分 120 分,考试时间 120 分钟. 3.在试卷(包括第Ⅰ卷和第Ⅱ卷)密封线内准确填写区(县)名称、毕 业学校、姓名、报名号和准考证号. 4.考试结束后,将试卷和答题卡一并交回.
第 n 个式子是 ( n 为正整数) . 三、解答题(共 5 道小题,共 25 分) 13. (本小题满分 5 分)
1 计算: 8 2sin 4. (本小题满分 5 分) 解不等式 5 x 12 ≤ 2(4 x 3) ,并把它的解集在数轴上表示出来. 解:
1 5
B.
2 5
C.
1 2
D.
3 5
7.若 x 2
y 3 0 ,则 xy 的值为(
)
A. 8 B. 6 C. 5 D. 6 8.已知 O 为圆锥的顶点, M 为圆锥底面上一点,点 P 在 OM 上.一只蜗牛从 P 点出发, 绕圆锥侧面爬行,回到 P 点时所爬过的最短路线的痕迹如右图所示.若沿 OM 将圆锥侧面 剪开并展开,所得侧面展开图是( ) O O P M M P A.
1 6
C.
1 6
D. 6
2.截止到 2008 年 5 月 19 日,已有 21 600 名中外记者成为北京奥运会的注册记者,创历届 奥运会之最.将 21 600 用科学记数法表示应为( ) A. 0.216 10
5
B. 21.6 10
3
C. 2.16 10
3
D. 2.16 10
4
3.若两圆的半径分别是 1cm 和 5cm,圆心距为 6cm,则这两圆的位置关系是( ) A.内切 B.相交 C.外切 D.外离 4.众志成城,抗震救灾.某小组 7 名同学积极捐出自己的零花钱支援灾区,他们捐款的数 额分别是 (单位: : 20, 30, 25, 元) 50, 50, 50, 135. 这组数据的众数和中位数分别是 ( ) A.50,20 B.50,30 C.50,50 D.135,50 5.若一个多边形的内角和等于 720 ,则这个多边形的边数是(
(3)
九、解答题(本题满分 8 分) 25.请阅读下列材料: P 问题: 如图 1, 在菱形 ABCD 和菱形 BEFG 中, A,B,E 在同一条直线上, 是线段 DF 点 的中点,连结 PG,PC .若 ABC BEF 60 ,探究 PG 与 PC 的位置关系及
PG 的 PC
值. 小聪同学的思路是:延长 GP 交 DC 于点 H ,构造全等三角形,经过推理使问题得到解决. C D P G A 图1 请你参考小聪同学的思路,探究并解决下列问题: B F E A 图2 P B E
C
O
E
B
五、解答题(本题满分 6 分) 20.为减少环境污染,自 2008 年 6 月 1 日起,全国的商品零售场所开始实行“塑料购物袋 有偿使用制度” (以下简称“限塑令”.某班同学于 6 月上旬的一天,在某超市门口采用问 ) 卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根 据 100 位顾客的 100 份有效答卷画出的统计图表的一部分: “限塑令”实施前,平均一次购物使 用不同数量塑料购物袋的人数统计图 .. 人数/位 40 35 30 25 20 15 10 5 0 37 26 11 4 2 3 4 图1 5 6 3 7 塑料袋数/个 图2 自备袋 46% 押金式环保袋 24% “限塑令”实施后,使用各种 购物袋的人数分布统计图 其它 5% 收费塑料购物袋 _______%
M
O M P B.
M
O M P C.
M
O M P D.
M
2008 年北京市高级中等学校招生考试 数 学 试 卷
第Ⅱ卷(非机读卷 共 88 分)
考 生 1.第Ⅱ卷从第 1 页到第 8 页,共 8 页,共八道大题,17 道小题. 须 知: 2.除画图可以用铅笔外,答题必须用黑色或蓝色钢笔、圆珠笔或签字笔. 二、填空题(共 4 道小题,每小题 4 分,共 16 分) 9.在函数 y
B 备用图
C
B 备用图
C
解: (1)重叠三角形 AB C 的面积为 ; (2)用含 m 的代数式表示重叠三角形 AB C 的面积为
; m 的取值范围为
.
七、解答题(本题满分 7 分) 23.已知:关于 x 的一元二次方程 mx2 (3m 2) x 2m 2 0(m 0) . (1)求证:方程有两个不相等的实数根; (2)设方程的两个实数根分别为 x1 , x2 (其中 x1 x2 ) .若 y 是关于 m 的函数,且
y x2 2x1 ,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量 m 的取值范围满足什么条件时,
y ≤ 2m .
(1)证明:
(2)解:
(3)解:
y 4 3 2 1 -4 -3 -2 -1 O 1 2 3 4 -1 -2 -3 -4 x
八、解答题(本题满分 7 分) 24. 在平面直角坐标系 xOy 中, 抛物线 y x bx c 与 x 轴交于 A,B 两点 (点 A 在点 B
D
C G F
PG 的值; PC (2)将图 1 中的菱形 BEFG 绕点 B 顺时针旋转,使菱形 BEFG 的对角线 BF 恰好与菱形 ABCD 的边 AB 在同一条直线上,原问题中的其他条件不变(如图 2) .你在(1)中得到
(1)写出上面问题中线段 PG 与 PC 的位置关系及 的两个结论是否发生变化?写出你的猜想并加以证明. (3)若图 1 中 ABC BEF 2 (0 90 ) ,将菱形 BEFG 绕点 B 顺时针旋转任
意角度,原问题中的其他条件不变,请你直接写出 解: (1)线段 PG 与 PC 的位置关系是 (2)
PG 的值(用含 的式子表示) . PC PG ; . PC
求 DC 的长. 解:
A
D
B
C
19. (本小题满分 5 分) 已知:如图,在 Rt△ ABC 中, C 90 ,点 O 在 AB 上,以 O 为圆心, OA 长为半径的
