关于污水池设计的数学建模
数学建模 污水处理

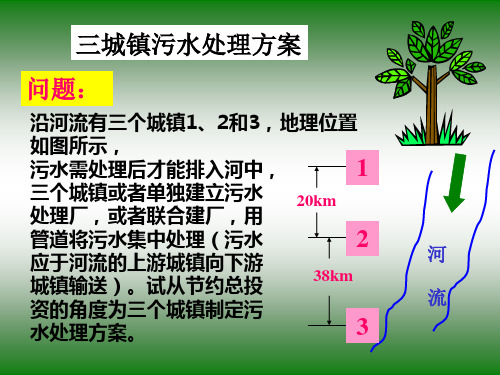
数学建模污水处理一、引言污水处理是指将废水中的污染物去除或转化为无害物质,以达到环境保护和资源利用的目的。
数学建模作为一种分析和解决实际问题的方法,在污水处理领域也发挥着重要作用。
本文将介绍如何利用数学建模来优化污水处理过程。
二、问题背景1.污水处理的重要性:污水中含有各种有害物质,如果不经过处理直接排放到环境中,将对水体、土壤和生态系统造成严重污染,甚至危害人类健康。
2.当前存在的问题:传统的污水处理方法存在着效率低、成本高等问题,需要寻找一种更加高效和经济的方法来处理污水。
三、问题描述1.污水处理过程概述:污水处理过程通常包括预处理、初级处理、二级处理和三级处理等环节。
其中,预处理主要是去除大颗粒、悬浮物和泥沙等杂质,初级处理用于去除有机物质,二级处理主要是进行生物降解,三级处理则是对水质进一步提升。
2.污水处理的数学模型:数学建模可以通过建立数学方程和模型来描述污水处理过程中涉及的物理和化学过程,包括质量平衡、浓度变化、反应速率等因素。
四、数学建模方法1.质量平衡方程:通过建立污水处理系统中物质的质量平衡方程,可以描述污水处理过程中物质的流动和转化情况,进而优化处理效果。
2.反应速率方程:污水处理过程中存在着各种化学和生物反应,通过建立反应速率方程,可以研究反应速率对处理效果的影响,为优化反应条件提供依据。
3.优化算法:针对污水处理过程中的复杂性和多变性,可以利用优化算法来寻求最佳的处理条件和方案,如线性规划、遗传算法等。
五、数学模型应用案例1.污水处理设备的优化设计:通过数学模型,可以优化污水处理设备的设计参数,使其具有更好的处理效果和经济性。
2.污水处理工艺的优化:通过数学模型,可以分析不同工艺条件下处理效果的差异,找到最优的处理工艺组合,提高处理效率和节约成本。
3.污水处理系统的模拟与预测:通过数学模型,可以模拟和预测污水处理系统中物质的流动和转化情况,为操作和管理提供科学依据。
六、附件本文档涉及的附件包括:数学模型的具体计算和分析过程、污水处理工艺的数据和图表、优化算法的代码和结果等。
数学建模 污水处理

数学建模污水处理近年来,随着我国城市化进程的加速和人口的快速增长,城市污水处理问题变得越来越严重,给人们生活环境带来了很大的压力和威胁。
然而,随着数学在各个领域中的应用越来越广泛,数学建模已经成为污水处理问题研究的一种重要的工具。
数学建模是指使用数学方法研究复杂现实问题的一种方法。
在污水处理中,数学建模的应用主要表现在以下几个方面。
第一,数学建模可以帮助我们精确地描述污水处理的过程。
通过数学建模,我们可以将污水处理过程中的各种因素分别进行量化,然后通过建立数学模型,来描述这些因素之间的相互作用。
例如,在污水的生化处理过程中,不同的微生物有不同的作用,通过建立数学模型,可以描述它们的生长、死亡、代谢和分解等过程。
第二,数学建模可以帮助我们优化污水处理流程。
建立完整的污水处理模型,可以用来优化流程,检测并解决污水处理中出现的问题,如过度臭氧化,过多沉淀等问题。
同时,我们还可以利用模型来确定适当的措施,降低成本并增加处理效率。
第三,数学建模可以帮助我们预测污水处理后的效果。
在实际污水处理中,我们需要经常监测处理后的效果。
通过建立数学模型,我们可以预测不同处理方案的效果,来寻找最佳的处理方案。
在建立数学模型时,我们通常需要考虑以下因素。
第一,建立模型的精度。
建立模型时,我们需要掌握一定的数学知识和分析技巧,同时,还需要收集大量的实验数据和相关信息,以保证模型的准确性和可靠性。
第二,建立模型的通用性。
我们需要注意到模型对不同场合的适用性,尽量的不受环境因素的影响才能确保它的通用性。
第三,建立模型的运算效率。
模型的运算效率与每次实现时的数据量密切相关,因此,我们需要充分的利用计算机来提高运算效率。
在污水处理领域中,数学建模已得到了广泛的应用,并取得了很好的效果。
例如,在研究污水生物处理技术时,我们可以利用微生物生长动力学、群体生态学和传质动力学等数学模型,对微生物生长和代谢等过程进行建模,从而研究和优化污水处理的过程。
数学建模 污水处理

污水处理问题摘要随着经济的快速发展,环保问题已经成为一个不容忽视的问题,而水资源更是关系着每个居民的日常生活,因此对于污水处理这一特殊的问题我们在解决时就应该本着高效的原则去实施,在这个污水处理问题中,我们先建立了一般情况下的模型,然后将该模型应用到实际问题中从而解决了实际问题。
在模型的建立中我们要考虑工厂的净化能力,江水的自净能力,在保证江水经这一系列的处理后在到达下一个居民点后要达到国家标准,还要花费最少,对该问题进行全面的分析后可知这是一个运筹学方面关于线性规划的最优解问题,在该模型的建立中我们针对江水污水浓度在每个居民点之前小于国家标准这一条件对其建立线性约束条件,然后综合考虑费用最小,在结合三个处理厂各自的情况后关于费用抽象数模型的目标函数,然后应用LINDO软件求解该问题得到当三个处理厂排出的污水浓度分别为40 mg/l,20 mg/l,50 mg/l时,此时我们得到使江面上所有地段的水污染达到国家标准,最少需要花费费用为500万元。
当从三个处理厂出来的污水浓度分别为62.222225mg/l,60mg/l,50mg/l,时,此时如果只要求三个居民点上游的水污染达到国家标准最少需要花费费用为188.8889万元。
问题的提出设上游江水流量为,污水浓度为0.8 mg/l,3个工厂的污水流量均为,污水浓度(从上游到下游排列)分别为100,60,50(mg/l),处理系数均为1万元( (mg/l)),3个工厂之间的两段江面的自净系数(从上游到下游)分别为0.9和0.6.国家标准规定水的污染浓度不能超过1mg/l.(1)为了使江面上所有地段的水污染达到国家标准,最少需要花费多少费用?(2)如果只要求三个居民点上游的水污染达到国家标准最少需要花费多少费用?问题的分析通过对该污水处理所花费用最少问题的分析,我们可知在此问题中有多个污水浓度,江水的原始污水浓度,工厂排出的污水浓度,处理厂排出的污水浓度,以及当处理厂排出污水与江水混合后再经江水自净后的浓度,在这几个浓度中只有经处理厂排出的污水的浓度是未知的,其关系着整个问题,要使总费用最少,江中每段的污水浓度都达到国家标准,江水中污水浓度在到达下一居民点之前须达到国家标准1(mg/l),那么问题的重点就在于对污水浓度的认识。
数学建模课件-污水处理
共有五种方案
方案五:城镇1、2、3合作
所需的投资分别为: C(1,2,3)=730* C6.6*30.51*38 =5560 ( 5+3+5 )
0.712+6.6*50.51*20
总投资为: S5= C(1,2,3) =5560。
比较五个方案可知: 应该选择三个城镇联合建厂的方案.
下面的问题是: 如何分担总额为S5=5560万元的费用。
污水处理问题中1(v)的计算 s v(s) v(s\1) v(s)-v(s\1) |s| w(|s|) 1 0 0 0 1 1/3 1U2 40 0 40 2 1/6 1U3 0 0 0 2 1/6 I 64 25 39 3 1/3
w(|s|)[v(s)&
0
13
1(v)=19.7(元),同法可计算出 2(v)=32.1 (元) 3(v)=12.2 (元)
其中Si是I中包含的所有子集,|s|是子集s中的元素 数目(人数),w(|s|)是加权因子。
例:甲乙丙三人经商,若单干,每人仅获利1元,甲乙合 作可获利7元,甲丙合作可获利5元,乙丙合作可获利4元, 三人合作则可获利10元,问三人合作时怎样合理地分配 10元的收入?
三人经商中甲的分配1(v)的计算
s v(s) v(s\1) v(s)-v(s\1) |s| w(|s|) 1 1 0 1 1 1/3 1U2 7 1 6 2 1/6 1U3 5 1 4 2 1/6 I 10 4 6 3 1/3
w(|s|)[v(s)+v(s\1)]
1/3
1
2 /3
2
1(v)=4(元),同法可计算出2(v)=3.5 (元) 3(v)=2.5 (元)
设I定义为n人集合,s为n人集合中的任一种合作, v(s)为合作s的效益。每一种合作都会得到一定的 效益,合作人数的增加不会引起效益的减少。
数学建模 污水处理

数学建模污水处理第一章引言\t污水处理是解决城市生活污水排放造成的环境污染问题的重要措施之一。
本文档旨在通过数学建模的方法,研究并分析污水处理过程中的关键问题,并提出相应的解决方案。
本文档主要涉及以下章节:问题定义、模型假设、问题分析、模型建立、模型求解和模型评价等。
第二章问题定义\t1.利用污水处理系统有效地去除污水中的污染物。
\t2.最小化处理过程中消耗的能源和化学药剂。
第三章模型假设\t1.假设污水处理过程中,污水的流量和污染物浓度稳定不变。
\t2.假设污水处理系统中的各个单元之间可以流动的混合液体为完全混合。
\t3.假设处理过程中没有发生反射现象,即所有反应都为一级反应。
\t4.假设污水处理系统中的温度、压力等外界影响因素保持不变。
第四章问题分析\t1.分析污水处理系统中的关键参数和指标。
\t2.分析污水处理系统中的关键问题。
\t3.设计合适的数学模型来描述和解决这些问题。
第五章模型建立\t1.建立污水处理系统的数学模型。
\t2.建立污水中污染物的浓度变化模型。
\t3.建立处理过程中能源和化学药剂的消耗模型。
第六章模型求解\t1.使用合适的数值计算方法求解模型。
\t2.通过计算得到的数值结果,分析污水处理系统的运行状况。
第七章模型评价\t1.对模型求解结果进行评价,判断模型的准确性和可用性。
\t2.提出对污水处理系统的改进措施和建议。
附件:\t1.污水处理系统的流程图。
\t2.污水处理系统中的关键参数和指标表格。
法律名词及注释:\t1.《环境保护法》:是中华人民共和国的一部法律,旨在保护和改善环境质量。
\t2.《水污染防治法》:是中华人民共和国的一部法律,旨在预防和控制水污染,保护水资源。
数学建模技术与案例 20151127

+ ⋯+
������
������
������������ ������!
������ − ������������
������
+ ������������ ������
只取泰勒展开的一次项������ ������ =
程 ������
������������ 近似为: ������������
a. 如何控制捕捞使持续产量最大化 b. 如何控制捕捞使效益最大化 c. 捕捞过度问题
∴ 渔场鱼量的变化量=增长量−捕捞量
案例6 捕鱼业的持续收获
分析
• 在鱼群自然增长和人工捕捞的情况下, 渔场鱼量如何变化?
– 渔场的鱼量按规律增长
– 捕捞
∴ 渔场鱼量的变化量=增长量−捕捞量
案例6 捕鱼业的持续收获
分析:渔场鱼量按规律增长
• 鱼量增长到一定程度后增长率下降:
– 原因:自然资源、环境条件等的阻滞作用。 – 趋势:随着鱼量的增加,阻滞作用也变大。
课程大纲
• • • • • • 第1章:什么是数学建模 第2章:数学建模的基本技能与方法 第3章:交通与运输案例分析 第4章:健康与医疗案例分析 第5章:环境与生态保护案例分析 第6章:生产与制造案例分析
2015/11/30
Mathematical Modeling
3
第5章:环境与生态保护案例分析
������→∞
lim ������ ������ = ������������ ⋯ ������
则平衡点������ = ������������ 是稳定的;否则是不稳定的。
微分方程的稳定性理论
•
������������ ������������
关于污水处理费用的数学模型

关于污水处理费用的数学模型污水处理费用是城市管理中一个重要的方面,它涉及到公共卫生和环境保护。
设计一个数学模型来估计污水处理费用可以帮助政府和水务部门制定合理的费用政策,提高污水处理效率,减少环境污染。
首先,我们需要确定污水处理费用和一些关键因素之间的关系。
污水处理费用可以分为固定成本和可变成本两部分。
固定成本是指与污水处理设施的建设和维护相关的固定费用,如设备购买和人工成本。
可变成本是指与实际的污水处理量相关的费用,如化学处理剂和电力消耗。
因此,我们可以将污水处理费用表示为:总费用 = 固定成本 + 可变成本固定成本通常是以年为单位计算的,而可变成本是以污水处理量为基础计算的。
关于固定成本部分的数学模型,我们可以考虑以下几个因素:设备购买费用、人工成本和维护费用。
设备购买费用可以用一个简单的数学方程来表示,如:设备购买费用 = 设备数量 * 单个设备价格其中,设备数量是根据城市的规模和污水处理需求进行估计的,单个设备价格可以通过市场调查获得。
人工成本可以根据城市工资水平和所需的人员数量进行计算。
我们可以使用以下公式来估计人工成本:人工成本 = 平均工资 * 人员数量维护费用是指设备维护和修理所需的费用。
我们可以根据设备购买费用的一定比例来估计维护费用,例如:维护费用 = 设备购买费用 * 年维护比例对于可变成本部分,我们可以考虑以下几个因素:污水处理量、化学处理剂和电力消耗。
污水处理量通常以每天处理的污水量为基础计算,可以由实际的污水排放量和人口规模来估算。
化学处理剂的使用量可以通过实际的污水处理效果和化学剂的投入量来决定。
电力消耗可以通过污水处理设备的能耗和运行时间来估算。
我们可以使用以下公式来计算可变成本:可变成本 = 污水处理量 * 单位处理成本其中,单位处理成本是可变成本中与污水处理量相关的部分。
综上所述,我们可以设计一个数学模型来估计污水处理费用:总费用 = 固定成本 + 可变成本固定成本 = 设备购买费用 + 人工成本 + 维护费用设备购买费用 = 设备数量 * 单个设备价格人工成本 = 平均工资 * 人员数量维护费用 = 设备购买费用 * 年维护比例可变成本 = 污水处理量 * 单位处理成本通过使用这个模型,政府和水务部门可以根据不同城市的特点和需求来确定合理的污水处理费用,从而实现资源的合理利用和环境的可持续发展。
建筑物排水 污水系统的数学模型及设计优化研究

建筑物排水污水系统的数学模型及设计优化研究建筑物排水污水系统的数学模型及设计优化研究建筑物排水污水系统是建筑设计中不可或缺的一部分,它的合理设计与优化对于建筑物的正常使用和环境保护都有着重要的作用。
本文将从数学模型和设计优化两个方面来探讨建筑物排水污水系统的研究。
一、数学模型建筑物排水污水系统的数学模型是对系统中涉及的各个工艺环节和参数进行定量描述和分析的方法。
常见的数学模型包括流量计算模型、水头计算模型和水力计算模型等。
1.流量计算模型流量计算模型用于确定建筑物排水污水系统中各个位置的流量大小。
在建筑物排水系统中,流量的计算是基于流体力学原理,其中包括根据建筑物的类型、用途和规模确定相应的排水标准,通过对建筑物内水源的产生和排放进行统计和计算,考虑水流的流速、压力、流量等参数,从而确定系统中各个位置的流量大小。
2.水头计算模型水头计算模型用于确定建筑物排水污水系统中水流的流速和压力变化。
水头是指水流在流动过程中所具有的能量,其大小和分布对于系统的运行和稳定性有着重要的影响。
水头计算模型通过对建筑物排水系统中涉及的水流路径、管道长度和管径、液位高差等参数进行定量分析,从而获得系统中水头的变化情况。
3.水力计算模型水力计算模型是建筑物排水污水系统的核心模型,它综合考虑了流量计算和水头计算的结果,以及建筑物排水系统中的液位变化、水压损失、管道摩阻和阀门等影响因素,通过建立动态平衡方程组进行求解,以获得系统中各个位置的流速、压力和液位等信息。
二、设计优化基于数学模型的建筑物排水污水系统设计优化是通过分析建筑物的实际需求和系统的运行特点,以提高系统效率和经济性为目标,优化系统的结构、参数和运行策略等,以达到更好的排水和处理效果。
1.结构优化结构优化主要包括对建筑物排水污水系统的布局和管网结构进行优化设计。
通过合理布置管道、排水设备和处理设备等,避免死角和堵塞点的产生,减少水头损失和能量消耗,提高系统的排水能力和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于污水池设计的数学建模
问题一
问题分析
需要建立一个已知最小体积的蓄水池,给予一个资金与蓄水池参数的函数关系,求所需的最少资金。
变量说明
问题假设
1.蓄水池是一个底部为正方形的长方体
2.地面对水的吸收比例在此不作考虑
3.总的费用可以写成c(x,y)=5(x2+4xy)+10xy
模型建立
高峰时期积水量:
M = T×V×N1
因为积水需要全部转移到蓄水池,因此蓄水池蓄水量应该大于高峰时期积水量,所以:
M≤X×X×Y
又因为
c(x,y)=5(x2+4xy)+10xy
通过Lingo软件解决,代入数据:
N1=20,T=60,V=2
运行得:
由运行结果可知,该模型的全局最优值为5593.019,最优解为X=19.30979,Y=6.436596
结果分析
结合现实情况,为了工程需要以及资金输出,无需精确到小数点后四位,因此,可以去X=19.3英尺Y=6.4英尺
此时的费用满足题目要求。
问题二
问题分析
用电问题,战士用电量与用电所处时间有关,而且由于受到本地经济的影响,供电量每个时刻均不会超过最大供电能力,由于日常作息的原因,战士会在一天中用电量不同,但均不能超过最大用电量,为了达到这一要求,看是否需要进行灯火管制。
知道部队用电的函数关系以后,需要知道那个时间点开始,超过了峰值的时间段就需要灯火管制。
问题假设
1.战士每天准时开始用电,即为每天用电起始时间一致
2.忽略电量在传输过程中的损失
模型建立
由f(t)即用电量与时间t存在函数关系:
f(t)=(1/4)*t^4—t^3+t^2—(1/6)
做出函数图像如下:
需要从图像分析,f(t)= 2 的X值为多少。
代入数据,可知由图知在t=2.986时,即为当时间为17时54分时,用电量开始超过最大供电量g=2,开始施行灯火管制,需要从此时管制直到夜里21:00活动时间结束。
结果分析
通过分析,得出当时间为17时54分的时候需要开始灯火管制,一个时间点也符合现实情况。
不过,从另外一个反面分析,部队是需要来打战的,而电力也是打仗必备的一个能源需要,如果,一个营队,需要为电力而调整作息时间,这未免也太麻烦,伤战斗力了。
所以希望,部队也能从根源解决问题,确实的提高部队的电力输送水平。
使一些问题吗,没必要考虑,没必要成为一个问题。
