第三章 地图数学基础
合集下载
地图之数学基础
X' Y' 2 1 2 m n
该方程证明:地球面上的微小圆， 投影后通常会变为椭圆，即︰
2
2
微小圆→变形椭圆
以O'为原点，以相交成θ角的两共 轭直径为坐标轴的椭圆方程式。
特别方向︰变形椭圆上相互垂直的两个方向(a,b)及 经向和纬向(m,n)
长轴方向（极大值）a
短轴方向（极小值）b
经线方向m；纬线方向n 据阿波隆尼定理，有 m2 + n2 = a2 + b2
地图投影
1地图投影的意义 地球椭球体表面是不可展曲面，要将曲面 上的客观事物表示在有限的平面图纸上，必 须经过由曲面到平面的转换。 地图投影︰在地球椭球面和平面之间建立 点与点之间函数关系的数学方法，称为地图 投影。 x =f (φ, λ)
y =f2(φ,λ)
1
地图投影的实质︰是将地球椭球面上的经 纬线网按照一定的数学法则转移到平面上。
面积比和面积变形︰投影平面上微小面积（变 形椭圆面积）dF′与球面上相应的微小面积（微小圆 面积）dF之比。
P表示面积比 Vp表示面积变形
dF ' πab P 2 a b dF πl
P = a‧b = m ‧ n
Vp p 1
(θ = 90)
= 0不变 > 0变大 < 0变小
P = m ‧ n ‧ sinθ
M为比例尺分母） • 当制图区域相当大，制图时对景物的缩小比率也相当大，在这种情况
下采用的地图投影比较复杂，地图上的长度也因地点和方向不同而有
所变化。在这种情况下所注明的比例尺含义，其实质是在进行地图投 影时，对地球半径缩小的比率，称为地图主比例尺，地图经过投影后， 地图上只有个别的点或线没有长度变形。其它大于或小于主比例尺的 比例尺称为局部比例尺。 • 地图比例尺的精确定义︰地图上沿某方向的微分线段和地面上相应微 分线段水平长度之比。
《地图数学基础》课件
表达的内容和尺度来决定。
03
地图比例尺
比例尺定义与表示
比例尺定义
地图上的长度与实际地面相应长度之 间的比例关系。
比例尺表示
通常以分数形式表示，如1:10000， 表示地图上1单位长度代表实际地面 10000单位长度。
比例尺与地图精度
比例尺越大，地图精 度越高，表示的地物 地貌越详细。
地图精度还受到地图 投影、制图方法等因 素的影响。
城市规划与管理
地图数学基础在城市规划与管理 中发挥着重要作用，如城市空间 布局规划、城市交通规划、城市 环境监测等。
自然资源管理
地图数学基础在自然资源管理中 应用广泛，如土地资源调查、森 林资源监测、水资源管理等。
灾害监测与应急响
应
地图数学基础能够为灾害监测和 应急响应提供精确的地理信息支 持，如地震、洪涝、火灾等灾害 的监测和预警。
展和地理信息系统的普及，地图数学基础逐渐成为地理信息科学领域的
研究热点。
02
当前研究热点
目前，地图数学基础的研究热点包括地图自动综合、空间数据挖掘、时
空数据分析等方向，这些方向的研究成果将不断推动地图数学基础的进
步和发展。
03
未来展望
随着人工智能、大数据等技术的不断发展，地图数学基础将在智慧城市
、环境保护、公共安全等领域发挥更加重要的作用，其理论和方法也将
THANKS
感谢观看
不断创新和完善。
02
地图投影
投影分类
等面积投影
等方位投影
保持面积不变，但形状和方向可能会 改变。
保持方向不变，但面积和距离可能会 改变。
等距离投影
保持距离不变，但面积和方向可能会 改变。
地图数学基础
3.地图数学基础
3.1地理坐标系
地理坐标系<Geographic Coordinate Systems），指地表实体经度面、纬度面与地心夹角，可理解为经纬度坐标。
在Geographic Coordinate Systems目录中，我们可以看到已定义的许多坐标系信息，典型的如Geographic Coordinate Systems\Asia目录下的Beijing 1954.prj，里面所定义的坐标参数描述了地理坐标系的名称、大地基准面、椭球体、起始坐标参考点、单位等。
b5E2RGbCAP
3.2投影坐标系
投影坐标系<Projected Coordinate Systems），可称为大地坐标系，指将地表弧面投影到平面坐标系的坐标值，可理解为公里网坐标。
在Projected Coordinate Systems目录中，我们可以看到已定义的许多坐标系信息，典型的如Projected Coordinate Systems\Gauss Kruger\Beijing1954目录下的Beijing 1954 GK Zonep1EanqFDPw
18N，里面所定义的坐标参数描述了投影坐标系的名称、地理坐标系、大地基准面、椭球体、起始坐标参考点、单位等。
DXDiTa9E3d
3.3 两大坐标系区别
关于地理坐标系和投影坐标系的区别，投影坐标系＝地理坐标系＋投影过程。
注意：详见压缩包“10-9.RAR、10-10.rar”中的视频RTCrpUDGiT
申明：
所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。
第三章 地图数学基础
第3章 地图数学基础
第1节 坐标系和高程系
1、地理坐标系 （2）常用地理坐标系 WGS84坐标系
第3章 地图数学基础
一种国际上采用的地心坐标系。坐标原点为地球质 心，其地心空间直角坐标系的Z轴指向BIH （国际时间
服务机构）1984.0定义的协议地球极（CTP)方向，X
轴指向BIH1984.0的零子午面和CTP赤道的交点，Y轴 与Z轴、X轴垂直构成右手坐标系，称为1984年世界大 地坐标系统。 a:6378137.0m f=1/298.257 223 563
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
每带带号与其中央经线的经度关系如下： ◆6°带：东半球λ中=（6n-3）° 西半球λ中=（6n-3）°-360° ◆3°带：东半球λ中=3n° 西半球λ中=3n°-360°
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
第3章 地图数学基础
第1节 坐标系和高程系
1、地理坐标系 （2）常用地理坐标系
第3章 地图数学基础
1954年北京坐标系 （北京坐标系） 采用苏联Krassovsky（克拉索夫斯基）椭球参数， 大地坐标原点不是在北京而在前苏联西部的普尔科夫。
1980年国家大地坐标系 （西安坐标系） 采用国际地理联合会（IGU）第十六届大会推荐的 椭球参数，大地坐标原点在陕西省西安市泾阳县永乐 镇北洪流村。
如 1:10 000（1:1万）；1:500
如 百万分之一；图上1cm相当于实地10km
第3章 地图数学基础
第2节 地图比例尺
第3章 地图数学基础
斜分比例尺，也称微分比例尺，是依据相似三角形原理制成 的图解比例尺。使量测精度达到三位数（10-3）
地图的数学基础03
2、磁北 过地面上任意一点，磁 针所指的北方，叫磁北。 其方向线叫磁方向线或 磁子午线。地图上P、 P′点或磁北、磁南点的 连线叫磁子午线。
3、坐标纵线北 地图上坐标纵线所指的 北方，叫坐标纵线北。
方位角
（二）三种方位角
1.真方位角：从真子午 线北端顺时针方向量至 某一直线的水平角，叫 真方位角。 2.磁方位角：从磁子午 线北端顺时针方向量至 某一直线的水平角，叫 磁方位角。 3.坐标方位角：从坐标 纵线北端顺时针方向量 至某一直线的水平角， 叫坐标方位角。
• 解： 1. 该点所在1:100万地形图编号为：G-49 2. 求所在1:50万地形图编号：
（1）绘制如右图 （2）注出经纬度 （3）可判断出1:50万
地形图编号为： G-49-B
3. 求1:10万地形图编号： （1）绘出1:10万图幅，如右图 （2）注出经纬度 （3）划分144幅 （4）注出经纬度 （5）根据该点位置
小比例尺地图定向
• 一般情况下，小比例尺地形图尽可能采
用北方定向
• 特殊情况，可采用斜方位定向
地图的比例尺比例尺使用
比例尺是地图缩小的比率，是指图上某线段与实地相应 水平距离之比。即
1 =l ML
地图上标注地图比例尺的形式
• 数字比例尺：例如，1:100000 • 文字比例尺（说明比例尺），例如，“十万分之一”“图
3、1：10万： 按经差30′纬差20′分幅，每幅1:100万图含144幅。代号1、2、 3……144。 例J-50-5 编号在1:100万幅编号后加上自然序数代号）
（三）1：5万 、 1：2.5万 、 1：1万；分幅编号 1、1：5万：分幅按经差15′纬差10′分幅，每幅1：10万图含4幅
编号是在1：10万幅后加上自己的序号A、B、C、D 例 J-50-5-B
3、坐标纵线北 地图上坐标纵线所指的 北方，叫坐标纵线北。
方位角
（二）三种方位角
1.真方位角：从真子午 线北端顺时针方向量至 某一直线的水平角，叫 真方位角。 2.磁方位角：从磁子午 线北端顺时针方向量至 某一直线的水平角，叫 磁方位角。 3.坐标方位角：从坐标 纵线北端顺时针方向量 至某一直线的水平角， 叫坐标方位角。
• 解： 1. 该点所在1:100万地形图编号为：G-49 2. 求所在1:50万地形图编号：
（1）绘制如右图 （2）注出经纬度 （3）可判断出1:50万
地形图编号为： G-49-B
3. 求1:10万地形图编号： （1）绘出1:10万图幅，如右图 （2）注出经纬度 （3）划分144幅 （4）注出经纬度 （5）根据该点位置
小比例尺地图定向
• 一般情况下，小比例尺地形图尽可能采
用北方定向
• 特殊情况，可采用斜方位定向
地图的比例尺比例尺使用
比例尺是地图缩小的比率，是指图上某线段与实地相应 水平距离之比。即
1 =l ML
地图上标注地图比例尺的形式
• 数字比例尺：例如，1:100000 • 文字比例尺（说明比例尺），例如，“十万分之一”“图
3、1：10万： 按经差30′纬差20′分幅，每幅1:100万图含144幅。代号1、2、 3……144。 例J-50-5 编号在1:100万幅编号后加上自然序数代号）
（三）1：5万 、 1：2.5万 、 1：1万；分幅编号 1、1：5万：分幅按经差15′纬差10′分幅，每幅1：10万图含4幅
编号是在1：10万幅后加上自己的序号A、B、C、D 例 J-50-5-B
地图数学基础
地图数学基础地图数学基础是地图上确定地理要素分布位置和几何精度的数学基础。
包括：①坐标网。
即控制制图资料转绘精度和方便用图的坐标网格。
古代以计里画方网格作为制图网，近代主要用地理坐标网和直角坐标网。
地理坐标网是按照一定投影方法，将地球椭球面上的经纬线描绘在平面上的网格。
因地图投影不同，坐标网常表现为不同系统和形状，构成有一定变形规律的经纬网格。
一般在<1：20万比例尺地形图上都绘有经纬网，>1：10万比例尺图上，图廓间绘有分度带，用以确定点位的地理坐标；②比例尺。
表示地图图形缩小程度。
通常绘注在地图上的为主比例尺，只有某些线或点符合比例尺。
一般大比例尺地图，内容较详，几何精度高，可用于图上量测，小比例尺地图，内容概括，不宜于图上量测；③大地控制网。
将地球上的自然表面转移到椭球面上，并使地图上的地理要素对于坐标网具有正确的位置。
包括平面控制网和高程控制网，前者作为平面位置的基本控制，由三角测量或导线测量方法建立，大地点的大地坐标通过投影换算成平面直角坐标，可直接控制地形测图；后者用水准测量方法建立，作为地形图上高程的基本控制。
比例尺愈大，要求表示控制点的种类和数量愈多；中小比例尺地图上由于坐标网为经纬度，一般不再表示控制点。
地图投影大比例尺：高斯-克吕格投影；中小比例尺：Lambert投影。
①我国基本比例尺地形图(1:100万、1:50万、1:25万、1:10万、1:5万、1:2.5万、1:1万、1:5000),除1:100万外均采用高斯—克吕格投影为地理基础；②我国1：100万地形图采用了Lambert投影（正轴等角割圆锥投影），其分幅原则与国际地理学会规定的全球统一使用的国际百万分之一地图投影保持一致。
为控制投影变形，高斯-克吕格投影采用6°带、3°带分带投影的方法。
我国：① 6°带： 1:2.5万-1:50万地形图② 3°带：≥1:1万比例尺地形图高斯投影坐标网经纬网①在1:5000～1:25万比例尺地形图上，经纬线只以内图廓线形式呈现，并在图幅四个角点处注明度数。
地图学的数学基础3
角度变形为零，ω =0，a=b（或θ =90°， m=n），变形椭圆是圆。在小区域内，投影后的 图形与实地是相似的，故又叫正形投影。
在一点上任何方向的长度比都相等，但在不 同地点是不同的，圆形大小不同，从大范围来讲， 投影后的图形与实地并不相似。
多用于编制航海图、洋流图和风向图等。
2）等积投影
面积变形等于零,Vp=0, P=a.b=m.n.sinθ =1。 在不同点上，变形椭圆的长、短轴发生变 化，但此消彼长，形状变化较大，角度变形比 别的投影亦大。 有利于图上面积对比。常用于对面积精度 要求较高的自然和经济地图。
正轴切圆锥投影示意图
圆锥投影变形规律图
等距正轴割圆锥投影：
特点：1.纬线呈同心圆弧，经线呈辐射的直线束； 2.两条标准纬线无长度变形； 3.两条标纬之间，变形为负，两外侧为正；
适于：东西方向长、南北方向稍宽的区域。如 苏联全图。
等积正轴割圆锥投影
特点：1.经纬线形状同等距正轴割圆锥投影。 2.由ｍ.ｎ.sinθ＝l 条件知，经线以纬线缩小 的程度放大。则两标纬外侧经线放大。内侧缩小；变 形情况如图示。 3.角度变形：离标纬愈远，变形则愈大。
一、在百万分一普通地图中应用 1. 1962年波恩百万分一国际地图会议 上提出了使用等角正割圆锥投影。 2. 1978年我国用作 1：100万分幅地形 图的投影。 3.投影特点： ①.投影带的划分：国际标准，纬差4° 为一带，从赤道起，由南到北共分15次（我 国位于北纬4°－60°）独立投影，单独计 算坐标。每带的两标纬按下式近似求出： 1=ｓ＋３0'；２=ｎ－３０ '
正轴圆柱投影示意图
切、割圆柱投影变形
等角正切圆柱投影
是荷兰学者墨卡托于1569年所创，又 名墨卡托投影。 其经线为竖直等距平行直线，纬线为 非等距垂直于经线的平行直线。
在一点上任何方向的长度比都相等，但在不 同地点是不同的，圆形大小不同，从大范围来讲， 投影后的图形与实地并不相似。
多用于编制航海图、洋流图和风向图等。
2）等积投影
面积变形等于零,Vp=0, P=a.b=m.n.sinθ =1。 在不同点上，变形椭圆的长、短轴发生变 化，但此消彼长，形状变化较大，角度变形比 别的投影亦大。 有利于图上面积对比。常用于对面积精度 要求较高的自然和经济地图。
正轴切圆锥投影示意图
圆锥投影变形规律图
等距正轴割圆锥投影：
特点：1.纬线呈同心圆弧，经线呈辐射的直线束； 2.两条标准纬线无长度变形； 3.两条标纬之间，变形为负，两外侧为正；
适于：东西方向长、南北方向稍宽的区域。如 苏联全图。
等积正轴割圆锥投影
特点：1.经纬线形状同等距正轴割圆锥投影。 2.由ｍ.ｎ.sinθ＝l 条件知，经线以纬线缩小 的程度放大。则两标纬外侧经线放大。内侧缩小；变 形情况如图示。 3.角度变形：离标纬愈远，变形则愈大。
一、在百万分一普通地图中应用 1. 1962年波恩百万分一国际地图会议 上提出了使用等角正割圆锥投影。 2. 1978年我国用作 1：100万分幅地形 图的投影。 3.投影特点： ①.投影带的划分：国际标准，纬差4° 为一带，从赤道起，由南到北共分15次（我 国位于北纬4°－60°）独立投影，单独计 算坐标。每带的两标纬按下式近似求出： 1=ｓ＋３0'；２=ｎ－３０ '
正轴圆柱投影示意图
切、割圆柱投影变形
等角正切圆柱投影
是荷兰学者墨卡托于1569年所创，又 名墨卡托投影。 其经线为竖直等距平行直线，纬线为 非等距垂直于经线的平行直线。
第三章 地图的数学基础2
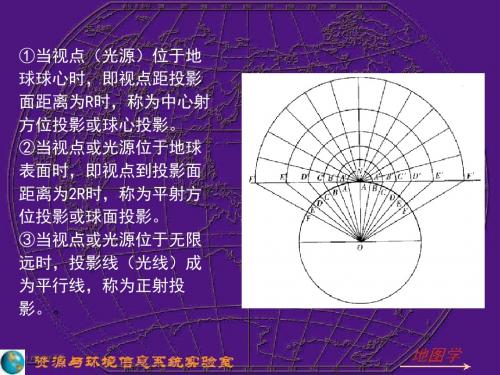
2.非透视方位投影
非透视方位投影是借助于透视 投影的方式，而附加上一定的条件， 如加上等积、等距等条件所构成的 投影。在这类投影中有等距方位投 影和等积方位投影。
二、正轴方位投影
投影中心为极点，纬线为 同心圆，经线为同心圆的半径， 两条经线间的夹角与实地相等。 等变形线都是以投影中心为圆 心的同心圆。 包括等角、等积、 等距三种变形性质，主要用于 制作两极地区图。
切圆锥投影，视点在球心，纬线投影到圆锥面上仍是圆，不同的纬线投 影为不同的圆，这些圆是互相平行的，经线投影为相交于圆锥顶点的一束直 线，如果将圆锥沿一条母线剪开展为平面，则呈扇形，其顶角小于360度， 在平面上纬线不再是圆，而是以圆锥顶点为圆心的同心圆弧，经线成为由圆 锥顶点向外放射的直线束，经线间的夹角与相应的经差成正比但比经差小。 在切圆锥投影上，圆锥面与球面相切的一条纬线投影后是不变形的线。叫做 标准纬线。它符合主比例尺，这条纬线通常位于制图区域的中间部位。从切 线向南向北，变形逐渐增大。
等角航线在墨卡托投影图 上表现为直线，这一点对于航 海航空具有重要意义。因为有 这个特征，航行时，在墨卡托 投影图上只要将出发地和目的 地连一直线，用量角器测出直 线与经线的夹角，船上的航海 罗盘按照这个角度指示船只航 行，就能达到目的地。 但是等角航线不是地球上两 点间的最短距离，地球上两点 间的最短距离是通过两点的大 圆弧，（又称大圆航线或正航 线）。大圆航线它各经线的夹 角是不等的，因此它在墨卡托 投影图上为曲线。
总
结
正轴圆柱投影特点：经纬线是互相垂直的直线，经纬 线方向是主方向。切圆柱投影，赤道是一条没有变形的线， 离开赤道越远变形越大，等变形线与纬线平行，呈平行线 状分布。 根据圆柱投影变形分布规律，这种投影适合绘制赤道附 近和沿赤道两侧呈东西方向延伸地区的地图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
线（中央经线）上；按照等角条件，用解析
法将中央经线两侧一定经差范围内椭球体面
上的经纬网投影到椭圆柱面上。
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
第3章 地图数学基础
第3节 高斯克吕格投影
一、高斯投影的基本条件
第3章 地图数学基础
1） 中央经线和赤道的投影为直线，且为投影的对 称轴； 2） 投影后无角度变形，即同一地点的各方向上长 度比不变； 3） 中央经线投影后保持长度不变，即m0=1。
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
第3章 地图数学基础
第3节 高斯克吕格投影 四、坐标网
第3章 地图数学基础
1、经纬线网：由经线和纬线所构成的坐标网，又称地理
坐标网。 意义：
（1）编制地图的控制系统之一，用以确定地面点和整
个地形的实地位置； （2）是计算和分析地图投影变形的依据，用来确定地 图比例尺和量测距离、角度和面积
的方里网，距离高斯投影带纵、横坐标轴均为整公里数。 因为是每隔整公里绘出坐标纵线和坐标横线，所以 称之为方里网，由于方里线同时又是平行于直角坐标轴 的坐标网线，故又称直角坐标网。 直角坐标网的坐标 系以中央经线投影后的直线为X轴，以赤道投影后的直 线为Y轴，它们的交点为坐标原点。这样，坐标系中就 出现了四个象限。纵坐标从赤道算起向北为正、向南为 负；横坐标从中央经线算起，向东为正、向西为负。
第3章 地图数学基础
第1节 坐标系和高程系
1、地理坐标系 （ຫໍສະໝຸດ ）常用地理坐标系第3章 地图数学基础
2000国家大地坐标系(CGCS2000) 2000国家大地坐标系是我国当前最新的大地坐标系，是 全球地心坐标系在我国的具体体现，其原点为包括海洋和 大气的整个地球的质量中心。Z轴指向BIH1984.0定义的协 议极地方向（BIH国际时间局），X轴指向BIH1984.0定义的 零子午面与协议赤道的交点，Y轴按右手坐标系确定。 a:6378137.0m f=1/298.257 222 101
第3节 高斯克吕格投影
四、坐标网
1、经纬线网
在1：50万－1： 100万地形图上， 直接绘出经纬 网，有时还绘 有供加密经纬 网的加密分割 线。
第3章 地图数学基础
第3章 地图数学基础
第3章 地图数学基础
第3节 高斯克吕格投影 四、坐标网
第3章 地图数学基础
2、方里网：由平行于投影坐标轴的两组平行线所构成
二、高斯投影变形分析
1. 2. 3. 4. 5.
第3章 地图数学基础
没有角度变形，面积比是长度比的平方; 中央经线投影后无长度变形，其余经线和全部纬线投影后 均有长度变形，长度比均大于1； 在同一经线上，纬度越低变形越大，最大值位于赤道上； 在同一纬线上，长度变形随着经差的增大而增大，且与经 差的平方近似成正比； 最大长度变形 ≤ 0.14% ，最大面积变形≤ 0.27%
第3章 地图数学基础
第3节 高斯克吕格投影
在我国1：1万－1： 25万地形图上，经 纬线只以图廓的形 式表现，经纬度数 值注记在内图廓的 四角，在内外图廓 间，绘有黑白相间 或仅用短线表示经 差、纬差1′的分度 带，需要时将对应 点相连接，就构成 很密的经纬网。
第3章 地图数学基础
第3章 地图数学基础
第3章 地图数学基础
第1节 坐标系和高程系
二、高程系
第3章 地图数学基础
高程是指由高程基准面起算的地面点高度。
海拔（绝对高程）：地面点对似大地水准面（海平面）的高度。
高程起算基准面： 黄海平均海水面 国家水准原点： 山东青岛 1985国家高程：72.260 4 m 1956年黄海高程：72.289 m
在高斯－克吕格投影上，规定以中央经线为 X 轴，赤道为 Y 轴，两轴的交点为坐标原点。 X 值 在赤道以北为正，以南为负， Y 坐标值在中经以 东为正，以西为负，我国的 X值均为正，但Y 值存 在中经西为负值的情况，运用起来很不方便，故 将各带的坐标纵轴西移 500km ，并冠以带号，称 通用坐标。
如：中国有两地面点分别为XA=432123.567米，YA=19623456.789米； XB=345678.912米，YB=38356789.123米。即此地面点A位于赤道以 北432123.567米、六度带投影的第19带，其中央子午线的经度为东 经111，位于中央子午线以东123456.789米；地面点B位于赤道以北 345678.912米、三度带投影的第38带，其中央子午线的经度为东经 114°，位于中央子午线以西143210.877米
第三章 地图数学基础
第3章
地图数学基础
• 1、坐标系和高程系
• 2、地图比例尺
• 3、高斯克吕格投影 • 4、双标准纬线圆锥投影
• 5、地图投影判别与选择
• 6、地图定向
第3章 地图数学基础
第1节 坐标系和高程系
一、坐标系
第3章 地图数学基础
与地图测绘相关的坐标系有地理坐标系和平 面坐标系。
1、地理坐标系 （1）地理坐标系的构成
最大变形点
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
第3章 地图数学基础
第3节 高斯克吕格投影 三、高斯投影分带
第3章 地图数学基础
中国国家基本比例尺地形图分带投影：
1∶1万（3°分带）从东经1°30´算起，自西向东全球共分为120个带， 我国领土位于东经72°-136°之间，共包含22个带，位于24－45带。 1∶2.5万、1∶5万、1∶10万、1∶25万、1∶50万（6°分带） 从格林威治0°经线（本初子午线），自西向东全球共分60个投影带. 我国位于13－23带,11带。
第3章 地图数学基础
第3节 高斯克吕格投影 四、坐标网
第3章 地图数学基础
3、邻带坐标网：指一幅地形图上所绘出的相邻投影带
的坐标网，即重叠绘出相邻投影带的坐标系统。 由于高斯克吕格投影的经线 是向投影带的中央经线收敛 的，它和坐标纵线有一定的 夹角，叫做子午线收敛角。 所以当相邻两带的图幅拼接 时，方里网就形成了折角， 这给地图拼接带来了很大的 困难。
第3章 地图数学基础
第3节 高斯克吕格投影
高斯投影的经纬网
第3章 地图数学基础
1）中央经线和赤道的是相互垂直的直线；
2）其余经线的投影为对称凹向中经的曲线； 3）其余纬线的投影为对称凸向赤道的曲线； 4）经纬线均正交； 5）整个图形呈东与西对称、南与北对称。
第3章 地图数学基础
第3节 高斯克吕格投影
根据地图投影变形情况，地图比例尺分为：
主比例尺 ： 在投影面上没有变形的点或线上的比例尺。 局部比例尺： 在投影面上有变形处的比例尺。
第3章 地图数学基础
第2节 地图比例尺
2. 地图比例尺的表示
① 数字式比例尺 ② 文字式比例尺 ③ 图解式比例尺
直线比例尺 斜分比例尺 复式比例尺
第3章 地图数学基础
第3章 地图数学基础
第1节 坐标系和高程系
2、平面坐标系
第3章 地图数学基础
将椭球面上的点通过地图投影的方法投影到平面上 时，通车使用平面坐标系，包括平面及坐标系和平面指 教坐标系。
（1）平面极坐标系：用某点至极点的距离和方向（矢量角） 表示该点位置的方法。
（2）平面直角坐标系：用直角坐标原理确定一点的平面位置的 方法。测绘中的平面直角坐标系与数学中所不同的地方在于X轴 和Y轴互换位置。
第3章 地图数学基础
第3节 高斯克吕格投影 四、坐标网
第3章 地图数学基础
绘有邻带方里网的区域 范围是沿经线呈带状分 布的，所以叫重叠带。 重叠带的实质是将投影 带的范围扩大，即西带 向东带延伸30′，东带 向西带延伸15′ （7.5′）。
比例尺 1:5千 1:1万 1:2.5万 1:5万 1:10万 1:25万 1:50万 1:100万
精度
0.5米
1米
2.5 米
5米
10 米
25 米
50 米
100 米
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
又名，横轴等角切椭圆柱投影。假设一
个椭圆柱面与地球椭球体面横切于某一条经
第3章 地图数学基础
国家高程控制网使用的是1985国家高程系统共有水准点成果114 041 个，水准路线长度为 416 619.1 km。 第3章 地图数学基础 10 本章首页
本节首页
10
第2节 地图比例尺
1. 地图比例尺的含义
第3章 地图数学基础
地图比例尺：地图上一直线段长度与地面相应直线水平投影 长度之比。 可表达为（d为图上距离，D为实地距离） d 1 — =— D M
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
每带带号与其中央经线的经度关系如下： ◆6°带：东半球λ 中=（6n-3）° 西半球λ 中=（6n-3）°-360° ◆3°带：东半球λ 中=3n° 西半球λ 中=3n°-360°
第3章 地图数学基础
第3节 高斯克吕格投影
第3章 地图数学基础
第3章 地图数学基础
第1节 坐标系和高程系
1、地理坐标系 （2）常用地理坐标系 WGS84坐标系
第3章 地图数学基础
一种国际上采用的地心坐标系。坐标原点为地球质 心，其地心空间直角坐标系的Z轴指向BIH （国际时间
服务机构）1984.0定义的协议地球极（CTP)方向，X
轴指向BIH1984.0的零子午面和CTP赤道的交点，Y轴 与Z轴、X轴垂直构成右手坐标系，称为1984年世界大 地坐标系统。 a:6378137.0m f=1/298.257 223 563
如 1:10 000（1:1万）；1:500