数字信号处理第三版(姚天任、江太辉) 答案 第五章-unprotected
数字信处理课后习题答案
数字信号处理(姚天任江太辉)第三版课后习题答案第二章2.1判断下列序列是否是周期序列。
若是,请确定它的最小周期(1)x(n)二Acos( 5 n86)(2)x(n )= e j(- 8 )(3) x(n )=Asi n(3 n4 3)解(1)对照正弦型序列的-般公式x(n)二 Acos( n ),得出5。
因此82 16是有理数,所以是周期序列。
5 最小周期等于N=^k 16(k取5)。
5(2)对照复指数序列的般公式x(n)二exp[ j ]n,得出1。
因此2168是无理数,所以不是周期序列。
(3)对照正弦型序列的般公式x(n)二 Acos( 3n ),又x(n)二Asin( n ) =Acos(— .门—)=Acos( —n 丄),得出3。
因此2 8是有理数,所以2 434 6 4 3是周期序列。
最小周期等于N=-k38(k 取3)2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解利用线性卷积公式y(n )= x(k)h( n k)k按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值(a) y(0)=x(0)h(0)=1y(l)=x(0)h(1)+x(1)h(0)=3y(n)=x(O)h( n)+x(1)h( n-1)+x(2)h( n-2)=4,n (b) x(n )=2 (n)- (n-1)h(n)=- (n)+2 (n-1)+ (n-2)y(n)=-2(n )+5(n-1)= (n-3)(c) y(n )=u(k)kn ka u(n k):n k 1 a n 1/ \=a = . a u(n)k i a2.3计算线性线性卷积(1) y(n )=u( n)*u( n)(2) y(n)= n u(n)*u(n)解:(1) y(n)二u(k)u(n k)ku(k)u(n k)=(n+1),n >0 k 0 即y(n)=(n+1)u(n)(2) y(n )=kku(k)u( n k)2.4图P2.4所示的是单位取样响应分别为 九(n)和h 2(n)的两个线性非移变系统的级联,已知 x(n)=u(n), h ^n)二(n)-(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出 y(n).解(n)=x( n)*h Jn)u(k)[(n-k)- (n-k-4)]k=u( n)-u( n-4)y(n)= (n)*h 2 (n)a k u(k)[u( n-k)-u( n-k-4)]k算线性卷积的方法,求系统的单位阶跃响应即 y(n)二ku(k)u(n1n 1——,n >n 1—u(n)2.5已知一个线性非移变系统的单位取样响应为h(n)二a n u(-n),0<a<1 用直接计2.6 试证明线性卷积满足交换率、结合率和加法分配率。
数字信号处理,第5章课后习题答案

第五章习题与上机题5.1 已知序列12()(),0 1 , ()()()nx n a u n a x n u n u n N =<<=--,分别求它们的自相关函数,并证明二者都是偶对称的实序列。
解:111()()()()()nn mx n n r m x n x n m a u n au n m ∞∞-=-∞=-∞=-=-∑∑当0m ≥时,122()1mmnx n ma r m aaa∞-===-∑ 当0m <时,122()1m mnx n a r m aaa -∞-===-∑ 所以,12()1mx ar m a =-2 ()()()()N x n u n u n N R n =--=22210121()()()()()1,0 =1,00, =()(1)x NN n n N mn N n m N r m x n x n m Rn R n m N m N m N m m Nm N m R m N ∞∞=-∞=-∞--=-=-=-=-⎧=--<<⎪⎪⎪⎪=-≤<⎨⎪⎪⎪⎪⎩-+-∑∑∑∑其他从1()x r m 和2()x r m 的表达式可以看出二者都是偶对称的实序列。
5.2 设()e()nTx n u n -=,T 为采样间隔。
求()x n 的自相关函数()x r m 。
解:解:()()()()e()e ()nTn m T x n n r m x n x n m u n u n m ∞∞---=-∞=-∞=-=-∑∑用5.1题计算1()x r m 的相同方法可得2e()1e m Tx Tr m --=-5.3 已知12()sin(2)sin(2)s s x n A f nT B f nT ππ=+,其中12,,,A B f f 均为常数。
求()x n 的自相关函数()x r m 。
解:解:()x n 可表为)()()(n v n u n x +=的形式,其中)2sin()(11s nT f A n u π=,=)(n v 22sin(2)s A f nT π,)(),(n v n u 的周期分别为 s T f N 111=,sT f N 221=,()x n 的周期N 则是21,N N 的最小公倍数。
《数字信号处理》第三版课后答案(完整版)

西安电子 ( 高西全丁美玉第三版 ) 数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列 (n) 及其加权和表示 题 1 图所示的序列。
解:x( n)(n4) 2 (n 2) ( n 1)2 (n)(n 1) 2 (n 2) 4 ( n 3)0.5(n 4)2 (n 6)2n 5, 4 n 12. 给定信号: x( n)6,0n 40, 其它(1)画出 x( n) 序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示 x(n) 序列;(3)令 x 1( n) 2x(n 2) ,试画出 x 1( n) 波形;(4)令 x 2 (n) 2x(n 2) ,试画出 x 2 (n) 波形;(5)令 x 3 (n) 2x(2 n) ,试画出 x 3 (n) 波形。
解:( 1) x(n) 的波形如 题 2 解图(一) 所示。
( 2)x(n)3 ( n 4)(n 3) (n 2) 3 ( n 1) 6 (n) 6 (n 1)6 ( n 2)6(n 3) 6 (n 4)( 3) x 1 (n) 的波形是 x(n) 的波形右移 2 位,在乘以 2,画出图形如 题 2 解图(二) 所示。
( 4) x 2 (n) 的波形是 x(n) 的波形左移 2 位,在乘以 2,画出图形如 题 2 解图(三) 所示。
( 5)画 x 3 (n) 时,先画 x(-n) 的波形,然后再右移2 位, x3 ( n) 波形如 题 2 解图(四) 所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1) x( n)Acos(3n) ,A 是常数;78(2)x(n)j ( 1n)e 8。
解:(1)w 3214T=14 ;7,,这是有理数,因此是周期序列,周期是w3(2)w 1 , 216 ,这是无理数,因此是非周期序列。
8w5. 设系统分别用下面的差分方程描述,x(n) 与 y(n) 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字图像处理第三版-第五章答案

第五章5.12一个带通滤波通过从相应的带阻滤波而获得:然后:(a)理想带通滤波:(b)巴特带通滤波:(c)高斯带通滤波:5.13带阻滤波器公式可以通过带通滤波器的公式得到。
两者的和为1.),(1),(v u H v u H np nr -=然后:(a) 理想带阻滤波:{01),(=v u H2.巴特带阻滤波:我不想输这个公式了,这个就是下面的巴特带通滤波的公式中1减的后面那个式子(b) 巴特带通滤波:3.高斯带阻滤波:我不想输这个公式了,这个就是下面的高斯带通滤波的公式中1减的后面中括号那个式子(c)高斯带通滤波:5.14二维连续余弦函数的傅里叶变换dxdye y v x u A dxdy e v uf v u F vy ux j vy ux j )(200)(2)cos(),(),(+-+-⎰⎰⎰⎰+==ππ余弦的变换)(21cos θθθj i e e -+=带入得到][2][2][2),()(2)2/2/(2)(2)2/2/(2)(2)()(00000000⎰⎰⎰⎰⎰⎰+-+-+-++-+-+--=+-=dxdy e e Adxdy e e A dxdy e e e A v u F vy ux j y v x u j vy ux j y v x u j vy ux j y v x u j y v x u j πππππππππ这些都是傅里叶变换的功能 并且结果变换成)]2,2()2,2([2),(0000ππδππδv v u u v v u u Av u F ++----=即可5.16从例子(5.5-13)即因此 得出当这是一个持续的形式,一个高斯密度方差或者减去的整体从无限数量的加上括号里面是1,因此这个两个题的区别比较小,但是结果有区别,在书上没有找到吧两者的答案都写上吧,英语的翻译版的估计大些,5.21解决这个问题的关键是要认识到下面给定的函数,是的二阶导数(拉普拉斯算子)的功能(参见3.6.2节有关拉普拉斯算子)即,所以,但是,我们知道这里因此,我们已经降低了计算的傅里叶变换的问题的高斯函数。
数字信处理课后习题答案

数字信号处理(姚天任江太辉)第三版课后习题答案第二章2.1判断下列序列是否是周期序列。
若是,请确定它的最小周期(1)x(n)二Acos( 5 n86)(2)x(n )= e j(- 8 )(3) x(n )=Asi n(3 n4 3)解(1)对照正弦型序列的-般公式x(n)二 Acos( n ),得出5。
因此82 16是有理数,所以是周期序列。
5 最小周期等于N=^k 16(k取5)。
5(2)对照复指数序列的般公式x(n)二exp[ j ]n,得出1。
因此2168是无理数,所以不是周期序列。
(3)对照正弦型序列的般公式x(n)二 Acos( 3n ),又x(n)二Asin( n ) =Acos(— .门—)=Acos( —n 丄),得出3。
因此2 8是有理数,所以2 434 6 4 3是周期序列。
最小周期等于N=-k38(k 取3)2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解利用线性卷积公式y(n )= x(k)h( n k)k按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值(a) y(0)=x(0)h(0)=1y(l)=x(0)h(1)+x(1)h(0)=3y(n)=x(O)h( n)+x(1)h( n-1)+x(2)h( n-2)=4,n (b) x(n )=2 (n)- (n-1)h(n)=- (n)+2 (n-1)+ (n-2)y(n)=-2(n )+5(n-1)= (n-3)(c) y(n )=u(k)kn ka u(n k):n k 1 a n 1/ \=a = . a u(n)k i a2.3计算线性线性卷积(1) y(n )=u( n)*u( n)(2) y(n)= n u(n)*u(n)解:(1) y(n)二u(k)u(n k)ku(k)u(n k)=(n+1),n >0 k 0 即y(n)=(n+1)u(n)(2) y(n )=kku(k)u( n k)2.4图P2.4所示的是单位取样响应分别为 九(n)和h 2(n)的两个线性非移变系统的级联,已知 x(n)=u(n), h ^n)二(n)-(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出 y(n).解(n)=x( n)*h Jn)u(k)[(n-k)- (n-k-4)]k=u( n)-u( n-4)y(n)= (n)*h 2 (n)a k u(k)[u( n-k)-u( n-k-4)]k算线性卷积的方法,求系统的单位阶跃响应即 y(n)二ku(k)u(n1n 1——,n >n 1—u(n)2.5已知一个线性非移变系统的单位取样响应为h(n)二a n u(-n),0<a<1 用直接计2.6 试证明线性卷积满足交换率、结合率和加法分配率。
数字信号处理(姚天任江太辉第三版)课后习题答案 清晰版

(2)y(n)= x(n)sin[
2 n+ ] 3 6
(3)y(n)=
k
x(k )
(4)y(n)=
k n0
x(k )
n
(5)y(n)= x(n)g(n)
解 (1)设 y 1 (n)=2x 1(n)+3,y 2 (n)=2x 2 (n)+3,由于 y(n)=2[x 1(n)+x 2 (n)]+3 ≠y 1 (n)+ y 2 (n) =2[x 1(n)+x 2 (n)]+6 故系统不是线性系统。 由于 y(n-k)=2x(n-k)+3,T[x(n-k)]=2x(n-k)+3,因而 y(n-k) = T[x(n-k)] 故该系统是非移变系统。 设|x(n)|≤M,则有 |y(n)|=|2x(n)+3|≤|2M+3|<∞ 故该系统是稳定系统。 因 y(n)只取决于现在和过去的输入 x(n),不取决于未来的输入,故该系统是因果系统。 (2)设
解 利用线性卷积公式 y(n)=
k
x ( k ) h( n k )
按照折叠、移位、相乘、相加、的作图方法,计算 y(n)的每一个取样值。 (a) y(0)=x(O)h(0)=1 y(l)=x(O)h(1)+x(1)h(O)=3 y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n≥2 (b) x(n)=2 (n)- (n-1) h(n)=- (n)+2 (n-1)+ (n-2) y(n)=-2 (n)+5 (n-1)= (n-3) (c) y(n)=
[
k
数字信号处理课后习题答案完整版

数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理(姚天任江太辉)第三版课后习题答案第二章判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n )(2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =在图中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
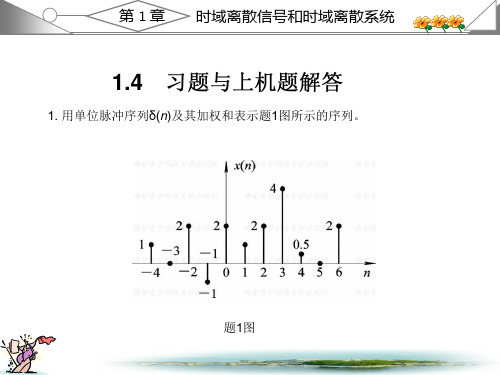
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于 x(n)和 y(n)是不相关的两个随机信号,所以在上列最后一个式子中
E[x(n) y(n)] = E[x(n)]E[ y(n)] = mxmy
因此
σ
2 ω
=
E[x2 (n)] +
E[ y 2 (n)] +
2mx m y
− 2(mx
+ my )2
+ (mx
+ my )2
=
E[x2 (n)] +
E[ y 2 (n)] −
2[Rxx (0)−
Rxx (1)]
x(n)的功率谱为
∞
∑ S xx (e jω ) = Rxx (m)e − jωn m=−∞
−∞
∞
∑ ∑ = Rxx (0) + Rxx (m)e− jωn + Rxx (m)e− jωn
m=−1
m=1
∞
∞
∑ ∑ = Rxx (0) + Rxx (−m)e jωn + e− jωn
∫ = 1
q
0 −q
xdx
=
1 2q
x2
|0−q =
−
q 2
∞
∫ mx2 = E[x2 ] = −∞ xpx2 (x)dx
∫ = 1
q
q/2 −q/2
xdx
=
1 2q
x2
|−q
/2 q/
2
=
0
∞
∫ mx3 = E[x3 ] = −∞ xpx3 (x)dx
∫ = 1
2π
2π 0
xdx =
1 4π
x2
|02π = π
cos[ω
0
(n
−
m)]
=
1 2
cos[ω 0
|
n
−
m
|]
因为 mxn 和 Rxx (m, n) 都与时间起点 n 无关, Rxx (m, n) 只与时间差|n-m|有关,所以
x(n)是广义平稳随机过程。
5.5 证明一个任意随机信号与一个与其不相关的白噪声序列相乘后,变成为一个白噪声序 列。 设任意随机信号为 x(n),白噪声序列为 e(n),它们的乘积 y(n)=x(n)e(n)。 白噪声序列 e(n)的自相关序列为
1
−(x−mx )2
e
2σ
2 x
求取样方差
2π
σ
2 x
σˆ
2 x
的方差
Var[ σˆ
2 x
]=E[( σˆ
2 x
-E[
σˆ
2 x
])]。
5.9 x(n)是零均值随机过程的取样序列,d(n)=x(n+1)-x(n)称为差分序列。设该随机过程的功
率谱是低通的即 S xx (e jω )= ⎩⎧⎨非0,ω零c ,<|ω| ω| ≤|<ωπc 此外还假设已知随机过程自相关序列的前
S xx
(e
jω
)dω
=
cosωc Rcc
(0)
=
(1 −
2 sin 2
ωc 2
) R xx
(0)
≥
(1 −
2(ωc 2
)2
) R xx
(0)
因此得
Rxx
(1)
≥
(1
−
ω
2 c
2
)
Rxx
(0)
即
Rxx (0) −
Rxx (1)
≤
ωc2 2
Rxx (0)
或
E[d 2 (n)] ≤ ωc2 E[x 2 (n)]
pxn ,ym (∞, n, y, m) = [xn ≤ ∞, ym ≤ y] 的概率=[ ym ≤ y] 的概率= Pym ( y, m)
pxn ,ym (x, n,−∞, m) = [xn ≤ x, ym ≤ −∞] 的概率=0
pxn ,ym (−∞, n, y, m) = [xn ≤ −∞, ym ≤ y] 的概率=0
因为 e(n)和 x(n)不相关,所以上式可写成
R yy
(n,
n
+
m)
=
E[ x(n) x *
(n
+
m)]E[e(n)e*
(n
+
m)]
=
Rxx
(m)Ree
(m)
=
σ
2 e
Rxx
(m)σ
(m)
因此 y(n)是白噪声序列。
5.6 遍历性过程一定是平稳的,平稳随机过程一定是遍历性的,这两个论断正确吗?为什 么?
E[x(i)x( j)] −
2
N −1 N −1
E[x(i)x( j)]
N n=0
N2 i=0 j=0
N2 i=0 j=0
∑ ∑∑ =
1 N
N −1
E[x2 (n)] −
n=0
1 N2
N −1 N −1
E[x(i)x( j)]
i=0 j=0
∑ ∑ ∑∑ =
1
N −1
E[x2 (n)] −
1
N −1
N −1 N −1
另一方面,有
∞
∞
∫ ∫ E[a xn ]= −∞ axpxn (x, n)dx =a −∞ xpxn (x, n)dx =aE[ xn ]
故随机变量的均值具有线性性质。
5.2
已知
x(n) 和
y(n) 是 不 相 关 的 两 个 随 机 信 号 , 它 们 的 方 差 分 别 是
σ
2 x
和
σ
2 y
,求
数字信号处理 答案 第五章
5.1 证明随机变量的均值的线性性质即式(5.16)和式(5.17)。 证明
∞∞
∞∞
∫ ∫ ∫ ∫ E( xn + ym )=
−∞
(x +
−∞
y) pxn ,ym (x, n, y, m)dxdy
=
−∞ −∞ xpxn ,ym (x, n, y, m)dxdy +
∞∞
∫ ∫−∞ −∞ ypxn ,ym (x, n, y, m)dxdy
=
π2 3
5.4 已知随机信号 x(n)=cos(ω0 n+φ )其中,角频率 ω0 是常数,初相φ 是在区间(0,2π )均匀分
布的随机变量。求 x(n)的均值和自相关序列,并判别 x(n)是否广义平稳随机过程。 x(n)的均值为
mxn =E[x(n)]
∫=
∞ −∞
x(n)
pθ
(θ
)dθ
∫1
= 2π
m
2 x
−
m
2 y
=
E[x 2
(n)
−
m
2 x
]
+
E[ y 2
(n)
−
m
2 y
]
= E[(x(n) = mx )2 ] + E[( y(n) − my )2 ]
=
σ
2 x
+σ
2 y
5.3 设有 3 个白噪声序列 x 1 (n)、x 2 (n)和 x 3 (n),它们分别在区间(-q,0)、(-q/2,q/2)和(0,2 π )
w(n)=x(n)+y(n)的方差
σ
2 ω
。
根据随机信号的均值的线性性质,得到
mx = E[ω(n)] = E[x(n) + y(n)] = E[x(n)] + E[ y(n)] = mx + my
σ
2 ω
=
E[(ω(n) − mω )2 ] =
E{[x(n) +
y(n) − mx
− my ]2}
其它
px3
(
x)
=
⎧⎪ ⎨
1 2π
,0
≤
⎪⎩0, 其它
x
≤
2π
其图形如图所示。
−q
px3 (x) 1 2π
px1 (x)
1 q
x
0
1 px2 (x) q
−q
qx 0
2
2
0
2π x
(2) x1(n) 、 x2 (n) 和 x3 (n) 的均值
∞
∫ mx1 = E[x1] = −∞ xpx1 (x)dx
其中
∫∞ −∞
xpxn , ym
(x, n,
y, m)dy =
x
∂ ∂x
pxn , ym
(x, n,
y, m)
|∞ y = −∞
∫∞ −∞
yp xn , ym
(x, n,
y, m)dx =
y
∂ ∂x
pxn , ym
(x, n,
y, m)
|∞
x=−∞
由于
pxn ,ym (x, n, ∞, m) = [xn ≤ x, ym ≤ ∞] 的概率=[xn ≤ x] 的概率= Pxn (x, n)
∞ −∞
(x
−
mx2
)2
px2
( x)dx
∫ = 1 q
q/2 −q / 2
x2dx
=
1 3q
x3
|q / 2
−q/
2
=
q2 12
∫ σ 2 x3
=
E[( x3
− mx3 )2 ] =
∞ −∞
(x
−
mx3
)2
px3
( x)dx
∫ = 1
2π
2π 0
(x
−π
)2 dx
=
1 6π
(x
−π )3
|02π
上呈均匀分布。 (1) 画出它们的概率密度函数图形。 (2) 计算它们各自的均值。 (3) 计算它们各自的方差。
