医学统计学第四版 课文例40-02
医学统计学第四版 课文例04-04

例4-4 某研究者采用随机区组设计进行实验,比较三种抗癌药物对小白鼠肉瘤的抑瘤效果,先将15只染有肉瘤小白鼠按体重大小配成5个区组,每个区组内3只小白鼠随机接受三种抗癌药物(具体分配方法见例4-3),以肉瘤的重量为指标,实验结果见表4-9。
问三种不同药物的抑瘤效果有无差别?表4-9 三种不同药物作用后小白鼠肉瘤重量(g )区组 A 药 B 药 C 药 1gij i X =∑1 0.82 0.65 0.51 1.98 2 0.73 0.54 0.23 1.50 3 0.43 0.34 0.28 1.05 4 0.41 0.21 0.31 0.93 5 0.68 0.43 0.24 1.351nijj X =∑3.07 2.17 1.57 6.81 ij X ∑∑i X0.6140.434 0.314 0.454 ()X21nij j X =∑2.02071.05870.54513.62452ij X ∑∑H 0:123μμμ==,即三种不同药物作用后小白鼠肉瘤重量的总体均数相等H 1:三种不同药物作用后小白鼠肉瘤重量的总体均数不全相等0.05α=按表4-8中的公式计算各离均差平方和SS 、自由度ν、均方MS 和F 值。
26.81/15 3.0917C ==3.6245 3.0917=0.5328SS =-总,ν总=15-1=14 2221(3.07 2.17 1.57) 3.09170.22805SS =++-=处理312ν=-=处理222221(1.98 1.50 1.050.93 1.35) 3.09170.22843SS =++++-=区组514ν=-=区组0.53280.22800.22840.0764SS =--=误差(51)(31)8ν=--=误差方差分析表见表4-10。
表4-10 例4-4的方差分析表变异来源 自由度 SS MS F P 总变异 14 0.5328 处理间 2 0.2280 0.1140 11.88 <0.01 区组间 4 0.2284 0.0571 5.95 <0.05 误 差80.07640.0096按ν1=2、 ν2=8查附表3的F 界值表,得F 0.05,(2,8)=4.46, F 0.01,(2,8)=8.65,11.88>F 0.01,(2,8),P <0.01。
《医学统计学》完整课件

,不损害受试者身心健康。
保护隐私
对受试者个人信息和数据进行严格保 密,防止数据泄露和滥用,确保个人
隐私不受侵犯。
公正选择受试者
遵循公平、公正原则,合理选择受试 者,避免任何形式的歧视和偏见。
数据安全与隐私保护
1 2
数据加密与备份
对医学统计数据进行加密处理,确保数据安全; 同时定期备份数据,防止数据丢失。
医学统计学的应用领域
临床试验
流行病学
在临床试验中,医学统计学用于分析试验 数据,评估治疗效果和安全性。
在流行病学研究中,医学统计学用于分析 疾病分布和影响因素,为预防和控制疾病 提供依据。
公共卫生
生物统计学
在公共卫生领域,医学统计学用于监测和 评估公共卫生状况,制定和评估公共卫生 政策。
在生物统计学中,医学统计学用于研究生 物学数据的分布和变化规律,为生物学研 究和医学研究提供支持。
生存分析中的多因素分析方法
多因素分析方法
考虑多个因素对生存时间的影响,常用方法有Cox比例风险模型和 分层分析等。
Cox比例风险模型
一种半参数模型,用于研究多个因素对生存时间的影响,并给出相 对风险比。
分层分析
将研究对象按照某些特征进行分层,然后在各层内进行统计分析,以 探讨各层内因素对生存时间的影响。
数据整理
对收集到的数据进行整理、核对和分类,确 保数据的规范化和标准化。
数据分析
选择合适的数据分析方法和技术,对数据进 行深入分析和挖掘,得出科学结论。
报告撰写
按照学术规范和要求,撰写研究报告或论文 ,客观地呈现研究结果和结论。
07
医学统计学中的伦理问题与数 据安全
《医学统计学》完整课件

详细描述
总结词
流行病学统计案例主要探讨如何运用统计学方法对流行病学数据进行分析,以评估疾病在人群中的分布和影响因素。
详细描述
流行病学研究旨在揭示疾病在人群中的分布特征和影响因素,为制定预防和控制策略提供科学依据。在流行病学研究中,统计方法的应用对于揭示疾病分布和影响因素至关重要。例如,在分析不同地区或不同人群的疾病发病率或死亡率时,研究者通常会采用描述性流行病学方法和比较流行病学方法,如率比、率差、相对危险度等指标来评估疾病分布和影响因素。此外,回归分析、逻辑回归等统计工具也被广泛应用于流行病学研究中。
详细描述
生存分析是一种专门针对生存时间数据的统计分析方法,包括描述生存时间的分布特征、比较不同组间的生存差异、预测生存时间等。在生存分析中,常用的统计方法包括Kaplan-Meier曲线、Cox比例风险模型、Log-rank检验等。这些方法可以帮助研究者了解患者的生存状况,为制定治疗方案和评估预后提供科学依据。
医学统计软件与数据分析
04
总结词
SPSS(Statistical Package for the Social Sciences)是一款广泛使用的统计软件,适用于各种社会科学数据分析。
总结词
在操作SPSS时,用户需要掌握基本的统计分析方法和数据管理技巧,以便更好地利用软件进行数据分析。
详细描述
SPSS的操作界面友好,易于上手。用户可以通过菜单和对话框选择需要的分析方法,并设置相应的参数。此外,SPSS还提供了丰富的帮助文档和教程,方便用户学习和掌握软件操作。
统计检验是用于判断样本数据是否符合某种假设或理论的过程。
统计检验的基本概念
包括提出假设、构造检验统计量、确定临界值、做出决策等步骤。
《医学统计学》完整课件课件

偏态分布及其应用
偏态分布
与正态分布不同,偏态分布的钟形曲线 存在偏斜,即数据向一侧倾斜。
VS
偏态分布的应用
在医学研究中,偏态分布的数据需要经过 适当的转换才能进行正态分布分析,如对 数转换或平方根转换。例如,一些免疫学 指标(如抗体滴度)通常呈偏态分布,需 要通过转换才能进行统计分析。
04
推论性统计方法与应用
01
利用医学统计学方法,对传染病的发生、流行趋势和影响因素
进行分析,为防控策略制定提供科学依据。
健康相关行为监测
02
通过收集和分析健康相关行为数据,如吸烟、饮酒、饮食等,
评估其与健康状况的关系,为制定干预措施提供支持。
健康相关环境监测
03
运用医学统计学方法,对空气质量、水质等环境因素进行监测
和分析,评估其对居民健康的影响。
离散程度指标
描述数据之间的差异程度,常用的指标有方差、标准差和四 分位数间距。
正态分布及其应用
正态分布
一种常见的概率分布,其特征是数据分布呈钟形曲线,且均值为正态分布的中心,标准差为分布的幅 度。
正态分布的应用
在医学研究中,正态分布被广泛应用于测量数据的统计分析,如身高、体重、血压等指标的测量值多 呈正态分布。
3
期望与方差
描述概率分布中心位置和离散程度的两个重要参 数。
参数估计与假设检验
参数估计
根据样本数据估计总体参数的过程, 常用的参数估计方法包括点估计和区 间估计。
假设检验
根据样本数据对总体参数进行假设检 验的过程,常用的假设检验方法包括t 检验、卡方检验和回归分析等。
03
描述性统计方法与应用
频数分布表与直方图
t检验与方差分析
图文《医学统计学》PPT课件

提出假设、构造检验统计量、确定拒绝域、计算p值、做出决策。
t检验和方差分析
t检验
用于比较两组均数是否有差别,包括单样本t检验、配对样本t检验和独立样本t检验。
方差分析
用于比较多组均数是否有差别,包括单因素方差分析和多因素方差分析。
卡方检验和秩和检验
卡方检验
用于推断两个或多个总体率或构成比之 间有无差别,多用于分类资料的统计分 析。
特点
以医学为背景,以数据为基础, 运用统计学方法揭示医学现象的 数量特征和规律。
发展历程及现状
发展历程
医学统计学经历了从描述性统计到推 断性统计,再到现代多元统计分析的 发展历程。
现状
随着计算机技术的发展和大数据时代 的到来,医学统计学在医学研究和实 践中发挥着越来越重要的作用。
研究对象与任务
研究对象
样本量
样本中所包含的个体数目 。
随机抽样与非随机抽样
随机抽样
按照随机原则从总体中抽取样本的方法,保证每个个体被抽 中的机会相等。
非随机抽样
根据研究者的主观意愿或方便性选择样本的方法,可能导致 选择偏倚。
变量与数据类型
变量
研究中观察或测量的特征或属性。
数据类型
根据变量的性质可分为定量数据和定性数据。定量数据包括连续型数据和离散型 数据,定性数据包括分类数据和顺序数据。
医学统计学的研究对象包括生物医学数据、临床医学数据、公共卫生数据等。
任务
医学统计学的任务包括描述医学数据的分布特征、比较不同组别间的差异、分 析影响医学现象的因素、预测医学现象的发展趋势等。
02
医学统计学基本概念
总体与样本
01
02
03
总体
《医学统计学》完整课件,超级经典!!!

对收集到的数据进行审核、分类、排序等处理,使其更加易 于分析的过程。数据的整理包括数据的清洗、分组、频数分 布等。
数据的描述性分析
描述性分析
对数据进行整理、计算和分析,以概括数据的基本特征和 规律的方法。描述性分析主要包括数据的频数分布、集中 趋势、离散程度等分析方法。
集中趋势
反映数据向某一点集中的程度,常用的指标包括平均数、 中位数和众数等。
古典概型
古典概型是概率论中最简单、最基本的概念之一, 常用于解决诸如掷骰子、摸球等问题。
条件概率与独立性
条件概率描述了两个事件之间发生的概率关 系,而独立性则描述了两个事件之间是否相 互影响。
数理统计的基本概念
总体与样本
总体是指包含所有可能观察值的集合,而样本则是总 体中的一部分,用于估计总体的特性。
复杂疾病通常受到多种因素的 影响,包括遗传、环境、生活 方式等,统计学方法需要发展 出能够处理多因素分析的工具 。
在复杂疾病研究中,确定因果 关系是至关重要的,统计学方 法需要提供更有效的工具来进 行因果推断。
医学伦理与隐私保护在统计学中的应用
伦理准则的遵循
在医学统计学研究中,需要遵循 伦理准则,尊重患者的权益和隐 私,确保研究结果的公正性和客 观性。
04
CATALOGUE
临床医学中的统计学应用
诊断试验评价
诊断试验评价的意义
对新的诊断试验方法进行科学的分析和评价 ,判断其是否具有临床应用价值。
诊断试验评价的内容
包括准确性、可靠性、可重复性、经济学评 价等方面。
常用评价指标
灵敏度、特异度、约登指数、ROC曲线等。
临床预后评估
预后评估的意义
01
《医学统计学》完整课件,超级经典!!!

GraphPad Prism等。
可视化工具的应用技巧
02
熟练使用可视化工具,掌握各种类型的图表制作方法,使数据
呈现更加专业、精准。
可视化工具的注意事项
03
注意数据呈现的规范性和科学性,避免出现错误的数据呈现方
式和解读方式。
06
医学统计Байду номын сангаас的实践应用
医学研究设计
要点一
实验设计和观察设计
介绍实验设计和观察设计的基本原则 和方法,包括随机对照试验、队列研 究、病例对照研究等。
概率与概率分布
要点一
概率
概率是用来描述某一事件发生的可能性大小的数值。在 医学统计学中,概率常常用来表示某种疾病发生的可能 性、某种治疗措施的效果等。
要点二
概率分布
概率分布是指随机变量取值对应的概率的分布情况。医 学统计学中常用的概率分布包括二项分布、正态分布和 泊松分布等。这些概率分布在医学研究中具有广泛的应 用,如样本均数和样本率的推断、相关分析和回归分析 等。
方差分析
总结词
方差分析是一种用于研究不同因素对总体 均数的影响的统计分析方法,它通过将方 差分解为各个因素的作用,从而确定因素 对总体均数的影响程度。
详细描述
方差分析的基本思想是将数据的方差分解 为各个因素的作用,从而将数据的变异分 解为可解释的变异和不可解释的变异。可 解释的变异包括因素的作用和随机误差, 不可解释的变异为随机因素的作用。通过 方差分析,我们可以判断因素的作用是否 显著,从而对总体均数的影响程度进行估 计。
20世纪中期以后,随着计算机技术和 数理统计方法的发展,医学统计学得 到了迅速发展和广泛应用。
当今,医学统计学在生命科学、临床 医学、预防保健和生物技术等领域发 挥着重要作用。
医学统计学第四版各章例题SAS与STATA实现第三章
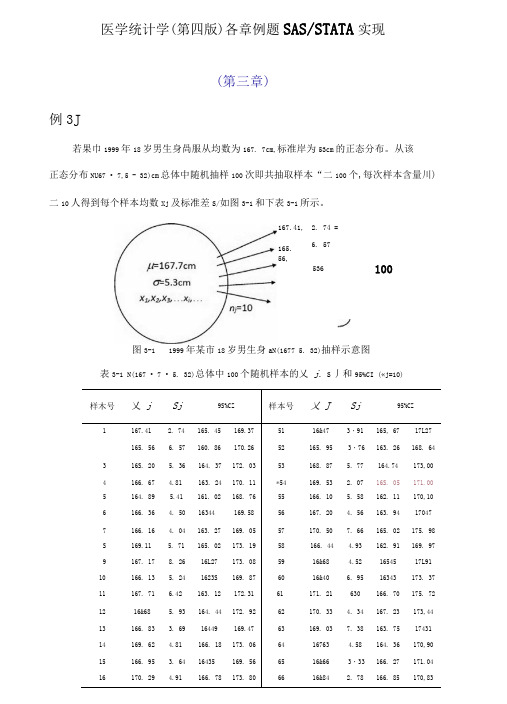
医学统计学(第四版)各章例题SAS/STATA 实现(第三章)例3J若果巾1999年18岁男生身咼服从均数为167. 7cm,标准岸为53cm 的正态分布。
从该 正态分布NU67 • 7,5 - 32)cm 总体中随机抽样100次即共抽取样本“二100个,每次样本含量川) 二10人得到每个样本均数Xj 及标准差S/如图3-1和下表3-1所示。
图3-1 1999年某市18岁男生身aN(1677 5. 32)抽样示意图表3-1 N(167 • 7 • 5. 32)总体中100个随机样本的乂 j. S 丿和95%CI («j=10)样木号乂 jSj9S%CZ样本号乂 JSj95%CZ1167.41 2. 74 165. 45 169.37 51 16&47 3・91 165, 67 17L27165. 566. 57 160. 86 170.26 52 165. 95 3・76 163. 26 168. 64 3 16S. 20 5. 36 164. 37 172. 03 53 168. 87 5. 77 164.74 173,00 4 166. 67 4.81 163. 24 170. 11 *54 169. 53 2. 07 16S. 05 171.00 5 164. 89 5.41 161. 02 168. 76 55 166. 10 5. 58 162. 11 170,10 6 166. 36 4. 50 16344 169.58 56 167. 20 4. 56 163. 94 17047 7 166. 16 4. 04 163. 27 169. 05 57 170. 50 7. 66 165. 02 175. 98 S 169.11 5. 71 165. 02 173. 19 58 166. 44 4.93 162. 91 169. 97 9 167. 178. 26 16L27 173. 08 59 16&68 4.52 16545 17L91 10 166. 13 5. 24 1623S 169. 87 60 16&40 6. 95 16343 173. 37 11 167. 71 6.42 163. 12 172.31 61 171. 21 630 166. 70 175. 72 12 16&68 5. 93 164. 44 172. 92 62 170. 33 4. 34 167. 23 173,44 13 166. 83 3. 69 16449 169.47 63 169. 03 7. 38 163. 75 17431 14 169. 62 4.81 166. 18 173. 06 64 16763 4.58 164. 36 170,90 15 166. 95 3. 64 16435 169. 56 65 16&66 3・33 166. 27 171.04 16170. 294.91166. 78173. 806616&842. 78166. 85170,83167.41, 165. 56,2. 74 = 6. 57 53610017 169. 20 5. 72 165. 11 173. 30 67 169. 31 5.31 165. 51 173. 11 1S 167. 65 2. 79 165. 65 169. 65 68 168. 46 4.81 16302 171.90 19 166. 51 5. 39 162. 65 170. 36 69 168. 60 5. 4S 164,68 172.52 •20163. 28 3. 19 16L00165. 5770 168.47 5. 05 164. 86 172,09 21 166. 29 4. 95 162.75 169. 84 71 165. 6S 5. 19 161.97 169. 40167. 65 5. 27 163S8 171.42 72 165. 68 8. 22 159. 80 171.5623 167. 64 4.61 16435 170. 94 73 168. 03 4.89 164. 53 171.5324 172.61 7. 74 167. 07 178.15 74 169. 37 5. 00 16579 172. 9425 166. 65 4. 12 163. 70 169. 59 75 169. 16 8. 36 163, 18 175,1426 165. 19 4.41 162. 04 168. 34 *76 171.27 4. 99 167.71174,8427 168. 80 7. 68 16331 174.30 77 16&36 4. 50 165, 14 171.5828 167如 2. 58 166.14 169. 83 78 168.50 3. 55 165, 96 171,0429 168.41 3.43 165. 95 170. 86 79 168. 08 5. 33 164. 27 171.9030 167. 75 7. 53 162.36 173. 13 80 165. 51 4.71 162.14 168. 88 ♦31 164. 25 4. 30 161. 17167. 33S1 167. 59 3. 73 164. 93 1702632 166. 42 5. 19 16271 170.13 *82 171. 12 4. 40 167. 98174, 2733 166. 90 4.41 163. 74 170. 05 83 165. 92 5. 11 162. 26 169.5834 166. 77 4. 34 163& 169& 84 16786 4. 44 164.69 171,0435 165. 77 5. 34 161.95 169.59 85 167. 43 6. 15 163. 03 171.8336 16442 6. 63 15938 168. 86 86 16790 6. 13 163. 51 172. 2837 169. 83 4. 20 166. 82 172. 84 87 167. 59 633 163. 06 172.1238 165. 16 4. 01 162. 29 168. 02 88 167. 744・60 16445 17L0339 166. 59 6. 20 1623 171.03 89 167. 408. 27 161. 49 173. 3240 165. 65 3. 56 163. 10 168. 20 90 167. 1S 6. 00 162. 89 171.4841 165. 72 4. 17 162.74 168.71 91 16643 3.87 163. 66 169,2142 166. 22 7. 44 1603 171.54 92 166. 62 4. 08 163. 70 169.5443 167.71 6. 12 163. 33 172. 09 93 166. 30 4.84 162. 83 169.7644 16725 5. 24 163. 50 170. 99 94 169. 70 5. 26 165. 94 1734545 165. 69 5.91 161.46 169. 92 95 169. 17 632 164. 65 173. 6946 169. 06 5. 65 165. 03 173. 10 96 167. 89 6. 07 163. 54 172. 2347 16&76 6. 14 16436 173. 15 97 167. 48 6. 03 163. 16 171.79 4S 16&64 4. 54 16539 171.89 98 169. 93 4.80 166. 50 173. 3749 167. 72 3. 82 164. 99 170. 45 99 16940 5. 57 16342 1733950 170. 39 4. 15 16742 173. 35 100 165. 69 5. 09 162, 06 16933*:表该样本资料算得的可信区间未包含已知总体均数167. 7cm例3 • 5某医生测量了36洛从事铅作业男性工人的血红蛋白含量,算得加均数为130. 83或L,标准差为25 - 74g/L.问从事铅作业工人的血红蛋白是否不同于正常成年男性平均值140gzL?⑴建立检验假设,确定检验水准Ho :严3=140g/L,即从事铅作业的男性工人平均血红蛋白含量与正常成年男性平均值H1: /岸MF140弓L 即从事铅作业的男性工人平均血红蛋白含量与正常成年男性平均值 不0=0. 05⑵讣算检验统il 嗤本例 «=36> 乂 =130 - 83g/L, 425 - 74g/L,“o=140g/L 。
