吉林省辽源市田家炳高级中学等五校2018届高三上学期期末联数学(理)试题 含解析
吉林省辽源市数学高三上学期理数期末考试试卷

吉林省辽源市数学高三上学期理数期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)设(是虚数单位),则复数的实部是()A .B .C .D .2. (2分)满足M且的集合M的个数是()A . 1B . 2C . 3D . 43. (2分)已知,则等于()A .B .C .D .4. (2分)已知向量满足,则等于()A . 2B . 3C .D . 45. (2分)球面上三点A、B、C,其中AB为球的直径,若∠ABC=30°,BC=2,则A、C两点的球面距离为()A .B .C .D .6. (2分)实数成等差数列,成等比数列,则的大小关系是()A .B .C .D .7. (2分) (2019高三上·广东月考) 已知变量,满足则的取值范围是()A .B .C .D .8. (2分) (2016高二下·渭滨期末) 从0,1,2,3,4中选取三个不同的数字组成一个三位数,其中奇数有()A . 18个B . 27个C . 36个D . 60个9. (2分)函数的值域为().A . [-2 ,2]B . [-,]C . [-1,1]D . [-, ]10. (2分) (2016高二上·大连期中) 过点M(﹣2,0)的直线m与椭圆 +y2=1交于P1、P2两点,线段P1P2的中点为P,设直线m的斜率为k1(k≠0),直线OP的斜率为k2 ,则k1k2的值为()A . 2B . ﹣2C .D . ﹣11. (2分)把1,3,6,10,15,21,…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,则第七个三角形数是()A . 21B . 28C . 32D . 3612. (2分)(2018·攀枝花模拟) 已知函数若对区间内的任意实数,都有,则实数的取值范围是()A .B .C .D .二、填空题 (共4题;共5分)13. (1分) (2017高一上·中山月考) 化简: =________.(用分数指数幂表示).14. (1分) (2017高二下·咸阳期末) (如图所示)程序框图能判断任意输入的正整数x是奇数或是偶数.其中判断框内的条件是________.15. (1分) (2015高三上·来宾期末) 已知双曲线﹣ =1(a>0,b>0)的两条渐近线与抛物线y2=2px (p>0)的准线分别交于A、B两点,O为坐标原点,若双曲线的离心率为2,△AOB的面积为,则该抛物线的标准方程是________.16. (2分)在等比数列中,若,,则(1)公比q=________;(2) |a1|+|a2|+ +|an|=________.三、解答题 (共7题;共60分)17. (10分)(2016·深圳模拟) 如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.(1)求cos∠B的值;(2)求sin∠BAC的值和边BC的长.18. (5分) (2018高二下·牡丹江月考) 一个袋中装有大小相同的黑球和白球共9个,从中任取2个球,记随机变量为取出2球中白球的个数,已知.(Ⅰ)求袋中白球的个数;(Ⅱ)求随机变量的分布列及其数学期望.19. (10分)(2018高三上·云南期末) 如图,四边形与均为菱形,,且 .(1)求证:平面;(2)求直线与平面所成角的正弦值.20. (10分)(2017·湖北模拟) 已知抛物线C:x2=2y的焦点为F,过抛物线上一点M作抛物线C的切线l,l交y轴于点N.(1)判断△MFN的形状;(2)若A,B两点在抛物线C上,点D(1,1)满足 + = ,若抛物线C上存在异于A,B的点E,使得经过A,B,E三点的圆与抛物线在点E处的有相同的切线,求点E的坐标.21. (5分)(2017·东城模拟) 已知函数f(x)=2lnx+ ﹣mx(m∈R).(Ⅰ)当m=﹣1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若f(x)在(0,+∞)上为单调递减,求m的取值范围;(Ⅲ)设0<a<b,求证:.22. (10分)(2017·新课标Ⅰ卷文) [选修4-4:坐标系与参数方程选讲]在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).(10分)(1)若a=﹣1,求C与l的交点坐标;(2)若C上的点到l距离的最大值为,求a.23. (10分) (2018高二下·阿拉善左旗期末) 设函数f(x)=|2x+1|-|x-4|.(1)解不等式f(x)>2;(2)求函数y=f(x)的最小值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、16-2、三、解答题 (共7题;共60分) 17-1、17-2、18-1、19-1、19-2、20-1、20-2、21-1、22-1、22-2、23-1、23-2、。
吉林省辽源市田家炳高级中学等五校2018届高三上学期期

友好学校第六十四届期末联考高三历史试卷说明:本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页。
考试时间90分钟,分值100分。
注意事项:1、答题前,考生必须将自己的姓名、考号填写清楚,并将条形码粘贴到指定区域。
2、选择题必须用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚。
3、请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草纸、试题卷上答题无效。
4、保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、选择题:本大题共30小题,每小题2分,共60分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.西周分封制在中国历史上影响深远。
下列各省中,其简称都不源自西周封国国名的是()A.山西、陕西 B.河南、湖北C.山东、山西 D.广东、山东2.苏东坡在《论养士》中对中国古代选官制度进行了总结:“三代以上出于学,战国至秦出于客,汉以后出于郡县吏,魏晋以来出于九品中正,隋唐至今出于科举。
”以下各项是对苏东坡这一总结的理解,其中不正确的是()A.三代时期,享有受教育及从政资格的主要是贵族B.“以客出仕”成为秦朝以前风行的做官途径C.汉代官员的选拔主要是来自全国范围的察举和征召D.古代选官制度大致可分为世官制、察举制和科举制等阶段3.中国古代常常通过分割和削弱相权来加强皇权。
下列表述正确的是()A.西汉通过削弱诸侯王势力分化相权B.宋代设立三司使来分割丞相的财权C.明太祖设立三司来分割丞相的军权D.清设军机处消除了皇权与相权矛盾4.希拉里访问希腊时曾笑称:“希腊应对实行民主政治的国家收取版税”,希拉里这样说主要是雅典政治开创了()①少数服从多数的原则②司法独立的原则③普遍选举的原则④“主权在民”的原则⑤集体领导的原则⑥“分权制衡”的原则A.①④⑤⑥B.②③④⑤ C.③④⑤⑥ D.①②③④5.英国《权利法案》、美国1787年宪法和法国1875年宪法的共同之处是()①规定了资产阶级国家政体②赋予全体公民以充分的选举权③资产阶级斗争成果的法律总结④体现了代议制民主的特征A.②③④ B.①②③ C.①②④ D.①③④6.甲午中日战争“以清政府惨败而告结束。
2018-2019学年吉林省辽源市田家炳高一上学期期末联考数学(理科)试题

2018-2019学年吉林省辽源市田家炳高级中学高一(第六十六届友好学校)上学期期末联考数学(理科)试题说 明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22小题,考试时间120分钟,分值150分。
注意事项:1. 答题前,考生必须将自己的姓名、准考证号填写清楚,并将条形码粘贴到指定区域。
2. 选择题必须用2B 铅笔填涂;非选择题必须用0.5毫米黑色中性笔书写,字体工整,笔迹清楚。
3. 按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草纸、试题卷上答题无效。
4. 保持卡面清洁,不要折叠,不要弄皱、弄破,不准使用涂改液,修正带,刮纸刀。
第Ⅰ卷 选择题(共60分)一、选择题:(本大题共12个小题,每小题5分,共60分,在每小题给出四个选项中,只有一项是符合题目要求的。
) 1. 计算cos(-780°)的值是 ( ) A .-32B .-12C. 12D. 322. 下列函数中,既是奇函数又是增函数的是 ( ) A .1+=x yB .x x y =C. xy 1=D .3x y -=3. 已知a =(1,1),b =(1,-1),则12a -32b 等于 ( ) A .(-1,2)B .(1,-2)C .(-1,-2)D .(1,2)4. 已知()mx m m y 52-+=是幂函数,且在第一象限内是单调递减的,则m 的值为 ( )A .-3B .2C .-3或2D .35. 若5.22=a , 5.2log 21=b ,5.221⎪⎭⎫ ⎝⎛=c , 则a ,b ,c 之间的大小关系是 ( )A. c > b > aB. c > a > bC. a > c > bD. b > a > c6. 要得到函数y =cos 23x π⎛⎫+ ⎪⎝⎭的图象,只需将函数y =cos 2x 的图象 ( ) A .向左平移π3个单位长度B .向左平移π6个单位长度 C .向右平移π6个单位长度 D .向右平移π3个单位长度7.函数⎪⎭⎫⎝⎛+=32tan 2πx y 的定义域为 ( ) A .{x |x ≠π12 } B .{x |x ≠-π12 } C .{x |x ≠π12+k π,k ∈Z } D .{x |x ≠π12+12k π,k ∈Z } 8. 方程3log 3=+x x 的解所在的区间为 ( )A .( 0 , 2 )B .( 1 , 2 )C .( 2 , 3 )D .( 3 , 4 )9. 设点D 为△ABC 中BC 边上的中点,O 为AD 边上靠近点A 的三等分点,则 ( ) A. =-16+12 B. =16-12 C. =56-16 D. =-56+1610. 若函数()()b x x f a +=log 的图象如图所示, 其中a ,b 为常数,则函数()b a x g x+=的图象大致是 ( )11. 在△ABC 中,若A =π4,cos B =1010,则sin C 等于 ( )A. 255 B .-255 C.55 D .-5512. 在△ABC 中,点M 是BC 的中点,AM =1,点P 在AM 上,且满足AP =2PM ,则 ·(+ ) 等于 ( )A . -43B . -49 C. 43 D. 49第Ⅱ卷 非选择题(共90分)二、填空题:(本大题共4个小题,每小题5分,共20分)13.已知函数)0f x >()1-x 32-=x ,则()2f 的值为________. 14. 设函数()0f x >=()⎪⎩⎪⎨⎧<-⎪⎭⎫ ⎝⎛≥-2,1212,1log 2x x x x ,若()10>x f ,则x 0的取值范围是________. 15.2sin 47°-3sin 17°2cos 17°=________. 16. 给出下列命题:① 函数y =cos ( 32x +π2)是奇函数;② 若α,β是第一象限角且α<β,则tan α< tan β; ③y =2 sin 32x 在区间[-π3,π2]上的最小值是-2,最大值是2;④x =π8是函数y =sin(2x +54π)的一条对称轴. 其中正确命题的序号是________.三、解答题:(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(10分) 已知集合A= {x |y =x m -+1错误!未找到引用源。
吉林省辽源市五校2018届高三数学上学期期末联考试题文

试卷答案和视频讲解课程请登录听课网 或者学霸网 下载吉林省辽源市五校2018届高三数学上学期期末联考试题 文说 明:本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
考试时间120分钟,分值150分。
注意事项:1、答题前,考生必须将自己的姓名、考号填写清楚,并将条形码粘贴到指定区域。
2、选择题必须用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚。
3、请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草纸、试题卷上答题无效。
4、保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、 选择题 (本大题共12小题,每小题5分,共60分) 1. 已知集合{}⎭⎬⎫⎩⎨⎧≤-=≤-=02,01x x xQ x x P ,则()Q P C R ⋂( ) A.()1,0 B.(]2,0 C.(]2,1 D.[]2,12. 下列命题中的假命题是( )A.0log ,2=∈∃x R xB.0,2>∈∀x R x C.1cos ,=∈∃x R x D.02,>∈∀xR x 3.已知两条直线n m 、,两个平面βα、,给出下面四个命题:①α∥m n m ⇒⊂⊂βαβ,,∥n ; ②m ∥n ,m ∥n ⇒α∥α; ③m ∥n ,⊥m αα⊥⇒n ; ④α∥m ,β∥βα⊥⇒⊥n m n ,。
其中正确命题的序号是( )A. ①③B. ③④C. ①④D. ②③ 4. 某几何体的三视图如图,则几何体的体积为 A. 8π+16 B. 8π-16 C. 16π﹣8 D. 8π+85. 已知变量x ,y 满足约束条⎪⎩⎪⎨⎧≤-≥+≥-4211y x y x y x ,则y x z +=3的最大值为()A. 2B.6C. 8D. 116. 已知等比数列{}n a 的前n 项和12-=nn S ,则数列{}n a 2log 的前12项和等于( )A. 66B. 55C. 45D.657. 如图所示,向量C B A c OC b OB a OA ,,,,,===在一条直线上,且CB AC 4-=则( )A. b a c 2321+=B.b a c 2123-= C.b a c 2+-= D.b a c 3431+-=8. 函数()()10log <<=a xx x x f a 图象的大致形状是( )A. B. C. D.9. 定义域为R 上的奇函数()x f 满足()()11+=+-x f x f ,且()11=-f ,则()=2017f ( )A. 2B. 1C. -1D. -210. 已知函数()()0cos 3sin >-=ωωωx x x f 的图象与x 轴的两个相邻交点的距离等于4π,若将函数()x f y =的图象向左平移6π个单位得到函数()x g y =的图象,则在下列区间中使()x g y =是减函数的是( ) A.⎪⎭⎫ ⎝⎛-0,3π B. ⎪⎭⎫ ⎝⎛247,24ππ C. ⎪⎭⎫⎝⎛3,0π D.⎪⎭⎫ ⎝⎛3,4ππ11. 设F 为双曲线()0,01:2222>>=-b a by a x C 的右焦点,过坐标原点的直线依次与双曲线C 的左、右支交于点Q P 、,若︒=∠=60,2PQF QF PQ ,则该双曲线的离心率为( ) A. 31+ B. 3 C. 32+D. 324+12. 设函数()x f '是奇函数()x f (x ∈R )的导函数, ()01=-f ,且当0>x 时,0)()(>-'x f x f x ,则使得()0>x f 成立的x 的取值范围是 ( )A. ()()∞+⋃,10,1- B. ()()1,01--⋃∞, C. ()()0,1-1--⋃∞, D.()()+∞⋃,11,0 第II 卷二、 填空题(本大题共4小题,每小题5分 ,共20分)13. 设向量()()1,1,2,1--==b a ,若b a -与b a m +垂直,则m 的值为__ __. 14. 若函数()b ax x x f ++=2的两个零点是-1和2,则不等式()02>-x af 的解集是_____.15. 数列{}n a 中, ==+=+1011,2,31a a a a a nnn 则 ______ .16. 已知a ,b ,c 分别是△ABC 的三个内角A ,B ,C 所对的边,若32=b ,三内角A ,B ,C 成等差数列,则该三角形的外接圆半径等于______________.三、 解答题(本大题共6小题,共70分。
吉林省辽源市田家炳高中友好学校高三上学期期末数学试卷(理科)含解析.doc

2016-2017学年吉林省辽源市田家炳高中友好学校高三(上)期末数学试卷(理科)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出四个选项中,只有一项是符合题目要求的.)1.若集合A={ - 1, 0, 1}, B={y|y=x2, x^A},贝lj AAB=()A. {0}B. {1} C・{0, 1} D. {0, - 1}2.下列函数屮,既不是奇函数,也不是偶函数的是()A. y二x+sinxB. y=xsinxC. y二x+cosxD. y=xcosx3.命题"3x o eR, 2 的否定为()A. VxeR, 2x^0B. VxeR, 2x^0C. VxeR, 2x<0 D・ VxeR, 2x>04.若aeR,贝Ija二2 是(a - 1)(a - 2)二0 的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.向量;二(・2,・1), b=(入,1),若;与7夹角为钝角,则入取值范围是()A.(一寺,2) U (2, +oo)B. (2, +8)C. (-*, +8)D. ( - 8,-6.一个几何体的三视图如图所示,则该几何体的表面积是()A. 6+8A/3B. 12+8^3C. 12+7嶺D. 18+2嶺7.设函数f (x) =xe x,贝I」( )侧视图A. x二1为f (x)的极大值点B. x"为f (x)的极小值点C. x=-l为f (x)的极大值点D. x=- 1为f (x)的极小值点&如果关于X 的不等式(a - 2) X 2+2 (a - 2) x - 4<0对一切实数x 恒成立,则实 数a 的取值范围是()A. ( 一 8, 2]B. ( 一 8, - 2)C. (一 2, 2]( )C.咔D.平2 211.已知数列{aj 的通项公式为a n =^YY (nGN ),其前n 项和S n =^,贝V 直线盘+討与坐标轴所围成三角形的面积为()A. 36B. 45C. 50D. 5512. 若直角坐标平面内A 、B 两点满足条件:①点A 、B 都在f (x)的图象上;②点A 、B 关于原点对称,则对称点对(A, B)是函数的一个〃姊妹点对〃(点对(A,(x)的“姊妹点对〃有( )个・A. 1B. 2C. 3D. 4二、填空题(本大题共4个小题,每小题5分,共20分)^-7>013. 己知x, y 满足< x+y- 4>0,则z=4x+y 的最小值为 ________ ・.x<414. T Q (e x +2x) dx= ______ ・15. 已知三棱锥S-ABC 的三条侧棱两两垂直,且SA=2, SB=SC=4,则该三棱锥的 外接球的半径为—・2 2D. ( - 2, 2) 9.己知向量;二(x- 1, A. 2 B. 2V3C. 6 2), b =( 4, y) 9 右 3 丄 b ,D. 9则9x +3y的最小值为( )10.已知两点A (・2,0), B (0, 2),点 C 是圆x 2+y 2 - 2x=0上的任意一点,则AABC 的面积最小值是 B)与(B, A)可看作同一个〃姊妹点对〃)・已知函数f (x)= X 2+2X 0_2_ Xe”则fA. 3 - V2 B ・ 3+V216.设椭圆C:七+冷■二1 (a>b>0)的左、右焦点分别为Fi,F2, P是C上的点,a bPF2丄FiF2, ZPF1F2=30°,则C的离心率为三、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.等差数列心讣中,a2=8, S6=66(1)求数列{aj的通项公式a.;、2 、(2)设bn二(n+])n , Tn二bi+b2+b3+.・.+bn,求Tn・18.已知函数f (x) =V3 (cos2x - sin'x) +2sinxcosx(1)求f (x)的最小正周期;(2)设xG[-^,中,求f (x)的值域和单调递减区间.19.设ZSABC的内角A、B、C所对的边长分别为a、b、c,且满足a2+c2 - b2=V3ac(1)求角B的大小;(2)若2bcosA=V3(ccosA+acosC), BC边上的中线AM的长为W,求△ABC的面积.20.如图,已知四棱锥P - ABCD,底面ABCD为菱形,PA丄平面ABCD, ZABC二60°, E, F 分别是BC, PC的中点.(1)证明:AE丄PD;(2)若PA=AB=2,求二而角E - AF - C的余弦值.21.已知椭圆青+冷二1 (a>b>0)的离心率e二耍,坐标原点到直线I: y二bx+2a b $的距离为伍,(1)求椭圆的方程;(2)若直线y二kx+2 (k#0)与椭圆相交于C、D两点,是否存在实数k,使得以CD为直径的圆过点E (- 1, 0) ?若存在,求出k的值,若不存在,请说明理由.22.已知函数f (x) =^x2+lnx.(1)求函数f (x)在区间[1, e]上的最小值及最大值(2)求证:在区间(1, +->)上,函数f (x)的图象在函数g (x)二^x3的图象的下方.2016-2017学年吉林省辽源市田家炳高中友好学校高三(上)期末数学试卷(理科)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出四个选项中,只有一项是符合题目要求的•)1.若集合A={ - 1, 0, 1}, B={y|y=x2, xGA},则AAB=( )A. {0}B. {1} C・{0, 1} D. {0, - 1}【考点】交集及其运算.【分析】把A中元素代入B中解析式求出y的值,确定出B,找出两集合的交集即可. 【解答】解:把A屮x= - 1, 0, 1代入B中得:y=0, 1,即B={0, 1},则AQB二{0, 1},故选:C.3.命题"3x0eR, 2 ®W0〃的否定为( )A. VxER, 2X^OB. VxER, 2X^O C・ VxER, 2x<0 D・ VxGR, 2x>02 下列函数中,既不是奇函数,也不是偶函数的是( )A. y二x+sinxB. y=xsinxC. y二x+cosxD. y=xcosx【考点】余弦函数的奇偶性.【分析】直接利用函数奇偶性的定义逐一判断四个选项得答案.【解答】解:函数y二f (x) =x+sinx的定义域为R,且f (・x)=-f (x), Ay=x+sinx 为奇函数;y=f (x) =xsinx 的定义域为R,且f ( - x) =f (x), /.y=xsinx 为偶函数;y二x+cosx 的定义域为R,由f ( -x) - f (x) =0,得-x+cosx - x - cosx=0,得x=0, 不满足对任意x都成立,由f ( - x) +f (x) =0,得-x+cosx+x+cosx=0,得COSX=0,不满足对任意X 都成立,・・.y二x+cosx为非奇非偶函数;y=f (x) =xcosx 的定义域为R,且f(-x) = - f (x), /. y=xcosx 为奇函数. 故选:C.【考点】命题的否定.【分析】直接利用特称命题的否定是全称命题写出结果即可.【解答】解:因为特称命题的否定是全称命题,所以命题T XO UR, 2 ®WO〃的否定为:VxER, 2x>0.故选:D.4.若aGR,贝I」a二2 是(a - 1) (a -2)二0 的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据一•元二次方程根的定义,我们判断出a=2^ (a-1) (a-2)二0及(a-1)(a-2) =0=>a=2的真假,进而根据充要条件的定义即可得到答案.【解答】解:当a=2时,(a - 1) (a - 2) =0成立故a二2今(a - 1) (a-2) =0为真命题而当(a - 1) (a-2) =0, a二1或a二2,即a=2不一定成立故(a - 1) (a - 2) =0=>a=2 为假命题故a=2是(a - 1) (a-2) =0的充分不必要条件故选A5.向量;二(-2, -1), b=(X, 1),若;与7夹角为钝角,则入取值范围是( ) A. ( -p 2) U (2, +oo) B. (2, +oo) C・(一寺,+G D. ( - p -【考点】平面向量数量积的运算.【分析】由于;与1夹角为钝角,可知;•©- 2X-K0,且亏与丫夹角不为平角,解出即可.【解答】解:Va 与7夹角为钝角,・・・;込=-2入-1<0,解得入〉-寺, 当入二2时,:与E 夹角为平角,不符合题意. 因此(一*, 2) U (2, +8). 故选:A.6. 一个儿何体的三视图如图所示,则该儿何体的表面积是( )A. 6+8価B. 12+8眉C. 12+7価D. 18+20【考点】由三视图求面积、体积.【分析】几何体是一个直三棱柱,.三棱柱的底面是一个腰长为2的,底边上的高 是1的等腰三角形,侧棱长是3,根据三棱柱的表面积包括三部分,写出表示式, 得到结果.【解答】解:・・•由题意知几何体是一个直三棱柱, 三棱柱的底面是一个腰长为2的,底边上的高是1的等腰三角形,侧棱长是3, ・•・三棱柱的表面积是2X-^X2^Xl+3 (2+2+2佝 二12+8佰 故选B.7. 设函数f (x) =xe x ,贝I 」( )A. x=l 为f (x)的极大值点B. x=l 为f (x)的极小值点C. x 二・1.为f (x)的极大值点D. x= - 1为f (x)的极小值点【考点】利用导数研究函数的极值.【分析】由题意,可先求出f‘ (x) = (x+1) e x ,利用导数研究出函数的单调性,即 可得出为f (x)的极小值点侧视图【解答】解:由于f(X)=xe x,可得F (x) = (x+1) e x,令F (x) = (x+1) M二o 可得x二-1令F (x) = (x+1)疋>0可得x> - 1,即函数在(-1, +8)上是增函数令f (x) = (x+1) e x<0可得x< - 1,即函数在(- 8, - 1)上是减函数所以x= - 1为f(X)的极小值点故选D8.如果关于x的不等式(a - 2) X2+2 (a-2) x-4<0对一切实数x恒成立,则实数a的取值范围是( )A. (-8, 2]B. ( - oo, - 2)C. ( -2, 2]D. ( - 2, 2)【考点】函数恒成立问题.【分析】分二次项系数为0和不为0讨论,当二次项系数不为0时,借助于二次函数的开口方向和判别式列不等式组求解.【解答】解:关于x的不等式(a-2) X2+2 (a-2) x - 4<0对一切实数x恒成立, 当a=2时,对于一切实数x,不等式(a-2) x2+2 (a-2) x - 4< 0恒成立;当时,要使对于一切实数x,不等式(a・2) x2+2 (a-2) x-4 VO恒成立,fa - 2<C0则「/ 「2 z 、f 、八解得:・2<a<2.I [2(a-2) ]2 - 4(a- 2)(- 4)<0综上,实数a的取值范围是(-2, 2].故选:C.9.已知向量;二(x- 1, 2), b=(4, y),若;丄丫,则9x+3y的最小值为( )A. 2B. 2V3C. 6D. 9【考点】基木不等式;数量积判断两个平面向量的垂直关系.【分析】由于;丄10;兀=0,即可得岀x, y的关系,再利用基本不等式即可得出9乂+3丫的最小值.【解答】解:V a 丄亍,・•・(x - 1, 2) • (4, y) =0,化为4 (x- 1) +2y=0,即2x+y=2.A9x+3y^ 2732x-3y= 2』32x+y二2佇二6,当且仅当2x=y=l 时取等号.故选C.10. 已知两点A ( - 2, 0), B (0, 2),点C 是圆x 2+y 2 - 2x=0 ±的任意一点,则AABC 的面积最小值是( )【考点】直线和圆的方程的应用.【分析】求出直线方程,圆心坐标与半径,从而可得圆上的点到直线距离的最小 值进而可求AABC 的面积最小值.【解答】解: 圆 x 2+y 2 - 2x=0,可化为(x - 1) 2+y 2=l, ・・・圆心(1,0)到直线的距离为」膵2L普・•・圆上的点到直线距离的最小值为型2 - 1AB =2近故选A.11. 已知数列{aj 的通项公式为a n =-4^Y(nGN9,其前n 项和S“二鲁,贝0直线 号+兰二1与坐标轴所围成三角形的面积为( )n+1 nA. 36B. 45C. 50 D ・ 55【考点】数列的求和;直线的截距式方程.【分析】利用裂项相消法求出S n ,由%二猪求出n 值,从而得到直线方程,易求 该直线与坐标轴的交点,利用三角形面积公式可得答案. 【解答】解:3产占=『禽’ 则Sn=i 44_14_i + …片「击 “ _ 禽,q1 a由 Sn=w‘ 即 1 - > 解得 n=9,A. 3 ・ B ・ 3+V2C..•.△ABC 的面积最小值是 (3孑 _1)x 2^/2= 3 ~ V2即 x - y+2=0D.直线AB 的方程为所以直线方程为斋亡二1,令x=0 得y=9,令y=0 得x=10,故选B.12.若直角坐标平面内A、B两点满足条件:①点A、B都在f (x)的图象上;② 点A、B关于原点对称,则对称点对(A, B)是函数的一个"姊妹点对〃(点对(A,(X2+2X X<COB)与(B, A)可看作同一个〃姊妹点对〃)・已知函数f (x) = 2 贝畀le(x)的"姊妹点对〃有( )个.A. 1B. 2C. 3D. 4【考点】函数的值.【分析】首先弄清关于原点对称的点的特点,进而把问题转化为求方程-I匸二-(X2+2X)的根的个数,再转化为求函数4)(x) =2e x+x2+2x零点的个数即可.e【解答】解:设P(X, y) (x<0),则点P关于原点的对称点为P f ( -X, -y),于是化为2e x+x2+2x=0,e令4>(X)=2e x+x2+2x,下面证明方程4)(x)二0有两解.2由X2+2X^0,解得-2WxW0,而二■>() (x$0),・•・只要考虑xe [ - 2, 0]即可.e求导& (x) =2e x+2x+2,令g (x) =2e x+2x+2,贝lj g (x) =2e x+2>0,・・・4)' (x)在区间[-2, 0]上单调递增,而& ( - 2) =2e'2 - 4+2<0, ^ ( - 1) =2e x>0,・・・4)(X)在区间(-2, 0)上只存在一个极值点x°・而4)( - 2) =2e_2>0, 4)( - 1) =2e_1 - 1<0, 4)(0) =2>0,・・・函数4)(X)在区间(・2,・1), ( - 1, 0)分别各有一个零点.也就是说f (x)的〃姊妹点对〃有两个.故选B.二、填空题(本大题共4个小题,每小题5分,共20分)fx-y>013.已知x, y满足《x+y - 4》0,则z=4x+y的最小值为10・、x<4【考点】简单线性规划.【分析】已知不等式组对应的平面区域是三角形ABC及其内部,在直线I: z二2x+y 扫过三角形区域的情况下,将它进行平移,可得当I经过点A (1, 0)时,z取得最小值2.y>0将直线I: z二4x+y进行平移,可得当直线I经过点B时,z取得最小值, fx _ y=0由丄川"解得B(2,2)时,z取得最小值,x+y一4=0A z mjn=2X 4+2=10.故答案为:10.14 ・ J $ (e x+2x) dx= e ・【考点】定积分.【分析】找出被积函数的原函数,然后计算.【解答】解:T Q (e x+2x) dx= (e x+x2) | g=e+l - l=e;故答案为:e;15.已知三棱锥S-ABC的三条侧棱两两垂直,且SA=2, SB=SC=4,则该三棱锥的外接球的半径为3・【考点】球的体积和表面积.【分析】三棱锥扩展为四棱柱(长方体),两个几何体的外接球是同一个球,求岀四棱锥的对角线的长度就是外接球的直径,即可求解半径.【解答】解:三棱锥S-ABC的三条侧棱两两垂直,且SA=2, SB=SC=4,则该三棱锥的外接球,就是三棱锥扩展为长方体的外接球,所以长方体的对角线的长度为:寸22 + 4?+42=6,所以该三棱锥的外接球的半径为:3.故答案为:3.2 216.设椭圆C:七+冷"(a>b>0)的左、右焦点分别为Fi,F2, P是C上的点, a bPF2丄FiF2, ZPF1F2二30°,则C的离心率为富・3【考点】椭圆的简单性质.【分析】设|PF2|=X,在直角三角形PF1F2中,依题意可求得|PFj与|FiF2|,利用椭圆离心率的性质即可求得答案.【解答】解:IPF2I二x,・・・PF2丄F1F2,ZPF1F2=30°,I PFi I =2x, I F I F2 =V3x>又|PF1| + |PF2|=2a,下卄2丨二2c•I2a=3x, 2c二眉x,・・・C的离心率为:e=-=^・a 3故答案为:三、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)17. 等差数列{a n }中,a 2=8, S 6=66 (1) 求数列{aj 的通项公式a.;2(2) 设 bn 二(口+1)务,T n =bi+b 2+b 3+...+bn ,求【考点】等差数列的前n 项和;等差数列的通项公式.(ai+d=8【分析】设等差数列{aj 的公差为d,则有。
2018届高三上学期期末联考数学(理)试题有答案-精品

2017—2018学年度第一学期期末联考试题高三数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分全卷满分150分,考试时间120分钟.注意:1. 考生在答题前,请务必将自己的姓名、准考证号等信息填在答题卡上.2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试卷上无效.3. 填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内.答在试题卷上无效.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.把答案填在答题卡上对应题号后的框内,答在试卷上无效.1.设集合{123}A =,,,{45}B =,,{|}M x x a b a A b B ==+∈∈,,,则M 中的元素个数为A .3B .4C .5D .62.在北京召开的第24届国际数学家大会的会议,会议是根据中国古代数学家赵爽的弦图(如图)设计的,其由四个全等的直角三角形和一个正方形组成,若直角三角形的直角边的边长分别是3和4,在绘图内随机取一点,则此点取自直角三角形部分的概率为 A .125B .925C .1625D .24253.设i 为虚数单位,则下列命题成立的是A .a ∀∈R ,复数3i a --是纯虚数B .在复平面内i(2i)-对应的点位于第三限象C .若复数12i z =--,则存在复数1z ,使得1z z ∈RD .x ∈R ,方程2i 0x x +=无解4.等比数列{}n a 的前n 项和为n S ,已知3215109S a a a =+=,,则1a =A .19B .19-C .13D .13-5.已知曲线421y x ax =++在点(1(1))f --,处切线的斜率为8,则(1)f -=试卷类型:A天门 仙桃 潜江A .7B .-4C .-7D .4 6.84(1)(1)x y ++的展开式中22x y 的系数是A .56B .84C .112D .1687.已知一个空间几何体的三视图如图,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 A .4cm 3B .5 cm 3C .6 cm 3D .7 cm 38.函数()sin()(0,0)f x A x A ωϕω=+>>的图像如图所示,则(1)(2)(3)(18)f f f f ++++的值等于ABC 2D .19.某算法的程序框图如图所示,其中输入的变量x 在1,2,3…,24 这24个整数中等可能随机产生。
吉林省辽源一中2018-2019学年高三上学期期末考试试题理(数学)
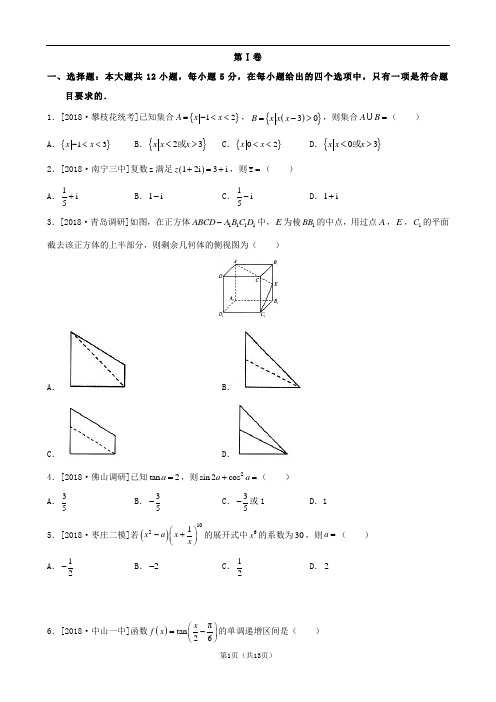
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2018·攀枝花统考]已知集合{}12A x x =-<<,(){}30B x x x =->,则集合AB =( ) A .{}13x x -<< B .{}23x x x <>或C .{}02x x <<D .{}03x x x <>或 2.[2018·南宁三中]复数z 满足()12i 3i z +=+,则z =( )A .1i 5+B .1i -C .1i 5-D .1i +3.[2018·青岛调研]如图,在正方体1111ABCD A B C D -中,E 为棱1BB 的中点,用过点A ,E ,1C 的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )A .B .C .D .4.[2018·佛山调研]已知tan 2a =,则2sin 2cos a a +=( )A .35B .35-C .35-或1 D .1 5.[2018·枣庄二模]若()1021x a x x ⎛⎫-+ ⎪⎝⎭的展开式中6x 的系数为30,则a =( ) A .12- B .2- C .12 D .26.[2018·中山一中]函数()πtan 26x f x ⎛⎫=- ⎪⎝⎭的单调递增区间是( )A .2π4π2π,2π33k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z B .2π4π2π,2π33k k ⎛⎫-+ ⎪⎝⎭,k ∈Z C .2π4π4π,4π33k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z D .2π4π4π,4π33k k ⎛⎫-+ ⎪⎝⎭,k ∈Z 7.[2018·山师附中]函数()f x 是R 上的偶函数,且()()1f x f x +=-,若()f x 在[]1,0-上单调递减,则函数()f x 在[]3,5上是( )A .增函数B .减函数C .先增后减的函数D .先减后增的函数8.[2018·棠湖中学]已知两点(),0A a ,()(),00B a a ->,若曲线22230x y y +--+=上存在点P ,使得90APB ∠=︒,则正实数a 的取值范围为( )A .(]0,3B .[]1,2C .[]2,3D .[]1,39.[2018·优创名校]函数()211ln 22f x x x =+-的图象大致为( ) A . B .C .D .10.[2018·南海中学]已知双曲线()222210,0x y a b a b-=>>的右焦点为F ,点A 在双曲线的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为( )A .2213x y -=B .2213y x -=C .221412x y -= D .221124x y -=11.[2018·黄陵中学]在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =,c =,tan 21tan A c B b+=,则C ∠=( )A .π6B .π4C .π4或3π4D .π312.[2018·开封月考]已知空间四边形ABCD ,2π3BAC ∠=,AB AC ==6BD CD ==,且平面ABC ⊥平面BCD ,则空间四边形ABCD 的外接球的表面积为( )A .60πB .36πC .24πD .12π第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2018·南康模拟]已知单位向量a ,b 的夹角为60︒,则()()23+⋅-=a b a b ________. 14.[2018·曲靖统测]随机变量ξ服从正态分布()2,N ξμσ~,若()20241P μξμ-<≤=.,则()2P ξμ>+=__________.15.[2018·高新区月考]若实数x ,y 满足不等式组00220y x y x y ≥⎧⎪-≥⎨⎪--≥⎩,则11y w x -=+的取值范围是__________. 16.[2018·盐城期中]已知函数()2221f x x ax a =-+-,()2g x x a =-,[]11,1x ∀∈-,[]21,1x ∃∈-,使()()21f x g x =,则实数a 的取值范围是__________.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(12分)[2018·华侨中学]已知数列{}n a 的前n 项和为n S ,且22n S n n =+.(1)求数列{}n a 的通项公式;(2)求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .18.(12分)[2018·唐山摸底]甲、乙两位工人分别用两种不同工艺生产同一种零件,已知尺寸在[]223,228(单位:mm )内的零件为一等品,其余为二等品,测量甲乙当天生产零件尺寸的茎叶图如图所示:。
2018-2019学年吉林省辽源市田家炳高级中学高一上学期期末联考(理)数学试题(答案+解析)

吉林省辽源市田家炳高级中学2018-2019学年高一上学期期末联考数学(理)试题一、选择题:(在每小题给出四个选项中,只有一项是符合题目要求的。
)1.计算cos(-780°)的值是()A. -B. -C.D.[答案]C[解析]cos(-780°)=cos780°=cos60°=.故选:C.2.下列函数中,既是奇函数又是增函数的是()A. B. C. D.[答案]B[解析]A.非奇非偶函数;B.奇函数且是单调递增函数;C.奇函数但在定义域上不是增函数;D. 奇函数,单调递减函数;故选B.3.已知a=(1,1),b=(1,-1),则a-b等于()A. (-1,2)B. (1,-2)C. (-1,-2)D. (1,2)[答案]A[解析]根据题意可得,故选A.4.已知是幂函数,且在第一象限内是单调递减的,则m的值为()A. -3B. 2C. -3或2D. 3[答案]A[解析]由y=(m2+m-5)x m是幂函数,知m2+m-5=1,解得m=2或m=-3.∵该函数在第一象限内是单调递减的,∴m<0.故m=-3.故选:A.5.若,,,则a,b,c之间的大小关系是()A. c>b>aB. c>a>bC. a>c>bD. b>a>c[答案]C[解析]∵a=22.5>1,<0,,∴a>c>b,故选:C.6.要得到函数y=cos的图象,只需将函数y=cos2的图象()A. 向左平移个单位长度B. 向左平移个单位长度C. 向右平移个单位长度D. 向右平移个单位长度[答案]B[解析]∵,∴要得到函数的图像,只需将函数的图像向左平移个单位.选B.7.函数的定义域为()A. {|≠}B. {|≠-}C. {|≠+kπ,k∈Z }D. {|≠+kπ,k∈Z }[答案]D[解析]由,k∈Z,即≠+kπ,k∈Z,即函数的定义域为{|≠+kπ,k∈Z },故选D.8.方程的解所在的区间为()A. (0,2 )B. (1,2 )C. (2,3 )D. (3,4 )[答案]C[解析]令,则在上单调递增.且,所以方程的解所在的区间为.故选C.9.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则()A. B.C. D.[答案]D[解析]由题意:.本题选择D选项.10.若函数的图象如图所示,其中a,b为常数,则函数的图象大致是( )A. B.C. D.[答案]D[解析]由于函数图像的单调性底数a小于1,则函数也是单调递减,则排除A,B,然后因为的定义域x>-1,则说明b=1,从而过点(0,2),排除C,选D.11.在△ABC中,若A=,cos B=,则sin C等于()A. B. -C. D. -[答案]A[解析]∵cos B=,∴B为锐角,则,则故选A. 12.在△ABC中,点M是BC的中点,AM=1,点P在AM上,且满足AP=2PM,则等于()A. -B. -C.D.[答案]B[解析]∵M是BC的中点,知AM是BC边上的中线,又由点P在AM上且满足,∴P是三角形ABC的重心,∴又∵AM=1,∴,∴.故选:B.二、填空题.13.已知函数,则的值为___.[答案]6[解析]令x-1=2,可得x=3,故f(2)=32-3=6,故答案为6.14.设函数=,若,则x0的取值范围是____.[答案](-∞,-1)∪(3,+∞)[解析]若x02,f(x0)>1即为>1,即>2,可得x0>3,;若,f(x0)>1即为>1,解得x0-1.综上可得,x0的取值范围是即答案为15.=________.[答案][解析]即答案为.16.给出下列命题:①函数=cos(+)是奇函数;②若α,β是第一象限角且α<β,则tanα<tanβ;③=2sin 在区间[-,]上的最小值是-2,最大值是;④=是函数=sin(2+π)的一条对称轴.其中正确命题的序号是________.[答案]①④[解析]①中,函数是奇函数,所以是正确的;②中,若、是第一象限角且,取时,则,所以不正确;③中,在区间上的最小值是,最大值是,所以不正确;④中,当时,函数,所以是函数的一条对称轴是正确的,故选①④.三、解答题(解答应写出文字说明、证明过程或演算步骤)17.已知集合A={|=},B={|<- 4或>2}.(1) 若m= -2, 求A∩(∁R B) ;(2)若A∪B=B,求实数m的取值范围.解:(1)m=-2,A={x|y=}={x|x≤-1},∁R B={x|-4≤x≤2},∴A∩(∁R B)={x|-4≤x≤-1}.(2)若A∪B=B,则A⊆B.∵A={x|x≤1+m},B={x|x<-4或x>2},∴1+m<-4.∴m<-5.18.已知函数.(1)求的值;(2)求的最大值和最小值.解:(1).(2)==,,因为,所以,当时,取最大值6;当时,取最小值. 19.已知向量m=(cos,sin ),n=(2+sin x,2-cos),函数=m·n,x∈R.(1) 求函数的最大值;(2) 若且=1,求的值.解:(1)因为f(x)=m·n=cos x(2+sin x)+sin x·(2-cos x)=2(sin x+cos x)=4sin(x∈R),所以f(x)的最大值是4.(2)因为f(x)=1,所以sin=.又因为x∈,即x+∈.所以cos=-,cos=cos=cos cos-sin sin=-×-×=-. 20.设函数是定义域(0,+∞)上的增函数,且=.(1)求的值;(2)若=1,求不等式的解集.解:(1)令,则.(2)令,即,且,即,由,得;又因为是定义在(0,+∞)上的增函数,所以,即,解得,即的解集为.21.设函数.(1)求函数的最大值及此时x的取值集合;(2)设A,B,C为△ABC的三个内角,已知cos B=,,且C为锐角,求sin A的值.解:(1),时,.此时的取值集合为.(2),,为锐角,,由,.22.已知函数=(1)写出该函数的单调区间;(2)若函数=-m恰有3个不同零点,求实数m的取值范围;(3)若≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.解:(1)函数f(x)的图象如图所示,则函数f(x)的单调递减区间是(0,1),单调递增区间是(-∞,0)及(1,+∞) .(2)作出直线y=m,函数g(x)=f(x)-m恰有3个不同零点等价于直线y=m与函数f(x)的图象恰有三个不同交点.根据函数f(x)=的图象,且f(0)=1,f(1)=,∴m∈.故实数m的取值范围为.(3)∵f(x)≤n2-2bn+1对所有x∈[-1,1]恒成立,∴[f(x)]ma x≤n2-2bn+1,又[f(x)]ma x=f(0)=1,∴n2-2bn+1≥1,即n2-2bn≥0在b∈[-1,1]上恒成立.令h(b)=-2nb+n2,∴h(b)=-2nb+n2在b∈[-1,1]上恒大于等于0.∴即由①得解得n≥0或n≤-2.同理由②得n≤0或n≥2.∴n∈(-∞,-2]∪{0}∪[2,+∞).故n的取值范围是(-∞,-2]∪{0}∪[2,+∞).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
友好学校第六十四届期末联考高三数学(理科)试卷一、选择题(本大题共12小题,每小题5分,共60分)1. 已知集合,则()A. B. C. D.【答案】C【解析】集合P={xǀx﹣1≤0}={x|x≤1},C R P={x|x>1},Q={xǀ0<x≤2},则(C R P)∩Q={x|1<x≤2}.故选:C.2. 下列命题中的假命题是( )A. B.C. D.【答案】B【解析】A. ,x=1;满足。
B. 不正确,当x=0时,。
C. ,当x=时,。
正确。
D. ,是正确的。
故答案为:B。
3. 已知两条直线,两个平面,给出下面四个命题:①∥∥;②∥,∥∥;③∥,;④∥∥。
其中正确命题的序号是()A. ①③B. ③④C. ①④D. ②③【答案】B【解析】①∥,则两条直线可以相交。
故不正确的。
②∥,∥,有可能其中一条直线n在平面内。
故不正确的。
③∥,,根据线面垂直的判定定理得到结论正确。
④∥∥,则,又因为∥,故。
结论正确;故正确的是③④。
故答案为:B。
4. 某几何体的三视图如图,则几何体的体积为........................A. 8π+16B. 8π-16C. 16π﹣8D. 8π+8【答案】B【解析】由已知中的三视图可得:该几何体是一个半圆柱切去一个三棱柱所得的组合体,半圆柱的底面半径为2,高为4,故体积V=π•22•4=8π,三棱柱的体积V=×4×2×4=16,故组合体的体积V=8π﹣16,故答案为:B。
5. 已知变量x,y满足约束条,则的最大值为()A. B. C. D.【答案】D【解析】根据题意得到可行域是封闭的三角形区域,交点为目标函数化简为,根据图像得到当目标函数过点A时取得最大值;代入得到11.故答案为:D .6. 已知等比数列的前项和,则数列的前12项和等于()A. 66B. 55C. 45D. 65【答案】A【解析】已知,,两式子做差得到,故,故是等差数列,首项为0,公差为1,则前12项和为66.故答案为:66.故答案为选择:A。
7. 如图所示,向量在一条直线上,且则( )A. B.C. D.【答案】D【解析】根据向量加法的三角形法则得到化简得到。
故答案为:D。
8. 函数图象的大致形状是()A. B.C. D.【答案】B【解析】根据表达式知道,故函数是奇函数,排除CD;当x>1时,故排除A选项,B是正确的。
故答案为:B。
9. 已知随机变量X服从正态分布N(3,δ2),且P(x≤6)=0.9,则P(0<x<3)=()A. 0.4B. 0.5C. 0.6D. 0.7【答案】A【解析】∵P(x≤6)=0.9,∴P(x>6)=1﹣0.9=0.1.∴P(x<0)=P(x>6)=0.1,∴P(0<x<3)=0.5﹣P(x<0)=0.4.故答案为:A。
10. 已知函数的图象与轴的两个相邻交点的距离等于,若将函数的图象向左平移个单位得到函数的图象,则在下列区间中使是减函数的是()A. B. C. D.【答案】B【解析】∵函数f(x)=sinωx﹣cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于,函数f(x)=sin4x﹣cos4x=2sin(4x﹣);若将函数y=f(x)的图象向左平移个单位得到函数y=g(x)=2sin(4x+)的图象.令2kπ+≤4x+≤2kπ+,可得k∈Z,当k=0时,故函数g(x)的减区间为。
故答案为B 。
11. 设为双曲线的右焦点,过坐标原点的直线依次与双曲线的左、右支交于点,若,则该双曲线的离心率为()A. B. C. D.【答案】A【解析】∵|PQ|=2|QF|,∠PQF=60°,∴∠PFQ=90°,设双曲线的左焦点为F1,连接F1P,F1Q,由对称性可知,F1PFQ为矩形,且故。
故答案为:A。
12. 设函数是奇函数(x∈R)的导函数,,且当时,,则使得>0成立的的取值范围是()A. B.C. D.【答案】A【解析】设g(x)=,则g(x)的导数为:g′(x)=,∵当x>0时,xf′(x)﹣f(x)>0,即当x>0时,g′(x)恒大于0,∴当x>0时,函数g(x)为增函数,∵f(x)为奇函数∴函数g(x)为定义域上的偶函数又∵g(﹣1)==0,∵f(x)>0,∴当x>0时,>0,当x<0时,<0,∴当x>0时,g(x)>0=g(1),当x<0时,g(x)<0=g(﹣1),∴x>1或﹣1<x<0故使得f(x)>0成立的x的取值范围是(﹣1,0)∪(1,+∞),故答案为:A。
点睛:本题考查函数的单调性与奇偶性的综合应用,注意奇函数的在对称区间上的单调性的性质;对于解抽象函数的不等式问题或者有解析式,但是直接解不等式非常麻烦的问题,可以考虑研究函数的单调性和奇偶性等,以及函数零点等,直接根据这些性质得到不等式的解集。
二、填空题(本大题共4小题,每小题5分,共20分)13. 设向量,,若-与垂直,则的值为_____【答案】【解析】根据题意得到-与垂直,得到代入公式得到故答案为:。
14. 若函数的两个零点是-1和2,则不等式的解集是 ___.【答案】【解析】∵f(x)=x2+ax+b的两个零点是﹣2,3.∴﹣1,2是方程x2+ax+b=0的两根,由根与系数的关系知∴f(x)=x2﹣x﹣2.∵不等式aƒ(﹣2x)>0,即﹣(4x2+2x﹣2)>0⇔2x2+x﹣1<0,解集为.故答案为.点睛:此题体现了一元二次不等式的解法,解决一元二次不等式的解法的问题,常常需要向方程或图象方面转化,而数形结合正是它们转化的纽带,求解不等式联系方程的根,不等中隐藏着相等.15. 设n= dx,则二项式展开式中常数项为 ________.【答案】60【解析】n= dx故得到n=6,=常数项k=2,代入得到60.故答案为:60.点睛:这个题目考查的是二项式定理的应用,和积分的应用。
一般二项式的小题,考查的有求某些项的和,求某一项的系数,或者求某一项。
要分清楚二项式系数和,和系数和。
求和时注意赋值法的应用。
16. 已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若,三内角A,B,C成等差数列,则该三角形的外接圆半径等于______________;【答案】2【解析】设△ABC的外接圆的半径为R,∵A,B,C成等差数列∴A+C=2B,且A+B+C=180°,所以B=60°,由正弦定理得,2R==4,则R=2.故答案为:2.三、解答题(本大题共6小题,共70分。
解答应写出文字说明,证明过程或演算步骤。
)17. △ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.【答案】(1) C=(2) △ABC的周长为+【解析】试题分析:(1)由正弦定理,两角和的正弦函数公式,三角形内角和定理化简已知可得2cosCsinC=sinC,结合范围C∈(0,π),解得cosC=,可得C的值.(2)由三角形的面积公式可求ab=3,利用余弦定理解得a+b的值,即可得解△ABC的周长.解析:(Ⅰ)∵在△ABC中,0<C<π,∴sinC≠0利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,整理得:2cosCsin(A+B)=sinC,即2cosCsin(π﹣(A+B))=sinC,2cosCsinC=sinC∴cosC=,∴C=(Ⅱ)由余弦定理得3=a2+b2﹣2ab•,∴(a+b)2﹣3ab=3,∵S= absinC= ab=,∴ab=16,∴(a+b)2﹣48=3,∴a+b=,∴△ABC的周长为+ .点睛:本题主要考查了正弦定理,两角和的正弦函数公式,三角形内角和定理,三角形的面积公式,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.一般三角形的题目已知两角和一对边则用正弦定理,用两边和夹角用余弦定理。
18. 记为差数列的前n项和,已知,.(1)求的通项公式;(2)令,,若对一切成立,求实数的最大值.【答案】(1) (2) 实数的最大值为【解析】试题分析:(1)根据等差数列的公式得到通项;(2)由第一问得到,故得到前n项和,是递增数列,,进而得到结果。
解析:(1)∵等差数列中,,.∴,解得.,.(2),是递增数列,,,∴实数的最大值为.点睛:这个题目考查的是数列通项公式的求法及数列求和的常用方法;数列通项的求法中有常见的已知和的关系,求表达式,一般是写出做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等。
19. 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求二面角F﹣BE﹣D的余弦值.【答案】(1)见解析(2)【解析】试题分析:(Ⅰ)因为D E⊥平面ABCD,所以DE⊥AC.因为ABCD是正方形,所以AC⊥BD,从而AC⊥平面BDE;(Ⅱ)建立空间直角坐标系D-xyz,分别求出平面BEF的法向量为和平面BDE的法向量,利用向量法能求出二面角的余弦值试题解析:(1)证明:因为DE⊥平面ABCD,AC⊂平面ABCD,所以DE⊥AC.因为ABCD是正方形,所以AC⊥BD.又BD,DE相交且都在平面BDE内,从而AC⊥平面BDE.(2)因为DA,DC,DE两两垂直,所以建立空间直角坐标系Dxyz,如图所示.因为DE⊥平面ABCD,所以BE与平面ABCD所成角就是∠DBE.已知BE与平面ABCD所成角为60°,所以∠DBE=60°,所以由AD=3可知DE=3,AF=.由A(3,0,0),F(3,0,),E(0,0,3),B(3,3,0),C(0,3,0),得=(0,-3,),=(3,0,-2).设平面BEF的法向量为n=(x,y,z),则即令z=,则n=(4,2,).因为AC⊥平面BDE,所以为平面BDE的法向量m=(3,-3,0),所以cos〈n,m〉==.因为二面角为锐角,所以二面角FBED的余弦值为.考点:1.用空间向量求平面间的夹角;2.直线与平面垂直的判定20. 某项竞赛分为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是且各阶段通过与否相互独立.(1)求该选手在复赛阶段被淘汰的概率;(2)设该选手在竞赛中回答问题的个数为ξ,求ξ的分布列与均值.【答案】(1) (2) ξ的分布列为:Eξ=2【解析】试题分析:(1)选手在复赛阶段被淘汰的概率P=P(A ),分别求出P(A)=,P(B)= ,代入公式P=P(A )=P(A)P()得到结果。
