《直线、射线、线段》同步练习题
2020年秋人教版七年级上册同步练习：4.2《直线、射线、线段》 含答案
2020年人教版七年级上册同步练习：4.2《直线、射线、线段》一．选择题1．“把弯曲的公路改直，就能缩短路程”，其中蕴含的数学道理是（）A．两点确定一条直线B．直线比曲线短C．两点之间直线最短D．两点之间线段最短2．如图，从A到B有三条路径，最短的路径是③，理由是（）A．两点确定一条直线B．两点之间，线段最短C．过一点有无数条直线D．因为直线比曲线和折线短3．某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是（）A．两点之间线段最短B．两点确定一条直线C．垂线段最短D．经过直线外一点，有且只有一条直线与这条直线平行4．如图，线段AB＝DE，点C为线段AE的中点，下列式子不正确的是（）A．BC＝CD B．CD＝AE﹣AB C．CD＝AD﹣CE D．CD＝DE5．如图，一根长为10厘米的木棒，棒上有两个刻度，若把它作为尺子，量一次要量出一个长度，能量的长度共有（）A．7个B．6个C．5个D．4个6．平面上有不同的三个点，经过其中任意两点画直线，一共可以画（）A．1条B．2条C．3条D．1条或3条7．观察图形，下列说法正确的个数是（）（1）直线BA和直线AB是同一条直线（2）射线AC和射线AD是同一条射线（3）AB+BD＞AD（4）三条直线两两相交时，一定有三个交点．A．1个B．2个C．3个D．4个8．直线a上有5个不同的点A、B、C、D、E，则该直线上共有（）条线段．A．8B．9C．12D．109．如图，下列说法正确的是（）A．点O在射线AB上B．点B是直线AB的一个端点C．射线OB和射线AB是同一条射线D．点A在线段OB上10．由唐山开往石家庄的G6738次列车，途中有5个停车站，这次列车的不同票价最多有（）A．21种B．10种C．42种D．20种11．已知线段AB＝8cm，点C是直线AB上一点，BC＝2cm，若M是AB的中点，N是BC 的中点，则线段MN的长度为（）A．5cm B．5cm或3cm C．7cm或3cm D．7cm12．两根木条，一根长20cm，另一根长24cm，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为（）A．2cm B．4cm C．2cm或22cm D．4cm或44cm 二．填空题13．把一段弯曲的河流改直，可以缩短航程，其理由是．14．如图，是从甲地到乙地的四条道路，其中最短的路线是，理由是．15．如图，已知AB＝8cm，BD＝3cm，C为AB的中点，则线段CD的长为cm．16．如图，A，B，C，D，E，P，Q，R，S，T是构成五角星的五条线段的交点，则图中共有线段条．17．直线AB，BC，CA的位置关系如图所示，则下列语句：①点B在直线BC上；②直线AB经过点C；③直线AB，BC，CA两两相交；④点B是直线AB，BC的交点，以上语句正确的有（只填写序号）18．已知线段AB和BC在同一条直线上，若AC＝6cm，BC＝2cm，则线段AC和BC中点间的距离为．19．如图，若CB＝4cm，DB＝7cm，且D是AC的中点，则AC＝cm．三．解答题20．如图，平面上有四个点A，B，C，D，根据下列语句画图：（1）画线段AC、BD交于E点；（2）作射线BC；（3）取一点P，使点P既在直线AB上又在直线CD上．21．已知：C为线段AB的中点，D在线段BC上，且AD＝7，BD＝5，求：线段CD的长度．22．如图，已知B是线段AC的中点，D是线段CE的中点，若AB＝4，CE＝AC，求线段BD的长．23．在一条不完整的数轴上从左到右有点A，B，C，其中AB＝2，BC＝1，如图所示，设点A，B，C所对应数的和是p．（1）若以B为原点，写出点A，C所对应的数，并计算p的值；若以C为原点，p又是多少？（2）若原点O在图中数轴上点C的右边，且CO＝28，求p．24．如图：A、B、C、D四点在同一直线上．（1）若AB＝CD．①比较线段的大小：AC BD（填“＞”、“＝”或“＜”）；②若BC＝AC，且AC＝12cm，则AD的长为cm；（2）若线段AD被点B、C分成了3：4：5三部分，且AB的中点M和CD的中点N之间的距离是16cm，求AD的长．25．如图，P是定长线段AB上一点，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上）（1）若C、D运动到任一时刻时，总有PD＝2AC，请说明P点在线段AB上的位置；（2）在（1）的条件下，Q是直线AB上一点，且AQ﹣BQ＝PQ，求的值．（3）在（1）的条件下，若C、D运动5秒后，恰好有，此时C点停止运动，D点继续运动（D点在线段PB上），M、N分别是CD、PD的中点，下列结论：①PM ﹣PN的值不变；②的值不变，可以说明，只有一个结论是正确的，请你找出正确的结论并求值．参考答案一．选择题1．解：由线段的性质可知：两点的所有连线中，可以有无数种连法，如折线、曲线、线段等，这些所有的线中，线段最短．故选：D．2．解：如图，最短路径是③的理由是两点之间线段最短，故B正确，故选：B．3．解：某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是两点之间线段最短．故选：A．4．解：因为点C为线段AE的中点，且线段AB＝DE，则BC＝CD，故本选项正确；B中CD＝AC﹣AB＝BC＝CD，故本选项正确；C中CD＝AD﹣BC﹣AB＝CD，故本选项正确；D中CD≠DE则在已知里所没有的，故本选项错误；故选：D．5．解：∵图中共有3+2+1＝6条线段，∴能量出6个长度，分别是：2厘米、3厘米、5厘米、7厘米、8厘米、10厘米．故选：B．6．解：如图，经过其中任意两点画直线可以画3条直线或1条直线，故选：D．7．解：（1）直线BA和直线AB是同一条直线，直线没有端点，此说法正确；（2）射线AC和射线AD是同一条射线，都是以A为端点，同一方向的射线，正确；（3）AB+BD＞AD，三角形两边之和大于第三边，所以此说法正确；（4）三条直线两两相交时，一定有三个交点，错误，可能有1个交点的情况．所以共有3个正确．故选：C．8．解：根据题意画图：由图可知有AB、AC、AD、AE、BC、BD、BE、CD、CE、DE，共10条．故选：D．9．解：A、点O不在射线AB上，点O在射线BA上，故此选项错误；B、点B是线段AB的一个端点，故此选项错误；C、射线OB和射线AB不是同一条射线，故此选项错误；D、点A在线段OB上，故此选项正确．故选：D．10．解：根据题意知这次列车的不同票价最多有6+5+4+3+2+1＝21（种），故选：A．11．解：如图1，由M是AB的中点，N是BC的中点，得MB＝AB＝4cm，BN＝BC＝1cm，由线段的和差，得MN＝MB+BN＝4+1＝5cm；如图2，由M是AB的中点，N是BC的中点，得MB＝AB＝4cm，BN＝BC＝1cm，由线段的和差，得MN＝MB﹣BN＝4﹣1＝3cm；故选：B．12．解：如图，设较长的木条为AB＝24cm，较短的木条为BC＝20cm，∵M、N分别为AB、BC的中点，∴BM＝12cm，BN＝10cm，∴①如图1，BC不在AB上时，MN＝BM+BN＝12+10＝22cm，②如图2，BC在AB上时，MN＝BM﹣BN＝12﹣10＝2cm，综上所述，两根木条的中点间的距离是2cm或22cm；故选：C．二．填空题13．解：把一段弯曲的河流改直，可以缩短航程，其理由是两点之间，线段最短，故答案为：两点之间，线段最短．14．解：由图可得，最短的路线为从甲经A到乙，因为两点之间，线段最短．故答案为：从甲经A到乙，两点之间，线段最短．15．解：∵C为AB的中点，AB＝8cm，∴BC＝AB＝×8＝4（cm），∵BD＝3cm，∴CD＝BC﹣BD＝4﹣3＝1（cm），则CD的长为1cm；故答案为：1．16．解：线段AC，BE，CE，BD，AD上各有另两个点，每条上有6条线段；所以共有6×5＝30条线段．17．解：由图可得，①点B在直线BC上，正确；②直线AB不经过点C，错误；③直线AB，BC，CA两两相交，正确；④点B是直线AB，BC的交点，正确；故答案为：①③④．18．解：设AC、BC的中点分别为E、F，∵AC＝6cm，BC＝2cm，∴CE＝AC＝3cm，CF＝BC＝1cm，如图1，点B不在线段AC上时，EF＝CE+CF＝3+1＝4（cm），如图2，点B在线段AC上时，EF＝CE﹣CF＝3﹣1＝2（cm），综上所述，AC和BC中点间的距离为4cm或2cm．故答案为：4cm或2cm．19．解：CD＝DB﹣BC＝7﹣4＝3cm，AC＝2CD＝2×3＝6cm．故答案为：6．三．解答题20．解：（1）如图所示：；（2）如图所示，（3）如图所示，．21．解：∵AD＝7，BD＝5∴AB＝AD+BD＝12∵C是AB的中点∴AC＝AB＝6∴CD＝AD﹣AC＝7﹣6＝1．22．解：∵点B、D分别是AC、CE的中点，∴BC＝AB＝AC，CD＝DE＝CE，∴BD＝BC+CD＝（AC+CE），∵AB＝4，∴AC＝8，∵CE＝AC，∴CE＝6，∴BD＝BC+CD＝（AC+CE）＝（8+6）＝7．23．解：（1）若以B为原点，则C表示1，A表示﹣2，∴p＝1+0﹣2＝﹣1；若以C为原点，则A表示﹣3，B表示﹣1，∴p＝﹣3﹣1+0＝﹣4；（2）若原点O在图中数轴上点C的右边，且CO＝28，则C表示﹣28，B表示﹣29，A 表示﹣31，∴p＝﹣31﹣29﹣28＝﹣88．24．解：（1）①∵AB＝CD，∴AB+BC＝CD+BC，即，AC＝BD，故答案为：＝；②∵BC＝AC，且AC＝12cm，∴BC＝×12＝9（cm），∴AB＝CD＝AC﹣BC＝12﹣9＝3（cm），∴AD＝AC+CD＝12+3＝15（cm），故答案为：15；（2）如图，设每份为x，则AB＝3x，BC＝4x，CD＝5x，AD＝12x，∵M是AB的中点，点N是CD的中点N，∴AM＝BM＝x，CN＝DN＝x，又∵MN＝16，∴x+4x+x＝16，解得，x＝2，∴AD＝12x＝24（cm），答：AD的长为24cm．25．解：（1）根据C、D的运动速度知：BD＝2PC ∵PD＝2AC，∴BD+PD＝2（PC+AC），即PB＝2AP，∴点P在线段AB上的处；（2）如图：∵AQ﹣BQ＝PQ，∴AQ＝PQ+BQ；又AQ＝AP+PQ，∴AP＝BQ，∴，∴．当点Q'在AB的延长线上时AQ'﹣AP＝PQ'所以AQ'﹣BQ'＝PQ＝AB所以＝1；（3）②．理由：当CD＝AB时，点C停止运动，此时CP＝5，AB＝30①如图，当M，N在点P的同侧时MN＝PN﹣PM＝PD﹣（PD﹣MD）＝MD﹣PD＝CD﹣PD＝（CD﹣PD）＝CP ＝②如图，当M，N在点P的异侧时MN＝PM+PN＝MD﹣PD+PD＝MD﹣PD＝CD﹣PD＝（CD﹣PD）＝CP＝∴＝＝当点C停止运动，D点继续运动时，MN的值不变，所以，＝．。
《4.2.1直线、射线、线段》练习题1
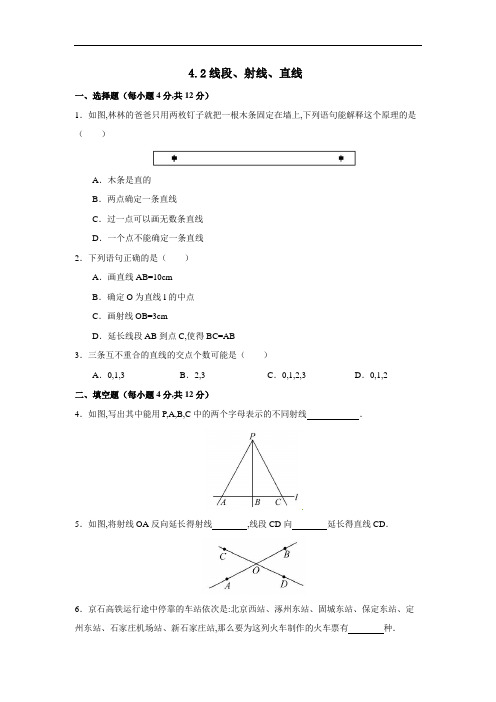
4.2线段、射线、直线一、选择题（每小题4分,共12分）1．如图,林林的爸爸只用两枚钉子就把一根木条固定在墙上,下列语句能解释这个原理的是（）A．木条是直的B．两点确定一条直线C．过一点可以画无数条直线D．一个点不能确定一条直线2．下列语句正确的是（）A．画直线AB=10cmB．确定O为直线l的中点C．画射线OB=3cmD．延长线段AB到点C,使得BC=AB3．三条互不重合的直线的交点个数可能是（）A．0,1,3 B．2,3 C．0,1,2,3 D．0,1,2二、填空题（每小题4分,共12分）4．如图,写出其中能用P,A,B,C中的两个字母表示的不同射线．5．如图,将射线OA反向延长得射线,线段CD向延长得直线CD．6．京石高铁运行途中停靠的车站依次是:北京西站、涿州东站、固城东站、保定东站、定州东站、石家庄机场站、新石家庄站,那么要为这列火车制作的火车票有种．三、解答题（共26分）7．（8分）数一数,图中共有多少条线段?并分别写出这些线段．8．（8分）A,B,C,D四点如图所示,读下列语句,按要求作出图形（不写画法）: （1）连接AD,并延长线段DA．（2）连接BC,并反向延长线段BC．（3）连接AC,BD,它们相交于点O．（4）DA延长线与BC反向延长线交于点P．【拓展延伸】9．（10分）动手画一画,再数一数．（1）过一点A能画几条直线?（2）过两点A,B能画几条直线?（3）已知平面上共有三个点A,B,C,过其中任意两点画直线,可画几条?（4）已知平面上共有n个点（n为不小于3的整数）,其中任意三个点都不在同一直线上,那么连接任意两点,可画多少条直线?答案解析1．【解析】选B．根据两点确定一条直线,故选B．2．【解析】选D．A,直线无限长;B,直线不能度量,没有中点;C,射线可向一方无限延长;D,延长线段AB到点C,使得BC=AB,正确．3．【解析】选C．分四种情况:1．三条直线平行,有0个交点;2．三条直线相交于同一点,有1个交点;3．一条直线截两条平行线有2个交点;4．三条直线两两相交有3个交点．4．【解析】图形中能用P,A,B,C中的两个字母表示的不同射线有:射线PA 、射线PB 、射线PC 、射线AB 、射线BC 、射线BA 、射线CB ．答案：射线PA 、射线PB 、射线PC 、射线AB 、射线BC 、射线BA 、射线CB5．【解析】将射线OA 反向延长得射线OB,线段CD 向两方延长得直线CD ．答案：OB 两方6．【解析】画一条直线,在直线上依次取A,B,C,D,E,F,G 七个点,它们依次表示北京西站、涿州东站、固城东站、保定东站、定州东站、石家庄机场站、新石家庄站．点A 分别与B,C,D,E,F,G 形成6条线段;点B 分别与C,D,E,F,G 形成5条线段;点C 分别与D,E,F,G 形成4条线段;点D 分别与E,F,G 形成3条线段;点E 分别与F,G 形成2条线段;点F 与G 形成1条线段,所以直线上共有线段的条数是6+5+4+3+2+1=21,考虑往返情况,所以应制作火车票21×2=42（种）．答案：42【知识拓展】若一条直线上有n 个点,那么以这n 个点中的任意两点为端点的线段共有（n-1）+（n-2）+…+2+1=21n （n-1）（条）． 7．【解析】由图形得:共有10条线段,分别为:线段AB 、线段BC 、线段CD 、线段DA 、线段AC 、线段AO 、线段CO 、线段BD 、线段BO 、线段DO ．8．【解析】如图所示．9．【解析】（1）过一点A 能画无数条直线．（2）过两点A,B 只能画一条直线．（3）①若三点共线则可画一条,②若三点不共线则可画三条．故可画1条或3条．（4）根据过两点的直线有1条,过不在同一直线上的三点的直线有3条,过任意三点都不在一条直线上的四点的直线有6条,按此规律由特殊到一般可得过任意三个点都不在同一直线上的n 个点共能画21n （n-1）条直线．。
人教版版四年级上册数学《线段 直线 射线》练习题(附答案)
人教版版四年级上册数学线段直线射线练习题（附答案）一、单选题1.一条（）长300米．A. 射线B. 直线C. 线段2.经过平面上的任意两点，可以画（）条直线。
A. 1B. 2C. 无数D. 不确定3.把线段的一端无限延长，就得到一条（）。
A. 垂线B. 射线C. 线段D. 直线4.下面图形中有条线段．（）A. 3B. 6C. 10D. 155.下图中共有（）线段。
A. 4条B. 5条C. 6条D. 8条二、判断题6.直线比射线长，射线比线段长．（）7.一条直线长25厘米。
（）8.一条直线长10分米．（）9.线段有两个端点，是直线的一部分。
（）三、填空题10.三角形由________条线段围成，长方形由________条线段围成。
11.在横线上填“经过”或“不经过”。
线段AB经过点C吗？________12.正方形是由________条线段围成的，三角形是由________条线段围成的．13.下图是由________条线段组成的，有________个直角。
14.手电筒发出的光是一条________。
四、解答题15.用两种不同的方法数出框中一共有（）条线段，并在图中画出你数线段的方法。
16.画一条比4厘米短5毫米的线段，并给这条线段标上长度。
五、作图题17.过AB两点画一条直线，并量出线段AB的长度。
线段AB长（）毫米。
答案一、单选题1. C2. A3. B4. C5. C二、判断题6. 错误7. 错误8. 错误9. 正确三、填空题10. 3；4 11. 不经过12. 4；3 13. 9；614. 射线四、解答题15. 解：，5+4+3+2+1=15（条）答：数出框中一共有15条线段。
16.五、作图题17.量得线段AB的长度是2厘米，即线段AB长20毫米。
人教版小学四年级数学上册《线段、直线、射线》同步练习(含答案)
人教版小学四年级数学上册同步练习3.1线段、直线、射线（含答案）一、填空题1．通过纸上一点，能画( )条直线，通过纸上两点，能画( )条直线。
2．下图中有( )条直线，有( )条射线，有( )条线段。
3．在直线、射线和线段中，( )有一个端点，( )有两个端点，( )没有端点。
4．手电筒发出的光束，舞台上的光束，都给人一种( )的形象。
5．两点之间的所有连线中( )最短，将它的一端无限延长，形成一条( )，将另一端也无限延长，形成一条( )。
二、选择题6．4个点可以连成（）条线段。
A．6B．5C．77．（）的长度是有限的。
A．直线B．射线C．线段8．经过一点画射线，可以画（）射线。
A．1条B．2条C．无数条9．下列线中，（）是直线。
A．B．C．D．10．直线与射线相比较，（）。
A．直线更长B．射线更长C．一样长D．无法比较11．小丽画了一条12厘米长的（）。
A．直线B．线段C．射线12．下面说法错误的是（）。
A．射线比直线短B．5时整，钟面上的时针与分针成钝角C．边长200米的正方形麦田的面积是4公顷D．角的大小与角两边的长短无关三、判断题13．一条直线长1.5米。
( )14．线段是有限长的。
( )15．直线的长度是射线长度的一半。
( )16．线段和射线都是直线的一部分，所以线段和射线都比直线长。
( ) 17．直线和射线都可以无限延伸。
( )四、解答题18．先画一画，再回答问题。
（1）如图1所示过点A可以画几条直线？（2）如图1所示以点A为端点可以画几条射线？（3）如图2所示每两点之间画一条线段，如下四点可以画几条线段？参考答案：1．无数 1 一2． 1 一 6 六 3 三3．射线线段直线4．射线5．线段射线直线6．A7．C8．C9．A10．D11．B12．A13．×14．√15．×16．×17．√18．（1）一条（2）无数条（3）六条答案第1页，共1页。
射线直线线段练习题
射线、直线、线段练习题一、选择题1. 下列说法正确的是：A. 射线有一个端点，无限长B. 直线有两个端点，有限长C. 线段有一个端点，有限长D. 射线与直线长度相等2. 在下列图形中，哪个是线段？A. 两条平行线B. 一个端点，向一方无限延伸C. 两个端点，有限长D. 一个端点，向两边无限延伸A. 两个端点，有限长B. 一个端点，向一方无限延伸C. 两个端点，无限长D. 无端点，无限长二、填空题1. 线段是由两个______和它们之间的______组成的。
2. 射线有一个______，向一方______延伸。
3. 直线无______，______延伸。
三、判断题1. 射线的长度大于线段的长度。
（）2. 直线比射线更长。
（）3. 线段有两个端点，有限长。
（）四、连线题请将下列射线、直线、线段的定义与相应的图形连线：1. 直线：______2. 射线：______3. 线段：______五、作图题1. 画出一条线段，长度为5厘米。
2. 画出一条射线，从一个端点出发，经过点A。
3. 画出一条直线，使它与线段AB平行。
六、简答题1. 请简要说明射线、直线和线段的特点。
2. 如何用直尺和三角板画出一条指定长度的线段？3. 在日常生活中，你能找到哪些射线、直线和线段的例子？请分别列举。
七、应用题1. 在平面直角坐标系中，点A(2,3)和点B(5,3)是线段AB的两个端点，求线段AB的长度。
2. 已知射线OC从点O(0,0)出发，经过点C(4,0)，求射线OC上距离点O 6个单位长度的点D的坐标。
3. 在直角坐标系中，直线l经过点P(1,2)和点Q(4,6)，请写出直线l的方程。
八、拓展题1. 如果一条射线逆时针旋转90度，它变成了什么？2. 在平面上，两条直线相交，形成的四个角中，有几个角是相等的？3. 有一根无限长的直线，你在上面任意取两点，这两点之间的是什么？九、探究题1. 如何证明两条平行线之间的距离处处相等？2. 在同一平面内，如果两条直线不相交，那么它们一定是平行的吗？3. 请设计一个实验，证明线段的长度是可以通过测量得到的。
直线、射线、线段同步练习题已整理
《直线、射线、线段》同步练习题1.经过一点,有______条直线;经过两点有_____条直线,并且______条直线.2.如图1,图中共有______条线段,它们是_________.1()2()3()3.如图2,图中共有_______条射线,指出其中的两条________.4.线段AB=8cm,C 是AB 的中点,D 是BC 的中点,A 、D 两点间的距离是_____cm.5.如图3,在直线I 上顺次取A 、B 、C 、D 四点,则AC=______+BC=AD-_____, AC+BD- BC=________.6.下列语句准确规范的是( )A.直线a 、b 相交于一点mB.延长直线ABC.反向延长射线AO(O 是端点)D.延长线段AB 到C,使BC=AB 7.下列四个图中的线段(或直线、射线)能相交的是( )1()2()3()4()A.(1)B.(2)C.(3)D.(4) 8.如果点C 在AB 上,下列表达式①AC=12AB;②AB=2BC;③AC=BC;④AC+BC=AB 中,能表示C 是AB 中点的有( )A.1个B.2个C.3个D.4个9.如图,从A 到B 有3条路径,最短的路径是③,理由是( )A.因为③是直的B.两点确定一条直线C.两点间距离的定义D.两点之间,线段最短10.如图,平面上有四个点A 、B 、C 、D,根据下列语句画图(1)画直线AB 、CD 交于E 点; (2)画线段AC 、BD 交于点F; (3)连接E 、F 交BC 于点G; (4)连接AD,并将其反向延长;(5)作射线BC;(6)取一点P,使P 在直线AB 上又在直线CD 上.11.在一条直线上取两上点A 、B,共得几条线段?在一条直线上取三个点A 、B 、 C,共得几条线段?在一条直线上取A 、B 、C 、D 四个点时,共得多少条线段? 在一条直线上取n 个点时,共可得多少条线段?B A线段、直线、射线1、关于线段，下列判断正确的是 ( ) A.只有一个端点； B.有两个以上的端点； C.有两个端点； D.没有端点。
北师版七上数学《1 线段、射线、直线》同步练习含答案解析
北师版七上数学第四章1线段、射线、直线同步练习一、选择题1.延长线段AB到C，下列说法正确的是（）A．点C在线段AB上B．点C在直线AB上C．点C不在直线AB上D．点C在直线BA的延长线上答案：B解析：解答：因为线段有两个端点，所以线段可以向两方延长，所以点C不在线段AB上，点C在直线AB上，故A、C错误，B正确，因为直线没有端点，可以向两方无限延伸，直线没有延长线的说法，故D错误．故选B．分析：本题根据直线、线段、以及射线的概念来解答即可．2.如图，图中共有线段的条数是（）A．4B．5C．6D．7答案：C解析：解答：图中的线段有AB、AC、AD、BC、BD、CD；故选：C．分析：根据图示数出线段即可．3.下列各直线的表示法中，正确的是（）A．直线AB．直线ABC．直线abD．直线Ab答案：B解析：解答：表示一条直线，可以用直线上的两个点表示，一般情况用两个大写字母表示；故选B．分析：此题考查直线的表示方法．4.如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A．两点确定一条直线B．两点之间线段最短C．垂线段最短D．在同一平面内，过一点有且只有一条直线与已知直线垂直答案：A解析：解答：经过刨平的木板上的两个点，能弹出一条笔直的墨线，此操作的依据是两点确定一条直线．故选：A．分析：根据公理“两点确定一条直线”来解答即可．5.如图，点A、B、C在一直线上，则图中共有射线（）A．1条B．2条C．4条D．6条答案：D解析：解答：根据射线的定义，这条直线上的每个点可以有两条射线，故图中共有射线6条．故选：D．分析：根据射线的定义，一条直线上的每个点可以有两条射线，分析图形可得答案．6.平面内的三个点A、B、C能确定的直线的条数是（）A．1条B．2条C．3条D．1条或3条答案：D解析：解答：∵若平面内的三个点A、B、C不在同一直线上，则能确定的直线的条数是：3条；若平面内的三个点A、B、C在同一直线上，则能确定的直线的条数是：1条．∴平面内的三个点A、B、C能确定的直线的条数是：1条或3条．故选D．分析：分别从若平面内的三个点A、B、C不在同一直线上与若平面内的三个点A、B、C在同一直线上去分析，则可求得答案．7.观察图形，下列说法正确的个数是（）（1）直线BA和直线AB是同一条直线（2）射线AC和射线AD是同一条射线（3）AB＋BD＞AD（4）三条直线两两相交时，一定有三个交点．A．1个B．2个C．3个D．4个答案：C解析：解答：（1）直线BA和直线AB是同一条直线，直线没有端点，此说法正确；（2）射线AC和射线AD是同一条射线，都是以A为端点，同一方向的射线，正确；（3）AB＋BD＞AD，三角形两边之和大于第三边，所以此说法正确；（4）三条直线两两相交时，一定有三个交点，错误，可能有1个交点的情况．所以共有3个正确．故选C．分析：结合图形，区别各概念之间的联系．8.如图，平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF，从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…，则数字“2008”在（）A．射线OA上B．射线OB上C．射线OD上D．射线OF上答案：C解析：解答：2008÷6＝334…4，所以在射线OD上．故选C．分析：根据规律，所写数字按6个一组循环，用2008除以6余数是几就在第几条线．9.如下图，直线l、射线PQ、线段MN中能相交的是（）A．B．C．D．答案：D解析：解答：根据线段不延伸，而射线只向一个方向延伸即可得到：正确的只有D．故选D．分析：根据线段与射线的定义，以及延伸性即可作出判断．10.将线段AB延长至C，再将线段AB反向延长至D，则共有线段（）条．A．8B．7C．6D．5答案：C解析：解答：线段上有4个点时，线段总条数是3＋2＋1条，即6条．故选C．分析：因为将线段AB延长至C，再将线段AB反向延长至D，线段上有4个点，则共有线段条数可求．11.下列说法中正确的是（）A．画一条3厘米长的射线B．画一条3厘米长的直线C．画一条5厘米长的线段D．在线段、射线、直线中直线最长答案：C解析：解答：A.射线可无限延长，不可测量，所以画一条3厘米长的射线是错误的；B.直线是无限长的，直线是不可测量长度的，所以画一条3厘米长的直线是错误的；C.线段有两个端点，有限长度，可以测量，所以画一条5厘米长的线段是正确的；D.直线、射线都是无限延长，不可测量，不能比较长短，只有线段可以比较长短，所以在线段、射线、直线中直线最长是错误的．故选：C．分析：利用直线、射线、线段的意义和特点，逐项分析，找出正确答案即可．12.下列说法正确的是（）A．过一点P只能作一条直线B．直线AB和直线BA表示同一条直线C．射线AB和射线BA表示同一条射线D．射线a比直线b短答案：B解析：解答：A.过一点P可以作无数条直线；故A错误．B.直线可以用两个大写字母来表示，且直线没有方向，所以AB和BA是表示同一条直线；故B正确．C.射线AB和射线BA，顶点不同，方向相反，故射线AB和射线BA表示不同的射线；故C 错误．D.射线和直线不能进行长短的比较；故D错误．故选B．分析：过一点可以做无数条直线，根据直线的表示方法，AB和BA是表示同一条直线．而射线AB和射线BA表示不同的射线，射线与直线不能进行长短的比较．13.下列说法正确的是（）A．经过两点有且只有一条线段B．经过两点有且只有一条直线C．经过两点有且只有一条射线D．经过两点有无数条直线答案：B解析：解答：A.线段有长短，例如过A、B两点的线段不止一条，故本选项错误；B.经过两点有且只有一条直线，是直线公理，正确；C.射线有一个端点，例如过B、C两点的射线有射线AB、射线BC，故本选项错误；D.因为两点确定一条直线，所以本选项错误．故选B．分析：根据两点确定一条直线的公理和直线、射线、线段的性质对各选项分析判断后利用排除法求解．14.“两条直线相交，有且只有一个交点”的题设是（）A．两条直线B．交点C．两条直线相交D．只有一个交点答案：C解析：解答：两条直线相交，有且只有一个交点这一命题题设是两条直线相交，结论是有且只有一个交点，故选C．分析：本题考查两直线相交，有且只有一个交点的命题，题设和结论要搞清楚．15.如图，给出的直线、射线、线段，根据各自的性质，能相交的是（）A．B．C．D．答案：D解析：解答：A.射线延伸后两直线不能相交，故本选项错误；B.直线延伸后两直线不能相交，故本选项错误；C.射线和直线延伸后两直线不能相交，故本选项错误；D.射线延伸后两直线能相交，故本选项正确；故选D．分析：根据直线可以沿两个方向延伸，射线可以沿一个方向延伸，线段不能延伸即可得出答案．二、填空题16.直线上有n个点，我们进行如下操作：在每相邻两点间插入2个点．经过2次这样的操作后，直线上共有______个点．（用含n的代数式表示）答案：9n－8解析：解答：第一次操作，共有n＋（n－1）×2＝3n－2个点，第二次操作，共有（3n－2）＋（3n－2－1）×2＝9n－8个点，故答案为：9n－8．分析：根据n个点中间可以有（n－1）个空插入，从而找出规律并得解．17.平面内三条直线两两相交，最多有a个交点，最少有b个交点，则a＋b＝______．答案：4解析：解答：∵平面内三条直线两两相交，最多有3个交点，最少有1个交点，∴a＋b＝4．故答案为：4．分析：分析可得：平面内三条直线两两相交，最多有3个交点，最少有1个交点，则即可求得a＋b的值．18.乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要安排不同的车票______种．（友情提示：A到B与B到A车票不同．）答案：20解析：解答：设点C、D、E是线段AB上的三个点，根据题意可得：图中共用()515102-⨯=条线段∵A到B与B到A车票不同．∴从A到B的车票共有10×2＝20种故答案为；20．分析：本题需先求出A、B之间共有多少条线段，根据线段的条数即可求出车票的种数．19.一条直线上立有10根距离相等的标杆，一名学生匀速地从第1杆向第10杆行走，当他走到第6杆时用了6.5s，则当他走到第10杆时所用时间是______．答案：11.7s解析：解答：从第1根标杆到第6根标杆有5个间隔，所以，每个间隔行进6.5÷5＝1.3s，从第1根标杆到第10根标杆共有9个间隔，所以，行进9个间隔共用1.3×9＝11.7s．故答案为：11.7s．分析：根据到第6杆时有5个间隔求出走1个间隔的时间，再求出到第10杆有9个间隔，然后列式计算即可得解．20.平面上有五条直线相交（没有互相平行的），则这五条直线最多有______个交点，最少有______个交点．答案：10|1解析：解答：最多时54102⨯=，相交于同一个点时最少，有1个交点．分析：直线交点最多时，根据公式()12n n-，把直线条数代入公式求解即可，直线相交于同一个点时最少，是1个交点．故答案为：10；1.三、解答题20.按要求画一画，再填空（1）延长AB到C，使BC＝AB；（2）延长BA到D，使AD＝2AB；答案：（3）根据画图过程，推想下列线段之间具有的等量关系，并将倍数填在横线上：CD＝______BC，BD＝______B C＝______AC．答案：4|3|32．解析：解答：（1）（2）如图：；（3）∵BC＝AB，AD＝2AB，∴CD＝4BC，BD＝3BC＝32 AC．故答案为：4；3；32．分析：（1）（2）根据题意画出图形即可；（3）根据图形得出线段之间的数量关系即可．22.①如图1直线l上有2个点，则图中有2条可用图中字母表示的射线，有1条线段②如图2直线l上有3个点，则图中有______条可用图中字母表示的射线，有______条线段；答案：4|3③如图3直线上有n个点，则图中有______条可用图中字母表示的射线，有______条线段；答案：2n－2|()12n n-；④应用③中发现的规律解决问题：某校七年级共有6个班进行足球比赛，准备进行循环赛（即每两队之间赛一场），预计全部赛完共需______场比赛． 答案：65152⨯=． 解析：解答：②射线有：12A A 、23A A 、21A A 、31A A 共4条，线段有：12A A 、13A A 、23A A 共3条；③2n －2，()1 2n n -； ④65152⨯=． 分析：②写出射线和线段后再计算个数；③根据规律，射线是每个点用两次，但第一个和最后一个只用一次；线段是从所有点中，任取两个；④代入③中规律即可．23.如图，C 是线段AB 外一点，按要求画图：（1）画射线CB ；（2）反向延长线段AB ；（3）连接AC ，并延长AC 至点D ，使CD ＝AC ．答案：解答：根据题意画图：解析：分析：根据作图的步骤即可画出图形．24.已知平面上四点A、B、C、D，如图：（1）画直线AB；（2）画射线AD；（3）直线AB、CD相交于E；（4）连接AC、BD相交于点F．（5）延长AC至M，使CM等于2AC．答案：解答：如图：解析：分析：利用直线，射线及线段的定义画图即可．25.如图，平面上有四个点A、B、C、D，根据下列语句画图．（1）画直线AB、CD交于E点；（2）画线段AC、BD交于点F；（3）连接E、F交BC于点G；（4）连接AD，并将其反向延长；（5）作射线BC；（6）取一点P，使P在直线AB上又在直线CD上．答案：解析：解答：如图所示．分析：分别根据直线、射线、线段的定义作出图形即可．。
北师大七年级上《4.1线段、射线、直线》课时练习含答案解析
北师大版数学七年级上册第四章4.1线段、射线、直线同步练习一、选择题1.延长线段AB到C，下列说法正确的是（）A．点C在线段AB上B．点C在直线AB上C．点C不在直线AB上D．点C在直线BA的延长线上答案：B解析：解答：因为线段有两个端点，所以线段可以向两方延长，所以点C不在线段AB上，点C在直线AB上，故A、C错误，B正确，因为直线没有端点，可以向两方无限延伸，直线没有延长线的说法，故D错误．故选B．分析：本题根据直线、线段、以及射线的概念来解答即可．2.如图，图中共有线段的条数是（）A．4B．5C．6D．7答案：C解析：解答：图中的线段有AB、AC、AD、BC、BD、CD；故选：C．分析：根据图示数出线段即可．3.下列各直线的表示法中，正确的是（）A．直线AB．直线ABC．直线abD．直线Ab答案：B解析：解答：表示一条直线，可以用直线上的两个点表示，一般情况用两个大写字母表示；故选B．分析：此题考查直线的表示方法．4.如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A．两点确定一条直线B．两点之间线段最短C．垂线段最短D．在同一平面内，过一点有且只有一条直线与已知直线垂直答案：A解析：解答：经过刨平的木板上的两个点，能弹出一条笔直的墨线，此操作的依据是两点确定一条直线．故选：A．分析：根据公理“两点确定一条直线”来解答即可．5.如图，点A、B、C在一直线上，则图中共有射线（）A．1条B．2条C．4条D．6条答案：D解析：解答：根据射线的定义，这条直线上的每个点可以有两条射线，故图中共有射线6条．故选：D．分析：根据射线的定义，一条直线上的每个点可以有两条射线，分析图形可得答案．6.平面内的三个点A、B、C能确定的直线的条数是（）A．1条C．3条D．1条或3条答案：D解析：解答：∵若平面内的三个点A、B、C不在同一直线上，则能确定的直线的条数是：3条；若平面内的三个点A、B、C在同一直线上，则能确定的直线的条数是：1条．∴平面内的三个点A、B、C能确定的直线的条数是：1条或3条．故选D．分析：分别从若平面内的三个点A、B、C不在同一直线上与若平面内的三个点A、B、C 在同一直线上去分析，则可求得答案．7.观察图形，下列说法正确的个数是（）（1）直线BA和直线AB是同一条直线（2）射线AC和射线AD是同一条射线（3）AB＋BD＞AD（4）三条直线两两相交时，一定有三个交点．A．1个B．2个C．3个D．4个答案：C解析：解答：（1）直线BA和直线AB是同一条直线，直线没有端点，此说法正确；（2）射线AC和射线AD是同一条射线，都是以A为端点，同一方向的射线，正确；（3）AB＋BD＞AD，三角形两边之和大于第三边，所以此说法正确；（4）三条直线两两相交时，一定有三个交点，错误，可能有1个交点的情况．所以共有3个正确．分析：结合图形，区别各概念之间的联系．8.如图，平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF，从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…，则数字“”在（）A．射线OA上B．射线OB上C．射线OD上D．射线OF上答案：C解析：解答：÷6＝334…4，所以在射线OD上．故选C．分析：根据规律，所写数字按6个一组循环，用除以6余数是几就在第几条线．9.如下图，直线l、射线PQ、线段MN中能相交的是（）A．B．C．D．答案：D解析：解答：根据线段不延伸，而射线只向一个方向延伸即可得到：正确的只有D．分析：根据线段与射线的定义，以及延伸性即可作出判断．10.将线段AB延长至C，再将线段AB反向延长至D，则共有线段（）条．A．8B．7C．6D．5答案：C解析：解答：线段上有4个点时，线段总条数是3＋2＋1条，即6条．故选C．分析：因为将线段AB延长至C，再将线段AB反向延长至D，线段上有4个点，则共有线段条数可求．11.下列说法中正确的是（）A．画一条3厘米长的射线B．画一条3厘米长的直线C．画一条5厘米长的线段D．在线段、射线、直线中直线最长答案：C解析：解答：A.射线可无限延长，不可测量，所以画一条3厘米长的射线是错误的；B.直线是无限长的，直线是不可测量长度的，所以画一条3厘米长的直线是错误的；C.线段有两个端点，有限长度，可以测量，所以画一条5厘米长的线段是正确的；D.直线、射线都是无限延长，不可测量，不能比较长短，只有线段可以比较长短，所以在线段、射线、直线中直线最长是错误的．故选：C．分析：利用直线、射线、线段的意义和特点，逐项分析，找出正确答案即可．12.下列说法正确的是（）A．过一点P只能作一条直线B．直线AB和直线BA表示同一条直线C．射线AB和射线BA表示同一条射线D．射线a比直线b短解析：解答：A.过一点P可以作无数条直线；故A错误．B.直线可以用两个大写字母来表示，且直线没有方向，所以AB和BA是表示同一条直线；故B正确．C.射线AB和射线BA，顶点不同，方向相反，故射线AB和射线BA表示不同的射线；故C 错误．D.射线和直线不能进行长短的比较；故D错误．故选B．分析：过一点可以做无数条直线，根据直线的表示方法，AB和BA是表示同一条直线．而射线AB和射线BA表示不同的射线，射线与直线不能进行长短的比较．13.下列说法正确的是（）A．经过两点有且只有一条线段B．经过两点有且只有一条直线C．经过两点有且只有一条射线D．经过两点有无数条直线答案：B解析：解答：A.线段有长短，例如过A、B两点的线段不止一条，故本选项错误；B.经过两点有且只有一条直线，是直线公理，正确；C.射线有一个端点，例如过B、C两点的射线有射线AB、射线BC，故本选项错误；D.因为两点确定一条直线，所以本选项错误．故选B．分析：根据两点确定一条直线的公理和直线、射线、线段的性质对各选项分析判断后利用排除法求解．14.“两条直线相交，有且只有一个交点”的题设是（）A．两条直线B．交点C．两条直线相交D．只有一个交点解析：解答：两条直线相交，有且只有一个交点这一命题题设是两条直线相交，结论是有且只有一个交点，故选C．分析：本题考查两直线相交，有且只有一个交点的命题，题设和结论要搞清楚．15.如图，给出的直线、射线、线段，根据各自的性质，能相交的是（）A．B．C．D．答案：D解析：解答：A.射线延伸后两直线不能相交，故本选项错误；B.直线延伸后两直线不能相交，故本选项错误；C.射线和直线延伸后两直线不能相交，故本选项错误；D.射线延伸后两直线能相交，故本选项正确；故选D．分析：根据直线可以沿两个方向延伸，射线可以沿一个方向延伸，线段不能延伸即可得出答案．二、填空题16.直线上有n个点，我们进行如下操作：在每相邻两点间插入2个点．经过2次这样的操作后，直线上共有______个点．（用含n的代数式表示）答案：9n－8解析：解答：第一次操作，共有n＋（n－1）×2＝3n－2个点，第二次操作，共有（3n－2）＋（3n－2－1）×2＝9n－8个点，故答案为：9n－8．分析：根据n个点中间可以有（n－1）个空插入，从而找出规律并得解．17.平面内三条直线两两相交，最多有a个交点，最少有b个交点，则a＋b＝______．解析：解答：∵平面内三条直线两两相交，最多有3个交点，最少有1个交点，∴a＋b＝4．故答案为：4．分析：分析可得：平面内三条直线两两相交，最多有3个交点，最少有1个交点，则即可求得a＋b的值．18.乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要安排不同的车票______种．（A到B与B到A车票不同．）答案：20解析：解答：设点C、D、E是线段AB上的三个点，根据题意可得：图中共用()515102-⨯=条线段∵A到B与B到A车票不同．∴从A到B的车票共有10×2＝20种故答案为；20．分析：本题需先求出A、B之间共有多少条线段，根据线段的条数即可求出车票的种数．19.一条直线上立有10根距离相等的标杆，一名学生匀速地从第1杆向第10杆行走，当他走到第6杆时用了6.5s，则当他走到第10杆时所用时间是______．答案：11.7s解析：解答：从第1根标杆到第6根标杆有5个间隔，所以，每个间隔行进6.5÷5＝1.3s，从第1根标杆到第10根标杆共有9个间隔，所以，行进9个间隔共用1.3×9＝11.7s．故答案为：11.7s．分析：根据到第6杆时有5个间隔求出走1个间隔的时间，再求出到第10杆有9个间隔，然后列式计算即可得解．20.平面上有五条直线相交（没有互相平行的），则这五条直线最多有______个交点，最少有______个交点．答案：10|1解析：解答：最多时54102⨯=，相交于同一个点时最少，有1个交点．分析：直线交点最多时，根据公式()12n n-，把直线条数代入公式求解即可，直线相交于同一个点时最少，是1个交点．故答案为：10；1.三、解答题20.按要求画一画，再填空（1）延长AB到C，使BC＝AB；（2）延长BA到D，使AD＝2AB；答案：（3）根据画图过程，推想下列线段之间具有的等量关系，并将倍数填在横线上：CD＝______BC，BD＝______B C＝______AC．答案：4|3|32．解析：解答：（1）（2）如图：；（3）∵BC＝AB，AD＝2AB，∴CD＝4BC，BD＝3BC＝32 AC．故答案为：4；3；32．分析：（1）（2）根据题意画出图形即可；（3）根据图形得出线段之间的数量关系即可．22.①如图1直线l上有2个点，则图中有2条可用图中字母表示的射线，有1条线段②如图2直线l上有3个点，则图中有______条可用图中字母表示的射线，有______条线段；答案：4|3③如图3直线上有n个点，则图中有______条可用图中字母表示的射线，有______条线段；答案：2n －2|()1 2n n -；④应用③中发现的规律解决问题：某校七年级共有6个班进行足球比赛，准备进行循环赛（即每两队之间赛一场），预计全部赛完共需______场比赛．答案：65152⨯=． 解析：解答：②射线有：12A A 、23A A 、21A A 、31A A 共4条，线段有：12A A 、13A A 、23A A 共3条；③2n －2，()1 2n n -； ④65152⨯=． 分析：②写出射线和线段后再计算个数；③根据规律，射线是每个点用两次，但第一个和最后一个只用一次；线段是从所有点中，任取两个；④代入③中规律即可．23.如图，C 是线段AB 外一点，按要求画图：（1）画射线CB ；（2）反向延长线段AB ；（3）连接AC ，并延长AC 至点D ，使CD ＝AC ．答案：解答：根据题意画图：解析：分析：根据作图的步骤即可画出图形．24.已知平面上四点A、B、C、D，如图：（1）画直线AB；（2）画射线AD；（3）直线AB、CD相交于E；（4）连接AC、BD相交于点F．（5）延长AC至M，使CM等于2AC．答案：解答：如图：解析：分析：利用直线，射线及线段的定义画图即可．25.如图，平面上有四个点A、B、C、D，根据下列语句画图．（1）画直线AB、CD交于E点；（2）画线段AC、BD交于点F；（3）连接E、F交BC于点G；（4）连接AD，并将其反向延长；（5）作射线BC；（6）取一点P，使P在直线AB上又在直线CD上．答案：解析：解答：如图所示．分析：分别根据直线、射线、线段的定义作出图形即可．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
- 2 -
《直线、射线、线段》同步练习题
轻松入门
1.经过一点,有______条直线;经过两点有_____条直线,并且______条直线.
2.如图1,图中共有______条线段,它们是_________.
1
C
B
A
2
B
A
3
CDBA
3.如图2,图中共有_______条射线,指出其中的两条________.
4.线段AB=8cm,C是AB的中点,D是BC的中点,A、D两点间的距离是_____cm.
5.如图3,在直线I上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,AC+BD- BC=________.
6.下列语句准确规范的是( )
A.直线a、b相交于一点m B.延长直线AB
C.反向延长射线AO(O是端点) D.延长线段AB到C,使BC=AB
7.下列四个图中的线段(或直线、射线)能相交的是( )
1
C
D
BA
2CDBA 3CDBA 4CDBAA.(1) B.(2) C.(3)
D.(4)
8.如果点C在AB上,下列表达式①AC=12AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是
AB中点的有( ) A.1个 B.2个 C.3个 D.4个
9.如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
10.如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)连接E、F交BC于点G;
(4)连接AD,并将其反向延长;
(5)作射线BC;
(6)取一点P,使P在直线AB上又在直线CD上.
11.在一条直线上取两上点A、B,共得几条线段?在一条直线上取三个点A、B、 C,共得几条
线段?在一条直线上取A、B、C、D四个点时,共得多少条线段? 在一条直线上取n个点时,
共可得多少条线段?
CBBA
A
C
D
BA
答案
1.无数;一,只有一 2.3条,线段AC,AB,CB 3.4,射线BA,射线AB 4.6 5. AB,CD,AD
6.D 7.A 8.C 9.D 11.2个点时1条线段,3个点时有2+1=3条线段;4个点时有3+2+1=6
③
①
②
C
D
B
A
- 2 -
条线段;n 个点时有(n-1)+(n-2)+……+3+2+1=(1)2nn条线段.
线段、直线、射线
[基础训练]
1、关于线段，下列判断正确的是 （ ）
A.只有一个端点； B.有两个以上的端点； C.有两个端点； D.没有端点。
2、下列说法不正确的是 （ ）
A.射线是直线的一部分； B.线段是直线的一部分；
C.直线是无限延长的； D.直线的长度大于射线的长度。
3、下列说法中，正确的是 （ ）
A.延长射线的OA； B.延长直线AB； C.延长线段CD D.反向延长直线AB
4、经过一点的直线有 条；经过两点的直线有 条，并且只有 条，经
过不在同一直线上的三点最多可画 条直线。
5、探照灯射出的光线，给我们的印象似 。
6、笔直的窗帘轨，至少需要 个钉子才能将它固定，理由是
7、观察如图，指出图形中有多少条线段，请用字母表示出来。
8、画出下列语句表达的图形：
（1）点A在直线a上，点B在直线a外；
（2）直线a、b、c相交于点M；
（3）直线a、b相交于点A，直线b、c相交于点B，直线a、c相交于点c。
[综合提高]
一、选择题：
1、数轴是一条： （ ）
（A）射线 （B）直线 （C）线段 （D）以上都是
2、下列说法中，正确的个数有 （ ）
（1）射线AB与射线BA一定不是同一条射线；（2）直线AB与直线BA一定是同一条直线；
（3）线段AB与线段BA一定是同一条线段。
（A）0个 （B）1个 （C）2个 （D）3个
3、任意画3条直线，则交点的个数是 （ ）
（A）1个 （B）1个或3个 （C）1个或2个或3个 （D）0个或1个或2个或3
个
4、在直线上取两点A、B则这条直线上共有射线 （ ）
（A）1条 （B）2条 （C）3条 （D）4条
5、下列说法正确的是 （ ）
（A）线段没有长度； （B）射线上有无数个端点；
（C）两条相同端点的射线连结在一起就是一条直线； （D）直线没有端点。
6、下列写法正确的是 （ ）
（A）直线A、B相交于点M （B）过A、B、C三点画直线L
（C）直线a、b相交于点M （D）直线a、b相交于点n
7、如图，下列说法正确的是
（ ）
（Ａ）点Ａ在线段ＢＯ上；（Ｂ）点Ａ在射线ＢＯ上；
E
C A B
D
A B O
- 2 -
（Ｃ）点Ａ在线段ＢＯ的延长线上；（Ｄ）点Ａ在线段ＢＯ的反向延长线上。
８、在同一平面内有４个点，过每两点画一条直线，则直线的条数是 （ ）
（A）1条 （B）4条（C）6条 （D）1条或4条或6条
二、填空题
9、如图，以0为端点的射线有 条，它们分别是
图中线段有 条。
10、同一平面内三条线直线两两相交，最少有 个交点，最多有 个交点。
11、如图，以A、B、C、D为端点的射线有 条，
线段有 条。
12、观察自己身边的物品，举出几种常见的线段 。
13、看图写话，用语言描述下列图形：
（1） （2）
描述： 描述：
14、经过平面上三点可以画 条直线。
三、解答题：
15、根据下列要求画图：
（1）连接线段AB；
（2）画射线OA，射线OB；
（3）在线段AB上取一点C，在射线OA上取一点D（点C、D不与点A重合），画直线CD，
使直线CD与射线OB交于点E。
16，数线段，找规律：
下列各图中，线段上的点依次增加，请你填写图中相应的线段数，
条线段； 条线段； 条线段； 条线段；
(1) 请猜想，当线段AB上有10个点时（含A、B两点），有几条线段？
（2）n个点呢（n≧2）
[学练点拨]
每增加一个点,可以发现增加线段条数与原来线段上点的个数关系。
[探究创新]
设平面上有5个点，任何三点不在一条直线上，那么过这些点中每两点画直线，可画 条
线，如果是n个点，可以画 条直线。
参考答案
基础训练：
1 . C 2 .D 3 .C 4、无数、1、2、3 ； 5.射线 6 .2，两点确定一条直线 ； 7.
D C B O A ·
B
M NA C
D
A
·
a
P
a
b
A · B · O ·
D
CEBCBABACBAA
- 2 -
8条 ； 8. 略 综合提高：选择题：1 .B 2 .D 3 .D 4 .D 5 .D 6 .C 7 .D 8. D
填空题：9. 4， 射线OA,射线OB, 射线OC, 射线OD； 8. 10、1,3; 11、 8, 6; 12. 略
13 （1）点A在直线a上，（2）直线a, b 相交于点p 14. 1 或3
解答题：15．略 16 . 1，3，6，10 ;（1）45条 （2）n(n-1)/2
探究创新： 1． 10条 ， n(n-1)/2 2. 能，图略