2020年7月20日湖南省邵阳市新邵县2019~2020学年度高二下学期期末考试试题及参考答案
2019-2020学年邵阳市新邵县高二下学期期末数学试卷(含答案解析)

2019-2020学年邵阳市新邵县高二下学期期末数学试卷一、单选题(本大题共12小题,共60.0分)1.设集合M={x|log2(x−1)<1},N={x|x≥2},则M∪N=()A. {x|2≤x<3}B. {x|x≥2}C. {x|x>1}D. {x|1≤x<3}2.已知复数z满足zi=2+i,i是虚数单位,则复数z=()A. −1+2iB. 1+2iC. −1−2iD. 1−2i3.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如表所示的列联表:优秀非优秀总计甲班10b乙班c30总计105,则下列说法.正确的是()已知在全部105人中随机抽取1人,成绩优秀的概率为27≈6.109参考公式及数据:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)附表:P(K2≥k0)0.0500.0100.001k0 3.841 6.63510.828A. 列联表中c的值为30,b的值为35B. 列联表中c的值为15,b的值为50C. 根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”D. 根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”4.在正方体中,点为上底面的中心,若,则,的值是A. ,B. ,C. ,D. ,5.已知,则的大小关系是()A. B. C. D.6.已知数列中,,,则的通项公式为()A. B.C. D.7.某校从高一(1)班和(2)班的某次数学考试(试卷满分为100分)的成绩中各随机抽取了3份数学成绩组成一个样本,如茎叶图所示,若分别从−(1)班、(2)班的样本中各随机抽取一份,则(2)班成绩更好的概率为()A. 29B. 13C. 12D. 498.若f(x)是R上的可导函数,且f(x)+xf′(x)>0则下列结论正确的是()A. 2014f(2014)>2015f(2015)B. 2014f(2015)>2015f(2014)C. 2014f(2014)<2015f(2015)D. 2014f(2015)<2015f(2014)9.从2、4、6、8、10五个数字中任取2个作为一个分数的分子与分母,则可组成分数值不同的分数个数为()A. 20B. 18C. 10D. 910.(文科做)甲乙两袋中各有大小相同的两个红球、一个黄球,分别从两袋中取一个球,恰有一个红球的概率是()A.B.C.D. (理科做)在棱长为2的正方体ABCD−A1B1C1D1中,点O为底面ABCD的中心,在正方体ABCD−A1B1C1D1内随机取一点P,则点P到点O的距离大于1的概率为()A.B.1−C.D.1−11. 在直三棱柱ABC −A 1B 1C 1中,AA 1=AB =6,BC =8,AC =10,则该三棱柱内能放置的最大球的表面积是( )A. 16πB. 24πC. 36πD. 64π12. 下列四个命题中正确的是( )A. 若n →∞lim a n 2=A 2,则n →∞lima n =AB. 若a n >0,n →∞lim a n =A ,则A >0C. 若n →∞lim a n =A ,则n →∞lima n 2=A 2D. 若n →∞lim (a n −b)=0,则n →∞lim a n =n →∞limb n二、单空题(本大题共3小题,共15.0分) 13. 函数的图象过点P(0,2),且在点M处的切线方程为.则b −c = .14. 在(1+3x)n (n ∈N ∗,n ≥6)的展开式中,若x 5与x 6的系数相等,则n 的值为______. 15. 在平面直角坐标系中,O 是坐标原点,两定点A ,B 满足||=||=·=2,则点集{P|=λ+μ,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是________.三、多空题(本大题共1小题,共5.0分)16. 点P 是直线kx +y +3=0(k >−43)上一动点,PA ,PB 是圆C :x 2−2x +y 2=0的两条切线,A ,B 为切点.若四边形PACB 的最小面积为2,则此时线段PC 的长为 ;实数k 的值是 . 四、解答题(本大题共6小题,共70.0分)17. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知B =2C ,3b =4c . (1)求cos C ;(2)若c =3,求△ABC 的面积.18. 已知数列{a n },b n 满足:a 1=14,a n +b n =1,b n+1=bn1−a n2.(1)求b 1,b 2,b 3,b 4; (2)求数列{b n }的通项公式;(3)设S n =a 1⋅a 2+a 2⋅a 3+⋯+a n ⋅a n+1,若4a ⋅S n >b n 对n ∈N ∗恒成立,求实数a 的取值范围.19.如图,在三棱柱ABC−A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1上运动(1)试问点P在何处时,AB//平面PNC,并证明你的结论;(2)在(1)的条件下,且AA1<AB,直线B1C与平面BCP的成角的正,求二面角A−BP−C的大小.弦值为√101020.2020年“双11”当天各大线上网站的消费额统计都创下新高,体现了中国在“新冠”疫情之后经济复苏的良好态势.某网站为了调查线上购物时“高消费用户”是否与性别有一定关系,随机调查200个“双11”当天在该网站消费的用户,得到了如下不完整的列联表;定义“双11”当天消费不高于10000元的用户为“非高消费用户”,消费10000元以上的用户为“高消费用户”.高消费用户非高消费用户总计男性用户20女性用户40总计80附:K2=n(ad−bc)2,(a+b)(c+d)(a+c)(b+d)P(K2≥k0)0.1000.0500.0100.001k0 2.706 3.841 6.63510.828(1)将列联表填充完整,并判断是否有99%的把握认为线上购物时“高消费用户”与性别有关?(2)若采用分层抽样的方法从随机调查的200个用户中抽出10个人,再随机抽4人,记高消费用户人数为X,求X的分布列和数学期望.21. 20.(本小题满分12分)已知椭圆的离心率为,且经过点.圆.(1)求椭圆的方程;(2)若直线与椭圆C有且只有一个公共点,且与圆相交于两点,问是否成立?请说明理由.22. 已知函数f(x)=e x−ax2,其中常数a∈R.(1)若a=1,令g(x)=f′(x),求g(x)的单调递增区间;(2)当x∈(0,+∞)时,不等式f(x)>0恒成立,求实数a的取值范围;(3)若a=1,且x∈[0,+∞)时,求证:f(x)>x2+4x−14.【答案与解析】1.答案:C解析:解:∵集合M={x|log2(x−1)<1}={x|1<x<3},N={x|x≥2},∴M∪N={x|x>1}.故选:C.先分别求出集合M,N,由此能求出M∪N.本题考查并集的求法,考查并集定义、不等式性质等基础知识,考查运算求解能力,是基础题.2.答案:D解析:解:由zi=2+i,得z=2+ii =−i(2+i)−i2=1−2i.故选:D.把已知等式变形,再利用复数代数形式的乘除运算化简得答案.本题考查了复数代数形式的乘除运算,是基础题.3.答案:C解析:解:∵在全部105人中随机抽取1人,成绩优秀的概率为27,∴成绩优秀的人数为:105×27=30(人),非优秀的人数为:105−30=75(人),∴c=30−10=20,b=75−30=45,∴则K的观测值:K2=105×(10×30−20×45)230×75×50×55=33655≈6.110>3.841,∴若按95%的可靠性要求,能认为“成绩与班级有关系”,故选:C.由成绩优秀的概率为27,可求得成绩优秀的人数,进而求出非优秀的人数,得到b,c的值,计算K 的观测值K2,对照题目中的表格,得出统计结论.本题考查了独立性检验的应用问题,也考查了计算能力的应用问题,是中档题.4.答案:A解析:试题分析:如下图:=,故选.考点:向量的加法5.答案:C解析:试题分析:根据指数函数与对数函数图像与性质可知,中a<0,b>1,0<c<1,那么可知a,b,c的大小关系为,故选C.考点:比较大小,指数式与对数式点评:解决该试题的关键是运用指数函数和对数函数的性质来得到值域的范围,比较大小属于基础题。
湖南省邵阳市新邵县2019-2020学年高二下学期期末考试物理答案

2020年上期高中二年级期末质量检测物理参考答案与评分标准一、单项选择题:本题共 8 小题,每小题 3 分,共 24 分。
在每个题给出的四个选项中, 只有一项是符合题目要求的。
二、多项选择题:本题共 4 小题,每小题 4 分,共 16 分。
在每个题给出的四个选项中, 有多项符合题目要求。
全部选对的得 4 分,选对但不全的得 2 分,有选错的得 0 分。
三、非选择题:本题共 6 小题,共 60 分。
13、(共6分) (1)AB (2分), (2)0.80 (2分), 0.40(2分)14、(共8分)(1)a (2分) (2) 偏小 (1分) 4.8(1分)1.2 (1分) (3)0.31-0.33都给3分 15.(8分)解:物体做匀加速直线运动,t 时间内的平均速度等于2t时刻的瞬时速度, 在第一段内中间时刻的瞬时速度为:1116m/s=4m/s 4v v -==;(3分) 在第二段内中间时刻的瞬时速度为:2216m/s=8m/s 2v v -==;(3分) 则物体加速度为:21844m/s m/s 33v v a t --===(2分) 16.(8分)解:(1)系统全过程动量守恒0223mv mv = (1分) v 2=023v (1分)(2)BC 发生完全非弹性碰撞,有 012mv mv = (1分) 得012v v =(1分)根据能量守恒有222012111(2)(3)222f mv m v m v W +=+ (1分) 则20112f W mv = (1分) A 在C 上滑动时摩擦力按线性关系增大,所以做功大小为2mgL W f μ=(1分)得L=206v gμ (1分)17.(14分)解:(1)对带电小球,从A 到B 过程小球做平抛运动,则有x 1=v 0t 1 (1分) 从B 到C 过程,有:x 2=v 0t 2; (1分) 由题意有:x 1=2x 2; (1分)则得:t 1=2t 2; (1分)即小球从A 到B 是从B 到C 运动时间的2倍.在竖直方向21112y gt =(1分)将小球在电场中的运动看成沿相反方向的类平抛运动,则有:21212y at =(1分)根据几何知识有:1122Y X Y X =;(1分) 解得:a=2g ;(1分) 在电场中,根据牛顿第二定律得:Eq-mg=ma=2mg ,(1分)解得:3mgE q =(1分)(2)由功能关系可得:23mgHW E -==∆电机(4分) 18.(16分)解:(1)线圈沿斜面向下运动,由动能定理有211sin 3002mgx mv ︒=- (2分)解得1 5 m/s v = (1分)(2)线圈进入磁场过程中,通过ab 边的电荷量q I t =⋅∆ (2分)又E I R =, (2分) ΔΔE t Φ= (2分) 解得2Δ0.5 C BL q R R Φ=== (1分)(3)线圈离开磁场时有2sin 30BLv B L mg R=︒ (2分) 222sin 3010 m/s mgR v B L︒== (1分) 由能量守恒可得2213=()sin 30 J 24Q mg d x L mv ++︒-=总 (2分)则ab 边产生的热量3= J 16Q (或0.187 5 J) (1分)。
湖南省邵阳市新邵县2019-2020学年高二下学期期末考试数学答案

2020年上期高中二年级期末考试数学参考答案一、选择题 D B C A C B D A B C B A 二、填空题 13.01=--y x 14.60 15.6π16.(1)3 (2)512三、解答题17.解:(1)由已知及正弦定理得:sin cos sin sin sin A B B A C +=,sin sin()sin cos cos sin C A B A B A B =+=+sin in cos sin Bs A A B ∴=, sin 0sin cos B A A≠∴=(0,)4A A ππ∈∴=………………5分(2)11sin 2242ABCSbc A bc ===∴=又22222cos 2()(2a b c bc A b c bc=+-∴=+-+所以,2()4, 2.b c b c +=+=. ………………10分 18.解:(1)∵1124,24n n n n S a S a --=-=-相减得:122n n n a a a -=- ∴12n n a a -=………………3分12,nn a a -= 又111124,4a S a a ==-∴= 11422n n n a -+∴=⨯=………………6分 (2)1222log 32log 2321n n n b a n +=-=-=-………………8分1111335(21)(21)n T n n =+++⨯⨯-+111111(1)233521(21)n n =-+-++--+ 11(1)2(21)21n n n =-=++………………12分 19.(1)证明:取AD 中点O ,连结OP ,OB ,BD ,∵底面ABCD 为菱形,60BAD ∠=,∴AD =AB BD =.又O 为AD 的中点,∴OB AD ⊥.……………1分在△APD 中,90APD ∠=, O 为AD 的中点,∴12PO AD AO ==. D CBAPO设2AD PB a ==,则OB =,PO OA a ==,∵22222234PO OB a a a PB +=+==,∴OP OB ⊥.………………2分 ∵OPAD O =,OP ⊂平面PAD ,AD ⊂平面PAD ,∴OB ⊥平面PAD .……3分又OB ⊂平面ABCD ,∴平面PAD ⊥平面ABCD .……………………4分 (2)解:∵AD PB ⊥,AD OB ⊥,OBPB B =,PB ⊂平面POB ,OB ⊂平面POB ,∴AD ⊥平面POB . ∴PO AD ⊥. 由(1)得PO OB ⊥,AD OB ⊥, ∴OA ,OB ,OP 所在的直线两两互相垂直.…………5分 以O 为坐标原点,分别以OA ,OB ,OP 所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系.………………………6分设2AD =,则(1,0,0)A ,(1,0,0)D -,()B ,()0,0,1P ,……………7分∴()1,0,1PD =--,()1PB =-,(2,0,0)BC AD ==-,…………………8分 设平面PBD 的法向量为()111,,x y z =n ,则11110,30,PD x z PB y z ⎧•=--=⎪⎨•=-=⎪⎩n n 令11y =,则1x =1z = ∴(=n .……………9分设平面PBC 的法向量为()222,,x y z =m ,则22220,30,BC x PB y z ⎧•=-=⎪⎨•=-=⎪⎩m m 令21y =,则20x =,2z =(=m .……………………………10分设二面角D PBC --为θ,由于θ为锐角,∴cos cos ,θ=<>m n …………11分==. 所以二面角D PB C --.……………12分 z yxOPA BCD20.解:(1)根据频率分布直方图得(20.0240.0200.004)101a b c +++++⨯=, 又2,2a c b c a +==,解得0.008a =,0.012b =,0.016c =, 故数学成绩的平均分850.04950.121050.161150.21250.241350.161450.08117.8x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=(分). …………4分(2)总人数为50,由物理成绩统计表知,中位数在区间[70,80)内, 所以物理成绩的中位数约为75分.…………6分(3)数学成绩为“优”的同学有4人,物理成绩为“优”的有5人, 因为至少有一科为“优”的同学共有6名,所以两科均为“优”的人数为3, 故X 的可能取值为0,1,2,3.3336C 1(0)C 20P X ===, 123336C C 9(1)C 20P X ===, 213336C C 9(2)C 20P X === 3336C 1(3)C 20P X ===. 所以X 的分布列为199130123202020202EX =⨯+⨯+⨯+⨯=. …………12分21.解:(1)由题意,1b =, …………1分 右焦点(,0)(0)c c >到直线分分∵椭圆E 的焦点在x 轴上,所以椭圆E 的方程为………………4分 (2)当k 不存在时,||2AB = ………………5分当k 存在时,设直线方程为1y kx =+,联立,得22(13)60k x kx ++=,6分分分令213,(1,),t k t =+∈+∞则分 ,即21k =,得1k =±时…………10分 2||AB 的最大值为,即||AB 的最大值为分 直线l 的方程为11y x y x =+=-+或. ………………12分 22.解:(1) 函数)(x f 的定义域为),0(+∞ 22'11)(xax x a x x f -=+-= ………1分 当0≤a 时,0)('<x f , ∴)(x f 在),0(+∞上单调递减; ………………2分当0>a 时,由0)('>x f 得a x 1>,由0)('<x f 得ax 10<< ∴)(x f 在)1,0(a 上单调递减,在),1(+∞a单调递增 ………………4分综上可知: 0≤a 时, )(x f 在),0(+∞上单调递减;0>a 时, )(x f 在)1,0(a 上单调递减,在),1(+∞a单调递增 ………………5分(2)因为0>x ,所以不等式等价于xxe ex e x ln 1>+- ………………6分设1)(+-=ex e x h x,e e x h x-=)(/,所以),1(+∞∈x 时, 0)(/>x h ,)(x h 单调递增,)1,0(∈x 时, 0)(/<x h ,)(x h 单调递减, ∴1)1()(min ==h x h ………………8分设x x e x g ln )(=,2/)ln 1()(xx e x g -=,所以),0(e x ∈时, 0)(/>x g ,)(x g 单调递增, ),(+∞∈e x 时, 0)(/<x g ,)(x g 单调递减, ∴1)()(max ==e g x g ………………10分虽然)(x h 的最小值等于)(x g 的最大值,但e ≠1,所以)(x h >)(x g , 即xxe ex e x ln 1>+-,故原不等式成立 ………………12分。
2019-2020学年湖南省邵阳市新邵县高二下学期期末考试数学试题 word版

湖南省邵阳市新邵县2019-2020学年高二下学期期末考试数学试题考生注意:1.答题前,先将自己的姓名,准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的做题:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域无效.3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区无效.一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.已知集合{}2|20A x x x =+-<,集合{}|0B x x =>,则集合A B =( )A.{}|1x x <B.{}|21x x -<<C.{}|01x x <<D.{}|2x x >-2.若复数z 满足1i z i ⋅=--,则在复平面内,z 所对应的点在( ) A.第一象限B.第二象限C.第三象限D.第四象限3.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下表的列联表:算得,27.8K ≈.见附表:参照附表,得到的正确结论是( )A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”4.甲、乙、两三人中,一人是律师,一个是医生,一人是记者.已知丙的年龄比医生大;甲的年龄和记者不同;记者的年龄比乙小.根据以上情况,下列判断正确的是( ) A.甲是医生,乙是律师,丙是记者 B.甲是医生,乙是记者,丙是律师 C.甲是律师,乙是医生,丙是记者D.甲是记者,乙是医生,丙是律师5.已知0.12tan 5a π⎛⎫= ⎪⎝⎭,3log 2b =,23log cos 7c π⎛⎫= ⎪⎝⎭,则( )A.c a b >>B.b a c >>C.a b c >>D.a c b >>6.设等差数列{}n a 的前n 项和为n S ,若452a S +=,714S =,则公差d 的值为( ) A.4B.2C.2-D.4-7.某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据丢失(如图),但甲得分的折线图完好,则下列结论正确的是( )A.甲得分的极差是11B.乙得分的中位数是18.5C.甲运动员得分有一半在区间[20,30]上D.甲运动员得分的平均值比乙运动员得分的平均值高8.函数()f x 在定义域R 内可导,若()(2)f x f x =-,且当(,1)x ∈-∞时,(1)()0x f x '-<,设(0)a f =,12b f ⎛⎫= ⎪⎝⎭,(3)c f =,则( )A.c a b <<B.c b a <<C.a b c <<D.b c a <<9.某班文艺晚会,准备从A 、B 等8个节目中选出4个节目,要求:A 、B 两个节目至少有一个选中,且A 、B 同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的种数为( )A.1020B.1140C.1320D.186010.盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一-个球,则此时取出黄色球的概率为( ) A.715B.79C.35D.314511.已知三棱锥S ABC -的所有顶点都在球O 的球面上,SA ⊥平面ABC ,2SA =,1AB =,2AC =,3BAC π∠=,则球O 的体积为( )A.3B.3C.D.312.已知函数()sin (0)3f x x πωω⎛⎫=+> ⎪⎝⎭,1()2f x =在区间[0,]π上有且仅有2个零点,对于下列4个结论:①在区间(0,)π上存在1x ,2x ,满足()()122f x f x -=;②()f x 在区间(0,)π有且仅有1个最大值点;③()f x 在区间0,15π⎛⎫ ⎪⎝⎭上单调递增;④ω的取值范围是115,162⎡⎫⎪⎢⎣⎭,其中所有正确结论的编号是( ) A.①③B.①④C.②③D.①③④二、填空题(本大题共4个小题,每小题5分,共20分) 13.曲线ln y x x =在点(1,0)处的切线方程为________.14.62x⎛⎝的展开式中的常数项的值是________.(用数字作答)15.已知a ,b 为单位向量,2c a b =-,且,3a b π〈〉=,则,a c 〈〉=________.16.2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:(0,3)Q -是圆Q 的圆心,圆Q 过坐标原点O ;点L 、S 均在x 轴上,圆L 与圆S 的半径都等于2,圆S 、圆L 均与圆Q 外切,已知直线l 过点O .(1)若直线l 与圆L ,圆S 均相切,则l 截圆Q 所得弦长为________; (2)若直线l 截圆L 、圆S 、圆Q 所得弦长均等于d ,则d =________. (本题第一个空2分,第二个空3分)三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)在ABC △中,内角A 、B 、C 的对边分别为a 、b 、c ,且cos sin a B b A c +=. (1)求角A 的大小;(2)若a =ABC △的面积为12,求b c +的值.18.(本小题满分12分)设数列{}n a 的前n 项和为n S ,已知24n n S a =-,*n N ∈. (1)求通项公式n a ;(2)设22log 3n n b a =-,求数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和n T .19.(本小题满分12分)如图,在四棱锥P ABCD -中,底面ABCD 为菱形,60BAD ∠=︒,90APD ∠=︒,且AD PB =.(1)求证:平面PAD ⊥平面ABCD ;(2)若AD PB ⊥,求二面角D PB C --的余弦值. 20.(本小题满分12分)高二年级某班50名学生的期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],其中a ,b ,c 成等差数列且2c a =.物理成绩统计如下表(说明:数学满分150分,物理满分100分)(1)根据频率分布直方图,请估计数学成绩的平均分; (2)根据物理成绩统计表,请估计物理成绩的中位数;(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一科为“优”的同学共有6人,从这6人中随机抽取3人,记X 为抽到两科为“优”的学生人数,求X 的分布列和数学期望.21.(本小题满分12分)已知椭圆E 的一个顶点为(0,1)A ,焦点在x轴上,若椭圆的右焦点到直线0x y -+=的距离是3. (1)求椭圆E 的方程;(2)设过点A 的直线l 与该椭圆交于另一点B ,当弦AB 的长度最大时,求直线l 的方程. 22.(本小题满分12分)已知函数1()ln f x a x x=+,()x e g x x =.(1)讨论函数()f x 的单调性;(2)证明:1a =时,2()()11n e f x g x x e x ⎛⎫+-+> ⎪⎝⎭.2020年上期高中二年级期末考试数学参考答案一、选择题 D B C A C B D A B C B A 二、填空题 13.01=--y x 14.60 15.6π16.(1)3 (2)512三、解答题17.解:(1)由已知及正弦定理得:sin cos sin sin sin A B B A C +=,sin sin()sin cos cos sin C A B A B A B =+=+sin in cos sin Bs A A B ∴=,sin 0sin cos B A A≠∴=(0,)4A A ππ∈∴=………………5分(2)11sin 2242ABCSbc A bc ===∴=又22222cos 2()(2a b c bc A b c bc=+-∴=+-+所以,2()4, 2.b c b c +=+=. ………………10分 18.解:(1)∵1124,24n n n n S a S a --=-=-相减得:122n n n a a a -=- ∴12n n a a -=………………3分12,nn a a -= 又111124,4a S a a ==-∴= 11422n n n a -+∴=⨯=………………6分(2)1222log 32log 2321n n n b a n +=-=-=-………………8分1111335(21)(21)n T n n =+++⨯⨯-+111111(1)233521(21)n n =-+-++--+ 11(1)2(21)21n n n =-=++………………12分 19.(1)证明:取AD 中点O ,连结OP ,OB ,BD ,∵底面ABCD 为菱形,60BAD ∠=,∴AD =AB BD =.又O 为AD 的中点,∴OB AD ⊥.……………1分 在△APD 中,90APD ∠=, O 为AD 的中点,∴12PO AD AO ==. 设2AD PB a ==,则OB =,PO OA a ==,∵22222234PO OB a a a PB +=+==,∴OP OB ⊥.………………2分 ∵OPAD O =,OP ⊂平面PAD ,AD ⊂平面PAD ,∴OB ⊥平面PAD .……3分又OB ⊂平面ABCD ,∴平面PAD ⊥平面ABCD .……………………4分 (2)解:∵AD PB ⊥,AD OB ⊥,OBPB B =,PB ⊂平面POB ,OB ⊂平面POB ,∴AD ⊥平面POB .∴PO AD ⊥. 由(1)得PO OB ⊥,AD OB ⊥, ∴OA ,OB ,OP 所在的直线两两互相垂直.…………5分以O 为坐标原点,分别以OA ,OB ,OP 所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系.………………………6分设2AD =,则(1,0,0)A ,(1,0,0)D -,()B ,()0,0,1P ,……………7分 ∴()1,0,1PD =--,()1PB =-,(2,0,0)BC AD ==-,…………………8分设平面PBD 的法向量为()111,,n x y z =,则1111•0,•30,n PD x z n PBy z ⎧=--=⎪⎨=-=⎪⎩ 令11y =,则1x =1z = ∴(3,1,n =-.……………9分设平面PBC 的法向量为()222,,m x y z =,则222•20,•30,m BC x m PB y z ⎧=-=⎪⎨=-=⎪⎩ 令21y =,则20x =,2z =∴(0,1,3m =. (10)分设二面角D PB C--为θ,由于θ为锐角,∴cos cos ,θ=<>m n …………11分==. 所以二面角D PB C --.……………12分20.解:(1)根据频率分布直方图得(20.0240.0200.004)101a b c +++++⨯=, 又2,2a c b c a +==,解得0.008a =,0.012b =,0.016c =, 故数学成绩的平均分850.04950.121050.161150.21250.241350.161450.08117.8x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=(分). …………4分(2)总人数为50,由物理成绩统计表知,中位数在区间[70,80)内, 所以物理成绩的中位数约为75分.…………6分(3)数学成绩为“优”的同学有4人,物理成绩为“优”的有5人, 因为至少有一科为“优”的同学共有6名,所以两科均为“优”的人数为3, 故X 的可能取值为0,1,2,3.3336C 1(0)C 20P X ===, 123336C C 9(1)C 20P X ===, 213336C C 9(2)C 20P X === 3336C 1(3)C 20P X ===. 所以X 的分布列为199130123202020202EX =⨯+⨯+⨯+⨯=. …………12分21.解:(1)由题意,1b =, (1)分 右焦点(,0)(0)c c >到直线 ……2分 分∵椭圆E 的焦点在x 轴上,所以椭圆E 的方程为………………4分 (2)当k 不存在时,||2AB = ………………5分当k存在时,设直线方程为1y kx =+,联立,得22(13)60k x kx ++=,6分 分 分令213,(1,),t k t =+∈+∞则分 ,即21k =,得1k =±时…………10分 2||AB 的最大值为,即||AB 的最大值为分直线l 的方程为11y x y x =+=-+或. ………………12分22.解:(1) 函数)(x f 的定义域为),0(+∞ 22'11)(x ax x a x x f -=+-= ………1分 当0≤a 时,0)('<x f , ∴)(x f 在),0(+∞上单调递减; ………………2分当0>a 时,由0)('>x f 得a x 1>,由0)('<x f 得ax 10<< ∴)(x f 在)1,0(a 上单调递减,在),1(+∞a单调递增 ………………4分综上可知: 0≤a 时, )(x f 在),0(+∞上单调递减;0>a 时, )(x f 在)1,0(a 上单调递减,在),1(+∞a单调递增 ………………5分(2)因为0>x ,所以不等式等价于xxe ex e x ln 1>+- ………………6分设1)(+-=ex e x h x,e e x h x-=)(/,所以),1(+∞∈x 时, 0)(/>x h ,)(x h 单调递增,)1,0(∈x 时,0)(/<x h ,)(x h 单调递减, ∴1)1()(min ==h x h ………………8分设x x e x g ln )(=,2/)ln 1()(xx e x g -=,所以),0(e x ∈时, 0)(/>x g ,)(x g 单调递增, ),(+∞∈e x 时, 0)(/<x g ,)(x g 单调递减, ∴1)()(max ==e g x g ………………10分虽然)(x h 的最小值等于)(x g 的最大值,但e ≠1,所以)(x h >)(x g , 即xxe ex e x ln 1>+-,故原不等式成立 ………………12分。
2019-2020学年湖南省邵阳市新邵县高二下学期期末数学试卷 (解析版)

2019-2020学年湖南省邵阳市新邵县高二第二学期期末数学试卷一、选择题(共12小题).1.已知集合A={x|x2+x﹣2<0},集合B={x|x>0},则集合A∪B=()A.{x|0<x<1}B.{x|x<1}C.{x|﹣2<x<1}D.{x|x>﹣2} 2.若复数z满足zi=﹣1﹣i,则在复平面内,z所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限3.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:男女总计爱好402060不爱好203050总计6050110P(K2≥k)0.0500.0100.001k 3.841 6.63510.828算得,K2≈7.8.见附表:参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”4.甲、乙、丙三人中,一人是律师,一人是医生,一人是记者.已知丙的年龄比医生大;甲的年龄和记者不同;记者的年龄比乙小.根据以上情况,下列判断正确的是()A.甲是律师,乙是医生,丙是记者B.甲是医生,乙是记者,丙是律师C.甲是医生,乙是律师,丙是记者D.甲是记者,乙是医生,丙是律师5.已知,则()A.a>b>c B.b>a>c C.c>a>b D.a>c>b6.设等差数列{a n}的前n项和为S n,若a4+S5=2,S7=14,则公差d=()A.﹣4B.﹣2C.2D.47.某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据丟失(如图),但甲得分的折线图完好,则下列结论正确的是()A.甲得分的极差是11B.乙得分的中位数是18.5C.甲运动员得分有一半在区间[20,30]上D.甲运动员得分的平均值比乙运动员得分的平均值高8.函数f(x)在定义域R内可导,若f(x)=f(x﹣2),且当x∈(﹣∞,1)时,(x﹣1)f'(x)<0,设a=f(0),b=f(),c=f(3),则()A.c<a<b B.c<b<a C.a<b<c D.b<c<a9.某班组织文艺晚会,准备从A,B等8个节目中选出4个节目演出,要求:A,B两个节目至少有一个选中,且A,B同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的和数为()A.1860B.1320C.1140D.102010.盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一个球,则此时取出黄色球的概率为()A.B.C.D.11.已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,∠BAC=,则球O的体积为()A.B.C.D.12.已知函数,在区间[0,π]上有且仅有2个零点,对于下列4个结论:①在区间(0,π)上存在x1,x2,满足f(x1)﹣f(x2)=2;②f(x)在区间(0,π)有且仅有1个最大值点;③f(x)在区间上单调递增;④ω的取值范围是.其中所有正确结论的编号是()A.①③B.①④C.②③D.①③④二、填空题(本大题共4个小题,每小题5分,共20分.)13.曲线y=xlnx在点(1,0)处的切线方程为.14.(2x﹣)6展开式中常数项为(用数字作答).15.已知,为单位向量,,且<,>=,则<,>=.16.2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:Q (0,﹣3)是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.(1)若直线l与圆L、圆S均相切,则l截圆Q所得弦长为;(2)若直线l截圆L、圆S、圆Q所得弦长均等于d,则d=.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.在△ABC中,内角A、B、C的对边分别为a、b、c,且a cos B+b sin A=c.(1)求角A的大小;(2)若,△ABC的面积为,求b+c的值.18.设数列{a n}的前n项和为S n,已知S n=2a n﹣4,n∈N*.(Ⅰ)求通项公式a n;(Ⅱ)设b n=2log2a n﹣3,求数列{}的前n项和T n.19.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,∠APD=90°,且AD=PB.(l)求证:平面PAD⊥平面ABCD;(2)若AD⊥PB,求二面角D﹣PB﹣C的余弦值.20.高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150.其中a,b,c成等差数列且c=2a.物理成绩统计如表.(说明:数学满分150分,物理满分100分)分组[50,60)[60,70)[70,80)[80,90)[90,100]频数6920105(1)根据频率分布直方图,请估计数学成绩的平均分;(2)根据物理成绩统计表,请估计物理成绩的中位数;(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从此6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和期望值.21.已知椭圆E的一个顶点为A(0,1),焦点在x轴上,若椭圆的右焦点到直线x﹣y+2=0的距离是3.(Ⅰ)求椭圆E的方程;(Ⅱ)设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.22.已知函数f(x)=,(1)讨论函数f(x)的单调性;(2)证明:a=1时,f(x)+g(x)﹣(1+)lnx>e.参考答案一、选择题(共12小题).1.已知集合A={x|x2+x﹣2<0},集合B={x|x>0},则集合A∪B=()A.{x|0<x<1}B.{x|x<1}C.{x|﹣2<x<1}D.{x|x>﹣2}【分析】利用并集定义直接求解.解:∵集合A={x|x2+x﹣2<0}={x|﹣2<x<1},集合B={x|x>0},∴集合A∪B={x|x>﹣2}.故选:D.2.若复数z满足zi=﹣1﹣i,则在复平面内,z所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【分析】利用复数的运算法则即可得出解:∵复数z满足zi=﹣1﹣i,∴﹣i•i•z=﹣i(﹣1﹣i),化为z=﹣1+i.∴z在复平面内所对应的点的坐标是(﹣1,1),在第二象限,故选:B.3.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:男女总计爱好402060不爱好203050总计6050110P(K2≥k)0.0500.0100.001k 3.841 6.63510.828算得,K2≈7.8.见附表:参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”【分析】根据条件中所给的观测值,同题目中节选的观测值表进行检验,得到观测值对应的结果,得到结论有99%以上的把握认为“爱好该项运动与性别有关”.解:由题意知本题所给的观测值K2≈7.8>6.635,∴这个结论有0.01=1%的机会说错,即有99%以上的把握认为“爱好该项运动与性别有关”故选:C.4.甲、乙、丙三人中,一人是律师,一人是医生,一人是记者.已知丙的年龄比医生大;甲的年龄和记者不同;记者的年龄比乙小.根据以上情况,下列判断正确的是()A.甲是律师,乙是医生,丙是记者B.甲是医生,乙是记者,丙是律师C.甲是医生,乙是律师,丙是记者D.甲是记者,乙是医生,丙是律师【分析】由甲的年龄和记者不同,记者的年龄比乙小,得到丙是记者,由丙的年龄比医生大,得到乙不是医生,从而乙是教师,甲是医生.解:由甲的年龄和记者不同,记者的年龄比乙小,得到丙是记者,从而排除B和D;由丙的年龄比医生大,得到乙不是医生,从而乙是教师,甲是医生.故选:C.5.已知,则()A.a>b>c B.b>a>c C.c>a>b D.a>c>b【分析】利用指数函数、对数函数三角函数的单调性即可得出.解:a=>=1,b∈(0,1),c<0.∴a>b>c.故选:A.6.设等差数列{a n}的前n项和为S n,若a4+S5=2,S7=14,则公差d=()A.﹣4B.﹣2C.2D.4【分析】利用通项公式与求和公式即可得出.解:∵a4+S5=2,S7=14,∴a1+3d+5a1+10d=2,7a1+21d=14,联立解得d=2.故选:C.7.某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据丟失(如图),但甲得分的折线图完好,则下列结论正确的是()A.甲得分的极差是11B.乙得分的中位数是18.5C.甲运动员得分有一半在区间[20,30]上D.甲运动员得分的平均值比乙运动员得分的平均值高【分析】根据茎叶图,折线图整合数据,判断选项.解:甲的极差为28﹣9=19,A错,乙的中位数为,B错,由甲得分的折线图可知甲运动员得分有3次在区间[20,30],C错,故选:D.8.函数f(x)在定义域R内可导,若f(x)=f(x﹣2),且当x∈(﹣∞,1)时,(x﹣1)f'(x)<0,设a=f(0),b=f(),c=f(3),则()A.c<a<b B.c<b<a C.a<b<c D.b<c<a【分析】由已知判断函数的单调性,再由f(x)=f(x﹣2)求得函数周期,得f(3)=f(﹣1),然后利用函数的单调性比较a、b、c的大小.解:当x∈(﹣∞,1)时,(x﹣1)f'(x)<0,得当x<1时,f′(x)>0,f(x)在(﹣∞,1)上为增函数.又f(x)=f(x﹣2),∴f(x+2)=f(x),即f(x)是周期为2的周期函数,∴f(3)=f(﹣1),且﹣1<0<<1,因此有f(﹣1)<f(0)<f(),即有f(3)<f(0)<f(),得c<a<b.故选:A.9.某班组织文艺晚会,准备从A,B等8个节目中选出4个节目演出,要求:A,B两个节目至少有一个选中,且A,B同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的和数为()A.1860B.1320C.1140D.1020【分析】分两类:第一类,A,B只有一个选中,第二类:A,B同时选中,利用加法原理即可得出结论.解:分两类:第一类,A,B只有一个选中,则不同演出顺序有种;第二类:A,B同时选中,则不同演出顺序有种.共有:+=1140(种).故选:C.10.盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一个球,则此时取出黄色球的概率为()A.B.C.D.【分析】若取出的是红色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1==,若取出的是黄色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1==,由此能求出再从盒中取出一个球,则此时取出黄色球的概率.解:盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,若取出的是红色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1==,若取出的是黄色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1==,∴再从盒中取出一个球,则此时取出黄色球的概率为:P=P1+P2==.故选:A.11.已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,∠BAC=,则球O的体积为()A.B.C.D.【分析】由AB=1,AC=2,∠BAC=,可得BC的值,又可得三角形ABC为直角三角形,可得外接圆的半径为斜边的一半,再由SA⊥平面ABC,可得三棱锥的外接球的球心是过底面外接圆的圆心作垂直于底面的直线与中截面的交点,进而求出外接球的半径,再求出外接球的体积.解:因为AB=1,AC=2,∠BAC=,可得BC===,所以可得AC2=AB2+BC2,所以三角形ABC的外接圆的圆心为AC的最中点O',所以外接圆的半径r==1因为SA⊥平面ABC,所以三棱锥的外接球的球心是过底面外接圆的圆心作垂直于底面的直线与中截面的交点,设为O,设球的半径为R,则R===,所以外接球的体积为V==()3=π,故选:B.12.已知函数,在区间[0,π]上有且仅有2个零点,对于下列4个结论:①在区间(0,π)上存在x1,x2,满足f(x1)﹣f(x2)=2;②f(x)在区间(0,π)有且仅有1个最大值点;③f(x)在区间上单调递增;④ω的取值范围是.其中所有正确结论的编号是()A.①③B.①④C.②③D.①③④【分析】对于①,f(x1)﹣f(x2)=2,则为f(x)最大值1减最小值﹣1,需要找到在(0,π)上是否存在最大值1和最小值﹣1;对于②,ωx+=对应的x值有可能在[0,π]上;对于④,f(x)=在区间[0,π]上有且仅有2个根,得≤ωπ+<,求出ω的范围;对于③,由ω的范围,确定ωπ+的范围,进而确定f(x)的单调性.【解答】解析:∵x∈[0,π],∴ωx+∈[,ωπ+],令z=ωx+,则z∈[,ωπ+]由题意,sin z=在[,ωπ+]上只能有两解z=和z=,∴≤ωπ+<,(*)因为在z∈[,ωπ+]上必有sin﹣sin =2,故在(0,π)上存在x1,x2满足f(x1)﹣f(x2)=2;①成立;z=对应的x(显然在[0,π]上)一定是最大值点,因z=对应的x值有可能在[0,π]上,故②结论错误;解(*)得≤ω<,所以④成立;当x∈(0,)时,z∈[,+],由于≤ω<,故z∈[,+]⊆[,],此时y=sin z是增函数,从而f(x)在(0,)上单调递增.综上,①③④成立.故选:D.二、填空题(本大题共4个小题,每小题5分,共20分.)13.曲线y=xlnx在点(1,0)处的切线方程为x﹣y﹣1=0.【分析】求出原函数的导函数,得到函数在x=1时的导数值,即切线的斜率,然后由直线方程的点斜式得答案.解:由f(x)=xlnx,得,∴f′(1)=ln1+1=1,即曲线f(x)=xlnx在点(1,0)处的切线的斜率为1,则曲线f(x)=xlnx在点(1,0)处的切线方程为y﹣0=1×(x﹣1),整理得:x﹣y﹣1=0.故答案为:x﹣y﹣1=0.14.(2x﹣)6展开式中常数项为60(用数字作答).【分析】用二项展开式的通项公式得展开式的第r+1项,令x的指数为0得展开式的常数项.解:(2x﹣)6展开式的通项为=令得r=4故展开式中的常数项.故答案为6015.已知,为单位向量,,且<,>=,则<,>=.【分析】根据题意,由数量积公式求出•,进而求出||和•的值,又由cos<,>=求出cos<,>的值,结合向量夹角的范围分析可得答案.解:根据题意,,为单位向量,且<,>=,则•=1×1×cos=,又由=2﹣,则||2=42+2﹣4•=3,即||=,则•=•(2﹣)=22﹣•=,则cos<,>===,又由0≤<,>≤π,则<,>=;故答案为:.16.2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:Q (0,﹣3)是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.(1)若直线l与圆L、圆S均相切,则l截圆Q所得弦长为3;(2)若直线l截圆L、圆S、圆Q所得弦长均等于d,则d=.【分析】(1)设出共切线方程,利用圆心到直线的距离等于半径列出方程求解即可;(2)设出方程,分别表示出圆心到直线的距离d1=,d2=,d3=,结合弦长公式求得k,m即可解:(1)根据条件得到两圆的圆心坐标分别为(﹣4,0),(4,0),设公切线方程为y=kx+m(k≠0)且k存在,则,解得k=±,m=0,故公切线方程为y=±x,则Q到直线l的距离d=,故l截圆Q的弦长=2=3;(2)设方程为y=kx+m(k≠0)且k存在,则三个圆心到该直线的距离分别为:d1=,d2=,d3=,则d2=4(4﹣d12)=4(4﹣d22)=4(9﹣d32),即有()2=()2,①4﹣()2=9﹣()2,②解①得m=0,代入②得k2=,则d2=4(4﹣)=,即d=,故答案为:3;.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.在△ABC中,内角A、B、C的对边分别为a、b、c,且a cos B+b sin A=c.(1)求角A的大小;(2)若,△ABC的面积为,求b+c的值.【分析】(1)利用正弦定理和三角形内角和定理与三角恒等变换求得A的值;(2)由三角形面积公式和余弦定理,即可求得b+c的值.解:(1)△ABC中,a cos B+b sin A=c,由正弦定理得:sin A cos B+sin B sin A=sin C,又sin C=sin(A+B)=sin A cos B+cos A sin B,∴sin B sin A=cos A sin B,又sin B≠0,∴sin A=cos A,又A∈(0,π),∴tan A=1,A=;(2)由S△ABC=bc sin A=bc=,解得bc=2﹣;又a2=b2+c2﹣2bc cos A,∴2=b2+c2﹣bc=(b+c)2﹣(2+)bc,∴(b+c)2=2+(2+)bc=2+(2+)(2﹣)=4,∴b+c=2.18.设数列{a n}的前n项和为S n,已知S n=2a n﹣4,n∈N*.(Ⅰ)求通项公式a n;(Ⅱ)设b n=2log2a n﹣3,求数列{}的前n项和T n.【分析】(Ⅰ)利用递推关系式,转化求出数列是等比数列,然后求解通项公式a n;(Ⅱ)化简b n=2log2a n﹣3,然后利用裂项相消法转化求解数列{}的前n项和T n.解:(Ⅰ)S n=2a n﹣4,S n﹣1=2a n﹣1﹣4相减得:a n=2a n﹣2a n﹣1a n=2a n﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣,又a1=S1=2a1﹣4,∴a1=4∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣==﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣19.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,∠APD=90°,且AD=PB.(l)求证:平面PAD⊥平面ABCD;(2)若AD⊥PB,求二面角D﹣PB﹣C的余弦值.【分析】(1)取AD中点O,连结OP,OB,BD,推导出OB⊥AD,OP⊥OB,从而OB⊥平面PAD,由此能证明平面PAD⊥平面ABCD.(2)法1:推导出AD⊥平面POB.PO⊥AD.PO⊥OB,AD⊥OB,以O为坐标原点,分别以OA,OB,OP所在直线为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出二面角D﹣PB﹣C的余弦值.法2:推导出AD⊥平面POB.从而PO⊥AD,过点D作DH⊥PB,H为垂足,过点H 作HG∥BC,交PC于点G,连接DG,则∠DHG为二面角D﹣PB﹣C的平面角,由此能求出二面角D﹣PB﹣C的余弦值.【解答】证明:(1)取AD中点O,连结OP,OB,BD,因为底面ABCD为菱形,∠BAD=60°,所以AD=AB=BD.因为O为AD的中点,所以OB⊥AD.………………………………………(1分)在△APD中,∠APD=90°,O为AD的中点,所以.设AD=PB=2a,则,PO=OA=a,因为PO2+OB2=a2+3a2=4a2=PB2,所以OP⊥OB.………………………………………因为OP∩AD=O,OP⊂平面PAD,AD⊂平面PAD,所以OB⊥平面PAD.……………………………………………………………………………………因为OB⊂平面ABCD,所以平面PAD⊥平面ABCD.…………………………………………………………………………解:(2)解法1:因为AD⊥PB,AD⊥OB,OB∩PB=B,PB⊂平面POB,OB⊂平面POB,所以AD⊥平面POB.所以PO⊥AD.由(1)得PO⊥OB,AD⊥OB,所以OA,OB,OP所在的直线两两互相垂直.………………………以O为坐标原点,分别以OA,OB,OP所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系.……………………………………………………………设AD=2,则A(1,0,0),D(﹣1,0,0),B(0,,0),P(0,0,1),………………………………所以=(﹣1,0,﹣1),=(0,,﹣1),=(﹣2,0,0),………………………………设平面PBD的法向量为=(x,y,z),则,令y=1,得=(﹣).…………………………………………………………………………………设平面PBC的法向量为=(x,y,z),则,令y=1,则=(0,1,).……………………………………………………………………………………设二面角D﹣PB﹣C为θ,由于θ为锐角,所以cosθ=|cos<>|===,……………………………………………………………………………所以二面角D﹣PB﹣C的余弦值为.…………………………………………………………解法2:因为AD⊥PB,AD⊥OB,OB∩PB=B,PB⊂平面POB,OB⊂平面POB,所以AD⊥平面POB.所以PO⊥AD.………………………………………所以PO=a,PD=.过点D作DH⊥PB,H为垂足,过点H作HG∥BC,交PC于点G,连接DG,……因为AD⊥PB,BC∥AD,所以BC⊥PB,即HG⊥PB.所以∠DHG为二面角D﹣PB﹣C的平面角.………在等腰△BDP中,BD=BP=2a,PD=,根据等面积法可以求得DH=a.…………………………………………………………………进而可以求得PH=a,所以HG=,PG=.…………………………………………………………………………在△PDC中,PD=,DC=2a,PC=2a,所以cos∠DPC==.在△PDG中,PD=,PG=a,cos∠DPC=,所以DG2=PD2+PG2﹣2×PD×PG×cos∠DPG=a2,即DG=a.…………………………在△DHG中,DH=,HG=,DG=a,所以cos∠DHG==,………………………………………………………………所以二面角D﹣PB﹣C的余弦值为.…………………………………………………………20.高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150.其中a,b,c成等差数列且c=2a.物理成绩统计如表.(说明:数学满分150分,物理满分100分)分组[50,60)[60,70)[70,80)[80,90)[90,100]频数6920105(1)根据频率分布直方图,请估计数学成绩的平均分;(2)根据物理成绩统计表,请估计物理成绩的中位数;(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从此6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和期望值.【分析】(1)根据题意,列方程,即可求得a,b和c值,根据频率分布值直方图,即可求得平均值;(2)根据频率分布直方图即可求得中位数;(3)由题意,求得X的取值,分别求得其分布列,求得其数学期望.解:(1)由于a+b+2c=0.052,a+c=2b,c=2a,解得a=0.008,b=0.012,c=0.016,故数学成绩的平均分:=85×0.04+95×0.12+105×0.16+115×0.2+125×0.24+135×0.16+145×0.08=117.8,(2)由表知,物理成绩的中位数为7.(3)数学成绩为“优”的同学有4人,物理成绩为“优”有5人,因为至少有一个“优”的同学总数为6名同学,故两科均为“优”的人数为3人,故X的取值为0、1、2、3.,,,.X0123PE(X)=0×+1×+2×+3×=.21.已知椭圆E的一个顶点为A(0,1),焦点在x轴上,若椭圆的右焦点到直线x﹣y+2=0的距离是3.(Ⅰ)求椭圆E的方程;(Ⅱ)设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.【分析】(Ⅰ)根据点到直线的距离列式求得c,再求得a;(Ⅱ)根据弦长公式求得弦长后,换元成二次函数求最值.解:(Ⅰ)由题意:b=1,右焦点(c,0)(c>0)到直线x﹣y+2=0的距离为:d==3,∴c=,又∵a2﹣b2=c2,∴a=,又∵椭圆E的焦点在x轴上,∴椭圆E的方程为:+y2=1(Ⅱ)①当直线l的斜率不存在时,|AB|=2;②当直线l的斜率存在时,设l:y=kx+1,联立,得:(1+3k2)x2+6kx=0,∵x A=0,∴x B=﹣,∴|AB|=|x B﹣x A|=•,∴|AB|2=,设1+3k2=t≥1,则k2=记f(t)==4[﹣2()2++1],∴=,即t=4,k=±1时,|AB|=f(t)取得最大值>2,此时直线l:y=x+1或y =﹣x+1.22.已知函数f(x)=,(1)讨论函数f(x)的单调性;(2)证明:a=1时,f(x)+g(x)﹣(1+)lnx>e.【分析】(1)f(x)=+alnx,(x∈(0,+∞)).f′(x)=﹣+=.对a分类讨论即可得出函数点单调性.(2)a=1时,f(x)+g(x)﹣(1+)lnx>e.即:+﹣lnx﹣e>0⇔e x﹣ex+1>.x∈(0,+∞).令F(x)=e x﹣ex+1,G(x)=,分别研究其单调性即可得出.【解答】(1)解:f(x)=+alnx,(x∈(0,+∞)).f′(x)=﹣+=.a≤0时,f′(x)<0,函数f(x)在x∈(0,+∞)上单调递减.a>0时,f′(x)=.可得函数f(x)在(0,)上单调递减,在(,+∞)上单调递增.(2)证明:a=1时,f(x)+g(x)﹣(1+)lnx>e.即:+﹣lnx﹣e>0⇔e x﹣ex+1>.x∈(0,+∞).令F(x)=e x﹣ex+1,F′(x)=e x﹣e,x∈(0,1)时,F′(x)=e x﹣e,x∈(0,1)时,F′(x)<0,此时函数F(x)单调递减;x∈(1,+∞)时,F′(x)>0,此时函数F(x)单调递增.可得x=1时,函数F(x)取得极小值即最小值,F(1)=1.令G(x)=,G′(x)=,可得x=e时,函数G(x)取得最大值,G(e)=1.1与e不同时取得,因此F(x)>G(x),即e x﹣ex+1>.x∈(0,+∞).故原不等式成立.。
湖南省邵阳市新邵县2019-2020学年高二下学期期末考试数学试题

w5i~ " ^L[w5b;^LRPb~0v
#E
&F
+G
2H
%%I J6#&+ 0:|= K 0@LJ#A #&+LJ#5!L#&5%L#+5!L
&#+5
0
LR
K
0v
#L
%C
! 0
&M
(
! 0
+N" !
$;)*+ ( ,- ).('*)%&/*012%( 34567/' 8
+<9:;<
/=9=;<
4>9>;<
8?9?;<
@A@ABCDE 33( FGHIJ6KLMNOPQRSTU%VWXYZ6[\Z]
½ PQ O( IPQ C(
¾ ¿À
C(
e(
@(
W(
l«BC1( (E(W( (E(3( (E((3
+;%&'
2<&'%
=>STUVWXLYZ[ #\& ] ( ^_`5ab " ^_`Lcde#\& f^_`gh:;^
a5LN #\& iPa5PLjk0lbmnopqrLstoilbmn0u#v
#?%.!.
&@%%".
+A%0!.
2B%(C.
%.Dw5:xy\z{|qi0 ! ^}~ 0 ^~L[5b;^L ~
O?$PQ.n?$oqr\
&'()$!"#$% &'$()'$ *(% *(+)'$,-./&0123456&017
邵阳市新邵县2019-2020学年高二下学期期末化学试卷(含答案解析)
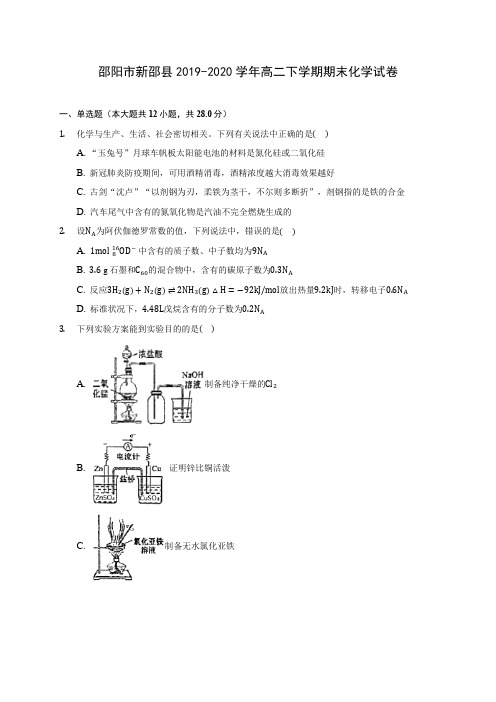
邵阳市新邵县2019-2020学年高二下学期期末化学试卷一、单选题(本大题共12小题,共28.0分)1.化学与生产、生活、社会密切相关。
下列有关说法中正确的是()A. “玉兔号”月球车帆板太阳能电池的材料是氮化硅或二氧化硅B. 新冠肺炎防疫期间,可用酒精消毒,酒精浓度越大消毒效果越好C. 古剑“沈卢”“以剂钢为刃,柔铁为茎干,不尔则多断折”,剂钢指的是铁的合金D. 汽车尾气中含有的氮氧化物是汽油不完全燃烧生成的2.设N A为阿伏伽德罗常数的值,下列说法中,错误的是()A. 1mol 816OD−中含有的质子数、中子数均为9N AB. 3.6 g石墨和C60的混合物中,含有的碳原子数为0.3N AC. 反应3H2(g)+N2(g)⇌2NH3(g)△H=−92kJ/mol放出热量9.2kJ时,转移电子0.6N AD. 标准状况下,4.48L戊烷含有的分子数为0.2N A3.下列实验方案能到实验目的的是()A. 制备纯净干燥的Cl2B. 证明锌比铜活泼C. 制备无水氯化亚铁D. 证明一水合氨是一元碱4.下列有关化学用语表示正确的是()①S2−的结构示意图:②MgCl2的电子式:③质量数为133、中子数为78的铯原子: 55133Cs④乙烯、乙酸结构简式依次为:CH2CH2、C2H4O2⑤用电子式表示HCl的形成过程A. ①③B. ③⑤C. ③④⑤D. ④⑤5.下列有机物的命名正确的是()A. 1,3,4−三甲苯B. 2−甲基−1,3−二丁稀C. 1,3−苯二酚D. 2−氯丙烷6.卤族元素及其化合物在生活中应用广泛.下列有关说法正确的是()A. 氟氯烃作制冷剂会加剧雾霾天气的形成B. 从海水中提取溴需经历氧化还原反应C. 加碘食盐中含有碘元素,能使淀粉溶液变蓝D. 工业上制漂白粉,所得的氯化物都具有漂白性7.25℃时,pH=2的HA和HB各1mL分别加水稀释,pH随溶液体积变化如图所示.下列叙述正确的是()A. K w的数值:a点大于c点B. 溶液中酸的总物质的量:a点大于b点C. HB的电离程度:b点大于c点D. 将a点与b点两溶液同时升高温度,则c(A−)减小c(B−)8.如图是三种有机物的结构简式下列说法正确的是()A. 三种有机物都能发生水解反应B. 三种有机物苯环上的氢原子若被氯原子取代,其一氯代物都只有2种C. 三种物质中,其中有两种互为同分异构体D. 三种物质在一定条件下,均可以被氧化反应9.下列有关实验的操作正确的是()实验操作A除去NaHCO3固体中混有的NH4Cl直接将固体加热B实验室收集Cu与稀硝酸反应成的NO向下排空气(CO2)法收集C检验乙酸具有酸性配制乙酸溶液,滴加NaHCO3溶液有气泡产生D比较碳、硫元素非金属性强弱测定同浓度Na2CO3和Na2SO4溶液的pHA. AB. BC. CD. D10.纳米ZnS具有独特的光电效应,在电学、磁学、光学等领域应用广泛。
2019-2020学年湖南省邵阳市新邵县高二下学期期末考试英语试题

湖南省邵阳市新邵县2019-2020学年高二下学期期末考试英语试题【参考『答案』】第一部分听力(30分,每小题1.5分)1~5 ACABB 6~10 AABCC 11~15 BCABC 16~20 ABCBC第二部分阅读( 共35分,21~30每小题2.5分; 31~35每小题2分)21~25 AAC DC 26~30 B DBAD 31~35 GABFD第三部分知识运用( 45分, 每小题1.5分)36~40 CDACB 41~45 ACDAB 46~50 ABDCD51~55 BADCB56. It 57. themselves 58. occurring 59. which 60. be bought61. disadvantages 62. to mention 63. busiest 64. dangerous 65. with/by*注意:大小写错误属于不正确形式,不给分。
第四部分写作(共两节,满分40)第一节应用文写作(15分)One possible version:Dear Leslie,I am very glad to receive your letter asking for a classical Chinese works to read.First of all, please allow me to show my earnest congratulations on you for having made such great progress on Chinese learning! As to the classical Chinese works you asked me for improvement, I strongly suggest you read The Journey to the West. Being one of the four greatest Chinese ancient novels, it has vivid plots and magic imaginations, which is certain to arouse your interest in reading. Furthermore, the book is comparatively simple in words but fairly rich in Chinese culture, which is not only helpful for you to read, but also beneficial for you to better understand Chinese culture.I bet you’ll make greater progress in Chinese after reading it!Yours Sincerely,Li Hua 第二节读后续写(25分)【参考范文1】Suddenly, Mary caught sight of a black box under the chair where Linda put her bag. She went over and then opened the box to find Linda’s tape was just inside. At that time, she was in adilemma. “This is my chance to defeat her.” But on a second thought, she changed her mind, “If I hide it, I will win the competition but I may lose something.” She placed it on the chair carefully, leaving a note saying “Take it easy, we are the best.” Soon, it’s her turn to come on the stage.Hearing her name called, Mary walked on the stage with her heart beating faster and faster. She kept reminding herself, “I have been practicing for so long, and I will certainly make it.” But the serious pain in her arm came again when she was performing the most difficult spin. She fell down on the stage. At that moment, Linda came back in low spirits. To her surprise and relief she saw the tape and Mary’s note. With Mary’s kindness and encouragement, Linda finished her performance calmly and skillfully. Finally, Mary lost the game but she believed she had won everything.【参考范文2】Suddenly, Mary caught sight of a black box under the chair where Linda put her bag. She bent over to pick it up. “Linda’s music tape!” She cried out in surprise. “It must have rolled out of her bag, while she got changed here.” At this moment, an idea flashed through her mind, which made her rooted to the spot. “Without her music tape, Linda will surely lose; without this real competitor, I will definitely win.” At the thought of this, Mary shivered slightly. She was in a dilemma, wondering what to do next. She hesitated for a second and then hurried out to give the music tape to Linda, who was extremely anxious in the corridor. Linda was so grateful to Mary, and finished her dancing successfully.Hearing her name called, Mary walked on the stage with her heart beating faster and faster. Nervous as she was, she stepped onto the stage with a big smile. She danced skillfully to the music and completed her most difficult spin smoothly. “Good,” she thought to herself, “my injured arm is awesome today.” As the music ended, thunderous applause filled the stadium. With the final marks announced, Mary knew she achieved her goal and tears began to well up in her eyes. (Possible ending 1) As she headed back to the dressing room, Linda came up to her cheerfully and held her hand tightly, “Congratulations! You’ve done an amazing performance! You win!” Mary smiled happily, “I win.” (Possible ending 2) As she headed back to the dressing room, she thought about the music tape. “No one will know how close I really came to losing.” Mary said softly to herself.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参考答案
一、选择题 1-12、DBCAC BDABC BA 二、填空题 13.01=--y x 14.60 15.6
π
16.(1)3 (2)512
三、解答题
17.解:(1)由已知及正弦定理得:sin cos sin sin sin A B B A C +=,
sin sin()sin cos cos sin C A B A B A B =+=+sin in cos sin Bs A A B ∴=,
sin 0sin cos B A A
≠∴=(0,)4
A A π
π∈∴=
………………5分
(2)
11
sin 2242
ABC
S
bc A bc bc ===∴=
又
22222cos 2()(2a b c bc A b c bc
=+-∴=+-+
所以,2
()4, 2.b c b c +=+=. ………………10分
18.解:(1)∵1124,24n n n n S a S a --=-=-
相减得:122n n n a a a -=- ∴12n n a a -=………………3分
1
2,n
n a a -= 又111124,4a S a a ==-∴= 11422n n n a -+∴=⨯=………………6分 (2)1
222log 32log 2321n n n b a n +=-=-=-………………8分
1111335
(21)(21)n T n n =
+++
⨯⨯-+1111
11
(1)2335
21(21)
n n =-+-+
+
--+ 11(1)2(21)21
n n n =
-=++………………12分 19.(1)证明:取AD 中点O ,连结OP ,OB ,BD ,
∵底面ABCD 为菱形,60BAD ∠=,
∴AD =AB BD =.又O 为AD 的中点,∴OB AD ⊥.………1分 在△APD 中,90APD ∠=, O 为AD 的中点,
∴1
2
PO AD AO ==.
设2AD PB a ==,则OB =
,PO OA a ==,
D C
B
A
P
O
∵22222234PO OB a a a PB +=+==,∴OP OB ⊥.………………2分 ∵OP
AD O =,OP ⊂平面PAD ,AD ⊂平面PAD ,∴OB ⊥平面PAD .……3分
又OB ⊂平面ABCD ,∴平面PAD ⊥平面ABCD .……………………4分 (2)解:∵AD PB ⊥,AD OB ⊥,OB
PB B =,
PB ⊂平面POB ,OB ⊂平面POB ,∴AD ⊥平面POB .
∴PO AD ⊥. 由(1)得PO OB ⊥,AD OB ⊥,
∴OA ,OB ,OP 所在的直线两两互相垂直.…………5分 以O 为坐标原点,分别以OA ,OB ,OP 所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系.……………6分 设
2
AD =,则
(1,0,0)A ,(1,0,0)D -
,()
B ,()0,0,1P ,………7分
∴
()1,0,1PD =--
,()
1PB =-,(2,0,0)BC AD ==-,…………………8分
设平面PBD 的法向量为()111,,x y z =n ,
则11110,
30,
PD x z PB y z ⎧•
=--=⎪⎨
•=-=⎪
⎩n n 令11y =
,
则1x =1z =∴(=n .……………9分
设平面PBC 的法向量为()222,,x y z =m ,则22220,
30,
BC x PB y z ⎧•=-=⎪⎨
•
=-=⎪⎩m m
令21y =,则20x =,2z =∴(=m .……………………………10分 设二面角D PB C
--为θ,由于
θ为锐角,∴cos cos ,θ=<>m n …………11分
7=
=. 所以二面角D PB C --的余弦值为
7
.……………12分 20.解:(1)根据频率分布直方图得(20.0240.0200.004)101a b c +++++⨯=,
z y
x
O P
A B
C
D
又2,2a c b c a +==,解得0.008a =,0.012b =,0.016c =, 故数学成绩的平均分
850.04950.121050.161150.21250.241350.161450.08117.8
x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=(分). …………4分
(2)总人数为50,由物理成绩统计表知,中位数在区间[70,80)内, 所以物理成绩的中位数约为75分.…………6分
(3)数学成绩为“优”的同学有4人,物理成绩为“优”的有5人,
因为至少有一科为“优”的同学共有6名,所以两科均为“优”的人数为3, 故X 的可能取值为0,1,2,3.
3336C 1(0)C 20P X ===, 12
33
3
6C C 9(1)C 20P X ===, 213336C C 9(2)C 20P X === 33
36C 1(3)C 20
P X ===
. 所以X 的分布列为
199130123
202020202EX =⨯
+⨯+⨯+⨯=. (12)
分
21.解:(1)由题意,1b =, …………1分 右焦点(,0)(0)
c c >到直线……2分 分
∵椭圆E 的焦点在x 轴上,所以椭圆E 的方程为………………4分 (2)当k 不存在时,||2AB = ………………5分
当k 存在时,设直线方程为1y kx =+,
得22(13)60k x kx ++=,6分
分
分 令213,(1,),t k t =+∈+∞则分 所以,
即21k =,得1k =±时…………10分 2||AB 的最大值为即||AB 的最大值为
分
直线l 的方程为11y x y x =+=-+或. ………………12分 22.解:(1) 函数)(x f 的定义域为),0(+∞ 2
2'
1
1)(x
ax x a x x f -=+-
= ………1分 当0≤a 时,0)('
<x f , ∴)(x f 在),0(+∞上单调递减; ………………2分
当0>a 时,由0)('
>x f 得a x 1>
,由0)('
<x f 得a
x 10<< ∴)(x f 在)1,0(a 上单调递减,在),1
(+∞a
单调递增 ………………4分
综上可知: 0≤a 时, )(x f 在),0(+∞上单调递减;
0>a 时, )(x f 在)1,0(a 上单调递减,在),1
(+∞a
单调递增 ………………5分
(2)因为0>x ,所以不等式等价于x
x e ex e x
ln 1>+- ………………6分
设1)(+-=ex e x h x
,e e x h x
-=)(/
,所以),1(+∞∈x 时, 0)(/
>x h ,)(x h 单调递增,
)1,0(∈x 时, 0)(/<x h ,)(x h 单调递减, ∴1)1()(min ==h x h ………………8分
设x x e x g ln )(=
,2
/
)ln 1()(x
x e x g -=,所以),0(e x ∈时, 0)(/>x g ,)(x g 单调递增, ),(+∞∈e x 时, 0)(/<x g ,)(x g 单调递减, ∴1)()(max ==e g x g ………………10分
虽然)(x h 的最小值等于)(x g 的最大值,但e ≠1,所以)(x h >)(x g , 即x
x
e ex e x
ln 1>+-,故原不等式成立 ………………12分。
