独立样本T检验操作
SPSS统计分析教程独立样本T检验doc

SPSS统计分析教程-独立样本T检验.docSPSS统计分析教程:独立样本T检验一、简介独立样本T检验(Independent Sample T-test)是统计分析中常见的一种方法,主要用于比较两组数据的均值是否存在显著差异。
这种检验的前提假设是,两组数据来自正态分布的独立样本。
独立样本T检验在SPSS中的实现相对简单,下面将详细介绍其操作步骤和解读结果。
二、数据准备在进行独立样本T检验之前,需要准备好数据。
数据通常存储在Excel或SPSS数据文件中。
为了方便起见,我们将使用SPSS数据文件进行说明。
三、操作步骤1.打开SPSS软件,点击“分析”(Analyze)菜单,然后选择“比较均值”(Compare Means)中的“独立样本T检验”(Independent Sample T-test)。
2.在弹出的对话框中,将左侧的“组别”(Grouped By)字段设置为一组变量,如“性别”(Gender),将右侧的“组1”(Group 1)和“组2”(Group 2)字段设置为另一组变量,如“年龄”(Age)。
3.点击“确定”(OK)按钮开始进行独立样本T检验。
四、结果解读1.假设检验(Hypothesis Test):在结果中,可以看到假设检验的结果。
如果p值小于显著性水平(通常为0.05),则拒绝原假设(即两组数据的均值无显著差异),认为两组数据的均值存在显著差异。
反之,如果p值大于显著性水平,则接受原假设,认为两组数据的均值无显著差异。
2.均值(Mean):在结果中,可以看到每组数据的均值。
如果两组数据的均值存在显著差异,则可以通过均值的大小来判断哪组数据更好或更优。
3.标准差(Standard Deviation):在结果中,还可以看到每组数据的标准差。
标准差反映了数据分布的离散程度,标准差越大,说明数据分布越不集中。
4.t统计量(t-statistic):t统计量是用来衡量两组数据之间差异大小的一个指标。
独立样本T检验课件

独立性
两个样本之间相互独立,没有关联性 ,即一个样本的数据不会对另一个样 本的数据产生影响。
目的与意义
比较两组数据的均值差异
通过独立样本t检验,可以比较两组数据的均值是否存在显 著差异,从而判断不同组别之间的差异是否具有统计学上 的意义。
探索潜在的分组因素
在研究过程中,有时需要探索不同分组之间的差异,独立 样本t检验可以帮助我们确定这些差异是否具有统计学上的 显著性。
假设检验
独立样本t检验是一种假设检验方法,通过设定原假设和备 择假设,进行统计推断,以决定是否拒绝原假设或接受备 择假设。
02
独立样本t检验的步骤
数据准备
确定样本来源
明确实验或调查的样本来 源,确保数据具有代表性 。
数据收集
按照研究目的和范围收集 数据,确保数据准确性和 完整性。
数据筛选与整理
对数据进行筛选,排除异 常值和缺失值,并进行数 据整理,使其满足分析要 求。
样本量的大小对独立样本t检验的结果具有重要影响。较小的样本量可能会导致 结果的不稳定和不可靠,而较大的样本量则可以提供更准确和可靠的结果。
确定合适的样本量
在进行分析之前,需要根据研究目的、研究设计和数据情况,确定合适的样本量 。如果样本量不足,可能需要重新收集数据或采用其他统计方法。
05
独立样本t检验的案例分析
数据正态性检验
正态分布检验
使用统计量或图形方法检验数据 是否符合正态分布,如直方图、 P-P图、Q-Q图等。
异常值处理
若数据不符合正态分布,需对异 常值进行处理,如用中位数或平 均数进行替代。
方差齐性检验
方差齐性检验方法
选择适当的方差齐性检验方法,如 Bartlett检验或Levene检验。
独立样本t检验原理

独立样本t检验原理
独立样本t检验是用于比较两个独立样本平均值差异是否显著
的统计方法。
根据中心极限定理,当样本容量大于30时,样
本平均值的抽样分布近似为正态分布。
独立样本t检验的原理
是基于此,计算两个样本平均值的差别和标准误差,进而得到
t值,并与t分布的临界值比较,判断两个样本平均值是否有
显著差异。
具体步骤如下:
1. 提出假设:设两个样本均值分别为μ1和μ2,零假设为H0:μ1=μ2,备择假设为Ha:μ1≠μ2。
2. 计算样本平均值差异:分别计算两个样本的平均值和标准差,计算两个样本平均值的差异。
3. 计算标准误差:通过两个样本的方差和样本大小计算标准误差。
4. 计算t值:用两个样本平均值的差异除以标准误差,得到t 值。
5. 比较t值:根据自由度和显著性水平查表得到t分布的临界值,将计算出的t值与临界值进行比较,如果t值小于临界值,则不能拒绝零假设,否则拒绝零假设,接受备择假设,认为两个样本的平均值存在显著差异。
两独立样本T检验---SPSS操作详解

两独立样本T检验-SPSS操作详解
为了解某一新药降血压的效果,将28名高血压患者随机分为实验组和对照组,实验组采用新药,对照组采用常规药,测得治疗前后的血压变化,问新药是否优于常规药?
1 打开SPSS软件,定义变量。
变量1设置:name-group , decimals-0 , label-分组, value-(1=新药,2=常规药) 变量2设置:name-value , decimals-0 , label-血压下降值
2 输入数据---血压差=用药前血压-用药后血压
3 单击菜单栏analyze/compare means/independent-samples t test
4 将血压下降值调入test variables下矩形框
5 将分组(group)调入grouping variable 下矩形框
6单击define groups…定义分组group1为1 定义group2为2 单击continue
7 options选项默认
8 bootstrap选项默认
9 单击OK 输出结果
10 结果界面
11 结果解释
表1表示两独立样本t检验基本统计量-group statistics
表2表示两独立样本t检验结果,方差方程的levene检验(Levene’s Test for Equality of Variances 方差齐性检验)F=3.115,P=0.93,认为两样本来自的总体方差齐。
T检验中t=3.18,P=0.005。
按α=0.05水准拒绝H0
,差异有统计学意义。
可认为新药组的降压效果优于常规药。
2017/06/06于深圳
随时交流:ammomeng@。
异质性检验操作方法

异质性检验操作方法异质性检验是一种用于比较两个或多个样本之间是否存在显著差异的统计方法。
常用于科学研究和数据分析中,以确定研究对象之间是否存在统计学意义上的差异。
异质性检验有多种方法,包括t检验、方差分析、卡方检验等。
以下将详细介绍一些常用的异质性检验方法的操作方法。
1. t检验:t检验是一种用于比较两个样本均值是否存在显著差异的统计方法。
它分为独立样本t检验和配对样本t检验两种形式。
(1)独立样本t检验:操作步骤如下:a. 确定研究的零假设和备择假设,即两个样本的均值是否相等。
b. 收集两个样本的数据,并计算样本均值和标准差。
c. 利用t分布表或统计软件计算得到t值。
d. 根据研究的显著水平(通常为0.05),确定临界值。
e. 比较计算得到的t值和临界值,判断两个样本的均值是否有显著差异。
(2)配对样本t检验:操作步骤如下:a. 确定研究的零假设和备择假设,即配对样本的均值是否相等。
b. 收集配对样本的数据,并计算差值。
c. 计算差值的平均值和标准差,并得到t值。
d. 根据研究的显著水平(通常为0.05),确定临界值。
e. 比较计算得到的t值和临界值,判断配对样本的均值是否有显著差异。
2. 方差分析:方差分析用于比较三个或更多个样本均值是否存在显著差异,适用于有一个自变量和一个因变量的情况。
操作步骤如下:a. 确定研究的零假设和备择假设,即各样本均值是否相等。
b. 收集各组样本的数据,并计算各组样本的均值和方差。
c. 计算组间变异和组内变异的比值(F值)。
d. 根据研究的显著水平(通常为0.05),确定临界值。
e. 比较计算得到的F值和临界值,判断各组样本的均值是否有显著差异。
3. 卡方检验:卡方检验用于比较两个或多个分类变量之间是否存在显著关联或差异。
操作步骤如下:a. 确定研究的零假设和备择假设,即各组之间是否独立。
b. 收集各组的实际统计数据,并计算预期频数。
c. 计算卡方值。
d. 根据研究的显著水平(通常为0.05),确定临界值。
T检验单样本与独立样本

T检验单样本与独立样本T检验是一种常用的统计方法,用于比较两组数据之间的差异是否显著。
在实际应用中,T检验可以分为单样本T检验和独立样本T检验两种情况。
本文将分别介绍单样本T检验和独立样本T检验的原理、应用场景以及计算方法。
## 单样本T检验单样本T检验用于检验一个样本的均值是否与已知的总体均值存在显著差异。
在进行单样本T检验时,需要满足以下假设:- 零假设(H0):样本均值与总体均值无显著差异。
- 备择假设(H1):样本均值与总体均值存在显著差异。
进行单样本T检验的步骤如下:1. 提出假设:设定零假设和备择假设。
2. 收集数据:获取样本数据。
3. 计算T值:根据样本数据计算T值。
4. 确定显著性水平:设定显著性水平(通常为0.05)。
5. 判断结果:比较计算得到的T值与临界T值,判断是否拒绝零假设。
## 独立样本T检验独立样本T检验用于比较两组独立样本的均值是否存在显著差异。
在进行独立样本T检验时,同样需要满足零假设和备择假设。
独立样本T检验的步骤如下:1. 提出假设:设定零假设和备择假设。
2. 收集数据:获取两组独立样本数据。
3. 计算T值:根据两组样本数据计算T值。
4. 确定显著性水平:设定显著性水平(通常为0.05)。
5. 判断结果:比较计算得到的T值与临界T值,判断是否拒绝零假设。
在实际应用中,单样本T检验常用于分析一个样本的均值是否与总体均值存在显著差异,例如某一产品的平均质量是否符合标准要求;而独立样本T检验常用于比较两组独立样本的均值,例如男性和女性在某项指标上的平均差异是否显著。
总之,T检验是一种重要的统计方法,可以帮助研究者判断样本数据之间的差异是否具有统计学意义。
通过合理应用T检验,可以更准确地进行数据分析和决策制定。
希望本文对T检验的单样本和独立样本应用有所帮助。
如何使用SPSS进行独立样本T检验
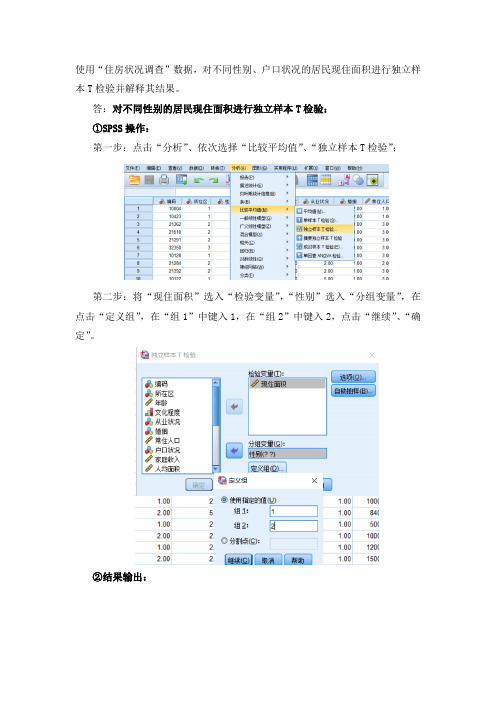
使用“住房状况调查”数据,对不同性别、户口状况的居民现住面积进行独立样本T检验并解释其结果。
答:对不同性别的居民现住面积进行独立样本T检验:①SPSS操作:第一步:点击“分析”、依次选择“比较平均值”、“独立样本T检验”;第二步:将“现住面积”选入“检验变量”,“性别”选入“分组变量”,在点击“定义组”,在“组1”中键入1,在“组2”中键入2,点击“继续”、“确定”。
②结果输出:③结果解读:先用F检验对不同性别的居民现住面积的方差是否向相等加以验证,然后利用t检验对不同性别的居民现住面积的均值是否存在差异进行检验。
从独立样本检验输出图中可以看到:F统计量为1.598,p值为0.206,在显著性水平0.05下,p值大于0.05,不拒绝原假设,即认为不同性别的居民现住面积的方差相等,没有差别。
由于不同性别的居民现住面积的方差没有差别,t检验将看假定等方差一栏。
t统计量为2.982,p值为0.003,在显著性水平0.05下,p值小于0.05,拒绝原假设,即认为不同性别的居民现住面积的均值有显著性差异。
对不同户口状况的居民现住面积进行独立样本T检验:④SPSS操作:第一步:点击“分析”、依次选择“比较平均值”、“独立样本T检验”;第二步:将“现住面积”选入“检验变量”,“户口状况”选入“分组变量”,在点击“定义组”,在“组1”中键入1,在“组2”中键入2,点击“继续”、“确定”。
⑤结果输出:⑥结果解读:先用F检验对不同户口状况的居民现住面积的方差是否向相等加以验证,然后利用t检验对不同户口状况的居民现住面积的均值是否存在差异进行检验。
从独立样本检验输出图中可以看到:F统计量为5.966,p值为0.015,在显著性水平0.05下,p值小于0.05,拒绝原假设,即认为不同户口状况的居民现住面积的方差存在显著差异。
由于不同户口状况的居民现住面积的方差存在显著差异,t检验将看不假定等方差一栏。
t统计量为3.314,p值为0.001,在显著性水平0.05下,p值小于0.05,拒绝原假设,即认为不同户口状况的居民现住面积的均值有显著性差异。
spss独立样本t检验

spss中有关独立样本T检验的详细介绍包含操作过程和结果分析分析>比较平均值3.独立样本T检验独立样本T检验类似于单样本T检验,不过独立样本T检验的内容比单样本T检验要复杂的多,特别是对其结果的分析,而独立样本T检验被使用的情况也比单样本T检验更广泛(因此也可以看到网络上关于独立样本T检验的文章远比关于单样本T检验的文章多)对比:二者都是将数据的平均值进行比较,不同之处在于单样本T检验是将一个样本与某一特定值进行对比,而独立样本T检验是对多个样本之间的平均值进行对比。
独立样本是指进行对比的多个样本之间是相互独立、互不干扰的,通过独立样本T检验我们可以判断多个样本之间的平均值是否可以认为是相等的。
没有什么比举个例子更容易理解独立样本T检验的用途了:假如我们有两个样本,分别是来自农村和城市两个不同地方的人们的身高数据,我们的目的是探讨农村和城市的差异会不会给当地的人们带来身高上的影。
这时我们算出城市的人群的平均身高为168.38cm,而农村的人们的平均身高为164.58cm,二者差了3.8cm,那我们是否就可以认为这3.8cm就可以很好的说明农村和城市的人们身高有差异呢?那如果是差了3cm呢?如果是差了1cm呢?这种时候就不可以单靠感觉来评判了,而是应该使用独立样本T检验来帮助我们判断得出结论检验变量——需要进行平均值比较的数据分组变量——用于区分不同样本的变量选项——选择置信区间百分比以及缺失值的处理方法对于分组变量我们操作时需要注意一下,在我们选入了分组变量后,我们必须要对其进行定义组操作,因为SPSS无法自行判断如何通过分组变量对数据进行分组点击定义组我们有两种分类的方法,分别是使用指定的值与分割点,指定值就是将所有分类变量等于该输入的数值的样本划分为一组,分割点就是以该输入的数值为分割点划分出大于和小于该值的两组进行比较,这些都是很简单的,不多废话了~~接下来就是重头戏了——对结果的分析简洁解释:得到结果后,首先将独立样本检验表格中莱文方差等同性检验的显著性数值与0.05进行比较大于0.05,两组假定等方差,看第一行数据的显著性(双尾)数值,如果大于0.05,两组差异不显著;如果小于0.05,两组差异显著;小于0.05,两组不假定等方差,看第二行数据的显著性(双尾)数值,如果大于0.05,两组差异不显著;如果小于0.05,两组差异显著。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.把各维度前后测均分选入成对变量
看sig的数值,小于0.000即差异显著
序号(Ordinal)变量:通常也称为有序分类变量,表示变量的值是离散的,相对有限个数的,但值之 间是有顺序关系的,如教育水平取值有:1 — 8 年,2 — 10 年,3 — 15 年,这些值之间存在顺序大 小关系。“序号”一般是用来定义等级差别的,例如对某个餐厅满意度,就可以用序号来表示,1、2和 3分别代表满意,一般和不满意。
5.输入已经打好分的数据
信效度
1.两个人同时进行打分
2.分别计算出两个人各维度的均分
3.分析—度量—可靠性分析
4.结果
实验组和控制组幼儿美术核心素养前测各维度差异比较
1.计算各维度平均分
2.分析—比较均值—独立样本T检验
3.将3个维度选入检验变量,将“班级”选入到“分组变量”中;同时点击 “定义组”按钮,在“使用指定值”下“组1”文本框中填入“1”,“组 2”文本框中填入“2”(因为我们的数据中“1”代表实验组,“2”代表 对照组)
“均值”和“标准差”在论文中的表示方法是“M±SD”(均数 加减标准差)
划线部分大于0.05,那么T、P值取第一行数值,即T=-0.85,P=0.40, P大于0.05,说明图像识读维度上,实验组和控制组没有显著差异。 如对样本T检验
实验组前后测对比:1.输入前测和后测分数,算出前后测均分
建模
1.编辑变量视图:用于管理变量的属性,包括变量名称,类型,标签,缺失 值,度量标准等属性。
2.在标签一栏填上对应的问卷题目
3.编辑值标签,在“值”一栏输入数值,在“标签 ”一栏输入问卷评分原则
4.度量标准
度量(Scale)变量:通常也称为连续变量,表示变量的值通常是连续的,无界限的,如员工收入,企 业销售额等。“度量”则表示可以不仅可以进行排序而且还能对结果进行加减的一种属性,例如“职工 收入”,“体重”等等。
名义(Nominal)变量:通常也称为无序分类变量,表示变量的值是离散的,相对有限个数的,通常变 量值的个数不超过 10 个,但值之间没有顺序关系的,如性别。“名义”一般是用来代表某物的一个属 性,没有任何比较排序的意义,只是说这个物有这个属性而已,例如人有男女之分,还有你说的“工号” 也只代表工人的一个属性而已。
