分振幅干涉—等厚干涉
光的干涉分振幅薄膜干涉等倾干涉

2
a1:4%×100=4 a2:100×96%×4%×96%=3.74 a3:100×96%×4%×4%×4% ×96% =5.9×10-3<<4
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
由于反射而引入的附加光程差2存在与否,可根据以下 条件判断 。 在不超过临界角的条件下,无论入射角的大小如 何,光在第一表面上反射和第二表面上反射并射出时: 若在薄膜上、下两个表面的两反射的物理性质不同,则两反 射相干光a1,a2(或b1,b2),或两透射光c1,c2(或d1,d2)之间将 有/2的附加光程差. 例如:如图
面甲等。为了增强反射能量,常在玻璃表面上镀一层高反射率
的透明薄膜,利用薄膜上、下表面的反射光的光程差满足干涉 相长条件,从而使反射光增强,这种薄膜叫增反膜。
在一光学元件的玻璃(折射率 n3 1.5 )表面上 镀一层厚度为e、折射率为 n2 1.38 的氟化镁薄膜, 为了使入射白光中对人眼最敏感的黄绿光 ( 5500 A) 反射最小,试求薄膜的厚度.
1
M1
2
i1
L 3
P
可见:波长一定、倾角i 相同的 入射光线,对应于同一级干涉 条纹—等倾条纹 .
n1
n2
A i 2
i2
i1
D C
d
M2
n1
B
4
E 5
光学
1.6 分振幅薄膜干涉(一)——等倾干涉
2d n
明纹条件:
2 2
n sin i1 ( ) 2
分振幅干涉

k R
20 R
由此得平凸透镜的曲率半径
R
r2 k 20
rk2
20
(14.96 / 2)2 (11.75 / 2)2 20 589.3106
mm
1.818m
1.4 增透膜
• 光在空气中垂直射到玻璃表面时,反射光能约占入射光能 的 5%,反射损失并不大。
• 但在各种光学仪器中为了矫正像差或其他原因,常常要用 多个透镜。例如,照相机的物镜有的用 6 个透镜,变焦距 物镜有十几个透镜,潜水艇用的潜望镜中约有 20 个透镜。
•
sin
2nl
700 109 2 1.4 0.25102
1.0 104
rad
等厚干涉在光学测量中有很多应用。如测量微小角度、细小 的直径、微小的长度,以及检查光学元件表面的不平度,都 可以利用光的等厚干涉。
1.3 牛顿环
• 把一个曲率半径R很大的平凸透镜A放在一块平面玻璃板B 上,其间有一厚度逐渐变化的劈尖形空气薄层。
端互相叠合,另一端夹一细金 属丝或薄金属片,形成的空气 薄膜称为空气劈尖。
1.2 劈尖的等厚干涉
• 考虑到空气的折射率 n<n1,在下边的玻璃片的上表面反
射时有半波损失,而在上边的玻璃片的下表面反射光没有
半波损失,则劈尖上下表面反射的两束光的光程差应为
劈尖反射光干涉极大(明纹)的条件为
2ne k, k 1, 2,3,
• 暗条纹对应
2e n2 n12 sin2 i k
2e
n2
n12
sin2
i
2k
1
2
• 由于直接透射的光比经过两次或更多次反射后透射出的光 强大得多,所以透射光的干涉条纹不如反射光条纹清晰。
第一章光的干涉5
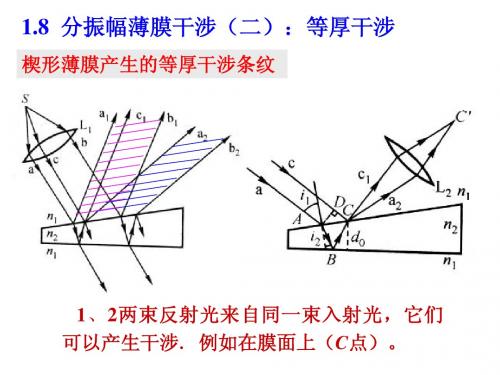
o·
光程差:
R d
2d
2
平凸透镜 平晶 暗环
r
r 2 R 2 ( R d )2 2 R d
r d 2R
2 ( 2 j 1)
2
(1)
暗环: 2d
2
,(j
1, = 0,2 …)(2)
(1)、(2)第j个暗环半径: rj
jR
j
∴
rj
1973年,国际计量局米定义咨询委员会推荐用氦氖 激光器的可见光632.8nm作为长度基准。
(632991399 0.0025) 10 m .
12
夏尔.法布里Charles Fabry (1867-1945) 阿尔弗雷德.珀罗 Alfred Perot (1863-1925)
1897年发明 法布里—珀罗空腔谐振器
迈克耳孙在工作
美籍德国人 因创造精密光学 仪器,用以进行 光谱学和度量学 的研究,并精确 测出光速,获 1907年诺贝尔 )观察迈克耳逊干 涉仪的等倾圆条纹,开始时视场中共看到10 个亮环,中心为亮斑,然后移动干涉仪一臂 的平面镜,先后看到共有10个亮环缩进中央, 而视场中除中心为亮斑外,还剩下5个亮环。 试求: 1. 平面镜移动的距离; 2. 开始时中心亮斑的干涉级次; 3. 移动平面镜后最外一个亮环的干涉级次。
d
k 1
k2
1 855 nm
2 412 .5nm
n3 1.5
k 3
3 275 nm
可见光波长范围 400~700nm
波长412.5nm的可见光有增反。
1.8 迈克耳孙干涉仪
仪器结构与光路:
分光板
物理光学主要公式

双光束干涉 1,201,21,21,201,2121221010212cos(-);()2cos cos --;E E t k r t I I I I I k r k r t ωϕωθϕϕϕϕωωωω=⋅+=++=⋅⋅++∆∆=-语言极大值:02;2(1cos );cos 1M m I I ϕπθϕ==+= 极小值:0(21);2(1cos );cos 1m m I I ϕπθϕ=+=-=- 条纹衬比度:()()01M m M m V I I I I V -+≤≤稳定干涉:①频率相同△w =0;②振动方向相同cos θ=1; ③相位差恒定;④光强尽量接近I 1≈I 2;(一)杨氏干涉——分波面法;22()R r k y d D R ϕπλπλ∆=∆+∆=∆=∆⋅≈⋅+∆干涉特点①属于非定域干涉;②光束受到限制强度小,难以应用; ③白光干涉除m=0级条纹仍为白色外其余呈现彩色条纹。
极值条件2;(21);(12)m y m D dm y m D d ϕπλϕπλ==⋅=+=+⋅2;()(21);[(12)]m y m R D dm y m R D dϕπλϕπλ==-∆⋅=+=+-∆⋅具体分析双缝上下平移或覆盖玻片的情况;图样发生平移。
条纹间距:y D d ελ=∆=⋅(二)等倾干涉——分振幅法2122cos (2);)nh I I I k θλ∆=+=++∆亮条纹位置:m λ∆=;暗条纹位置:(12)m λ∆=+ 条纹特点①亮环对透镜中心的张角就是入射角,愈靠近中心,光程差愈大,干涉级数愈高;反之远离中心干涉级数愈小; ②平板越厚边缘条纹越密集;④平板反射率较小时,应用反射光干涉条纹,衬比度大; ⑤平板反射率较大时,应用透射光条纹。
中心点干涉级0001212;22nhnh m m m λλελ∆=+==+=+ 中心向外数第N 个亮环的干涉级次为[m 1-(N-1)]。
条纹半径和条纹间距2111tan N N N N N N N N Nr e r f e r r θθθ+≈=∆→→=→=-思路:(三)等厚干涉——分振幅法22cos (2)nh θλ∆=+从一个条纹过渡到另一个条纹,光程差改变λ,平板的厚度均改变λ/2n ;入(折)射角θ视为常数。
1-8 双光束分振幅薄膜干涉(二)等厚干涉 _投影稿
加热时,待测 材料膨胀,上表 面上升,条纹有 什么变化?
待测材料膨胀后,空气膜变薄,条纹向远离劈棱 的方向移动。 每移动一个条纹,空气膜厚度变化为:h=/2 移过m条,则说明膨胀: h=m(/2)
next next
2
13
14
白光入射薄膜时,条纹如何分布? 白光照射下的肥皂膜
例:检查光学平面的平整度 标准平面 空气 待测平面
next
3、光程差
/ 2 2hn 2 cos i 2 0 0
3
二、劈尖干涉 劈尖:上下表面都是平面的透明体,两表面之间有 一个很小的夹角。 1. 条纹形状
4
上、下表面夹角很小时,在局部可近似认为是平行膜:
0和i2固定,只与h 有关, 同一级条纹出现 在薄膜厚度相同处,故称 等厚条纹。 条纹的特点由薄膜厚h度变化的规律决定。
n2 2n2
21
22
r1 : r2 : r3 : ...... 1 : 2 : 3 : ...... 无额位光程差时, r1 : r2 : r3 : ...... 1 : 3 : 5 : ...... 有额位光程差时,
条纹内疏外密,级次内低外高 透镜上移时: 条纹收缩,中心条纹被吞没。 透镜下移时: 条纹扩展,中心有条纹冒出。 球面半径变化时,条纹如何变化?
25
两个力在竖直方向平衡: d·Fn·cos= g·dm 水平方向满足:d·Fn·sin=2r·dm tan = 2r/g
tan dy dr
26
水旋转时表面为旋转对称曲面,取过水面最低点的 竖直线为y轴,原点o在水盘底面。 取水表面上某一点P处质量为dm的水元。
y
1 2 2 r C 表示水膜的厚度 2 g
3.2薄膜干涉一等厚条纹(修正版)解析

氟化镁: n1.38
4)增反膜
n1 nn2
L 2 n h 0/2 0, h
0 4n
I A 1 2 A 2 2 2 A 1 A 2 c o s 2 ( A 1 A 2 ) 2
多层介质高反射膜的光强反射率
可达99%以上
例 为了增加透射率,求氟化镁膜的最
级次,不影响条纹的形状、间 隔和反衬度。
3)正入射时,等厚条纹的形状
垂直入射时,cosi1 L (P )2 n h 0/2
可知,干涉条纹与薄膜的等厚度线重合, 干涉条纹的形状就是薄膜等厚线的形状, 所以成为等厚条纹。
4)等厚条纹的特点
(1)条纹定位于薄膜的表面附近
(2)薄膜厚度不均匀,条纹与等厚线重合
B
n2
2 n h s in 2i/c o si
( A B P ) 2 ( A B ) 2 n h / c o s i L (P ) 2 n h c o si
2)讨论 (1)这是一个近似公式
(2)干涉区域位于薄膜表面附近
(3)满足n1 nn2或 n1 nn2时 有半波损 L (P ) 2 n h c o s i0 /2 (4)有无半波损只影响条纹的绝对
2
rk R (k0,1 ,2, )
(1)从反射光中观测,中心点是暗点还 是亮点?从透射光中观测,中心点是暗点还 是亮点?
(2)属于等厚干涉,条纹间距不等,为 什么?
(3)将牛顿环置于 n1的液体中,条 纹如何变?
(4)应用例子:可以用来测量光波波长, 用于检测透镜质量,曲率半径等.
工件 标准件
测量透镜的曲率半径
半球形水膜
正在破裂的半球形水膜
双层肥皂水膜
11-3分振幅干涉--等厚干涉

§11-2 分振幅干涉 —— 薄膜干涉一、等厚干涉平行光不是垂直入射 结论:光程差不但与膜厚度 有关,还与入射角有关。
平行光垂直入射 结论:光程差与膜厚有关反射光1 单色平行光 反射光2λan1 n2n3θA e单色平行光反射光1 反射光2 aλn1 n2n3θAe1计算1光与2光的光程差:单色平行光反射光1 反射光2 a关键----考虑是否有半波损失 讨论:(1)λn1 > n2 > n3 δ = 2n2 e (2) n1 < n2 < n3 δ = 2n2 e (3) n1 > n2 , n2 < n3 λ δ = 2n2 e + 2 (4) n1 < n2 , n2 > n3n1 n2n3θAe注意:涉及反射 时务必注意是否 存在半波损失!δ = 2n2 e +λ22当薄膜很薄且折射率均匀时,光程差仅与膜厚有关。
因此,膜上厚度相同的各点反射的每一对相干光有 相同的光程差,因此这些点对应同一级条纹,光强 相等。
从垂直于膜面的方向观察,且视场角范围很 小时,薄膜上的干涉条纹与膜表面的等厚线形状相 同,故这种干涉条纹称为等厚干涉条纹,这类干涉 称为等厚干涉。
等厚干涉典型实验:劈尖和牛顿环3二、劈尖空气劈尖分析劈尖的等厚条纹特点 ——光程差是出发点δ = 2ne或δ = 2 ne +λ2厚度相同的点构成同一级条纹1、条纹位置λ ⎧ kλ ⎪ δ = 2ne + = ⎨ λ (2k + 1) 2 ⎪ 2 ⎩ ⎧ kλ ⎪ λ 或 δ = 2ne = ⎨ (2k +1) ⎪ 2 ⎩( k = 1, 2 ,3 , L ) ( k = 0 ,1, 2 , L ) ( k = 0 ,1, 2 , L ) ( k = 0 ,1, 2 , L )θ明纹 暗纹 明纹 暗纹42、相邻明(暗)条纹对应的膜厚差Δe = ek+1 −ek =λ2 nλ2nθλ2n即明(暗)条纹的级次每增加一级,对应的膜厚就增加3、相邻明(暗)条纹间距Δe Δe λ Δl = ≈ = sinθ θ 2nθ若劈尖角固定,则条纹间距固定. 劈尖干涉条纹是等间距的分布.ΔlθΔeek lek+1n劈尖角越小,条纹间距越大,条纹越疏;反之,条纹越密.54、条纹特点对于劈尖角固定的劈尖而言,劈尖干涉条纹是一系列平行 于棱边的明暗相间的等间距的直条纹.5、应用(1)测量微小长度和微小角度λ标 准 块 规 待 测 块 规平晶Δh(2)测量长度的微小变化等厚条纹 平晶(3)检测平面质量待测工件6例1 在半导体元件生产中,为测定硅(Si)表面氧化硅(SiO )薄膜的2厚度,可将该膜一端用化学方法腐蚀成劈尖状。
等厚干涉原理

等厚干涉原理
干涉原理是光学中的一个基本原理,描述了当两束光波相遇时,它们的干涉现象。
在干涉实验中,我们通常会使用一对光栅或两个狭缝来产生干涉效应。
干涉现象的产生源于光波的波动性质。
等厚干涉是其中一种干涉现象,它指的是当两个处于同一平面上的玻璃或空气薄膜之间被光所填充时,光在两个界面之间的反射和折射所引起的干涉现象。
等厚干涉主要是由于光在介质中传播速度不同而引起的。
当入射光波垂直于两个界面时,会发生垂直入射等厚干涉。
在这种情况下,入射光波在第一个界面上发生反射,并在第二个界面上发生折射,然后再次反射回来。
这两束光波具有不同的光程差,这会导致干涉现象的出现。
干涉现象的强度取决于光的波长、介质的折射率以及两个界面的厚度差。
根据等厚条件,当两个界面之间的厚度差等于光的波长的整数倍时,我们就会观察到明纹或暗纹。
等厚干涉广泛应用于光学领域,例如在干涉测量中,我们可以利用等厚干涉现象来测量薄膜的厚度或者根据干涉纹的形态来判断介质的性质。
此外,等厚干涉还可以用于图像处理和光学元件的设计等方面。
总之,等厚干涉原理是一种重要的光学现象,通过研究光的波
动性质,我们可以深入理解光的行为,并将其应用于实际生活和科学研究中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.4分振幅干涉 12.5迈克尔孙干涉仪
大连理工大学余虹
1
二,等厚干涉
1.劈尖薄膜的等厚干涉(4=0 4=叫洪 __ R卜"*:
11噸
2如/”一诚(k = 1,2,3,:)明 ° Al
[砍 (& = 0,1,2,…)暗
第■暗纹中心对应膜厚响第&级 相邻条[厚度差峭 纹
牛 顿 环
级次--内低外高;
=R2—2R2古" 2Rh
间距——内疏外密
大连理工大学余虹
5
(5)牛顿环在光学冷加工中的应用
加压环外扩——
加压环内缩——
要打磨中央部分
要打磨边缘部分
大连理工大学余虹
6
中心l间距一
sin 0 2nOຫໍສະໝຸດ 大连理工大学余虹2
2.等厚干涉的应用
(1)增透膜与增反膜 玻璃(赤3=1.5)镀MgF? ("2=1.38),放在空气中,白 光垂直 射到膜的表面,欲使反射光中X=550nm的成分相 消,求: 膜的最小悍度。..“ 一“
. “1、"2 、“3
=1
~h n7 = 1.38
w3 = 1.5
思考• 〃2> 〃3
到什么结果?
• 2hn =(2k + Vi— 相消
• • “""2 、谷" > 旦丿 2 M H/H
2 心=>
会得 反射光相消=増透 效果取好
大连理工大学余虹
3
(2)测长度微小变化 玻璃板向上平移
千涉条纹移动\温度升高
(3)检查光学平面的缺陷
相邻两条纹中聞=&
心对应高度差 2
根,咼度变化
2
材料膨胀系数〃= AH
平面上有凹坑,条纹偏向空气 膜变薄方向;平面上有凸起, 条纹偏向空气膜曾后厚方向。
大连理工大学余虹
4
(4)测凸透镜的曲率半径
k人 明环中心 2 (2A + 1)?暗环中心
中心接触点血=0 ; & =。 暗环 r半径
第k级暗环对应
L膜厚
R2=(R-hk)2 + r^ 衍
