类比探究(习题及答案)
九年级思维拓展:类比探究(一)(讲义及答案)

九年级思维拓展:类比探究(一)【知识点睛】➢引言:类比:就是由两个对象的某些相同或相似的性质,推断它们在其他性质上也有可能相同或相似的一种推理形式.探究:是指学生在学习情境中通过观察、阅读,发现问题,搜集数据,形成解释,获得答案并进行交流、检验、探究性学习.学习过程的本质 类比与探究.处处皆类比!!!➢综合几何题中的类比探究问题:1.解题策略:①类比——类比字母、辅助线、思路②不变特征——相同或相似的性质(可类比的关键)③应用——类比思路、应用结论④作图——关注待确定点的特征及轨迹,尝试分析转化2.类比探究常见结构:①旋转结构:找“等线段共端点”,借助全等整合条件②直角结构:斜直角放正,找全等或相似③平行结构:作平行,造相似,转比例(A型、X型)④中点结构:构造全等或中位线,转移、整合条件【精讲精练】1.如图,在Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形的对角线交于点O,连接OC,已知AC=5,OC=62,则另一直角边BC的长为________.第1题图第2题图2.如图,在Rt△ABC中,∠ACB=90°,以斜边AB为边向外作等腰直角三角形ABO,∠AOB=90°,连接OC,已知AC=5,OC=2BC的长为________.3.如图,抛物线272 2y x x 与直线122y x交于C,D两点.点P是y轴右侧抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.若存在点P,使∠PCF=45°,则点P的坐标为________________.4.(1)阅读理解:如图1,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.AB,AD,DC之间的等量关系为_____________;(2)问题探究:如图2,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论;(3)问题解决:如图3,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB,DF,CF之间的等量关系,并证明你的结论.CDBA Oyx PC FDBEA Oyx5. 【问题背景】如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,BE ,点P 为DC 的中点.(1)【观察猜想】观察图1,猜想线段AP 与BE 的数量关系是________,位置关系是_________.(2)【拓展探究】把△ADE 绕点A 逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立,请证明;否则写出新的结论并说明理由. (3)【问题解决】把△ADE 绕点A 在平面内自由旋转,若DE =4,BC =8,请直接写出线段AP 长的取值范围.图1EDC BA PPABCDE图26. 如图,在Rt △ABC 中,∠ACB =90°,BC mAC n,CD ⊥AB 于点D ,点E 是直线AC 上一动点,连接DE ,过点D 作FD ⊥ED ,交直线BC 于点F .(1)探究发现:如图1,若m =n ,点E 在线段AC 上,则DE DF__________.(2)数学思考:①如图2,若点E 在线段AC 上,则DEDF_______(用含m ,n 的代数式表示);②当点E 在直线AC 上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明.(3)拓展应用:若ACBC=DF=CE 的长.图1F E DCBA图2BCF E AD图3DAEFC B备用图DCBA7. 在△ABC 中,已知D 是BC 边的中点,G 是△ABC 的重心,过点G 的直线分别交AB ,AC 于点E ,F .(1)如图1,当EF ∥BC 时,求证:1=+AFCFAE BE . (2)如图2,当EF 和BC 不平行,且点E ,F 分别在线段AB ,AC 上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由. (3)如图3,当点E 在AB 的延长线上或点F 在AC 的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.图1G F E D CBA 图2ABCD E FG 图3GFED CBA8.(1)问题发现如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.填空:①∠AFB的度数是________;②线段AD,BE之间的数量关系为__________.(2)类比探究如图2,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F.请判断∠AFB的度数及线段AD,BE之间的数量关系,并说明理由.(3)解决问题如图3,在平面直角坐标系中,点A坐标为(4,0),点B为y轴上任意一点,连接AB,将BA绕点B逆时针旋转90°至BC,连接OC,请直接写出OC的最小值.FEDCBA图2FED CBA图3图1【参考答案】1. 72. 73. ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛1813,62327,21或4. (1)AD =AB +DC (2)AB =AF +CF(3)DF CF AB +=235. (1)BE =2AP ;BE ⊥AP(2)成立(3)232≤≤AP 6. (1)1(2)①mn;②成立 (3)52552或=CE 7. (1)证明略(2)成立 (3)不成立,理由:当点E 在AB 的延长线上时,1>AFCF;点F 在AC 的延长线上时,1>AE BE 8. (1)60°;AD =BE(2)45°;AD =BE (3)22。
02类比、拓展探究题(解析版)

类比、拓展探究题类比、拓展探究题是近两年中考热门考题,题型的模式基本分为三步:初步尝试、类比发现、深入探究,考查的知识点有:三角形旋转、平行四边形性质、相似、全等、矩形折叠、勾股定理等.此类问题解答往往是层层深入,从特殊到一般,然后是拓展运用.在解题时需要牢牢把握特殊情况、特殊位置下的结论,然后探寻一般情况下是否也成立,最后是类比应用.类比模仿是解决此类问题的重要手段.例1数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD (∠BAD =120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD 所在平面内旋转,且60°角的顶点始终与点C 重合,较短的直角边和斜边所在的两直线分别交线段AB ,AD 于点E ,F (不包括线段的端点).(1)初步尝试如图①,若AD =AB ,求证:①△BCE ≌△ACF ,②AE +AF =AC ; (2)类比发现如图②,若AD =2AB ,过点C 作CH ⊥AD 于点H ,求证:AE =2FH ; (3)深入探究如图③,若AD =3AB ,探究得AE +3AFAC的值为常数t ,则t =________.例题分层分析(1)①先证明△ABC ,△ACD 都是________三角形,再证明∠BCE =________,即可解决问题. ②根据①的结论得到________,由此可证明.(2)设DH =x ,由题意,可得CD =________,CH =________(用含x 的代数式表示),由△ACE ∽△HCF ,得AE FH =AC CH,由此即可证明.(3)如图③,过点C 作CN ⊥AD 于N ,CM ⊥BA ,交BA 的延长线于点M ,CM 与AD 交于点H .先证明△CFN ∽△CEM ,得CN CM =FN EM ,由AB ·CM =AD ·CN ,AD =3AB ,推出CM =3CN ,所以CN CM =FN EM =13,设CN =a ,FN=b ,则CM =3a ,EM =3b ,想办法求出AC ,AE +3AF 即可解决问题.对应练习:我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.(1)概念理解请你根据上述定义举一个等邻角四边形的例子; (2)问题探究如图①,在等邻角四边形ABCD 中,∠DAB =∠ABC ,AD ,BC 的中垂线恰好交于AB 边上一点P ,连结AC ,BD ,试探究AC 与BD 的数量关系,并说明理由;(3)应用拓展如图②,在Rt △ABC 与Rt △ABD 中,∠C =∠D =90°,BC =BD =3,AB =5,将Rt △ABD 绕着点A 顺时针旋转角α(0°<∠α<∠BAC )得到Rt △AB ′D ′(如图③),当凸四边形AD ′BC 为等邻角四边形时,求出它的面积.解题方法点析(1)矩形或正方形邻角相等,满足“等邻角四边形”的条件;(2)连结PD,PC,根据PE,PF分别为AD,BC的垂直平分线,可得到PA=________,PB=________,∠DAP=________=∠ABC=________,从而可得∠APC=∠DPB,利用SAS可证得△APC≌△DPB,即可得到AC=BD.(3)分两种情况考虑:(i)当∠AD′B=∠D′BC时,延长AD′,CB交于点E,由S四边形ACBD′=S△ACE-S△BED′,求出四边形ACBD′的面积;(ii)当∠D′BC=∠ACB=90°时,过点D′作D′E⊥AC于点E,由S四边形ACBD′=S△AED′+S矩形ECBD′,求出四边形ACBD′的面积即可.课后练习:1.【操作发现】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连结BB′;(2)在(1)所画图形中,∠AB′B=________.【问题解决】如图,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.小明同学通过观察、分析、思考,对上述问题形成了如下想法:想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连结PP′,寻找PA,PB,PC三条线段之间的数量关系;想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连结PP′,寻找PA,PB,PC三条线段之间的数量关系.……请参考小明同学的想法,完成该问题的解答过程.(―种方法即可)【灵活运用】如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).2.问题呈现:如图①,点E,F,G,H分别在矩形ABCD的边AB,BC,CD,DA上,AE=DG.求证:2S四边形EFGH=S矩形ABCD.(S表示面积)实验探究:某数学实验小组发现:若图①中AH≠BF,点G在CD上移动时,上述结论会发生变化.分别过点E,G 作BC边的平行线,再分别过点F,H作AB边的平行线,四条平行线分别相交于点A1,B1,C1,D1,得到矩形A1B1C1D1.如图②,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+S矩形A1B1C1D1.如图③,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与S矩形A1B1C1D1之间的数量关系,并说明理由.迁移应用:请直接应用“实验探究”中发现的结论解答下列问题.(1)如图,点E,F,G,H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH =11,HF=29,求EG的长.(2)如图,在矩形ABCD中,AB=3,AD=5,点E,H分别在边AB,AD上,BE=1,DH=2,点F,G分别是边BC,CD上的动点,且FG=10,连结EF,HG,请直接写出四边形EFGH面积的最大值.3.【探索发现】如图①是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE,EF剪下时,所得的矩形的面积最大.随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为________.【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P,N分别在边AB,AC上,顶点Q,M在边BC上,则矩形PQMN面积的最大值为________.(用含a,h的代数式表示) 【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.【实际应用】如图,现有一块四边形的木板余料ABCD,经测量AB=50 cm,BC=108 cm,CD=60 cm,且tan B=tan C=43,木匠徐师傅从这块余料中裁出了顶点M,N在边BC上且面积最大的矩形PQMN,求该矩形的面积.答案与解析【例1】【解答】解:(1)AE+AF=AC;理由如下:∵四边形ABCD是平行四边形,∠BAD=120°,∴∠D=∠B=60°,∵四边形ABCD是菱形,∴AD=AB,∴△ABC,△ACD都是等边三角形,∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,∵∠ECF=60°,∴∠BCE+∠ACE=∠ACF+∠ACE=60°,∴∠BCE=∠ACF,在△BCE和△ACF中,,∴△BCE≌△ACF(ASA).∴BE=AF,∴AE+AF=AE+BE=AB=AC;故答案为:AE+AF=AC;(2)设DH=x,由由题意,CD=2x,CH=,∴AD=2AB=4x,∴AH=AD﹣DH=3x,∵CH⊥AD,∴AC==,∴AC2+CD2=AD2,∴∠ACD=90°,∴∠BAC=∠ACD=90°,∴∠CAD=30°,∴∠ACH=60°,∵∠ECF=60°,∴∠HCF=∠ACE,∴△ACE∽△HCF,∴,(3),理由如下:如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.∵∠ECF+∠EAF=180°,∴∠AEC+∠AFC=180°,∵∠AFC+∠CFN=180°,∴∠CFN=∠AEC,∵∠M=∠CNF=90°,∴△CFN∽△CEM,∴,∵AB•CM=AD•CN,AD=4AB,∴CM=4CN,∴,设CN=a,FN=b,则CM=4a,EM=4b,∵∠MAH=60°,∠M=90°,∴∠AHM=∠CHN=30°,∴HC=2a,HM=2a,HN=a,∴AM=,AH=,∴AC==,AE+4AF=(EM﹣AM)+4(AH+HN﹣FN)=EM﹣AM+4AH+4HN﹣4FN=4AH+4HN﹣AM=,∴.∴t=,故答案为:.【对应练习】【解答】解:(1)矩形或正方形;(2)AC=BD,理由为:连接PD,PC,如图1所示:∵PE是AD的垂直平分线,PF是BC的垂直平分线,∴P A=PD,PC=PB,∴∠P AD=∠PDA,∠PBC=∠PCB,∴∠DPB=2∠P AD,∠APC=2∠PBC,即∠P AD=∠PBC,∴∠APC=∠DPB,∴△APC≌△DPB(SAS),∴AC=BD;(3)分两种情况考虑:(i)当∠AD′B=∠D′BC时,延长AD′,CB交于点E,如图3(i)所示,∴∠ED′B=∠EBD′,∴EB=ED′,设EB=ED′=x,由勾股定理得:42+(3+x)2=(4+x)2,解得:x=4.5,过点D′作D′F⊥CE于F,∴D′F∥AC,∴△ED′F∽△EAC,∴=,即=,解得:D′F=,∴S△ACE=AC×EC=×4×(3+4.5)=15;S△BED′=BE×D′F=×4.5×=,则S四边形ACBD′=S△ACE﹣S△BED′=15﹣=10;(ii)当∠D′BC=∠ACB=90°时,过点D′作D′E⊥AC于点E,如图3(ii)所示,∴四边形ECBD′是矩形,∴ED′=BC=3,在Rt△AED′中,根据勾股定理得:AE==,∴S△AED′=AE×ED′=××3=,S矩形ECBD′=CE×CB=(4﹣)×3=12﹣3,则S四边形ACBD′=S△AED′+S矩形ECBD′=+12﹣3=12﹣.【课后练习】1.【解答】解:【操作发现】(1)如图所示,△AB′C′即为所求;(2)连接BB′,将△ABC绕点A按顺时针方向旋转90°,∴AB=AB′,∠B′AB=90°,∴∠AB′B=45°,故答案为:45°;【问题解决】如图②,∵将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,∴△APP′是等边三角形,∠AP′C=∠APB=360°﹣90°﹣120°=150°,∴PP′=AP,∠AP′P=∠APP′=60°,∴∠PP′C=90°,∠P′PC=30°,∴PP′=PC,即AP=PC,∵∠APC=90°,∴AP2+PC2=AC2,即(PC)2+PC2=72,∴PC=2,∴AP=,∴S△APC=AP•PC=7;【灵活运用】如图③中,∵AE⊥BC,BE=EC,∴AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,∵∠BAD=∠CAG,∴∠BAC=∠DAG,∵AB=AC,AD=AG,∴∠ABC=∠ACB=∠ADG=∠AGD,∴△ABC∽△ADG,∵AD=kAB,∴DG=kBC=4k,∵∠BAE+∠ABC=90°,∠BAE=∠ADC,∴∠ADG+∠ADC=90°,∴∠GDC=90°,∴CG==.∴BD=CG=.2.【解答】问题呈现:证明:如图1中,∵四边形ABCD是矩形,∴AB∥CD,∠A=90°,∵AE=DG,∴四边形AEGD是矩形,∴S△HGE=S矩形AEGD,同理S△EGF=S矩形BEGC,∴S四边形EFGH=S△HGE+S△EFG=S矩形ABCD.实验探究:结论:2S 四边形EFGH=S矩形ABCD﹣.理由:∵=,=,=,=,∴S 四边形EFGH=+++﹣,∴2S 四边形EFGH=2+2+2+2﹣2,∴2S 四边形EFGH=S矩形ABCD﹣.迁移应用:解:(1)如图4中,∵2S四边形EFGH=S矩形ABCD﹣.∴=25﹣2×11=3=A1B1•A1D1,∵正方形的面积为25,∴边长为5,∵A1D12=HF2﹣52=29﹣25=4,∴A1D1=2,A1B1=,∴EG2=A1B12+52=,∴EG=.(2)∵2S 四边形EFGH=S矩形ABCD+.∴四边形A1B1C1D1面积最大时,四边形EFGH的面积最大.①如图5﹣1中,当G与C重合时,四边形A1B1C1D1面积最大时,四边形EFGH的面积最大.此时矩形A1B1C1D1面积=1•(﹣2)=,∴2S 四边形EFGH=S矩形ABCD+=15+(﹣2)=13+,∴S四边形EFGH=②如图5﹣2中,当G与D重合时,四边形A1B1C1D1面积最大时,四边形EFGH的面积最大.此时矩形A1B1C1D1面积=2•1=2,∴2S 四边形EFGH=S矩形ABCD+=15+2=17,∴S四边形EFGH=8.5∵8.5>,∴四边形EFGH的面积最大值8.5.3.【解答】解:【探索发现】设EF=x,ED=y,∵EF、ED为△ABC中位线,∴ED∥AB,EF∥BC,EF=BC,ED=AB,∴AB=2ED=2y,BC=2EF=2x,又∠B=90°,∴四边形FEDB是矩形,则===,故答案为:;【拓展应用】设PN=b,∵PN∥BC,∴△APN∽△ABC,∴,∵BC=a,BC边上的高AD=h,∴,PQ=,∴S=b•PQ==﹣+bh,∴S的最大值为:=;则矩形PQMN面积的最大值为;故答案为:;【灵活应用】如图1,延长BA、DE交于点F,延长BC、ED交于点G,延长AE、CD交于点H,取BF中点I,FG 的中点K,由题意知四边形ABCH是矩形,∵AB=32,BC=40,AE=20,CD=16,∴EH=20、DH=16,∴AE=EH、CD=DH,在△AEF和△HED中,∵,∴△AEF≌△HED(ASA),∴AF=DH=16,同理△CDG≌△HDE,∴CG=HE=20,∴BI==24,∵BI=24<32,∴中位线IK的两端点在线段AB和DE上,过点K作KL⊥BC于点L,由【探索发现】知矩形的最大面积为×BG•BF=×(40+20)×(32+16)=720,答:该矩形的面积为720;【实际应用】如图2,延长BA、CD交于点E,过点E作EH⊥BC于点H,∵tan B=,设EH=4x,BH=3x,∵tan C=2=,∴CH=2x,∵BC=BH+CH=105=3x+2x,x=21,∴BH=63,CH=42,EH=84,由勾股定理得:BE===105,CE===42,∵AB=60,∴AE=45,∴BE的中点Q在线段AB上,∵CD=70,∴CE的中点P在线段CD上,∴中位线PQ的两端点在线段AB、CD上,由【拓展应用】知,矩形PQMN的最大面积为BC•EH==2205cm2,答:该矩形的面积为2205cm2.。
类比探究问题(习题及答案)

类比探究问题(习题)>例题示范例1:如图1,在正方形ABCD中,E, F分别是BC, CD上的点, 且ZE4F=45。
,则有结论EF=BE+DF成立.(1)如图2,在四边形ABCD中,AB=AD. ZB=ZD=90。
, E, F分别是BC, CD上的点,且ZEAF是ZB4D的一半,那么结论EF二BE+DF 是否仍然成立?若成立,请证明;若不成立,请说明理山.⑵ 如图3,若恪(1)中的条件改为:在四边形ABCD 4^,AB=AD.ZB+上ADC=180。
,延长SC到点E,延长CD到点F,使得ZEAF 仍然是ZBAD的一半,则结论EF二BE+DF是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.图1D图2F思路分析:1.题目中有旋转结构,可以类比.题U结论思路:如图1,延长CB到G,使BG二DF,根据已知条件容易证明^ ABG幻△ADF,由此可以推出ZBAG=ZD4F, AG=AF.而Z EAF』ABAD.2 所以得到ZDAF+ZBAE二ZEAF,进一步得到ZEAF二上EAG, 所以故EF=EG=BE+BG=BE+DF ・2.类比上面思路,解决笫一问•如图2,延长CB到G,使BG=DF, 根据已知条件容易证明^ABG^^ADF.山此可以推出ZBAG=ZD4F, AG=AF.而Z EAF=_ ZBAD,2 所以得到ZDAF+ZBAE二ZEAF,进一步得到ZEAF二上EAG, 所以△故EF=EG=BE+BG=BE+DF ・3.照搬思路解决第二问•结论EF=BE+DF不成立,应为EF=BE-DF.如图3,在BC上截取BG=DF, 山于ZB+ZAQC=180。
,Z/1DF+Z/IDC=18O^ 可以得到ZB=ZADF,所以△ABG幻△ADF,山此可以推出ZBAG=ZD4F, AG=AF.而Z EAF』ZBAD.2 所以得到ZEAF=ZEAG,所以△AEF竺△AEG,A)90。
△ADF空△ABG (SAS)I AAEF^AAEG (SAS)I故EF=EG=BE-BG=BE-DF ・D>巩固练习1.如图1,在正方形ABCD和正方形CGEF (CG>BC)中,点C, G在同一直线上,M是AE的中点.(1)探究线段MD, MF的位置关系及数量关系,并证明.(2)若将图1中的正方形CGEF绕点C顺时针旋转,使D, C, G三点在同一直线上,如图2,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.(3)若将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边在同一直线上,如图3,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.图2E2.在△ABC中,已知BC >AC.动点D绕△ABC'的顶点A逆时针旋转,丄LAD=BC,连接CD. E, F分别为AB, CD的中点,直线EF与直线AD眈分别交于点M, N.如图1,当点D旋转到BQ 的延长线上时,点N恰好与点Fifi合,取AC的中点H,连接HE, HF.根据三角形中位线定理和平行线的性质,可得结论ZAMF二ZBNE (无需证明).(1)当点D旋转到图2中的位置时,ZAMFLj ZBNE有何数量关系?请写出猜想,并给出证明.(2)当点Q旋转到图3中的位置时,ZAMF与ZBNE有何数量关系?请直接写出结论.3.已知AABC,以△ABC的边4C为直角边向外作等腰直角三角形ABE和等腰直角三角形ACD AB=AE. AC=AD. ZBAE= ZCAD=90\ M 是BC中点,连接AM, DE.(1)如图1,在△ABC中,当ZB4C二90。
四边形之类比探究(一)(习题及答案)

四边形之类比探究(一)(习题)例题示范例1:已知等腰三角形ABC 中,∠ACB =90°,点E 在AC 的延长线上,且∠DEC =45°,M ,N 分别是DE ,AE 的中点,连接MN ,交直线BE 于点F .当点D 在CB 的延长线上时,如图1所示,易证MF +FN =1BE .2(1)如图2,当点D 在CB 边上时,上述结论是否成立?若成立,请给出证明;若不成立,请写出你的猜想,并说明理由.(2)当点D 在BC 的延长线上时,如图3所示,请直接写出线段MF ,FN ,BE 之间的数量关系(不需要证明).1【思路分析】1.里面有多个中点,考虑中位线,先证明易证的思路.连接AD ,由中位线定理可知MN =1AD ,2由题意可证△ACD ≌△BCE ,得到AD =BE ,即MN =1BE ,2所以MF +FN =1BE .22.照搬易证的思路解决第一问.连接AD ,由中位线定理可知MN =1AD ,2由题意可证△ACD ≌△BCE ,得到AD =BE ,即MN =1BE ,2所以NF -MF =1BE .23.照搬易证的思路解决第二问.连接AD ,由中位线定理可知MN =1AD ,2由题意可证△ACD ≌△BCE ,得到AD =BE ,即MN =1BE ,2所以MF -NF =1BE .2【过程书写】证明:(1)不成立,理由如下:连接AD ,在△AED 中,M 是DE 的中点,N 是AE 的中点,∴MN 是中位线∴MN =1AD2在等腰三角形ABC 中,∠ACB =90°∴AC =CB ,∵∠ACB =90°,∠DEC =45°∴CD =CE∴△ACD ≌△BCE (SAS )∴AD =BE∴MN=1BE 2∴FN-MF=1BE 2(2)MF-FN=1BE 2巩固练习1.已知△ABC是等边三角形,D是直线BC上一动点(不与点B,C重合),以AD为边作菱形ADEF(A,D,E,F按逆时针排列),使∠DAF=60°,连接CF.(1)如图1,当点D在BC边上时,求证:①BD=CF;②AC=CD+CF.(2)如图2,当点D在BC的延长线上时,其他条件不变,结论AC=CD+CF是否仍成立?若成立,请证明;若不成立,请写出AC,CD,CF之间的数量关系,并说明理由.(3)如图3,当点D在CB的延长线上时,其他条件不变,探究AC,CD,CF之间的数量关系.图1图2图32.如图1,C是线段BG上一点,分别以BC,CG为边,向外作正方形BCDA和正方形CGEF,使点D落在线段CF上,M是AE的中点,连接DM,FM.(1)求证:DM=FM,DM⊥FM.(2)如图2,将正方形CGEF绕点C顺时针旋转45°,其他条件不变,探究线段DM,FM之间的关系,并加以证明.(3)如图3,将正方形CGEF绕点C旋转任意角度,其他条件不变,探究线段DM,FM之间的关系,并加以证明.图1图2图33.(1)如图1,△ABC和△BDE都是等腰直角三角形,AB⊥AC,BD⊥DE,点D在AB边上.取CE的中点F,连接AF,DF,猜想AF,DF之间的数量关系和位置关系,并加以证明.(2)将△BDE旋转至如图2所示的位置,使点E在AB的延长线上,点D在CB的延长线上,其他条件不变,判断(1)中AF,DF之间的数量关系和位置关系是否发生变化,并加以证明.图1图2【参考答案】巩固练习1.(1)证明略.提示:证明△ABD≌△ACF,得到BD=CF,进而得到AC=CD+CF.(2)AC=CF-CD,理由略.(3)AC=CD-CF.2.(1)证明略.提示:延长DM,交EF于点H.证明△ADM≌△EHM(ASA),得到AD=EH,DM=HM,进而得到△DFH是等腰直角三角形,所以DM=FM,DM⊥FM.(2)DM=FM,DM⊥FM,证明略.提示:延长DM,交CE于点H,连接DF,HF.证明△ADM≌△EHM(ASA),得到AD=EH,DM=HM,再证明△CDF≌△EHF(SAS),得到DF=HF,∠CFD=∠EFH,进而得到△DFH是等腰直角三角形,则可得证.(3)DM=FM,DM⊥FM,证明略.提示:过点E作EH∥AD,交DM的延长线于点H,连接DF,HF.3.(1)AF=DF,AF⊥DF,证明略.提示:延长DF,交AC于点H.证明△DEF≌△HCF,得到DE=HC,DF=HF,进而得到△ADH是等腰直角三角形,所以AF=DF,AF⊥DF.(2)(1)中AF,DF之间的数量关系和位置关系不发生变化,证明略.提示:过点C作CH∥DE,交DF的延长线于点H,连接AD,AH.。
类比常见常识单选题100道及答案解析

类比常见常识单选题100道及答案解析1. 鸟:羽毛相当于人:()A. 衣服B. 皮肤C. 头发D. 骨骼答案:A解析:鸟的羽毛起到保护和装饰的作用,人的衣服也起到保护和装饰的作用。
2. 蜡烛:照明相当于汽车:()A. 运输B. 装饰C. 比赛D. 展览答案:A解析:蜡烛的主要功能是照明,汽车的主要功能是运输。
3. 蜜蜂:蜂巢相当于蜘蛛:()A. 蛛网B. 洞穴C. 树枝D. 草丛答案:A解析:蜜蜂居住在蜂巢里,蜘蛛织蛛网并居住在上面。
4. 电脑:键盘相当于手机:()A. 屏幕B. 电池C. 外壳D. 摄像头答案:A解析:键盘是电脑的输入设备,屏幕是手机的重要组成部分用于显示。
5. 森林:树木相当于海洋:()A. 船只B. 鲸鱼C. 波浪D. 水滴答案:B解析:树木是森林的主要组成部分,鲸鱼是海洋中的主要生物之一。
6. 书包:书本相当于冰箱:()A. 蔬菜B. 水果C. 饮料D. 食物答案:D解析:书本可以装在书包里,食物可以放在冰箱里。
7. 月亮:地球相当于卫星:()A. 行星B. 恒星C. 彗星D. 流星答案:A解析:月亮是地球的卫星,卫星围绕行星运转。
8. 医生:手术刀相当于厨师:()A. 锅铲B. 菜刀C. 勺子D. 盘子答案:A解析:医生做手术常用手术刀,厨师烹饪常用锅铲。
9. 水稻:农田相当于绵羊:()A. 草原B. 猪圈C. 鸡舍D. 鱼塘答案:A解析:水稻通常种植在农田里,绵羊主要生活在草原上。
10. 作家:作品相当于画家:()A. 画笔B. 画布C. 画作D. 颜料答案:C解析:作家创作作品,画家创作画作。
11. 麦克风:唱歌相当于相机:()A. 拍照B. 录像C. 展览D. 收藏答案:A解析:麦克风用于唱歌,相机用于拍照。
12. 飞机:天空相当于轮船:()A. 陆地B. 港口C. 海洋D. 江河答案:C解析:飞机在天空中飞行,轮船在海洋中航行。
13. 图书馆:书籍相当于超市:()A. 顾客B. 商品C. 收银员D. 货架答案:B解析:图书馆存放书籍,超市陈列商品。
七年级下册数学中考数学类比探究实战演练(含答案)

中考数学类比探究实战演练1.(本小题4分)如图1,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,连接EF并延长,与BA,CD的延长线分别交于点M,N,则∠BME=∠CNE(不必证明).(1)如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交CD,AB于点M,N,判断△OMN的形状,并说明理由.(2)如图3,在△ABC中,,点D在AC边上,且AB=CD.E,F分别是BC,AD的中点,连接EF并延长,与BA的延长线交于点G,连接DG,若∠EFC=60°,判断△AGD形状,并说明理由.(1)中△OMN的形状为( )∙ B.等边三角形∙ C.等腰直角三角形∙ D.含30°角的直角三角形知识点:中考数学几何中的类比探究解题思路见第2题中解析2.(本小题6分)(上接第1题)(2)中△AGD的形状为( )∙ A.等腰三角形∙ B.等边三角形∙ D.含30°角的直角三角形知识点:中考数学几何中的类比探究解题思路3.(本小题7分)小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:(1)问题情境:如图1,四边形ABCD中,AD∥BC,E为CD边的中点,连接AE 并延长,交BC的延长线于点F,求证:(S表示面积).(2)问题迁移:如图2,在已知锐角∠AOB内有一个定点P,过点P任意作一条直线,分别交射线OA,OB于点M,N.小明在直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,请问当直线MN在什么位置时,△MON的面积最小?并说明理由.(3)实际应用:如图3,若在道路OA,OB之间有一村庄Q发生疫情,防疫部门计划以公路OA,OB和经过防疫站P的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66°,∠POB=30°,OP=4km,试求△MON的面积.(参考数据:sin66°≈0.91,tan66°≈2.25,)(2)中当直线MN在什么位置时,△MON的面积最小?( )∙ A.当直线MN旋转到与OA垂直的位置时∙ B.当直线MN旋转到与OP垂直的位置时∙ C.当直线MN旋转到与OB垂直的位置时知识点:中考数学几何中的类比探究解题思路见第4题中解析4.(本小题3分)(上接第3题)(3)中△MON的面积为( )∙ A.∙ B.∙ C.∙ D.正确答案: C 你的答案:C,回答正确答题总人数:497该试题正确率:39.03%平均用时:50秒实际用时:2分37秒知识点:中考数学几何中的类比探究解题思路。
类比探究综合测试(通用版)(含答案)

类比探究综合测试(通用版)试卷简介:测试学生在处理类比探究问题过程中,有没有类比照搬的意识,能否根据题干或者问与问之间的联系,照搬辅助线,照搬思路来解决问题,同时考查学生对于类比探究中中点结构、旋转结构、平行结构这三种特殊结构的处理思路。
一、单选题(共6道,每道16分)1.如图1,△ABC和△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,点D在AB边上.连接EC,取EC的中点F,连接AF,DF.为了证明AF⊥DF,AF=DF,我们只需要延长DF交线段AC于点G,说明AF是等腰直角三角形ADG的中线即可.现将△BDE旋转至如图2所示的位置,使点E在AB的延长线上,点D在CB的延长线上,其他条件不变,类比上面的做法,为了证明AF⊥DF,AF=DF,我们需要作的辅助线是( )A.连接ADB.过点C作CG⊥DF,交DF的延长线于点GC.延长DF交AC的延长于点G,连接ADD.延长DF到G,使DF=FG,连接CG,AD,AG答案:D解题思路:在图1中,给出的辅助线达到的一个效果就是保证F是等腰直角三角形ADG斜边的中点,满足DF=FG.若在图2中达到同样的效果,需要延长DF到G,使DF=FG,这样再连接AD,AG之后才能保证F是等腰直角三角形ADG斜边的中点.试题难度:三颗星知识点:中考数学几何中的类比探究2.(上接第1题)在试题1图2的证明中,说明△ADG是等腰直角三角形之前,证明AD=AG 需要直接使用到某对三角形全等,则判定这对三角形全等的条件是( )A.AASB.ASAC.SSSD.SAS答案:D解题思路:要证明AD=AG,我们需要证明△ABD≌△ACG.根据上一题的分析,如图,延长DF到G,使DF=FG,连接CG,AD,AG,容易证明△DEF≌△GCF,∴CG=ED=BD,∠DEF=∠GCF,∴DE∥CG,∴∠GCD=∠BDE=90°,∴∠GCA=∠DBA=135°.又∵AC=AB,∴△ABD≌△ACG(SAS).(为了证明AF⊥DF,AF=DF,接下来需要根据得出的条件,说明∠DAG=90°,进而说明AF是等腰直角三角形ADG斜边上的中线)试题难度:三颗星知识点:中考数学几何中的类比探究3.如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF.利用旋转的思想很容易证明DE+BF=EF;如图2,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且.则DE,BF,EF之间的数量关系为( )A. B.C.DE+2BF=EFD.DE+BF=EF答案:D解题思路:在图1中,旋转思想考虑了两个方面,一个是AB=AD,能够实现旋转,一个是,能够将角度放在一起,所以图1中的证明是将△DAE旋转,使得AD 与AB重合,这是一种思想,作辅助线的时候是延长CB到点G,使得BG=DE,最后证明GF=EF.图2中有同样的两个结构:AB=AD,,所以照搬分析图1的思路来研究数量关系.如图,延长CB到点G,使得BG=DE,连接AG.易证△ADE≌△ABG,∴AE=AG,BG=DE,∠DAE=∠BAG,∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF.∵,∴∠GAF=∠EAF.又∵AF=AF,∴△GAF≌△EAF,∴GF=EF,∴EF=GB+BF=DE+BF,即DE,BF,EF满足的数量关系是DE+BF=EF.试题难度:三颗星知识点:类比探究问题4.(上接第3题)如图3,在四边形ABCD中,AB=AD,E,F分别为DC,BC边上的点,且满足,当∠ABC与∠ADC满足( )时,可使得DE+BF=EF.A.∠ABC=∠ADCB.∠ABC+∠ADC=180°C.∠ABC=2∠ADC-180°D.∠ABC+2∠ADC=270°答案:B解题思路:试题3中图1和图2的证明,都是利用旋转的思想来证明DE+BF=EF,从作辅助线开始到结束,整个分析有以下几点:延长CB到点G,使得BG=DE,证明△ABG≌△ADE(SAS),导出∠GAF=∠EAF,进而证明△GAF≌△EAF(SAS),之后导出线段关系.若在图3中用此方法证明,首先延长CB到点G,使得BG=DE,要证明△ABG和△ADE全等,需要保证∠ABG=∠ADE,也就是需要∠ABC+∠ADC=180°,所以需要添加的条件是∠ABC+∠ADC=180°.添加条件之后的证明如下:如图,延长CB到点G,使得BG=DE,连接AG.∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,∴∠ABG=∠ADE.又∵AB=AD,BG=DE,∴△ADE≌△ABG,∴AE=AG,BG=DE,∠DAE=∠BAG,∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF.∵,∴∠GAF=∠EAF.又∵AF=AF,∴GF=EF,∴EF=GB+BF=DE+BF.试题难度:三颗星知识点:类比探究问题5.如图,D是△ABC的边BC上一点,过点D的一条直线交AC于点F,交BA的延长线于点E.若BD=2CD,CF=mAF,则的值是( )A. B.C. D.答案:B解题思路:如图,过点D作DG∥AC,交AB于点G.设CD=a,BD=2a,AF=b,CF=mb.∵△BDG∽△BCA,∴∴,BG=2AG.设AG=c,BG=2c,∴,即∴∴试题难度:三颗星知识点:中考数学几何中的类比探究6.如图,D是△ABC的边BC上一点,过点D的一条直线交AC的延长线于点F,交AB于点E.若BD=aCD,CF=bAF,则的值是( )A. B.C. D.答案:D解题思路:如图,过点D作DG∥AC,交AB于点G.设CD=m,BD=am,AF=n,CF=bn.∵△BDG∽△BCA,∴∴,BG=aAG.设AG=c,BG=ac,∵△EAF∽△EGD,∴,即∴∴.试题难度:三颗星知识点:中考数学几何中的类比探究。
类比探究(讲义)
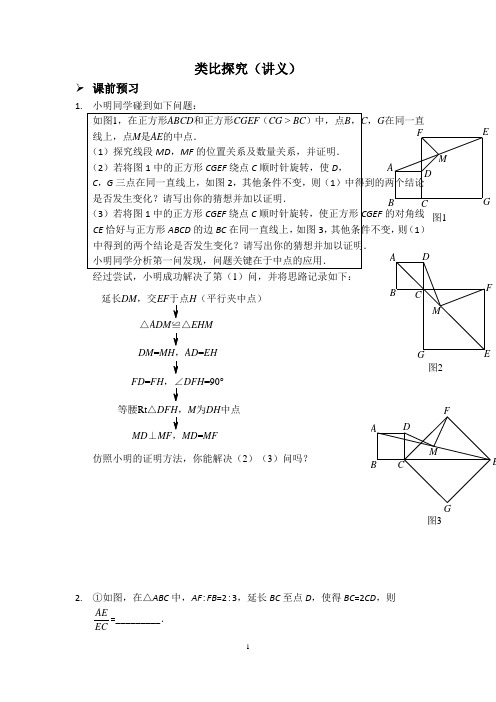
图1AB CDGEF M图2A BCDG EFM图3AB CDG EFM类比探究(讲义)➢ 课前预习1.小明同学碰到如下问题:如图1,在正方形ABCD 和正方形CGEF (CG > BC )中,点B ,C ,G 在同一直线上,点M 是AE 的中点.(1)探究线段MD ,MF 的位置关系及数量关系,并证明. (2)若将图1中的正方形CGEF 绕点C 顺时针旋转,使D , C ,G 三点在同一直线上,如图2,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.(3)若将图1中的正方形CGEF 绕点C 顺时针旋转,使正方形CGEF 的对角线CE 恰好与正方形ABCD 的边BC 在同一直线上,如图3,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明. 小明同学分析第一问发现,问题关键在于中点的应用. 经过尝试,小明成功解决了第(1)问,并将思路记录如下:MD ⊥MF MD =MF等腰Rt △M 为DH 中点FD =FH DFH =90°DM =AD =EH △ADM ≌△EHM 延长DM ,交EF H (平行夹中点)仿照小明的证明方法,你能解决(2)(3)问吗?2. ①如图,在△ABC 中,AF :FB =2:3,延长BC 至点D ,使得BC =2CD ,则AEEC=_________.提示:求比例,找相似.利用平行线构造“A 型”或“X 型”相似是我们常用的一种做法.A BEF②如图,AB =4,射线BM 和AB 相互垂直,点D 是AB 上的一个动点,点E 在射线BM 上,2BE =DB ,作EF ⊥DE 并截取EF =DE ,连接AF 并延长交射线BM 于点C .设BE =x ,BC =y ,则y 关于x 的函数解析式是( )A .124xy x =--B .21xy x =--C .31xy x =-- D .84x y x =-- 提示:结合直角特征考虑分析,可构造一线三等角,利用相似整合信息.➢ 知识点睛类比探究问题的处理思路1. 若属于类比探究常见的结构类型,调用结构类比解决.类比探究结构举例:中点结构、直角结构、旋转结构、平行 结构.2. 若不属于常见结构类型:①根据题干条件,结合_______________先解决第一问.M FE DC B A②类比解决下一问.如果不能,分析条件变化,寻找______________.③结合所求目标,依据__________,大胆猜测、尝试、验证.➢ 精讲精练1. 已知梯形ABCD ,AD ∥BC ,AB ⊥BC ,AD =1,AB =2,BC =3.(1)如图1,P 为AB 边上的一点,以PD ,PC 为边作□PCQD ,则当点P 与点A 重合时,PQ 的长为__________.(2)如图2,若P 为AB 边上任意一点,以PD ,PC 为边作□PCQD ,请问对角线PQ 的长是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.(3)若P 为AB 边上任意一点,延长PD 到E ,使DE =PD ,再以PE ,PC 为边作□PCQE ,请探究对角线PQ 的长是否也存在最小值.如果存在,请求出最小值;如果不存在,请说明理由.(4)如图3,若P 为直线DC 上任意一点,延长PA 到E ,使AE =nPA (n 为常数),以PE ,PB 为边作□PBQE ,请探究对角线PQ 的长是否也存在最小值.如果存在,请求出最小值;如果不存在,请说明理由.DQCBA (P )图1AP BCQD图2AC D EPQ图3A B CDA B CD2. 已知△ABC 为直角三角形,∠ACB =90°,点P 是射线CB 上一点(点P 不与点B ,C 重合),线段AP 绕点A 顺时针旋转90°得到线段AQ ,连接QB 交射线AC 于点M .(1)如图1,当AC =BC ,点P 在线段CB 上时,线段PB ,CM 的数量关系是__________.(2)如图2,当AC =BC ,点P 在线段CB 的延长线上时,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由.(3)如图3,若52AC BC ,点P 在线段CB 的延长线上时,CM =2,AP =13,求△ABP 的面积.图1M QPABC图2M QPAB CMC BAPQ图33. (1)问题发现如图1,△ACB 和△DCE 均为等边三角形,点A ,D ,E 在同一直线上,连接BE .填空:①∠AEB 的度数为___________;②线段AD ,BE 之间的数量关系为___________.图1CDABE(2)拓展探究如图2,△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE =90°,点A ,D ,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接BE .请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系,并说明理由.图2MEDCBA(3)解决问题如图3,在正方形ABCD 中,CD.若点P 满足PD =1,且∠BPD =90°,请直接写出点A 到BP 的距离.A BCD图34. 如图1,在Rt △ABC 中,∠B =90°,BC =2AB =8,点D ,E 分别是边BC ,AC的中点,连接DE .将△EDC 绕点C 按顺时针方向旋转,记旋转角为α. (1)问题发现①当α=0°时,=BD AE ______;②当α=180°时,=BDAE______. (2)拓展探究试判断:当0°≤α<360°时,AEBD的大小有无变化?请仅就图2的情形给出证明. (3)问题解决当△EDC 旋转至A ,D ,E 三点共线时,直接写出线段BD 的长.图3图2图1ABCAEBDCDECB A【参考答案】 ➢ 课前预习1. 能,证明略2. ①2②A➢ 知识点睛2. ①分支条件 ②不变特征 ③不变特征➢ 精讲精练1. (1)(2)存在,最小值为4. (3)存在,最小值为5.(44)n +. 2. (1)PB =2CM .(2)成立,证明略. (3)△ABP 的面积为25. 3. (1)①60°;②AD =BE .(2)AE =2CM +BE .(3)点A 到BP .4. (1 (2)0360α︒<︒≤时,AEBD的大小没有变化,证明略.(3)线段BD 的长为5. 类比探究(随堂测试)1. 如图1,将三角板放在正方形ABCD 上,使三角板的直角顶点E 与正方形ABCD 的顶点A 重合,三角板的一边交CD 于点F ,另一边交CB 的延长线于点G .(1)求证:EF =EG .(2)如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)如图3,将(2)中的“正方形ABCD ”改为“矩形ABCD ”,且使三角板的一边经过点B ,其他条件不变,若AB =a ,BC =b ,求EFEG的值.E (A )BC D FGG FDC BAEEACDFG (B )图1图2图3【参考答案】1. (1)证明略.(2)成立,证明略. (3)EF bEG a.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢例题示范
类比探究(习题)
例1:如图1,在□ABCD 中,点E 是BC 边的中点,点F 是线段AE 上一点,BF 的延长线交射线CD 于点G.
(1)尝试探究:如图1,若AF
= 3 ,则
CD
的值是.EF CG
(2)类比延伸:如图2,在原题的条件下,若AF
=m (m>EF
0),则CD
的值是CG
解答过程.
(用含m 的代数式表示),试写出(3)拓展迁移:如图3,在梯形ABCD 中,DC∥AB,点E
是BC 延长线上一点,AE 和BD 相交于点F.若AB
=a ,CD
BC
=b(a>0,b>0),则AF
的值是(用含a,b 的代
BE EF 数式表示).
1
【思路分析】
根据特征确定问题结构,设计方案解决第一问.
问题背景是平行四边形,且已知线段比例关系,考虑通过相
似传递比例关系,进而求 CD
的值.
CG
构造相似利用作平行线的方法,即过中点 E 作 EH ∥AB 交 BG
于点 H ,可得“A ”字型相似△BEH ∽△BCG ,“X ”型相似
△EFH ∽△AFB ,结合 AF
= 3 ,可得 CG =2EH ,AB =3EH ,故
EF
CD = 3 .
CG 2
类比第一问思路,解决第二问.
分析不变特征,此时平行四边形、中点特征均不变,变化的是 AF ,EF 的比例,照搬第一问思路,过点 E 作 EH ∥AB 交BG 于点 H ,同样可得△BEH ∽△BCG ,△EFH ∽△AFB ,此
时 CG =2EH ,AB =mEH ,故 CD = m
.
CG 2
照搬思路解决第三问.
虽然此问中图形、中点 E 、比例关系均发生变化,但 DC ∥AB 不变,依然可利用相似来整合条件,可照搬前面思路处理, 依然构造平行.过点 E 作 EH ∥AB 交 BD 的延长线于点 H ,
可得△BCD ∽△BEH ,△AFB ∽△EFH ,可得 BC = CD
,
BE EH
AF = AB ,结合 AB = a , BC = b ,可知 EF EH CD BE AF = AB = a ⋅CD = ab . EF EH EH
2
1
2 3
➢巩固练习
1.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=
∠DEF=90°,∠EDF=30°.
【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上,再将三角板DEF 绕点E 旋转,并使边DE 与边AB 交于点P,边EF 与边BC 交于点Q.
【探究】在旋转过程中,
(1)如图2,当CE
=1时,EP 与EQ 满足怎样的数量关系?EA
并给出证明.
(2)如图3,当CE
= 2 时,EP 与EQ 满足怎样的数量关系?EA
并给出证明.
(3)根据你对(1),(2)的探究结果,试写出当CE
=m时,EA
EP 与EQ 满足的数量关系式为.
3
,=
2.如图1,在等边三角形ABC 中,线段AD 为其内角角平分线,
过点D 的直线B1C1⊥AC 于C1,交AB 的延长线于B1.
(1)请你探究:AC =CD AC1 C1D 是否都成立?
AB BD AB
1
DB
1
(2)请你继续探究:如图2,若△ABC 为任意三角形,线段
AD 为其内角角平分线,请问
AC
=
CD
一定成立吗?并证明
AB BD
你的判断.
(3)如图3,在Rt△ABC 中,∠ACB=90°,AC=8,AB=
40
,
3
E 为AB 上一点且AE=5,CE 交其内角角平分线AD 于F.试
求
DF
的值.
FA
4
3.
如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C =90°,∠B =∠E =30°.
(1) 操作发现
如图 2,固定△ABC ,使△DEC 绕点 C 旋转,当点 D 恰好落在 AB 边上时,填空:
①线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S 1,△AEC 的面积为 S 2,则 S 1 与 S 2 的
数量关系是
.
图 1
图 2
(2) 猜想论证
当△DEC 绕点 C 旋转到图 3 所示的位置时,小明猜想(1) 中 S 1 与 S 2 的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中 BC ,CE 边上的高,请你证明小明的猜想.
(3) 拓展探究
如图 4 , 已知∠ ABC =60°, 点 D 是其角平分线上一点, BD =CD =4,DE ∥AB 交 BC 于点 E .若在射线 BA 上存在点 F , 使 S △DCF =S △BDE ,请直.接.写.出.
相应的 BF 的长.
5
➢思考小结
总结类比探究问题中的常见结构
①旋转结构
始终含有等腰结构(正方形、等腰直角三角形等),并且经过旋转后,能将各条件重新组合应用.
②中点结构
平行夹中点(类)倍长中线中位线始终含有中点,常考虑利用中点结构补全图形,然后将所证目标放在一个较大的背景下(等腰三角形、直角三角形、等腰直角三角形等)研究.
③直角结构
始终含有直角,常构造直角与斜直角配合,得到同角的余角相等;再配合构造的其他直角证明相似,所求目标往往和比例关系相关.
6
④平行结构
所求目标为线段间的比例关系,题目中没有相似三角形,往往考虑利用平行线构造相似求解.
7
8 3 3 【参考答案】 ➢ 巩固练习
1. (1)EP =EQ ,证明略;
(2) EP = 1
EQ ,证明略;
2 (3) EP = 1
EQ .
m
2. (1)都成立,证明略; (2)一定成立,证明略;
(3) DF = 5 .
FA 8
3. (1)①DE ∥AC ;②S 1=S 2.
(2) 证明略; (3) BF 的长为
4 3
或 .
3
8。
