因子分析在STATA中实现和案例
因子分析︱使用Stata做主成分分析

因子分析︱使用Stata做主成份分析因子分析是一种常用的多变量数据分析方法,可以用于降维、变量筛选和构建综合指标等方面。
在实际应用中,Stata是一款功能强大的统计软件,可以方便地进行因子分析。
本文将介绍如何使用Stata进行主成份分析。
首先,我们需要准备好需要进行因子分析的数据。
假设我们有一份包含10个变量的数据集,每一个变量都代表了某种特征或者指标。
我们希翼通过因子分析来找出这些变量的共同因素,并将其转化为更少的几个主成份。
在Stata中,我们可以使用“factor”命令来进行主成份分析。
首先,我们需要加载数据集。
假设我们的数据集名为“data”,我们可以使用以下命令加载数据:```use data```接下来,我们可以使用“factor”命令进行主成份分析。
以下是一个示例命令:```factor var1-var10, pcf```在上述命令中,“var1-var10”表示我们要进行因子分析的变量范围,而“pcf”表示使用主成份法进行因子分析。
执行该命令后,Stata会输出一份关于因子分析结果的报告。
报告中的一项重要指标是共同度(communality),它表示每一个变量与所有因子的相关程度。
共同度越高,说明变量与因子之间的关联越强。
我们可以根据共同度来判断每一个变量对应的主成份是否合适。
此外,报告还会给出每一个主成份的解释方差比例(proportion of variance explained)。
解释方差比例表示每一个主成份能够解释原始数据中的多少方差。
通常,我们希翼选择解释方差比例较高的主成份,以便更好地代表原始数据。
在进行因子分析后,我们还可以使用“rotate”命令对主成份进行旋转,以便更好地解释数据。
Stata提供了多种旋转方法,如方差最大旋转(varimax rotation)和直角旋转(orthogonal rotation)等。
我们可以根据需要选择合适的旋转方法。
除了使用命令行进行因子分析,Stata还提供了可视化工具来匡助我们更好地理解和解释数据。
因子分析在STATA中实现和案例

因子分析在STATA中实现和案例因子分析是一种统计方法,用来研究一组变量之间的相关性,以及这些变量是否可以被归纳为更少的无关变量,即因子。
在STATA软件中,我们可以使用factor命令进行因子分析。
在本文中,我们将介绍STATA中因子分析的实现步骤,并给出一个案例来说明。
实现步骤:1. 数据准备:将需要进行因子分析的变量导入STATA软件,并确保变量为连续型变量。
如果变量中存在缺失值,可以使用命令“dropmiss”删除缺失值。
2. 因子分析模型的选择:在因子分析中,我们需要选择合适的因子数和因子分析模型。
常见的因子数选择方法有Kaiser准则、斯科马洛维准则和Cattell准则等。
常见的因子分析模型有主成分分析和最大似然估计法。
在STATA中,我们可以使用命令“factor”来估计主成分分析模型或最大似然估计法模型。
3. 进行因子分析:在STATA中,我们可以使用命令“factor”进行因子分析。
命令的一般语法如下:factor 变量列表,选项常用的选项有:-pca:使用主成分分析模型-ml:使用最大似然估计法模型-factors(n):指定因子的个数为n-rotation(r):选择因子旋转方法,常见的有方差最大旋转法(varimax)和极大似然估计法(method=ml)等4.结果解读:进行因子分析后,STATA会生成一份结果报告,其中包括每个因子的因子载荷、特征值、解释方差比等指标。
因子载荷可以用来解释原始变量与因子之间的关系,特征值可以用来衡量因子的重要性,解释方差比可以用来衡量因子分析模型的拟合度。
案例:假设我们现在有一组数据,包括10个变量:x1、x2、x3、x4、x5、x6、x7、x8、x9和x10。
我们希望对这组变量进行因子分析,以便找出潜在的结构。
步骤如下:1.数据准备:将数据导入到STATA软件中,并确保变量为连续型变量。
2. 因子分析模型的选择:我们首先通过计算相关性矩阵来选择合适的因子数。
stata fama french三因子代码

Stata Fama French三因子代码一、介绍Stata是一种统计分析软件,非常适合进行数据分析和数据管理。
而Fama-French三因子模型是用来解释股票回报的经典模型,在资产定价和投资组合管理中具有重要意义。
结合Stata和Fama-French三因子模型,可以对股票市场进行深入的分析和研究。
本文将详细介绍如何在Stata中使用Fama-French三因子模型进行分析,并给出相应的代码和操作步骤。
二、获取数据在使用Stata进行Fama-French三因子模型分析之前,首先需要获取所需的数据。
一般来说,可以从金融数据库或者股票交易所获取股票收益率和市值数据,以及市场大盘收益率和无风险利率数据。
在本文的案例中,我们将使用一家股票交易所提供的样本数据来进行模型分析。
三、安装Stata模块Stata并没有直接内置Fama-French三因子模型的计算功能,但是可以通过安装相应的模块来实现。
在Stata中,可以通过输入以下命令来安装ff运行Stata模块:```statassc install ff```这样就可以安装ff模块并准备好进行Fama-French三因子模型分析。
四、导入数据在安装好ff模块后,接下来可以导入所需的数据进行分析。
以导入月度股票收益率、市值和市场大盘收益率数据为例,可以按照以下步骤进行操作:```statause yourfile, clear```五、运行Fama-French三因子模型在导入数据后,就可以利用ff模块来运行Fama-French三因子模型了。
以运行单因子模型为例,可以按照以下步骤进行操作:```stataff reg stock_return, famafrench(market smb hml)```其中,stock_return为股票收益率变量名称,market为市场大盘收益率变量名称,smb为规模因子变量名称,hml为价值因子变量名称。
运行以上命令后,就可以得到Fama-French三因子模型的回归结果了。
stata迭代主因子法

stata迭代主因子法【实用版】目录1.引言2.Stata 迭代主因子法的概述3.Stata 迭代主因子法的操作步骤4.Stata 迭代主因子法的应用实例5.总结正文1.引言在数据分析中,主因子分析是一种常用的降维方法,它能够将原始变量转化为少数几个线性无关的主因子,从而实现变量的简化。
而 Stata 作为一款功能强大的统计分析软件,提供了迭代主因子法这一有效的主因子分析方法。
本文将对 Stata 迭代主因子法进行详细介绍,包括其概述、操作步骤和应用实例。
2.Stata 迭代主因子法的概述Stata 迭代主因子法是一种基于迭代计算的主因子分析方法,其主要目的是通过迭代计算来逼近原始变量的协方差矩阵,从而得到更准确的主因子。
这种方法在处理高维数据和大规模数据时具有较好的效果,能够提高主因子分析的准确性和可靠性。
3.Stata 迭代主因子法的操作步骤在 Stata 中,可以使用“factor”命令进行迭代主因子分析。
以下是具体的操作步骤:(1) 首先,输入原始数据。
假设我们有一个包含 10 个变量的数据集,可以使用以下命令:```* 示例数据* insheet using "data.csv", clear```(2) 进行迭代主因子分析。
在 Stata 中,可以使用“factor”命令进行迭代主因子分析,具体操作如下:```factor```(3) 查看迭代主因子分析的结果。
Stata 会输出迭代主因子分析的结果,包括每个主因子的方差贡献率、累积方差贡献率和特征值等。
4.Stata 迭代主因子法的应用实例假设我们有一个包含 10 个变量的数据集,希望通过主因子分析来提取其中的关键信息。
具体操作如下:(1) 首先,输入原始数据。
```* 示例数据* insheet using "data.csv", clear```(2) 进行迭代主因子分析。
```factor```(3) 查看迭代主因子分析的结果。
stata 共同因子方法

stata 共同因子方法
共同因子方法是一种统计技术,用于识别和解释多个变量之间的共同因子或潜在结构。
这种方法在许多领域都有应用,包括心理学、社会学、经济学等。
在Stata中,可以使用以下步骤进行共同因子分析:
确定要分析的变量。
这些变量应该是可以测量的,并且它们之间应该存在一定的相关性,以便可以识别出共同因子。
对变量进行因子分析。
在Stata中,可以使用factor命令进行因子分析。
该命令将计算每个变量的因子载荷,并确定共同因子的数量。
解释因子结构。
因子载荷是变量与共同因子之间的相关系数。
通过观察因子载荷的大小和符号,可以解释每个共同因子所代表的概念或结构。
解释因子得分。
因子得分可以帮助您了解每个观测值的共同因子结构。
可以使用Stata中的score命令来计算因子得分。
解释结果。
解释因子得分和因子载荷可以帮助您理解共同因子的含义和作用。
此外,您还可以使用这些结果进行进一步的统计分析或预测模型的开发。
总之,共同因子方法是分析多个变量之间关系的有力工具,可以帮助您揭示潜在的结构和模式。
在Stata中,使用factor命令可以轻松地进行共同因子分析,并解释结果。
stata 主成分 提取公因子 cfa

文章题目:深度探讨Stata中主成分分析和提取公因子的应用和理解1. 引言在社会科学研究中,主成分分析(PCA)和确认性因子分析(CFA)是常用的数据分析方法。
本文将深入探讨Stata中主成分分析和提取公因子的应用和理解,帮助读者更全面地掌握这两种方法的使用。
2. Stata中的主成分分析(PCA)主成分分析即PCA是一种用于降维和发现变量间相关性的方法。
在Stata中,我们可以使用“factor”命令进行主成分分析。
我们需要加载数据集并选择感兴趣的变量,然后使用“factor”命令进行主成分分析。
得到主成分之后,我们可以根据主成分载荷来解释每个主成分所代表的变量间关系。
在解释主成分时,我们需要关注载荷大小和方向,以确定不同变量之间的相关性和主成分的解释性。
3. Stata中的确认性因子分析(CFA)确认性因子分析即CFA是一种用于验证构念和测量模型的方法,常用于问卷调查和心理学领域。
在Stata中,我们可以使用“sem”命令进行CFA。
我们需要构建测量模型,并指定潜在变量和观测变量之间的关系。
我们可以使用“sem”命令进行模型拟合和参数估计。
得到CFA模型之后,我们可以通过拟合指标和因子载荷来评估模型的拟合度和测量指标的效度。
4. 应用实例分析以一个实际的研究案例为例,我们将结合主成分分析和确认性因子分析,探讨如何使用Stata进行数据分析和模型验证。
我们将使用实际数据集,并按照从简到繁的方式,逐步进行主成分分析和CFA。
通过具体的数据分析过程,读者可以更加直观地了解这两种方法的应用和解释。
5. 总结与展望主成分分析和确认性因子分析是重要的数据分析工具,对于研究者来说具有重要的实用价值。
通过本文的讨论,读者可以更深入地理解Stata中主成分分析和提取公因子的方法和意义。
未来,我们可以进一步探讨如何结合主成分分析和CFA,做出更加全面和深入的数据分析和模型验证。
6. 个人观点和理解个人认为,主成分分析和确认性因子分析是研究中不可或缺的方法,能够帮助我们更好地理解变量之间的关系和构念的测量。
stata迭代主因子法

stata迭代主因子法
stata迭代主因子法(Iterative Principal Factor Method in Stata)是一种数据降维技术,用于发现和提取数据集中的主要因子。
该方法基于主成分分析(PCA)和因子分析的原理,通过迭代的方式逐渐确定数据中的主要因子,并计算每个因子对原始数据的贡献程度。
本文将一步一步回答有关stata迭代主因子法的相关问题。
第一部分:概述和背景
- 什么是迭代主因子法(Iterative Principal Factor Method)?
- 迭代主因子法在数据降维中的作用是什么?
第二部分:迭代主因子法的基本原理
- 迭代主因子法是如何通过迭代的方式确定数据中的主要因子的?
- 主成分分析(PCA)和因子分析的原理是什么?它们是如何与迭代主因子法相关联的?
第三部分:实施迭代主因子法
- 在Stata中如何使用迭代主因子法进行数据降维?
- 通过一个简单的示例数据集介绍如何使用迭代主因子法。
- 如何根据迭代主因子法的结果进行数据的解释和分析?
第四部分:迭代主因子法的应用领域和限制
- 迭代主因子法在哪些领域中得到广泛应用?
- 迭代主因子法存在哪些限制?如何根据限制进行结果的解释和分析?
第五部分:比较和结论
- 迭代主因子法与其他主成分分析方法的比较与评估。
- 在不同情景下,迭代主因子法的优势与劣势是什么?
- 结论和未来研究展望。
以上是对于stata迭代主因子法的一个大致的解析,根据需要可以进一步展开和详细讨论每一个部分。
根据不同的情况和背景,文章长度可能在3000-6000字之间。
STATA中主成分分析与使用主成分法的因子分析的区别
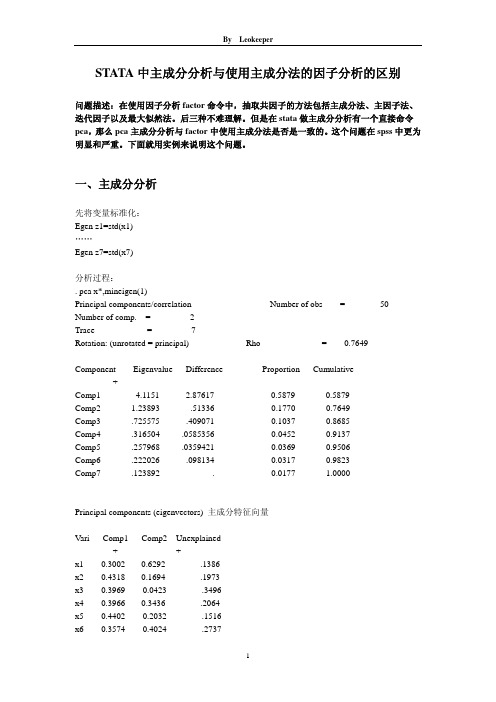
STATA中主成分分析与使用主成分法的因子分析的区别问题描述:在使用因子分析factor命令中,抽取共因子的方法包括主成分法、主因子法、迭代因子以及最大似然法。
后三种不难理解。
但是在stata做主成分分析有一个直接命令pca,那么pca主成分分析与factor中使用主成分法是否是一致的。
这个问题在spss中更为明显和严重。
下面就用实例来说明这个问题。
一、主成分分析先将变量标准化:Egen z1=std(x1)……Egen z7=std(x7)分析过程:. pca x*,mineigen(1)Principal components/correlation Number of obs = 50 Number of comp. = 2Trace = 7Rotation: (unrotated = principal) Rho = 0.7649--------------------------------------------------------------------------Component Eigenvalue Difference Proportion Cumulative-------------+------------------------------------------------------------Comp1 4.1151 2.87617 0.5879 0.5879Comp2 1.23893 .51336 0.1770 0.7649Comp3 .725575 .409071 0.1037 0.8685Comp4 .316504 .0585356 0.0452 0.9137Comp5 .257968 .0359421 0.0369 0.9506Comp6 .222026 .098134 0.0317 0.9823Comp7 .123892 . 0.0177 1.0000--------------------------------------------------------------------------Principal components (eigenvectors) 主成分特征向量------------------------------------------------Vari Comp1 Comp2 Unexplained-------------+--------------------+-------------x1 0.3002 -0.6292 .1386x2 0.4318 -0.1694 .1973x3 0.3969 0.0423 .3496x4 0.3966 -0.3436 .2064x5 0.4402 0.2032 .1516x6 0.3574 0.4024 .2737x7 0.2952 0.5023 .3288------------------------------------------------. loadingplot. estat loading,cnorm(eigen)Principal component loadings (unrotated) 主成分负荷component normalization: sum of squares(column) = eigenvalue----------------------------------Comp1 Comp2-------------+--------------------x1 .6091 -.7003x2 .8758 -.1886x3 .8051 .04705x4 .8046 -.3825x5 .8929 .2262x6 .725 .4479x7 .5988 .5591----------------------------------注:主成分向量=负荷/特征值的开方. estat kmo KMO检验Kaiser-Meyer-Olkin measure of sampling adequacy-----------------------Variable kmo-------------+---------x1 0.6759x2 0.8398x3 0.8517x4 0.8675x5 0.7961x6 0.6731x7 0.7318-------------+---------Overall 0.7836-----------------------. estat smcSquared multiple correlations of variables with all other variables-----------------------Variable smc-------------+---------x1 0.6093x2 0.7300x3 0.5951x4 0.6453x5 0.7948x6 0.7275x7 0.4858-----------------------. estat antiAnti-image correlation coefficients --- partialing out all other variables------------------------------------------------------------------------------------Va x1 x2 x3 x4 x5 x6 x7-------------+----------------------------------------------------------------------x1 1.0000x2 -0.3698 1.0000x3 -0.2740 -0.0700 1.0000x4 -0.2669 -0.3694 -0.0779 1.0000x5 -0.1825 -0.0386 -0.1297 -0.2412 1.0000x6 0.4149 -0.3903 -0.0029 0.1277 -0.6471 1.0000x7 0.2781 -0.0107 -0.4681 0.0538 -0.2887 0.0757 1.0000------------------------------------------------------------------------------------注:KMO、SMC和ANTI结合判断是否适合做主成分分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第13章因子分析因子分析始于1904年Chars Spearman对学生成绩的分析,在经济领域有着极为广泛的用途。
在多个变量的变化过程中,除了一些特定因素之外,还受到一些共同因素的影响。
因此,每个变量可以拆分成两部分,一是共同因素,二是特殊因素。
这些共同因素称为公因子,特殊因素称为特殊因子。
因子分析即是提出多个变量的公共影响因子的一种多元统计方法,它是主成分分析的推广。
因子分析主要解决两类问题:一是寻求基本结构,简化观察系统。
给定一组变量或观察数据,是否存在一个子集,特别是一个加权子集,来解释整个问题,即将为数众多的变量减少为几个新的因子,以再现它们之间的内在联系。
二是用于分类,将变量或样本进行分类,根据因子得分值,在因子轴所构成的空间中进行分类处理。
p个变量X的因子模型表达式为:=Λ'efX+f称为公因子,Λ称为因子载荷。
X的相关系数矩阵分解为:∑'=+ΛΦΛψ对于未旋转的因子,1Φ。
ψ称为特殊度,即每个变量中不属于共性的部=分。
13.1 因子估计Stata可以通过变量进行因子分析,也可以通过矩阵进行。
命令为factor 或factormat。
webuse bg2,cleardescribefactor bg2cost1-bg2cost6factor bg2cost1-bg2cost6, factors(2)* pf 主因子方法,用复相关系数的平方作为因子载荷的估计量(默认选项)factor bg2cost1-bg2cost6, factors(2) pcf* pcf 主成分因子,假定共同度=1factor bg2cost1-bg2cost6, factors(2) ipf* ipf 迭代主因子,重复估计共同度factor bg2cost1-bg2cost6, factors(2) ml* ml 极大似然因子,假定变量(至少3个)服从多元正态分布,对偏相关矩阵的行列式进行最优化求解,等价于Rao的典型因子方法13.2 预测Stata可以通过predict预测变量得分、拟合值和残差等。
webuse bg2,clearfactor bg2cost1-bg2cost6predict f1 f2* factor1 factor2因子分得分predict stdp residuals* 预测标准差和残差13.3 EstatEatat给出了几个非常有用的工具,包括KMO、SMC等指标。
webuse bg2,clearfactor bg2cost1-bg2cost6estat antiestat kmoestat residualsestat smcestat summarize13.4 因子旋转与作图因子分析的旋转方法以及碎石图、得分图、因子载荷图与主成分分析的方法相同,请参见”主成分分析”一章。
webuse bg2,clearfactor bg2cost1-bg2cost6screeplot /*碎石图*/scoreplot /*得分图*/loadingplot /*因子载荷图*/rotate /*旋转*/例:利用2009年的数据对中国社会发展状况进行综合考察,原始数据如下表:省份人均GDP(元)新增固定资产(亿元)城镇居民人均年可支配收入(元)农村居民家庭人均纯收入(元)高等学校数(所)卫生机构数(个)area x1 x2 x3 x4 x5 x6北京63029 2385.8 24724.89 10661.92 85 6497 天津55473 1676.8 19422.53 7910.78 55 2784 河北23239 4734.2 13441.09 4795.46 105 15632 山西20398 1772.6 13119.05 4097.24 69 9431 内蒙古32214 3309.3 14432.55 4656.18 39 7162 辽宁31259 5056.7 14392.69 5576.48 104 14627 吉林23514 3279.9 12829.45 4932.74 55 9659 黑龙江21727 2405.4 11581.28 4855.59 78 7928 上海73124 2523.2 26674.9 11440.26 66 2822 江苏39622 7645.9 18679.52 7356.47 146 13357 浙江42214 3434.8 22726.66 9257.93 98 15290 安徽14485 2849.5 12990.35 4202.49 104 7837 福建30123 1768.3 17961.45 6196.07 81 4478 江西14781 2962.5 12866.44 4697.19 82 8229山东33083 6852.5 16305.41 5641.43 125 14973 河南19593 6414 13231.11 4454.24 94 11683 湖北19860 3053.4 13152.86 4656.38 118 10305 湖南17521 2478.2 13821.16 4512.46 115 14455 广东37589 5529.2 19732.86 6399.79 125 15819 广西14966 1419 14146.04 3690.34 68 10427 海南17175 230.2 12607.84 4389.97 16 2220 重庆18025 1381.9 14367.55 4126.21 47 6265 四川15378 2918.7 12633.38 4121.21 90 20738 贵州8824 903 11758.76 2796.93 45 5848 云南12587 1551 13250.22 3102.6 59 9249 西藏13861 137.4 12481.51 3175.82 6 1326 陕西18246 2262.8 12857.89 3136.46 88 8812 甘肃12110 575.2 10969.41 2723.79 39 10534 青海17389 322.8 11640.43 3061.24 9 1582 宁夏17892 403.9 12931.53 3681.42 15 1629 新疆19893 1162.9 11432.1 3502.9 37 6739程序:clear*定义变量的标签label var area 省份label var x1 "人均GDP(元)"label var x2 "新增固定资产(亿元)"label var x3 "城镇居民人均年可支配收入(元)"label var x4 "农村居民家庭人均纯收入(元)"label var x5 "高等学校数(所)"label var x6 "卫生机构数(个)"describefactor x1-x6screeplot /* 碎石图(特征值等于1处的水平线标示保留主成分的分界点)*/*检验estat kmo /*KMO检验,越高越好*/estat smc /*SMC检验,值越高越好*/rotate /*旋转*/loadingplot , yline(0) xline(0)/*载荷图 */*预测predict score fit residual q /*预测变量得分、拟合值和残差以及残差的平方和*/ predict f1 f2label var f1 收入因子label var f2 "投资、社会因子"list area f1 f2summarize f1 f2correlate f1 f2scoreplot,xtitle("收入因子") ytitle("投资、社会因子") ///mlabel(area) yline(0) xline(0) /*得分图*/分析:首先通过主因子分析(factor),得到主成分因子:Factor analysis/correlation Number of obs = 31Method: principal factors Retained factors = 3Rotation: (unrotated) Number of params = 15--------------------------------------------------------------------------Factor | Eigenvalue Difference Proportion Cumulative-------------+------------------------------------------------------------Factor1 | 3.28193 1.42544 0.6554 0.6554Factor2 | 1.85648 1.81677 0.3707 1.0261Factor3 | 0.03971 0.06244 0.0079 1.0341Factor4 | -0.02272 0.03972 -0.0045 1.0295Factor5 | -0.06244 0.02293 -0.0125 1.0170Factor6 | -0.08538 . -0.0170 1.0000--------------------------------------------------------------------------LR test: independent vs. saturated: chi2(15) = 211.52 Prob>chi2 = 0.0000Factor loadings (pattern matrix) and unique variances-----------------------------------------------------------Variable | Factor1 Factor2 Factor3 | Uniqueness-------------+------------------------------+--------------x1_s | 0.8609 -0.4463 -0.1125 | 0.0469x2_s | 0.6274 0.6026 -0.1061 | 0.2320x3_s | 0.8800 -0.3931 0.0998 | 0.0611x4_s | 0.9120 -0.3658 0.0365 | 0.0332x5_s | 0.6508 0.6526 0.0349 | 0.1494x6_s | 0.3427 0.7616 0.0572 | 0.2993-----------------------------------------------------------从上面的分析可以看出,只有两个成分大于1大于的特征值,同时两个成分解释了全部六个变量组合的方差还多。
