互余角的正切值关系
互余角的三角函数关系

1 / 6
互余角的三角函数关系
sin(90°-α)=cosα, cos(90°-α)=sinα,
tan(90°-α)=cotα, cot(90°-α)=tanα。
3.同角三角函数间的关系
商数关系:
sinA/cosA=tanA
·平方关系:
sin^2(A)+cos^2(A)=1
三角函数值
(1)特殊角三角函数值
(2)0°~90°的任意角的三角函数值,查三角函数表。
(3)锐角三角函数值的变化情况
(i)锐角三角函数值都是正值
(ii)当角度在0°~90°间变化时,
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
余切值随着角度的增大(或减小)而减小(或增大)
(iii)当角度在0°≤∠A≤90°间变化时,
0≤sinα≤1, 1≥cosA≥0,
当角度在0°<∠A<90°间变化时,
tanA>0, cotA>0.
·对称性
180度-α的终边和α的终边关于y轴对称。
-α的终边和α的终边关于x轴对称。
180度+α的终边和α的终边关于原点对称。
90度-α的终边和α的终边关于y=x对称
诱导公式
公式一:
设α为任意角,终边相同的角的同一三角函数的值相等
k是整数 sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
sec(2kπ+α)=secα
csc(2kπ+α)=cscα
公式二:
设α为任意角,π+α的三角函数值与α的三角函数值之间的关系 sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα 2 / 6
互余角的三角函数关系 2

1 / 6
互余角的三角函数关系
sin(90°-α)=cosα, cos(90°-α)=sinα,
tan(90°-α)=cotα, cot(90°-α)=tanα。
3.同角三角函数间的关系
商数关系:
sinA/cosA=tanA
·平方关系:
sin^2(A)+cos^2(A)=1
三角函数值
(1)特殊角三角函数值
(2)0°~90°的任意角的三角函数值,查三角函数表。
(3)锐角三角函数值的变化情况
(i)锐角三角函数值都是正值
(ii)当角度在0°~90°间变化时,
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
余切值随着角度的增大(或减小)而减小(或增大)
(iii)当角度在0°≤∠A≤90°间变化时,
0≤sinα≤1, 1≥cosA≥0,
当角度在0°<∠A<90°间变化时,
tanA>0, cotA>0.
·对称性
180度-α的终边和α的终边关于y轴对称。
-α的终边和α的终边关于x轴对称。
180度+α的终边和α的终边关于原点对称。
90度-α的终边和α的终边关于y=x对称
诱导公式
公式一:
设α为任意角,终边相同的角的同一三角函数的值相等
k是整数 sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
sec(2kπ+α)=secα
csc(2kπ+α)=cscα
公式二:
设α为任意角,π+α的三角函数值与α的三角函数值之间的关系 sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα 2 / 6
一、课题:互余角的锐角三角函数关系
第1页 一、课题:互余角的锐角三角函数关系
二、教学目标:
1、掌握互余角的概念以及互余角的锐角三角函数关系
2、会用互余角的三角函数关系进行运算
三、教学重点:互余角的概念以及互余角的锐角三角函数关系
四、教学难点:灵活运用互余角的锐角三角函数关系进行运算
五、教学过程
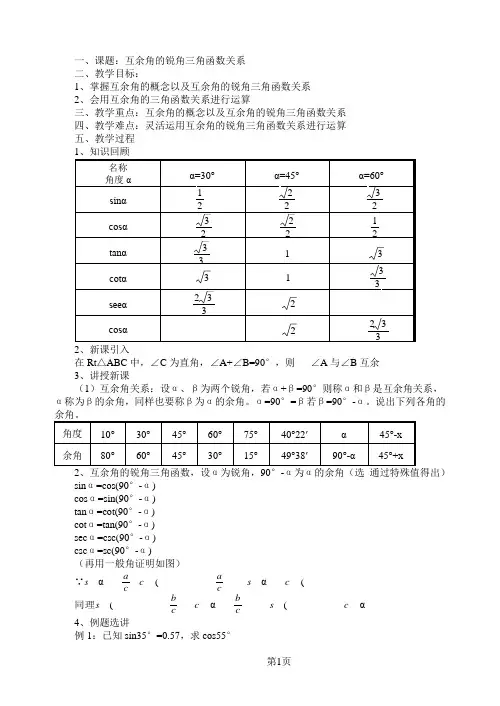
1、知识回顾
2、新课引入
在Rt△ABC中,∠C为直角,∠A+∠B=90°,则 ∠A与∠B互余
3、讲授新课
(1)互余角关系:设α、β为两个锐角,若α+β=90°则称α和β是互余角关系,α称为β的余角,同样也要称β为α的余角。α=90°=β若β=90°-α。说出下列各角的余角。
角度 10° 30° 45° 60° 75° 40°22′ α 45°-x
余角 80° 60° 45° 30° 15° 49°38′ 90°-α 45°+x
2、互余角的锐角三角函数,设α为锐角,90°-α为α的余角(选 通过特殊值得出)
sinα=cos(90°-α)
cosα=sin(90°-α)
tanα=cot(90°-α)
cotα=tan(90°-α)
secα=csc(90°-α)
cscα=sc(90°-α)
(再用一般角证明如图)
∵sα ac c(ac sα c(
同理s(bc cα bc s(cα 4、例题选讲
例1:已知sin35°=0.57,求cos55° 名称
角度α α=30° α=45° α=60°
sinα
cosα
tanα
cotα
seeα
cosα
12 22 3232 22 12 3 1 33233 2
2 23333 13
第2页 解:因为cos55°=cos(90°-55°)=sin35° 所以cos55°=0.57
练一练:已知cos70°=0.342,则sin20°= .
例2:化简
sin(90°-α)-cosαtan45°+tanα·cot(90°-α)
九年级数学下册基础知识专项讲练(北师大版)专题 三角函数的应用

试卷第1页,共4页 专题1.8 三角函数的应用(知识讲解)
【学习目标】
会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题.
【要点梳理】
要点一、锐角三角函数之间的关系
如图所示,在Rt△ABC中,△C=90°.
(1)互余关系:sincosAB,0csin(9)snosiAAB;
(2)平方关系:22sincos1AA;
(3)倒数关系:tan(90)1tanAA或1tnanatAB;
(4)商数关系:itnanscosAAA.
要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.
【典型例题】
类型一、利用同角三角函数关系求值
1.计算:
(1)2tan452sin30cos30; (2)22tan1tan89sin1sin89.
举一反三:
【变式1】
2.已知△A为锐角且sinA=12,则4sin2A-4sinAcosA+cos2A的值是多少。
【变式2】
3.如图,在ABCD中,E,F是对角线BD上的两点(点E在点F左侧),且90AEBCFD. 试卷第2页,共4页
(1)求证:四边形AECF是平行四边形.
(2)当5AB,3tan4ABE,CBEEAF时,求BD的长.
【变式3】
4.求值:
(1)260453456cossintantan;
2已知2tanA,求245sinAcosAsinAcosA的值.
类型二、求证同角三角函数关系式
5.已知:1sin15cos15sin302,1sin20cos20sin402,1sin30cos30sin602,请你根据上式写出你发现的规律________.
举一反三:
【变式1】
6.已知:实常数abcd、、、同时满足下列两个等式:△sincos0abc;△cossin0abd(其中为任意锐角),则abcd、、、之间的关系式是:___________
任意角的三角函数及基本公式

任意角的三角函数及基本公式
三角函数是数学中的一个重要概念,它们描述了角度与三角比之间的关系。任意角的三角函数包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。下面将详细介绍这些函数的定义、基本公式以及它们之间的关系。
1. 正弦函数(sine function):在单位圆上,从x轴正向到射线与单位圆的交点之间的弧度即为角的弧度。正弦函数将给定角度的正弦值映射到数轴上。其定义如下:
sin(θ) = y/r
其中θ为角度,y为对边,r为斜边。
2. 余弦函数(cosine function):余弦函数表示角的余弦值在数轴上的投影长度。其定义如下:
cos(θ) = x/r
其中θ为角度,x为邻边,r为斜边。
3. 正切函数(tangent function):正切函数表示角的正切值在数轴上的投影比。其定义如下:
tan(θ) = y/x
其中θ为角度,y为对边,x为邻边。
4. 余切函数(cotangent function):余切函数表示角的余切值在数轴上的投影比。其定义如下:
cot(θ) = x/y 其中θ为角度,y为对边,x为邻边。
5. 正割函数(secant function):正割函数表示角的正割值在数轴上的投影长度。其定义如下:
sec(θ) = r/x
其中θ为角度,x为邻边,r为斜边。
6. 余割函数(cosecant function):余割函数表示角的余割值在数轴上的投影长度。其定义如下:
csc(θ) = r/y
其中θ为角度,y为对边,r为斜边。
这些函数在不同的角度上有不同的值,可以通过查表或计算器得到具体数值。同时,它们之间存在一些基本公式和关系,如下:
1. 互余关系(co-function identities):
sin(θ) = cos(90° - θ)
cos(θ) = sin(90° - θ)
tan(θ) = cot(90° - θ)
正弦、余弦、正切

直角三角形的边角关系—正弦.余弦.正切
常识要点
1.正弦:在直角三角形中,一个锐角所对的直角边与斜边的比,叫做这个角的正弦.
即:caAA斜边的对边sin; cbBB斜边的对边sin.
2.余弦:在直角三角形中,一个锐角的邻边与斜边的比,叫做这个角的余弦.
即:cbAA斜边的邻边cos; caBB斜边的邻边cos
3.正切:在直角三角形中,一个锐角所对的直角边与邻边的比,叫做这个角的正切.
即:baAAA的邻边的对边tan; abBBB的邻边的对边tan.
4.特别角的正弦,余弦值:
0sin0;30sin21;45sin22;60sin23;90sin1;
0cos1;30cos23;45cos22;60cos21;90cos0.
0tan 0 ;30tan33;45tan 1 ;60tan3;90tan 不消失 ;
5.正.余弦.正切值随锐角大小的变更(即增减性):
正弦值随锐角的增大而增大,余弦值随锐角的增大而减小,正切值随锐角的增大而增大.
6.互余两角的正弦,余弦间的关系:
随意率性锐角的正弦值等于它的余角的余弦值,随意率性锐角的余弦值等于它的余角的正弦值.
cos90sin; sin90cos.
7.同角的正弦,余弦间的关系:
(1)平方和的关系:1cossin22AA.
(2)大小比较:当450A时,AAsincos.当9045A时,AAsincos. (3)正切.余切与正弦.余弦间的关系:cossintan
例题讲授
例1依据下列图中给出的ABCRt的数据,求Asin,Acos,Bsin,Bcos,tanA,tanB的值.
例2已知等腰梯形ABCD中,上底CD=2cm,下底AB=5cm,腰AD=3cm,试求Asin,Acos,tanA的值.
《直角三角形边角关系》知识点
《直角三角形边角关系》知识点 姓名____________
一、锐角三角函数的概念
1、如图,在△ABC中,∠C=90°
①锐角A的对边与斜边的比叫做∠A的正弦,记为sinA,即
casin斜边的对边AA
②锐角A的邻边与斜边的比叫做∠A的余弦,记为cosA,即
cbcos斜边的邻边AA
③锐角A的对边与邻边的比叫做∠A的正切,记为tanA,即batan的邻边的对边AAA
2、锐角三角函数的概念: 锐角A的正弦、余弦、正切 都叫做∠A的锐角三角函数
3、一些特殊角的三角函数值
三角函数 30° 45° 60°
sinα 21 22 23
cosα 23 22 21
tan α 33 1 3
4、各锐角三角函数之间的关系 (以下 ∠A+∠B=90°)
(1)互余关系: sinA = cosB, cosA = sinB
(2)平方关系: 1cossin22AA
(3)倒数关系 tanA•tanB=1
(4)弦切关系: tanA=AAcossin
5、锐角三角函数的增减性: 当角度在0°~90°之间变化时,
(1)正弦值随着角度的增大(或减小)而增大(或减小)
(2)余弦值随着角度的增大(或减小)而减小(或增大)
(3)正切值随着角度的增大(或减小)而增大(或减小)
∠A的对边
二、解直角三角形
1、解直角三角形的概念
在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。
2、解直角三角形的理论依据
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c
(1)三边之间的关系:222cba(勾股定理)
(2)锐角之间的关系:∠A+∠B=90°
第1章-锐角三角函数-知识梳理
-----WORD格式--可编辑--专业资料-----
--完整版学习资料分享---- 锐角三角函数
一、基础知识
1.定义:如图在△ABC中,∠C为直角,
我们把锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA;sinA= asinAc
把锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA;cosbAc
把锐角∠A的对边与邻边的比叫做∠A的正切,记作tanA 。tanaAb
把锐角∠A的邻边与对边的比叫做∠A的余切,记作cosA。cosbAa
2、三角函数值
(1)特殊角的三角函数值
角度
三角函数 0° 30° 45° 60° 90°
sinA 0 12 22
32
1
cosA 1 32 22 12 0
tanA 0 33 1 3 不存在
(2)锐角三角函数值的性质。
锐角三角函数的大小比较:
在900A时,随着A的增大,正弦值越来越大,而余弦值越来越小.
即:Asin是增函数,Acos减函数。
○1锐角三角函数值都是正数。
○2当角度在090间变化时:正弦、正切值随着角度的增大而增大;余弦、余切随着角度的增大而减小。
3、 同角、互余角的三角函数关系:
1、同角三角函数关系:1cossin22AA.sintancos;coscotsin;tancot1•
2、互余锐角的三角函数关系:)90cos(cossinABA,)90sin(sincosABA。
-----WORD格式--可编辑--专业资料-----
--完整版学习资料分享---- 解直角三角形:
由直角三角形中除直角以外的两个已知元素(其中至少有一条边),求出所有未知元素的过程,叫做解直角三角形。
直角三角形的可解条件及解直角三角形的基本类型
已知条件 解法
一条边和一个锐角 斜边c和锐角A B=90°-A,a=csinA,b=ccosA,s=c2sinAcosA
专题28 锐角三角函数(解析版)
专题28 锐角三角函数
知识点一:锐角三角函数
1.三角函数定义
在Rt△ABC中,若∠C=90°
A sinA ac的对边斜边
A cosA bc的邻边斜边
A tanA A ab的对边的邻边
A cotA A ba的邻边的对边
2.同角三角函数的关系
(1)平方关系:22sincos1AA
(2)商数关系: sintancosAAA coscotsinAAA
(3)倒数关系:
tancot1AA
3.互为余角的三角函数关系
sin(90)cosAA,
cos(90)sinAA
tan(90)cotAA,
cot(90)tanAA
或者:若∠A+∠B=90°,则
sinA=cosB,cosA=sinB,tanA=cotB,cotA=tanB
4. 特殊角的三角函数值
α sinα Cosα tanα cotα
0° 0 1 0 不存在
30° 12 32 33 3
45° 22 22 1 1
60° 32 12 3 33
5.锐角三角函数的增减性(0°--90°)
(1)锐角的正弦值(或正切值)随着角度的增大而增大,随着角度的减小而减小。
(2)锐角的余弦值(或余切值)随着角度的增大而减小,随着角度的减小而增大。
6.锐角三角函数的取值范围
0≤sinα≤1,0≤cosα≤1,tanα≥0,cotα≥0.
知识点二:解直角三角形
1.直角三角形中边角关系
在直角三角形ABC中,如果∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,那么
(1)三边之间的关系为222abc(勾股定理)
(2)锐角之间的关系为∠A+∠B=90°
(3)30°角所对直角边等于斜边的一半。 90° 1 0 不存在 0 (4)直角三角形斜边上的中线等于斜边的一半。
浙教版九年级(下)数学教学内容整理
第一章 解直角三角形
1、锐角三角函数
(1)锐角A的对边与斜边 的比叫做A的正弦,记作Asin;caAA斜边的对边sin
(2)锐角A的邻边与斜边 的比叫做A的余弦,记作Acos;cbAA斜边的邻边cos
(3)锐角A的对边与邻边 的比叫做A的正切,记作Atan;baAAA的邻边的对边tan
特殊的三角函数值
度数
三角函数 030 045 060
sin 21 22
23
cos 23 22 21
tan 33 1 3
互余两角的正弦值、余弦值和正切值之间的关系
若090BA,则BAcossin,即)90cos(sin0AA;
BAsincos,即)90sin(cos0AA; BAtan1tan
正切与正余弦之间的关系: AAAcossintan
同角的正余弦关系:1cossin22AA
2、有关三角函数的计算
用计算器求相应的三角函数的值
3、解直角三角形
概念:在直角三角形中,除了直角外的5个元素,只要知道其中的2个元素(至少要有一个是边),求其它3个元素的过程叫解直角三角形。
依据:(1)三边间的关系:勾股定理222cba
(2)锐角间的关系:090BA;
(3)边角间的关系:caAsin,cbAcos,baAtan;
cbBsin,cabcos,abbtan; (4)面积公式:chabSABC2121
直角三角形可解的条件及可直接解的直角三角形的解
(1) 已知两边或已知一边及一锐角,则此三角形可解,即在已知的两个条件中,至少有一个是边。
(2) 可直接解求解的直角三角形分为以下四种情况:
① 已知两条直角边a,b其解法为
22bac,由baAtan得A,AB090.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
互余角的正切值关系
互余角是三角函数中的一个重要概念,它具有解决三角形问题的作用。
上面介绍了互余角的定义,下面将主要介绍它的正切值关系。
一、正切值关系定义
正切值关系就是,当中心角A与角A的互余角B满足正切值关系:tgA=1/tgB时,A与B就是正切值关系。
二、互余角的正切值
1、互余角的正切值是一个倒数概念:
互余角是指两个角之间的夹角是相等的,即A+B=180°,因此,正切值关系应当满足tgA=1/tgB,表示它们之间的倒数关系。
2、在当中心角A和B满足正切值关系时可以求出两角的大小:
若互余角A和B满足正切值关系:tgA=1/tgB,则可以由tgA和tgB算出角A、B的大小,如:若A+B=180°,则tgA=1/tgB,2tgA=tgA+tgB=180°,tgA=90°,此时A=90°,B=90°
三、正切值的应用
通过正切值关系在图形分析中可以有效解决三角函数中的问题。
1、可以通过正切值关系求出三角形的剩余边长:
在满足正切值关系的情况下,可以通过已知角A和边a的正切值关系来求取三角形的剩余两边长,如已知角A和角B及它们的正切值,可以求出其余三角形的边长。
2、可以通过正切值关系求出两个相邻角所变换出的角:
在两个相邻角之间存在正切值关系时,只要满足A+B=360°的条件,可以求出两个相邻角所变换出的角,即:A/B=tgA/tgB=tg(A+B)。
四、总结 由上文可知,互余角的正切值关系是一个重要概念,它可以帮助我们在解决三角形问题中及时准确地使用正切值来求出三角形的剩余边长或求出变换出的角,并能有效地帮助我们解决图形的问题。
