人教版九年级数学上册单课件-直接开平方法解次方程.ppt
合集下载
人教版数学九年级上册解一元二次方程—直接开平方法课件

(x+2)2=64
2(x-5)2=72
x+2=±8
(x-5)2=36
x1=-2 +8 或 x2=-2-8
x-1=±6
x1= x2=-10 x1=11 或 x2=-1
直接开平方法 解一元二次方程
步骤
平方根的意义
通过“降次”将一元二次 方程转化为一元一次方程
①将方程转化为x2=p(p≥0)或(x+m)2=p(p≥0)的情势 ②方程两边同时开平方,得到两个一元一次方程
根据平方根意义求下列方程的解:
(1)x2=25;
解:∵(±5)2 =25 ∴x= ±5
即:x1=5,x2=-5
(2)x2= 4 ;
9
解:
2 2
4
3 9
x 2 3
即:x1
2 3
,
x2
2 3
市区有一块边长为15米的正方形绿地,经城市 计划,需扩大绿化面积,估计计划后的正方形绿 地面积将到达400平方米,请问这块绿地的边长 增加了多少米?
开方得x 1 2
x1 1 2, x2 1- 2
(4)、x2 4x 4 25
解:原方程整理得 (x 2)2 25
开方得x 2 5
x1 7, x2 3
(5).(x+2)2-64=0 (6).2(x-5)2-12=0
解1:(x+2)2-64=0
解2: 2(x-5)2-72=0
(15+x)2=400 转化
一元二次方程
降次
15+x=20 15+x=-20 一元一次方程
化繁为简
例1:利用直接开平方法解下列方程
(1)、x2 100
(2)、x2 25 0
一元二次方程的解法(一)直接开平方法(课件)数学九年级上册(人教版)

即 x-5=1或x-5=-1
∴x1=6,x2=4.
(4)8x2-8x+2=-6
解: 4x2-4x+1=-3,
(2x-1)2=-3,
∵ (2x-1)2≥0,
∴ (2x-1)2≠-3,
∴此方程无实数根.
15.已知关于x的方程(x+1)2=k2+3的一个根是x=2,求k的值及另
一个根.
解:把x=2代入原方程得k2+3=9,
1.会把一元二次方程降次转化为两个一元一次方程.(难点)
2.运用开平方法解形如x2=p或(x+n)2=p (p≥0)的方程.(重点)
1.什么是平方根?一个数的平方根怎样表示?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
a(a≥0)的平方根记作:± .
x2=a(a≥0),则根据平方根的定义知,x=± .
C.当n≥0时,有两个解=± −
D.当n≤0时,无实数解
B
)
2=1则x=_________.
±8
-1或-3
7.若x2=64,则x=______;若(x+2)
m≥1
8.若关于x的方程2(x-1)2=m-1有实数根,则m的取值范围是_______.
2−4
9.当x=_____时,分式
值为零.
−2
∴k2=6.解得k=± 6.
把k2=6代入原方程,得(x+1)2=9,可解得方程的另一个根为x=—4.
A.10cm
B)
B.5cm
C.±10cm
5.下列方程可以用直接开方法求解的有(
①(x-1)2-1=O
A.①和②
②x2-2=0
B.①和③
D.±5cm
∴x1=6,x2=4.
(4)8x2-8x+2=-6
解: 4x2-4x+1=-3,
(2x-1)2=-3,
∵ (2x-1)2≥0,
∴ (2x-1)2≠-3,
∴此方程无实数根.
15.已知关于x的方程(x+1)2=k2+3的一个根是x=2,求k的值及另
一个根.
解:把x=2代入原方程得k2+3=9,
1.会把一元二次方程降次转化为两个一元一次方程.(难点)
2.运用开平方法解形如x2=p或(x+n)2=p (p≥0)的方程.(重点)
1.什么是平方根?一个数的平方根怎样表示?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
a(a≥0)的平方根记作:± .
x2=a(a≥0),则根据平方根的定义知,x=± .
C.当n≥0时,有两个解=± −
D.当n≤0时,无实数解
B
)
2=1则x=_________.
±8
-1或-3
7.若x2=64,则x=______;若(x+2)
m≥1
8.若关于x的方程2(x-1)2=m-1有实数根,则m的取值范围是_______.
2−4
9.当x=_____时,分式
值为零.
−2
∴k2=6.解得k=± 6.
把k2=6代入原方程,得(x+1)2=9,可解得方程的另一个根为x=—4.
A.10cm
B)
B.5cm
C.±10cm
5.下列方程可以用直接开方法求解的有(
①(x-1)2-1=O
A.①和②
②x2-2=0
B.①和③
D.±5cm
新人教版九年级数学上册全册ppt课件

10x - 4.9x2. 你能根据上述规律求出物体经过多少秒落回地面吗 (精确到 0.01 s)?
1.探究因式分解法
你认为该如何解决这个问题?你想用哪种方法解这 个方程?
10x - 4.9x2 = 0
配方法 降 公式法 次
?
x
1
=
0,x
2
=
100 49
1.探究因式分解法
问题3 观察方程 10x - 4.9x2 = 0,它有什么特点? 你能根据它的特点找到更简便的方法吗?
x2 + 6x = -4 x2 + 6x + 9 = -4 + 9 (x + 3)2 = 5
x3 5
移项
两边加 9,左边 配成完全平方式 左边写成完全 平方形式
降次
x 3 5 ,或 x 3 5
解一次方程
x1 3 5, x2 3 5
2.推导求根公式
想一想:以上解法中,为什么在方程③两边加 9? 加其他数可以吗?如果不可以,说明理由.
• 学习重点: 一元二次方程的概念.
1.创设情境,导入新知
思考以下问题如何解决: 1.要设计一座高 2 m 的人体雕像,使它的上部 (腰以上)与下部(腰以下)的高度比,等于下部与全 部(全身)的高度比,求雕像的下部应设计为高多少米?
1.创设情境,导入新知
思考以下问题如何解决: 2.有一块矩形铁皮,长 100 cm,宽 50 cm,在它 的四角各切去一个同样的正方形,然后将四周突出部分 折起,就能制作一个无盖方盒,如果要制作的无盖方盒 的底面积为 3 600 cm2,那么铁皮各角应切去多大的正方 形?
1.复习配方法,引入公式法
问题2 能否用公式法解决一元二次方程的求根问 题呢?
1.探究因式分解法
你认为该如何解决这个问题?你想用哪种方法解这 个方程?
10x - 4.9x2 = 0
配方法 降 公式法 次
?
x
1
=
0,x
2
=
100 49
1.探究因式分解法
问题3 观察方程 10x - 4.9x2 = 0,它有什么特点? 你能根据它的特点找到更简便的方法吗?
x2 + 6x = -4 x2 + 6x + 9 = -4 + 9 (x + 3)2 = 5
x3 5
移项
两边加 9,左边 配成完全平方式 左边写成完全 平方形式
降次
x 3 5 ,或 x 3 5
解一次方程
x1 3 5, x2 3 5
2.推导求根公式
想一想:以上解法中,为什么在方程③两边加 9? 加其他数可以吗?如果不可以,说明理由.
• 学习重点: 一元二次方程的概念.
1.创设情境,导入新知
思考以下问题如何解决: 1.要设计一座高 2 m 的人体雕像,使它的上部 (腰以上)与下部(腰以下)的高度比,等于下部与全 部(全身)的高度比,求雕像的下部应设计为高多少米?
1.创设情境,导入新知
思考以下问题如何解决: 2.有一块矩形铁皮,长 100 cm,宽 50 cm,在它 的四角各切去一个同样的正方形,然后将四周突出部分 折起,就能制作一个无盖方盒,如果要制作的无盖方盒 的底面积为 3 600 cm2,那么铁皮各角应切去多大的正方 形?
1.复习配方法,引入公式法
问题2 能否用公式法解决一元二次方程的求根问 题呢?
专题(二) 一元二次方程的解法课件(人教版)

解:x1=3+ 10,x2=3- 10
7. 2x-2=2x2. 解:原方程无实数根
四、用因式分解法解方程
此解法合适于右边为0,左边能进行因式分解的一元二次方程 8.(x-1)2-2(x-1)=0.
解:x1=3,x2=1 9.(x+2)2-10(x+2)+25=0.
解:x1=x2=3
五、用适当的方法解方程 解一元二次方程时,先视察方程的特征,然后选择适当的方法求 解 10.2(x-3)2=x2-9.
九年级上册人教版数学 专题(二) 一元二次方程的解法
一、用直接开平方法解方程 一元二次方程若能化成 x2=p 或(mx+n)2=p(p≥0)的形式,适 合用此方法求解 1.(4x-1)2=225.
解:x1=4,x2=-72 .13(x-2)2=8.
解:x1=2+2 6,x2=2-2 6
3.(2x+1)2=(x-1)2. 解:x1=-2,x2=0
二、用配方法解方程 此解法适合所有的一元二次方程,配方的关键是方程二次项系 数化为 1 后,方程两边同时加上一次项系数一半的平方 4.2t2-3t=-1.
解:t1=1,t2=12
5.(2x-1)2=x(3x+2)-7. 解:x1=4,x2=2
三、用公式法解方程 此解法适合所有的一元二次方程,关键是找准 a,b,c 的值及 熟记求根公式 6.x2=6x+1.
解:x1=3,x2=9
11.(2x+1)(4x-2)=(2x-1)2+2.
解:x1=-1+2 6,x2=-1-2 6
12.(x+1)(x-1)+2(x+3)=8. 解:x1=1,x2=-3
7. 2x-2=2x2. 解:原方程无实数根
四、用因式分解法解方程
此解法合适于右边为0,左边能进行因式分解的一元二次方程 8.(x-1)2-2(x-1)=0.
解:x1=3,x2=1 9.(x+2)2-10(x+2)+25=0.
解:x1=x2=3
五、用适当的方法解方程 解一元二次方程时,先视察方程的特征,然后选择适当的方法求 解 10.2(x-3)2=x2-9.
九年级上册人教版数学 专题(二) 一元二次方程的解法
一、用直接开平方法解方程 一元二次方程若能化成 x2=p 或(mx+n)2=p(p≥0)的形式,适 合用此方法求解 1.(4x-1)2=225.
解:x1=4,x2=-72 .13(x-2)2=8.
解:x1=2+2 6,x2=2-2 6
3.(2x+1)2=(x-1)2. 解:x1=-2,x2=0
二、用配方法解方程 此解法适合所有的一元二次方程,配方的关键是方程二次项系 数化为 1 后,方程两边同时加上一次项系数一半的平方 4.2t2-3t=-1.
解:t1=1,t2=12
5.(2x-1)2=x(3x+2)-7. 解:x1=4,x2=2
三、用公式法解方程 此解法适合所有的一元二次方程,关键是找准 a,b,c 的值及 熟记求根公式 6.x2=6x+1.
解:x1=3,x2=9
11.(2x+1)(4x-2)=(2x-1)2+2.
解:x1=-1+2 6,x2=-1-2 6
12.(x+1)(x-1)+2(x+3)=8. 解:x1=1,x2=-3
人教版九年级数学上用直接开平方法解一元二次方程
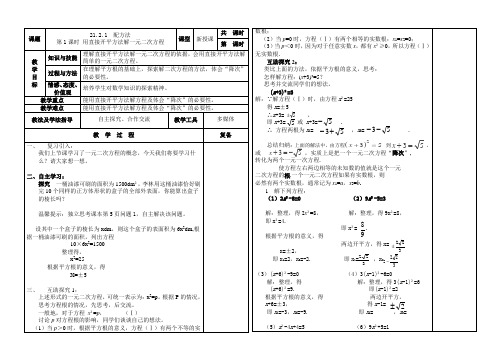
一般地,对于方程x²=p,(Ⅰ)
讨论p对方程根的影响,同学们谈谈自己的想法。
(1)当p>0时,根据平方根的意义,方程(Ⅰ)有两个不等的实数根;
(2)当p=0时,方程(Ⅰ)有两个相等的实数根:x1=x2=0;
(3)当p<0时,因为对于任意实数x,都有x²≥0,所以方程(Ⅰ)无实数根.
互助探究2:
类比上面的方法,依据平方根的意义,思考:
课题
21.2.1配方法
第1课时用直接开平方法解一元二次方程
课型
新授课
共课时
第课时
教
学
目
标
知识与技能
理解直接开平方法解一元二次方程的依据,会用直接开平方法解简单的一元二次方程。
过程与方法
在理解平方根的基础上,探索解二次方程的方法,体会“降次”的必要性。
情感、态度、价值观
培养学生对数学知识的探索精神。
教学重点
4.如果实数a,b满足+b2-12b+36=0,那么ab的值是.
5.解下列方程:
(1)x2=16(2)x2-0.81=0
(3)9x2=4(4)y2-144=0
6.解下列方程:
(1)(x-1)2=4 (2)(x+2)2=3
(3)(x-4)2-25=0
(4)(2x+3)2-5=0
(5)(2x-1)2=(3-x)2
(3)(x+6)²-9=0(4)3(x-1)²-6=0
解:整理,得解:整理,得3(x-1)²=6
(x+6)²=9.即(x-1)²=2
根据平方根的意义,得两边开平方,
x+6=±3,得x-1=
即x1=-3,x2=-9.即x1=,x2=
(5)x²-4x+4=5(6)9x²+5=1
讨论p对方程根的影响,同学们谈谈自己的想法。
(1)当p>0时,根据平方根的意义,方程(Ⅰ)有两个不等的实数根;
(2)当p=0时,方程(Ⅰ)有两个相等的实数根:x1=x2=0;
(3)当p<0时,因为对于任意实数x,都有x²≥0,所以方程(Ⅰ)无实数根.
互助探究2:
类比上面的方法,依据平方根的意义,思考:
课题
21.2.1配方法
第1课时用直接开平方法解一元二次方程
课型
新授课
共课时
第课时
教
学
目
标
知识与技能
理解直接开平方法解一元二次方程的依据,会用直接开平方法解简单的一元二次方程。
过程与方法
在理解平方根的基础上,探索解二次方程的方法,体会“降次”的必要性。
情感、态度、价值观
培养学生对数学知识的探索精神。
教学重点
4.如果实数a,b满足+b2-12b+36=0,那么ab的值是.
5.解下列方程:
(1)x2=16(2)x2-0.81=0
(3)9x2=4(4)y2-144=0
6.解下列方程:
(1)(x-1)2=4 (2)(x+2)2=3
(3)(x-4)2-25=0
(4)(2x+3)2-5=0
(5)(2x-1)2=(3-x)2
(3)(x+6)²-9=0(4)3(x-1)²-6=0
解:整理,得解:整理,得3(x-1)²=6
(x+6)²=9.即(x-1)²=2
根据平方根的意义,得两边开平方,
x+6=±3,得x-1=
即x1=-3,x2=-9.即x1=,x2=
(5)x²-4x+4=5(6)9x²+5=1
九年级数学上册第二十一章一元二次方程21.2解一元二次方程21.2.1配方法(第一课时直接开平方法)课件人教版

∴ x3 5 或 x3- 5 .
∴ x1= 5-3 ,x2 = - 5-3 .
解一元二次方程的基本思路是:
把一个一元二次方程“ 降次 ”,转化 为两个一元一次方程.
由应用直接开平方法解形如:
x2=p(p≥0),那么x=± p
由应用直接开平方法解形如:
(mx+n)2=p(p≥0),则mx+n=____p_ .
问题:一桶油漆可刷的面积为1500 dm2 , 李林用这桶油漆恰好刷完10个同样的正方体 形状的盒子的全部外表面,你能算出盒子的 棱长吗?
提示
可以根据正方体表面积 S=6a2求解. 同时要注意 所得的结果要符合实际
意义.
解:设正方体的棱长为x dm,则一个正方 体的表面积为__6_x_2_dm2 .根据一桶油漆可 刷面积列出方程 1_0_×_6_x_2_=_1_5_0_0____.
解下列方程:
(1)9x2 5 3;
解:移项,得 9x2 8.
系数化为1,得 x2 8 .
9
直接开平方,得
x
8. 9
x1
22 3
,x2
22 3
.
注意:二次根 式必须化为最 简二次根式。
(2)9x2 5 1.
解:先移项,得 9x2 4. 系数化为1,得 x2 4 0 9
1
x1
, 3
x2
1.
整理,得_x_2_=_2_5 , 根据平方根的意义得x=___±_5__. 即x1=___5___,x2=__-_5___. 因为_棱__长__不_能__为__负__值__,所以正方体的棱长 是_5_d_m__.
21.2 一元二次方程的解法——直接开平方法课件 2024-2025学年人教版数学九年级上册

2
(2) x -18=0.
2
解: x -18=0
2
x =18
x2=36
∴x1=6,x2=-6
10.解方程:
(1)(2-x)2=8;
解:(2-x)2=8
2-x=±2
∴x1=2-2 ,x2=2+2
(2)3(x-1)2-6=0.
解:3(x-1)2-6=0
3(x-1)2=6
(x-1)2=2
小结:通过移项、系数化为1,化为x2=p(p≥0)的形式求
解.
6.解方程:
(1)(x-2)2=4;
(2)(x+6)2-9=0.
解:(x-2)2=4
解:(x+6)2-9=0
x-2=±2
(x+6)2=9
∴x1=4,x2=0
x+6=±3
∴x1=-3,x2=-9.
小结:将方程化为(x+n)2=p(p≥0)的形式,直接开平方.
7.解方程:
(1)(2x-3)2-9=0;
(2)(2x-1)2=(x-3)2.
解:(2x-3)2-9=0
解:(2x-1)2=(x-3)2
2x-1=±(x-3)
∴x1=-2,x2= .
(2x-3)2=9
2x-3=±3
∴x1=3,x2=0.
小结:(1)中化为(mx+n) 2=p(p≥0)的形式;(2)中
(3)(x-1)2-25=0.
解: (x-1)2-25=0
(x-1)2=25
x-1=±5
∴x1=-4, x2 =6
(2)(x-2)2=3;
解:(x-2)2=3
x-2=±
∴x1=2+ ,x2=2-
人教版初三数学上册一元二次方程的解法1(直接开方法).2 一元二次方程的解法1(直接开方)(定稿) (1)

一元二次方程的解法( --直接开平方法
复习回顾:
什么是一元二次方程?一元二次方程的一般形式?
等式两边都是整式,只含有一个未知数(一元), 并且未知数的最高次数是2(二次)的方程,叫做一 元二次方程.
一般形式:ax2+bx+c=0(a≠0).
复习旧知
2、你学过的整式方程有哪些?它们是如 何求解去?分母➔去括号➔移项、合并同类项➔
的形式,那么等式两边直接开平方可得
xp或 m xnp.
3 x24x45
解: x 22 5,
x2 5,
x2 5,x25,
方程的两 x1 2 5
根为
x2 2 5.
解下列方程: 1、2x2-8=0; 2、(x+6)2-9=0 3、9x2+6x+1=4 4、x2-4x=-4
独立 作业
教材:P42 习题22.2 1; 订正走进名校P31-32 (中午)
《节节高》p22-23页 (晚上)
或:依一题个意正得方1体0×的6表x2面=1积50=0刷漆①的面积
x2=25
即 x1=5,x2=-5
棱长不能是负值,所以正方体的 棱长为5dm。
如果方程能化成 x2p(p0)
的形式,那么等式两边直接开平方可得
xp或mxnp.
解下列方程:
(1)9x2 53
解:移项 9x2 8,
方程 未知数的系数化为1➔得解
一元一次方程 二元一次方程组
一元二次方程
消元 降次
类比 猜想
问题1一桶某种油漆可刷的面积为1500dm2,李明 用这桶油漆恰好刷完10个同样的正方体形状的盒 子的全部外表面,你能算出盒子的棱长吗?
一解桶:漆设可正刷方的体面的积棱=长刷为的x正d方m,体则(一表个面正积方)的体总的表 面数积为6x2dm2,
复习回顾:
什么是一元二次方程?一元二次方程的一般形式?
等式两边都是整式,只含有一个未知数(一元), 并且未知数的最高次数是2(二次)的方程,叫做一 元二次方程.
一般形式:ax2+bx+c=0(a≠0).
复习旧知
2、你学过的整式方程有哪些?它们是如 何求解去?分母➔去括号➔移项、合并同类项➔
的形式,那么等式两边直接开平方可得
xp或 m xnp.
3 x24x45
解: x 22 5,
x2 5,
x2 5,x25,
方程的两 x1 2 5
根为
x2 2 5.
解下列方程: 1、2x2-8=0; 2、(x+6)2-9=0 3、9x2+6x+1=4 4、x2-4x=-4
独立 作业
教材:P42 习题22.2 1; 订正走进名校P31-32 (中午)
《节节高》p22-23页 (晚上)
或:依一题个意正得方1体0×的6表x2面=1积50=0刷漆①的面积
x2=25
即 x1=5,x2=-5
棱长不能是负值,所以正方体的 棱长为5dm。
如果方程能化成 x2p(p0)
的形式,那么等式两边直接开平方可得
xp或mxnp.
解下列方程:
(1)9x2 53
解:移项 9x2 8,
方程 未知数的系数化为1➔得解
一元一次方程 二元一次方程组
一元二次方程
消元 降次
类比 猜想
问题1一桶某种油漆可刷的面积为1500dm2,李明 用这桶油漆恰好刷完10个同样的正方体形状的盒 子的全部外表面,你能算出盒子的棱长吗?
一解桶:漆设可正刷方的体面的积棱=长刷为的x正d方m,体则(一表个面正积方)的体总的表 面数积为6x2dm2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
难点: 探究( x-m)2=a的解的情况,具有分类 讨论的意识.
知识回顾
问题1.什么叫做平方根?用式子如何表示?
如果一个数的平方等于a,那么这个数就叫 做a的平方根。
若x2=a,则x叫做a的平方根。记作x= a
即x= a 或x= a
问题如2:.9平的方平根方根有是哪_些_±__性_3_质2?54 的平方根是____52__
方程: x2 pp0或
mxn2 pp0;
思想方法
1. 降次的实质:将一个二次方程转化为两个 一次方程;
降次的方法:直接开平方法; 降次体现了:转化思想; 2. 用直接开平方法解一元二次方程的一般步 骤:先要将方程化为左边是含有未知数的完全平方 式,右边是非负数的形式,再利用平方根的定义求 解.
检测与评价
x1= a +m, x2=- a +m.
4.完成课前的实际问题 课本第5页
5、真刀实枪,实战演练:
1x2 90;
2t2 450
316x2 490; 42x32 5;
5x52 360; 66x12 25;
●总结梳理 整合提高
1.直接开平方法的依据是什么?
(平方根)
2.用直接开平方法可解下列类型的一元二次
方程 x3220
将方程化成
(mx n) p 2
例2、 解方程
x3220
解: x32 2
x3 2
(p≥0)的形 式,再求解
即: x3 2,或x3 2;
x13 2,x2 3 2;
•练习:解方程: (1)2(x 1)2 6 0 (2)(3x 1 )2 0 2
•用直接开平方法还可以解形如_(m_x___n)_2__p_(_p___0)_方
认为他解的对吗?如果有错,指出具体位置并帮他改正。
( 1 y+1)2-5=0
解:
3 (
1
y+1)2=5
13 y+1=
5
31 3 y= 5 -1
(×)
y=3 5 -1 ( × )
3、实力比拼
探究( x-m)2=a的解的情况。
( x-m)2=a 当a<0时,此一元二次方程无解.
当a≥0时, x-m=± a
C层 解下列方程: 1.(4x- 5 )(4x+ 5 )=3 2.(ax+b) 2=b 3. x2-2 x-7=0 4. (2x-1)2 =x2
什么叫直接开平方法?
像解x2=4,x2-2=0这样,利用平方根的 定义用直接开平方解一元二次方程的方法
叫做直接开平方法。
•能利用直接开平方法解的一元二次方程应
满足的形式为__x_2 __p_(_p___0)___ •例:解方程:(1)x2 16 0 (2)x2 3 0
•一元二次方程如果有解,则解的个数一定为
(1)一个正数有两个平方根,这两个平方根是互为相反
问题4.根据平方根的意义你能解下列方程吗?
如何解方程(1)x2=4,(2)x2-2=0呢?
解(1)∵x是4的平方根 ∴x=±2
即此一元二次方程的解(或根)为: x1=2,x2 =-2
(2)移向,得x2=2 ∵ x就是2的平方根
∴x= 2Leabharlann 概括总结程•从 (mx n)2 p 变形mx n p
转化
归纳:直接开平方法
如 果 方 程 能 化 成 x2p或 (m xn)2p(p0) 的 形 式 , 那 么 可 得 xp或 m xnp.
用直接开平方法来解的方程有什么 特征?
小结 直接开平方法适用于A2p p0 形式的一元二次方 程的求解。这里的A既可以是字母,单项式,也可 以是含有未知数的多项式。换言之:只要经过变 形可以转化为 A2p p0 形式的一元二次方程 都可以用直接开平方法求解。
初中数学九年级上册
解一元二次方程
——直接开平方法
分享
▪ 人生重要的不是所站的位置,而是所 朝的方向。
●学习目标
▪ 1.理解解一元二次方程降次的转化思想;
▪ 2.会利用直接开平方法解形如x2=p或(mx +n)2=p(p≥0)的一元二次方程;
重点: 能够熟练而准确的运用直接开平方法 求一元二次方程的解.
A层
1用求平方根的方法解一元二次方程的方法叫 __________.
2. 如果x2=121,那么x1=__________,x2=___________. 3. 如果3x2=18那么x1=__________,x2=___________. 4. 如果25x2-16=0那么x1=__________,x2=___________. 5. 如果x2=a(a≥0)那么 x1=__________,x2=___________. B层
1.小试身手 :
判断下列一元二次方程能否用直接开平方法 求解并 说明理由.
1) x2=2
(√ )
2) p2 - 49=0
( √)
3) 6 x2=3 4) (5x+9)2+16=0 5) 121-(y+3) 2 =0
(√ ) (× ) ( √)
2、明察秋毫。
下面是李昆同学解答的一道一元二次方程的具体过程,你
_2_个__ •方程 x2 0 解为 x1 x2 0 •方程 x2 3 无解
用直接开平方法解下列方程:
(1) y2 121 0 ;
y 11
(2) x2 2 0
x 2
(3) 16x2250
x5 4
将方程化成
x2 p
(p≥0)的形 式,再求解
思考:类比上面解方程的过程,你认为应怎样解
知识回顾
问题1.什么叫做平方根?用式子如何表示?
如果一个数的平方等于a,那么这个数就叫 做a的平方根。
若x2=a,则x叫做a的平方根。记作x= a
即x= a 或x= a
问题如2:.9平的方平根方根有是哪_些_±__性_3_质2?54 的平方根是____52__
方程: x2 pp0或
mxn2 pp0;
思想方法
1. 降次的实质:将一个二次方程转化为两个 一次方程;
降次的方法:直接开平方法; 降次体现了:转化思想; 2. 用直接开平方法解一元二次方程的一般步 骤:先要将方程化为左边是含有未知数的完全平方 式,右边是非负数的形式,再利用平方根的定义求 解.
检测与评价
x1= a +m, x2=- a +m.
4.完成课前的实际问题 课本第5页
5、真刀实枪,实战演练:
1x2 90;
2t2 450
316x2 490; 42x32 5;
5x52 360; 66x12 25;
●总结梳理 整合提高
1.直接开平方法的依据是什么?
(平方根)
2.用直接开平方法可解下列类型的一元二次
方程 x3220
将方程化成
(mx n) p 2
例2、 解方程
x3220
解: x32 2
x3 2
(p≥0)的形 式,再求解
即: x3 2,或x3 2;
x13 2,x2 3 2;
•练习:解方程: (1)2(x 1)2 6 0 (2)(3x 1 )2 0 2
•用直接开平方法还可以解形如_(m_x___n)_2__p_(_p___0)_方
认为他解的对吗?如果有错,指出具体位置并帮他改正。
( 1 y+1)2-5=0
解:
3 (
1
y+1)2=5
13 y+1=
5
31 3 y= 5 -1
(×)
y=3 5 -1 ( × )
3、实力比拼
探究( x-m)2=a的解的情况。
( x-m)2=a 当a<0时,此一元二次方程无解.
当a≥0时, x-m=± a
C层 解下列方程: 1.(4x- 5 )(4x+ 5 )=3 2.(ax+b) 2=b 3. x2-2 x-7=0 4. (2x-1)2 =x2
什么叫直接开平方法?
像解x2=4,x2-2=0这样,利用平方根的 定义用直接开平方解一元二次方程的方法
叫做直接开平方法。
•能利用直接开平方法解的一元二次方程应
满足的形式为__x_2 __p_(_p___0)___ •例:解方程:(1)x2 16 0 (2)x2 3 0
•一元二次方程如果有解,则解的个数一定为
(1)一个正数有两个平方根,这两个平方根是互为相反
问题4.根据平方根的意义你能解下列方程吗?
如何解方程(1)x2=4,(2)x2-2=0呢?
解(1)∵x是4的平方根 ∴x=±2
即此一元二次方程的解(或根)为: x1=2,x2 =-2
(2)移向,得x2=2 ∵ x就是2的平方根
∴x= 2Leabharlann 概括总结程•从 (mx n)2 p 变形mx n p
转化
归纳:直接开平方法
如 果 方 程 能 化 成 x2p或 (m xn)2p(p0) 的 形 式 , 那 么 可 得 xp或 m xnp.
用直接开平方法来解的方程有什么 特征?
小结 直接开平方法适用于A2p p0 形式的一元二次方 程的求解。这里的A既可以是字母,单项式,也可 以是含有未知数的多项式。换言之:只要经过变 形可以转化为 A2p p0 形式的一元二次方程 都可以用直接开平方法求解。
初中数学九年级上册
解一元二次方程
——直接开平方法
分享
▪ 人生重要的不是所站的位置,而是所 朝的方向。
●学习目标
▪ 1.理解解一元二次方程降次的转化思想;
▪ 2.会利用直接开平方法解形如x2=p或(mx +n)2=p(p≥0)的一元二次方程;
重点: 能够熟练而准确的运用直接开平方法 求一元二次方程的解.
A层
1用求平方根的方法解一元二次方程的方法叫 __________.
2. 如果x2=121,那么x1=__________,x2=___________. 3. 如果3x2=18那么x1=__________,x2=___________. 4. 如果25x2-16=0那么x1=__________,x2=___________. 5. 如果x2=a(a≥0)那么 x1=__________,x2=___________. B层
1.小试身手 :
判断下列一元二次方程能否用直接开平方法 求解并 说明理由.
1) x2=2
(√ )
2) p2 - 49=0
( √)
3) 6 x2=3 4) (5x+9)2+16=0 5) 121-(y+3) 2 =0
(√ ) (× ) ( √)
2、明察秋毫。
下面是李昆同学解答的一道一元二次方程的具体过程,你
_2_个__ •方程 x2 0 解为 x1 x2 0 •方程 x2 3 无解
用直接开平方法解下列方程:
(1) y2 121 0 ;
y 11
(2) x2 2 0
x 2
(3) 16x2250
x5 4
将方程化成
x2 p
(p≥0)的形 式,再求解
思考:类比上面解方程的过程,你认为应怎样解
