投入产出分析论文
投入产出分析论文

投入产出分析课程论文投入产出模型应用与分析投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统内各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一张棋盘式平衡表。
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1 =B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976(3)价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081(3)价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A :直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T —总产出的列向量;Y=(y 1 y 2.......y N )T —最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
中国投入产出表中投入系数变化的分析(学术论文)

中国投入产出表中投入系数变化的分析段志刚1,李善同2,王其文1(1.北京大学 光华管理学院,北京 100086;2.国务院发展研究中心,北京 100010)摘 要:比较分析中国从1992-2000年投入产出表的时序数据,概括了部门间中间投入系数的变化趋势。
分析表明:随着经济水平的提高,中国经济系统和大多数部门的中间投入率均有所提高,但部门间的投入系数变化却差异较大。
总体而言,大多数部门偏向于对基础能源部门的使用,而减少了对消费品制造业、采掘业和服务业的使用份额;且绝大多数部门均增加了对自身部门的使用比重。
投入系数的变化反映了这些年来中国经济部门技术水平和经济结构方面的系统性变化特征。
关键词:消耗系数变化;投入产出表中图分类号:F224 文献标识码:A 文章编号:1002-9753(2006)08-0058-07Study on I nput Coeff i c i en t Change i n Ch i n ese I nput-O utput TableDUAN Zhi-gang1,L I Shan-t ong2,WANG Q i-wen1(1.Guanghua School of M anage m ent,Peking U niversity,B eijing100086,China;2.D evelop m ent Research Center of S tate Council of P.R.China,B eijing100010,China)Abstract:The general trends of the direct input coefficient change are su mmarized by the comparis on of Chinese series input-out put tables fr om1992t o2000.The studies show that both the whole input rati on in the t otal out put and inter2 mediate consu mp ti on in the t otal consu mp ti on are rising with the elevati on of Chinese econom ic level.Generally s peak2 ing,most of the industries tend t o use more utilities-intensive p r oducts while reduce the inputs shares of consu mp ti on manufacturing,m ining p r oduct and service.Besides,self-e mp l oy ment rati os within most of the industries increase. The coefficient changes indicate the syste matic characters of Chinese industries’technol ogy i m p r ove ment and the econom2 ic structural syste m trans m issi on.Key words:input coefficient change;input-out put table 一、引言经济部门之间相互直接或间接的投入与使用,是部门之间经济联系变得错综复杂的一个重要原因。
农业发展趋势的投入产出分析

农业发展趋势的投入产出分析随着经济的快速发展和人民生活水平的提高,农业发展成为一个备受关注的领域。
投入产出分析是评估农业发展趋势的一种有效方法。
本文将从不同的角度分析农业发展趋势的投入产出,并探讨其可能带来的影响。
一、农业发展的背景农业作为国民经济的基础,是保障人民饮食安全的关键。
在农业现代化的推动下,农业结构不断优化,农业产出也持续增长。
同时,农民收入也得到了较大幅度的提升。
二、农业发展的投入农业发展需要充足的投入,包括土地、人力、资金和技术等。
在土地方面,不仅需要保障耕地质量,还需要合理规划土地利用,提高土地利用效率。
在人力方面,培养专业技术人员和农村劳动力,提高农业从业人员素质。
资金投入是农业发展的重要保障,政府需要加大资金支持力度,鼓励农业科技创新。
技术投入也是农业发展的关键,农业科技的进步将有效提高农业产量。
三、农业的产出农业发展的投入应当能够实现相应的产出。
随着科技的进步、管理的改善以及农业生产方式的创新,农业产出逐年增加。
农产品的种植和养殖方式不断改进,生产效益不断提高。
此外,农产品的质量和品种也得到了大幅度提升,满足了人们对安全和高品质食品的需求。
四、农业对经济的影响农业不仅与农村经济密切相关,还对整个国民经济有重要影响。
农业发展的投入将带动农村经济的发展,提高农民收入水平,拉动内需。
同时,农业产出的增加也为其他行业提供了原料和市场,促进了产业链的完善和拓展。
五、农业对环境的影响农业发展虽然带来了经济效益,但也对环境带来了一定的压力。
农业投入过多可能导致土地水肥资源的过度利用,扰乱生态平衡。
农业生产的化肥和农药使用也可能对土壤和水源造成污染。
因此,在农业发展中要注重生态环境保护,推广可持续农业生产方式。
六、农业发展的现状与问题当前,农业发展面临着一些问题。
一方面,农民收入增长缓慢,农民创业热情不高。
另一方面,农产品价格波动较大,农民收益不稳定。
此外,农业现代化水平不够高,技术创新和科研投入相对不足。
投入产出分析论文 投入产出模型应用与分析
投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统内各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一张棋盘式平衡表。
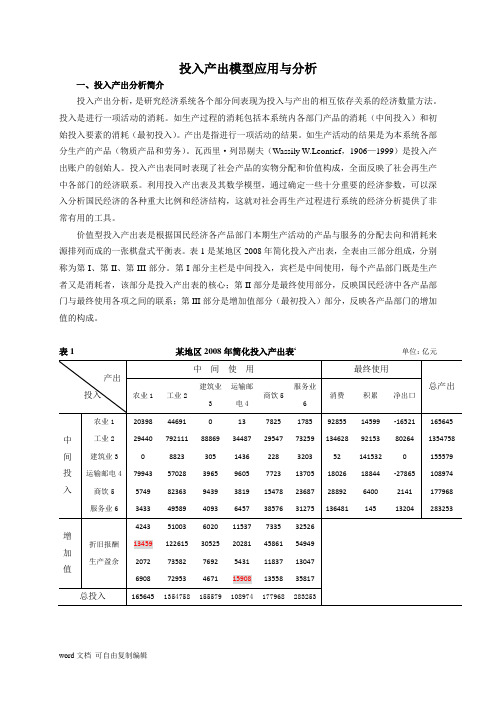
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1 =B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976(3)价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081(3)价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A :直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T —总产出的列向量;Y=(y 1 y 2.......y N )T —最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
农户农业投入产出的分析

农户农业投入产出的分析【摘要】本文主要围绕农户农业投入与产出进行分析,通过对农户投入和产出的详细比较分析,探讨影响因素并进行效益评价。
研究发现,农户的投入主要包括劳动力、资金、物资等,而产出则受到市场需求、气候等多方面因素影响。
在投入产出比较分析中,也揭示了农户经营的现状和问题。
通过对农户农业投入产出效益的评价,提出建议与展望,并总结结论,为农户经营提供参考和指导。
本研究对于了解农户经营情况、提高农业效益具有一定的理论和实践意义。
【关键词】农户、农业、投入、产出、效益、分析、比较、因素、评价、建议、展望、结论、总结1. 引言1.1 研究背景农户农业投入产出效益一直是农业领域研究的热点问题,不同地区、不同农作物种植方式下,农户的投入和产出情况不尽相同。
由于我国农业的主要特点是以家庭农场经营为主,农户对于农业投入产出的关注尤为重要。
在当前市场经济体制下,农户的投入主要包括土地、劳动力、农资、机械等方面,而产出则主要包括农作物、畜禽产品等。
了解农户农业投入产出情况,有助于政府农业政策制定、农业生产企业经营决策、农户增收致富等方面的工作。
随着我国农业产业化、现代化的不断推进,农户对于农业投入产出的关注也越来越重要。
本研究旨在探讨农户农业投入产出情况,分析其影响因素,评价其效益,并提出相应建议和展望。
通过深入研究,可以为我国农业农村发展提供科学的参考依据,促进农业现代化、提高农户收入水平。
的这一部分将进一步解读农户农业投入产出效益评价的重要性和必要性。
1.2 研究目的农户农业投入产出的研究目的主要是为了深入理解农户在农业生产过程中的投入和产出情况,从而为农户提供更科学的经营决策和政策制定提供依据。
具体来说,研究目的包括以下几个方面:通过分析农户的投入情况,可以了解农户在农业生产中投入的成本和资源配置情况,从而帮助农户优化经营管理,提高农业生产效率。
通过分析农户的产出情况,可以评估农户的农业生产绩效和产出水平,为农户提供实际可行的经营建议,帮助他们提高农业生产的竞争力和盈利能力。
投入产出分析课程论文

盐城师范学院投入产出分析课程论文学生姓名瞿潇雨学院数学与统计学院专业应用统计班级 131班学号 ******** 成绩投入产出模型的应用——基于价值型投入产出数学模型引言投入产出分析主要通过编制投入产出表来实现的。
投入产出表是由投入表与产出表交叉而成的。
前者反映各种产品的价值,包括物质消耗,劳动报酬,剩余产品。
后者反映各种产品分配使用情况。
在投入产出表的基础上,可以建立相应的数学模型。
例如,产品平衡模型,价值构成模型等,用以进行经济分析,政策模拟,计划论证,和经济预测。
它的基本作用,通过编制投入产出表和模型,能够清晰地揭示国民经济各部门,产业结构之间的内在联系,能够反映国民经济中各部门,各产业之间在生产过程中的直接与间接联系,各部门、各产业生产与分配使用、生产与消耗之间的平衡(均衡)关系。
因此,投入产出法又称为部门联系平衡法。
1 投入产出简介投入产出分析是一种特定的经济数量分析方法。
投入产出分析是由俄罗斯裔美国经济学家瓦西里·里昂惕夫创立的。
主要应用数学方法和电子计算机,研究各部门间这种平衡关系的一种现代管理方法。
其理论基础是瓦尔拉的一般均衡理论。
投入产出是国民经济各部门间投入原料和产出产品的平衡关系正如前述,这里的“投入产出”有着自己的特定含义,它与通常所讲的一般的“投入产出”并不相同。
经济学和经济活动都要注重经济效益,增强提高经济效果的意识。
投入产出分析在我国的应用主要经历以下几个阶段:1.初步研究及引入阶段。
五十年代九十年代初,在著名经济学家孙治方和著名学家钱学森倡导下,经济理论和一些高等院校开始研究投入产出理论。
“文革”期间,此项工作几乎中断。
2.快速发展阶段。
1974年,为了研究宏观经济发展情况的需要,在国家统计局和国家计委的组织下,由国家统计局,国家计委,中国科学院,中国人民大学等单位联合编制了1973年全国61种产品的实物型投入产出表。
利用该表开展的分析开展的分析应用工作,在制定社会经济发展计划等方面发挥了积极的作用。
投入产出论文

新疆产业结构分析摘要:通过对2007年新疆各产业部门影响力系数与感应度系数的比较计算,发现产业在新疆的经济体系中地位非常重要,属于经济体系中的关键部门,应予以大力发展。
同时,根据新疆产业结构的实际情况提出了相对应的政策建议。
关键词:产业结构;影响力系数;感应度系数引言经济发展的程度决定产业结构的状况,而合理的产业结构则会对经济的持续、有效、健康发展产生积极的作用。
在经济持续高速发展过程中,一方面传统产业结构渐渐无法满足经济发展的需要,会对经济水平的继续提升构成制约;另一方面,经济发展引起的生产需求改变将导致传统产业结构中部分行业产能过剩,造成经济资源的巨大浪费。
因此,在现有基础上对一个地区的产业结构的特征和关联性进行进一步的研究,有助于确定该地区未来的主导产业,为地区产业结构调整提供有益的参考。
投入产出分析作为整个国民经济各产业以及各产业之间相互联系、相互依赖和相互制约关系的重要模型,在研究产业结构变动方面具有一定的优势。
本文以新疆产业结构为研究对象,运用投入产出表数据对近年来新疆产业部门影响力系数与感应度系数进行计算,并据此对新疆产业结构调整方向提出相应的政策建议。
1.2009年新疆三次产业结构分析改革开放以来,新疆国民经济快速增长,产业结构不断优化升级。
国内生产总值由1978年的39.07亿元上升到2009年的4277.05亿元,年均增长15.71%;2009年国民生产总值按可比价格计算,比上年增长8.1%,其中,第一产业增加值759.74亿元,增长4.5%;第二产业增加值1929.59亿元,增长8.5%;第三产业增加值1587.72亿元,增长9.2%,三次产业比例为17.8∶45.1∶37.1。
由表1可以看出,新疆1990年-2009年三次产业比重变化特点为一次产业比重逐渐降低,二次和三次产业比重逐渐增大,三次产业比重在1998-2003年间高于二次产业比重,在其余年份低于二次产业比重,说明新疆产业结构中工业和服务业成为经济的支柱,尤其是工业成为拉动经济增长的主要动力。
【论文】投入产出论文

【关键字】论文基于“快车道”模型的江苏省产业结构优化控制摘要:针对江苏省产业结构存在的问题,利用列昂惕夫“快车道”模型计算出江苏省最优产业结构及最优发展速度。
并结合经济控制论思想,利用动态线性规划,建立江苏省产业结构发展的动态线性规划模型。
最后,利用2007年江苏省投入产出表,以2012年为实现最优结构为目标,计算得到江苏省2007年到2012年间每年产业结构的优化调整方案。
结果表明,目前江苏省的产业结构发展应仍以第二产业为核心,应加大力度发展第三产业,逐步引导并深化服务业体系建设,提高其在国民经济中的比重。
关键词:“快车道”模型,产业结构,投入产出,优化控制Analysis of Industrial Structure Adjustment in Jiangsu Province based on the “Turnpike” ModelWang JunjieCollege of Economics&Management, NUAA, Nanjing, 211100Abstract—To solve the existing problems of the industrial structure in jiangsu province, using the turnpike model to calculate the optimal model of jiangsu province industrial structure and the optimal development speed. By using the dynamic linear programming, to set up the development of industrial structure dynamic linear programming model. At last, using 2007 input-output table of jiangsu province to calculated the optimization of the industrial structure of jiangsu province from 2007 to 2012 each year which goal is to achieve the optimal structure at 2012. The result indicated that the development of jiangsu province industrial structure should be still with the second industry as the core, should intensify efforts to the development of the third industry, and gradually lead and deepening service system construction, improve its proportion in the national economy.Keywords—Turnpike Model; Industrial Structure; Input-output table; Optimization contro1、引言产业结构是经济资源配置的结果反映,产业结构的变动对经济增长有着决定性影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一棋盘式平衡表。
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1=B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A:直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T—总产出的列向量;Y=(y 1 y 2.......y N )T—最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
.(二)主要系数计算与分析: 1分配系数分配系数是第i 部门提供的产品和服务在各种用途之间的分配使用比例。
中间产品分配系数为ij h =ijx /i X ,根据数据计算H=(66)(⨯=ij h H ,Hi (主对角线为∑=61j ij h 的对角矩阵)。
H =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.13620.0228 0.0144 0.1751 0.0121 0.1331 0.0870 0.0215 0.0530 0.4628 0.0323 0.1258 0.0709 0.08810.0364 0.5233 0.7336 0.206 0.00150.0092 0.0020 0.0567 0.0000 0.0541 0.0218 0.0255 0.0656 0.5847 0.0217 0.0108 0.04720.0001 0.0000 0.2698 0.1231H i =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.4710000000 0.7897000000 1.5781000000 0.0900000000 0.77340000000.4510 可用中间分配系数矩阵建立投入产出模型: 行模型:HiX+Y=X 即X=(I-Hi)-1Y 列模型:H TX+N=X 即X=(I-H T )-1N 2增加值系数: (1)折旧系数直接折旧系数dj a = j d /j X ,完全折旧系数dj b =dj a + ∑=ni ij a di b 1 (j i ,=1,2,...,n)直接折旧系数行向量61)(⨯=dj d a A ,完全折旧系数B d = A d (I-A)-1,计算结果如下:直接折旧系数行向量A d =()0.11480.04120.10580.03860.03760.0256完全折旧系数行向量B d =A d (I-A)-1=() 0.0896 0.1008 0.0888 0.1140 0.1283 0.1548(2)劳动者报酬系数直接劳动者报酬系数行向量A v =(0.0813 0.0905 0.1962 0.1861 0.2577 0.1940) 完全劳动者报酬系数行向量B v = Av(I-A)-1=(0.3431 0.3181 0.2855 0.2127 0.2373 0.2202)(3)生产税净额系数:直接生产税净额系数行向量A t =(0.01250.0543 0.0494 0.0498 0.0665 0.0461)完全生产税净额系数行向量B t = At(I-A)-1=(0.1263 0.1384 0.1268 0.0888 0.0865 0.0869)(4)营业盈余系数:直接营业盈余系数行向量As =(0.0417 0.0538 0.0300 0.1460 0.0762 0.1264) 完全营业盈余系数行向量Bs= As(I-A)-1=(0.2146 0.1790 0.1595 0.1219 0.13390.1219)劳动报酬、社会纯收入等完全系数又称为影响乘数,可以分析调整措施的影响程度。
3 综合直接消耗系数:cj a =∑=ni ij a 1(j =1,2,3,4,5,6)混合直接消耗系数:ei a =∑=nj ij a 1(i =1,2,3,4,5,6)分析:下标1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门。
从计算结果中分析,农业的综合直接消耗系数最大,说明农业对所有部门的直接依存强度最高,其他服务部门次之。
运输邮电部门的混合直接消耗系数最小,服务业部门次之,说明两者对所有部门的感应程度较强,两部门已成为国民经济发展的支柱产业,且是“瓶颈部门”。
