胡松瀛数模讲义
《自动控制原理》胡寿松自动控制原理简明教程第5章详解

bm1s bm an1s an
➢ 惯性环节:1/(Ts+1),式中T>0
➢ 一阶微分环节:(Ts+1),式中T>0
➢ 积分环节:1/s
➢ 微分环节:s
➢ 振荡环节:1/[(s/ωn)2+2ξs/ωn+1];式中ωn>0,0 < ξ <1 ➢ 二阶微分环节:(s/ωn)2+2 ξ s/ωn+1;式中ωn>0,0 < ξ <1
线性分度,单位是分贝(dB);对数相频曲线的纵坐标按 φ(ω) 线性分度,单位是度(°)。由此构成的坐标系称为 半对数坐标系。
ω和lgω的关系表
① ω轴为对数分度, 即采 用相等的距离代表相等的 频率倍增,在伯德图中横 坐标按μ=lgω均匀分度。 ② ω=0在对数分度的坐标系中的负无穷远处,ω =0不可能 在横坐标上表示出来,横坐标上表示的最低频率由所感兴 趣的频率范围确定。 ③ 从表中可以看出,ω的数值每变化10倍, 在对数坐标 上lgω相应变化一个单位。 频率变化10倍的一段对数刻度 称为“十倍频程”, 用“dec”表示。
arctg
2
曲线起自幅角
为-v90°的
无穷远处。
1. 极坐标图的起点
2T T 2
2
tan
1
2T T 2 2
1
0 L 0dB
-40
0 90
0
180
L 20 lgT 2 40 lgT
180
n
1 T
90
1 10 TT
40dB dec
(a) (b)
➢ 延迟环节
Gs eTs
G j e jT G j 1 G j T
精确曲线
第4章 线性规划模型3_Lingo软件

数据按行依次分配给变量的(1,1), (1,2), … ,(1,n), (2,1),…(2,n),…(m,n) 位置。
3 模型的初始化
init: X, Y = 0, .1; endinit min=X+Y; X^2+Y^2<=1; 好的初始点会减少模型的求解时间。 好的初始点会减少模型的求解时间。而 在非线性规划之中, 在非线性规划之中,初始点的选择还影 响结果的最优性。 响结果的最优性。
i=5 67.4 71 83.8 62.4
如何选拔队员组 100米混合泳 成4×100米混合泳 接力队? 接力队?
Min Z = ∑∑cij xij
∑x
j =1
5 i=1
4
ij
≤1, i =1,⋯5
=1, j =1,⋯4
∑x
ij
model: sets: workers/w1..w5/; jobs/j1..j4/; links(workers,jobs): cost,volume; endsets min=@sum(links: cost*volume); @for(workers(I): @sum(jobs(J): volume(I,J))<=1); @for(jobs(J): @sum(workers(I): volume(I,J))=1); @for(links(i,j): @bin(volume(i,j))); data: cost= 66.8 57.2 78 70 67.4 75.6 66 67.8 74.2 71 87 66.4 84.6 69.6 83.8 58.6 53 59.4 57.2 62.4; enddata end
sets: students/John Jill Rose endsets Mike/:sex, age;
自动控制原理(胡寿松版)课件第四章

第一节 根轨迹的基本概念
二、根轨迹与系统性能
根轨迹图可以分析系统的各种性能: ω j ∞ ↑ 稳定性: 根轨迹均在s的左半平 Kr 面,则系统对所有k>0的值是稳定的。 s K =0 1 1 s1 2 r 0 σ -1 稳态性能:如图有一个开环极点 -2 -1 s=0,说明属于I型系统,阶跃作用 Kr ∞ 下的稳态误差为0。 动态性能:过阻尼 临界阻尼 欠阻 尼。 K越大,阻尼比 越小,超调量σ%越大。
第四章 根轨迹分析法
第一节 根轨迹的基本概念
当系统的某个参数变化时,特征方程的根随 之在S平面上移动,系统的性能也跟着变化。研究 S 平面上根的位置随参数变化的规律及其与系统 性能的关系是根轨迹分析法的主要内容。
第一节 根轨迹的基本概念
一、根轨迹
设系统的结构如图 K r变化时,闭环特征 Kr 根在 s平面上的轨迹 : 极点;右半平面为 C(s) 2+2s+K s1 s2 Kr 不稳定极点;虚轴 R(s) =s∞ ω r j ↑ -2 0 0 上为临界极点。 闭环特征方程式 Kr 1 -1 -1 1 2 (2) 0<Kr<1时,系统 s 0 s2 +2s+K Kr=0 1r= s1 -1-j -1+j 2 0 σ -1 有呈过阻尼状态。 -2 特征方程的根 -1 -1+j∞ -1-j∞ Kr (3) 当 时,系统 ∞Kr=1 s1.2 =-1± 1-Kr ∞ 呈临界阻尼状态 。 得相应的闭环特征根值: (4) 1<Kr<∞时,系统呈欠阻尼状态。
↑
↑
第一节 根轨迹的基本概念
三、闭环零、极点与开环零、极点的关系
系统传递函数为
G( s) ( s) 1 G(s) H (s)
自动控制原理(胡寿松) 第二章PPT课件

mdd 2x2 (tt)fdd(tx)tk(x t)F(t)
F
k
m
x
k和f分别为弹簧的弹性系数和阻尼器的粘性摩擦系数。 负号表示弹簧力的方向和位移的方向相反; 粘性摩擦力的方向和速度的方向相反。
9
例2 电气系统
电气系统中最常见的装置是由电阻、电感、电容、运算放大器
等元件组成的电路,又称电气网络。仅由电阻、电感、电容(无源 器件)组成的电气网络称为无源网络。如果电气网络中包含运算放 大器(有源器件),就称为有源网络。
i(t) C duo (t) dt
消去中间变量i (t ),可得
Ld C 2 d u o 2 (tt)Rd C d o( u t)t u o(t)u i(t)
11
Ld C 2 d u o 2 (tt)Rd C d o( u t)t u o(t)u i(t) mdd 2x2 (tt)fdd(tx)tk(x t)F(t)
4
2. 1 系统微分方程的建立
2.1 控制系统的微分方程
控制系统的数学模型是指描述系统或元件输入量、输出量 以及内部各变量之间关系的数学表达式。而把描述各变量动 态关系的数学表达式称为动态模型。常用的动态数学模型有 微分方程、传递函数及动态结构图。
建立数学模型,可以使用解析法和实验法
对根实据际系系统统及或元元件件各加变入量一之定间形所式遵的循输的 入物信理号、,化根学据定输律入,信列号写与出输各出变信量号间间的 的数关学系表来达建式立,数从学而模建型立的起方数法学模型的 方法
F
k
m x
8
解:在物体受外力F的作用下,质量m相对于初始状态的位移、速度、 加速度分别为x、dx/dt、d2x/dt2 。设外作用力F为输入量,位移 x 为输 出量。根据弹簧、质量、阻尼器上力与位移、速度的关系和牛顿第二 定律,可列出作用在上的力和加速度之间的关系为
自动控制原理胡寿松第六版第一张

电机拖动考虑:纪录笔有惯性,希望电机速度能按所需位移量进行控制,所 以将电机转速测量出来,用来反馈。
输入量
放大器
伺服电机
传动机构
笔位置
纪录笔
测速电机
位置测量
内反馈可增加 系统的阻尼
第13页,共24页。
•飞机自动驾驶仪系统
第3页,共24页。
•例1:人用手拿物品。
控制目标:手拿到物品。
相关部件:1.手。抓取物品。功能:受控对象、执行部 件。 2.大脑。协调眼、手工作。功能:比较物品与手 之间的接近程度(比较元件);控制手的动作(控制部 件)。3 .眼睛。观察物品与手的位置。功能:检测元 件。
物品
位置
眼睛
大脑
手 手臂、手
较,若液位降低,则加大阀门开度,反之则减小。
设定水位
调节器
阀门
干扰
水位
锅炉
液位测量
第16页,共24页。
§1-3 自动控制系统的分类
1.线性连续控制系统
2.线性定常离散控制系统 3.非线性控制系统
第17页,共24页。
•线性连续控制系统
线性:系统的输入输出满足线性关系。
即有:若a输1u 入1时ua1,2u输输2出出为为 ;输ay入11y1 时,a。u2 输y2 出2为 。则输y入2 为
t
t
4.正弦函数:
u
f(t) 0 Asi nt()
t0 t0
t
第24页,共24页。
不稳定系统
稳定系统
2.快速性:系统稳定快慢程度的性能描述。一般用过渡过程的时间
来描述。
过渡过程:系统从开始运动到回到平衡点稳定下来的过程,也叫动 态过程、动态。
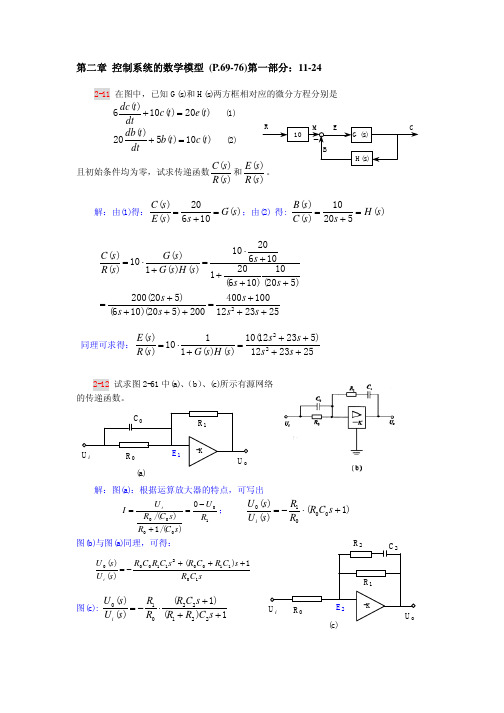
胡寿松_第二章_数学模型_参考解答_11-24
C (s) 。 R(s)
答案:信号流图略。 参见题 2-17 的答案。
2-20
递函数
画出图 2-66 中各系统结构图相对应的信号流图,并用梅逊增益公式求系统的传
C (s) C (s) 和 。 R(s) N ( s)
答案:信号流图略。 参见题 2-18 的答案。
2-21 试绘制图 2-67 中系统结构图对应的信号流图,并用梅逊增益公式求系统的传递函
胡寿松第二章数学模型参考解答1124数学模型习题参考解答自动控制原理胡寿松胡寿松七年级上册数学第二章高一数学必修1第二章八年级上册数学第二章高中数学必修一第二章数学必修二第二章高一数学必修一第二章
第二章 控制系统的数学模型 (P.69-76)第一部分:11-24
2-11 在图中,已知 G(s)和 H(s)两方框相对应的微分方程分别是
图(c)答案:存在 2 条前向通道,3 个回路(2 对不相交回路) ∆ = 1 + 10 + 2 + 0.5 + 0.5 *10 + 0.5 * 2 = 19.5
P1 = 5 * 10 = 50 ; P2 = 10 * 2 = 20 ;
故有:
∆ 1 = 1 + 0.5 = 1.5 ∆ 2 = 1 + 10 = 11
图(b): 图(c):
图(d): 图(e):
C ( s) G1G2G3 = R( s ) 1 + G1H1 + G2 H 2 + G3 H 3 + G1G3 H1H 3
C ( s ) G1G2 G3 + G4 (1 + G2 H 1 + G2 G3 H 2 − G1G2 H 1 ) = R( s) 1 + G2 H 1 + G2 G3 H 2 − G1G2 H 1 = G4 + G1G2 G3 1 + G2 H 1 + G2 G3 H 2 − G1G2 H 1
胡寿松自控第六版2.1
令K = f `(x0) , 则 y – f(x0) = K(x- x0) 再令 y=y-f(x0)
y= K x
x = x- x0,则
此式表明在工作点附近,输出的增量与输 入的增量之间是成线性关系的,上式是 环节的增量化方程式。
为了符号的方便,仍用y表示 y, x表示 x
则 y=Kx
写微分方程时,常习惯于把输出写在方程的 左边,输入写在方程右边,而且微分的次数 由高到低排列 。 机械平移系统的微分方程为:
mx(t) fx(t) kx(t) F(t)
这两个例子的微分方程很相似,故可用电 子线路来模拟机械平移系统,这也证明了我们 前面讲到的,看似完全不同的系统,具有相同 的运动规律,可用相同的数学模型来描述。
r(t)=1(t)
C(t) K
惯性环节的特点:
T
t
输出量迟缓地反应 输入量的变化规律。
当输入量发生突跳时,输出量并不能阶跃,而是按指 数规律上升。
(5)举例
R
r(t)
C
C(t)
C R1
R0
-
ur
+
uc
3、积分环节 (1)微分方程
T—积分时间常数 环节的输出量与输入量对时间的积分成正比。 (2)传递函数
(3)动态结构图
R(s)
s
C(s)
(4)动态响应
C(t)
k (t)
t
t=0+时,c(t)为-面积(强度)为K,宽度为0, 幅值为无穷大的理想脉冲。
(5)举例
C
ur(t)
R
+
uc(t)
直流测速发电机 以电机转角作为输出量,电枢 电压Ufn为输出量,则
胡寿松简明教程ch2
用拉氏变换法求解微分方程的步骤可归纳为: 微分方程
拉氏变换
输出的象函数
拉氏反变换
输出的时域函数(微分方程的解)
2.1.2
传递函数的定义
① ②
对于线性定常系统,在零初始条件下,输出的L变换与输入的L变换之比. n 阶线性定常系统:
n n 1 m m 1 d d d d a c ( t ) a c ( t ) ... a c ( t ) b r ( t ) b r ( t ) ... b r ( t ) 0 1 n 0 1 m n n 1 m m 1 dt dt dt dt
Uo(s) 1 Ui (s) RCs 1
du RC o u u o i dt
事实上,对于此类电网络,可以 直接用电路上所学的运算法得到 其传递函数。
1 Uo (s) 1 Cs Ui (s) R 1 RCs1 Cs
2.2.1
环节数学模型的建立
归纳分析法建立环节数学模型的一般步骤:
m s b s b C ( s ) b 0 1 m G ( s ) n 1m n 1 R ( s ) a s a s a 0 1 n
熟记对应关系
◆ 传递函数的反拉氏变换是系统的单位脉冲响应。 ◆ 传递函数只是对系统的数学描述,并不反映系统的物理构成。
2.2
R2
R
P37例2-12 某速度控制系统如下图所示,建立其数学模型。
+
ui R 1
R1 -K1 u1
C
-ut
R1
-K2
u2
功 率 放 大 K3
ua
SM
ωm
ω
负 载
-ut
TG
自动控制原理(胡寿松版)课件第三章
第一节 系统(xìtǒng)时间响应的性能指 标
二、典型输入(shūrù)信号
1. 典型初始状态
通常规定控制系统的初始状态为零状态。
即在外作用加于系统之前,被控量及其各阶导数相对于 平衡工作点的增量为零,系统处于相对平衡状态。
精品资料
第一节 系统(xìtǒng)时间响应的性能指
标 2. 典型 (diǎnxíng)外作 用①单位阶跃函数1(t)
(tiáojié)时间t s (±5%),如果要求 t s= 0.1s,求反
馈系数。
Kk= 100 KH= 0.1 解:闭环传递函数 ФФ(s()s=)=1+CR1((10sss0))0s0=K1H+=KKs0kksKK.0HHK11sH+1
t s==3×s1K+0H10.00=10/=.K30H.11=s0+.11
ess 是系统控制精度或抗扰动能力的一种度量。
精品资料
第三章 线性系统的时域分析法
第二节 一阶系统(xìtǒng)的时域分析 根据系统的输出响应求取系统的性能 指标,从而分析系统的性能,是时域分析法 分析系统性能的基本(jīběn)方法。 一、一阶系统的数学模型
二、一阶系统的时域响应及性能分析
精品资料
单位斜坡响应曲线
h(t)
=t-(t-T+Te-t/T )
r(t) T c(t)
=T(1-e-t/T )
ess=
lim
t→∞
e(t)
=T
0
t
精品资料
第二节 一阶系统(xìtǒng)的时域分析
4.单位(dānwèi)加速度 响应
设系统的输出信号为单位加速度函数,则求得一阶系 统的单位加速度响应为:
数学建模BUPT上学期讲义
第一章课程概述§1.1 数学模型与数学建模一.基本概念数学是研究现实世界中数量关系和空间形式的科学。
其产生以及许多重大发展都是和现实世界的生产活动和其他相应学科的需要密切相关的;同时,作为认识和改造世界的强有力的工具,又促进了科学技术和生产建设的发展。
特别在当今时代,由于计算机软硬件的迅速发展和普及,数学方法被广泛应用于生产实践、社会管理的各个领域和层面。
对具体的应用问题或问题类进行合理的简化假设以及适当的抽象并最终表述为某种数学结构,即我们在这里讨论的数学模型,是现代生产实践与社会生活实现优化决策和科学管理的必要环节。
而数学建模则是指根据实际需要或最终管理目标,对现实问题构建数学模型,对模型进行分析求解,并最终将模型解翻译为决策方案应用于实际的一个由诸多环节组成的一个完整过程。
为理解现实对象与数学模型的关系,以下给出数学建模的一个流程图:二.(引例1)椅子的平稳放置问题将(四脚)椅子置于不平的地面,通常只有三只脚着地,放不稳;然而只需稍挪动几次,就可以使四只脚同时着地,放稳了——这是我们在日常生活中遇到的一件很普通的事实。
这一现象是偶然的呢,还是有其必然性呢?三.(引例2)商人过河设有三名商人,各带一个随从,欲乘一小船渡河,小船只能容纳两人,须由他们自己划行。
随从们密约,在河的任何一岸,一旦随从的人数比商人多,就杀人越货。
而如何乘船渡河的大权掌握在商人们的手中。
商人们怎样才能安全渡河呢?第二章 初等数学方法建模数学建模的核心是力求对实际应用问题的解决,而不在于所采用方法的深奥程度。
事实上,在对一个问题能够做到完好解决的前提下,朴素性简洁性恰好是构成一个完美的数学模型或数学建模过程的一个重要侧面。
本章介绍的几个例子即能够用相对初等的方法得以很好地解决,这里强调选用怎样的工具通常是由问题本身内在决定的,切忌为了炫耀方法而使问题的解决变的烦琐——这正如在良医的眼里,各种药材的价值在其用并在行医中总能做到对症,而不在其名贵程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
胡松瀛数模讲义对策与决策模型古人云:“世事如棋。
”人生就像下棋一样,每天都要面对许多的对策与决策问题。
有些是生活琐事的对策与决策,如要不要买你看中的一件商品;今天中午你点什么菜,喝什么酒?有些则可能是决定你命运的重大事情的对策与决策,如高考填志愿你该填什么学校,什么专业?许多人在竞争某一职位,你应当怎样做才能最好的表现自己,使自己脱颖而出?等等,等等。
对策与决策问题都要求你面对几种方案做出选择,不同之处在于遇到对策问题时,你面对的是一个或几个与你一样可以可以选择行动方案的对手;而遇到决策问题时则不然,你面对的并非一些对手,而是将来会出现的几种可能结果,它们虽不会故意为难你(即不会和你博弈),但你一般却不知道究竟哪一种结果会真正出现。
当然,两类问题也有一定的联系,不必分得过于清楚。
例如,在某些情况下,如果我们把可能出现的若干种情况看成是竞争对手可以采取的几种策略,那么求解对策问题的方法也可以用来求解决策问题。
对策问题对策论的思想早就有之,我国战国时期的“田忌赛马”就是一例。
传说齐王欲与大将田忌赛马,双方约定每人挑选上、中、下三个等级的马个一匹进行比赛,每局赌局诶一千金。
齐王同等级的马均比田忌的马略胜一筹,似乎必胜无疑。
田忌的朋友孙膑给他除了一个主意,让他用下等马对齐王的上等马,上等马对齐王的中等马,中等马对齐王的下等马,结果田忌两胜一败,反而赢得了一千金。
然而,对策论作为一门真正独立的学科,其发展的历史却并不久远。
1912年,策墨罗利用集合论思想研究下棋,发表了题为《关于集合论在象棋对策中的应用》的论文。
1928年与1937年著名美籍匈牙利科学家冯.诺伊曼和摩根斯藤合著了《对策论与经济行为》一书。
这些研究成果被公认为是对策论作为一门学科创立的标志,他们引进了严格的定义,构建了对策论的理论框架,使对策论研究走上了系统化、公理化的道路。
1950年,美国数学家纳什将冯.诺伊曼等人的合作对策理论发展到非合作对策情况,提出了纳什平衡点概念(纳什本人也因此而获得了诺贝尔经济学奖)。
此后,对策论围饶着纳什平衡点这一核心问题发展,又有了新的重大突破。
对策问题的参与者为利益相互冲突的各方,其结局不取决于其中任意一方的努力而是各方所采取的策略的综合结果。
究竟什么是对策问题呢?让我们先来考察两个简单的实例。
例 1 (囚犯的困惑)警察同时逮捕了两人,并将他们分别关押在两处,逮捕的原因是他们持有大量伪币。
警方怀疑他们伪造钱币,但尚未找到充分的证据,希望他们能自己供认。
这两个人都知道:如果他们双方都不供认,将被以持有和使用大量伪币罪各判刑18个月;如果双方都供认伪造了钱币,将因伪造钱币罪各判刑3年;如果一方供认另一方不供认,则供认方将被从宽处理仅关押半年,但未供认一方将被判刑7年。
将嫌疑犯A、B被判刑的几种可能情况如表一所示。
表一表中每对数字表示嫌疑犯A、B被判刑的年数。
让我们来分析一下囚犯们会怎样决策。
囚犯A也许会这样想:若B招认了,我如果不招认会被判7年,但我也招认的话只有3年;若B不招认,我如果招认判刑只有半年,而不招认则被判刑1.5年。
也就是说,不论B招认还是不招认,对A来说,招认都比不招认要好。
既然如此,除非A是傻瓜,他肯定会采取招认的策略。
同样道理,如果B不是傻瓜,他也会这样想,从而采取招认的策略。
看来这一案件的最终结果一定是,A、B均供认并各被判刑3年,不管他们真的有没有伪造钱币。
由此可以看出,在这种情况下,过分的强调了坦白从宽、抗拒从严,即使不使用刑罚,也完全有可能制造冤案,这就是为什么法律界人士要再三强调量刑时应当重事实、重证据的原因之一。
在上面这个简单实例的分析中,我们其实已经先验地做了一条假设:“防人之心不可无”,不管对方怎么做,我们的策略应当保证我不会成为牺牲品。
例如,假如A、B都不招认,他们都只需服刑1.5年(而不是3年)。
可是双方都会这样想,凭什么我要相信对方,有什么对东西能保证对方不会出卖我呢?“囚徒的困惑”是一个很出名的实例,它之所以出名是因为它揭示了一种现象,即在自然状态下,动物(包括人)是趋利避害的。
假如你将一批猴子关进笼子里并每天从中选出一只来杀掉,你只要稍加留意就会发现,在你选猴子的时候,猴子们非常紧张,一动都不敢动生怕引起你的注意,而当你选中一只准备杀时,被选中的猴子拼命挣扎,其余的猴子却在笼子里幸灾乐祸的观望,可能庆幸自己未被选中。
不少人认为,认总是利己的,只要不出伤害别人就算是好人了(经济学中将这种人称为“理性人”)。
其实不然,如果不崇尚奉献精神,人人都事不关己高高挂起,人人都满足于当“理性人”,就会对整个社会带来灾难,最后也一定会殃及作为社会一员的个人。
例如,我们经常看到有消息报道,某处罪犯正在作案,旁观看热闹的人不少,却没有人挺身而出去加以制止(或只有很少的几个见义勇为者),大概就是因为事不关己吧。
这些人和关在笼子里的猴子没有多大区别,他们的举动其实在助长犯罪分子的威风,如果每一个人都能挺身而出,罪犯的气焰就不会这样嚣张了,敢于犯罪的人也就少了。
例 2 (商业竞争)两家生产相同产品的工厂在竞争市场,甲厂拟定了三套行动计划1α,2α,3α,乙厂拟定了四套行动计划1β,2β,3β,4β。
预测在甲厂采取方案i α,而乙厂采取方案j β时,甲已两厂的市场盈利分别为(ij α,ij β)(注:前者为甲厂盈利,后者为乙厂盈利)。
问两厂各应采取哪一种策略才能使本厂的盈利最大。
在例2中,根据预测我们得到的其实是一个赢得“矩阵”(注:我们给矩阵两字加了引号是因为,严格地讲,它并不是矩阵,因为其每一个元素是一个向量而不是一个数):⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=),(),(),(),(,(),(343431312424212114141111b a b a b a b a b a b a A 分析上面两个对策问题的实例,我们可以发现一些共同的规律。
一、 对策问题的基本要素给定一个对策问题的实例必须给定以下信息:(1)局中人。
参加对策的各方被称为决策问题的局中人,一个对策问题可以包含两名局中人(如棋类比赛等),也可以包含多于两名局中人(如大多数商业中的竞争、 政治派别间的斗争等)。
每一局中人都必须拥有可供其选择并能影响最终结局的策略,在例1中,局中人是A 、B 两名疑犯,警方不是局中人。
两名疑犯最终被如何判刑取决于他们各自采取的态度,警方不能为他们做出选择。
(2)策略集合。
局中人能采取的可行方案称为策略,每一局中人存在着一个策略集合,而每一策略集合中至少要有两个策略,否则该局中人可从此对策问题中删去,因为对他来讲,不存在选择策略的余地。
应当注意的是,所谓策略是指在整个竞争过程中对付他方的完整方法,而并非指竞争过程中某步所采取的具体局部办法。
例如,下棋中的某一步只能看作一个完整策略的组成部分,而不能看成一个完整的策略。
当然,有时可将它看成一个多阶段对策中的子对策。
策略集合可以是有限集也可以是无限集。
策略集合为有限集时被称为有限对策,否则被称为无限对策。
(3)赢得函数(或称支付函数)。
记局中人i 的策略集合为i S 。
当对策问题的各方都从各自的策略集合中选定了一个策略后,各方采取的策略全体可用一个矢量表示,称之为一个纯局势(简称局势)。
例如,若一个对策问题中包含着A 、B 两名局中人,其策略集合分别为},,{1m A S αα =,},,{1n B S ββ =。
若A 选择策略i α,而B 选择策略j β,则),(j i βα就构成此策略的一个纯局势。
显然,A S 与B S 一共可构成n m ⨯个纯局势,它们构成了表二。
对策问题的全体纯局势构成的集合S 称为此对策问题的局势集合。
表 二对策的结果用矢量表示,称之为赢得函数。
赢得函数F 是定义在局势集合S 上的失值函数,对于S 中的每一纯局势s ,)(s F 指出了每一局中人在此对策结果下应赢得(或支付)的值。
综上所述,一个对策模型由局中人、策略集合喝赢得函数三部分组成。
记局中人集合为},,2,1{k I =,对每一I i ∈,有一策略集合i S ,当I 中每一局中人i 选定策略后得一个局势s ;将s 代入赢得函数F ,即得一矢量())(,),()(1s F s F s F k =,其中)(s F i 为在局势s 下局中人i 的赢得(或支付)。
本节讨论只有两名局中人的对策问题,即两人对策,其结果可以被推广到一般的对策模型中去。
对于只有两名局中人的对策问题,其局势集合和赢得函数均可用表格表示。
例如,表二就给出了一般两人对策问题的局势集合喝赢得函数。
二、 零和对策存在一类特特殊的对策问题。
在这类对策问题中,当纯局势确定后,A 之所得恰为B 之所失,或A 之所失恰为B 之所得,即双方所得之和总为零,这样的对策问题被称为零和对策问题。
在零和对策中,因)()(21s F s F -=,故只需指出其中一人的赢得值即可,此时,赢得函数可用真正的赢得矩阵来表示。
例如若A 有m 中策略,B 有n 种策略,赢得矩阵可写成⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⨯mn m m n n nm a a a a a a a a a R 212222111211 n m R ⨯的元素ij a 表示若A 选取策略i 而B 选取策略j ,则A 之所得为ij a (当0<ij a 时为为支付)。
在有些两人对策的赢得表中,A 之所得并非明显为B 之所失,但双方赢得数之和为一常数。
例如在表三中,无论A ,B 怎样选取策略,双方赢得总和均为10,此时,若将各人赢得数减去两人的平均赢得数,即可将赢得表化为零和赢得表。
表三中的对策在转化为零和对策后,具有赢得矩阵R .表 三综上所述可知,要给定一个两人零和对策只需给出局中人A ,B 的策略集合A S 、B S 及表示赢得值的赢得矩阵R 。
当遇到零和对策或可转化为零和对策的问题时,R 可用通常意义下的矩阵表示,否则R 中的元素为一个两维矢量。
故两人对策G 又被称为矩阵对策并可简记为},,{R S S G B A =例 3 给定一个零和对策},,{R S S G B A =,其中},,{321ααα=A S ,},,,{4321ββββ=B S4321ββββ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=16100610182142230612R 321ααα (1) 零和对策不存在合作基础,A 之所得即B 之所失,故在求解两人零和对策时只能根据利己原则。
从R 中可以看出,若A 希望获得最大盈利30,需采取策略1α,但此时若B 采取策略4β,A 非但得不到30,反而会失去22。
此时任何一方都不应当抱有侥幸心理,根据利己原则,双方都应考虑到对方为了使自己能获得最大利益,都有使对手遭受最大损失的动机,为稳妥起见,应当从最坏的可能中去争取最好的结果。
