(推荐下载)热力学知识点总结及习题373
热力学小结与习题
= 0,∴∆E = 0
Q = ∆ E + W = W = 1 .25 × 10 J
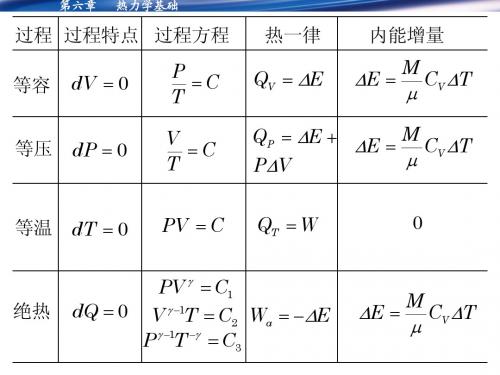
第六章
热力学基础
双原子分子理想气体经过如图的过程, 例 1mol 双原子分子理想气体经过如图的过程,其 为绝热过程、 中1— 2 为直线过程 、2— 3 为绝热过程、3— 1 为等温 过程.已知 T1, T2 = 2T1 , V3 = 8V1 .求:1)各过程的功、 过程 已知 求 )各过程的功、 热量和内能变化; )此循环热机效率. 热量和内能变化;2)此循环热机效率 p 解 1): 1— 2
第六章
热力学基础
例:讨论理想气体下图过程中,各过程 讨论理想气体下图过程中,
P A* 1 O 2 绝热 *B V
Q 的正负。
A— B
QAB = 0
WAB = −∆E AB > 0
A— 1— B
QA1B = ∆EAB + WA1B = WA1B −WAB ∵W A1B < W AB ∴ Q A1B < 0
p
A
p=C
解
B
QAB = ∆EAB + WAB
Q AC = W AC
T =C
C
QAD = 0
∵ W AB > W AC > W AD
dQ = 0
D
∆EAB > 0 , ∆EAD < 0
o VA
VB V
∴ Q AB > Q AC > Q AD = 0
第六章
热力学基础
例 一定量理想气体的 图所示, 循环过程如 P-V 图所示, 请填写表格中的空格. 请填写表格中的空格
P A 等温 B
绝热
o
内能增量ΔE/J Δ 0 A→B 过程 B→C C→D D→A ABCD -50 -100 150 50 50 -50 0
热力学复习题及答案

热力学复习题及答案1. 热力学的定义是什么?答:热力学是研究能量转化和能量传递规律的一个物理学分支。
2. 什么是热力学系统?答:热力学系统是指被选定的一部分物质或空间,用于研究热力学性质和过程的对象或范围。
3. 请简要解释热力学过程中的熵变。
答:热力学过程中的熵变指系统熵的变化,代表了系统无序度的改变。
熵增加表示系统的无序度增加,熵减少表示系统的无序度减少。
4. 热力学第一定律是什么?答:热力学第一定律,也称能量守恒定律,表示能量不会被创造或破坏,只能从一种形式转化为另一种形式,能量的总量保持不变。
5. 温度和热量有什么区别?答:温度是物体分子运动的程度,用来衡量热力学系统的热平衡状态。
热量是能量的传递形式,表示因温度差而引起的能量传递。
6. 请解释等温过程和绝热过程。
答:等温过程是指系统与外界保持恒定温度的热力学过程。
绝热过程是指系统与外界无能量交换的热力学过程。
7. 热力学循环是什么?答:热力学循环是指能量转化过程中系统从一个状态经过一系列过程最终回到原来状态的过程。
8. 请解释热力学可能性原理。
答:热力学可能性原理,也称热力学第二定律,表示任何孤立系统都不可能完全转化热能为有效的功。
9. 热力学第三定律是什么?答:热力学第三定律,也称绝对温标定律,指出在绝对零度(0K)下,所有物质的熵可以达到最低值,即熵的极限为零。
10. 请解释吉布斯自由能。
答:吉布斯自由能,简称G,是热力学系统在等温等压条件下的可用能量。
它在化学平衡时取最小值,可用于预测化学反应的方向。
热学热力学知识点总结

热学热力学知识点总结热学热力学是物理学中的重要分支,研究物质热现象和热传递规律,深入了解这一领域的知识对于我们理解自然界的运行机制至关重要。
本文将对热学热力学的一些重要知识点进行总结。
一、热力学基本概念1. 系统与环境:热力学中,我们将要研究的物体或者系统称为“系统”,而其周围的一切称为“环境”。
2. 边界与界面:系统与环境之间通过一条虚线或者实际存在的物理情况进行分界,在这个分界线上,称为“边界”。
而边界之间的物理现象发生的地方称为“界面”。
二、热力学定律1. 第一定律:能量守恒定律,描述了能量的转化和守恒规律。
能量从一个系统传递到另一个系统,既不会凭空产生,也不会消失。
2. 第二定律:熵增原理,描述了自然界热现象的方向性。
热量不会自动从低温物体传递到高温物体,而是相反的。
这个定律也说明了热量的传递需要有势差。
3. 第三定律:绝对零度定律,描述了当温度接近绝对零度时,物体的一些性质将趋近于零。
三、热力学过程1. 等压过程:系统中的压强恒定,系统对外界做功或者从外界接收到的功相等。
2. 等温过程:系统内部温度恒定,根据热容量对外界做功或者从外界接收到的功相等。
3. 绝热过程:系统与环境没有热量交换,系统内部熵不变。
四、热力学函数1. 内能:系统中分子的热运动所具有的能量总和称为内能。
内能是状态函数,与系统的初始状态和末状态有关。
2. 焓:系统的内能加上对外做的功,称为焓。
焓也是状态函数。
3. 熵:描述了系统的无序程度,并且是一个状态函数。
熵增原理通过熵的变化来预测自然界的趋势,即系统熵会不断增大。
4. 自由能:描述了系统能做到的最大非体积功。
分为Helmholtz自由能和Gibbs自由能两种。
五、热力学循环1. 卡诺循环:由两个等温过程和两个绝热过程组成的循环,是一个理想的热力学循环。
卡诺循环的效率反映了热机的工作效率。
2. 标准焓:在25摄氏度和1 atm压强下,各物质的标准热力学性质,如标准焓变等。
热力学复习知识点汇总

概 念 部 分 汇 总 复 习第一章 热力学的基本规律1、热力学与统计物理学所研究的对象:由大量微观粒子组成的宏观物质系统其中所要研究的系统可分为三类孤立系:与其他物体既没有物质交换也没有能量交换的系统; 闭系:与外界有能量交换但没有物质交换的系统; 开系:与外界既有能量交换又有物质交换的系统。
2、热力学系统平衡状态的四种参量:几何参量、力学参量、化学参量和电磁参量。
3、一个物理性质均匀的热力学系统称为一个相;根据相的数量,可以分为单相系和复相系。
4、热平衡定律(热力学第零定律):如果两个物体各自与第三个物体达到热平衡,它们彼此也处在热平衡.5、符合玻意耳定律、阿氏定律和理想气体温标的气体称为理想气体。
6、范德瓦尔斯方程是考虑了气体分子之间的相互作用力(排斥力和吸引力),对理想气体状态方程作了修正之后的实际气体的物态方程。
7、准静态过程:过程由无限靠近的平衡态组成,过程进行的每一步,系统都处于平衡态。
8、准静态过程外界对气体所作的功:,外界对气体所作的功是个过程量。
9、绝热过程:系统状态的变化完全是机械作用或电磁作用的结果而没有受到其他影响。
绝热过程中内能U是一个态函数:A B UU W -= 10、热力学第一定律(即能量守恒定律)表述:任何形式的能量,既不能消灭也不能创造,只能从一种形式转换成另一种形式,在转换过程中能量的总量保持恒定;热力学表达式:Q W U U A B +=-;微分形式:W Q Ud d d +=11、态函数焓H :pV U H +=,等压过程:Vp U H ∆+∆=∆,与热力学第一定律的公式一比较即得:等压过程系统从外界吸收的热量等于态函数焓的增加量。
12、焦耳定律:气体的内能只是温度的函数,与体积无关,即)(T U U =。
13.定压热容比:ppT H C ⎪⎭⎫⎝⎛∂∂=;定容热容比:V V T U C ⎪⎭⎫⎝⎛∂∂= 公式:nR C C V p=-14、绝热过程的状态方程:const =γpV ;const =γTV ;const 1=-γγT p 。
高考热力学知识点归纳总结

高考热力学知识点归纳总结热力学是自然科学中的一个重要分支,它研究能量转化和能量传递的规律。
作为高考物理的一部分,热力学知识占据了相当重要的位置,以下是对高考热力学知识点的归纳总结。
一、热力学基本概念1. 系统与环境:热力学研究的对象被称为系统,系统与系统的外界称为环境。
2. 定态与非定态:当系统的温度、压强、体积等宏观性质保持不变时,系统处于定态;反之则为非定态。
3. 热平衡与热不平衡:当系统与环境达到温度相等且无任何宏观性质发生变化时,称为热平衡;反之则为热不平衡。
二、温度和热量1. 温度:温度是物体冷热程度的度量,常用单位为摄氏度(℃)。
2. 热量:热量是能量的一种传递方式,是由高温物体向低温物体传递的能量。
3. 内能:内能是系统中各个微观粒子的能量总和,表示为U。
4. 热容:热容是单位质量的物质在温度变化下所吸收(释放)的热量,表示为C。
- 定压热容:在恒定压力下吸收(释放)的热量,表示为Cp。
- 定容热容:在恒定体积下吸收(释放)的热量,表示为Cv。
三、热力学第一定律1. 能量守恒定律:能量不会自发消失,也不会自发产生。
2. 系统的内能变化:系统的内能变化等于系统所吸收的热量减去对外界所做的功。
△U = Q - W其中,△U为内能变化,Q为系统吸收的热量,W为对外界所做的功。
四、热容与焓1. 热容与温度变化关系:当物体的温度变化很小的情况下,热容可以看作是与温度变化成正比的。
C = △Q / △T其中,C为热容,△Q为物体吸收(释放)的热量,△T为温度变化。
2. 焓:焓是系统在恒定压力下的热力学函数,表示为H。
H = U + PV其中,H为焓,U为内能,P为压强,V为体积。
五、等容、等压、等温过程1. 等容过程:系统发生变化时,体积保持不变的过程称为等容过程。
2. 等压过程:系统发生变化时,压强保持不变的过程称为等压过程。
功W = P△V其中,W为对外界所做的功,P为压强,△V为体积变化。
热力学基础知识点总结

热力学基础知识点总结热力学是研究热现象中物质系统在平衡时的性质和建立能量的平衡关系,以及状态发生变化时系统与外界相互作用(包括能量传递和转换)的学科。
以下是对热力学基础知识点的详细总结。
一、热力学系统与状态热力学系统是指被研究的对象,它可以是一个封闭的容器中的气体,也可以是一个热机的工作物质等。
根据系统与外界的物质和能量交换情况,热力学系统可分为三类:1、孤立系统:与外界既无物质交换,也无能量交换。
2、封闭系统:与外界只有能量交换,无物质交换。
3、开放系统:与外界既有物质交换,又有能量交换。
系统的状态是由一些宏观物理量来描述的,比如压强(P)、体积(V)、温度(T)等,这些物理量被称为状态参量。
当系统的状态参量确定时,系统的状态就确定了。
二、热力学第零定律如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡(温度相同),那么它们彼此也必定处于热平衡。
这一定律为温度的测量提供了理论依据。
三、热力学第一定律热力学第一定律就是能量守恒定律在热现象中的应用。
其表达式为:ΔU = Q + W,其中ΔU 表示系统内能的变化,Q 表示系统吸收的热量,W 表示系统对外所做的功。
当系统从外界吸收热量时,Q 为正;向外界放出热量时,Q 为负。
当系统对外做功时,W 为正;外界对系统做功时,W 为负。
例如,在一个绝热容器中,有一个热的物体和一个冷的物体,热的物体向冷的物体传热,最终两者温度相同。
这个过程中,没有对外做功或外界对系统做功,也没有与外界进行热交换,系统的内能变化就等于热传递的热量。
四、热力学第二定律热力学第二定律有多种表述方式,常见的有克劳修斯表述和开尔文表述。
克劳修斯表述:热量不能自发地从低温物体传到高温物体。
开尔文表述:不可能从单一热源吸取热量,使之完全变为有用功而不产生其他影响。
热力学第二定律揭示了热现象的方向性和不可逆性。
例如,热机在工作过程中,总是会有一部分能量以废热的形式散失到环境中,无法将所有的输入能量都转化为有用功。
热力学重点知识总结(期末复习必备)

热力学重点知识总结(期末复习必备)热力学重点知识总结 (期末复必备)1. 热力学基本概念- 热力学是研究物质和能量转化关系的科学领域。
- 系统:研究对象,研究所关注的物体或者物质。
- 环境:与系统相互作用的外部世界。
- 边界:系统与环境之间的分界面。
2. 热力学定律第一定律:能量守恒定律- 能量既不会凭空产生,也不会凭空消失,只会在不同形式之间转化。
- $\Delta U = Q - W$,其中 $U$ 表示内能,$Q$ 表示传热量,$W$ 表示对外界做功。
第二定律:热力学箭头定律- 热量不会自发地从低温物体传递到高温物体,而是相反的方向。
- 热量自发地会沿着温度梯度从高温物体传递到低温物体。
- 第二定律的一个重要应用是热机效率计算:$\eta =\frac{W}{Q_H}$,其中 $Q_H$ 表示从高温热源吸收的热量,$W$ 表示对外界做的功。
第三定律:绝对零度定律- 温度无法降低到绝对零度,即 $0$K 是一个温度的下限。
- 第三定律提供了热力学的温标基准,即绝对温标。
3. 热力学过程绝热过程- 绝热过程是指在过程中不与环境发生热量交换的过程。
- 绝热过程中,系统的内能会发生改变,但传热量为零。
等温过程- 等温过程是指在过程中系统与环境保持恒定的温度。
- 在等温过程中,系统的内能不变,但会发生热量交换。
绝热可逆过程- 绝热可逆过程是指绝热过程与可逆过程的结合。
- 在绝热可逆过程中,系统不仅不与环境发生热量交换,还能够在过程中达到热力学平衡。
4. 热力学系统分类封闭系统- 封闭系统是指与环境隔绝,但能够通过物质和能量交换来进行工作的系统。
开放系统- 开放系统是指与环境可以进行物质和能量交换的系统,也称为流体系统。
孤立系统- 孤立系统是指与环境既不进行物质交换,也不进行能量交换的系统。
5. 热力学熵- 熵是热力学中一个重要的物理量,表示系统的无序程度或混乱程度。
- 熵的增加反映了系统的混乱程度的增大,熵的减少反映了系统的有序程度的增大。
热力学基础习题及总结

绝 热 点火等体吸热
吸 气 排 气 等体放热 绝热膨胀 压 缩
等体吸热
等体放热
奥托
主体 两个绝热 过程 两个等体
均为绝热过程,有
大气压
奥托
图中两卡诺循环 1 2 吗 ?
p
W1 W 2
p
T1
T3
W1
W1 W 2
T1
W1
T2
W2
W2
T2
o
V
o
V
1 2
1 2
不同过程的熵变
m 2 c p T
T
dT T
m 2 c p ln
T
'
203 J K
1
1
T2
S S 1 S 2 21 J K
显然孤立系统中不可逆过程熵是增加的 .
将1kg 20oC的水放到100oC的炉上加热后达100oC, 水的比热C=4.18103J/kg · k.求水和炉子的熵变。 解: 设水依次与一系列温度逐渐升高彼此相差无限小 dT的热源接触,从而逐个吸热dQ达到热平衡进行 可逆加热最后达100oC
解 系统为孤立系统 , 混合是不可逆的等压过程. 为计算熵变 , 可假设一可逆等压混合过程. 设 平衡时水温为 T 由能量守恒得
0 . 30 c p ( 363 K T ) 0 . 70 c p ( T 293 K )
T 314 K
'
'
, 水的定压比热容为
3 1
c p 4 . 18 10 J kg
'
K
1
'
m 1 0 . 3 kg
T1 363 K
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.热力学第零定理:如果两个物体各自与第三个物体达到热平衡,他们彼此也必然处于热平衡2.热力学第一定律:能量可以从一种形式转变为另一种形式,但在转化过程中能量的总量保持不变3.热力学第二定理:实质:自然界中一切与热现象有关的实际过程都是不可逆过程,他们有一定的自发进行的方向开式:不可能从单一热源吸热使之完全变成有用的功而不引起其他变化克式:不可能把热量从低温物体传到高温物体而不引起其他变化热力学第三(绝对零度定理):不可能通过有限步骤是一个物体冷却到热力学温度的零度4.孤立系统:与外界无物质、无能量交换dQ=0 dW=05.封闭系统:与外界无物质交换、有能量交换dQ≠0 dW=06.准静态过程:是一个进行得无限缓慢以致系统连续不断的经历着一些列平衡态的过程。
只有系统内部各部分之间及系统与外界之间始终同时满足力学、热学、化学平衡条件的过程才是准静态过程(准静态过程是一个理想过程)7.熵增加原理:系统经可逆绝热过程熵不变,经不可逆绝热过程熵增加,在绝热条件下,熵减少过程是不可能实现的。
8.广延量:与系统大小成正比的热力学量(如质量M、体积V、内能U等)强度量:不随系统大小变化的热力学量(如系统的P、T、ρ等)9.获得低温的方法:节流过程、节流过程与绝热膨胀相结合、绝热去磁制冷、激光制冷、核绝热去磁10.特性函数的定义:在适当选择独立变量条件下,只要知道系统的一个热力学函数,就可以用只求偏导数的方法求出系统的其他基本热力学函数,从而完全确定均匀系统的平衡性质,这个热力学函数就称为特性函数。
11.一级相变:在相变点两点的化学势连续,但化学势的一阶偏导数存在突变12.二级相变:在相变点两点的化学势及一阶导数连续,但二阶导数存在突变13.单元复相系平衡条件:一个单元两个系统(ɑ相和β相)组成一孤立系统,其总内能总体积和总物质的量恒定。
14.中肯半径:在一定的蒸气压下,于正其达到平衡的液滴半径称为中肯半径15.能量均分定理:对于外在温度为T 的平衡状态的经典系统,例子的能量中每一个平方项的平均值等于(1/2)KT16.微观粒子全同性原理:微观粒子全同性原理指出,全同粒子是不可分辨的,在含有多个全同粒子的系统中,将任何两个全同粒子加以对换,不改变整个系统的微观运动状态。
17.等概率原理:对于处在平衡状态的孤立系统,系统各个可能的微观状态出现的概率是相等的18.经典极限条件:在所有能量级,粒子数都远远小于量子)(对所有l 1a l l pp ϖ态数。
19.能态方程:就是给出温度与状态参量之间的函数20.卡诺定理:(可逆机)在相同的高温热源与相同的低温热源之间工作的一切可逆机,不论用什么工作物质,效率相等。
(不可逆机)在相同的高温热源与相同的低温热源之间工作的一切不可逆机的效率小于可逆机的效率2.7 实验发现,一气体的压强与体积V 的乘积以及内能U 都只是温度的函数,即p (),().pV f T U U T ==试根据热力学理论,讨论该气体的物态方程可能具有什么形式.解:根据题设,气体具有下述特性:(1)(),pV f T =(2)().U U T =由式(2.2.7)和式(2),有 (3)0.T V U p T p V T ∂∂⎛⎫⎛⎫=-= ⎪ ⎪∂∂⎝⎭⎝⎭而由式(1)可得(4).V p T df T T V dT ∂⎛⎫= ⎪∂⎝⎭将式(4)代入式(3),有(5).df dT f T =积分得ln ln ln ,f T C =+或式中C 是常量.,pV CT =3.8 在三相点附近,固态氨的蒸气压(单位为Pa )方程为3754ln 27.92.p T=-液态氨的蒸气压力方程为3063ln 24.38.p T=-试求氨三相点的温度和压强,氨的汽化热、升华热及在三相点的熔解热.解:固态氨的蒸气压方程是固相与气相的两相平衡曲线,液态氨的蒸气压方程是液相与气想的两相平衡曲线. 三相点的温度可由两条相平衡曲线的交点确定:t T (1)3754306327.9224.38,t t T T -=-由此解出195.2.t T K =将代入所给蒸气压方程,可得t T 5934Pa.t p =将所给蒸气压方程与式(3.4.8) (2)In L p A RT =-+比较,可以求得443.12010J,2.54710J.L L =⨯=⨯升汽氨在三相点的熔解热等于L 溶40.57310J.L L L =-=⨯溶升汽1.17 温度为的1kg 水与温度为的恒温热源接触后,水温达到。
试分别0C o 100C o 100C o求水和热源的熵变以及整个系统的总熵变。
欲使参与过程的整个系统的熵保持不变,应如何使水温从升至?已知水的比热容为0C o 100C o 114.18J g K .--⋅⋅解:设有一系列彼此温差为无穷小的热源,其温度分布在与之间。
令水依次从0C o 100C o这些热源吸热,使水温由升至。
在这可逆过程中,水的熵变为0C o 100C o (1)37331273373373ln 10 4.18ln 1304.6J k .273273p p mc dT S mc T -∆===⨯⨯=⋅⎰水水从升温至所吸收的总热量为0C o 100C oQ 3510 4.18100 4.1810J.p Q mc T =∆=⨯⨯=⨯为求热源的熵变,可令热源向温度为的另一热源放出热量。
在这可逆过程中,热100C oQ 源的熵变为 (2)514.18101120.6J K .373S -⨯∆=-=-⋅热源由于热源的变化相同,式(2)给出的熵变也就是原来的不可逆过程中热源的熵变。
则整个系统的总熵变为 (3)1184J K .S S S -∆=∆+∆=⋅总水热源 (4)37312731304.6J K .p mc dT S T -∆=-=-⋅⎰%热源参与过程的整个系统的总熵变为 (5)0.S S S ∆=∆+∆=%%%总水热源3.12 蒸气与液相达到平衡. 以表示在维持两相平衡的条件下,蒸气体积随温度的变mdV dT 化率. 试证明蒸气的两相平衡膨胀系数为111.m m dV L V dT T RT ⎛⎫=- ⎪⎝⎭解:蒸气的两相平衡膨胀系数为 (1)11.m m m p m m T dV V V dp V dT V T p dT ⎡⎤⎛⎫∂∂⎛⎫=+⎢⎥ ⎪ ⎪∂∂⎝⎭⎢⎥⎝⎭⎣⎦将蒸气看作理想气体,,则有m pV RT =在克拉珀龙方程中略去液相的摩尔体积,因而11,11.m p m m m T V V T TV V p p ∂⎛⎫= ⎪∂⎝⎭⎛⎫∂=- ⎪∂⎝⎭(3)2.m dp L Lp dT TV RT ==将式(2)和式(3)代入式(1),即有(4)111.m m dV L V dT T RT ⎛⎫=- ⎪⎝⎭4.7实验测得碳燃烧为二氧化碳和一氧化碳燃烧为二氧化碳的燃烧热,其数值分Q H =-∆别如下:522CO C O 0,3.951810J;H --=∆=-⨯5221CO CO O 0, 2.828810J.2H --=∆=-⨯试根据赫斯定律计算碳燃烧为一氧化碳的燃烧热.解:本题给出了两个实验数据,在291K 和下,有1n p(1)522CO C O 0, 3.951810J;H --=∆=-⨯ (2)5221CO CO O 0, 2.828810J.2H --=∆=-⨯式(1)的含义是,的与的燃烧为的,放出燃烧热1mol C 1mol 2O 1mol 2CO 由于等压过程中系统吸收的热量等于焓的增量,所以燃烧热为53.951810J.Q =⨯11.Q H =-∆式(2)的含义是,的与的燃烧为的,放出燃烧热1mol CO 1mol 22O 1mol 2CO 52222.828810J,.Q Q H =⨯=-∆ 焓是态函数,在初态和终态给定后,焓的变化就有确定值,与中间经历的过程无H ∆关. 将式(1)减去式(2),得(3)5221CO CO O 0, 1.123010J.2H --=∆=-⨯式中 式(3)意味着,的与的燃烧为的312.H H H ∆=∆-∆1mol C 1mol 22O 1mol 将放出燃烧热燃烧为CO 的燃烧热是不能直接测量的. 上面的计算CO 51.123010J.C ⨯表明,它可由C 燃烧为CO2和CO 燃烧为CO2的燃烧热计算出来. 这是应用赫斯定律的一个例子.7.11 表面活性物质的分子在液面上作二维自由运动,可以看作二维气体. 试写出二维气体中分子的速度分布和速率分布,并求平均速率,最概然速率和方均根速率υm υs .υ 解: 参照式(7.3.7)—(7.3.9),可以直接写出在液面上作二维运动的表面活性物质分子的速度分布和速率分布. 速度分布为(1)()222e d d .2x y m υυkT x y m υυkT π-+速率分布为(2)222e d .2m υkT m υυkT ππ-平均速率为2220e d m υkT m υυυkT -+∞=⎰(3)=速率平方的平均值为22320e d 2.m υkT m υυυkT kT m -+∞==⎰因此方均根速率为(4)s υ==最概然速率条件m υ22d e 0d m υkT υυ-⎛⎫= ⎪ ⎪⎝⎭确定. 由此可得(5)m υ=值得注意,上述三种速率均小于三维气体相应的速率,这是由于二维和三维气体,,s m υυυ中速率在到中的分子数分别与速度空间的体积元和成正比,因而υd υυ+2d υυπ24d υυπ二维气体中大速率分子的相对比例低于三维气体的缘故.7.16 已知粒子遵从经典玻耳兹曼分布,其能量表达式为()22221,2x y z p p p ax bx mε=++++其中是常量,求粒子的平均能量.,a b 解: 应用能量均分定理求粒子的平均能量时,需要注意所难能量表达式中和两面ε2ax bx三刀项都是的函数,不能直接将能量均分定理用于项而得x 2ax 出的结论. 要通过配方将表达为212ax kT =ε (1)()222221.224x y z b b p p p a x m a a ε⎛⎫=++++- ⎪⎝⎭在式(1)中,仅第四项是的函数,又是平方项. 由能量均分定理知x ()22222124x y z b b p p p a x m a a ε⎛⎫=++++- ⎪⎝⎭ (2)22.4b kT a =-证明:1.14试根据热力学第二定律证明两条绝热线不能相交。
解:假设在图中两条绝热线交于点,如图所示。
设想一等温线与pV -C 两条绝热线分别交于点和点(因为等温线的斜率小于绝热线的斜率,这样的等温线总A B 是存在的),则在循环过程中,系统在等温过程中从外界吸取热量,而在循ABCA AB Q 环过程中对外做功,其数值等于三条线所围面积(正值)。
