大学物理第06章补充例题
大学物理6-8单元课后习题答案（详解）
第六章 静电场中的导体与电介质 6 －1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近，则导体B 的电势将（ ）（A ） 升高 （B ） 降低 （C ） 不会发生变化 （D ） 无法确定 分析与解 不带电的导体B 相对无穷远处为零电势。
由于带正电的带电体A 移到不带电的导体B 附近时，在导体B 的近端感应负电荷；在远端感应正电荷，不带电导体的电势将高于无穷远处，因而正确答案为（A ）。
6 －2 将一带负电的物体M 靠近一不带电的导体N ，在N 的左端感应出正电荷，右端感应出负电荷。
若将导体N 的左端接地（如图所示），则（ ）（A ） N 上的负电荷入地 （B ）N 上的正电荷入地（C ） N 上的所有电荷入地 （D ）N 上所有的感应电荷入地分析与解 导体N 接地表明导体N 为零电势，即与无穷远处等电势，这与导体N 在哪一端接地无关。
因而正确答案为（A ）。
6 －3 如图所示将一个电量为q 的点电荷放在一个半径为R 的不带电的导体球附近，点电荷距导体球球心为d ，参见附图。
设无穷远处为零电势，则在导体球球心O 点有（ ）（A ）d εq V E 0π4,0== （B ）dεq V d εq E 020π4,π4== （C ）0,0==V E（D ）Rεq V d εq E 020π4,π4==分析与解 达到静电平衡时导体内处处各点电场强度为零。
点电荷q 在导 体球表面感应等量异号的感应电荷±q′，导体球表面的感应电荷±q′在球心O 点激发的电势为零，O 点的电势等于点电荷q 在该处激发的电势。
因而正确答案为（A ）。
6 －4 根据电介质中的高斯定理，在电介质中电位移矢量沿任意一个闭合曲面的积分等于这个曲面所包围自由电荷的代数和。
下列推论正确的是( )（A ） 若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内一定没有自由电荷（B ） 若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内电荷的代数和一定等于零（C ） 若电位移矢量沿任意一个闭合曲面的积分不等于零，曲面内一定有极化电荷（D ） 介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关 （E ） 介质中的电位移矢量与自由电荷和极化电荷的分布有关分析与解 电位移矢量沿任意一个闭合曲面的通量积分等于零，表明曲面 内自由电荷的代数和等于零；由于电介质会改变自由电荷的空间分布，介质中的电位移矢量与自由电荷与位移电荷的分布有关。
大学物理第六章课后习题答案
第六章 静电场中的导体与电介质 6 －1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近，则导体B 的电势将（ ）（A ） 升高 （B ） 降低 （C ） 不会发生变化 （D ） 无法确定 分析与解 不带电的导体B 相对无穷远处为零电势。
由于带正电的带电体A 移到不带电的导体B 附近时，在导体B 的近端感应负电荷；在远端感应正电荷，不带电导体的电势将高于无穷远处，因而正确答案为（A ）。
6 －2 将一带负电的物体M 靠近一不带电的导体N ，在N 的左端感应出正电荷，右端感应出负电荷。
若将导体N 的左端接地（如图所示），则（ ）（A ） N 上的负电荷入地 （B ）N 上的正电荷入地（C ） N 上的所有电荷入地 （D ）N 上所有的感应电荷入地分析与解 导体N 接地表明导体N 为零电势，即与无穷远处等电势，这与导体N 在哪一端接地无关。
因而正确答案为（A ）。
6 －3 如图所示将一个电量为q 的点电荷放在一个半径为R 的不带电的导体球附近，点电荷距导体球球心为d ，参见附图。
设无穷远处为零电势，则在导体球球心O 点有（ ）（A ）d εq V E 0π4,0== （B ）dεq V d εq E 020π4,π4== （C ）0,0==V E（D ）Rεq V d εq E 020π4,π4==分析与解 达到静电平衡时导体内处处各点电场强度为零。
点电荷q 在导 体球表面感应等量异号的感应电荷±q′，导体球表面的感应电荷±q′在球心O 点激发的电势为零，O 点的电势等于点电荷q 在该处激发的电势。
因而正确答案为（A ）。
6 －4 根据电介质中的高斯定理，在电介质中电位移矢量沿任意一个闭合曲面的积分等于这个曲面所包围自由电荷的代数和。
下列推论正确的是( )（A ） 若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内一定没有自由电荷（B ） 若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内电荷的代数和一定等于零（C ） 若电位移矢量沿任意一个闭合曲面的积分不等于零，曲面内一定有极化电荷（D ） 介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关 （E ） 介质中的电位移矢量与自由电荷和极化电荷的分布有关分析与解 电位移矢量沿任意一个闭合曲面的通量积分等于零，表明曲面 内自由电荷的代数和等于零；由于电介质会改变自由电荷的空间分布，介质中的电位移矢量与自由电荷与位移电荷的分布有关。
大学物理学(课后答案)第5-6章
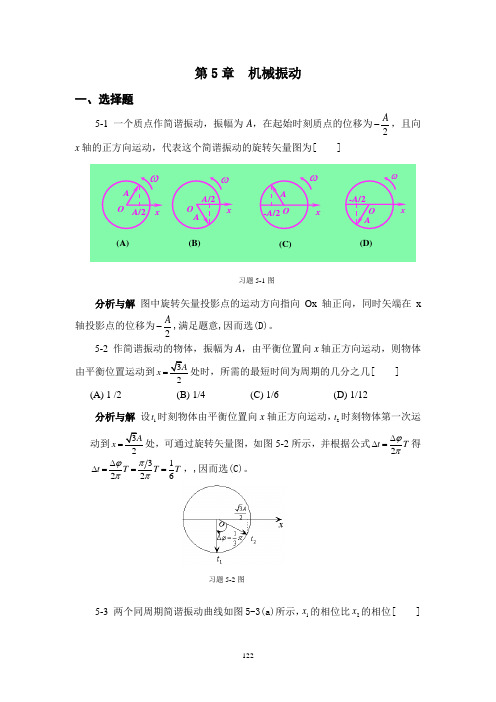
第5章 机械振动一、选择题5-1 一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为2A-，且向x 轴的正方向运动，代表这个简谐振动的旋转矢量图为[ ]分析与解 图中旋转矢量投影点的运动方向指向Ox 轴正向，同时矢端在x轴投影点的位移为2A-,满足题意,因而选(D)。
5-2 作简谐振动的物体，振幅为A ，由平衡位置向x 轴正方向运动，则物体由平衡位置运动到32Ax =处时，所需的最短时间为周期的几分之几[ ] (A) 1 /2 (B) 1/4 (C) 1/6 (D) 1/12分析与解 设1t 时刻物体由平衡位置向x 轴正方向运动，2t 时刻物体第一次运动到32A x =处，可通过旋转矢量图，如图5-2所示，并根据公式2t T ϕπ∆∆=得31226t T T T ϕπππ∆∆===，,因而选(C)。
5-3 两个同周期简谐振动曲线如图5-3(a)所示，1x 的相位比2x 的相位[ ]O O OO A Axxx(A) (B)(D)(C)A /2-A /2 A /2 -A /2A Aωωωωx习题5-1图习题5-2图(A) 落后2π(B) 超前2π(C) 落后π (D) 超前π分析与解 可通过振动曲线作出相应的旋转矢量图（b ），正确答案为（B ）。
5-4 一弹簧振子作简谐振动，总能量为E ，若振幅增加为原来的2倍，振子的质量增加为原来的4倍，则它的总能量为[ ](A) 2E (B) 4E (C) E (D) 16E 分析与解 因为简谐振动的总能量2p k 12E E E kA =+=，因而当振幅增加为原来的2倍时，能量变为原来的4倍，因而答案选(B)。
5-5 两个同振动方向、同频率、振幅均为A 的简谐振动合成后，振幅仍为A ，则这两个简谐振动的相位差为[ ](A) 60 (B) 90 (C) 120 (D) 180分析与解 答案（C ）。
由旋转矢量图可知两个简谐振动的相位差为 120时,合成后的简谐运动的振幅仍为A 。
大学物理学第06章补充例题
8
物理学
第五版
第六章补充例题
4 如图，一平行板电容器极板面积为S， 厚度为d1 ，中间一半体积内充有电容率为1 的介质，另一半体积内充有电容率为2的介 质，求该电容器的电容. S/2 S/2
1
2
d
第六章 静电场中的导体和电介质
9
物理学
第五版
第六章补充例题
解 此题可看成两个电容器的串联
C1
2
2
R
1
0
Qr ε0 4 πε R 3 2 0
2
4 πr 2dr
1
R
Q ε0 4 πε r 2 2 0
Q
40 π ε 0 R 3Q
2
Q
2
8πε0 R
R r
Q
20 π ε 0 R
第六章 静电场中的导体和电介质
16
3
1
πr πR
3
E1
E2
Qr 4ε0 R
Q 4ε0r
2
R r
Q
r R
r R
第六章 静电场中的导体和电介质
15
物理学
第五版
第六章补充例题
We
(
1 2
DE ) d V
2
V
1 2
V1
ε 0 E1 d V
2
1 2
V2
ε0 E 2 dV
4 πr 2dr
Q
A
第六章 静电场中的导体和电介质
B
11
物理学
第五版
第六章补充例题
解 两球接触后电势相等，电荷重新分配 .
大学物理学习指导详细标准答案
大学物理学习指导详细答案————————————————————————————————作者：————————————————————————————————日期：2第六章 相对论【例题精选】例6-1 当惯性系S 和S ′的坐标原点O 和O ′重合时，有一点光源从坐标原点发出一光脉冲，在S 系中经过一段时间t 后（在S ′系中经过时间t ′），此光脉冲的球面方程（用直角坐标系）分别为：S 系 ； S ′系 ．22222t c z y x =++ 22222t c z y x '='+'+'例6-2 下列几种说法中正确的说法是： (1) 所有惯性系对物理基本规律都是等价的．(2) 在真空中，光的速度与光的频率、光源的运动状态无关． (3) 在任何惯性系中，光在真空中沿任何方向的传播速率都相同．(A) 只有(1)、(2) 正确． (B) 只有(1)、(3) 正确． (C) 只有(2)、(3) 正确． (D) (1)、(2)、(3)都正确． [ D ] 例6-3 经典的力学相对性原理与狭义相对论的相对性原理有何不同？答：经典力学相对性原理是指对不同的惯性系，牛顿定律和其它力学定律的形式都是相同的．狭义相对论的相对性原理指出：在一切惯性系中，所有物理定律的形式都是相同的，即指出相对性原理不仅适用于力学现象，而且适用于一切物理现象。
也就是说，不仅对力学规律所有惯性系等价，而且对于一切物理规律，所有惯性系都是等价的． 例6-4 有一速度为u 的宇宙飞船沿x 轴正方向飞行，飞船头尾各有一个脉冲光源在工作，处于船尾的观察者测得船头光源发出的光脉冲的传播速度大小为 ；处于船头的观察者测得船尾光源发出的光脉冲的传播速度大小为 ． c c 例6-5 关于同时性的以下结论中，正确的是(A) 在一惯性系同时发生的两个事件，在另一惯性系一定不同时发生．(B) 在一惯性系不同地点同时发生的两个事件，在另一惯性系一定同时发生．(C) 在一惯性系同一地点同时发生的两个事件，在另一惯性系一定同时发生．(D) 在一惯性系不同地点不同时发生的两个事件，在另一惯性系一定不同时发生． [ C ] 例6-6静止的μ子的平均寿命约为 τ0 =2×10-6 s ．今在8 km 的高空，由于π介子的衰变产生一个速度为v = 0.998 c (c 为真空中光速)的μ子，试论证此μ子有无可能到达地面． 证明：考虑相对论效应，以地球为参照系，μ子的平均寿命：62106.31)/(1-⨯=-=c v ττ s则μ 子的平均飞行距离： =⋅=τv L 9.46 km ．μ 子的飞行距离大于高度，有可能到达地面．例6-7 两惯性系中的观察者O 和O ′以0.6 c (c 为真空中光速)的相对速度互相接近．如果O 测得两者的初始距离是20 m ，则O 相对O ′运动的膨胀因子γ= ；O ′测得两者经过时间∆t ′= s 后相遇．1.25(或5/4) 8.89×10-8例6-8 两个惯性系S 和S ′，沿x (x ′)轴方向作匀速相对运动. 设在S ′系中某点先后发生两个事件，用静止于该系的钟测出两事件的时间间隔为τ0 ，而用固定在S 系的钟测出这两个事件的时间间隔为τ ．又在S ′系x ′轴上放置一静止于该系、长度为l 0的细杆，从S 系测得此杆的长度为l, 则 (A) τ < τ0；l < l 0． (B) τ < τ0；l > l 0．(C) τ > τ0；l > l 0． (D) τ > τ0；l < l 0． [ D ]例6-9 α 粒子在加速器中被加速，当其质量为静止质量的3倍时，其动能为静止能量的(A) 2倍． (B) 3倍． (C) 4倍． (D) 5倍． [ A ] 例6-10 匀质细棒静止时的质量为m 0，长度为l 0，当它沿棒长方向作高速的匀速直线运动时，测得它的长为l ，那么，该棒的运动速度v = ；该棒所具有的动能E K = ．c)(020lll c m - 例6-11 观察者甲以0.8c 的速度（c 为真空中光速）相对于静止的观察者乙运动，若甲携带一长度为l 、截面积为S ，质量为m 的棒，这根棒安放在运动方向上，则甲测得此棒的密度为 ；乙测得此棒的密度为 ．lSm925 例6-12 根据相对论力学，动能为0.25 MeV 的电子，其运动速度约等于(A) 0.1c (B) 0.5 c (C) 0.75 c (D) 0.85 c (c 表示真空中的光速，电子的静能m 0c 2 = 0.51 MeV) [ C ] 例6-13 令电子的速率为v ，则电子的动能E K 对于比值v / c 的图线可用下列图中哪一个图表示？ （c 表示真空中光速）OE K v /c1.0(A)OE K v /c 1.0(B)OE K v /c1.0(C)OE K v /c1.0(D)[ D ]【练习题】6-1 在某地发生两件事，静止位于该地的甲测得时间间隔为4 s ，若相对于甲作匀速直线运动的乙测得时间间隔为5 s ，则乙相对于甲的运动速度是(c 表示真空中光速) (A) (4/5) c ． (B) (3/5) c ． (C) (2/5) c ． (D) (1/5) c ． [ B ] 6-2 假定在实验室中测得静止在实验室中的μ+子(不稳定的粒子)的寿命为2.2×10-6 s ，当它相对于实验室运动时实验室中测得它的寿命为1.63×10-5s ．则 μ+子相对于实验室的速度是真空中光速的多少倍？为什么？ 答：设μ+子相对于实验室的速度为v μ+子的固有寿命τ0 =2.2×10-6 s μ+子相对实验室作匀速运动时的寿命τ0 =1.63×10-5 s按时间膨胀公式：20)/(1/c v -=ττ移项整理得： 202)/(τττ-=c v 20)/(1ττ-=c = 0.99c则 μ+子相对于实验室的速度是真空中光速的0.99倍．6-3 在S 系中的x 轴上相隔为∆x 处有两只同步的钟A 和B ，读数相同．在S ＇系的x ＇轴上也有一只同样的钟A ＇，设S ＇系相对于S 系的运动速度为v , 沿x 轴方向, 且当A ＇与A 相遇时，刚好两钟的读数均为零．那么，当A ＇钟与B 钟相遇时，在S 系中B 钟的读数是 ；此时在S ＇系中A ＇钟的读数是 ．x /v 2)/(1)/(c x v v -∆6-4 两个惯性系K 与K ＇坐标轴相互平行，K ＇系相对于K 系沿x 轴作匀速运动，在K ＇系的x ＇轴上，相距为L ＇的A ＇、B ＇两点处各放一只已经彼此对准了的钟，试问在K 系中的观测者看这两只钟是否也是对准了？为什么？答：没对准．根据相对论同时性，如题所述在K ＇系中同时发生，但不同地点(x ＇坐标不同)的两事件(即A ＇处的钟和B ＇处的钟有相同示数)，在K 系中观测并不同时；因此，在K 系中某一时刻同时观测，这两个钟的示数必不相同． 6-5 边长为a 的正方形薄板静止于惯性系K 的Oxy 平面内，且两边分别与x ，y 轴平行．今有惯性系K ＇以 0.8c （c 为真空中光速）的速度相对于K 系沿x 轴作匀速直线运动，则从K ＇系测得薄板的面积为 (A) 0.6a 2． (B) 0.8 a 2． (C) a 2． (D) a 2／0.6 ． [ A ] 6-6 狭义相对论确认，时间和空间的测量值都是 ，它们与观察者的 密切相关．相对的 运动6-7 地球的半径约为R 0 = 6376 km ，它绕太阳的速率约为=v 30 km ·s -1，在太阳参考系中测量地球的半径在哪个方向上缩短得最多？缩短了多少？ (假设地球相对于太阳系来说近似于惯性系) 答：在太阳参照系中测量地球的半径在它绕太阳公转的方向缩短得最多．20)/(1c R R v -=其缩短的尺寸为： ∆R = R 0- R ))/(11(20c R v --= 220/21c R v ≈∆R =3.2 cm6-8 有一直尺固定在K ′系中，它与Ox ′轴的夹角θ′＝45°，如果K ′系以匀速度沿Ox 方向相对于K 系运动，K 系中观察者测得该尺与Ox 轴的夹角(A) 大于45°． (B) 小于45°． (C) 等于45°．(D) K ′系沿Ox 正方向运动时大于45°，K ′系沿Ox 负方向运动时小于45°． [ A ]6-9 在狭义相对论中，下列说法中哪些是错误的？ (A) 一切运动物体相对于观察者的速度都不能大于真空中的光速．(B) 质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的． (C) 在一惯性系中发生于同一时刻，不同地点的两个事件在其他一切惯性系中也是同时发生的． (D) 惯性系中的观察者观察一个与他作匀速相对运动的时钟时，会看到这只时钟比与他相对静止的相同的时钟走得慢些． [ C ] 6-10 观察者甲以 0.8c 的速度（c 为真空中光速）相对于静止的观察者乙运动，若甲携带一质量为1 kg 的物体，则甲测得此物体的总能量为 ；乙测得此物体的总能量为 ．9×1016 J 1.5×1017 J 6-11 一个电子以0.99 c 的速率运动，电子的静止质量为9.11×10-31 kg ，则电子的总能量是 J ，电子的经典力学的动能与相对论动能之比是 ．5.8×10-13 8.04×10-2 6-12 一匀质矩形薄板，在它静止时测得其长为a ，宽为b ，质量为m 0．由此可算出其面积密度为m 0 /ab ．假定该薄板沿长度方向以接近光速的速度v 作匀速直线运动，此时再测算该矩形薄板的面积密度则为(A) ab c m 20)/(1v - (B) 20)/(1c ab m v - (C) ])/(1[20c ab m v - (D) 2/320])/(1[c ab m v - [ C ] 6-13 一体积为V 0，质量为m 0的立方体沿其一棱的方向相对于观察者A 以速度v 运动．观察者A 测得其密度是多少？为什么？ 答：设立方体的长、宽、高分别以x 0，y 0，z 0表示，观察者A 测得立方体的长、宽、高分别为2201c x x v -=，0y y =，0z z =． 相应体积为 2201cV xyz V v -==∵质量 2201cm m v -=故相应密度为 V m /=ρ2222011/cV c m v v --=)1(2200c V m v -=6-14 质子在加速器中被加速，当其动能为静止能量的4倍时，其质量为静止质量的(A) 4倍． (B) 5倍． (C) 6倍． (D) 8倍． [ B ]。
大学物理6,7章作业答案
⼤学物理6,7章作业答案第六章机械振动参考答案⼀. 选择题1. ( C )2. ( B )3.( D )4. ( D )5. ( B )6. ( D )7. ( D )8. ( D )9. ( C )⼆. 填空题10. （,）11. （；；）12. （；）13. （）14. （ 0 ）三. 计算题15. 质量为10g 的⼩球与轻弹簧组成的系统，按 cm )3 8cos(5.0ππ+=t x 的规律振动，式中t 的单位为S 。
试求：（1）振动的圆周期、周期、初相、速度及加速度的最⼤值；（2）t =1s 、2s 时的相位各为多少？解：（1）将原式与简谐振动的⼀般表达式⽐较圆频率，初相，周期速度最⼤值加速度最⼤值（2）相位将代⼊，得相位分别为．16. ⼀质点沿x 轴作简谐振动，平衡位置在x 轴的原点，振幅cm 3=A ，频率Hz 6=ν。
（1）以质点经过平衡位置向x 轴负⽅向运动为计时零点，求振动的初相位及振动⽅程；（2）以位移 cm 3-=x 时为计时零点，写出振动⽅程.解: (1) 设振动⽅程为当t =0, x =0, 做旋转⽮量图，可得初相位振动⽅程为(2) 当t =0 , x = －3cm , 做旋转⽮量图，可得初相位所以振动⽅程为17. 在⼀轻弹簧下端悬挂砝码时，弹簧伸长8cm ，现在此弹簧下端悬挂的物体，构成弹簧振⼦。
将物体从平衡位置向下拉动4cm ，并给以向上的21cm/s 初速度（设这时t = 0）令其振动起来，取x 轴向下，写出振动⽅程。
解: 设振动⽅程为由，可知振幅A初相位由旋转⽮量图可得振动⽅程为18. 两质点同时参与两个在同⼀直线上的简谐振动,其表达式为：)652cos(03.0,)62cos(04.021ππ-=+=t x t x试求其合振动的振幅和初相位（式中x 以m 计，t 以s 计）．解：⼆振动的频率相同，它们的相位差因⽽合振动的振幅设合振动的初相为，则第七章机械波参考答案⼀. 选择题1. (B)2. (D)3. (B)4.（C ）5. （C ）6. (D)7.（C ）8.（B ）9.（C ）⼆. 填空题 10. ( 503 m/s )11. ( 1 Hz ； 1m/s ； 1m )12. (；)13. ( )14. ( 5J ) 15. ( - π/2 ) 16. ( - 2π/3 )三. 计算题17. ⼀横波沿绳⼦传播时的波动表式为 )410cos(05.0x t y ππ-=[SI] . 求：（1）此波的振幅、波速、频率和波长;（2）绳⼦上各质点振动的最⼤速度和最⼤加速度; 解：（1）波动⽅程可得振幅频率波长波速（2）绳上各质点振动时的最⼤速度绳上各质点振动时的最⼤加速度18. ⼀平⾯简谐纵波沿线圈弹簧传播．设波沿着x 轴正向传播，弹簧中某圈的最⼤位移为3.0cm ，振动频率为Hz 5.2，弹簧中相邻两疏部中⼼的距离为cm 24. 当0=t 时，在0=x 处质元的位移为零并向x 轴正向运动, 试写出该波的波动表式．解: 设平⾯简谐波的波动⽅程为已知：，，⼜时，原点处质点的位移，速度，故该质点的初相cm19. ⼀平⾯波在介质中以速度1s m 20-?=u 沿x 轴负⽅向传播，已知a 点的振动表式为t y a π4cos 3= [SI]．（1）以a 为坐标原点写出波动⽅程；（2）以与a 点相距m 5处的b 点为坐标原点，写出波动⽅程．解：（1）已知A = 3m ，,因波沿x 轴负⽅向传播，以a 点为坐标原点的波动⽅程为（2）以a 点为坐标原点时，b 点的坐标为代⼊上式得b 点的振动⽅程为若以b 点为坐标原点，则波动⽅程为20. 如图所⽰，已知和时的波形曲线分别为图中实线曲线Ⅰ和虚线曲线Ⅱ，波沿x 轴正向传播. 根据图中给出的条件，求：（1）波动⽅程；（2）P 点质元的振动⽅程.解：(1) 设波动⽅程为由图知A= 0.1m，λ= 4m⼜时，原点处质点的位移，速度，故该质点的初相（2）将代⼊波动⽅程，得点质元振动⽅程为21. 如图所⽰，两相⼲波源分别在P、Q两点，它们发出频率为ν，波长为λ，初相相同的两列相⼲波，振幅分别为A1和A2 ，设2/3λPQ，R为PQ连线上的⼀点．求：=（1）⾃P、Q发出的两列波在R处的相位差；（2）两波在R处⼲涉时的合振幅．解：（1）两列波的初相位相同，在R处的相位差为（2）两波在R处的振动⽅向相同，频率相同，相位差，则合振幅为。
《大学物理学》第1-6章课后习题解答
大学物理学习题答案习题一答案 习题一1.1 简要回答下列问题：(1) 位移和路程有何区别？在什么情况下二者的量值相等？在什么情况下二者的量值不相等？(2) 平均速度和平均速率有何区别？在什么情况下二者的量值相等？(3) 瞬时速度和平均速度的关系和区别是什么？瞬时速率和平均速率的关系和区别又是什么？(4) 质点的位矢方向不变，它是否一定做直线运动？质点做直线运动，其位矢的方向是否一定保持不变？ (5) r ∆和r ∆有区别吗？v ∆和v ∆有区别吗？0dvdt =和0d v dt=各代表什么运动？ (6) 设质点的运动方程为：()x x t =，()y y t =，在计算质点的速度和加速度时，有人先求出r =drv dt= 及 22d r a dt =而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即v = 及 a =你认为两种方法哪一种正确？两者区别何在？(7) 如果一质点的加速度与时间的关系是线性的，那么，该质点的速度和位矢与时间的关系是否也是线性的？(8) “物体做曲线运动时，速度方向一定在运动轨道的切线方向，法向分速度恒为零，因此其法向加速度也一定为零.”这种说法正确吗？(9) 任意平面曲线运动的加速度的方向总指向曲线凹进那一侧，为什么？(10) 质点沿圆周运动，且速率随时间均匀增大，n a 、t a 、a 三者的大小是否随时间改变？ (11) 一个人在以恒定速度运动的火车上竖直向上抛出一石子，此石子能否落回他的手中？如果石子抛出后，火车以恒定加速度前进，结果又如何？1.2 一质点沿x 轴运动，坐标与时间的变化关系为224t t x -=，式中t x ,分别以m 、s 为单位，试计算：(1)在最初s 2内的位移、平均速度和s 2末的瞬时速度；(2)s 1末到s 3末的平均加速度；(3)s 3末的瞬时加速度。
解：(1) 最初s 2内的位移为为： (2)(0)000(/)x x x m s ∆=-=-= 最初s 2内的平均速度为： 00(/)2ave x v m s t ∆===∆ t 时刻的瞬时速度为：()44dxv t t dt==- s 2末的瞬时速度为：(2)4424/v m s =-⨯=-(2) s 1末到s 3末的平均加速度为：2(3)(1)804/22ave v v v a m s t ∆---====-∆ (3) s 3末的瞬时加速度为：2(44)4(/)dv d t a m s dt dt-===-。
三峡大学大学物理第六章答案
第6章 真空中的静电场 习题答案1. 电荷为q +和q 2-的两个点电荷分别置于1=x m 和1-=x m 处。
一试验电荷置于x 轴上何处，它受到的合力等于零？解：根据两个点电荷对试验电荷的库仑力的大小及方向可以断定，只有试验电荷0q 位于点电荷q +的右侧，它受到的合力才可能为0，所以200200)1(π4)1(π42-=+x qq x qq εε 故 223+=x2. 电量都是q 的三个点电荷，分别放在正三角形的三个顶点。
试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解：(1) 以A 处点电荷为研究对象，由力平衡知，q '为负电荷，所以2220)33(π4130cos π412a q q a q '=︒εε故 q q 33-=' (2)与三角形边长无关。
3. 如图所示，半径为R 、电荷线密度为1λ的一个均匀带电圆环，在其轴线上放一长为l 、电荷线密度为2λ的均匀带电直线段，该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解：先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dl dq 1λ=，dq 在带电圆环轴线上x 处产生的场强大小为)(4220R x dqdE +=πε 根据电荷分布的对称性知，0==z y E E23220)(41 cos R x xdqdE dE x +==πεθ式中：θ为dq 到场点的连线与x 轴负向的夹角。
⎰+=23220)(4dq R x xE x πε 232210)(24R x R x +⋅=πλπε232201)(2R x xR +=ελ 下面求直线段受到的电场力。
在直线段上取dx dq 2λ=，dq 受到的电场力大小为dq E dF x =dx R x xR 2322021)(2+=ελλ方向沿x 轴正方向。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章 静电场中的导体和电介质
物理学
第五版
第六章补充例题
3 一球型导体，带电荷量为q，置于一 任意形状的空腔导体内，当用导线将两者 连接后，与未连接前相比，系统的静电场 能量将 （A）增大 q （B）减少 -q +q （C）不变 （D）无法确定
第六章 静电场中的导体和电介质
7
物理学
第五版
第六章补充例题
s
D 4r 2 q
0 D Q 2 4πr 0r a ar
Q
a b
c
r
第六章 静电场中的导体和电介质
2
物理学
第五版
第六章补充例题
D ε0 εr E
0ra 0 Q a r b 2 4ε r 0 E Q brc 4ε ε r 2 0 r Q cr 4ε r 2 0
第六章 静电场中的导体和电介质
R r
Q
9
物理学
第五版
第六章补充例题
1 1 1 2 2 We ( DE )dV ε0 E1 dV ε0 E2 dV V 2 V1 2 V2 2 2 2 R1 1 Qr Q 2 2 ε0 4 π r d r ε 4 π r dr 0 3 2 0 2 R 2 4 π ε R 0 4πε0 r
物理学
第五版
第六章补充例题
1 一半径为a的导体球, 被围在内半径为 b、外半径为c，相对介电系数为r 的介质同 心球壳内，若导体球带电荷量为Q, 求D(r), E (r)和导体表面电势.
Q
a b
c
r
第六章 静电场中的导体和电介质
1
物理学
第五版
第六章补充例题
解
D dS q
Q Q 40πε0 R 8πε0 R 3Q 2 20πε0 R
第六章 静电场中的导体和电介质
2
2
R r
Q
10
4 一均匀带电荷量Q的球体, 半径为R, 试求其电场储存的能量.
R
Q
第六章 静电场中的导体和电介质
8
物理学
第五版
第六章补充例题
1 解 We we dV DE dV 2 q SE dS ε0 4 3 πr 1 2 E1 4πr Q 3 0 4 πR 3 3 Qr E1 rR 3 4ε0 R Q rR E2 2 4ε0 r
Q 4ε0 εr Q 4ε0 c
1 1 b c
Q
a b
c
r
第六章 静电场中的导体和电介质
4
物理学
第五版
第六章补充例题
2 一空气平行板电容器电容为C，两极板 间距为d, 充电后，两极板间相互作用力为F, 求两极板间的电势差和极板上电荷量的大小.
+Q
+ + + + + +
Q
a b
c
r
第六章 静电场中的导体和电介质
3
物理学
第五版
Hale Waihona Puke 第六章补充例题ua
a
b
E dr
c Q Q Q dr dr dr 2 2 2 a 4ε r b 4ε ε r c 4ε r 0 0 r 0 Q 1 1 4ε0 a b
F
-Q
d
- - - - - 5
第六章 静电场中的导体和电介质
物理学
第五版
第六章补充例题
ε0 s 解 C d Q E 2ε 0 2ε 0 s 2 Q F EQ 2ε 0 s
Q 2ε0 sF 2CdF
Q u 2dF / C C
+Q
+ + + + + +
F
-Q
d
- - - - - 6