人教版数学九年级下册数学:27.1 --27.3 同步复习题 (附答案)
新课程课堂同步练习册(九年级数学下册人教版)答案

数学课堂同步练习册(人教版九年级下册)参考答案第二十六章 二次函数26.1 二次函数及其图象(一)一、 D C C 二、 1. ≠0,=0,≠0,=0,≠0 =0, 2. x x y 62+=3. )10(x x y -= ,二三、1. 23x y = 2.(1)1,0,1 (2)3,7,-12 (3)-2,2,0 3. 2161x y = §26.1 二次函数及其图象(二)一、 D B A 二、1. 下,(0,0),y 轴,高 2. 略 3. 答案不唯一,如22x y -= 三、1.a 的符号是正号,对称轴是y 轴,顶点为(0,0) 2. 略3. (1) 22x y -= (2) 否 (3)()6-;(),6-§26.1 二次函数及其图象(三)一、 BDD 二、1.下, 3 2. 略 三、1. 共同点:都是开口向下,对称轴为y 轴.不同点:顶点分别为(0,0);(0,2);(0,-2) .2. 41=a 3. 532+-=x y §26.1 二次函数及其图象(四)一、 DCB 二、1. 左,1, 2. 略 3. 向下,3-=x ,(-3,0) 三、1. 3,2a c ==- 2. 13a =3. ()2134y x =-§26.1 二次函数及其图象(五)一、C D B 二、1. 1=x ,(1,1) 2. 左,1,下,2 3.略三、1.略2.(1)()212y x =+- (2)略 3. (1)3)2(63262--=-===x y k h a(2)直线2223x =>-小2.(1)()212y x =+- (2)略 §26.1 二次函数及其图象(六) 一、B B D D 二、1.23)27,23(=x 直线 2. 5;5;41<-3. < 三、1. ab ac a b x a y x y x y 44)2(32)31(36)4(2222-++=---=--= 略2. 解:(1)设这个抛物线的解析式为2y ax bx c =++.由已知,抛物线过(20)A -,,(10)B ,,(28)C ,三点,得4200428a b c a b c a b c -+=⎧⎪++=⎨⎪++=⎩,,.解这个方程组,得 224a b c =⎧⎪=⎨⎪=-⎩.∴所求抛物线的解析式为2224y x x =+-.(2)222192242(2)222y x x x x x ⎛⎫=+-=+-=+- ⎪⎝⎭.∴该抛物线的顶点坐标为1922⎛⎫-- ⎪⎝⎭,. §26.2 用函数观点看一元二次方程一、 C D D 二、1.(-1,0);(2,0) (0,-2) 2. 一 3. 312-或; 231<<-x ; 312x x <->或 三、1.(1)1x =-或3x = (2)x <-1或x >3(3)1-<x <3 2.(1)()21232y x =--+ (2)()20和()20 §26.3 实际问题与二次函数(一)一、 A C D 二、1. 2- 大 18 2. 7 3. 400cm 2三、1.(1)当矩形的长与宽分别为40m 和10m 时,矩形场地的面积是400m 2(2)不能围成面积是800m 2的矩形场地.(3)当矩形的长为25m 、宽为25m 时,矩形场地的面积最大,是625m 22.m ,矩形的一边长为2x m .其相邻边长为((2041022xx -+=-+∴该金属框围成的面积(121022S x x ⎡⎤=⋅-++⎣⎦(2320x x =-++ (0<x<10-当30x ==-.此时矩形的一边长为)260x m =-,相邻边长为((()10210310m -+⋅-=.()21003300.S m =-=-最大26.3 实际问题与二次函数(二)一、A B A 二、1. 2 2. 250(1)x + 3.252或12.5 三、1. 40元 当5.7=x 元时,625=最大W 元 2. 解:(1)降低x 元后,所销售的件数是(500+100x ),y=-100x 2+600x+5500 (0<x ≤11 )(2)y=-100x 2+600x+5500 (0<x ≤11 )配方得y=-100(x -3)2+6400 当x=3时,y 的最大值是6400元。
人教版数学九年级下《27.3位似》测试(含答案)
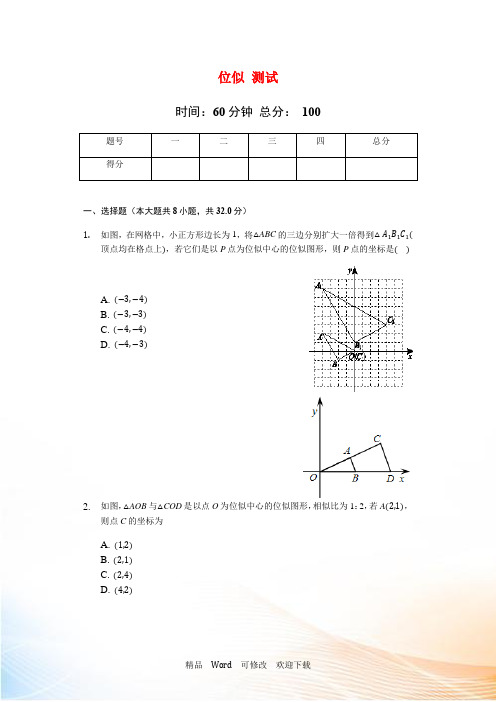
位似测试时间:60分钟总分:100题号一二三四总分得分一、选择题(本大题共8小题,共32.0分)1.如图,在网格中,小正方形边长为1,将△ABC的三边分别扩大一倍得到△A1B1C1(顶点均在格点上),若它们是以P点为位似中心的位似图形,则P点的坐标是()A. (−3,−4)B. (−3,−3)C. (−4,−4)D. (−4,−3)2.如图,△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,若A(2,1),则点C的坐标为A. (1,2)B. (2,1)C. (2,4)D. (4,2)3.如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段CD.若点A(1,2),B(2,0),D(5,0),则点A的对应点C的坐标是()A. (2,5),5)B. (52C. (3,5)D. (3,6)4.下列说法:①有一个锐角相等的两个直角三角形相似;②顶角相等的两个等腰三角形相似;③任意两个菱形一定相似;④位似图形一定是相似图形;其中正确的个数是()A. 1个B. 2个C. 3个D. 4个5.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为()A. 4:9B. 2:5C. 2:3D. √2:√36.按如下方法,将△ABC的三边缩小的原来的1,如图,任取一点O,连AO、BO、2CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是()①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形③△ABC与△DEF的周长比为1:2 ④△ABC与△DEF的面积比为4:1.A. 1B. 2C. 3D. 47.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的1后得到线段CD,则端点C的坐标为()2A. (3,3)B. (4,3)C. (3,1)D. (4,1)8.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是()A. −2aB. 2a−2C. 3−2aD. 2a−3二、填空题(本大题共8小题,共32.0分)9.△OAB三个顶点的坐标分别为O(0,0),A(4,6),B(3,0),以O为位似中心,将△OAB缩小为原来的12,得到△OA′B′,则点A的对应点A′的坐标为______.10.如图,四边形ABCD与四边形EFGH位似,位似中心点是O,OEOA =35,则FGBC=______.11.如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=______.12.如图,在平面直角坐标系xOy中,△ABC与△A′B′C′顶点的横、纵坐标都是整数.若△ABC与△A′B′C′是位似图形,则位似中心的坐标是______.13.如图,△ABO三个顶点的坐标分别为A(2,4),B(6,0),O(0,0),,可以原点O为位似中心,把这个三角形缩小为原来的12以得到△A′B′O,已知点B′的坐标是(3,0),则点A′的坐标是______.14.已知,如图,A′B′//AB,B′C′//BC,且OA′:A′A=4:3,则△ABC与______ 是位似图形,位似比为______ ;△OAB与______ 是位似图形,位似比为______ .15.已知在平面直角坐标系中,点A(−3,−1)、B(−2,−4)、C(−6,−5),以原点为位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为______.16.如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为______.三、计算题(本大题共4小题,共20.0分)17.如图,在每个小正方形边长为1个单位长的网格中,建立直角坐标系xOy,点A,B,C均在格点上.(1)请在该网格内部画出△A1BC1,使其与△ABC关于点B成位似图形,且位似比为2:1;(2)直接写出(1)中C1点的坐标为______.18.(10分)在平面直角坐标系中,△ABC的位置如下图所示,其中点B(−3,1),解答下列问题:(1)将△ABC绕着点O(0,0)顺时针旋转90∘得到△A1B1C1,并写出B1的坐标;(5分)(2)在网格图中,以O为位似中心在另一侧将△A1B1C1放大2倍得到△A′B′C′,并写出B′的坐标.(5分)19.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是______ ;(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是______ .20.如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).(1)请你根据位似的特征并结合点B的坐标变化回答下列问题:,3),则A′的坐标为______ ;①若点A(52②△ABC与△A′B′C′的相似比为______ ;(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)四、解答题(本大题共2小题,共16.0分)21.如图,网格图的每个小正方形边长均为1.△OAB的顶点均在格点上.已知△OA′B′与△OAB是以O为位似中心的位似图形,且位似比为1:3.(1)请在第一象限内画出△OA′B′;(2)试求出△OA′B′的面积.22.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(0,4),B(−2,0),C(4,0)(1)以原点O为位似中心,画出所有满足条件的△DEF,使△DEF和△ABC位似,且DE:AB=EF:BC=1:2。
人教版九年级下册数学 27.1--27.3分节测试题含答案

人教版九年级下册数学 27.1--27.3分节测试题含答案27.1图形的相似一、单选题1.下列说法正确的是( )A .对应边都成比例的多边形相似B .对应角都相等的多边形相似C .边数相同的正多边形相似D .矩形都相似2.如图,D E 、分别是ABC △边,AB AC 上的点,ADE ACB ∠=∠,若2,6,4AD AB AC ===,则AE 的长是( ).A .1B .2C .3D .43.如图,AB ⊥BD ,CD ⊥BD ,垂足分别为B 、D ,AC 和BD 相交于点E ,EF ⊥BD 垂足为F .则下列结论错误的是( )A .AE EC =BE EDB .AE ED =AB CDC .EF AB =DF DBD .AD BD =AE BF 4.如图,有三个矩形,其中是相似图形的是( )A .甲和乙B .甲和丙C .乙和丙D .甲、乙和丙5.如图,在△ABC 中,点D ,E ,F 分别是边AB ,AC ,BC 上的点,DE ∥BC ,EF ∥AB ,且A.5∶8 B.3∶8 C.3∶5 D.2∶56.如图,在矩形ABCD中,点E、F分别在BC,AD上,四边形ABEF是正方形,矩形ABCD∼矩形ECDF,AD=2,则DF的值为()A.√5−1B.√5+1C.√5−3D.3−√57.如果两个相似多边形的面积比为4:9,那么它们的周长比为()A B.2:3 C.4:9 D.16:818.如图,有三个直角三角形,其中OA=AB=BC=CD=1,则线段OA,OD的比例中项线段的长度为( )A B C D9.如图,△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC.则BN:NQ:QM 等于()二、填空题10.已知线段a =2cm 、b =8cm ,那么线段a 、b 的比例中项等于_________cm..11.如图,在△ABC 中,点D 、E 分别在AB 、AC 边上,DE ∥BC ,若23AD AB =,AE=4,则EC 等于_____.12.已知AB ∥CD ,AD 与BC 相交于点O.若BO OC =23,AD =10,则AO =____.13.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为_____14.在ABC 中,AB AC =,点D 在直线BC 上,3DC DB =,点E 为AB 边的中点,连接AD ,射线CE 交AD 于点M ,则AM MD的值为________. 15.小芳的房间有一面积为3 m 2的玻璃窗,她站在室内离窗子4 m 的地方向外看,她能看到窗前面一幢楼房的面积有____m 2(楼之间的距离为20 m).16.在长8cm ,宽6cm 的矩形中,截去一个矩形,使留下的矩形与原矩形相似,那么留下的矩形面积是_______cm217.如图,Rt △ABC 中,∠C =90°,AB =5,AC =3,D 是AB 的中点,E 是直线BC 上一点,把△BDE 沿直线ED 翻折后,点B 落在点F 处,当FD ⊥BC 时,线段BE 的长为_____.18.如图,在正方形ABCD 中,AB=8,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且BM=6. P 为对角线BD 上一点,则PM —PN 的最大值为___.三、解答题19.知四条线段的长度为 1.5a = cm ,2b = cm , 2.8c = cm , 2.1d = cm ,判断它们是不是成比例线段.20.如图,已知E 是平行四边形ABCD 中DA 边的延长线上一点,且AD =2AE ,连接EC 分别交AB ,BD 于点F ,G .(1)求证:BF =2AF ;(2)若BD =20cm ,求DG 的长.1.C 2.C 3.A 4.B 5.A 6.D 7.B 8.D 9.C10.411.212.4.13.2 514.23或4315.108 16.2717.54或518.2.19.略20.(1)略;(2)12cm.27.2相似三角形一、选择题1、能判定与相似的条件是()A. B.,且C.且D.,且2、已知两个相似三角形的周长比为4:9,则它们的面积比为()A.4:9 B.2:3 C.8:18 D.16:493、下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC 相似的三角形所在的网格图形是()A. B. C. D.4、已知△ABC∽△A′B′C′,下列图形中,△ABC与△A′B′C′不存在位似关系的是( )5、如图,在△ABC中,∠ADE = ∠B,DE :BC = 2 :3,则下列结论正确的是()A. AD : AB = 2 : 3; B.AE : AC = 2:5;C. AD : DB = 2 : 3; D.CE : AE= 3 : 2.6、如图,已知DE∥BC,那么下列结论正确的是()A. B. C. D.7、如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是()A. B. C. D.8、如图,在△ABC中,∠AED=∠B,DE=6,AB=10,AE=8,则BC的长度为()A.B.C.3 D.9、如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有()A.1个 B.2个 C.3个 D.4个10、如图所示,在河的一岸边选定一个目标A,再在河的另一岸边选定B和C,使AB⊥BC,然后选定E,使EC⊥BC,用视线确定BC和AE相交于D,此时测得BD=120米,CD=60米,为了估计河的宽度AB,还需要测量的线段是()A.CEB.DEC.CE或DED.无法确定11、如图,,∠1=∠2,则对于结论:①△ABE∽△ACF;②△ABC∽△AEF;③;④.其中正确的结论的个数是()A.1 B.2 C.3 D.412、如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM 为()时,△ABE与以D、M、N为顶点的三角形相似A. B. C.或 D.或二、填空题13、如图,在△ABC中,D、E分别是AB、AC边上的点(DE不平行于BC),当时,△AED与△ABC相似.14、如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是.(只需写一个条件,不添加辅助线和字母)15、如图,在△ABC 中,D. E 分别是 AB、AC 边的中点,则的值为16、如图,两条直线被第三条直线所截,DE=,EF=,AB=1,则AC= .17、如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB、AC上,将△ABC沿DE折叠,使点A 落在点处,若为CE的中点,则折痕DE的长为.18、在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为秒.三、简答题19、在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4,。
2023-2024学年人教版九年级数学下册27.3位似第1课时位似图形的概念及画法 作业课件

知识点3:位似图形的画法 7.如图所示,分别按下列要求作出四边形ABCD以点O为位似中心的位似四边形. (1)沿AO方向放大为原图的2倍; (2)沿OA方向放大为原图的2倍.
解:(1)如图,四边形A1B1C1D1即为所求 (2)如图,四边形A2B2C2D2即为所求
8.如图,△ABO与△A′B′O是位似图形,其中AB∥A′B′,则A′B′的长y与AB的长x
解:(2)∵E′C′∥EC,E′D′∥ED,∴△OCE∽△OC′E′,△ODE∽△OD′E′.∴CE∶C′E′ =OE∶OE′,DE∶D′E′=OE∶OE′,∠CEO=∠C′E′O,∠DEO=∠D′E′O,∴CE∶C′E′ = DE∶D′E′ , ∠CED = ∠C′E′D′.∴△CDE∽△C′D′E′.∵△CDE 是 等 边 三 角 形 , ∴△C′D′E′是等边三角形
的面积为( C )
Hale Waihona Puke A.(43 )3B.(43 )7
C.(43 )6
D.(34 )6
11.如图,矩形ABCD与矩形A′B′C′D′是位似图形,点A是位似中心,矩形ABCD 的周长是24,BB′=4,DD′=2,则AB=____. 8
12.如图所示,图中的小方格都是边长为1的正方形,△ABC的顶点和点O都在正 方形的顶点上.
第二十七章 相似
27.3 位似
第1课时 位似图形的概念及画法
知识点1:位似图形 1.图中的两个相似三角形不是位似图形的是( D )
2.图中两个四边形是位似图形,它们的位似中心是( D ) A.点M B.点N C.点O D.点P
知识点2:位似图形的性质
3.(温州中考)如图,图形甲与图形乙是位似图形,O是位似中心,相似比为2∶3,
之间函数关系的图象大致是( )
(完整版)人教九年级数学下册同步练习题及答案

第二十六章二次函数26.1二次函数(第一课时)一、课前小测1.已知函数y=(k+2)x+3是关于x的一次函数,则k_______.2.已知正方形的周长是ccm,面积为Scm2,则S与c之间的函数关系式为__ ___. 3.填表:4.在边长为4m的正方形中间挖去一个长为xm的小正方形, 剩下的四方框形的面积为y,则y与x间的函数关系式为_________.5.用一根长为8m的木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系式为________.二、基础训练121.形如_______ ________的函数叫做二次函数.2.扇形周长为10,半径为x ,面积为y ,则y 与x 的函数关系式为_______________。
3.下列函数中,不是二次函数的是( )x 2 B.y=2(x-1)2+4 C.y=12(x-1)(x+4) D.y=(x-2)2-x 2 4.在半径为4cm 的圆中, 挖去一个半径为xcm 的圆面, 剩下一个圆环的面积为ycm 2,则y与x 的函数关系式为( )A.y=πx 2-4 B.y=π(2-x)2; C.y=-(x 2+4) D.y=-πx 2+16π 5.若y=(2-m)22m x -是二次函数,则m 等于( )A.±2 B.2 C.-2 D.不能确定三、综合训练1.已知y 与x 2成正比例,并且当x=1时,y=2,求函数y 与x 的函数关系式,并求当x=-3时,y的值.当y=8时,求x 的值.2.已知函数y =(m 2-m )x 2+(m -1)x +m +1.(1)若这个函数是一次函数,求m 的值;(2)若这个函数是二次函数,则m 的值应怎样?326.1二次函数(第二课时)一、课前小测1.函数y =ax 2+bx +c (a ,b ,c 是常数)是二次函数的条件是( )A.a ≠0,b ≠0,c ≠0B.a <0,b ≠0,c ≠0C.a >0,b ≠0,c ≠0D.a ≠02.下列函数中:①y =-x 2;②y =2x ;③y =22+x 2-x 3;④m =3-t -t 2是二次函数的是__ __(其中x 、t 为自变量).3.当k=__ ___时,27(3)k y k x -=+是二次函数。
人教版数学九年级下册 27.1 ---27.3随堂练(含答案)

A B
C
二、填空题
6 / 36
9. (2020·盐城) 如图, BC / /DE, 且 BC DE, AD BC 4, AB DE 10 ,则 AE 的值 AC
为 .
10. (2020·吉林)如图, AB // CD // EF .若 AC 1 , BD 5 ,则 DF ______. CE 2
人教版数学九年级下册 27.1《图形的相似》
一、选择题 1.下图是大众汽车的标志示意图,下面的图形中与其相似的是( )
2.下列各组图形中,两个图形形状不一定相同的是( ) A.两个等边三角形 B.有一个角是 35°的两个等腰三角形 C.两个正方形 D.两个圆
3.一个多边形的边长为 2,3,4,5,6,另一个和它相似的多边形的最长边为 24,则这个多边形的 最短边为( )
A.6
B.8
C.10
D.12
4.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 5 cm,6 cm 和 9 cm,另 一个三角形的最短边长为 2.5 cm,则它的最长边为( )
A.3 cm
B.4 cm
C.4.5 cm D.5 cm
5.小张用手机拍摄得到图(1),经放大后得到图(2),图(1)中的线段 AB 在图(2)中的对应线段是 ()
(1)如果四周的小路的宽均相等,都是 x,如图 1,那么小路四周所围成的矩形 A′B′C′D ′和矩形 ABCD 相似吗?请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为 x,y,如图 2,试问小路的宽 x 与 y 的 比值为多少时,能使得小路四周所围成的矩形 A′B′C′D′和矩形 ABCD 相似?请说明理由.
(含答案)九年级数学人教版下册课时练第27章《27.3 位似 》(1)
答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!课时练第27章相似27.3位似一、选择题1.下列说法中正确的是()A.位似图形可以通过平移而相互得到B.位似图形的对应边平行且相等C.位似图形的位似中心不只有一个D.位似中心到对应点的距离之比都相等2.如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A、C、E是x轴正半轴上的点,B、D是第一象限的点,BC=2,则点D的坐标是()A.(9,6)B.(8,6)C.(6,9)D.(6,8)3.如图,△ABC经过位似变换得到△DEF,点O是位似中心且OA=AD,则△ABC与△DEF的面积比是()A.1:8B.1:6C.1:4D.1:24.如图,在3×3正方形网格中,顶点是网格线的交点的三角形叫做格点三角形.给出下列命题:①一定存在全等的两个格点三角形②一定存在相似且不全等的两个格点三角形③一定存在两个格点三角形是位似图形④一定存在周长和面积均为无理数的格点三角形其中真命题的个数是()A.4个 B.3个 C.2个 D.1个5.如图,在56´的网格中,每个小正方形边长均为1,ABC 的顶点均为格点,D 为AB 中点,以点D 为位似中心,相似比为2,将ABC 放大,得到'''A B C ,则'BB =()6.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则下列叙述不正确的是()A.△AMO 与△ABC 位似B.△AMO 与△BCD 位似C.△ANO 与△ACD 位似D.△AMN 与△ABD 位似7.如图,已知△ABO 与△DCO 位似,且△ABO 与△DCO 的面积之比为1:4,点B 的坐标为(﹣3,2),则点C 的坐标为()A.(3,﹣2)B.(6,﹣4)C.(4,﹣6)D.(6,4)8.如图,在平面直角坐标系中,△ABC 与△A1B1C1是以点P 为位似中心的位似图形,且顶点都在格点上,则点P的坐标为()A.(﹣4,﹣3)B.(﹣3,﹣4)C.(﹣3,﹣3)D.(﹣4,﹣4)二、填空题9.△ABC与△A/B/C/是位似图形,且△ABC与△A/B/C/的位似比是1:2,已知△ABC的面积是3,则△A/B/C/的面积是10.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为.11.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是.12.在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:2.把三角形ABC缩小,得到△AB1C1,则点C的对应点C1的坐标为.13.如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是.三、作图题14如图,图中的小方格都是边长为1的正方形,△ABC 与△A′B′C′是关于点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)求出△ABC 与△A′B′C′的位似比;(3)以点O 为位似中心,再画一个△A 1B 1C 1,使它与△ABC 的位似比等于1.5.15.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形.(1)在图②中,请在网格中画一个与图①△ABC 相似的△DEF ;(2)在图③中,以O 为位似中心,画一个△A 1B 1C 1,使它与△ABC 的位似比为2:1.16.如图,在正方形格中,每一个小正方形的边长都为1,△ABC 的顶点分别为A (2,3),B(2,1),C(5,4).(1)写出△ABC的外心P的坐标.(2)以(1)中的外心P为位似中心,按位似比2:1在位似中心的同侧将△ABC放大为△A′B′C′,放大后点A、B、C的对应点分别为A′、B′,C′,请在图中画出△ABC.17.如图,在10×10的正方形网格中,每个小正方形的边长均为1,点O是格点,△ABC是格点三角形(顶点在网格线交点上),且点A1是点A以点O为位似中心的对应点.(1)画出△ABC以点O为位似中心的位似图形△A1B1C1.(2)△A1B1C1与△ABC的位似比为;(3)△A1B1C1的周长为.参考答案1.D2.A3.C4.B5.D6.B7.B8.D9.答案为:1210(,2)或(﹣,﹣2).11.(﹣1,0).12.(2,3)或(0,﹣1).13.答案为:(﹣2,).14.解:(1)连接A′A,C′C,并分别延长相交于点O,即为位似中心(2)位似比为1∶2(3)略15.解:(1)如图②,△DFE为所作;(2)如图③,△A1B1C1为所作.16.解:(1)如图.P点坐标为(4,2);故答案为(4,2);(2)如图,△A′B′C′为所作.17.解:(1)如图所示:△A1B1C1即为所求;(2)△A1B1C1与△ABC的位似比为:1:3;(3)△A1B1C1的周长为:9++=9+3+3.故答案为:(2)1:3;(3)9+3+3.。
2022-2023学年人教版九年级数学下册《27-3位似》同步题型分类练习题(附答案)
2022-2023学年人教版九年级数学下册《27.3位似》同步题型分类练习题(附答案)一.位似变换1.如图,已知△ABC与△DEF位似,位似中心为O,且△ABC的面积与△DEF的面积之比是16:9,则AO:AD的值为()A.4:7B.4:3C.6:4D.9:52.如图平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,点A,B,E在x轴上,若正方形ABCD的边长为3,则F点坐标为()A.(16.5,9)B.(18,12)C.(16.5,12)D.(16,12)3.在如图所示的网格中,以点O为位似中心,能够与四边形ABCD是位似图形的为()A.四边形NGMF B.四边形NGME C.四边形NHMF D.四边形NHME 4.如图所示,在平面直角坐标系中,A(1,0),B(0,2),C(﹣2,1),以A为位似中心,把△ABC在点A同侧按相似比1:2放大,放大后的图形记作△A'B'C',则C'的坐标为()A.(﹣6,2)B.(﹣5,2)C.(﹣4,2)D.(﹣3,2)5.如图,在直角坐标系中,矩形ABCD与矩形EFGO位似,矩形ABCD的边CD在y轴上,点B的坐标为(﹣4,4),矩形EFGO的两边都在坐标轴上,且点F的坐标为(2,1),则矩形ABCD与EFGO的位似中心的坐标是.6.如图,平面直角坐标系中,点A在x轴正半轴上,且OA=4,∠BOA=30°,∠B=90°,以点O为位似中心,在第一象限内将△AOB放大,使相似比为2:1,则点B的对应点B′的坐标为.7.如图,在平面直角坐标系中,A、B两点的坐标分别为A(﹣1,2)、B(0,2),C、D 两点的坐标分别为C(0,﹣1)、D(2,﹣1).若线段AB和线段CD是位似图形,且位似中心在y轴上,则位似中心的坐标为.8.《墨子•天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为4,以它的对角线的交点为位似中心,作它的位似图形A'B'C'D',若A'B':AB=2:1,则四边形A'B'C'D'的外接圆的周长为.9.如图,△ABC与△A1B1C1是以原点O为位似中心的位似图形,且位似比为1:2,则点A(1,2)在第一象限的对应点A1的坐标是.10.如图,在平面直角坐标系中,O是坐标原点,以点O为位似中心,△A1B1C1和△ABC 相似比为2:1,在网格中画出新图象△A1B1C1,若每个小正方形边长均为1,请写出A1,B1,C1的坐标.11.如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△A n B n∁n组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…A n是OA n﹣1的中点,顶点B2,B3,…,B n.C2,C3,…,∁n都在B1C1边上.(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心;(2)求出第n个三角形△A n B n∁n(n≥2)的周长.12.如图,△ABC中,P′是边AB上一点,四边形P'Q'M'N'是正方形,点Q',M'在边BC上,点N′在△ABC内.连接BN′,并延长交AC于点N,过点N作NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.(1)求证:四边形PQMN为正方形;(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.13.(1)对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴t,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是,若点B′表示的数是2,则点B表示的数是;已知线段AB上的点E经过上述操作后得到的对应点E'点E重合,则点E表示的数是.(2)在平面直角坐标系xOy中,已知△ABC的顶点A(﹣2,0),B(2,0),C(2,4),对△ABC及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同个实数a,将得到的点先向右平移m单位,再向上平移n个单位(m>0,n>0),得到△A′B′C′及其内部的点,其中点A,B的对应点分别为A′(1,2),B′(3,2).△ABC内部是否存在点F,使得点F经过上述操作后得到的对应点F′与点F重合,若存在,求出点F 的坐标;若不存在请说明理由.14.在平面直角坐标系中,抛物线L:y=﹣x2+x+2与y轴交于点C,与x轴交于A、B两点(点A在点B的左侧).(1)求A、B、C三点的坐标;(2)连接AC、BC,以点C为位似中心,将△ABC扩大到原来的2倍得到△A1B1C,其中点A1、B1分别是点A、B的对应点,如何平移抛物线L才能使其同时经过点A1、B1,求出所有的平移方式.二.作图-位似变换15.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是()A.4B.3C.2D.116.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为()A.(0,0),2B.(2,2),C.(2,2),2D.(1,1),17.如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为()A.(m,n+3)B.(m,n﹣3)C.(m,n+2)D.(m,n﹣2)18.如图,以点O为位似中心,把△AOB缩小后得到△COD,使△COD∽△AOB,且相似比为,已知点A(3,6),则点C的坐标为.19.如图,以点O为位似中心,把△ABC放大2倍得到△A'B'C'',①AB∥A'B';②△ABC∽△A'B'C';③AO:AA'=1:2;④点C、O、C'三点在同一直线上.则以上四种说法正确的是.20.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA =2.OC=1,则矩形AOCB的对称中心的坐标是;在第二象限内,将矩形AOCB 以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是.21.在平面直角坐标系中,△ABC的顶点A的坐标为(2,﹣5),若以原点O为位似中心,作△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的位似比为2:1,且点A1和点A 不在同一象限内,则点A1的坐标为.22.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是.23.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,0),B(3,1),C (2,3).请在所给直角坐标系中按要求画图和解答下列问题:(1)以原点O为位似中心,在原点的另一侧画出△ABC的位似三角形△DEF,△ABC 与△DEF的位似比为;(2)如果△ABC内部一点M的坐标为(a,b),请写出M的对应点M'的坐标(,).24.如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.(1)在平面直角坐标系中画出位似中心;(2)设点P(a,b)为△ABC内一点,确定点P在△A1B1C1内的对应点P1的坐标.25.如图,小明在学习图形的位似时,利用几何画板软件,在平面直角坐标系中画出了△ABC的位似图形△A1B1C1.(1)在图中标出△ABC和△A1B1C1的位似中心M点的位置并写出M点的坐标.(2)若以点A1为位似中心,请你帮小明在图中画出△A1B1C1的位似图形△A2B2C2,且△A1B1C1与△A2B2C2的位似比为2:1.(3)直接写出(2)中C2点的坐标.26.如图,△ABC三个顶点分别为A(0,﹣3),B(3,﹣2),C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.(1)画出△ABC向上平移5个单位得到的△A1B1C1;(2)以点C为位似中心,在网格中画出△A2B2C2,使得△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并写出A2的坐标.27.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).(1)以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1.(2)画出△ABC绕O点顺时针旋转90°后得到的△A2B2C2.28.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)直接写出△ABC与△A′B′C′的位似比;(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出△A′B′C′各顶点的坐标.参考答案一.位似变换1.解:∵△ABC与△DEF位似,∴△ABC∽△DEF,AC∥DF,∵△ABC的面积与△DEF的面积之比是16:9,∴=,∵AC∥DF,∴△AOC∽△DOF,∴==,∴AO:AD=4:7,故选:A.2.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,∴==,即==,解得:EF=12,OB=4,∴F(16,12).故选:D.3.解:如图,四边形ABCD的位似图形是四边形NGMF.故选:A.4.解:∵以A为位似中心,把△ABC按相似比1:2放大,放大后的图形记作△AB'C',∴AC=AC′,∴点C是线段AC′的中点,∵A(1,0),C(﹣2,1),∴C'的坐标为(﹣5,2).故选:B.5.解:连接BF交y轴于点P,∵C和F是对应点,∴点P为位似中心,由题意得,GF=2,AD=4,GC=4﹣1=3,∵BC∥GF,∴△BPC∽△FPG,∴=,即=2,解得,GP=1,∴OP=2,∴位似中心的坐标是(0,2),故答案为:(0,2).6.解:作BE⊥OA于E,则∠BEO=90°,∵∠ABO=90°,∠BOA=30°,∴OB=OA•cos30°=4×=2,∴BE=OB=,OE=OB•cos30°=2×=3,∴点B的坐标为:(3,),∵以点O为位似中心,在第一象限内将△AOB放大,使相似比为2:1,∴点B的对应点B'的坐标为:(3×2,×2),即(6,2),故答案为:(6,2).7.解:连接AD交BC于E,则点E为位似中心,∵A(﹣1,2)、B(0,2),C(0,﹣1)、D(2,﹣1).∴AB=1,CD=2,BC=3,∵线段AB和CD是位似图形,∴AB∥CD,∴=,即=,解得BE=1,∴OE=OB﹣BE=1,∴位似中心点E的坐标为(0,1),故答案为:(0,1).8.解:如图,连接B′D′.设B′D′的中点为O.∵正方形ABCD∽正方形A′B′C′D′,相似比为1:2,又∵正方形ABCD的面积为4,∴正方形A′B′C′D′的面积为16,∴A′B′=A′D′=4,∵∠B′A′D′=90°,∴B′D′=A′B′=4,∴正方形A′B′C′D′的外接圆的周长=4π,故答案为:4π.9.解:∵△ABC与△A1B1C1是以原点O为位似中心的位似图形,且位似比为1:2,∵A(1,2),点A(1,2)在第一象限的对应点是A1,∴点A1的坐标为:(2,4).故答案为:(2,4).10.解:如图,△A1B1C1即为所求,A1(0,8),B1(6,6),C1(6,2).11.解:(1)∵△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,∴正△A2B2C2的边长为,正△A3B3C3的边长为()2,正△A10B10C10和的边长为()9,正△A7B7C7的边长为()6,∴正△A10B10C10和正△A7B7C7的相似比==;它们的位似中心为点O;(2)∵第n个三角形△A n B n∁n(n≥2)的边长为()n﹣1,∴第n个三角形△A n B n∁n(n≥2)的周长为.12.(1)证明:∵NM⊥BC,NP⊥MN,PQ⊥BC,∴四边形PQMN为矩形,∵四边形P'Q'M'N'是正方形,∴PN∥P′N′,∴=,∵MN∥M′N′,∴=,∴=,而P′N′=M′N′,∴PN=MN,∴四边形PQMN为正方形;(2)解:作AD⊥BC于D,AD交PN于E,如图,∵△ABC的面积=1.5,∴AB•AC=1.5,∴AB=2,∴BC==2.5,∵BC•AD=1.5,∴AD==,设PN=x,则PQ=DE=x,AE=﹣x,∵PN∥BC,∴△APN∽△ABC,∴=,即=,解得x=,即PN的长为m.13.解:(1)点A′:﹣3×+1=﹣1+1=0,设点B表示的数为a,则a+1=2,解得a=3,设点E表示的数为b,则b+1=b,解得b=;故答案为:0,3,;(2)根据题意,得:,解得:,设点F的坐标为(x,y),∵对应点F′与点F重合,∴x+2=x,y+2=y,解得x=y=4,所以,点F的坐标为(4,4),∵点F的坐标为(4,4)不在△ABC内,故△ABC内部不存在点F,使得点F经过上述操作后得到的对应点F′与点F重合.14.解:(1)在y=﹣x2+x+2中,令y=0,即0=﹣x2+x+2,解得:x1=2,x2=﹣1,∴A(﹣1,0),B(2,0),令x=0,即y=2,∴C(0,2);(2)如图,当抛物线经过A1(2,6),B1(﹣4,6)时,设抛物线的解析式,y=﹣x2+bx+c,则有,解得,,∴抛物线的解析式为y=﹣x2﹣2x+14=﹣(x+1)2+15,当抛物线经过A2(﹣2,﹣2),B2(4,﹣2)时,同法可得抛物线的解析式为:y=﹣x2+2x+6=﹣(x﹣1)2+7.∵原来的抛物线的解析式为y=﹣(x﹣)2+,∴+1=,15﹣=,∴原来抛物线向左平移,再向上平移单位得到y=﹣x2﹣2x+14.1﹣=,7﹣=,原来抛物线向右平移单位,再向上平移单位得到y=﹣x2+2x+6.二.作图-位似变换15.解:第一个图形中的位似中心为A点,第二个图形中的位似中心为AD与BC的交点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.故选:A.16.解:如图所示:位似中心F的坐标为:(2,2),k的值为:=.故选:B.17.解:过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,设C(x,y),则CD=y﹣2、AD=﹣x,C′D′=2﹣n,AD′=m,∵△AB′C′与△ABC的位似比为2:1,∴==,即==,解得:x=﹣m,y=﹣n+3,∴点C的坐标为(﹣m,﹣n+3),故选:A.18.解:由题意得,点A与点C是对应点,△AOB与△COD的相似比是3,∴点C的坐标为(3×,6×),即(1,2),当点C值第三象限时,C(﹣1,﹣2)故答案为:(1,2)或(﹣1,﹣2).19.解:∵以点O为位似中心,把△ABC放大2倍得到△A'B'C'',∴AB∥A'B,△ABC∽△A'B'C';AO:AA'=2:1;点C、O、C'三点在同一直线上,①①②④正确,故答案为:①②④.20.解:∵OA=2.OC=1,∴B(﹣2,1),∴矩形AOCB的对称中心的坐标为(﹣1,),∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,∴B1(﹣3,),同理可得B2(﹣,),B3(﹣,),B4(﹣,),∴矩形A4OC4B4的对称中心的坐标是(﹣,).故答案为(﹣1,),(﹣,).21.解:在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),∴则点A′的坐标为:(1,﹣2.5),不在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),∴则点A′的坐标为:(﹣1,2.5),故答案为:(﹣1,2.5).22.解:如图所示:△A1B1C1和△A′B′C′与△ABC的相似比为2,点B的对应点B1的坐标是:(4,2)或(﹣4,﹣2).故答案为:(4,2)或(﹣4,﹣2).23.解:(1)如图,△DEF即为所求;(2)M′(﹣2a,﹣2b).故答案为:﹣2a,﹣2b.24.解:(1)如图点O即为位似中心;(2)设点P(a,b)为△ABC内一点,则点P在△A1B1C1内的对应点P1的坐标(2a,2b).25.解:(1)如图,点M为所作,M点的坐标为(0,2);(2)如图,△A2B2C2即为所求;(3)C2(﹣4,2).26.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求.A2的坐标(﹣2.,﹣2).27.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求.28.解:(1)如图,(2)2:1,(3)A′(﹣6,0),B′(﹣3,2),C′(﹣4,4).。
人教版初3数学9年级下册 第27章(相似)期末综合复习训练2(含答案)
人教版九年级数学下册《第27章相似》期末综合复习训练2(附答案)1.若x===,则x等于( )A.﹣1或B.﹣1C.D.不能确定2.已知===,则=( )A.B.C.D.3.线段AB=8,P是AB的黄金分割点,且AP<BP,则BP的长度为( )A.4﹣4B.8+8C.8﹣8D.4+44.一个五边形ABCDE各边的边长为2,3,4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( )A.8B.6C.4D.25.如图,在正方形ABCD中,E,F分别是BC、AB上一点,且AF=BE,AE与DF交于点G,连接CG.若CG=BC,则AF:FB的比为( )A.1:1B.1:2C.1:3D.1:46.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )A.B.C.D.7.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,点H为AF与DG的交点.若AC=9,则DH为( )A.1B.2C.D.38.有一个三角形木架三边长分别是15cm,20cm,24cm,现要再做一个与其相似的三角形木架,而只有长为12cm和24cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )A.一种B.两种C.三种D.四种9.如图,四边形ABCD与四边形A'B'C'D'是位似图形,点O是位似中心,若OA:AA′=2:1,则四边形ABCD与四边形A'B'C'D'的面积之比等于( )A.1:2B.1:4C.2:3D.4:910.如图,在平面直角坐标系中,有一个Rt△OAB,∠ABO=90°,∠AOB=30°,直角边OB在y轴正半轴上,点A在第一象限,且OA=1,将Rt△OAB绕原点逆时针旋转30°,同时把各边长扩大为原来的两倍(即OA1=2OA).得到Rt△OA1B1,同理,将Rt△OA1B1绕原点O逆时针旋转30°,同时把各边长扩大为原来的两倍,得到Rt△OA2B2,…,依此规律,得到三角形Rt△OA2021B2021,则OB2021的长度为( )A.B.×22020C.×22021D.×2201911.已知=,则= .12.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .13.四边形ABCD∽四边形A1B1C1D1,他们的面积比为16:9,四边形ABCD的周长是16,则四边形A1B1C1D1的周长为 .14.如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则DF的长度为 .15.如图,在直角坐标系中,已知点A(2,0),B(0,4),在x轴上找到点C(1,0)和y轴的正半轴上找到点D,使△AOB与△DOC相似,则D点的坐标是 .16.如图,Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从点A出发,沿着A→C→A的方向运动,设点E的运动时间为秒(0≤t≤12),连接DE,当△CDE是直角三角形时,t的值为 .17.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为 .18.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上,若正方形BEFG的边长为5,则C 点坐标为 .19.阅读理解:已知:a,b,c,d都是不为0的数,且=,求证:=.证明:∵=,∴+1=+1.∴=.根据以上方法,解答下列问题:(1)若=,求的值;(2)若=,且a≠b,c≠d,证明=.20.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.请回答下列问题:(1)你认为上述两个观点是否正确?请说明理由.(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为1,DE=15,求△DEF的面积.21.阅读与计算,请阅读以下材料,并完成相应的问题.角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.证明:如图2,过C作CE∥DA.交BA的延长线于E.…任务:(1)请按照上面的证明思路,写出该证明的剩余部分;(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .22.在等腰△AMB中,AM=AB,点C在边AM上,△MCD是直角三角形,∠CMD=90°,∠MCD=∠MAB,连接BC,BD,点O是BC的中点,连接AO.(1)如图1,作AE⊥MB于E,连接OE.当∠AMB=45°时,求证:△AOE相似于△BDM;(2)如图2,当∠AMB=30°时,线段BD与线段AO存在怎样的数量关系?写出证明过程.23.数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF 上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.24.如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.(1)求证:△AEF∽△ABD.(2)若△AEF的面积为1,求△ABC的面积.参考答案1.解:∵x===,∴当a+b+c≠0时,x==;当a+b+c=0时,x===﹣1,故选:A.2.解:∵===,∴b=2a,d=2c,f=2e,把b=2a,d=2c,f=2e代入===,故选:C.3.解:∵线段AB=8,P是AB的黄金分割点,且AP<BP,∴BP=AB=×8=4﹣4.故选:A.4.解:设五边形A1B1C1D1E1的最短边长为m.由相似多边形的性质可知:=,∴m=4,故选:C.5.解:作CH⊥DF于点H,如图所示.在△ADF和△BAE中,,∴△ADF≌△BAE(SAS).∴∠ADF=∠BAE,又∠BAE+∠GAD=90°,∴∠ADF+∠GAD=90°,即∠AGD=90°.由题意可得∠ADG+∠CDG=90°,∠HDC+∠CDG=90°,.∴∠ADG=∠HDC.在△AGD和△DHC中,,∴△AGD≌△DHC(AAS).∴DH=AG.又CG=BC,BC=DC,∴CG=DC.由等腰三角形三线合一的性质可得GH=DH,∴AG=DH=GH.∴tan∠ADG=.又tan∠ADF==,∴AF=AB.即F为AB中点,∴AF:FB=1:1.故选:A.6.解:设CF=x,∵EF∥AC,∴=,∴=,解得x=,∴CF=,∵EF∥DB,∴===.故选:A.7.解:∵D、E为边AB的三等分点,EF∥DG∥AC,∴BE=DE=AD,BF=GF=CG,AH=HF,∴AB=3BE,DH是△AEF的中位线,∴DH=EF,∵EF∥AC,∴△BEF∽△BAC,∴=,即=,解得:EF=3,∴DH=EF=×3=,故选:C.8.解:长24cm的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长24cm 的木条不能作为一边,设从24cm的木条上截下两段长分别为xcm,ycm(x+y≤24),由于长12cm的木条不能与15cm的一边对应,否则x+y>24cm,当长12cm的木条与20cm的一边对应,则==,解得:x=9,y=14.4;当长12cm的木条与24cm的一边对应,则==,解得:x=7.5,y=10.∴有两种不同的截法:把24cm的木条截成9cm、14.4cm两段或把24cm的木条截成7.5cm、10cm两段.故选:B.9.解:∵OA:AA′=2:1,∴OA:OA′=2:3.∵四边形ABCD与四边形A′B′C′D′位似,∴AB∥A′B′,四边形ABCD∽四边形A′B′C′D′,∴△OAB∽△OA′B′,∴==,∴四边形ABCD与四边形A′B′C′D′的面积比=()2=,故选:D.10.解:在Rt△AOB中,∠AOB=30°,OA=1,∴OB=OA•cos∠AOB=,由题意得,OB1=2OB=×2,OB2=2OB1=×22,……OB n=2OB1=×2n=×2n﹣1,∴OB2021=×22020.故选:B.11.解:∵=,∴=,∴﹣=,∴=.故答案为:.12.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.13.解:∵四边形ABCD∽四边形A1B1C1D1,他们的面积比为16:9,∴相似比为4:3,∴周长比等于4:3,∴四边形A1B1C1D1的周长=×16=12,故答案为:12.14.解:∵点B是线段AC的中点,∴AB=BC,∴=1,∵直线a∥b∥c,∴==1,∵DE=2,∴EF=2,∴DF=DE+EF=2+2=4,故答案为:4.15.解:若△AOB∽△DOC,点D在x轴上方:∠B=∠OCD,∴=,即=.∴OD=.∴D(0,),若△AOB∽△COD,点D在x轴上方:可得D(0,2).综上所述,D点的坐标是(0,)或(0,2).故答案是:(0,)或(0,2).16.解:在Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=4cm,∴AC=2BC=8cm,∵D为BC中点,∴CD=2cm,∵0≤t≤12,∴E点的运动路线为从A到C,再从C到AC的中点,按运动时间分为0≤t≤8和8<t≤12两种情况,①当0≤t≤8时,AE=tcm,CE=BC﹣AE=(8﹣t)cm,当∠EDC=90°时,则有AB∥ED,∵D为BC中点,∴E为AC中点,此时AE=4cm,可得t=4;当∠DEC=90°时,∵∠DEC=∠B,∠C=∠C,∴△CED∽△BCA,∴,即,解得t=7;②当8<t≤12时,则此时E点又经过t=7秒时的位置,此时t=8+1=9;当t=12时,此时E点在AC的中点,DE∥AB,此时△CDE是直角三角形.综上可知t的值为4或7或9或12,故答案为:4或7或9或1217.解:∵C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,∴A(6,6),B(8,2),∵E是AB中点,∴E(7,4),故答案为:(7,4).18.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,∴=,∵BG=5,∴AD=BC=,∵AD∥BG,∴△OAD∽△OBG,∴=,∴=,解得:OA=,∴OB=+=,∴C点坐标为:(,),故答案为:(,).19.解:(1)∵=,∴=+1=+1=.(2)∵=,∴﹣1=﹣1,∴=,∵=,∴÷=÷,∴=.20.解:(1)观点一正确;观点二不正确.理由:①如图(1)连接并延长DA,交FC的延长线于点O,∵△ABC和△DEF对应的边的距离都为1,∴AB∥DE,AC∥DF,∴∠FDO=∠CAO,∠ODE=∠OAB,∴∠FDO+∠ODE=∠CAO+∠OAB,即∠FDE=∠CAB,同理∠DEF=∠ABC,∴△ABC∽△DEF,∴观点一正确;②如图(2)由题意可知,原矩形的邻边为6和10,则新矩形邻边为4和8,∵=,=,∴,∴新矩形于原矩形不相似,∴观点二不正确;(2)如图(3),延长DA、EB交于点O,∵A到DE、DF的距离都为1,∴DA是∠FDE的角平分线,同理,EB是∠DEF的角平分线,∴点O是△ABC的内心,∵AC=6,BC=8,AB=10,∴△ABC是直角三角形,设△ABC的内切圆的半径为r,则6﹣r+8﹣r=10,解得r=2,过点O作OH⊥DE于点H,交AB于G,∵AB∥DE,∴OG⊥AB,∴OG=r=2,∴==,同理===,∴DF=9,EF=12,∴△DEF的面积为:×9×12=54.21.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,∵CE∥AD,∴=,∠2=∠ACE,∠1=∠E,∵∠1=∠2,∴∠ACE=∠E,∴AE=AC,∴=;(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,∴AC=5,∵AD平分∠BAC,∴=,即=,∴BD=BC=,∴AD===,∴△ABD的周长=+3+=.故答案为.22.解:(1)证明:∵AM=AB,AE⊥MB,∴E为MB的中点,∵∠AMB=45°,∴∠MAB=180°﹣2×45°=90°,∴AE=MB,∵点O是BC的中点,∴OE∥MC且OE=MC,∴∠OEB=∠CMB=45°,∴∠AEO=45°,∵∠CMD=90°,∴∠BMD=45°,∴∠BMD=∠AEO,∴△BMD∽△AEO;(2)BD=2AO;证明:如图,作AF⊥MB于F,连接OF,∵AM=AB,AF⊥MB,∴F为MB的中点,∵∠AMB=30°,∴∠MAB=180°﹣2×30°=120°,∴∠MCD=∠MAB=60°,∵∠CMD=90°,∴∠CDM=30°,∴tan AMB=tan∠CDM=tan30°==,∴MB=2AF,∵点O是BC的中点,∴OF∥MC且OF=MC,∴∠OFB=∠CMB=30°,MD=2OF,∴∠AFO=60°,∴∠BMD=∠AFO,∴△BMD∽△AFO,∴BD=2AO.23.解:设广告牌的高度EF为xm,依题意知:DB=11m,BG=2m,DH=1m,AB=CD=1.6m.∴GD=DB﹣BG=9m,∵CD⊥BF,EF⊥BF,∴CD∥EF.∴△EFH∽△CDH.∴=,即=.∴=.∴DF=x﹣1.由平面镜反射规律可得:∠EGF=∠AGB.∵AB⊥BF,∴∠ABG=90°=∠EFG.∴△EFG∽△ABG.∴=,即=.∴=.∴x=12.8.故树的高度EF为12.8m.24.(1)证明:∵DC=AC,CF是∠ACB的平分线,∴AF=DF,∵点E是AB的中点,即AE=BE,∴EF是△ABD的中位线,∴EF∥BD,∴△AEF∽△ABD;(2)∵△AEF∽△ABD,∴,∵AE=AB,S△AEF=1,∴S△ABD=4,∵BD=CD,∴S△ABC=2S△ABD=8。
人教版九年级下册数学第二十七章测试卷及答案
人教版九年级下册数学第二十七章测试题一、单选题1.如图,在△ABC中,DE∥BC分别交AB,AC于点D,E,若23ADDB=,则下列说法不正确的是()A.AD AEAB AC=B.23AEEC=C.23DEBC=D.421ADEDBCESS=四边形2.在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则EFFC等于()A.13B.12C.23D.323.如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为()A.60mm B.16013mm C.20mm D.24013mm4.如图,在△ABC中,AB=6,AC=8,BC=10,D是△ABC内部或BC边上的一个动点(与B、C不重合),以D为顶点作△DEF,使△DEF∽△ABC(相似比k>1),EF∥BC.两三角形重叠部分是四边形AGDH,当四边形AGDH的面积最大时,最大值是多少?()A.12B.11.52C.13D.25.已知线段AB的长为4,点P是线段AB的黄金分割点(AP>BP),则PA的长为() A.52B.6﹣2√5C.512D.4﹣56.如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,DF∥AC,若△ADE与四边形DBCE的面积相等,则△DBF与△ADE的面积之比为()A.12B.14C21D.27.如图,正方形OABC的边长为8,点P在AB上,CP交OB于点Q.若S△BPQ=19OQC S,则OQ长为()A.6B.2C.1623D.1638.在△ABC中,点D在边BC上,联结AD,下列说法错误的是()A.如果∠BAC=90°,AB2=BD•BC,那么AD⊥BCB.如果AD⊥BC,AD2=BD•CD,那么∠BAC=90°C.如果AD⊥BC,AB2=BD•BC,那么∠BAC=90°D.如果∠BAC=90°,AD2=BD•CD,那么AD⊥BC9.如图,在△ABC中,点O是∠ABC和∠ACB两个内角平分线的交点,过点O作EF∥BC 分别交AB,AC于点E,F,已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是()A.B.C.D.10.如图,已知△ABO与△DCO位似,且△ABO与△DCO的面积之比为1:4,点B的坐标为(﹣3,2),则点C的坐标为()A.(3,﹣2)B.(6,﹣4)C.(4,﹣6)D.(6,4)11.在比例尺是1:8000的南京市城区地图上,太平南路的长度约为25cm,它的实际长度约为()A.320cm B.320m C.2000cm D.2000m12.△DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是()A.2B.4C.6D.8二、填空题13.如图,△ABC 中,D 、E 分别是AB 、AC 上的点(DE 不平行BC ),若使△ADE 与△ABC 相似,则需要添加_____即可(只需添加一个条件).14.如图,已知△ABC 和△ADE 都是等边三角形,点D 在边BC 上,且BD =4,CD =2,那么AF =_____.15.如图,矩形ABCD 中,AB =2,BC =4,剪去一个矩形ABEF 后,余下的矩形EFDC ∽矩形BCDA ,则FC 的长为_____.16.若23a b =,则2a ba +=_____.17.如图,平行四边形ABCD 中,点E 是AD 边上一点,连结EC 、BD 交于点F ,若AE :ED =5:4记△DFE 的面积为S 1,△BCF 的面积为S 2,△DCF 的面积为S 3,则DF :BF =_____,S 1:S 2:S 3=_____.18.如图,在四边形ABCD 中,AD ∥BC ∥EF ,EF 分别与AB ,AC ,CD 相交于点E ,M ,F ,若EM :BC =2:5,则FC :CD 的值是_____.19.如图,已知△ABC ,AB=6,AC=5,D 是边AB 的中点,E 是边AC 上一点,∠ADE=∠C ,∠BAC 的平分线分别交DE 、BC 于点F 、G ,那么AFAG的值为__________.三、解答题20.如图,在△ABC 中,AB =AC ,D 是边BC 的中点,DE ⊥AC ,垂足为点E .(1)求证:DE •CD =AD •CE ;(2)设F 为DE 的中点,连接AF 、BE ,求证:AF •BC =AD •BE.21.如图,已知菱形ABCD ,点E 是AB 的中点,AF ⊥BC 于点F ,联结EF 、ED 、DF ,DE 交AF 于点G ,且AE 2=EG •ED .(1)求证:DE ⊥EF ;(2)求证:BC 2=2DF •BF.22.如图,在ABC 中,D 、E 分别是边AB 、AC 上的点,// DE BC ,点F 在线段DE 上,过点F 作//FG AB 、//FH AC 分别交BC 于点G 、H ,如果::2:4:3BG GH HC .求ADEFGHS S △△的值.23.如图,△ABC的面积为12,BC与BC边上的高AD之比为3:2,矩形EFGH的边EF 在BC上,点H,G分别在边AB、AC上,且HG=2GF.(1)求AD的长;(2)求矩形EFGH的面积.24.如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请在图中找出与△HBC相似的三角形,并说明它们相似的理由.25.如图,在△ABC中,点D为边BC上一点,且AD=AB,AE⊥BC,垂足为点E.过点D作DF∥AB,交边AC于点F,连接EF,EF2=12BD•EC.(1)求证:△EDF∽△EFC;(2)如果14EDFADCSS,求证:AB=BD.参考答案1.C 【分析】根据题意可以得到△ADE ∽△ABC ,然后根据题目中的条件即可推出选项中的说法是否正确,从而可以解答本题.【详解】∵DE ∥BC ,∴△ADE ∽△ABC ,∴AD AE AB AC =,AE AD EC DB ==23,DE BC==AD AB =25,ADE ABC S S ∆∆=(AD AB )2=425,∴ADE DBCE S S ∆四边形=421,故A 、B 、D 选项正确,C 选项错误,故选C .【点睛】本题考查相似三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用相似三角形的性质解答问题.2.A 【详解】试题分析:如图,∵四边形ABCD 为平行四边形,∴ED ∥BC ,BC=AD ,∴△DEF ∽△BCF ,∴EF DEFC CB =,设ED=k ,则AE=2k ,BC=3k ,∴EF FC =3k k =13,故选A .考点:1.相似三角形的判定与性质;2.平行四边形的性质.3.A【分析】利用相似三角形的性质构建方程即可解决问题.【详解】如图,设AD交PN于点K,∵PM:PQ=3:2,∴可以假设MP=3k,PQ=2k,∵四边形PQNM是矩形,∴PM∥BC,∴△APM∽△ABC,∵AD⊥BC,BC∥PM,∴AD⊥PN,∴PM AK BC AD=,∴3802 12080k k-=,解得k=20mm,∴PM=3k=60mm,故选A.【点睛】本题考查相似三角形的应用,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.4.A【分析】先判断面积最大时点D的位置,由△BGD∽△BAC,找出AH=8-43GA,得到S矩形AGDH=-43AG2+8AG,确定极值,AG=3时,面积最大,于是得到结论.【详解】∵AB2+AC2=100=BC2,∴∠BAC=90°,∵△DEF∽△ABC,∴∠EDF=∠BAC=90°,如图1延长ED交BC于M,延长FD交BC于N,∵△DEF∽△ABC,∴∠B=∠E,∵EF∥BC,∴∠E=∠EMC,∴∠B=∠EMC,∴AB∥DE,同理:DF∥AC,∴四边形AGDH为平行四边形,∵∠EDF=90°,∴四边形AGDH为矩形,∵GA⊥AC,∴四边形AGDH为正方形,当点D在△ABC内部时,四边形AGDH的面积不可能最大,如图2,点D在内部时(N在△ABC内部或BC边上),延长GD至N,过N作NM⊥AC于M,∴矩形GNMA面积大于矩形AGDH,∴点D在△ABC内部时,四边形AGDH的面积不可能最大,只有点D在BC边上时,面积才有可能最大,如图3,点D在BC上,∵△DEF∽△ABC,∴∠F=∠C,∵EF∥BC.∴∠F=∠BDG,∴∠BDG=∠C,∴DG∥AC,∴△BGD∽△BAC,∴BG GD AB AC=,∴AB AG AH AB AC-=,∴668AG AH -=,∴AH=8-43 GA,S矩形AGDH=AG×AH=AG×(8-43AG)=-43AG2+8AG,当AG=-842()3⨯-=3时,S矩形AGDH最大,S矩形AGDH最大=12.故选A.【点睛】此题主要考查了相似三角形的性质和判定,平行四边形,矩形,极值的确定,勾股定理的逆定理,解本题的关键是作出辅助线,5.A【分析】利用黄金分割的定义得到PA=12AB ,然后把AB=4代入计算即可.【详解】∵点P 是线段AB 的黄金分割点(AP >BP ),∴12AB=12.故选A .【点睛】本题考查了黄金分割:把线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC=AC :BC ),叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点.其中,并且线段AB 的黄金分割点有两个.6.D【分析】根据矩形的性质得到DE=CF ,根据相似三角形的性质得到ADE ABC S S =(DE BC )2=12,求得DE BC=2,设k ,BC=2k ,得到k ,根据相似三角形的性质即可得到结论.【详解】∵DE ∥BC ,DF ∥AC ,∴四边形DFCE 是平行四边形,∴DE=CF ,∵△ADE 与四边形DBCE 的面积相等,∴ADE ABC S S =12,∵DE ∥BC ,∴△ADE ∽△ABC ,∴ADE ABC S S =(DE BC )2=12,∴DE BC=2,设k ,BC=2k ,∴,∵DF ∥AC ,∴△BDF ∽△BAC ,∴△DBF ∽△ADE ,∴BDF ADE S S =(BF DE )2=2⎛⎫⎪⎪⎭=)2故选D .【点睛】本题考查了相似三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质是解题的关键.7.B【分析】根据正方形的性质得到AB ∥OC ,推出△PBQ ∽△COQ ,根据相似三角形的性质得到OC=3PB ,求得PB=83,于是得到结论.【详解】∵四边形ABCO 是正方形,∴AB ∥OC ,∴△PBQ ∽△COQ ,∴BPQOQC S S =(PB OC)2=19,∴OC=3PB ,∵OC=8,∴PB=83,∵BQ OQ =PB OC =13,∴OQ=34故选B .【点睛】本题考查相似三角形的判定和性质、正方形的性质、平行线分线段成比例定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.D根据相似三角形的判定定理证明相应的三角形相似,根据相似三角形的性质判断即可.【详解】如图:A、∵AB2=BD•BC,∴AB BC BD AB=,又∠B=∠B,∴△BAD∽△BCA,∴∠BDA=∠BAC=90°,即AD⊥BC,故A选项说法正确,不符合题意;B、∵AD2=BD•CD,∴AD CD BD AD=,又∠ADC=∠BDA=90°,∴△ADC∽△BDA,∴∠BAD=∠C,∵∠DAC+∠C=90°,∴∠DAC+∠BAD=90°,∴∠BAC=90°,故B选项说法正确,不符合题意;C、∵AB2=BD•BC,∴AB BC BD AB=,又∠B=∠B,∴△BAD∽△BCA,∴∠BAC=∠BDA=90°,即AD⊥BC,故C选项说法正确,不符合题意;D、如果∠BAC=90°,AD2=BD•CD,那么AD与BC不一定垂直,故D选项错误,不符合题意;故选D.本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.9.A【分析】根据角平分线和平行证明△EBO和△OFC是等腰三角形,再由周长关系得y=8-x,即可解题.【详解】解:∵点O是∠ABC和∠ACB两个内角平分线的交点,EF∥BC,∴∠OBC=∠EOB,∠OBC=∠EBO,∴△EBO是等腰三角形,同理,△OFC是等腰三角形,即BE=EO,CF=OF,∴△AEF的周长y=AE+EF+AF=AB+AC,∵△ABC的周长为8,BC=x,∴y=8-x,即x是关于y的一次函数,图像是递减的直线,故选A【点睛】本题考查了一次函数的实际应用,中等难度,证明等腰三角形,找到函数关系是解题关键. 10.B【分析】利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky).【详解】∵△ABO与△DCO位似,且△ABO与△DCO的面积之比为1:4,∴△ABO与△DCO为1:2,∵点B的坐标为(-3,2),∴点C的坐标为(6,-4),故选B.【点睛】此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.11.D【分析】首先设它的实际长度是xcm ,然后根据比例尺的定义,即可得方程:1:800025:x =,解此方程即可求得答案,注意统一单位.【详解】设它的实际长度是xcm ,根据题意得:1:800025:x =,解得:200000x =,2000002000cm m =,∴它的实际长度为2000m .故选D .【点睛】此题考查了比例线段.此题难度不大,解题的关键是理解题意,根据比例尺的定义列方程,注意统一单位.12.D【分析】先根据三角形中位线的性质得到DE=12AB ,从而得到相似比,再利用位似的性质得到△DEF ∽△ABC ,然后根据相似三角形的面积比是相似比的平方求解即可.【详解】∵点D ,E 分别是OA ,OB 的中点,∴DE=12AB ,∵△DEF 和△ABC 是位似图形,点O 是位似中心,∴△DEF ∽△ABC ,∴DEF ABC S S ∆∆=14,∴△ABC 的面积=2×4=8故选D .【点睛】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.13.∠ADE=∠C【分析】根据相似三角形判定定理:两个角相等的三角形相似;夹角相等,对应边成比例的两个三角形相似,即可解题.【详解】∵∠A是公共角,如果∠ADE=∠C,∴△ADE∽△ABC,故答案为∠ADE=∠C.【点睛】本题主要考查相似三角形的判定,掌握相似三角形的判定方法是解题的关键,即①有两组角对应相等的三角形相似,②三边对应成比例的两个三角形相似,③两组边对应成比例且夹角相等的两个三角形相似.14.143【分析】根据三角形的角性质定理、相似三角形的性质进行求解.【详解】∵△ABC和△ADE都是等边三角形,∴∠B=∠ADE=∠C=60°,∵∠B+∠BAD=∠ADF+∠FDC,∴∠BAD=∠FDC,∴△ABD∽△FDC,∴DC FC AB BD=,∵BD=4,CD=2,且△ABC是等边三角形,∴AB=BC=BD+DC=6,∴2=6 DC FCAB BD=,∴FC=4 3 ,AF=AC-FC=14 3 .【点睛】本题主要考查的是三角形的角性质定理、相似三角形的性质,熟练掌握是本题的解题关键. 15【分析】根据相似多边形的性质得CD CEAD AB=,即242CE=,然后利用比例性质求出CE,再利用勾股定理计算FC即可.【详解】∵四边形ABCD是矩形,∴AB=CD=2,AD=BC=4,∵四边形EFCD是矩形,∴EF=CD=2,CF=DE,∵余下的矩形EFCD∽矩形BCDA,∴CD CEAD AB=,即242CE=,∴CE=1,∴FC的长【点睛】本题考查了相似多边形的性质:如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形;相似多边形对应边的比叫做相似比.16.4【分析】设a b k23==,则a=2k,b=3k,再代入式子中即可求得结果.【详解】设a b k23==,则a=2k,b=3k,a 2b a+=2k 6k 2k +=8k 2k =4故答案为4【点睛】此题考查了比例的基本性质,熟练掌握性质是解答此题的关键.17.4:916:81:36.【分析】由AE :ED=5:4,得到DE :AD=4:9,根据平行四边形的性质得到AD ∥BC ,AD=BC ,根据相似三角形的性质即可得到结论.【详解】∵AE :ED=5:4,∴DE :AD=4:9,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD=BC ,∴△DEF ∽△BCF ,∴49DE DF BC BF ==,∴12S S =(49)2=1681,23S S =94,∴S 1:S 2:S 3=16:81:36,故答案为4:9,16:81:36.【点睛】本题考查了相似三角形的判定和性质,平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.18.35【分析】首先得出△AEM ∽△ABC ,△CFM ∽△CDA ,进而利用相似三角形的性质求出即可.【详解】∵AD ∥BC ∥EF ,∴△AEM ∽△ABC ,△CFM ∽△CDA ,∵EM :BC=2:5,∴25 AM EMAC BC==,设AM=2x,则AC=5x,故MC=3x,∴35 CM CFAC CD==,故答案为3 5.【点睛】此题主要考查了相似三角形的判定与性质,得出25AMAC=是解题关键.19.3 5【分析】由题中所给条件证明△ADF~△ACG,可求出AFAG的值.【详解】解:在△ADF和△ACG中,AB=6,AC=5,D是边AB的中点AG是∠BAC的平分线,∴∠DAF=∠CAG∠ADE=∠C∴△ADF~△ACG∴35 AF AD AG AC==.故答案为3 5 .【点睛】本题考查了相似三角形的判定和性质,难度适中,需熟练掌握.20.(1)证明见解析;(2)证明见解析.【分析】(1)由AB=AC,D是边BC的中点,利用等腰三角形的性质可得出∠ADC=90°,由同角的余角相等可得出∠ADE=∠DCE,结合∠AED=∠DEC=90°可证出△AED∽△DEC,再利用相似三角形的性质可证出DE•CD=AD•CE;(2)利用等腰三角形的性质及中点的定义可得出CD=12BC,DE=2DF,结合DE•CD=AD•CE可得出CE BCDF AD=,结合∠BCE=∠ADF可证出△BCE∽△ADF,再利用相似三角形的性质可证出AF•BC=AD•BE.【详解】(1)∵AB=AC,D是边BC的中点,∴AD⊥BC,∴∠ADC=90°,∴∠ADE+∠CDE=90°.∵DE⊥AC,∴∠CED=90°,∴∠CDE+∠DCE=90°,∴∠ADE=∠DCE.又∵∠AED=∠DEC=90°,∴△AED∽△DEC,∴DE CE AD CD=,∴DE•CD=AD•CE;(2)∵AB=AC,∴BD=CD=12 BC,∵F为DE的中点,∴DE=2DF.∵DE•CD=AD•CE,∴2DF•12BC=AD•CE,∴CE BC DF AD=,又∵∠BCE=∠ADF,∴△BCE∽△ADF,∴BC BE AD AF=,∴AF•BC=AD•BE.【点睛】本题考查了相似三角形的判定与性质、等腰三角形的性质以及余角,解题的关键是:(1)利用相似三角形的判定定理证出△AED∽△DEC;(2)利用相似三角形的判定定理证出△BCE∽△ADF.21.(1)证明见解析;(2)证明见解析.【分析】(1)根据直角三角形的性质得到AE=FE,根据相似三角形的性质得到∠EAG=∠ADG,求得∠DAG=∠FEG,根据菱形的性质得到AD∥BC,求得∠DAG=∠AFB=90°,于是得到结论;(2)由AE=EF,AE2=EG•ED,得到FE2=EG•ED,推出△FEG∽△DEF,根据相似三角形的性质得到∠EFG=∠EDF,根据相似三角形的判定和性质即可得到结论.【详解】(1)∵AF⊥BC于点F,∴∠AFB=90°,∵点E是AB的中点,∴AE=FE,∴∠EAF=∠AFE,∵AE2=EG•ED,∴AE DE EG AE,∵∠AEG=∠DEA,∴△AEG∽△DEA,∴∠EAG=∠ADG,∵∠AGD=∠FGE,∴∠DAG=∠FEG,∵四边形ABCD是菱形,∴AD∥BC,∴∠DAG=∠AFB=90°,∴∠FEG=90°,∴DE⊥EF;(2)∵AE=EF,AE2=EG•ED,∴FE2=EG•ED,∴EF EG DE EF=,∵∠FEG =∠DEF ,∴△FEG ∽△DEF ,∴∠EFG =∠EDF ,∴∠BAF =∠EDF ,∵∠DEF =∠AFB =90°,∴△ABF ∽△DFE ,∴AB BF DF EF=,∵四边形ACBD 是菱形,∴AB =BC ,∵∠AFB =90°,∵点E 是AB 的中点,∴FE =12AB =12BC ,∴BC DF =12BF BC ,∴BC 2=2DF•BF .【点睛】本题考查了相似三角形的判定和性质,菱形的性质,直角三角形的性质,正确的识别图形是解题的关键.22.2516ADE FGH S S ∆=△.【分析】设BG=2k ,GH=4k ,HC=3k ,根据平行四边形的性质可得DF=BG=2k ,EF=HC=3k ,可得DE=5k ,根据△ADE ∽△FGH 可得22516ADE FGH S DE SGH == ().【详解】解:∵DE BC ‖,∴ADE B∠=∠∴FG AB ‖,∴FGH B∠=∠∴ADE FGH∠=∠同理:AED FHG∠=∠∴ADE FGH∽△△∴2ADE FGH S DE S GH ⎛⎫= ⎪⎝⎭△△∵DE BC ‖,FGAB ‖,∴DF BG =同理:FE HC=∵::2:4:3BG GH HC =,∴设2BG k =,4GH k =,3HC k=∴2DF k =,3FE k =,∴5DE k=∴2525416ADE FGH S k S k ∆⎛⎫== ⎪⎝⎭△【点睛】此题考查相似三角形的判定和性质,平行四边形判定和性质,熟练掌握相似三角形的性质是解题的关键.23.(1)AD =4;(2)矩形EFGH 的面积28849.【分析】(1)设BC=3x ,根据三角形的面积公式列式计算即可;(2)设GF=y ,根据矩形的性质得到HG ∥BC ,得到△AHG ∽△ABC ,根据相似三角形的性质列出比例式,计算即可.【详解】(1)设BC =3x ,则AD =2x ,∵△ABC 的面积为12,∴12×3x×2x =12,解得,x 1=2,x 2=﹣2(舍去),则AD 的长=2x =4;(2)设GF =y ,则HG =2y ,∵四边形EFGH 为矩形,∴HG ∥BC ,∴△AHG ∽△ABC ,∴HG AM BC AD =,即2464y y -=,解得,y =127,HG =2y =247,则矩形EFGH 的面积=127×247=28849.【点睛】本题考查的是相似三角形的判定和性质,矩形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.24.△DBH ∽△HBC ,理由见解析.【分析】根据正方形的性质得到∠A=90°,设AB=x ,则AH=BC=CD=x ,推出BH BD BC BH=,由∠HBC=∠HBC ,即可得到结论.【详解】△DBH ∽△HBC ,理由:∵四边形ABGH ,四边形BCFG ,四边形CDEF 都是正方形,∴A ,B ,C ,D 在一条直线上,∠A =90°,设AB =x ,则AH =BC =CD =x ,∴BHx ,BD =2x ,∴BH BD BC BH =,∵∠HBC =∠HBC ,∴△DBH ∽△HBC .【点睛】此题主要考查了相似三角形的判定方法:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;需注意的是所有的全等三角形都相似.25.(1)证明见解析;(2)证明见解析.【分析】(1)利用两边成比例夹角相等两个三角形相似即可证明;(2)由△EDF ∽△ADC ,推出EDF ADC S S =(ED AD )2=14,推出ED AD =12,即ED=12AD ,由此即可解决问题.【详解】(1)∵AB =AD ,AE ⊥BC ,∴BE =ED =12DB ,∵EF 2=12•BD•EC ,∴EF 2=ED•EC ,即得EF EC =ED EF,又∵∠FED =∠CEF ,∴△EDF ∽△EFC ;(2)∵AB =AD ,∴∠B =∠ADB ,又∵DF ∥AB ,∴∠FDC =∠B ,∴∠ADB =∠FDC ,∴∠ADB+∠ADF =∠FDC+∠ADF ,即得∠EDF =∠ADC ,∵△EDF ∽△EFC ,∴∠EFD =∠C ,∴△EDF ∽△ADC ,∴EDF ADC S S =(ED AD )2=14,∴ED AD =12,即ED =12AD ,又∵ED =BE =12BD ,∴BD =AD ,∴AB =BD .【点睛】本题考查等腰三角形的性质,相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27.1 图形的相似知识点1 相似图形1.下列选项中,哪个才是相似图形的本质属性()A.大小不同B.大小相同C.形状相同 D.形状不同2.下列各组图形相似的是()知识点2 比例线段3.下列各线段的长度成比例的是()A.2 cm,5 cm,6 cm,8 cm B.1 cm,2 cm,3 cm,4 cmC.3 cm,6 cm,7 cm,9 cm D.3 cm,6 cm,9 cm,18 cm4.在比例尺为1∶40 000的地图上,某条道路的长为7 cm,则该道路的实际长度是km.知识点3 相似多边形5.两个相似多边形一组对应边分别为3 cm,4.5 cm,那么它们的相似比为()A.23B.32C.49D.946.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 5 cm,6 cm和9 cm,另一个三角形的最短边长为2.5 cm,则它的最长边长为()A.3 cm B.4 cm C.4.5 cm D.5 cm7.如下的各组多边形中,相似的是()A.(1)(2)(3) B.(2)(3)C.(1)(3) D.(1)(2)8.在一张复印出来的纸上,一个多边形的一条边由原图中的2 cm变成了6 cm,这次复印的放缩比例是.9.如图所示是两个相似四边形,求边x、y的长和α的大小.10.已知三条线段的长分别为1 cm、2 cm、 2 cm,如果另外一条线段与它们是成比例线段,那么另外一条线段的长为 . 11.下列说法:①放大(或缩小)的图片与原图片是相似图形;②比例尺不同的中国地图是相似图形;③放大镜下的五角星与原来的五角星是相似图形;④放电影时胶片上的图象和它映射到屏幕上的图象是相似图形;⑤平面镜中,你的形象与你本人是相似的.其中正确的说法有()A.2个 B.3个C.4个 D.5个12.如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是()A.2DE=3MNB.3DE=2MNC.3∠A=2∠FD.2∠A=3∠F13.如图所示,它们是两个相似的平行四边形,根据条件可知,α=,m=.14.如图,左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形,要求大小与左边四边形不同.15.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:(1)每块地砖的长与宽分别为多少?(2)这样的地砖与所铺成的矩形地面是否相似?试说明你的结论.16.如图,矩形ABCD的长AB=30,宽BC=20.(1)如图1,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD 与A′B′C′D′相似吗?请说明理由;(2)如图2,x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?参考答案:1.C2.B3.D4.2.8 .5.A6.C7.B8.1∶3.9.解:∵两个四边形相似,∴ADA′D′=BCB′C′=ABA′B′,即416=6x=7y.∴x=24,y=28.∵∠B=∠B′=73°,∴α=360°-∠A-∠D-∠B=83°.102__cm或2__cm. 11.D12.B13.α=125°,m=12.14.解:如图所示.15.解:(1)设矩形地砖的长为a cm ,宽为b cm ,由题图可知4b =60,即b =15.因为a +b =60,所以a =60-b =45,所以矩形地砖的长为45 cm ,宽为15 cm. (2)不相似.理由:因为所铺成矩形地面的长为2a =2×45=90(cm ),宽为60 cm ,所以长宽=9060=32,而a b =4515=31,32≠31,即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.所以它们不相似. 16.解:(1)不相似,AB =30,A ′B ′=28,BC =20,B ′C ′=18, 而2830≠1820, 故矩形ABCD 与矩形A ′B ′C ′D ′不相似. (2)矩形ABCD 与A ′B ′C ′D ′相似, 则A ′B ′AB =B ′C ′BC 或A ′B ′BC =B ′C ′AB .即30-2x 30=20-220或30-2x 20=20-230.解得x =1.5或9,故当x =1.5或9时,矩形ABCD 与A ′B ′C ′D ′相似.27.2 相似三角形(满分120分;时间:120分钟)一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )1. 如图,在△ABC 中,AB =8,AC =6,点D 在AC 上,且AD =2,如果要在AB 上找一点E,使△ADE与△ABC相似,则AE的长为()A.8 3B.32C.3D.83或322. 在△ABC中,点D,E分别在边AB,AC上,AD:BD=1:2,那么下列条件中能够判断DE // BC的是()A.DEBC =12B.DEBC=13C.AEAC=12D.AEAC=133. 能说明△ABC和△A1B1C1相似的条件是()A.AB:A1B1=AC:A1C1B.AB:A1C1=BC:A1C1且∠A=∠C1C.AB:A1B1=BC:A1C1且∠B=∠A1D.AB:A1B1=AC:A1C1且∠B=∠B14. 如图,在Rt△ABC中,∠ACB=90∘,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为()A.3 2B.92C.3√32D.3√35. 如图,在Rt△ABC中,∠BAC=90∘,AD⊥BC,AB=10,BD=6,则BC的值为()A.185B.2√5 C.1003D.5036. 已知两个相似三角形的对应边长分别为9cm和11cm,它们的周长相差20cm,则这两个三角形的周长分别为()A.45cm,65cmB.90cm,110cmC.45cm,55cmD.70cm,90cm7. 如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,图中点D,E,F也都在格点上,则下列与△ABC相似的三角形是()A.△ACDB.△ADFC.△BDFD.△CDE8. 如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为()m.A.2B.4C.6D.89. 如图,在△ABC中,D、E分别是AB、AC上一点,下面有四个条件:(1)ADAB =AEAC;(2)DBAB=ECAC;(3)ADDB=AEEC;(4)ADDB=DEBC.其中一定能判定DE // BC有()A.1个B.2个C.3个D.4个10. 如图,AD⊥BC于D,CE⊥AB于E交AD于F,则图中相似三角形的对数是()A.3个B.4个C.5个D.6个二、填空题(本题共计8 小题,每题3 分,共计24分,)11. 在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请你在4×4的方格纸中,画一个格点三角形A1B1C1,使△A1B1C1与格点三角形ABC相似(相似比不为1).________.12. 如图,在△ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC于点F.若∠AED=∠B,且AG:GF=2:1,则DE:BC=________.13. 在△ABC中,∠ACB=90∘,CD⊥AB,垂足为D,若AD=3,BD=1.则∠ABC的度数为________度.14. 如图,已知△ABC中,DE // BC,连接BE,△ADE的面积是△BDE面积的1,则2S△ADE:S△ABC=________.15. 如图所示,CD是一个平面镜,光线从A点射出经CD上的E点反射后照射到B点,设入射角为α(入射角等于反射角).AC⊥CD,BD⊥CD,垂足分别为点C,D.若AE=4,BE=8,CD=6.则CE=________.16. 如图,AB⊥BC于B,AC⊥CD于C,添加一个条件:________,使△ABC∽△ACD.17. 四边形ABCD中,AD // BC,∠A=90∘,AD=2cm,AB=7cm,BC=3cm,试在AB边上确定P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似,则AP的长是________cm.18. 如图,C、D是△PAB的边AB上的两点,以CD为边作平行四边形CDEF,EF经过点P,且∠APB=∠ADE.试写出四对相似三角形________.三、解答题(本题共计8 小题,共计66分,)19. 已知,如图,D为△ABC的边BC的中点,O为AD上的任一点,CD的延长线交AB于点E,BD的延长线交AC于点F,求证:EF // BC.20. 已知,如图,ABBD =BCBE=CAED,那么△ABD与△BCE相似吗?为什么?21. 如图,已知AB:AC=AE:AD.求证:△ODB∽△OEC.22. 如图,CD为Rt△ABC的斜边AB上的高线,∠BAC的平分线交BC,CD于点E,F,求证:△ABE∽△ACF.23. 如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且ADAC =DFCG.(1)求证:△ADF∼△ACG;(2)若ADAC =12,求AFFG的值.24. 如图,已知:梯形ABCD中,AD // BC,AC、BD交于点O,E是BC延长线上一点,点F在DE上,且DFEF =AOOC.求证:OF // BC.25. 如图,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区,已知亮区到窗口下的墙脚距离EC=7.2m,窗口高AB=1.8m.求窗口底边离地面的高BC.26. 定义:顶点都在网格点上的四边形叫做格点四边形,端点都在网格点上的线段叫做格点线.如图1,在正方形网格中,格点线DE、CE将格点四边形ABCD分割成三个彼此相似的三角形.请你在图2、图3中分别画出格点线,将阴影四边形分割成三个彼此相似的三角形.参考答案一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 ) 1. 【答案】 D 【解答】解:∵ ∠A 是公共角, ∵ 当AEAB =ADAC,即AE 8=26时,△AED ∼△ABC , 解得:AE =83; 当AE AC=AD AB,即AE 6=28时,△ADE ∼△ABC ,解得:AE =32, ∵ AE 的长为:83或32.故选D . 2. 【答案】 D 【解答】 解:如图,可假设DE // BC ,则可得AD DB=AE EC=12,AD AB=AE AC=13,但若只有DEBC =ADAB =13,并不能得出线段DE // BC .故选D .3. 【答案】【解答】解:∵ 相似三角形的判定定理之一是:有①两边对应成比例,且②夹角相等的两个三角形相似,①②两个条件缺一不可,∵ A、只符合条件①,不符合条件②,即这两个三角形不相似,故本选项错误;B、符合条件①,但是夹角是∠B=∠A1,不是∠A=∠C1,即这两个三角形不相似,故本选项错误;C、符合条件①②,即这两个三角形相似,故本选项正确;D、符合条件①,但是夹角是∠A=∠A1,不是∠B=∠B1,即这两个三角形不相似,故本选项错误;故选C.4.【答案】A【解答】解:∵ 在Rt△ABC中,∠ACB=90∘,CD⊥AB,∵ AC2=AD⋅AB.又∵ AC=3,AB=6,∵ 32=6AD,则AD=32.故选A.5.【答案】D【解答】解:根据射影定理得:AB2=BD×BC,∵ BC=1006=503.故选D.6.【答案】【解答】解:∵ 两个相似三角形的对应边长分别为9cm和11cm,∵ 两个相似三角形的相似比为9:11,∵ 两个相似三角形的周长比为9:11,设两个相似三角形的周长分别为9x、11x,由题意得,11x−9x=20,解得,x=10,则这两个三角形的周长分别为90cm,110cm,故选:B.7.【答案】C【解答】解:由网格可知:AB=2√2,BC=4,AC=2√10,BD=1,DF=√2,BF=√5,则BDAB =DFBC=BFAC=√24,故与△ABC相似的三角形是△BDF.故选C.8.【答案】B【解答】解:根据题意,作△EFC;树高为CD,且∠ECF=90∘,ED=2,FD=8;∵ ∠E+∠ECD=∠E+∠CFD=90∘∵ ∠ECD=∠CFD∵ Rt△EDC∽Rt△FDC,有EDDC =DCFD;即DC2=ED⋅FD,代入数据可得DC2=16,DC=4;故选:B.9.【答案】C【解答】解:根据对应线段成比例两直线平行,有ADAB =AEAC,DBAB=ECAC,ADDB=AEEC,得到(1)(2)(3)正确,(4)的线段不对应(如图所示)DE′=DE时,DE′不平行于BC,所以不正确.故选C.10.【答案】D【解答】解:∵ AD⊥BC于D,CE⊥AB于E,∵ ∠ADB=∠CEB=90∘,而∠AFE=∠CFD,∵ ∠A=∠C,∵ Rt△AFE∽Rt△CFD∽Rt△ABD∽Rt△CBF.故选D.二、填空题(本题共计8 小题,每题 3 分,共计24分)11.【答案】答案如图【解答】解:如图所示:12.【答案】2:3【解答】解:∵ ∠AED=∠B,而∠DAE=∠CAB,∵ △ADE∽△ACB,∵ DEBC =AGAF,∵ AG:GF=2:1,∵ DEBC =AGAF=23.故答案为2:3.13.【答案】60∘【解答】解:由射影定理得,CD2=AD⋅DB=3,则CD=√3,tan∠B=CDDB=√3,则∠ABC=60∘.故答案为:60∘.14.【答案】1:9【解答】解:∵ △ADE的面积是△BDE面积的12,∵ ADBD =12,∵ ADAB =13,∵ DE // BC,∵ △ADE∼△ABC,∵ S△ADES△ABC =(ADAB)2=(13)2=19.故答案为:1:9.15.【答案】2【解答】解:由镜面反射对称可知:∠A=∠B,∠AEC=∠BED.∵ △AEC∽△BED.∵ AEBE =CEDE.又∵ AE=4,BE=8,CD=6,∵ 48=CE6−CE,求得EC=2.故答案为:2.16.【答案】∠BAC=∠CAD或∠BCA=∠CDA或ABBC =ACCD【解答】解:∵ AB ⊥BC 于B ,AC ⊥CD 于C , ∵ ∠ABC =∠ACD =90∘,∵ 当∠BAC =∠CAD 或∠BCA =∠CDA 或AB BC=AC CD时,△ABC ∽△ACD . 故答案为:∠BAC =∠CAD 或∠BCA =∠CDA 或AB BC=AC CD.17. 【答案】 1, 6或145【解答】解:①若点A ,P ,D 分别与点B ,C ,P 对应,即△APD ∽△BCP , ∵ ADBP =APBC , ∵27−AP =AP 3,∵ −AP 2+7AP −6=0, ∵ AP =1或AP =6,检测:当AP =1时,由BC =3,AD =2,BP =6, ∵ APBC =ADBP ,又∵ ∠A =∠B =90∘,∵ △APD ∽△BCP . 当AP =6时,由BC =3,AD =2,BP =1, 又∵ ∠A =∠B =90∘, ∵ △APD ∽△BCP .②若点A ,P ,D 分别与点B ,P ,C 对应,即△APD ∽△BPC . ∵ APBP =ADBC , ∵ AP7−AP =23, ∵ AP =145.检验:当AP =145时,由BP =215,AD =2,BC =3,∵ APBP =ADBC ,又∵ ∠A =∠B =90∘, ∵ △APD ∽△BPC .故答案为:1,6或145.18.【答案】△PMF∽△AMC;△AMC∽△ABP;△PMF∽△ABP;△BDN∽△PEN【解答】解:△PMF∽△AMC;△AMC∽△ABP;△PMF∽△ABP;△BDN∽△PEN,∵ 平行四边形CDEF,∵ EF // AB,CF // ED,∵ ∠F=∠MCA,∠FPM=∠A,∵ △PMF∽△AMC;∵ ∠A=∠A,∠ACM=∠ADE=∠APB,∵ △AMC∽△ABP;∵ ∠F=∠ACM=∠APB,∠FPM=∠A,∵ △PMF∽△ABP;∵ EF // AB,∵ ∠E=∠NDB,∠EPN=∠B,∵ △BDN∽△PEN.故答案为:△PMF∽△AMC;△AMC∽△ABP;△PMF∽△ABP;△BDN∽△PEN三、解答题(本题共计8 小题,每题10 分,共计80分)19.【答案】证明:∵ D为△ABC的边BC的中点,∵ BD=CD,∵ S△ABD=S△ACD,S△BOD=S△COD,∵ S△ABO=S△ACO,∵ AEBE =S△ACES△BCE=S△AOES△BOE=S△ACE−S△AOES△BCE−S△BOE=S△AOCS△BOC,同理可得AFCF =S△AOBS△BOC,∵ AEBE =AFCF,∵ EF // BC.【解答】证明:∵ D为△ABC的边BC的中点,∵ BD=CD,∵ S△ABD=S△ACD,S△BOD=S△COD,∵ S△ABO=S△ACO,∵ AEBE =S△ACES△BCE=S△AOES△BOE=S△ACE−S△AOES△BCE−S△BOE=S△AOCS△BOC,同理可得AFCF =S△AOBS△BOC,∵ AEBE =AFCF,∵ EF // BC.20.【答案】∵ ABBD =BCBE=CAED,∵ △ABC∽△DBE,∵ ∠ABC=∠DBE,∵ ∠ABC−∠DBC=∠DBE−∠DBC,即∠ABD=∠CBE,∵ ABBD =BCBE,∵ ABBC =BDBE,∵ △ABD∽△CBE.【解答】∵ ABBD =BCBE=CAED,∵ △ABC∽△DBE,∵ ∠ABC=∠DBE,∵ ∠ABC−∠DBC=∠DBE−∠DBC,即∠ABD=∠CBE,∵ ABBD =BCBE,∵ ABBC =BDBE,∵ △ABD∽△CBE.21.【答案】证明:∵ AB:AC=AE:AD,即AB:AE=AC:AD,∠A为公共角,∵ △ACD∽△ABE,∵ ∠BDO=∠CEO,又∵ ∠BOD=∠COE,∵ △ODB∽△OEC.【解答】证明:∵ AB:AC=AE:AD,即AB:AE=AC:AD,∠A为公共角,∵ △ACD∽△ABE,∵ ∠BDO=∠CEO,又∵ ∠BOD=∠COE,∵ △ODB∽△OEC.22.【答案】证明:∵ ∠ACB=90∘,∠CDB=90∘,∵ ∠ACD=90∘−∠DCB,∠B=90∘−∠DCB,∵ ∠ACD=∠B,∵ AE平分∠CAB,∵ ∠CAE=∠EAB,∵ △ACF∽△ABE.【解答】证明:∵ ∠ACB=90∘,∠CDB=90∘,∵ ∠ACD=90∘−∠DCB,∠B=90∘−∠DCB,∵ ∠ACD=∠B,∵ AE平分∠CAB,∵ ∠CAE=∠EAB,∵ △ACF∽△ABE.23.【答案】(1)证明:∵ ∠AED=∠B,∠DAE=∠CAB,∵ △ADE∼△ACB,∵ ∠ADF=∠C.又∵ ADAC =DFCG,∵ △ADF∼△ACG.(2)解:∵ △ADF∼△ACG,∵ ADAC =AFAG.∵ ADAC =12,∵ AFAG =12,∵ AFFG =AFAG−AF=1.【解答】(1)证明:∵ ∠AED=∠B,∠DAE=∠CAB,∵ △ADE∼△ACB,∵ ∠ADF=∠C.又∵ ADAC =DFCG,∵ △ADF∼△ACG.(2)解:∵ △ADF∼△ACG,∵ ADAC =AFAG.∵ ADAC =12,∵ AFAG =12,∵ AFFG =AFAG−AF=1.24.【答案】证明:∵ AD // BC,∵ AOCO =DOBO,∵ DFEF =AOOC,∵ DOBO =DFEF,∵ DODB =DFEF,∵ ∠ODF=∠BDE,∵ △DOF∽△DBE,∵ ∠DOF=∠DBE,∵ OF // BC.【解答】证明:∵ AD // BC,∵ AOCO =DOBO,∵ DFEF =AOOC,∵ DOBO =DFEF,∵ DODB =DFEF,∵ ∠ODF=∠BDE,∵ △DOF∽△DBE,∵ ∠DOF=∠DBE,∵ OF // BC.25.【答案】窗口底边离地面的高BC为3m.【解答】解:∵ BF // AE,∵ △CBF∽△CAE,∵ CBCA =CFCE,即CBCB+1.8=7.2−2.77.2,∵ BC=3(m).26.【答案】解:(1)作答如图所示图2中,连接AC、CE,得△ABC∽△CDE∽△ECA,相似比为√2:2;图3中,连接BE、CE,得△BCE∽△EBA∽△CED,相似比为√2:2.【解答】解:(1)作答如图所示图2中,连接AC、CE,得△ABC∽△CDE∽△ECA,相似比为√2:2;图3中,连接BE、CE,得△BCE∽△EBA∽△CED,相似比为√2:2.27.3 位似(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 在平面直角坐标系中,A(3,4),B(−2,3),C(−4,−2),以原点为位似中心,将△ABC扩大到原来的3倍,若A点的对应点坐标为(9,12),则B点的对应点的坐标为()A.(6,−9)B.(−6,9)C.(6,9)D.(−6,−9)2. 在平面直角坐标系中,点A(6,3),以原点O为位似中心,在第一象限内把线段OA缩小为原来的1得到线段OC,则点C的坐标为()3A.(2,1)B.(2,0)C.(3,3)D.(3,1)3. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a, b)对应大鱼上的点( )A.(−2a, 2b)B.(−2a, −2b)C.(−2b, −2a)D.(−2a, −b)4. 在如图所示的网格中,正方形ABCD与正方形EFGH是位似图形,则位似中心是()A.点O或点MB.点O或点NC.点P或点MD.点P或点N5. 如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是()A.点OB.点PC.点MD.点N6. 点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为()A.点EB.点FC.点HD.点G7. 如图,四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,四边形ABCD的面积等于4,则四边形A′B′C′D′的面积为()A.3B.4C.6D.98. 在平面直角坐标系中,△ABO的三个顶点的坐标分别为A(−4,2),B(−4,0),O(0,0),,得到△CDO,则点A的对应点C的坐以原点O为位似中心,把这个三角形缩小为原来的12标是()A.(−2,1)B.(2,2)C.(−2,1)或(2,−1)D.(2,2)或(−2,−2)9. 下列各组图形中不是位似图形的是()A. B. C. D.10. 在平面直角坐标系中,把△ABC以原点O为位似中心放大,得到△A′B′C′若点A和它的对应点A′的坐标分别为(2,5),(−6,−15),则△A′B′C′与△ABC的相似比为()A.−3B.3C.13D.−13二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是________.12. 如图,在Rt△ABC∠B=90∘,AB,=3,BC=4,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C′EF,C′F,交BC于点G,当△CFG,△ABC相似时,CF的长为________.13. 在平面直角坐标系中,△ABO三个顶点的坐标分别为A(−2, 4),B(−4, 0),O(0, 0).以原点O为位似中心,把这个三角形缩小为原来的12,得到△CDO,则点A的对应点C的坐标是________.14. 大矩形的周长是与它位似的小矩形的2倍,小矩形的面积是5cm2,大矩形的长为5cm,则大矩形的宽为________cm.15. 已知四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4),以0为位似中心,作四边形A′B′C′D′位似与四边形ABCD位似,对应边的比为12,则点A′、B′、C′、D′的对应点的坐标分别为________,________,________,________.16. 把一个三角形变成和它位似的另一个三角形,若边长缩小到12倍,则面积缩小到原来的________倍..若五边形ABCDE 17. 如图,五边形A′B′C′D′E′与五边形ABCDE是位似图形,且位似比为12的,面积为20cm2,那么五边形A′B′C′D′E′的面积为________.18. 在△ABC中,AB=BC,∠B=90∘,将△ABC沿BC方向平移,得到△A′CC′,以C为位似的值为中心,作△DEC与△ABC位似,位似比为1:2,F为CC′的中点,连接DF, A′F,则A′FDF________.19. 如图,△ABC与△DEF是位似图形,位似比为2:3,已知AB=4,则DE的长为________.20. 如图,△ABC的顶点在格点上,且点A(−5, −1),点C(−1, −2).以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出________放大后的图形△A′B′C′并写出△A′B′C′各顶点坐标.三、解答题(本题共计6 小题,共计60分,)21. 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0, 3),B(3, 4),C(2, 2).(正方形网格中,每个小正方形的边长是1个单位长度)请以点B为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,并求出△A1B1C1的面积.22. 如图,已知O是坐标原点,A,B的坐标分别为(3,1),(2,−1).(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD.(要求:新图与原图的相似比为2:1);(2)分别写出A,B的对应点C,D的坐标;(3)若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为________.23. 如图,在平面直角坐标系中,A(2, 1),B(1, −2).(1)画出△OAB向左平移2个单位长度,再向上平移1个单位长度后的△O1A1B1;(2)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1;(3)判断△O1A1B1与△OA2B2是否关于某一点M为位似中心的位似图形?若是,请在图中标出位似中心M,并写出点M的坐标.24. 如图,已知O是坐标原点,B、C两点的坐标分别为(3, −1)、(2, 1).(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;(2)分别写出B、C两点的对应点B′、C′的坐标.25. 如图,BD,AC相交于点P,连结AB,BC,CD,DA,∠DAP=∠CBP.(1)求证:△ADP∼△BCP;(2)△ADP与△BCP是不是位似图形?并说明理由;(3)若AB=8,CD=4,DP=3,求AP的长.26. 如图,已知O是原点,B、C两点的坐标分别为(3, −1),(2, 1).(1)以点O为位似中心,在y轴的左侧将△OBC扩大为原来的两倍(即新图与原图的相似比为2),画出图形并写出点B,C的对应点的坐标;(2)如果△OBC内部一点M的坐标为(a, b),写出点M的对应点M′的坐标.参考答案与试题解析一、选择题(本题共计10 小题,每题 3 分,共计30分)1.【答案】B【解答】解:∵ 以原点O为位似中心,将△OAB放大为原来的3倍,点A(3,4)的对应点是(9,12),则点B(−2,3)的对应点为(−6,9).故选B.2.【答案】A【解答】解:在平面直角坐标系中,点A(6,3),以原点O为位似中心,在第一象限内把线段OA缩小为原来的13得到线段OC,则点A的对应点C的坐标为(6×13,3×13),即C点坐标为(2,1).故选A.3.【答案】B【解答】解:根据图形可得,两个图形的位似比是1:2,∵ 对应点是(−2a, −2b).故选B.4.【答案】D【解答】解:如图,连接AG,EC,FD,BH交于点P;连接AE,BF,DH,CG并分别延长交于点N,则位似中心为点P或点N.故选D.5.【答案】B【解答】如图所示:两个三角形的位似中心是:点P.故选:B.6.【答案】B【解答】解:点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为点F,故选B.7.【答案】D【解答】解:∵ 四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,OA:OA′=2:3,∵ 四边形ABCD与四边形A′B′C′D′的面积比为:4:9.∵ 四边形ABCD的面积等于4,∴ 四边形A′B′C′D′的面积为9.故选D.8.【答案】C【解答】,解:∵ 点A(−4,2),且相似比为12∵ 当△CDO与△ABO在y轴同侧时,点C的坐标为(−2,1),当△CDO与△ABO在y轴异侧时,点C的坐标为(2,−1).故选C.9.【答案】D【解答】解:根据位似图形的定义,可得A,B,C是位似图形,B与C的位似中心是交点,A的位似中心是圆心;D不是位似图形.故选D.10.【答案】B【解答】解:∵ △ABC和△A′B′C′关于原点位似,且点A和它的对应点A′的坐标分别为(2,5),(−6,−15),对应点的坐标乘以−3,∵ △A′B′C′与△ABC的相似比为3.故选B.二、填空题(本题共计10 小题,每题 3 分,共计30分)11.【答案】【解答】解:由题图可知,直线与直线的交点坐标为,所以位似中心的坐标为.故答案为:.12.【答案】4或2.8【解答】解:①当FG⊥BC时,将△CEF沿EF折叠得△C′EF,∵ ∠C′=∠C,C′E=CE=2,∵ sin∠C=sin∠C′,∵ ABAC =EGC′E,∵ EG=1.2,∵ FG//AB,∵ CGBC =CFAC,即3.2 4=CF5,∵ CF=4;②当GF⊥AC时,如图,将△CEF沿EF折叠得△C′EF,∵ ∠1=∠2=45∘,∵ HF=HE,∵ sin∠C=sin∠C′=EHC′E =ABAC,∵ EH=2×35=65,∵ C′H=√C′E2−EH2=85,∵ CF=C′F=C′H+HF=1.6+1.2=2.8.综上所述,当△CFG与△ABC相似时,CF的长为4或2.8.故答案为∵4或2.8.13.【答案】(−1, 2)或(1, −2)【解答】解:以原点O为位似中心,把这个三角形缩小为原来的12,点A的坐标为(−2, 4),∵ 点C的坐标为(−2×12, 4×12)或(2×12, −4×12),即(−1, 2)或(1, −2).故答案为:(−1, 2)或(1, −2).14.【答案】4【解答】解:∵ 大矩形与小矩形位似,∵ 位似比等于相似比为2:1.∵ 其对应的面积比等于相似比的平方为4:1,∵ 大矩形面积为20cm2.∵ 大矩形的宽为4cm.故大矩形的宽为4cm.15.【答案】(1,3),(2,1),(3,1),(3,2)【解答】解:如图,连接OA、OB、OC、OD,分别取它们的中点A′,B′,C′,D′,即四边形A′B′C′D′即为所求.∵ A′(1,3),B′(2,1),C′(3,1),D′(3,2).故答案为:(1,3);(2,1);(3,1);(3,2).16.【答案】14【解答】解:∵ 把一个三角形变成和它位似的另一个三角形,若边长缩小了2倍∵ 位似比等于1:2∵ 面积比等于1:4倍.∵ 面积缩小到原来的1417.【答案】5【解答】,解:∵ 五边形A′B′C′D′E′与五边形ABCDE是位似图形,且位似比为12∵ 五边形A′B′C′D′E′的面积与五边形ABCDE的面积比为:1:4,∵ 五边形ABCDE的面积为20cm2,∵ 五边形A′B′C′D′E′的面积为:5.故答案为:5.18.【答案】【解答】解:设AB=BC=2x,①如图1,当点D在AC上时,∵ △ABC≅△A′CC′,∵ A′C=CC′=2x,∵ F为CC′的中点,∵ CF=x,则A′F=√A′C2+CF2=√5x,又∵ △DEC∼△ABC,且DEAB =CECB=12,∵ DE=CE=x,则EF=2x,∵ DF=√DE2+EF2=√5x,∵ A′FDF =√5x√5x=1;②如图2,当点D在AC延长线上时,由①知A′F=√A′C2+CF2=√5x,DF=DE=x,∵ A′FDF =√5xx=√5.故答案为:1或√5.19.6【解答】解:∵ △ABC与△DEF是位似图形,位似比为2:3,∵ AB:DE=2:3,∵ DE=6.故答案为:6.20.【答案】△ABC【解答】解:如图所示:△A′B′C′即为所求,A′(10, 2),B′(10, 6),C′(2, 4).三、解答题(本题共计6 小题,每题10 分,共计60分)21.【答案】解:如图所示:△A1B1C1即为所求,△A1B1C1的面积为:4×6−12×2×6−12×2×4−12×2×4=10.【解答】解:如图所示:△A1B1C1即为所求,△A1B1C1的面积为:4×6−12×2×6−12×2×4−12×2×4=10.22.【答案】解:(1)如图:△OCD即为所求.(2)由图可知:C:(−6,−2),D:(−4,2).(−2m,−2n)【解答】解:(1)如图:△OCD即为所求.(2)由图可知:C:(−6,−2),D:(−4,2).(3)根据原点位似的特点可知P′(−2m,−2n).故答案为:(−2m,−2n).23.【答案】解:如图所示:如图:如图所示,与是关于为位似中心的位似图形.【解答】解:如图所示:如图:如图所示,与是关于为位似中心的位似图形.24.【答案】解:是所求的三角形;的坐标是,的坐标是.【解答】解:是所求的三角形;的坐标是,的坐标是.25.【答案】(1)证明:∵ ∠DAP=∠CBP,∠DPA=∠CPB,∴ △ADP∼△BCP;(2)解:△ADP与△BCP不是位似图形,因为它们的对应边不平行;(3)∵ △ADP∼△BCP,∴APDP =BPCP,又∠APB=∠DPC,∴ △APB∼△DPC,∴APPD =ABCD,即AP3=84,解得,AP=6.【解答】(1)证明:∵ ∠DAP=∠CBP,∠DPA=∠CPB,∴ △ADP∼△BCP;(2)解:△ADP与△BCP不是位似图形,因为它们的对应边不平行;(3)∵ △ADP∽△BCP,∴APDP =BPCP,又∠APB=∠DPC,∴ △APB∽△DPC,∴APPD =ABCD,即AP3=84,解得,AP=6.26.【答案】解:(1)如图,△OB1C1为所作,点B1,C1点的坐标分别为(−6, 2),(−4, −2);(2)把M点的横纵坐标分别乘以−2即可得到M1的坐标,所以点M的对应点M′的坐标为(−2a, −2b).【解答】解:(1)如图,△OB1C1为所作,点B1,C1点的坐标分别为(−6, 2),(−4, −2);(2)把M点的横纵坐标分别乘以−2即可得到M1的坐标,所以点M的对应点M′的坐标为(−2a, −2b).亲爱的读者:纸上得来终觉浅,绝知此事要躬行!+读书不觉已春深,一寸光阴一寸金;少壮不努力,老大徒伤悲春去燕归来,新桃换旧符。
