2021学年高中数学2.2第14课时超几何分布作业课件北师大版选修2_3.ppt
高中高中数学北师大版选修2-3练习课件2.2 超几何分布精选ppt课件

答案:59
知识点二
超几何分布的分布列
5. 从装有3个红球,2个白球的袋中随机取
出2个球,设其中有X个白球,求X的分布列.
解:X 的可能取值为 0,1,2. P(X=0)=CC2325=130=0.3, P(X=1)=CC12·C52 13=160=0.6, P(X=2)=CC2225=110=0.1.
选修2-3 §2 超几何分布
课时作业40 超几何分布
[目标导航] 1. 通过实例,理解超几何分布及其导出过 程. 2. 运用超几何分布解决一些简单的问题.
1 课堂对点训练 2 课后提升训练
课堂对点训练
知识点一
超几何分布问题
1. 一个小组有 6 人,任选 2 名代表,其中甲当选的
概率是( )
A.12
则正好取到 1 件次品的概率是( )
A.2485
B.1465
C.4115
D.1475
解析:由题意 10 件产品中有 2 件次品,故所求概率为
P=B
4. 从分别标有数字1,2,3,4,5,6,7,8,9的9张卡 片中任取2张,则所取卡片上数字之和是奇数的概 率是________.
故 X 的分布列为
X
0
1
2
P
0.3
0.6
0.1
课后提升训练
温馨提示:请点击按扭进入WORD文档作业
再见
B.13
C.14 解析:P=CC1526=13.
答案:B
D.15
2. 盒中有 4 个白球,5 个红球,从中任取 3 个球,则
取出 1 个白球和 2 个红球的概率是( )
课堂设计高中数学 2.2 超几何分布课件 北师大版选修23

学的概率为
P(X≥1)=P(X=1)+P(X=2)+P(X=3)=CC4113C062
+
C42C61 C130
+
C43C60 C130
=
56或
P(X≥1)=1-P(X=0)=1-CC4013C063 = 56.
探究一
探究二
探究三
探究四
点评超几何分布问题的解题关键在于判断,先确定问题是否属于
此类,然后确定各个量,代入公式运算.
§2 超几何分布
课程目标
1.通过实例,理解超几何分布及其特点. 2.通过对实例的分析,掌握超几何分布 的导出过程. 3.能用超几何分布解决简单的实际问 题.
学习脉络
超几何分布
一般地,设有 N 件产品,其中有 M(M≤N)件次品.从中任取 n(n≤N)件产
品,用 X 表示取出的 n 件产品中次品的件数,那么 P(X=k)=C������������CC������������������������--������������(其中 k 为 非负整数).
探究一
探究二
探究三
探究四
【例 3】厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家 时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收 这批产品.
若厂家发给商家 20 件产品,其中有 3 件不合格,按合同规定该商家从中 任取 2 件进行检验,只有 2 件产品都合格时才接收这批产品,否则拒收.求该 商家可能检验出不合格产品数 ξ 的分布列,并求该商家拒收这批产品的概 率.
如果一个随机变量的分布列由上式确定,则称 X 服从参数为 N,M,n 的 超几何分布.
特别提醒 1.超几何分布是概率分布的一种形式,一定要注
超几何分布-北师大版选修2-3教案

超几何分布-北师大版选修2-3教案一、知识背景超几何分布(hypergeometric distribution)是离散随机变量的一种,描述从有限个物品中抽出固定数量的物品,其中有指定种类的物品数量的概率分布。
它在统计学中有广泛的应用,例如在品质控制中,抽检商品的次数以及在实验设计中选定目标人群的样本数量。
二、教学目标•理解超几何分布的概念、特点、条件和性质;•掌握超几何分布的基本计算方法和公式应用;•能够解答超几何分布的实际问题,如品质控制的样本检测等;•培养学生的逻辑思维能力和应用数学知识解决实际问题的能力。
三、教学内容1. 超几何分布的概念和特点超几何分布指从总数为N(不放回)的物品中,其中有m个种类的物品共k 个,随机抽取n个物品,其中有m0个种类的物品的个数X的分布律,用H(n, m, k)表示。
因此,超几何分布的性质为:•该分布实验不满足独立性;•分布变量的取值只能是非负整数;•总体中有k个成功物品,n个样本,成为超几何分布的参数。
2. 超几何分布的计算方法和公式超几何分布的概率函数公式为:其中,C表示组合数。
3. 超几何分布的应用品质控制中,经常需要检验样本是否达到质量标准。
对于超过某个标准值的样本,则认为该样本不符合质量要求。
超几何分布在此类问题中应用广泛。
四、教学方法•讲授法:通过讲解概念、公式和解题方法,让学生掌握超几何分布的知识;•举例法:通过实际问题,让学生在操作中掌握超几何分布的应用方法;•配套练习:在课堂上或课后布置超几何分布的练习题,检验学生掌握程度。
五、教学内容安排第一课时•教学内容:超几何分布的概念和特点;•教学重点:超几何分布的性质;•教学难点:掌握超几何分布的条件。
第二课时•教学内容:超几何分布的计算方法和公式;•教学重点:掌握超几何分布的公式和应用;•教学难点:掌握超几何分布的计算方法。
第三课时•教学内容:超几何分布的应用;•教学重点:学习超几何分布在品质控制中的应用;•教学难点:掌握超几何分布在实际问题中的运用。
高中数学第二章概率2.2超几何分布课件北师大版选修2_3

=
C22C113 C135
=
315.
所以 ξ 的分布列如下表:
ξ
0
1
2
P
22
12
1
35
35
35
故至少取得一件次品的概率为
P(ξ=1)+P(ξ=2)=
12 35
+
1 35
=
1335.
目标导航
题型一
题型二
题型三
知识梳理
典例透析
随堂演练
反思解决此类问题的关键是先判断出所给问题是否属于超几何分 布问题,建立超几何分布列的关键是求得P(ξ=k)的组合关系式,利用 超几何分布的概率公式进行验证,然后利用公式求出取其他值的概 率,从而建立ξ的分布列.
典例透析
随堂演练
题型一
题型二
题型三
题型二 超几何分布的综合应用
【例2】 生产方提供一批产品共50箱,其中有2箱不合格产品,采 购方接收该批产品的原则是:从该批产品中任取5箱产品进行检验, 若至多有1箱不合格产品,便接收该批产品,问该批产品被接收的概 率是多少?
分析:用X表示“5箱中的不合格产品的箱数”,则X服从参数 N=50,M=2,n=5的超几何分布,再利用超几何分布的概率公式求解.
正解:P(A)=
C31C73 C140
=
12.
目标导航
知识梳理
典例透析
随堂演练
123456
1.下列随机事件中的随机变量X服从超几何分布的是 ( ) A.将一枚硬币连抛3次,正面向上的次数为X B.从7名男生,3名女生共10名学生干部中选出5名优秀学生干部,选 出女生的人数为X C.某射手的命中率为0.8,现对目标射击1次,记命中目标的次数为X D.盒中有4个白球和3个黑球,每次从中摸出1球且不放回,X是首次 摸出黑球时的总次数 答案:B
高中数学 2.2 超几何分布(一)教案 北师大选修2-3
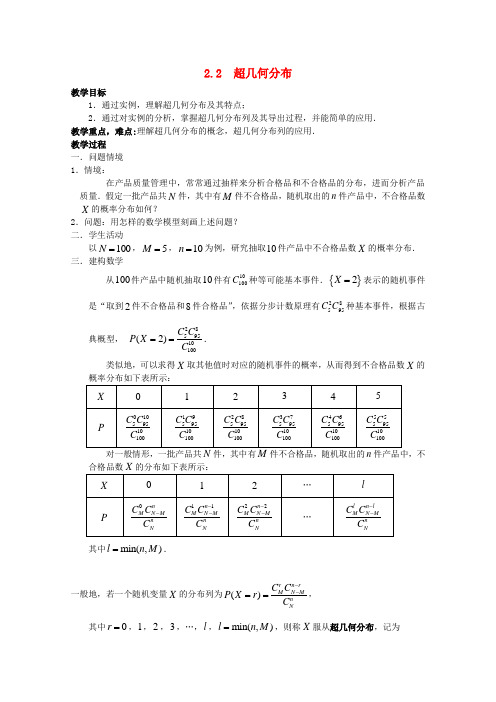
2.2 超几何分布教学目标1.通过实例,理解超几何分布及其特点;2.通过对实例的分析,掌握超几何分布列及其导出过程,并能简单的应用. 教学重点,难点:理解超几何分布的概念,超几何分布列的应用. 教学过程 一.问题情境 1.情境:在产品质量管理中,常常通过抽样来分析合格品和不合格品的分布,进而分析产品 质量.假定一批产品共N 件,其中有M 件不合格品,随机取出的n 件产品中,不合格品数X 的概率分布如何?2.问题:用怎样的数学模型刻画上述问题? 二.学生活动以100N =,5M =,10n =为例,研究抽取10件产品中不合格品数X 的概率分布. 三.建构数学从100件产品中随机抽取10件有10100C 种等可能基本事件.{}2X =表示的随机事件是“取到2件不合格品和8件合格品”,依据分步计数原理有28595C C 种基本事件,根据古典概型, 2859510100(2)C C P X C ==. 类似地,可以求得X 取其他值时对应的随机事件的概率,从而得到不合格品数X 的对一般情形,一批产品共件,其中有件不合格品,随机取出的件产品中,不合格品数X 的分布如下表所示:其中min(,)l n M =.一般地,若一个随机变量X 的分布列为()r n r M N MnNC C P X r C --==, 其中0r =,1,2,3,…,l ,min(,)l n M =,则称X 服从超几何分布,记为(,,)XH n M N ,并将()r n r M N MnNC C P X r C --==记为(;,,)H r n M N . 说明:(1)超几何分布的模型是不放回抽样; (2)超几何分布中的参数是M ,N ,n . 四.数学运用 1.例题:例1.高三(1)班的联欢会上设计了一项游戏:在一个口袋中装有10个红球,20个白球,这些球除颜色外完全相同.现一次从中摸出5个球,(1)若摸到4个红球1个白球的就中一等奖,求中一等奖的概率. (2)若至少摸到3个红球就中奖,求中奖的概率.解:(1)若以30个球为一批产品,其中红球为不合格产品,随机抽取5个球,X 表示取到的红球数,则X 服从超几何分布(5,10,30)H .由公式得4541020530700(4;5,10,30)0.029523751C C H C -==≈, 所以获一等奖的概率约为2.95%.(2)根据题意,设随机变量X 表示“摸出红球的个数”,则X 服从超几何分布(5,10,30)H ,X 的可能取值为0,1,2,3,4,5,根据公式可得至少摸到3个红球的概率为:324150102010201020555303030(3)(3)(4)(5)0.1912C C C C C C P X P X P X P X C C C ≥==+=+==++≈, 故中奖的概率为0.1912.例2.生产方提供50箱的一批产品,其中有2箱不合格产品.采购方接收该批产品的准则是:从该批产品中任取5箱产品进行检测,若至多有1箱不合格产品,便接收该批产品.问:该批产品被接收的概率是多少?解:以50箱为一批产品,从中随机抽取5箱,用X 表示“5箱中不合格产品的箱数”,则X 服从超几何分布(5,2,50)H .这批产品被接收的条件是5箱中没有不合格的箱或只有1箱不 合格,所以被接收的概率为(1)P X ≤,即0514248248555050243(1)245C C C C P X C C ≤=+=. 答:该批产品被接收的概率是243245(约为0.99184).说明:(1)在超几何分布中,只要知道N 、M 和n ,就可以根据公式,求出X 取不同m 值时的概率()P X m =,从而列出X 的分布列.(2)一旦掌握了X 的分布列,就可以算出相应试验的很多事件的概率,从而就完全掌握了该试验.思考:该批产品中出现不合格产品的概率是多少?例3.50张彩票中只有2张中奖票,今从中任取n 张,为了使这n 张彩票里至少有一张中奖的概率大于0.5,n 至少为多少?解:设随机变量X表示“抽出中奖票的张数”,则X服从超几何分布(,2,50)H n,根据公式可得至少有一张中奖的概率11222482485050(1)0.5n nn nC C C CP XC C--≥=+>,解得15n≥.答:n至少为15张.2.练习:课本第51页练习第1,2题.五.回顾小结:1.超几何分布的特点;2.超几何分布列的简单应用.六.课外作业:课本第52页习题2.2第4题.。
高中数学 第2章 概率 2.2 超几何分布学案 北师大版选修2-3(2021年整理)

§2 超几何分布1.理解超几何分布及其推导过程.(重点)2.能用超几何分布解决一些简单的实际问题.(难点)[基础·初探]教材整理 超几何分布阅读教材P 38~P 40部分,完成下列问题. 1.超几何分布的概念一般地,设有N 件产品,其中有M (M ≤N )件次品.从中任取n (n ≤N )件产品,用X 表示取出的n 件产品中次品的件数,那么P (X =k )=____________(其中k 为非负整数).如果一个随机变量的分布列由上式确定,则称X 服从参数为N ,M ,n 的超几何分布. 2.超几何分布的表格形式【答案】错误!错误!错误!错误!错误!1.判断(正确的打“√",错误的打“×”)(1)在产品检验中,超几何分布描述的是放回抽样.( ) (2)在超几何分布中,随机变量X 取值的最大值是M .( )(3)从4名男演员和3名女演员中选出4名,其中女演员的人数X 服从超几何分布.( )(4)在超几何分布中,只要知道N ,M 和n ,就可以根据公式,求出X 取不同值m 时的概率P (X =m).()【答案】(1)×(2)×(3)√(4)√2.设袋中有80个红球,20个白球,若从袋中任取10个球,则其中恰有6个红球的概率为( )A.错误!B。
错误!C。
错误! D.错误!【解析】设X表示任取10个球中红球的个数,则X服从参数为N=100,M=80,n=10的超几何分布,取到的10个球中恰有6个红球,即X=6,P(X=6)=错误!。
【答案】D[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们"探讨交流:疑问1:解惑:疑问2:解惑:疑问3:解惑:[小组合作型]盒中共有9个球,其中有4个红球,3个黄球和2个白球,这些球除颜色外完全相同.(1)若用随机变量X表示任选4个球中红球的个数,则X服从超几何分布,其参数为()A.N=9,M=4,n=4 B.N=9,M=5,n=5C.N=13,M=4,n=4 D.N=14,M=5,n=5(2)若用随机变量Y表示任选3个球中红球的个数,则Y的可能取值为________.(3)若用随机变量Z表示任选5个球中白球的个数,则P(Z=2)=________.【精彩点拨】着眼点:(1)超几何分布的概念;(2)参数的意义;(3)古典概型概率的计算公式.【自主解答】(1)根据超几何分布的定义知,N=9,M=4,n=4。
2020_2021学年高中数学第二章概率2_2超几何分布课件北师大版选修

第59页
第60页
培根曾说:“读史使人明智,读诗使人聪慧,演算使人精密,哲理使人 深刻,道德使人高尚,逻辑修辞使人善辩。”生活里没有书籍,就好像没有 阳光;智慧中没有书籍,就好像鸟儿没有翅膀。知识是人类进步的阶梯,阅 读则是了解人生和获取知识的重要手段和最好途径。那些主人公具有美好品 格的书籍,那些富有人文精神的书籍,很容易在阅读者的内心引起震荡。比 如读鲁迅的书,会被鲁迅“我以我血荐轩辕”的赤子之心打动;读李白的诗, 会被李白“安能摧眉折腰事权贵”的傲骨打动;读《钢铁是怎样炼成的》,会 被主人公保尔不向命运屈服的钢铁般的意志所折服……此外,读书能够祛除 内心的浮躁,让一颗心沉浸在文字宁静的世界里,给心灵以慰藉和滋润;还
1.“超几何分布”模型的识别、判断 “超几何分布”是常见的概率模型,广泛地取材于现实生 活、生产实践中的问题,如产品中的合格品与不合格品,盒中 的红球与黑球,学生中的男生与女生等等.应用“超几何分 布”模型求概率,关键在于这种模型的识别与判断.具体来 说,这类问题的特点是:
(1)总体中含有两类不同的个体; (2)不放回抽取,且无先后顺序; (3)随机变量是指从总体中所抽取的n个个体中某一类个体的 数量.
X2
6
10
P
28 45
16 45
1 45
探究3 根据超几何分布的意义,所摸2球的钱数之和X并不 服从超几何分布,若设摸到的2个球中1元球的个数为ξ,则ξ~ H(10,8,2).X与ξ之间存在着对应关系:X=2对应于ξ=2,X =6对应于ξ=1,X=10对应于ξ=0,在求解时一定要注意到这 一点.
课后巩固
X5
6
7
8
P
4 35
18 35
12 35
高中数学 2.2 超几何分布课件 北师大版选修23

教师(jiàoshī)用书独具演示
●三维目标 1.知识与技能 (1)理解超几何分布及其推导过程. (2)能用超几何分布解决一些简单的实际问题.
第一页,共47页。
2.过程与方法 通过具体实例,感受现实生活中的数学原型,经历概念 的形成过程,体会概念的内涵. 3.情感、态度与价值观 体会数学来源于生活,也应该服务于生活,增强学习数 学的兴趣.
第四页,共47页。
●教学流程
第五页,共47页。
第六页,共47页。
第七页,共47页。
第八页,共47页。
第九页,共47页。
第十页,共47页。
演示(yǎnshì)结 束
第十一页,共47页。
课标 解读
1.理解超几何分布及其推导过 程.
2.能用超几何分布解决一些简 单的实际问题.
第十二页,共47页。
∴C1200=4 950 为基本事件总数. (1)100 件产品中有 95 件合格品,取到 2 件合格品的结果 数,就是从 95 个元素中任取 2 个的组合数 C925,记“任取 2 件都是合格品”为事件 A1,那么事件 A1 的概率为 P(A1)=CC2129050 =899930,
第二十二页,共47页。
第二十五页,共47页。
超几何分布的综合(zōnghé)应用
在 2010 年上海世博会期间,小红计划对事先选 定的 10 个场馆进行参观,在她选定的 10 个场馆中,有 4 个 场馆分布在 A 片区,3 个场馆分布在 B 片区,3 个场馆分布在 C 片区.由于参观的人很多,在进入每个场馆前都需排队等 候,已知 A 片区的每个场馆的排队时间为 2 小时,B 片区和 C 片区的每个场馆的排队时间都为 1 小时.参观前小红突然 接到公司通知,要求她一天后务必返回,于是小红决定从这 10 个场馆中随机选定 3 个场馆进行参观.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C26C14 C310
+
C36C04 C310
=16200+12200=23.
三、解答题(本大题共2小题,共25分.解答应写出文字说 明,证明过程或演算步骤)
12.(12分)某校高二年级某班的数学课外活动小组有6名男 生,4名女生,从中选出4人参加数学竞赛,用X表示其中男生的 人数,
(1)列出X的分布列; (2)求选出的4人中至少有3名男生的概率.
解:(1)依题意,得随机变量X服从超几何分布,且X的所有可 能取值为0,1,2,3,4.P(X=k)=Ck6CC41440-k,k=0,1,2,3,4,
所以X的分布列为
X0
123 4
P
1 210
4 35
3 7
8 21
1 14
(2)由分布列可知选出的4人中至少有3名男生的概率为P(X≥3)
=P(X=3)+P(X=4)=281+114=1492.
1 27 A.220 B.55
27 21 C.220 D.25
解析:由X=4,知取出的3个球必为2个旧球、1个新球, 故P(X=4)=CC233C1219=22270.
2.从4名男生和2名女生中任选3人参加演讲比赛,则所选3 人中至少有1名女生的概率是( D )
12 A.5 B.5
34 C.5 D.5
抽出3道题2 进行测试,至少答对2道题才能入选,则李明入选的概 率为____3___.
解析:设所选的3道题中李明能答对的题数为X,则X服从参
数为N=10,M=6,n=3的超几何分布,且P(X=k)=
Ck6C34-k C310
(k=
0,1,2,3),故所求概率为P(X≥2)=P(X=2)+P(X=3)=
第二章 概率
§2 超几何分布 第14课时 超几何分布
课时作业基设础训计练(45分钟)
——作业目标—— 1.理解超几何分布及其导出过程. 2.运用超几何分布解决一些简单的问题.
——基础巩固—— 一、选择题(本大题共8小题,每小题5分,共40分) 1.一个盒中有12个乒乓球,其中9个新的,3个旧的,从盒 中任取3个球来用(用完即为旧的),用完后装回盒中,记此时盒中 旧球的个数为X,则P(X=4)的值为( C )
解析:设所选3人中的女生人数为X,则X服从参数为N=6,
M=2,n=3的超几何分布,且P(X=k)=
Ck2C34-k C36
(k=0,1,2),故所
求概率为P(X≥1)=P(X=1)+P(X=2)=C12C24+ C36C22C14=122克牌中任意抽出5张,则至
4.12人的兴趣小组中有5人是“三好学生”,现从中任选6
人参加竞赛,若随机变量X表示参加竞赛的“三好学生”的人
数,则CC35C61237为( C ) A.P(X=6) B.P(X=5)
C.P(X=3)
D.P(X=7)
解析:由题意可知随机变量X服从参数为N=12,M=5,n=6 的超几何分布,易知P(X=3)=CC356C1237,故选C.
A.都不是白球 B.恰有1个白球 C.至少有1个白球 D.至多有1个白球
解析:P(都不是白球)=
C22 C25
=
1 10
,P(恰有1个白球)=
C13C12 C25
=
35,
P(至少有1个白球)=C13CC12+25 C23=190, P(至多有1个白球)=C22+CC25 13C12=170. 故选D.
5.10名同学中有a名女生,若从中抽取2个人作为学生代
表,则恰抽取1名女生的概率是1465,则a等于( B )
A.1
B.2或8
C.2
D.8
解析:设X表示抽取的女生人数,则X服从超几何分布,P(X =1)=C1aCC211100-a=a1405-a=1465,解得a=2或a=8.
6.袋中有除颜色外完全相同的3个白球和2个红球,从中任 取2个,那么下列事件中发生的概率为170的是( D )
解析:由超几何分布的概念判断.
10.10张奖券中有3张有奖,5个人每人购买1张,至少有1人 11
中奖的概率是__1_2___.
解析:可求得没有人中奖的概率为CC03C51057=112, 所以至少有1人中奖的概率为1-112=1112.
11.李明参加江苏卫视《一站到底》节目的选拔,已知备选
的10道题中,李明能答对其中的6道.规定:从备选题中随机地
7.有10件产品,其中3件是次品,从中任取两件,若X表示
取得次品的个数,则P(X<2)等于( C )
7
8
A.15
B.15
14 C.15
D.1
解析:由题意知X可能取0,1,2,X服从超几何分布,它取每个
值的概率都符合等可能事件的概率公式,即P(X=0)=
C27 C210
=
7 15
,
P(X=1)=CC17·21C0 13=175,P(X=2)=CC21230=115,于是P(X<2)=P(X=0)+
少有3张A的概率为( D )
34C552248 C.1-CC14855C2 44
34855C2 24 D.C34C248C+552C44C148
解析:设X为抽出的5张扑克牌中A的张数,则P(X≥3)=P(X =3)+P(X=4)=CC34C552248+CC44C552148=C34C248C+552C44C148.
B.3
C.4
D.5
解析:由题意,可得
C1nC310-n C140
=
8 21
,∴n(10-n)(9-n)(8-n)=
480,将选项中的值代入检验,知选C.
二、填空题(本大题共3小题,每小题5分,共15分) 9.下列随机事件中的随机变量X服从超几何分布的有②__④__. ①将一枚硬币连抛3次,正面向上的次数记为X; ②从7男3女的10名学生干部中选出5个优秀学生干部,其中 女生的人数记为X; ③某射手射击的命中率为0.8,现对目标射击1次,记命中的 次数为X; ④盒中有4个白球和3个黑球,从中摸出3个球,每次摸出1个 球且不放回,X是摸出黑球的个数.
P(X=1)=175+175=1145.
8.在一次抽奖中,一个箱子里有编号为1至10的10个号码球
(球的大小、质地完全相同,但编号不同),其中有n个号码为中奖
号码,若从中任意取出4个号码球,其中恰有1个球的号码是中奖
号码的概率为
8 21
,则这10个号码球中,其号码是中奖号码的球的
个数为( C )
A.2
