13-14(1)高等数学(64学时)试题(A)
高等数学A(一)期末试题及答案

济南大学2013~2014学年第一学期课程考试试卷(A 卷) 课 程 高等数学A (一) 考试时间 2013 年 12 月 31 日………………注:请将答案全部答在答题纸上,直接答在试卷上无效。
………………一、填空题(每小题2分,共10分)(1) =-∞→x x x )11(lim e1 . (2) 设)tan(2x x y +=,则=dy dx x x x )(sec )21(22++ .(3) 曲线36223+++=x x x y 的拐点是 )6,1(- 。
(4) =-⎰10211dx x 2π . (5) =⎰∞+121dx x1 . 二、选择题(每小题2分,共10分)(1) =∞→x x x 2sin lim (A ) (A ) 0. (B ) 1。
(C ) 2. (D)21。
(2) 设xx x f tan )(=,则0=x 是函数)(x f 的(A) (A ) 可去间断点. (B) 跳跃间断点。
(C) 第二类间断点。
(D ) 连续点.(3) 当0→x 时,下列变量中与x 是等价无穷小的是(B)(A) x 3sin . (B ) 1-x e 。
(C) x cos 。
(D ) x +1.(4) 函数)(x f 在0x 点可导是它在该点连续的(C)(A ) 充分必要条件. (B ) 必要条件。
(C ) 充分条件. (D ) 以上都不对.(5) 设)(x f 在),(∞+-∞内有连续的导数,则下列等式正确的是(D )(A) ⎰=')()(x f dx x f 。
(B ) C x f dx x f dx d +=⎰)()(. (C) )0()())((0f x f dt t f x-='⎰. (D ) )())((0x f dt t f x ='⎰.三、计算下列极限、导数(每小题6分,共18分)(1) 213lim 21-++--→x x x x x .解: )13)(2()13)(13(lim 213lim 2121x x x x x x x x x x x x x x ++--+++-+--=-++--→→ 62)13)(2(1lim 2)13)(2)(1(22lim 11-=++-+-=++-+--=→→x x x x x x x x x x(2) 22)2(sin ln lim x x x -→ππ.解:)2(4sin cos lim )2(sin ln lim 222x x xx x x x --=-→→ππππ 812sin lim 41sin 12cos lim 4122-=---=⋅--=→→x x x x x x πππ (3) 设函数)(x y y =由方程0ln =+-y x y y 所确定,求:dxdy 和22dx y d 。
13-14北京信息科技大学高等数学一(B卷)期末考题答案

2013~2014学年 第一学期《高等数学A(1)》课程期末考试试卷B 答案一.简答题(本题满分30分,共含6道小题,每小题5分)1. 求极限 x →解法一:用等价无穷小,0lim212x x xx →→==解法二:用有理化,01)lim2x x x x→→==解法三:用洛必达法则,01lim2112x x →→==2.已知函数ln y =,求微分 .dy解:1(22y ′=−⋅=dy =−3.求由方程 所确定的隐函数1sin y x y −−=0()y y x =的导数.dy dx解:方程两边同时关于x 求导得sin cos 0y y x y y ′′−−⋅=解得 sin 1cos dy y y dx x y′==−4. 求函数13y =−x 的驻点。
解:y ′=, 令得0y ′=3x =212x =取x =5. 求不定积分2(x e d +∫.x解:22(arcsin x xe ++∫x C + 6. 写出二阶常系数非齐次微分方程32x y y y xe −′′′++=的特解待定形式。
解:特征方程为, 两相异实根为2320r r ++=122, 1.r r =−=−由于右端项为()x m P x e λ型且1, 1m λ==−.这样1λ=−是特征方程的单根,故可设特解的待定形式为()x x ax b e −+二.计算题(本题满分30分,共含6道小题,每小题5分)1. 求极限: 03(1cos ) d limx x t t x →−∫。
解: 2320001(1cos ) d 1cos 12limlim lim 33x x x x x t t x x x →→→−−==∫26x =t2. 已知函数由参数方程所确定,求()y y x =cos sin cos x t y t t =⎧⎨=−⎩22, .dy d ydx dx 解:/cos (cos sin )/sin dy dy dt t t t t t dx dx dt t −−===−− 221/c sin d y d dy dx t dx dt dx dt t −⎛⎞==⎜⎟−⎝⎠sc = 3.求定积分83∫解:3∫4. 求定积分()222sin cos d .x x x x ππ−−∫解:()2222 0 02sin cos d 02cos d (1cos 2)d x x x x x x x πππ−−=−=−+∫∫∫2x π201(sin 2)22x x ππ=−+=−5. 判断反常积分1201x e dx x+∞−∫是否收敛,若收敛求出其值。
《高等数学》教学日历
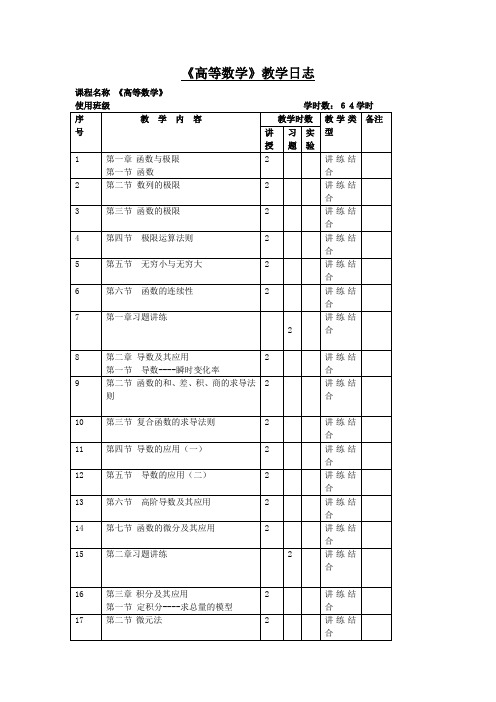
课程名称《高等数学》
使用班级学时数:64学时
序
号
教 学 内 容
教学时数
教学类型
备注
讲授
习题
实验
1
第一章函数与极限
第一节 函数
2
讲练结合
2
第二节 数列的极限
2
讲练结合
3
第三节 函数的极限
2
讲练结合
4
第四节 极限运算法则
2
讲练结合
5
第五节 无穷小与无穷大
2
讲练结合
6
第六节 函数的连续性
第一节 微分方程的概念及可分离微分方程
2
讲2
讲练结合
24
第三节 二阶常系数齐次线性微分方程
2
讲练结合
25
第四章 习题讲练
2
讲练结合
26
第五章数学实验
第一节 Matlab简介及函数极限实验
2
27
第二节 微分实验
2
讲练结合
28
第三节 积分实验
2
29
第四节 微分方程实验
2
14
第七节 函数的微分及其应用
2
讲练结合
15
第二章习题讲练
2
讲练结合
16
第三章积分及其应用
第一节 定积分----求总量的模型
2
讲练结合
17
第二节微元法
2
讲练结合
18
第三节 微积分基本公式
2
讲练结合
19
第四节 积分方法
2
讲练结合
20
第五节 定积分的应用
2
讲练结合
21
第三章习题讲练
13级《高等数学I、II》(上)期末考试卷及答案

2013—2014学年第一学期《高等数学I 、II 》考试试卷(A 卷)一、填空题(每小题3分,共48分)1. 2()ln(1)f x x =-, 已知 000()(2)3lim2h f x f x h h →--=, =0x 13- .2. 2sin 10()0ax x e x f x x a x ⎧+-≠⎪=⎨⎪=⎩在0x =处连续,则a = 1- . 3. 函数32()391f x x x x =--+的既递减又上凸的区间是 (1,1)- .4. 21tx t y e ⎧=+⎨=⎩,则22d d y x 4t t. 5. 设)(x f 在0=x 点处连续,且0()lim12x f x x→=,那么(0)f '= 2 6. 222||2x x dx x -++⎰ ln3 .7.x y dye dx+=的通解为 y x e e c --=+ 8. 设3(1)f x x +=,则(1)f x '-= 23(2)x - .9. 方程2610y e xy x ++-=确定隐函数()y y x =,则(0)y '= 0 。
10. 若函数)(x f 具有二阶连续导数,,0)()(21='='x f x f ),(0)( 21x f x f ''<<''则12(),().f x f x 的大小关系为 ).()(21x f x f >11. 变上限函数⎰21sin x tdt 的导数等于 2sin 2x x12. 设x ,x e ,x e -是二阶非齐次线性微分方程)()()(x f y x b y x a y =+'+''的三个特解,则该方程的通解为x x e C x e C y x x +-+-=-)()(21。
得 分13. 广义积分21(ln )edx x x +∞⎰= 1 。
14. 微分方程052=+'-''y y y 的通解为12(cos 2sin 2)x y e c x c x =+ 15. ⎰⎰'+=dx x f x c x dx x f )( ,sin )(2 2sin 2sin x x x C -+ .16. 函数x e x f -=)(的四阶麦克劳林公式是)(!!!443243211x o xx x x ++-+-二、计算题(满分24分,每小题6分)17.求020()lim (0,0)ln(1)xt t xx a b dt a b t dt→->>+⎰⎰)(b a ≠原式=-+→limln()x x x a b x 0212 3分=-+→lim ln ln x x x a a b b x 0412=14lna b 3分18、求曲线xex y 12-+=)(的渐近线。
公共基础课程介绍稿

公共基础课课程介绍九、课程介绍(一)公共基础课程介绍1.思想政治课(130学时,其中课内98学时,课外32学时,共8学分)本课程是我院各专业的公共基础必修课程,是根据《<中共中央宣传部教育部关于进一步加强和改进高等学校思想政治理论课的意见>实施方案》(教社政[2005]9号)而设立,包括三门课程:《思想道德修养与法律基础》内容:主要进行社会主义道德教育和法制教育,帮助学生增强社会主义法制观念,提高思想道德素质,解决成长成才过程中遇到的实际问题。
本课程3学分,45课时,按2+1形式排课,课堂授课30课时,实践教学15课时;在第一学期开设。
考核方式:开卷考试。
《毛泽东思想和中国特色社会主义理论体系概论》内容:主要讲授中国共产党把马克思主义基本原理与中国实际相结合的历史进程及马克思主义中国化的理论成果,帮助学生系统掌握毛泽东思想和中国特色社会主义理论体系,增强中国特色社会主义的道路自信、理论自信、制度自信,坚定在中国共产党领导下走中国特色社会主义道路的理想信念。
本课程4学分,68课时,按2+2形式排课,课堂授课34课时,实践教学34课时;在第二学期开设。
考核方式:开卷考试。
《形势与政策》内容:主要以马克思列宁主义、毛泽东思想和中国特色社会主义理论体系为指导,针对学生关注的热点问题和思想特点,帮助学生认清国内外形势,全面准确地理解党的路线、方针和政策,积极投身中国特色社会主义建设的伟大事业。
本课程1学分,共16课时,按专题讲座形式排课,课堂讲座12课时,实践教学4课时;分别在二、四学期开设。
考核方式:开卷考试。
2.职业指导(60学时,其中课内44学时,课外16学时,共4学分)本课程是我院各专业的公共基础必修课程,是根据《教育部办公厅关于印发<大学生职业发展与就业指导课程教学要求>的通知》(教高厅〔2007〕7号)要求开设的。
结合我院实际,具体开设两门课程:《大学生职业生涯规划》内容:本课程主要对学生进行职业生涯规划与发展的教育。
高等数学历年真题汇总

目录第一部分计算机科学与技术山东省2005年普通高等教育专升本入学统一考试《高等数学》试题 (3)山东省2006年普通高等教育专升本入学统一考试《高等数学》试题 (4)山东省2007年普通高等教育专升本入学统一考试《高等数学》试题 (6)山东省2008年普通高等教育专升本入学统一考试《高等数学》试题 (8)山东省2009年普通高等教育专升本入学统一考试《高等数学》试题 (10)山东省2010年普通高等教育专升本入学统一考试《高等数学》试题 (12)山东省2011年普通高等教育专升本入学统一考试《高等数学》试题 (14)山东省2012年普通高等教育专升本入学统一考试《高等数学》试题 (16)山东省2013年普通高等教育专升本入学统一考试《高等数学》试题 (18)山东省2015年普通高等教育专升本入学统一考试《高等数学》试题 (22)山东省2014年普通高等教育专升本入学统一考试《高等数学》试题 (20)山东省2016年普通高等教育专升本入学统一考试《高等数学》试题 (24)山东省2017年普通高等教育专升本入学统一考试《高等数学》试题 (25)山东省2018年普通高等教育专升本入学统一考试《高等数学》试题 (27)第二部分土木工程山东省2009年普通高等教育专升本入学统一考试《高等数学》试题(土木工程) (29)山东省2010年普通高等教育专升本入学统一考试《高等数学》试题(土木工程).......................................30山东省2013年普通高等教育专升本入学统一考试《高等数学》试题(土木工程) (31)山东省2014年普通高等教育专升本入学统一考试《高等数学》试题(土木工程) (32)山东省2015年普通高等教育专升本入学统一考试《高等数学》试题(土木工程) (33)山东省2017年普通高等教育专升本入学统一考试《高等数学》试题(土木工程) (34)山东省2018年普通高等教育专升本入学统一考试《高等数学》试题(土木工程) (35)第三部分其他专业山东省2009年普通高等教育专升本入学统一考试《高等数学》试题(电气工程) (37)山东省2009年普通高等教育专升本入学统一考试《高等数学》试题(机械自动化) (38)山东省2009年普通高等教育专升本入学统一考试《高等数学》试题(国际经济与贸易) (39)山东省2009年普通高等教育专升本入学统一考试《高等数学》试题(工商管理) (41)山东省2009年普通高等教育专升本入学统一考试《高等数学》试题(会计) (42)山东省2010年普通高等教育专升本入学统一考试《高等数学》试题(电气工程) (44)山东省2010年普通高等教育专升本入学统一考试《高等数学》试题(机械自动化) (45)山东省2010年普通高等教育专升本入学统一考试《高等数学》试题(国际经济与贸易) (46)山东省2010年普通高等教育专升本入学统一考试《高等数学》试题(工商管理) (47)山东省2010年普通高等教育专升本入学统一考试《高等数学》试题(会计) (48)山东省2011年普通高等教育专升本入学统一考试《高等数学》试题(机械自动化) (49)山东省2011年普通高等教育专升本入学统一考试《高等数学》试题(会计) (50)山东省2012年普通高等教育专升本入学统一考试《高等数学》试题(会计) (51)山东省2013年普通高等教育专升本入学统一考试《高等数学》试题(电气工程) (52)山东省2013年普通高等教育专升本入学统一考试《高等数学》试题(机械自动化) (53)山东省2013年普通高等教育专升本入学统一考试《高等数学》试题(国际经济与贸易) (54)山东省2013年普通高等教育专升本入学统一考试《高等数学》试题(工商管理) (55)山东省2013年普通高等教育专升本入学统一考试《高等数学》试题(会计) (56)山东省2014年普通高等教育专升本入学统一考试《高等数学》试题(电气工程) (57)山东省2014年普通高等教育专升本入学统一考试《高等数学》试题(机械自动化) (58)山东省2014年普通高等教育专升本入学统一考试《高等数学》试题(国际经济与贸易) (59)山东省2014年普通高等教育专升本入学统一考试《高等数学》试题(工商管理) (60)山东省2014年普通高等教育专升本入学统一考试《高等数学》试题(会计) (61)山东省2015年普通高等教育专升本入学统一考试《高等数学》试题(电气工程) (62)山东省2015年普通高等教育专升本入学统一考试《高等数学》试题(机械自动化) (63)山东省2015年普通高等教育专升本入学统一考试《高等数学》试题(国际经济与贸易) (64)山东省2015年普通高等教育专升本入学统一考试《高等数学》试题(工商管理) (65)山东省2015年普通高等教育专升本入学统一考试《高等数学》试题(会计) (66)山东省2018年普通高等教育专升本入学统一考试《高等数学》试题(财经类) (67)山东省普通高等教育专升本入学统一考试《高等数学》试题 (69)机密★启用前试卷类型:公共课科目代码:102山东省2005年普通高等教育专升本入学统一考试《高等数学》试题一、单项选择题(本大题共10个小题,每题1分,共10分。
汽车技术服务与营销专业

7 汽车技术服务与营销专业2006级人才培养方案专业类别:汽车类专业代码:580405学制:三年一、培养目标面向“汽车中、后市场”,培养拥护党的领导,具有与汽车技术服务与营销专业(汽车维修与营销方向)(汽车维修与营销方向)相适应的文化水平和良好的职业道德,相适应的文化水平和良好的职业道德,相适应的文化水平和良好的职业道德,掌握本专业掌握本专业必需的专业理论知识、充分的实践技能和较强的实际工作能力和经营管理能力,从事汽车检测、维修、营销、管理的德、智、体、美等方面全面发展的高等技术应用型人才。
通过理论学习和实践训练,学生应具备良好的思想政治素质和文化素质,掌握扎实的汽车结构、性能、维修以及营销、电子商务、汽车保险与理赔、管理知识和技能。
学生在校期间应获得的证书包括:大学英语三级、计算机一级、汽车修理工中级、营销师、汽车驾驶执照C 级以上。
学生可以在汽车及汽车零部件制造、维修、运用、营销行业从事汽车及零部件生产、维修、售前售后技术服务、销售、企业管理等方面的工作。
二、职业导向本专业毕业生就业面向的单位与部门:汽车及其他行业营销部门、本专业毕业生就业面向的单位与部门:汽车及其他行业营销部门、4S 4S 店、汽车销售公司、汽车修理厂、汽车运输公司、汽车及零部件制造厂,以及汽车安全管理部门、汽车质量行政管理部门等。
能从事的职业岗位:汽车营销、汽车保险与理赔、汽车销售现场服务、汽车售前售后服务,汽车驾驶、汽车运行管理、汽车企业管理、汽车修理、汽车维护、汽车装配、汽车装配、质量管理、质量管理、质量管理、汽车零部件修理、汽车零部件修理、汽车零部件修理、汽车配件营销与保管以及其他行业营销汽车配件营销与保管以及其他行业营销工作等。
在二手车贸易市场从事旧车性能评估、旧车估价工作和二手车的贸易工作;可在汽车保险公司从事汽车贷款、汽车保险与事故车的理赔等工作三、职业岗位能力分析职业职业能力能力 专业能力专业能力 知识与技能构成知识与技能构成课程序号课程序号 基 本 素 质 与 能 力 基本政治素质基本政治素质 公共道德与职业道德公共道德与职业道德 法律法规及政策水平法律法规及政策水平 身体素质与劳动素质身体素质与劳动素质 社交能力社交能力 合作精神合作精神 应用文写作应用文写作 数学计算与逻辑思维数学计算与逻辑思维 大学英语三级水平大学英语三级水平 计算机一级水平计算机一级水平 知识:知识:毛泽东思想、邓小平理论与“三个代表”思想、思想道德修养和法律基础、形势与政策、体育、应用文写作、军训及军事理论、体育、高等数学、大学英语、计算机信息技术算机信息技术技能:技能:体能、社会活动能力、组织能力、语言表达能力、写作能力、英语日常会话、计算机打字、计算机检索检索职 业 专 业 基 础 能 力 读懂中等复杂装配图读懂中等复杂装配图 运用CAD 绘制简单零件图绘制简单零件图 机械零件的公差与测量机械零件的公差与测量 液压与气动技术液压与气动技术 钳工操作能力钳工操作能力 会计与统计能力会计与统计能力 知识:知识:机械制图、机械制图、CAD CAD CAD、机械设计基础、、机械设计基础、液压与气动技术、基础会计、市场调研与预测、消费者行为学场调研与预测、消费者行为学技能:技能:CAD 绘图、计算机办公软件应用、装配图读图、简单零件车钳加工、零部件技术测量、液压与气动技术的运用、会计与统计基本技能基本技能汽车技术服务与营销应用能力 1.1.对汽车发动机、对汽车发动机、底盘、整车的性能与故障进行检测、诊断的能力能力 2.对汽车零件与性能进行检测与合格性评价的能力和零件修复能力修复能力 3.3.对汽车整车、对汽车整车、总成及部件拆装、检修、装、检修、维护的能力。
2013-2014第一学年期末考试高数C参考答案

2013—2014学年第一学期高等数学期末考试试题参考答案一、 选择题(每小题4分,共20分)D B D C A二、 填空题(每小题4分,共20分)1.(0,2)2. cos sin x dy xe dx =-3. (1)x e x C --++4.15.0 三、 计算题(每小题5分,共20分) 1. 31lim (2cos )1x x x x →∞++-解:由于2333111lim lim 0111x x x x x x x →∞→∞++==--或者3211lim lim 013x x x x x →∞→∞+==-―――(2分) 2cos x +为x →∞时的有界量,――――――――――――――(4分)所以原式极限为0. ―――――――――――――――――――(5分) 2.设0x >时,可导函数()f x 满足:13()2()f x f x x+=,求'()f x (0)x > 令1t x =,则原式变为:1()2()3f f t t t +=――――――――――――――――――――――(2分) 连立得13()2(),1()2()3f x f x x f f x x x⎧+=⎪⎪⎨⎪+=⎪⎩解得1()2f x x x =-―――――――――(4分) 所以21()2f x x '=+. ――――――――――――――――――――(5分) 3.设2cos xy e x =,求y '' 解:21(cos sin )2x y e x x '=-―――――――――――――――――(3分)23[cos sin ]4x y e x x ''=-+―――――――――――――――――――(5分)4.x 011lim()1x x e →-- 解:原式=x 01lim (1)x x e x x e →---――――――――――――――――――(1分) =01lim (1)1x x x e e x →-+-―――――――――――――――――(3分) =01lim 2x x →+=12――――――――――――――――――(5分) 四.计算题(每小题5分,共20分) 1.2arctan 1x x dx x ++⎰解:原式=22arctan 11x x dx dx x x +++⎰⎰――――――――――――――(1分) =2211(1)arctan arctan 21d x xd x x+++⎰⎰―――――――――――――(3分) =221[ln(1)(arctan )]2x x +++C ―――――――――――――――――(5分) 2.2156dx x x -+⎰ 解:原式=11()32dx x x ---⎰―――――――――――――――――(3分) =3ln2x C x -+-―――――――――――――――――――(5分) 3.3cos()3x dx πππ+⎰解:法一:原式=3cos()()33x d x ππππ++⎰―――――――――――(2分)=3sin()3x πππ+――――――――――――――――――(4分)=(5分)法二:原式=3cos()()33x d x ππππ++⎰――――――――――――――――(2分) 43323cos x tdt πππ+==⎰t=换元―――――――――――――――――――(4分)4323sin tππ=-=――――――――――――――――――(5分) 4.120arcsin xdx ⎰解:原式=1212001arcsin 2x x +⎰―――――――――――――(2分)=12π――――――――――――――――――(4分)=122π+――――――――――――――――――――(5分) 五.求由抛物线21y x =+与直线1y x =+所围成的面积.解:如图所示――――――――――――――――――――――(2分) 联立方程,解出交点:(0,1)(1,2)――――――――(6分) 积分:1122300111()()236x x dx x x -=-=⎰―――――――――――(10分) 六.某服装有限公司确定,为卖出x 套服装,其单价为1500.5p x =-.同时还确定,生产x 套服装的总成本为:2()40000.25C x x =+.(10分)(1)写出边际成本'()C x 的表达式;(2)求总利润()L x 以及边际利润'()L x ;(3)服装产量x 为多少时,利润达到最大,最大利润是多少?解:1.()0.5C x x '=――――――――――――――――――――(2分) 2.2()()()0.751504000L x R x C x x x =-=-+-―――――――(4分) () 1.5150L x x '=-+――――――――――――――――――――(6分)3.令()0L x '=得到唯一驻点100x =,由题设可知此唯一驻点即使总利润最大时的服装产量,则(100)3500L =――――――――――――――――(10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州大学2013-2014学年第一学期考试卷
课 程:高等数学Ⅱ(64学时) 考 试 形 式:闭卷考试
学院:____________ 专业班级:__________ 学号:____________ 姓名:___________
一.填空题(每空3分,本大题满分15分)
1.3sin lim 3x x x x
→∞+=______. 2.曲线321y x =+在点(1,3)处的切线方程是____________________.
3.函数431341,[,1]2
y x x x =-+∈的拐点为__________. 4.若4()tan f x dx x c =+⎰,则()f x =________________.
5.设3()y f x =,且()y f u =可导,则dy dx
=__________.
二.选择题 (每小题3分, 本大题满分15分)
1.当0x →时,4sin x 是4x 的( )无穷小.
(A) 高阶; (B) 低阶; (C) 同阶但不等价; (D) 等价.
2.函数()f x 在[,]a b 上连续是()f x 在[,]a b 上可导的( ).
(A) 充分条件; (B) 必要条件; (C) 充要条件; (D) 无关条件.
3.()F x dx '=⎰( ).
(A) ()F x ; (B) ()()F x F a -; (C) ()dF x ; (D) ()F x C +.
4.50x e dx +∞
-=⎰( ).
(A) 1/5; (B) 1; (C) 3; (D) 5.
5.设3cos ,0(),0
x x x f x e a x ≥⎧=⎨+<⎩在0x =处连续,则a =( ). (A) 0; (B) -1; (C) 1; (D) 2.
1
.x →+∞.
2.0lim sin x x
x e e x -→-.
3.1
sin 0lim(12)x
x x →+.
四.讨论21
sin ,00,0
x x y x
x ⎧≠⎪=⎨⎪=⎩ 在0x =处的连续性与可导性.
(本题满分7分)
1.求3cos5x y e x -=的微分和二阶导数.
2.求由方程2sin()0xy y π-=所确定的隐函数的导数dx
dy .
六.求(y x =-.(本题满分10分)
七.计算下列积分(每小题5分,本大题满分15分)
1.(12ln )
dx x x +⎰.
2
..
3.
1
2
arccos xdx ⎰.
八.求4
y x
=-与22
y x
=围成图形的面积S.(本题满分8分)。
