模式识别实验最小错误率下贝叶斯决策
【模式识别与机器学习】——2.1贝叶斯判别法

【模式识别与机器学习】——2.1贝叶斯判别法⼀.作为统计判别问题的模式分类 模式识别的⽬的就是要确定某⼀个给定的模式样本属于哪⼀类。
可以通过对被识别对象的多次观察和测量,构成特征向量,并将其作为某⼀个判决规则的输⼊,按此规则来对样本进⾏分类。
在获取模式的观测值时,有些事物具有确定的因果关系,即在⼀定的条件下,它必然会发⽣或必然不发⽣。
但在现实世界中,由许多客观现象的发⽣,就每⼀次观察和测量来说,即使在基本条件保持不变的情况下也具有不确定性。
只有在⼤量重复的观察下,其结果才能呈现出某种规律性,即对它们观察到的特征具有统计特性。
特征值不再是⼀个确定的向量,⽽是⼀个随机向量。
此时,只能利⽤模式集的统计特性来分类,以使分类器发⽣错误的概率最⼩。
⼆.贝叶斯判别原则2.1 两类模式集的分类⽬的:要确定x是属于ω1类还是ω2类,要看x是来⾃于ω1类的概率⼤还是来⾃ω2类的概率⼤。
2.2 贝叶斯判别规则对于⾃然属性是属于ωi类的模式x来说,它来⾃ωi类的概率应为P(ωi |x)根据概率判别规则,有:由贝叶斯定理,后验概率P(ωi | x)可由类别ωi的先验概率P(ωi)和x的条件概率密度p(x | ωi)来计算,即:这⾥p(x | ωi)也称为似然函数。
将该式代⼊上述判别式,有:或其中,l12称为似然⽐,P(ω2)/P(ω1)=θ21称为似然⽐的判决阈值,此判别称为贝叶斯判别。
2.3 贝叶斯判别⽰例问题描述: 对某⼀地震⾼发区进⾏统计,地震以ω1类表⽰,正常以ω2类表⽰统计的时间区间内,每周发⽣地震的概率为20%,即P(ω1)=0.2,当然P(ω2)=1-0.2=0.8 在任意⼀周,要判断该地区是否会有地震发⽣。
显然,因为P(ω2)> P(ω1),只能说是正常的可能性⼤。
如要进⾏判断,只能其它观察现象来实现。
通常地震与⽣物异常反应之间有⼀定的联系。
若⽤⽣物是否有异常反应这⼀观察现象来对地震进⾏预测,⽣物是否异常这⼀结果以模式x代表,这⾥x为⼀维特征,且只有x=“异常”和x=“正常”两种结果。
《模式识别》实验报告-贝叶斯分类

《模式识别》实验报告---最小错误率贝叶斯决策分类一、实验原理对于具有多个特征参数的样本(如本实验的iris 数据样本有4d =个参数),其正态分布的概率密度函数可定义为112211()exp ()()2(2)T d p π-⎧⎫=--∑-⎨⎬⎩⎭∑x x μx μ 式中,12,,,d x x x ⎡⎤⎣⎦=x 是d 维行向量,12,,,d μμμ⎡⎤⎣⎦=μ是d 维行向量,∑是d d ⨯维协方差矩阵,1-∑是∑的逆矩阵,∑是∑的行列式。
本实验我们采用最小错误率的贝叶斯决策,使用如下的函数作为判别函数()(|)(),1,2,3i i i g p P i ωω==x x (3个类别)其中()i P ω为类别i ω发生的先验概率,(|)i p ωx 为类别i ω的类条件概率密度函数。
由其判决规则,如果使()()i j g g >x x 对一切j i ≠成立,则将x 归为i ω类。
我们根据假设:类别i ω,i=1,2,……,N 的类条件概率密度函数(|)i p ωx ,i=1,2,……,N 服从正态分布,即有(|)i p ωx ~(,)i i N ∑μ,那么上式就可以写为1122()1()exp ()(),1,2,32(2)T i i dP g i ωπ-⎧⎫=-∑=⎨⎬⎩⎭∑x x -μx -μ对上式右端取对数,可得111()()()ln ()ln ln(2)222T i i i i dg P ωπ-=-∑+-∑-i i x x -μx -μ上式中的第二项与样本所属类别无关,将其从判别函数中消去,不会改变分类结果。
则判别函数()i g x 可简化为以下形式111()()()ln ()ln 22T i i i i g P ω-=-∑+-∑i i x x -μx -μ二、实验步骤(1)从Iris.txt 文件中读取估计参数用的样本,每一类样本抽出前40个,分别求其均值,公式如下11,2,3ii iii N ωωω∈==∑x μxclear% 原始数据导入iris = load('C:\MATLAB7\work\模式识别\iris.txt'); N=40;%每组取N=40个样本%求第一类样本均值 for i = 1:N for j = 1:4w1(i,j) = iris(i,j+1); end endsumx1 = sum(w1,1); for i=1:4meanx1(1,i)=sumx1(1,i)/N; end%求第二类样本均值 for i = 1:N for j = 1:4 w2(i,j) = iris(i+50,j+1);end endsumx2 = sum(w2,1); for i=1:4meanx2(1,i)=sumx2(1,i)/N; end%求第三类样本均值 for i = 1:N for j = 1:4w3(i,j) = iris(i+100,j+1); end endsumx3 = sum(w3,1); for i=1:4meanx3(1,i)=sumx3(1,i)/N; end(2)求每一类样本的协方差矩阵、逆矩阵1i -∑以及协方差矩阵的行列式i ∑, 协方差矩阵计算公式如下11()(),1,2,3,41i ii N i jklj j lk k l i x x j k N ωωσμμ==--=-∑其中lj x 代表i ω类的第l 个样本,第j 个特征值;ij ωμ代表i ω类的i N 个样品第j 个特征的平均值lk x 代表i ω类的第l 个样品,第k 个特征值;iw k μ代表i ω类的i N 个样品第k 个特征的平均值。
模式识别第二章贝叶斯理论

4、分类器设计:
x1 x X 2 ... xn
g1(x) g2(x)
...
Max g(x)
x i
gn(x)
判别计算
最大值选择器
决策
特征向量
贝叶斯公式可以有几种形式的判别法则,针对具体问 题可以选取合适的形式。不管选取何种形式,其基本思想均 是要求判别归属时依概率最大作出决策,这样的结果就是分 类的错误率最小。
由上例中计算出的后验 概率:P (1 x) 0.818, P ( 2 x) 0.182 条件风险:R (1 x) 1 j P ( j x) 12 P( 2 x) 1.092
j 1 2
R ( 2 x) 21 P (1 x) 0.818 因为R (1 x) R ( 2 x) x 异常细胞,因决策1类风险大。 因12=6较大,决策损失起决定 作用。
31
N-P决策规则 如果:
Px | 2
当
P x | 1
则:
N-P决策规则归结为找阈值
1 x 2
。
P ( x 1 ) 时, 作1 2的分界线. P( x 2 )
t
2 P ( x 2 ) dx, 为 2的函数在取 2为常数时, 可确定, 这时 2一定 1最小
1 j M
另一种形式: g i ( x ) ln P ( x i ) ln P ( i ) max ln P ( x j ) ln P ( i ) x i
1 j M
3、决策面方程: g i ( x )
g j ( x ), 即 g i ( x ) g j ( x ) 0
i , 1 i , 2
第2章_贝叶斯决策理论
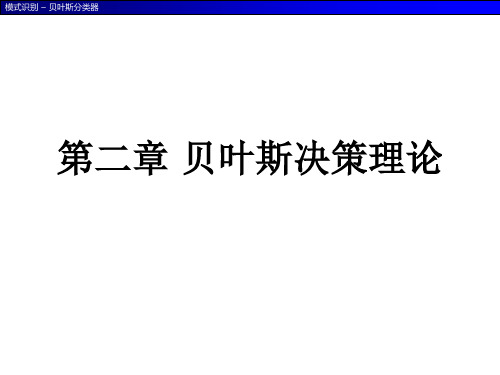
px
1
2
exp
1 2
x
2
模式识别 – 贝叶斯分类器
多元正态分布函数
p x i
1
2 d 2
Σi
12
exp
1 2
x
μi
t
Σi1 x μi
模式识别 – 贝叶斯分类器
正态分布的判别函数
• 贝叶斯判别函数可以写成对数形式:
gi x ln px i ln Pi
• 类条件概率密度函数为正态分布时:
P x 阳性 1 0.95,P x 阳性 2 0.01
现有一人化验结果为阳性,问此人是否患癌症?
模式识别 – 贝叶斯分类器
2.2 最小平均风险准则贝叶斯分 类器
•问题的提出: 有c个类别ω1, ω2 ,... , ωc, 将ωi类的样本
判别为ωj类的代价为λij。
•将未知模式x判别为ωj类的平均风险:
gi
x
1 2
xt
Σi1x
μit
Σi1x
1 2
μit
Σi1μiຫໍສະໝຸດ 1 ln 2Σiln
P
i
• 判别函数为二次判别函数,分类界面为2次 曲线(面)。
模式识别 – 贝叶斯分类器
二次分类曲线
模式识别 – 贝叶斯分类器
二次分类曲面
模式识别 – 贝叶斯分类器 •
每 一 次 的 加 油,每 一次的 努力都 是为了 下一次 更好的 自己。 21.1.1221.1.12Tuesday, January 12, 2021
•
每 天 都 是 美 好的一 天,新 的一天 开启。 21.1.1221.1.1221:5021:50:2321:50:23Jan-21
模式识别实验一(最小贝叶斯决策及ROC曲线)

实验一一、 实验原理1. 最小错误率贝叶斯决策规则:对于两类问题,最小错误率贝叶斯决策有如下判决规则:1212(|)(|),;P x P x x x ωωωω>∈∈则反之,则。
由于先验概率i (P ω)可以确定,与当前样本x 无关,所以决策规则也可整理成下面的形式:121212(|)()(),()(|)P x P l x x x P P x ωωωωωω=>∈∈若,则否则。
2. 平均错误率决策边界把x 轴分割成两个区域,分别称为第一类和第二类的决策区域.样本在中但属于第二类的错误概率和样本在中但属于第一类的错误概率就是出现错误的概率,再考虑到样本自身的分布后就是平均错误率:212211()(|)()(|)()(|)P()(|)P()ttt tP e P x p x dx P x p x dxp x dx p x dxωωωωωω∞-∞∞-∞=+=+⎰⎰⎰⎰3. 此实验中的判决门限和平均错误率 (1) 判决门限假设随机脉冲信号f 中0的概率为,高斯噪声信号n 服从,信号叠加时的放大倍数为a ,叠加后的信号为*s f a n =+。
由最小错误率贝叶斯决策可得:1122()(|)()(|)P p x P p x ωωωω→→>化简计算得:220022(ln(1)ln )2aa a p p t μσ+---=(2) 平均错误率 由上述积分式可计算。
二、 实验内容1、 已知均值和方差,产生高斯噪声信号,计算其统计特性 实验中利用MATLAB 产生均值为0,方差为1的高斯噪声信号,信号统计分布的程序和结果如下:%产生高斯噪声并统计其特性x=0;%均值为0 y=1;%方差为1n=normrnd(x,y,[1 1000000]);%产生均值为0,方差为1的高斯噪声 m1=mean(n);%高斯噪声的均值 v1=var(n); %高斯噪声的方差 figure(1)plot(n(1:400)); title('均值为0,方差为1的高斯噪声'); figure(2)hist(n,10000); title('高斯噪声的统计特性');得到m1=-4.6534e-005;v1= 0.9971。
模式识别课后习题答案

– (1) E{ln(x)|w1} = E{ln+1(x)|w2} – (2) E{l(x)|w2} = 1 – (3) E{l(x)|w1} − E2{l(x)|w2} = var{l(x)|w2}(教材中题目有问题) 证∫ 明ln+:1p对(x于|w(12)),dxE={ln∫(x()∫p(|wp(x(1x|}w|w=1)2))∫n)+nl1nd(xx)所p(x以|w∫,1)Ed{xln=(x∫)|w(1p(}p(x(=x|w|Ew1)2{))ln)n+n+11d(xx)又|wE2}{ln+1(x)|w2} = 对于(2),E{l(x)|w2} = l(x)p(x|w2)dx = p(x|w1)dx = 1
对于(3),E{l(x)|w1} − E2{l(x)|w2} = E{l2(x)|w2} − E2{l(x)|w2} = var{l(x)|w2}
• 2.11 xj(j = 1, 2, ..., n)为n个独立随机变量,有E[xj|wi] = ijη,var[xj|wi] = i2j2σ2,计 算在λ11 = λ22 = 0 及λ12 = λ21 = 1的情况下,由贝叶斯决策引起的错误率。(中心极限 定理)
R2
R1
容易得到
∫
∫
p(x|w2)dx = p(x|w1)dx
R1
R2
所以此时最小最大决策面使得P1(e) = P2(e)
• 2.8 对于同一个决策规则判别函数可定义成不同形式,从而有不同的决策面方程,指出 决策区域是不变的。
3
模式识别(第二版)习题解答
实验一贝叶斯决策

实验一贝叶斯决策一、 实验原理1. 最小错误率贝叶斯决策规则:对于两类问题,最小错误率贝叶斯决策有如下判决规则:1212(|)(|),;P x P x x x ωωωω>∈∈则反之,则。
由于先验概率i (P ω)可以确定,与当前样本x 无关,所以决策规则也可整理成下面的形式:121212(|)()(),()(|)P x P l x x x P P x ωωωωωω=>∈∈若,则否则。
2. 平均错误率决策边界把x 轴分割成两个区域,分别称为第一类和第二类的决策区域.样本在中但属于第二类的错误概率和样本在中但属于第一类的错误概率就是出现错误的概率,再考虑到样本自身的分布后就是平均错误率:212211()(|)()(|)()(|)P()(|)P()ttt tP e P x p x dx P x p x dxp x dx p x dxωωωωωω∞-∞∞-∞=+=+⎰⎰⎰⎰3. 此实验中的判决门限和平均错误率 (1) 判决门限假设随机脉冲信号f 中0的概率为,高斯噪声信号n 服从,信号叠加时的放大倍数为a ,叠加后的信号为*s f a n =+。
由最小错误率贝叶斯决策可得:1122()(|)()(|)P p x P p x ωωωω→→>化简计算得:220022(ln(1)ln )2aa a p p t μσ+---=(2) 平均错误率 由上述积分式可计算。
二、 实验内容1、 已知均值和方差,产生高斯噪声信号,计算其统计特性 实验中利用MATLAB 产生均值为0,方差为1的高斯噪声信号,信号统计分布的程序和结果如下:%产生高斯噪声并统计其特性x=0;%均值为0 y=1;%方差为1n=normrnd(x,y,[1 1000000]);%产生均值为0,方差为1的高斯噪声 m1=mean(n);%高斯噪声的均值 v1=var(n); %高斯噪声的方差 figure(1)plot(n(1:400)); title('均值为0,方差为1的高斯噪声'); figure(2)hist(n,10000); title('高斯噪声的统计特性');得到m1=-4.6534e-005;v1= 0.9971。
模式识别实验报告

实验一Bayes 分类器设计本实验旨在让同学对模式识别有一个初步的理解,能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识,理解二类分类器的设计原理。
1实验原理最小风险贝叶斯决策可按下列步骤进行:(1)在已知)(i P ω,)(i X P ω,i=1,…,c 及给出待识别的X 的情况下,根据贝叶斯公式计算出后验概率: ∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…,x(2)利用计算出的后验概率及决策表,按下面的公式计算出采取i a ,i=1,…,a 的条件风险∑==cj j jii X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…,a 进行比较,找出使其条件风险最小的决策k a ,即则k a 就是最小风险贝叶斯决策。
2实验内容假定某个局部区域细胞识别中正常(1ω)和非正常(2ω)两类先验概率分别为 正常状态:P (1ω)=0.9; 异常状态:P (2ω)=0.1。
现有一系列待观察的细胞,其观察值为x :-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531 -2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752 -3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682 -1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532 已知类条件概率密度曲线如下图:)|(1ωx p )|(2ωx p 类条件概率分布正态分布分别为(-2,0.25)(2,4)试对观察的结果进行分类。
3 实验要求1) 用matlab 完成分类器的设计,要求程序相应语句有说明文字。
2) 根据例子画出后验概率的分布曲线以及分类的结果示意图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
文档收集于互联网,已重新整理排版.word版本可编辑,有帮助欢迎下载支持.《模式识别》实验报告题目:最小错误率贝叶斯决策
一、实验内容
1,实验原理
2,实验步骤
1)从iris.txt 文件(课程邮箱-文件中心)中读取估计参数用的样本,每一类样本抽出前40个,分别求其均值;
(2)求每类样本的协方差矩阵、逆矩阵以及协方差矩阵的行列式;
(3)对三个类别,分别取每组剩下的 10个样本,每两组进行分类。
由于每类样本都相等,
且每类选取用作训练的样本也相等,在每两组进行分类时,待分类样本的类先验概率为0.5。
将各个样本代入判别函数既公式(5),进行分类。
3,实验要求
(1)复习最小错误率贝叶斯决策原理,写出实验代码,实现对三类样本的分类;
(2)计算分类的正确率,画出三维空间的样本分类图;
(3)分析实验结果,完成实验报告。
二、实验代码
(1),
clear
% 原始数据导入
iris=load('iris.txt');
N=40;%每组取N=40个样本
%求第一类样本均值
for i = 1:N
for j = 1:4
w1(i,j) = iris(i,j+1);
end
end
sumx1 = sum(w1,1);
for i=1:4
meanx1(1,i)=sumx1(1,i)/N;
end
%求第二类样本均值
for j = 1:4
w2(i,j) = iris(i+50,j+1);
end
end
sumx2 = sum(w2,1);
for i=1:4
meanx2(1,i)=sumx2(1,i)/N;
end
%求第三类样本均值
for i = 1:N
for j = 1:4
w3(i,j) = iris(i+100,j+1);
end
end
sumx3 = sum(w3,1);
for i=1:4
meanx3(1,i)=sumx3(1,i)/N;
end
(2),
%求第一类样本协方差矩阵
z1(4,4) = 0;
var1(4,4) = 0;
for i=1:4
for j=1:4
for k=1:N
z1(i,j)=z1(i,j)+(w1(k,i)-meanx1(1,i))*(w1(k,j)-meanx1(1,j)); end
var1(i,j) = z1(i,j) / (N-1);
end
end
%求第二类样本协方差矩阵
z2(4,4) = 0 ;
var2(4,4) = 0;
for j=1:4
for k=1:N
z2(i,j)=z2(i,j)+(w2(k,i)-meanx2(1,i))*(w2(k,j)-meanx2(1,j)); end
ar2(i,j) = z2(i,j) / (N-1);
end
end
%求第三类样本协方差矩阵
z3(4,4) = 0 ;
var3(4,4) = 0;
for i=1:4
for j=1:4
for k=1:N
z3(i,j)=z3(i,j)+(w3(k,i)-meanx3(1,i))*(w3(k,j)-meanx3(1,j)); end
var3(i,j) = z3(i,j) /( N-1);
end
end
%求各类的协方差矩阵逆矩阵及行列式
var1_inv = [];var1_det = [];
var2_inv = [];var2_det = [];
var3_inv = [];var3_det = [];
var1_inv = inv(var1);
var2_inv = inv(var2);
var3_inv = inv(var3);
var1_det = det(var1);
var2_det = det(var2);
var3_det = det(var3);
(3),
M=10;
for i = 1:M
for j = 1:4
test(i,j) = iris(i+50,j+1); % 取测试数据
end
end
t1=0;t2=0;t3=0;
for i = 1:M
x=test(i,1);y=test(i,2);
z=test(i,3);h=test(i,4);
g1 = (-0.5)*([x,y,z,h]-meanx1)*var1_inv*([x,y,z,h]'-meanx1') - 0.5*log(abs(var1_det)) +log(0.5); % p1
g2 = (-0.5)*([x,y,z,h]-meanx2)*var2_inv*([x,y,z,h]'-meanx2') - 0.5*log(abs(var2_det)) +log(0.5); % p2
if g1>g2
t1=t1+1; %若g1>g2,则属于第一类,否则属于第二类,并统计属于每一类的个数
else
t2=t2+1;
end
end
三、实验结果
(1)
第一类样本均值:5.0375 3.4525 1.46 0.235
第二类样本均值:6.01 2.78 4.3175 1.35
第三类样本均值:6.6225 2.96 5.6075 1.99
(2)每类样本的协方差矩阵、逆矩阵以及协方差矩阵的行列式
第一类样本的协方差矩阵:
0.4871795 0.09721 0.03333333 0.07692308
0.09721 0. 0.005384614 0.01196
0.03333333 0.005384614 0.02964 0.002564103
0.07692308 0.01196 0.002564103 0.001282051
逆矩阵:18.42527 -13.86752 -6.800065 -5.772421
-13.86752 18.45718 5.788004 -7.317483
-6.800065 5.788004 39.94642 -19.32768
-5.772421 -7.317483 -19.32768 133.0711
协方差矩阵的行列式:1.563e-06
第二类样本的协方差矩阵:
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
逆矩阵:
Inf Inf Inf Inf
Inf Inf Inf Inf
Inf Inf Inf Inf
Inf Inf Inf Inf
协方差矩阵的行列式:0
第三类样本的协方差矩阵:
0.7692308 0.1104 0. 0.02564103
0.1104 0.9230769 0.00769231 0.02564103
0. 0.00769231 0.3076923 0.03076923
0.02564103 0.02564103 0.03076923 0.02564103 逆矩阵:
12.04511 -4.889 -12.12238 4.494952
-4.889 14.82 3.001398 -8.361937
-12.12238 3.001398 15.29687 -6.556262
4.494952 -8.361937 -6.556262 20.47
协方差矩阵的行列式:0.0005162081
(3)各类样本代入公式分类得:
第一类样本:
5.000000 3.000000 0. 0.
3.000000 5.000000 0.09999996 0.
0. 0.09999996 1.000000 0.
0. 0. 0. 0.
第二类样本:
10.00000 3.000000 6.000000 2.000000
3.000000
4.000000 3.000000 1.000000
6.000000 3.000000
7.000000 2.000000
2.000000 1.000000 2.000000 1.000000
第三类样本:
18.00000 4.000000 13.00000 1.000000
4.000000 4.000000 3.000000 1.000000
13.00000 3.000000 13.00000 2.000000
1.000000 1.000000
2.000000 2.000000
三维空间分类图:
四实验心得
首先感谢老师给予我们这次试验的机会,通过这次试验,我更深入了解了最小错误率贝叶斯决策原理,通过计算期望,可以对现实问题进行数学计算,从而获得最优解。
通过自己对相关程序的理解和老师的帮助下我们完成了程序,并仔细阅读了程序,希望对以后的学习有一定的帮助。
经过实验,我对模式识别的认识更深入了,希望能学好模式识别。
实验报告成绩评定表。
