数字信号第2节
合集下载
数字信号处理第2章
Z变换与拉氏变换的关系:
这一关系实际上是通过 到了Z平面。
若将Z平面用极坐标表示
标表示
，代入
将S平面的函数映射
，S平面用直角坐 ，得：
上述关系表明： z 的模 r 仅与 s 的实部 相对应， z 的幅角 则仅与 s 的虚部 对应。
映射关系：
Z变换与拉氏变换的关系
0 0,2 (S平面实轴映射到Z平面的正实轴)
解：
，求它的傅立叶变换。
其幅度谱和相位谱分别为：
典型例题
❖ 例2 已知序列的傅立叶变换如下，求它的反变换。
解：
显然序列 h(n)不是绝对可和的，而是平方可和 的 ，但其依然存在傅立叶变换。 Parseval定理
典型例题
❖ 例3 证明复指数序列 x(n) e j0n 的傅立叶变换为：
证：根据序列的傅立叶反变换定义，利用冲击函 数 的性质，有：
即序列绝对可和
某的有 立些序些叶既列序变不，列换满若虽依足引然然绝入不存对频满在可 域足。和的以见的冲上后条击条例件函件。也数，不但满满，足足其平平傅方方立可可叶和和变条，换件其傅
也存在。如
、某些周期序列，见后例。
序列傅立叶变换的定义
5．常用序列的傅立叶变换
序列
(n)
傅立叶变换
1
1
典型例题
❖ 例1 已知
A形k(式k=求0,X取1(…：z),N)B，(此z) A( z )
时
为了方bi 便z i通常利用
i0
N
1 ai z i
X(z)/z的
i 1
若序列为因果序列，且N≥M，当X(z)的N个极点都是单
极点时，可以展开成以下的部分分式的形式：
则其逆Z变换为：
电子技术基础与技能第八章 数字信号
3.集成逻辑门电路的选用 以上讨论了 TTL和CMOS两种集成逻辑门电路 ，在具体的应用中可以根据要求来选用相关的器件 。器件的主要技术参数有传输延迟时间、功耗、噪 声容限、带负载能力等。若要求功耗低、抗干扰能 力强，则应选用CMOS 电路。其中 CMOS4000 系 列一般用于工作频率在1 MHz 以下、驱动能力要 求不高的场合；HCMOS 常用于工作频率在20 MHz 以下、要求较强驱动能力的场合。 若对功耗 和抗干扰能力没有特殊要求，可选用TTL 电路。
13
第三节 逻辑门电路 逻辑门电路是数字电路中最基本的逻辑元件。 所谓门就是一种开关，它能按照一定的条件去控制 信号的通过或不通过。逻辑即是门电路的输入和输 出之间存在一定的因果关系。电路的输入输出端只 有两种状态：一是高电平，用“１”表示；二是低 电平，用“０”表示。为了便于理解，这里用简单 的开关控制灯的电路来说明基本逻辑门电路的真值 表、电路符号和逻辑功能。
3
4
5
二、脉冲波形 1.脉冲波形的主要参数图8-1脉冲波形的主要 参数在数字电路中，加工和处理的都是脉冲波形， 而应用最多的是矩形脉冲。下面以图8-1所示的实 际矩形脉冲来描述脉冲波形的主要参数。
6
（１）脉冲幅度Ｕｍ：脉冲电压波形变化的最大 值。
（２）脉冲上升时间ｔｒ：脉冲波形从０．１Ｕ ｍ 到０．９Ｕｍ 所需要的时间。 （３）脉冲下降时间ｔｆ：脉冲波形从０．９Ｕ ｍ 到０．１Ｕｍ 所需要的时间。 （４）脉冲宽度ｔｗ：脉冲上升沿０．５Ｕｍ 到下降沿０．５Ｕｍ 所需要的时间，单位与ｔｒ、 ｔｆ相同。 （５）脉冲周期Ｔ：在周期性脉冲中，相邻两个 脉冲波形重复出现所需要的时间，单位和ｔｒ、ｔｆ 相同。 7
（６）脉冲频率ｆ：每秒时间内，脉冲出现的 次数，单位为赫兹（Ｈｚ）、千赫兹（ｋＨｚ）、 兆赫兹（ＭＨｚ）。
数字信号处理_第二章
试画出其级联型网络结构。
解： 将H(z)分子、分母进行因式分解，然后两两组合， 得到：
(2 0.379 z 1 )(4 1.24 z 1 5.264 z 2 ) H ( z) (1 0.25z 1 )(1 z 1 0.5z 2 )
5.3
IIR系统的基本网络结构
5.3
IIR系统的基本网络结构
系数ai 、bi对滤波器性能的控制关系不直接，调 整不方便。 响应对系统变化过于灵敏，也就是对有限精度 （有限字长）运算过于灵敏，容易出现不稳定 或产生较大误差。
直接型结构的缺点：
极点对系数的变化过于灵敏，从而使系统频率
5.3
IIR系统的基本网络结构
二、级联型 把H(z) 分解（因式分解）成几个一阶或二阶 数字网络的级联形式：
H ( z) A H1 ( z) H 2 ( z) ... H K ( z)
式中 H j ( z) 表示一个一阶或二阶的数字网络的 系统函数，每个 H j ( z) 的网络结构均采用前面 介绍的直接型网络结构。
5.3
IIR系统的基本网络结构
实现步骤： （1）先将系统函数按零、极点进行因式分解
第五章 时域离散系统的基本网络结构
5.1 引言
1、滤波器的差分方程
y (n) ai y(n i) bi x(n i)
i 1 i 0 N M
所以，一个滤波系统的输出是其过去 N 点输出 的线性组合加上当前输入序列与过去 M 点输入序列 的线性组合。输出 y (n) 除了与当前的输入 x(n) 有 关，同时还与过去的输入和过去的输出有关，系统 是带有记忆的。
z 1
y(n 2)
5.3
IIR系统的基本网络结构
数字信号处理西安邮电大学第一章 (2)
x(n N ) A sin[(n N )0 ] A sin( N0 n0 )
若Nω0=2πk, 当k为正整数时，则
x(n) x(n N )
这时的正弦序列就是周期性序列，其周期满足N=2πk/ω0
（N，k必须为整数）。可分几种情况讨论如下。 （1） 当2π/ω0为正整数时，周期为2π/ω0。 （2） 当2π/ω0不是整数，而是一个有理数时（有理数可表示 成分数），设
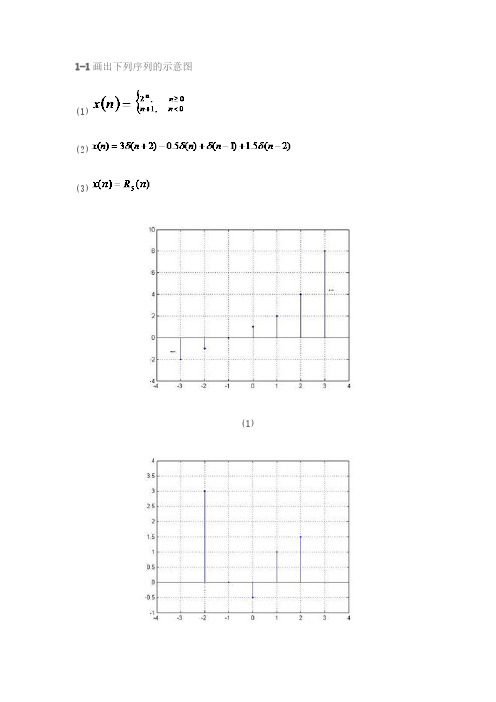
x(n)
x(0) x(－1) x(－2) x(－3)
x(1)
x(2)
x(3)
－5 －4 x(－5)
－3 －2 －1 0
1
2
3 4
5
6
n
x(－4) x(4)
x(5) x(6)
图 1-1 离散时间信号x(n)的图形表示
离散时间信号常常可以由对模拟信号(如语音信号)进行等 间隔采样而得到。例如，对于一个连续时间信号xa(t)，以每秒
y(n)=T［x(n)］
y(n-n0)=T［x(n-n0)］ 例1.3.2 检查y(n)=ax(n)+b代表的系统是否是时不变系统， a和b是常数。 解： y(n)=ax(n)+b y(n-n0)=ax(n- n0)+b y(n- n0)=T［x(n- n0)］ 因此该系统是时不变系统。
例1.3.3 检查y(n)=nx(n)所代表的系统是否是时不变系统。 解 ： y(n)=nx(n) y(n-n0)=(n- n0)x(n- n0) T［x(n- n0)］=nx(n- n0) y(n- n0)≠T［x(n- n0)］ 因此该系统是时变系统。 同样方法可以证明
x(n)* (n) x(n)
x(n)* (n m) x(n m)
数字信号处理课后习题答案
（修正：此题有错，
(3)系统的单位脉冲响应 而改变，是两个复序列信号之和）
(4)
（修正： 随上小题答案
（修正：此图错误，乘系数应该为 0.5，输出端 y(n)应该在两个延迟器 D 之间）
1-25 线性移不变离散时间系统的差分方程为
(1)求系统函数 ； (2)画出系统的一种模拟框图； (3)求使系统稳定的 A 的取值范围。 解：(1)
(2)
(3)
解：（1）
（2）
（3）
1-7 若采样信号 m(t)的采样频率 fs=1500Hz，下列信号经 m(t)采样后哪些信号不 失真？ (1) (2) (3) 解：
(1)
采样不失真
(2)
采样不失真
(3)
，
采样失真
1-8 已知
,采样信号 的采样周期为 。
(1) 的截止模拟角频率 是多少？
(2)将 进行 A/D 采样后， 如何？
（3）最小阻带衰减 5-4
由分式（5.39）根据 A 计算 ，如下： 由表 5.1 根据过度带宽度 计算窗口：
单位脉冲响应如下：
单位脉冲响应如下：
其中 为凯泽窗。 5-5 答：减小窗口的长度 N，则滤波器的过度带增加，但最小阻带衰减保持不变。 5-6：图 5.30 中的滤波器包括了三类理想滤波器，包括了低通，带通和高通，其响应的单位
(1)
，
(2)
1-18 若当 时
；时
(1)
，其中
(2) 证明：
，收敛域
,其中 N 为整数。试证明： ，
(1) 令 其中
，则 ,
(2)
,
1-19 一系统的系统方程及初时条件分别如下： ，
(1)试求零输入响应 ，零状态响应 ，全响应 ； (2)画出系统的模拟框图 解： (1)零输入响应
数字信号处理(第三版)第2章习题答案
第２章 时域离散信号和系统的频域分析
2.3
求信号与系统的频域特性要用傅里叶变换。 但分析频 率特性使用Z变换却更方便。 我们已经知道系统函数的极、 零点分布完全决定了系统的频率特性， 因此可以用分析极、 零点分布的方法分析系统的频率特性， 包括定性地画幅频 特性， 估计峰值频率或者谷值频率， 判定滤波器是高通、 低通等滤波特性， 以及设计简单的滤波器（内容在教材第5 章）等。
X e (e j ) FT[xr (n)]
Hale Waihona Puke 1 1 ej2 1 e j2 1 (1 cos 2)
24
4
2
因为 所以
Xe
(e j
)
1 2
[X
(e j
)
X
(e j
)]
X(ejω)=0π≤ω≤2π
X(e-jω)=X(ej(2π-ω))=0 0≤ω≤π
第２章 时域离散信号和系统的频域分析
当0≤ω≤π时，
用留数定理求其逆变换， 或者将z=ejω代入X(ejω)中， 得到X(z)函数， 再用求逆Z变换的方法求原序列。 注意收 敛域要取能包含单位圆的收敛域， 或者说封闭曲线c可取 单位圆。
第２章 时域离散信号和系统的频域分析
例如， 已知序列x(n)的傅里叶变换为
X
(e
j
)
1
1 ae
j
a 1
1 求其反变换x(n)。 将z=ejω代入X(ejω)中， 得到 X (z) 1 az 1
三种变换互有联系， 但又不同。 表征一个信号和系统 的频域特性是用傅里叶变换。 Z变换是傅里叶变换的一种推 广， 单位圆上的Z变换就是傅里叶变换。
第２章 时域离散信号和系统的频域分析
第二十一章信息的传递(知识清单)九年级物理全一册(人教版)(教师版)
第二十一章信息的传递（知识清单）第1节现代顺风耳——一、电流把信息传到远方1. 的结构及工作原理最简单的由话筒和听筒组成。
为了完成通话，话筒和听筒之间要连上一对线。
话筒把声音转换成变化的电流，电流沿着导线把信息传到远方。
在另一端，电流使听筒的膜片振动，携带信息的电流又转换成了声音。
话筒听筒（1）话筒①主要组成：碳粒和膜片等。
②作用：把声信号变成电信号（即变化的电流）。
③工作原理：当人对着话筒讲话时，声波使膜片振动，膜片忽松忽紧地挤压碳粒，电阻随之发生变化，在电路中产生随声音振动而变化的电流，话筒相当于一个可变电阻器。
（2）听筒①主要组成：电磁铁、膜片。
②作用：把电信号还原成声信号。
③工作原理：当从话筒中传来随说话声音的振动而产生强弱变化的电流时，电磁铁对膜片的吸引力大小也发生变化，使膜片振动起来，产生和对方说话声音相同的声音，把电信号转换为声信号。
2. 机工作电路图同一部中，话筒和听筒是并联的；两部中（对方的），话筒与对方的听筒是串联的，对方的话筒与自己的听筒是串联的（选填“串联”或“并联”）。
二、交换机1. 交换机的作用交换机的作用：减少线的数量，提高线路的利用率。
便于通话时接通，通话完毕断开。
交换机交换机的连接2. 交换机的连接（1）一个地区的都接到同一台交换机上，每部都编上号码。
使用时，交换机把需要通话的两部接通，通话完毕再将线路断开。
（2）如果在一台交换机与另一台交换机之间连上若干线，这样两个不同的交换机的用户就能互相通了。
例如：北京地区交换机的编号（即区号）010，上海地区交换机的编号（即区号）021。
使用时，交换机把需要通话的两部接通，通话完毕再将线路断开。
3. 交换机的发展（1）早期的交换机是依靠话务员手工操作来接线和断线的，工作效率低，劳动强度大。
（2）1891年出现了自动交换机，它通过电磁继电器进行接线。
（3）现代的程控交换机利用了电子计算机技术，只要事先给交换机中的电脑输入所需的程序，电脑就能“见机行事”，能按用户所拨的号码自动接通话机。
《数字信号处理》第二章 离散信号和抽样定理
性延拓，因而采样信号xs(t)就包含了的原信号x(t)全部
信息。
重要结论
第三节 抽样定理
*带限信号抽样定理:
要想连续信号抽样后能够不失真的还原 出原信号，则抽样频率必须大于或等于两 倍原信号频谱的最高频率(2fm≤ fs)，这就是 奈奎斯特抽样定理。
第三节 抽样定理
二、如何从抽样信号恢复出带限信号x(t)
n
其中
1 g (t)
0
t
2
t
2
Ts
第二节 连续信号的离散化
xa (t)
抽样器
（电子开关） P(t)
T
xa (t)
xˆs (t)
fs
1 T
xˆs (t)
第二节 连续信号的离散化
理想抽样：当τ 趋于零的极限情况时，抽样脉冲
方波p(t)变成了冲激函数序列δT(t)，这些冲击函数 的强度准确地为采样瞬间的xa(t)幅值，这样的抽 样称为理想抽样。
余弦与正弦序列示意图如下：
第一节 离散时间信号
5、 用单位脉冲序列表示任意序列
任意序列x(n)都可用单位脉冲序列δ(n)表示成 加权和的形式，即
x(n) x(m) (n m) m
如:
a n x(n)
可表示为 0
10 n 10 其他
10
x(n) am (n m)
样品集合可以是本来就存在的，也可以是由模拟 信号通过采样得来的或者是用计算机产生的。
第一节 离散时间信号
离散时间信号的时域表示 1） 表示离散时间信号可采用枚举的方式。例如
{x(n)}={…，-1.5，-8.7，2.53，0.0，6，7.2， …}
信息。
重要结论
第三节 抽样定理
*带限信号抽样定理:
要想连续信号抽样后能够不失真的还原 出原信号，则抽样频率必须大于或等于两 倍原信号频谱的最高频率(2fm≤ fs)，这就是 奈奎斯特抽样定理。
第三节 抽样定理
二、如何从抽样信号恢复出带限信号x(t)
n
其中
1 g (t)
0
t
2
t
2
Ts
第二节 连续信号的离散化
xa (t)
抽样器
（电子开关） P(t)
T
xa (t)
xˆs (t)
fs
1 T
xˆs (t)
第二节 连续信号的离散化
理想抽样：当τ 趋于零的极限情况时，抽样脉冲
方波p(t)变成了冲激函数序列δT(t)，这些冲击函数 的强度准确地为采样瞬间的xa(t)幅值，这样的抽 样称为理想抽样。
余弦与正弦序列示意图如下：
第一节 离散时间信号
5、 用单位脉冲序列表示任意序列
任意序列x(n)都可用单位脉冲序列δ(n)表示成 加权和的形式，即
x(n) x(m) (n m) m
如:
a n x(n)
可表示为 0
10 n 10 其他
10
x(n) am (n m)
样品集合可以是本来就存在的，也可以是由模拟 信号通过采样得来的或者是用计算机产生的。
第一节 离散时间信号
离散时间信号的时域表示 1） 表示离散时间信号可采用枚举的方式。例如
{x(n)}={…，-1.5，-8.7，2.53，0.0，6，7.2， …}
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
前面的M-1个点跟上一段后面的 M-1个点重合，后面的M-1个点跟 下一段前面的M-1个点重叠相加
15
16
x2 (n)* h(n) [ L, 2L M 2]
L，2L M 2点分段后不同
前面的M-1点不同，后面的M-1点也不同
17
h(m)
C b a
任取一段数据：x'(n) [A,B]
同序列号的序列 值逐项对应相乘
4
5)时间尺度变换
x(mn) 抽取
x(n) xa (t ) t nT x(mn) xa (t ) t mnT
5
6)序列的卷积：
定义： y (n) x(n) * h(n) x(m)h(n m) 解卷积步骤：
m
1）将 x ( n)与h( n) 用 x(m) 和 h(m) 表示，并将 h(m) 翻转，形成 h(m) 2）将 h( m) 移位n,得到 h(n m) ， n>0 时，序列右移；n<0时，序列左移 3）将 x(m) 和 h(n m) 相同m的序列值对应 相乘后，再相加。
m
h(m) x(n m) x(m)h(n m)
m
4 m 0
m
R ( m) a
5
( nm)
U (n m) a ( n m )U (n m)
0, n 0 n ( nm) a ,0 n 4 m 0 4 ( nm) ,n 4 a m 0
按照上述三个步骤可得到卷积结果 y (n)
6
例： x(n)
h ( n ) R ( n) R (n) ， 求：y (n) x(n) * h(n)
3
4
解：由定义可以得到
y(n) R (m) R (n m)
m 3 4
R 3 (m)
0m2
R 4 (n m)
0 nm 3 0n5
x(n)*[h1 (n) h 2 (n)] x(n)*h1 (n) x(n)*h 2 (n)
13
7）用 (n) 表示任意序列 x(n):
x(n)=x(n)* (n) =
特别的， u(n)
m
x(m) (n m)
(m)
14
m
u(m) (n m)
'
h(n) RM (n)
然后将序列x (n)分成长度为L的许多段 每一段和前一度重叠M-1个点
’ x1 (n)* h(n) [0, L M 2] 舍掉前面的M-1个点
19
20
n m
(n m)
m 0
h(n) RM (n)
x ( m)
x1 (m)
0 L-1 L
x2 (m)
2L-1 2L
x2 (m)
3L-1
h(m)
M-1 0
x(n)* h(n) [ x1 (n) x2 (n)] [0, 2L M 2] x1 (n)* h(n) [0, L M 2] x2 (n)* h(n) [ L, 2L M 2] x3 (n)* h(n) [2L,3L M 2]
12
卷积性质说明：
卷积中主要运算是反转、移位、相乘和相加，这类 卷积称为序列的线性卷积。设两序列的长度是N和M， 线性卷积后的序列长度为（N+M-1). 线性卷积服从交换律、结合律和分配律： x(n)*h(n)=h(n)*x(n)
x(n)*[h1 (n)*h 2 (n)] (x(n)*h1 (n))*h 2 (n)
4
R (1 m)
4
R (m) R (1 m)
m 0 3 4
=2
-3-2-1 0 1
m
9
R (1 m)
4
R ( 1 m )
4
-3-2-1 0 1
m
-3-2-1 0 1
m
y(1) R (m) R (1 m)
m 3 4
R (m) R (1 m)
三、序列的运算
1)移位 序列X(n),m>0时
X(n-m): 延时/右移m位
X(n+m): 超前/左移m位
1
2)翻转
X(-n)是以 n=0的纵轴 为对称轴将序列 X(n) 对称翻转
2
3）和
x(n) x1 (n) x2 (n)
同序列号的序列 值逐项对应相加
3
4）积
x(n) x1 (n) x2 (n)
线性卷积后的输出：x'(n) h(n) [A,B+M-1] 从A开始的前面M-1个点不正确，B以后的M-1个点也不正确
只有中间一段输出数据是正确的
不正确舍掉，保留正确的部分 不正确时刻的输出，上一 段已经算出，且是正确的
18
不正确
正确
2)重叠保留法
将序列x(n)右移M-1得到x (n),
'
7
y(n) R 3 (m)R 4 (n m), 0 n 5
m 0
2
R (n)
4
R ( m)
4
1
0 1 2 3
n
-3-2-1 0
m
8
R ( m)
3
R (1 m
※
-3-2-1 0 1
m
y(1) R (m) R (1 m)
m
2
3
m 0 3 4
2
=0
10
n 1, 0 n 2 y(n) 6 n,3 n 5 0, 其他
11
下面采用解析法进行求解．
例：h(n) a u (n), x(n) R5 (n),
n
求：y(n) h(n) * x(n)
解．
y ( n) h( n) * x ( n)
15
16
x2 (n)* h(n) [ L, 2L M 2]
L，2L M 2点分段后不同
前面的M-1点不同，后面的M-1点也不同
17
h(m)
C b a
任取一段数据：x'(n) [A,B]
同序列号的序列 值逐项对应相乘
4
5)时间尺度变换
x(mn) 抽取
x(n) xa (t ) t nT x(mn) xa (t ) t mnT
5
6)序列的卷积：
定义： y (n) x(n) * h(n) x(m)h(n m) 解卷积步骤：
m
1）将 x ( n)与h( n) 用 x(m) 和 h(m) 表示，并将 h(m) 翻转，形成 h(m) 2）将 h( m) 移位n,得到 h(n m) ， n>0 时，序列右移；n<0时，序列左移 3）将 x(m) 和 h(n m) 相同m的序列值对应 相乘后，再相加。
m
h(m) x(n m) x(m)h(n m)
m
4 m 0
m
R ( m) a
5
( nm)
U (n m) a ( n m )U (n m)
0, n 0 n ( nm) a ,0 n 4 m 0 4 ( nm) ,n 4 a m 0
按照上述三个步骤可得到卷积结果 y (n)
6
例： x(n)
h ( n ) R ( n) R (n) ， 求：y (n) x(n) * h(n)
3
4
解：由定义可以得到
y(n) R (m) R (n m)
m 3 4
R 3 (m)
0m2
R 4 (n m)
0 nm 3 0n5
x(n)*[h1 (n) h 2 (n)] x(n)*h1 (n) x(n)*h 2 (n)
13
7）用 (n) 表示任意序列 x(n):
x(n)=x(n)* (n) =
特别的， u(n)
m
x(m) (n m)
(m)
14
m
u(m) (n m)
'
h(n) RM (n)
然后将序列x (n)分成长度为L的许多段 每一段和前一度重叠M-1个点
’ x1 (n)* h(n) [0, L M 2] 舍掉前面的M-1个点
19
20
n m
(n m)
m 0
h(n) RM (n)
x ( m)
x1 (m)
0 L-1 L
x2 (m)
2L-1 2L
x2 (m)
3L-1
h(m)
M-1 0
x(n)* h(n) [ x1 (n) x2 (n)] [0, 2L M 2] x1 (n)* h(n) [0, L M 2] x2 (n)* h(n) [ L, 2L M 2] x3 (n)* h(n) [2L,3L M 2]
12
卷积性质说明：
卷积中主要运算是反转、移位、相乘和相加，这类 卷积称为序列的线性卷积。设两序列的长度是N和M， 线性卷积后的序列长度为（N+M-1). 线性卷积服从交换律、结合律和分配律： x(n)*h(n)=h(n)*x(n)
x(n)*[h1 (n)*h 2 (n)] (x(n)*h1 (n))*h 2 (n)
4
R (1 m)
4
R (m) R (1 m)
m 0 3 4
=2
-3-2-1 0 1
m
9
R (1 m)
4
R ( 1 m )
4
-3-2-1 0 1
m
-3-2-1 0 1
m
y(1) R (m) R (1 m)
m 3 4
R (m) R (1 m)
三、序列的运算
1)移位 序列X(n),m>0时
X(n-m): 延时/右移m位
X(n+m): 超前/左移m位
1
2)翻转
X(-n)是以 n=0的纵轴 为对称轴将序列 X(n) 对称翻转
2
3）和
x(n) x1 (n) x2 (n)
同序列号的序列 值逐项对应相加
3
4）积
x(n) x1 (n) x2 (n)
线性卷积后的输出：x'(n) h(n) [A,B+M-1] 从A开始的前面M-1个点不正确，B以后的M-1个点也不正确
只有中间一段输出数据是正确的
不正确舍掉，保留正确的部分 不正确时刻的输出，上一 段已经算出，且是正确的
18
不正确
正确
2)重叠保留法
将序列x(n)右移M-1得到x (n),
'
7
y(n) R 3 (m)R 4 (n m), 0 n 5
m 0
2
R (n)
4
R ( m)
4
1
0 1 2 3
n
-3-2-1 0
m
8
R ( m)
3
R (1 m
※
-3-2-1 0 1
m
y(1) R (m) R (1 m)
m
2
3
m 0 3 4
2
=0
10
n 1, 0 n 2 y(n) 6 n,3 n 5 0, 其他
11
下面采用解析法进行求解．
例：h(n) a u (n), x(n) R5 (n),
n
求：y(n) h(n) * x(n)
解．
y ( n) h( n) * x ( n)