基于Burg算法的AR模型功率谱估计简介
AR模型谱估计方法研究及其应用

AR模型谱估计方法研究及其应用摘要数字信号处理(DSP)重要的应用领域之一,是建立在周期信号和随机信号基础上的功率谱估计。
在实际应用中往往不能获得具体信号的表达式,需要根据有限的数据样本来获得较好的谱估计效果,因而谱估计被广泛的应用于各种信号处理中[1]。
本论文研究了功率谱估计的几种常用的方法,包括经典谱估计和现代谱估计的各种方法,且对每种方法的估计质量做了数学推导,并给出仿真程序及仿真图。
经典法主要包括周期图法、自相关法,但这两种方法都存在缺陷,即认为观测数据之外的数据都为零,所以对经典法中的周期图法进行了加窗、平均等修正,因此提出了周期图法的改进方法;现代谱估计的方法分类比较多,AR模型法,MA 模型法和ARMA模型法是现代功率谱估计中最主要的参数模型,本论文着重讨论了AR模型参数法[2]。
同时论文将通过对经典谱估计和现代谱估计的实现方法及仿真图的比较,得出经典功率谱估计方法的方差性较差,分辨率较低,而现代谱估计的目标正是在于努力改善谱估计的分辨率,因此能得到较好的谱估计效果,为此应用更为广泛[3]。
关键字:数字信号处理,功率谱估计,周期图法,自相关法,AR模型法ABSTRACTDigital signal processing (DSP) important application of one of the field. Actually, we can’t get the expression of a specific signal, so we need to estimate the power spectral of a signal according to some sample data sequences.So spectrum estimation which is widely used in various signal processing.In this thesis, some common methods of Power Spectral Estimation, such as classical spectral estimation and modern spectral estimation, are studied. The quality of each estimation method is derived, simulation program and simulation figure is given. Classical methods of Power Spectral Estimation mainly include the Periodogram and the BT method. But both of them have a common drawback: the data sequences, beyond the area of the observed sequences, are all presumed to zero. So the Windows and the average method are introduced to improve the quality of the Periodogram. Therefore the improvement of The Periodogram estimation method is proposed. The classification of modern spectral estimation methods are more , AR,MA, and ARMA is the most important parameters of modern spectral estimation. This thesis will focus on discussion of AR model parameters method. At the same time , It can be seen from the comparison and realization of classical spectral estimation and modern spectral estimation, classical power spectrum estimation variance is poor, low resolution .The goal of modern spectral estimation is working to improve the resolution of spectral estimation, better results of the estimation of the power spectrum can be obtained, so it is applied more widely.Keywords: digital signal processing, Power Spectrum Estimation, The Periodogram, the BT methods,AR model目录摘要 (I)1 绪论 (1)1.1功率谱简介 (1)1.2经典谱估计 (2)1.3现代谱估计 (3)1.4功率谱估计应用及用途 (4)2 谱估计简介 (5)2.1随机信号简介 (5)2.2平稳随机信号 (7)2.3估计质量的评价标准 (10)3 现代谱估计 (12)3.1平稳随机信号的参数模型 (12)3.2 AR模型的正则方程与参数计算 (13)3.3 MA模型谱估计 (16)3.4 ARMA模型谱估计 (17)3.5 AR模型功率谱估计实验 (19)3.5.1、实验内容 (19)3.5.2、实验分析 (20)3.5.3、实验结果及分析 (20)3.5.4、实验思考 (24)3.5.5、实验源代码 (25)3.6 AR模型的应用 (30)3.7 小结 (36)4论文总结 (36)参考文献 (38)1 绪论1.1功率谱简介1.功率谱估计技术渊源流长,在过去的几十年获得了飞速的发展。
经典功率谱和Burg法的功率谱估计

现代信号处理作业实验题目:设信号)()8.0cos(25.0)47.0cos()35.0cos()(321n v n n n n x ++++++=θπθπθπ,其中321,,θθθ是[]ππ,-内的独立随机变量,v(n)是单位高斯白噪声。
1.利用周期图法对序列进行功率谱估计。
数据窗采用汉明窗。
2.利用BT 法对序列进行功率谱估计,自相关函数的最大相关长度为M=64,128,256,512采用BARTLETT 窗。
3.利用Welch 法对序列进行功率谱估计,50%重叠,采用汉明窗,L=256,128,64。
4.利用Burg 法对序列进行AR 模型功率谱估计,阶数分别为10,13.要求每个实验都取1024个点,fft 作为谱估计,取50个样本序列的算术平均,画出平均的功率谱图。
实验原理:1)。
周期图法:又称间接法,它把随机信号的N 个观察值x N (n)直接进行傅里叶变换,得到X N (e jw ),然后取其幅值的平方,再除以N ,作为对x (n )真实功率谱的估计。
2^)(1)(jw e X Nw P N per =, 其中∑-=-=1)()(N n jwn N jwN e n x e X 2)。
BT 法:对于N 个观察值x(0),x(1),。
,x(N-1),令x N (n)=a(n)x(n)。
计算r x (m )为∑--=-≤+=mN n N Nx N m m n x n xN m r 101),()(1)(,计算其傅里叶变换∑-=--≤=MMm jwm xBT N M e m rm v w P 1 ,)()()(^^,作为观察值的功率谱的估计。
其中v(m)是平滑窗。
3)。
Welch 法:假定观察数据是x(n),n=0,1,2...,N-1,现将其分段,每段长度为M,段与段之间的重叠为M-K,第i 个数据段经加窗后可表示为 1,...,1,0 )()()(-=+=M i iK n x n a n x i M其中K 为一整数,L 为分段数,该数据段的周期图为2)(1)(^w X MU w P i M iper =,其中∑-=-=10)()(M n j w n iM i M e n x w X 。
burg算法谱估计

burg算法谱估计
Burg算法谱估计是一种基于递归最小二乘法的谱估计方法,通过迭代计算自回归(AR)模型的系数来估计信号的频谱。
其特点在于,只需要知道有限长的时间信号序列,不需计算其自相关函数值,所得的解保证是稳定的。
具体来说,Burg算法谱估计的步骤如下:
1.初始化AR模型的系数。
2.计算AR模型的预测误差和功率谱。
3.更新AR模型的系数,使预测误差和功率谱最小。
4.重复步骤2和步骤3,直到收敛。
这种算法在许多领域得到应用,尤其在信号处理、通信、声学等领域中表现出较好的稳定性和抗干扰性。
但是,其缺点是计算量较大,对于实时处理等场景可能存在较大的延迟。
AR模型谱估计方法研究及其应用

的功率谱密度。
Kalman滤波器的优点是能够实时处理数据,并且能够自适应
03
地调整估计精度。
最小二乘法
最小二乘法是一种常用的参数估计方法,它通 过最小化预测值与实际值之间的残差平方和来 估计模型参数。
在谱估计中,最小二乘法可以用于估计信号的 功率谱密度。
最小二乘法的优点是简单易用,但是它的估计 精度较低,可能会出现偏差。
VS
AR模型可以提取信号中的特征信息 ,从而实现信号的有效分类和识别 ,在语音识别、图像识别等领域有 着广泛的应用前景。
AR模型在信号检测中的应用
利用AR模型对信号进行检测,可以快速准确地检测出信号的 存在和变化情况,及时发现信号中的异常情况。
AR模型可以有效地提取信号中的突变信息,从而实现信号的 有效检测,在雷达、声呐、无线通信等领域有着广泛的应用 。
AR模型的优势
与其他频谱估计方法相比,AR模型具 有多个优点。首先,它可以更加准确 地估计信号的频谱特性,特别是当信 号的噪声水平较高时。其次,它可以 更加灵活地适应不同的信号和系统特 性,从而适用于更广泛的领域。此外 ,AR模型还具有计算复杂度低、易于 实现等优点。
研究内容与方法
研究内容
本文主要研究了AR模型谱估计方法的关键技术,包括 模型的建立、参数估计、性能分析和优化等。在此基 础上,本文还探讨了AR模型在信号处理中的应用,以 及其未来发展趋势和应用前景。
AR模型的参数估计可以采用多种方法,如 最小二乘法、卡尔曼滤波器等。
AR模型的一个重要应用是谱估计, 它可以用于估计信号的频谱特性。
kalman滤波器
01
Kalman滤波器是一种递归滤波器,它通过使用状态空间方法 来估计动态系统的状态变量。
报告2AR过程的线性建模与功率谱估计

实验报告2——AR过程的线性建模与功率谱估计一、实验目的1.理解AR过程的产生机理,复习实验1估计自相关序列的方法。
2.利用估计出的自相关序列来求解信号的功率谱,即用周期图法来估计功率谱。
3.分别采用自相关法(Yule-Walker法),协方差法,Burg法,修正协方差法来估计功率谱,并与周期图法进行比较,分析性能孰优孰劣。
4.学习matlab在数字信号处理中的应用。
二、实验过程和分析AR过程的线性建模与功率谱估计。
考虑AR过程:=-+-+-+-+()(1)(1)(2)(2)(3)(3)(4)(4)(0)()x n a x n a x n a x n a x n b v n v n是单位方差白噪声。
()(a) 取b(0)=1, a(1)=2.7607, a(2)=-3.8106, a(3)=2.6535, a(4)=-0.9238,产生x(n)的N=256个样点。
用randn(1,N)产生单位方差高斯白噪声v(n),用v(n)激励滤波器产生AR(4)过程,即用x=filter(b,a,v)产生x(n),b是滤波器分子系数,这里为b(0)=1,a是滤波器分母系数,a=[1 -2.7607 3.8106 -2.6535 0.9238]。
(b) 计算其自相关序列的估计ˆ()r k,并与真实的自相关序列值相比较。
x结论:真实自相关序列与估计出的序列对比如上图所示,两者在100点之前的形状相似,幅度有一定差异,而且估计出的自相关序列有较大的波动,这是因为估计的点数较少,使得估计精度不够,另外,估计自相关序列的下标越大,用来估计的点数就越少,因而后面的估计值是很不精确的。
因为假设n>= 500 处的数据为0,所有估计自相关不精确,误差较大。
(c) 将ˆ()x rk 的DTFT 作为x (n )的功率谱估计,即: 1211ˆˆ()()|()|N j jk j xx k N P e rk e X e Nωωω--=-+==∑。
现代信号处理论文_AR模型的功率谱估计BURG算法的分析与仿真

AR 模型的功率谱估计BURG 算法的分析与仿真一.引言现代谱估计法主要以随机过程的参数模型为基础,也可以称其为参数模型方法或简称模型方法。
现代谱估计技术的研究和应用主要起始于20世纪60年代,在分辨率的可靠性和滤波性能方面有较大进步。
目前,现代谱估计研究侧重于一维谱分析,其他如多维谱估计、多通道谱估计、高阶谱估计等的研究正在兴起,特别是双谱和三谱估计的研究受到重视,人们希望这些新方法能在提取信息、估计相位和描述非线性等方面获得更多的应用。
现代谱估计从方法上大致可分为参数模型谱估计和非参数模型谱估计两种。
基于参数建摸的功率谱估计是现代功率谱估计的重要内容,其目的就是为了改善功率谱估计的频率分辨率,它主要包括AR 模型、MA 模型、ARMA 模型,其中基于AR 模型的功率谱估计是现代功率谱估计中最常用的一种方法,这是因为AR 模型参数的精确估计可以通过解一组线性方程求得,而对于MA 和ARMA 模型功率谱估计来说,其参数的精确估计需要解一组高阶的非线性方程。
在利用AR 模型进行功率谱估计时,必须计算出AR 模型的参数和激励白噪声序列的方差。
这些参数的提取算法主要包括自相关法、Burg 算法、协方差法、 改进的协方差法,以及最大似然估计法。
本章主要针对采用AR 模型的两种方法:Levinson-Durbin 递推算法、Burg 递推算法。
实际中,数字信号的功率谱只能用所得的有限次记录的有限长数据来予以估计,这就产生了功率谱估计这一研究领域。
功率谱的估计大致可分为经典功率谱估计和现代功率谱估计,针对经典谱估计的分辨率低和方差性能不好等问题提出了现代谱估计,AR 模型谱估计就是现代谱估计常用的方法之一。
信号的频谱分析是研究信号特性的重要手段之一,通常是求其功率谱来进行频谱分析。
功率谱反映了随机信号各频率成份功率能量的分布情况,可以揭示信号中隐含的周期性及靠得很近的谱峰等有用信息,在许多领域都发挥了重要作用。
基于Burg算法的AR模型功率谱估计简介

基于Burg 算法的AR 模型功率谱估计简介摘要:在对随机信号的分析中,功率谱估计是一类重要的参数研究,功率谱估计的方法分为经典谱法和参数模型方法。
参数模型方法是利用型号的先验知识,确定信号的模型,然后估计出模型的参数,以实现对信号的功率谱估计。
根据wold 定理,AR 模型是比较常用的模型,根据Burg 算法等多种方法可以确定其参数。
关键词:功率谱估计;AR 模型;Burg 算法随机信号的功率谱反映它的频率成分以及各成分的相对强弱, 能从频域上揭示信号的节律, 是随机信号的重要特征。
因此, 用数字信号处理手段来估计随机信号的功率谱也是统计信号处理的基本手段之一。
在信号处理的许多应用中, 常常需要进行谱估计的测量。
例如, 在雷达系统中, 为了得到目标速度的信息需要进行谱测量; 在声纳系统中, 为了寻找水面舰艇或潜艇也要对混有噪声的信号进行分析。
总之, 在许多应用领域中, 例如, 雷达、声纳、通讯声学、语言等领域, 都需要对信号的基本参数进行分析和估计, 以得到有用的信息, 其中, 谱分析就是一类最重要的参数研究。
1 功率谱估计简介一个宽平稳随机过程的功率谱是其自相关序列的傅里叶变换,因此功率谱估计就等效于自相关估计。
对于自相关各态遍历的过程,应有:)()()(121lim *k r n x k n x N N x N N n =⎭⎬⎫⎩⎨⎧++∞→∑-= 如果所有的)(n x 都是已知的,理论上功率谱估计就很简单了,只需要对其自相关序列取傅里叶变换就可以了。
但是,这种方法有两个个很大的问题:一是不是所有的信号都是平稳信号,而且有用的数据量可能只有很少的一部分;二是数据中通常都会有噪声或群其它干扰信号。
因此,谱估计就是用有限个含有噪声的观测值来估计)(jw x e P 。
谱估计的方法一般分为两类。
第一类称为经典方法或参数方法,它首先由给定的数据估计自相关序列)(k r x ,然后对估计出的)(ˆk rx 进行傅里叶变换获得功率谱估计。
Burg算法估计模型参数
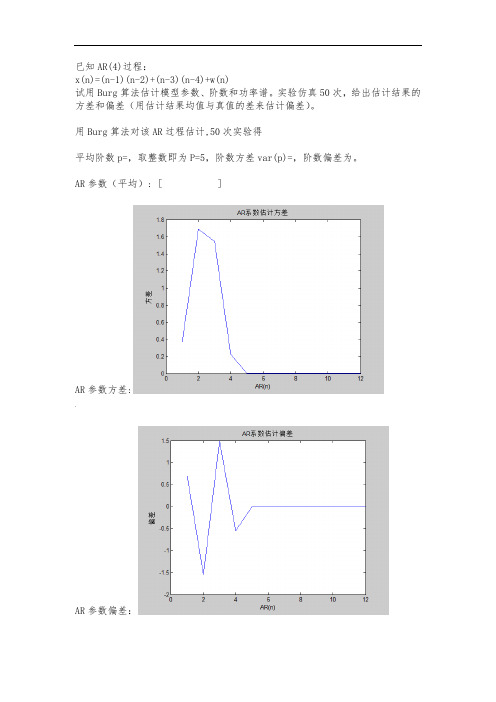
已知AR(4)过程:x(n)=(n-1)(n-2)+(n-3)(n-4)+w(n)试用Burg算法估计模型参数、阶数和功率谱。
实验仿真50次,给出估计结果的方差和偏差(用估计结果均值与真值的差来估计偏差)。
用Burg算法对该AR过程估计,50次实验得平均阶数p=,取整数即为P=5,阶数方差var(p)=,阶数偏差为。
AR参数(平均): [ ]AR参数方差:,AR参数偏差:Burg最大熵谱估计:matlab代码:u=1;while u<=50 %50次仿真实验n=10000;|w=randn(1,n);%生成零均值,方差为的白噪声w=w-mean(w);w=w/std(w);w=sqrt*w;x(1)=1+w(1);x(2)=2+w(2);x(3)=3+w(3);x(4)=4+w(4);%由ar模型生成含噪信号;for i=5:nx(i)=*x(i-1)*x(i-2)+*x(i-3)*x(i-4)+w(i);endP(1+1)=1/n*sum(x.^2);%计算预测误差功率的初始值-g(1,:)=x;f(1,:)=g(1,:);m=1;k=0;l=0;a(1,1)=1;P(1)=1;while abs(P(m+1)-P(m))/P(m)>=for j=m+1:nk=k+f(m,j)*g(m,j-1);l=l+f(m,j)^2+g(m,j-1)^2;endK(m)=-k/(1/2*l);%求反射系数a(1,1)=1;、if m>=2for j=1:m-1%计算前向预测滤波器系数a(m,j)=a(m-1,j)+K(m)*a(m-1,m-j);a(m,m)=K(m);endendP(m+1+1)=(1+abs(K(m))^2)*P(m+1);%计算预测误差功率for j=1:n%计算滤波器输出f(m+1,j)=f(m,j)+K(m)*g(m,n-1);g(m+1,j)=K(m)*f(m,j)+g(m,n-1);end(m=m+1;endM(u)=m-1;%记录每次实验的阶数u=u+1;endfor i=1:50ar=arburg(x,M(i));%估计AR系数ar_coef(i,1:length(ar))=ar;[Px,fx]=pburg(x,M(i));%估计功率谱Pxx(i,1:length(Px))=10*log10(Px');…fxx(i,1:length(fx))=fx';end%%求阶数和AR系数的方差和偏差var_p=var(M);for i=1:max(M)var_ar(i)=var(ar_coef(:,i+1));endbias_p=mean(M)-4;ar_r(max(M))=0;ar_r(1)=;ar_r(2)=;ar_r(3)=;ar_r(4)=;for i=1:max(M)`mean_ar(i)=mean(ar_coef(:,i+1));bias_ar(i)=mean(ar_coef(:,i+1))-ar_r(i);end%%50次实验功率谱平均for i=1:length(Pxx(1,:))mean_Pxx(i)=mean(Pxx(:,i));end%%作图plot(fxx(1,:),mean_Pxx);%作功率谱图title('burg最大熵估计功率谱'); xlabel('频率');ylabel('功率谱密度');》figure(2);plot(var_ar);%AR系数估计方差title('AR系数估计方差');xlabel('AR(n)');ylabel('方差');figure(3);plot(bias_ar);%AR系数估计偏差title('AR系数估计偏差');xlabel('AR(n)');ylabel('偏差');disp('阶数方差:');disp(var_p);disp('阶数偏差:');disp(bias_p);disp('AR系数:');disp(mean_ar);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Burg 算法的AR 模型功率谱估计简介
摘要:在对随机信号的分析中,功率谱估计是一类重要的参数研究,功率谱估计的方法分为经典谱法和参数模型方法。
参数模型方法是利用型号的先验知识,确定信号的模型,然后估计出模型的参数,以实现对信号的功率谱估计。
根据wold 定理,AR 模型是比较常用的模型,根据Burg 算法等多种方法可以确定其参数。
关键词:功率谱估计;AR 模型;Burg 算法
随机信号的功率谱反映它的频率成分以及各成分的相对强弱, 能从频域上揭示信号的节律, 是随机信号的重要特征。
因此, 用数字信号处理手段来估计随机信号的功率谱也是统计信号处理的基本手段之一。
在信号处理的许多应用中, 常常需要进行谱估计的测量。
例如, 在雷达系统中, 为了得到目标速度的信息需要进行谱测量; 在声纳系统中, 为了寻找水面舰艇或潜艇也要对混有噪声的信号进行分析。
总之, 在许多应用领域中, 例如, 雷达、声纳、通讯声学、语言等领域, 都需要对信号的基本参数进行分析和估计, 以得到有用的信息, 其中, 谱分析就是一类最重要的参数研究。
1 功率谱估计简介
一个宽平稳随机过程的功率谱是其自相关序列的傅里叶变换,因此功率谱估计就等效于自相关估计。
对于自相关各态遍历的过程,应有:
)()()(121lim *k r n x k n x N N x N N n =⎭
⎬⎫⎩⎨⎧++∞→∑-= 如果所有的)(n x 都是已知的,理论上功率谱估计就很简单了,只需要对其自相关序列取傅里叶变换就可以了。
但是,这种方法有两个个很大的问题:一是不是所有的信号都是平稳信号,而且有用的数据量可能只有很少的一部分;二是数据中通常都会有噪声或群其它干扰信号。
因此,谱估计就是用有限个含有噪声的观测值来估计)(jw x e P 。
谱估计的方法一般分为两类。
第一类称为经典方法或参数方法,它首先由给定的数据估
计自相关序列)(k r x ,然后对估计出的)(ˆk r
x 进行傅里叶变换获得功率谱估计。
第二类称为非经典法,或参数模型法,是基于信号的一个随机模型来估计功率谱。
非参数谱估计的缺陷是其频率分辨率低,估计的方差特性不好, 而且估计值沿频率轴的起伏甚烈,数据越长, 这一现象越严重。
为了改善谱分辨率,研究学者对基于模型的参数方法进行了大量研究。
参数方法的第一步是对信号选择一个合适的模型,这种选择可能是基于有关信号如何产生的先验知识,也可能是多次试验后获得的结果。
通常采用的模型包括AR 、MA 、ARMA 模型和谐波模型(噪声中含有复指数)。
一旦模型选择好后,下一步就是计算模型的参数。
最后将计算得到的参数带
入模型中就可以获得估计功率谱。
2 AR 谱估计
2.1 简介
AR 模型叫做自回归模型, 信号由本身的若干次过去值和激励时的现实值线性组合产生, 由于传递函数中只有极点, 没有零点, 所以又叫作全极点模型。
MA 模型叫做移动平均模型, 信号由现时的激励和若干次过去值线性组合产生, 由于传递函数中只有零点, 没有极点, 所以又叫作全零点模型。
ARMA 模型叫做自回归移动平均模型, 它是前两种模型的结合, 因为它既有极点又有零点, 所以也叫做极零点模型。
根据wold 定理, 即任何ARMA 过程, 或者任何 MA 过程都能用无限的 AR 过程表示。
如果在三种模型中选择了一个错误的模型, 我们仍然可以通过一个很高的阶数获得一个合理的逼近。
因此, MA 、ARMA 模型可以用一个足够高阶的AR 模型来近似。
AR 谱估计是最常用的时间序列建模方法, 这是因为 AR 参数的精确估计值可以用一组线性方程的方法求得, 而对于 ARMA 或MA 过程参数的精确计算, 则需要解一组高阶非线性方程,。
正是由于这个缘故, 有关有理式传递函数的许多研究工作都喜欢采用 AR 模型作近似研究。
一个AR 过程)(n x 可以表示为单位方差白噪声的驱动的全极点滤波器的输出,p 阶AR 过程的功率谱是:
()jw x e P =21
2
)(1)0(∑=-+p k ikw
p e k a b
因此,若)0(b 和)(k a p 可以由数据进行估计,则功率谱估计可以写成如下形式;
显然,()
jw AR e P ˆ的精确程度决定于模型参数能多准确地被估计,且更重要的是取决于选择的AR 模型是否与数据产生的方式相一致。
确定AR 模型系数的方法有很多,每种方法会得出不同的的参数,但是最终实现的方式是完全相同,利用的是同一个估计形式。
常用的估计方法有:Lenvinson-Durbin 方法、Burg 方法、无约束最小二乘法等等。
2.2 Burg 算法AR 模型参数估计
这里主要对Burg 算法进行介绍。
这种方法通常称为最大熵法(MEM )。
Burg 通过最大化观测序列的熵,得到这种方法,定义为:
1
4a f ln(())a a f f P f df -⎰
式中观测数据序列假定为带宽a f f ≤的静态高斯过程,()P f 是一个实的正函数,最大化式
1
4a f ln(())a a f f P f df -⎰,并受限于自相关采样的约束过程,即:
m r =2()a
s a f j fmT f P f e df π-⎰
这个优化结果可以用来计算最小二乘估计,它涉及观测数据前向和后向预测的MSE 之和。
计算中,预测系数必须满足Lenvinson-Durbin 递推关系,并且可直接计算而无需首先计算自相关系数。
这种方法的优点就是对未知数据不需要做任何假设,估计精度较高。
其缺点是在分析噪声中的正弦信号时,会引起谱线分裂,且谱峰的位置和正弦信号的相位有很大的关系。
Burg 算法是使前向预测误差和后向预测误差均方误差之和最小来求取Km 的,它不对已知数据段之外的数据做认为假设。
计算m 阶预测误差的递推表示公式如下:
x(n)
(n)(n)(n)
1)-(n (n)1)
-(n (n)(n)0f 0f 1-m m 1-b m 1-m f 1-m m e e e e ==+=+=e k e e k e b b m b m f
求取反射系数的公式如下: }1)]-(n [(n)]{[1)]-(n (n)[2-2
b 1-m 2f 1-m b
1-m f 1-m m e e e e +=E E k 对于平稳随机过程,可以用时间平均代替集合平均,因此上式可写成:
[][][][]{}p ,2,1,1)-(n (n)1)-(n (n)2-1-21-21-1-m n 1-1-,⋯=+=∑∑==m N m n b
m f m N b m f m m e e e e k
这样便可求得AR 模型的反射系数。
将m 阶AR 模型的反射系数和m-1阶AR 模型的系数代入到Levinson 关系式中,可以求得AR 模型其他的p-1个参数。
Levinson 关系式如下:
1-m 1,2,i i),-(m (i)(i)1
-m 1-m m ,⋯=+=a k a a m m 阶AR 模型的第m+1个参数G ,2m G ρ=其中m ρ是预测误差功率,可由递推公式
m ρ=21(1)m m
K ρ--求得。
易知为进行该式的递推,必须知道0阶AR 模型误差功率0ρ,
20()(0)x E X n R ρ⎡⎤==⎣⎦
可知该式由给定序列易于求得。
完成上述过程,即最终求得了表征该随机信号的AR 模型的p+1个参数 。
然后根据
2
2()()jw jw x w S e H e σ 即可求得该随机信号的功率谱密度。
3 实验仿真分析
假定信号序列为两个正弦信号与白噪声的叠加,其功率谱估计的matlab 仿真结果如图1和图2。
图1 基于matlab 的Burg 算法功率谱估计仿真(p=130)
图2 基于matlab 的Burg 算法功率谱估计仿真(p=300)
从图中我们可以清晰的看到Burg 算法求解AR 模型的过程是非常稳定的,而且具有很高的分辨率。
当然对于Burg 算法来说,P 即阶数的选择是至关重要的。
在多次实验中发现,当
P介于50和80之间时,得到的频谱图是较优越的,P在130左右时频谱图是最优越的,这也符合了经验定理,对于512点的频谱图分析,P应介于130和250之间。
而当P的阶数过小的时候,会无法分辨出离的较近的两个频谱,P过大频谱图会出现过多伪峰,导致分辨率严重下降。
参考文献:
[1]张贤达,现代信号处理[M],北京:清华大学出版社,2002
[2]杨绿溪,现代数字信号处理[M],北京:科学出版社,2007
[3]关欣、杨爱萍、白煜、李锵等译,信号检测与估计-理论与应用[M],北京:电子工业出版社,2012
[4]张威、张路纲,Burg算法最大熵谱估计的VC++仿真分析[J],北京石油化工学院学报,2002年9月,第10卷第3期
[5]马秉伟、刘会金、周莉、崔福鑫,一种基于自回归模型的间谐波谱估计的改进算法[J],中国电机工程学报,2005年8月第25卷第15期
[6]周巍、郝守玲、赵树元,最大熵谱分析中Burg算法和Marple算法比较[J],石油物探,1998年6月第37卷第2期。
