八年级数学上学期期中试题B卷扫描版新人教版
人教版八年级(上)期中数学试卷B(含解析)
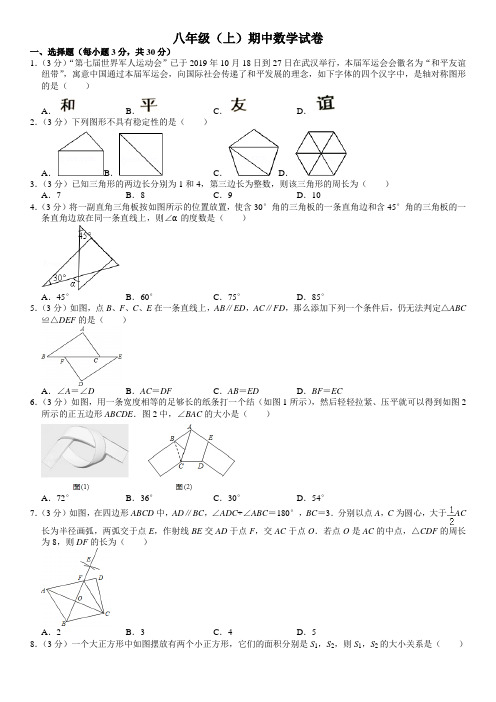
八年级(上)期中数学试卷一、选择题(每小题3分,共30分)1.(3分)“第七届世界军人运动会”已于2019年10月18日到27日在武汉举行,本届军运会会徽名为“和平友谊纽带”,寓意中国通过本届军运会,向国际社会传递了和平发展的理念,如下字体的四个汉字中,是轴对称图形的是()A.B.C.D.2.(3分)下列图形不具有稳定性的是()A.B.C.D.3.(3分)已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为()A.7B.8C.9D.104.(3分)将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是()A.45°B.60°C.75°D.85°5.(3分)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC ≌△DEF的是()A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC6.(3分)如图,用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图2中,∠BAC的大小是()A.72°B.36°C.30°D.54°7.(3分)如图,在四边形ABCD中,AD∥BC,∠ADC+∠ABC=180°,BC=3.分别以点A,C为圆心,大于AC长为半径画弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,△CDF的周长为8,则DF的长为()A.2B.3C.4D.58.(3分)一个大正方形中如图摆放有两个小正方形,它们的面积分别是S1,S2,则S1,S2的大小关系是()A.S1>S2B.S1<S2C.S1=S2D.无法确定9.(3分)如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE 交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F;②∠AGH=∠BAE+∠ACB;③S△AEB:S△AEC=AB:AC,其中正确的结论有()个.A.0B.1C.2D.310.(3分)如图,△ABC中,BC=10,AC﹣AB=4,AD是∠BAC的角平分线,CD⊥AD,则S△BDC的最大值为()A.40B.28C.20D.10二、填空题(每题3分,共18分)11.(3分)点A(1,2)与点B关于x轴对称,则点B的坐标是.12.(3分)在△ABC中,∠A=50°,∠B=30°,点D在边AB上,连接CD,若AC=AD,则∠BCD的大小是.13.(3分)一个多边形的内角和比它的外角和多540°,并且这个多边形的各个内角都相等,则这个多边形每个内角是.14.(3分)如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有3条对称轴,则n的最小值是.15.(3分)如图,△ABC为等腰直角三角形,∠ACB=90°,∠BDC=90°,CD=4,那么△ADC的面积为.三、解答题(共72分)17.(8分)已知一个等腰三角形的周长是18cm,其中一边长是4cm,求这个三角形的边长.18.(8分)如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.求证:AE=CE.19.(8分)如图△ABC中,AB,AC的垂直平分线分别交BC于D,E,垂足分别是M,N (1)若BC=10,求△ADE的周长.(2)若∠BAC=100°,求∠DAE的度数.20.(8分)图①,图②都是由四条边长均为1的小四边形构成的网络,每个小四边形的顶点称为格点.点O,M,N,A,B均在格点上,请仅用无刻度直尺在网格中完成下列画图(保留连线痕迹)(1)在图①中,画出△OMP≌△ONP,要求点P在格点上;(2)在图②中,画一个Rt△ABC,∠ACB=90°,要求点C在格点上.21.(8分)△ABC和△CDE都是等腰直角三角形,其中∠ACB=∠DCE=90°,AC=BC,DC=EC,连接BD,BE,AE.(1)求证:BD=AE;(2)若∠AEB=50°,求∠EBD的度数.22.(10分)请按要求完成下面三道小题(本题作图不要求尺规作图)(1)如图1,AB=AC.这两条线段一定关于∠BAC的所在直线对称,请画出该直线.(2)如图2,已知线段AB和点C.求作线段CD,使它与AB成轴对称,且A与C是对称点,对称轴是线段AC 的.(3)如图3,任意位置(不成轴对称)的两条线段AB,CD,AB=CD.你能从(1),(2)问中获得的启示,对其中一条线段作两次轴对称使它们重合吗?如果能,请画出图形并简要描述操作步骤;如果不能,请说明理由.23.(10分)已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=BC,点E,F分别在射线DA,DC上,满足EF=AE+CF.(1)如图1,若点E,F分别在线段DA,DC上,求证:∠EBF=90°﹣∠ADC;(2)如图2,若点E,F分别在线段DA延长线与DC延长线上,请直接写出∠EBF与∠ADC的数量关系.24.(12分)【实验操作】如图①,在△ABC中,AB=AC,现将AB边沿∠ABC的平分线BD翻折,点A落在BC边的点A1处;再将线段CA1沿CD翻折到线段CA2,连接DA2.【探究发现】若点B,D,A2三点共线,则∠ADB的大小是,∠BAC的大小是,此时三条线段AD,BD,BC之间的数量关系是【应用拓展】(1)如图②,将图①中满足【实验操作】与【探究发现】的△ABC的边AB延长至E,使得AE=BC,连接CE,直接写出∠BCE的度数.(2)如图③,在△MNP中,∠MNP=60°,∠MPN=70°,Q为NP上一点,且∠NMQ=20°,求证:MN+NQ =MQ+QP.参考答案与试题解析一、选择题(每小题3分,共30分)1.【解答】解:A、不是轴对称图形,故本选项不合题意;B、是轴对称图形,故本选项符合题意;C、不是轴对称图形,故本选项不合题意;D、不是轴对称图形,故本选项不合题意.故选:B.2.【解答】解:根据三角形的稳定性可得,B、C、D都具有稳定性.不具有稳定性的是A选项.故选A.3.【解答】解:设第三边为x,根据三角形的三边关系,得:4﹣1<x<4+1,即3<x<5,∵x为整数,∴x的值为4.三角形的周长为1+4+4=9.故选:C.4.【解答】解:如图,∵∠ACD=90°、∠F=45°,∴∠CGF=∠DGB=45°,则∠α=∠D+∠DGB=30°+45°=75°,故选:C.5.【解答】解:选项A、添加∠A=∠D不能判定△ABC≌△DEF,故本选项正确;选项B、添加AC=DF可用AAS进行判定,故本选项错误;选项C、添加AB=DE可用AAS进行判定,故本选项错误;选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项错误.故选:A.6.【解答】解:∵∠ABC==108°,△ABC是等腰三角形,∴∠BAC=∠BCA=36°.故选:B.7.【解答】解:如图,连接FC,则AF=FC.∵AD∥BC,∴∠F AO=∠BCO.在△FOA与△BOC中,,∴△FOA≌△BOC(ASA),∴AF=BC=3=CF,且AF∥BC,∴四边形ABCF是平行四边形,∴∠ABC=∠AFC,∵∠ADC+∠ABC=180°,∠AFC+∠CFD=180°,∴∠CDF=∠CFD,∴CF=CD=AF=3,∵△CDF的周长为8,∴DF=2,故选:A.8.【解答】解:如图,设大正方形的边长为x,根据等腰直角三角形的性质知,AC=BC,BC=CE=CD,∴AC=2CD,CD=.∴S2的边长为,S2的面积为,S1的边长为,S1的面积为,∴S1>S2,故选:A.9.【解答】解:如图,AE交GF于M,①∵AD⊥BC,FG⊥AE,∴∠ADE=∠AMF=90°,∵∠AED=∠MEF,∴∠DAE=∠F;故①正确;②∵∠DAE=∠F,∠FDG=∠FME=90°,∴∠AGH=∠MEF,∵AE平分∠BAC交BC于E,∴∠BAE=∠CAE,∵∠MEF=∠CAE+∠ACB,∴∠AGH=∠CAE+∠ACB,∴∠AGH=∠BAE+∠ACB;故②正确;③∵AE平分∠BAC交BC于E,∴,∵S△AEB:S△AEC=,∴S△AEB:S△AEC=AB:CA;故③正确,故选:D.10.【解答】解:如图:延长AB,CD交点于E,∵AD平分∠BAC,∴∠CAD=∠EAD,∵CD⊥AD,∴∠ADC=∠ADE=90°,在△ADE和△ADC中,,∴△ADE≌△ADC(ASA),∴AC=AE,DE=CD;∵AC﹣AB=4,∴AE﹣AB=4,即BE=4;∵DE=DC,∴S△BDC=S△BEC,∴当BE⊥BC时,S△BDC面积最大,即S△BDC最大面积=××10×4=10.故选:D.二、填空题(每题3分,共18分)11.【解答】解:点A与点B关于x轴对称,点A的坐标为(1,2),则点B的坐标是(1,﹣2).故答案为:(1,﹣2).12.【解答】解:∵在△ABC中,∠A=50°,∠B=30°,∴∠ACB=180°﹣50°﹣30°=100°,∵AD=AC,∴∠ADC=∠ACD=(180°﹣50°)=65°,∴∠BCD=∠ACB﹣∠ACD=100°﹣65°=35°,故答案为:35°;13.【解答】解:设这个多边形的边数为n,则有(n﹣2)•180°=360°+540°,解得n=7.∵这个多边形的每个内角都相等,∴它每一个内角的度数为900°÷7=()°.故答案为:()°.14.【解答】解:如图所示,n的最小值为3,故答案为:3.15.【解答】解:如图,作DM⊥AC于M.DN⊥BC于N.∵∠BDC=90°,BC=5,CD=4,∴BD==3,∵S△BCD=•BC•DN=•BD•DC,∴DN=,∴CN=,∵DM⊥AC,∴∠DMC=∠MCN=∠CND=90°,∴四边形DMCN是矩形,∴DM=CN=,∴S△ADC=•AC•DM=×5×=8,故答案为8.三、解答题(共72分)17.【解答】解:∵等腰三角形的周长为18cm,三角形的一边长4cm,∴若4cm是底边长,则腰长为:=7(cm),∵4cm,7cm,7cm能组成三角形,∴此时其它两边长分别为7cm,7cm;若4cm为腰长,则底边长为:18﹣4﹣4=10(cm),∵4+4=8<10,∴不能组成三角形,故舍去.∴这个三角形的边长分别为4cm,7cm,7cm.18.【解答】证明:∵FC∥AB,∴∠A=∠FCE,且DE=EF,∠AED=∠CEF∴△AED≌△CEF(AAS)∴AE=CE19.【解答】解:(1)∵AB、AC的垂直平分线分别交BC于D、E,垂足分别是M、N,∴AD=BD,AE=CE,∴△ADE的周长=AD+DE+AE=BD+DE+CE=BC=10.(2)∵∠BAC=100°,∴∠B+∠C=180°﹣∠BAC=80°,∵AD=BD,AE=CE,∴∠BAD=∠B,∠CAE=∠C,∴∠BAD+∠CAE=80°,∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=100°﹣80°=20°.20.【解答】解:(1)如图所示,射线OP即为所求.(2)如图所示,点C即为所求;21.【解答】证明:(1)∵∠ACB=∠DCE=90°,∴∠DCB=∠ECA,且AC=BC,DC=EC,∴△DBC≌△ECA(SAS)∴BD=AE;(2)∵△DBC≌△ECA,∴∠CDB=∠CEA,∵∠AEB=50°=∠CEA+∠CEB,∴∠CDB+∠CEB=50°,∵∠CDB+∠BDE+∠CEB+∠BED=90°∴∠BDE+∠BED=40°,∴∠EBD=180°﹣(∠BDE+∠BED)=140°.22.【解答】解:(1)如图1,作∠ABC的平分线所在直线a,则a即为所求.(答案不唯一)故答案为:角平分线;(2)如图2所示:①连接AC;②作线段AC的垂直平分线,即为对称轴b;③作点B关于直线b的对称点D;④连接CD即为所求.故答案为:垂直平分线;(3)如图3所示,连接BD;作线段BD的垂直平分线,即为对称轴c;作点C关于直线c的对称点E;连接BE;作∠ABE的角平分线所在直线d即为对称轴,故其中一条线段作2次的轴对称即可使它们重合.23.【解答】证明:(1)如图1,延长DA,使AH=CF,连接BH,∵∠ABC+∠BCD+∠ADC+∠DAB=360°,∠ABC+∠ADC=180°,∴∠DAB+∠BCD=180°,且∠DAB+∠HAB=180°,∴∠BCD=∠HAB,且AB=BC,AH=CF,∴△HAB≌△FCB(SAS)∴BH=BF,∠HBA=∠CBF,∵EF=AE+CF,∴EF=AE+AH=EH,且BH=BF,BE=BE,∴△BEH≌△BEF(SSS)∴∠EBF=∠EBH,∴∠EBF=∠EBH=∠EBA+∠CBF,∴∠EBF=∠ABC=(180°﹣∠ADC)=90°﹣∠ADC;(2)在CD的延长线上截取CH=AE,连接BH,∵∠ABC+∠BCD+∠ADC+∠DAB=360°,∠ABC+∠ADC=180°,∴∠DAB+∠BCD=180°,且∠DAB+∠EAB=180°,∴∠BCD=∠EAB,且AB=BC,AE=CH,∴△AEB≌△CHB(SAS)∴BE=BH,∠EBA=∠HBC,∵EF=AE+CF,∴EF=CH+CF=HF,且BF=BF,BE=BH,∴△EBF≌△HBF(SSS)∴∠EBF=∠HBF,∵∠EBF+∠HBF+∠EBA+∠ABH=360°,∴2∠EBF+∠HBC+∠ABH=360°,∴2∠EBF+∠ABC=360°,∴2∠EBF+180﹣∠ADC=360°,∴∠EBF=90°+∠ADC.24.【解答】解:【探究发现】∵将AB边沿∠ABC的平分线BD翻折,点A落在BC边的点A1处;再将线段CA1沿CD翻折到线段CA2,∴∠ADB=∠A1DB,∠CDA1=∠CDA2,∠ABD=∠DBC,∠DCA1=∠DCA2,AD=A1D=A2D,∵点B,D,A2三点共线,∴∠A2DC=∠ADB,∴∠ADB=∠A1DB=∠CDA1=∠CDA2,∵∠ADB+∠A1DB+∠CDA1=180°,∵AB=AC,∴∠ABC=∠ACB,∴∠ACB=2∠DBC,∵∠ADB=∠DBC+∠ACB=3∠DBC=60°,∴∠DBC=20°,∴∠ACB=40°,∴∠BAC=180°﹣∠ABC﹣∠ACB=100°,∵∠DCA1=∠DCA2=40°∴∠BCA2=80°,∠BA2C=180°﹣80°﹣20°=80°,∴∠BCA2=∠BA2C,∴BC=A2B=BD+A2D=BD+AD,故答案为:60°,100°,BC=BD+AD;【应用拓展】(1)如图,将AB边沿∠ABC的平分线BD翻折,点A落在BC边的点A1处;再将线段CA1沿CD 翻折到线段CA2,以A2C为边作等边三角形A2CF,连接BF,由【探究发现】可知:∠ABC=∠ACB=∠A2CD=40°,A1C=A2C,A2B=BC,AB=BA1,∠BCA2=∠BA2C=80°,∴∠CBE=140°,∵AE=BC,AB=A1B,∴BE=A1C,∵△A2CF是等边三角形,∴∠A2CF=∠CA2F=60°,A2F=A2C=CF,∴A2F=CF=BE,∠BA2F=140°=∠BCF=∠EBC,且BC=BC,∴△EBC≌△FCB(SAS),∴∠FBC=∠ECB,∵A2F=BE,∠BA2F=140°=∠EBC,BC=A2B∴△EBC≌△F A2B(SAS)∴∠BCE=∠A2BF,∴∠BCE=∠A2BF=∠FBC,且∠A2BC=20°∴∠BCE=10°;(2)如图3,将△MNQ沿MN翻折,得到△MNC,延长MC交直线PN于点E,将△MPQ沿MP翻折,得到△MP A,延长MA,交直线NP于点B,延长MN使NF=NQ,连接EF,∵∠MNP=60°,∠MPN=70°,∴∠NMP=50°,且∠NMQ=20°,∴∠MQP=80°,∵将△MNQ沿MN翻折,得到△MNC,将△MPQ沿MP翻折,得到△MP A,∴∠NMQ=∠NMC=20°,∠CNM=∠MNQ=60°,CN=NQ,∠QMP=∠PMA=30°,MQ=AM,QP=AP,∠QPM=∠MP A=70°,∠MQP=∠MAP=80°,∴∠APB=180°﹣∠QPM﹣∠MP A=40°,∠EMB=100°∵∠MAP=∠B+∠APB,∴∠B=40°=∠APB,∴AP=AB,∠MEB=180°﹣∠B﹣∠EMB=40°,∴∠B=∠MEB=40°,∴ME=MB=AM+AB=MQ+PQ,∵∠ENF=∠MNQ=60°=∠MNC,∴∠CNE=∠ENF=60°,且CN=NQ=NF,EN=EN,∴△EFN≌△ECN(SAS)∴∠CEN=∠FEN=40°,∴∠MEF=80°,∴∠MFE=180°﹣∠EMF﹣∠MEF=80°,∴∠MEF=∠MFE=80°,∴MF=EM,∴MN+NF=MQ+PQ,∴MN+NQ=MQ+PQ.。
人教版2022--2023学年度第一学期八年级数学上册期中测试卷及答案

故选:C.
【点睛】本题考查了三角形的高线,中线,角平分线的定义,掌握以上知识是解题的关键.
8. B
【解析】
【分析】直接根据三角形中线定义解答即可.
【详解】解:∵ 是 的中线, ,
∴BM= ,
故选:B.
【点睛】本题考查三角形的中线,熟知三角形的中线是三角形的顶点和它对边中点的连线是解答的关键.
【详解】解:∵△ABF和△BCE均为等边三角形,
∴AB=FB,BC=BE,∠ABF=∠CBE=60°,
∴∠MBN=180°﹣∠ABF﹣∠CBE=60°,
∵∠ABE=∠ABF+∠MBN=60°+60°=120°,
∠FBC=∠CBE+∠MBN=60°+60°=120°,
∴∠ABE=∠FBC,
在△ABE和△FBC中,
21.已知在△ABC中,AC=BC,分别过A,B两点作互相平行的直线AM,BN,过点C的直线分别交直线AM,BN于点D,E.
(1)如图1,若AM⊥AB,求证:CD=CE;
(2)如图2,∠ABC=∠DEB=60°,判断线段AD,DC与BE之间的关系,并说明理由.
22.如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上.
∴BD是∠ADC的角平分线,故⑤正确;
故选:B.
【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质与判定,角平分线的判定定理,综合运用以上知识是解题的关键.
二.填空题(共7小题,满分28分,每小题4分)
11.108°
【解析】
【分析】设∠A=x,然后利用等边对等角表示出各个角的度数,然后利用三角形内角和定理求得x的值后即可求得答案.
人教版八年级上册数学期中考试试卷带答案

人教版八年级上册数学期中考试试题一、单选题1.下列图形中,其中不是轴对称图形的是()A .B .C .D .2.若正多边形的一个外角是60°,则该正多边形的边数是()A .4B .5C .6D .73.如图,△ABC 中BC 边上的高是()A .BDB .AEC .BED .CF4.若△ABC ≌△DEF ,AB =2,AC =4,且△DEF 的周长为奇数,则EF 的值为()A .3B .4C .3或5D .3或4或55.如图,在△ABC 中,点D 为BC 边上一点,连接AD ,取AD 的中点P ,连接BP ,CP .若△ABC 的面积为4cm 2,则△BPC 的面积为()A .4cm 2B .3cm 2C .2cm 2D .1cm 26.如图,在ABC 中,D 、E 分别为AB 、AC 边上的点,DA DE =,DB BE EC ==.若130ABC ∠=︒,则C ∠的度数为()A .20︒B .22.5︒C .25︒D .30°7.如图,将一副含30°,45°的直角三角板如图摆放,则∠1+∠2等于()A.200°B.210°C.180°D.225°8.如图,在△ABD与△ACD中,已知∠CAD=∠BAD,在不添加任何辅助线的前提下,依据“ASA”证明△ABD≌△ACD,需再添加一个条件,正确的是()A.∠B=∠C B.∠BDE=∠CDE C.AB=AC D.BD=CD9.在△ABC中,∠A=40°,∠B=60°,则∠C=()A.40°B.80°C.60°D.100°10.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是()A.AD=AE B.DB=AE C.DF=EF D.DB=EC二、填空题11.若三角形三个内角度数的比为2:3:4,则此三角形是______三角形(填锐角、直角或钝角).12.已知ABC∆是等腰三角形,若它的周长为18,一条边的长为4,则它的腰长为__________.13.若△ABC的边AB、BC的长是方程组93x yx y+=⎧⎨-=⎩的解,设边AC的长为m,则m的取值范围是_____.14.如图,在△ABC 中,∠ACB =90º,∠ABC =60º,CD ⊥AB ,垂足为D ,若BD =1,则AD 的长为___________.15.如图,△ABC ≌△ADE ,且点E 在BC 上,若∠DAB =30°,则∠CED =_____.16.如图,ABC 为等边三角形,以边AC 为腰作等腰ACD △,使AC CD =,连接BD ,若32ABD ∠=︒,则CAD ∠=__________°.三、解答题17.如图,已知CD 为ACB ∠的平分线,AM CD ⊥于,46,8M B BAM ∠=︒∠=︒,求ACB ∠的度数.18.如图,∠C =∠E ,AC =AE ,点D 在BC 边上,∠1=∠2,AC 和DE 相交于点O .求证:△ABC ≌△ADE .19.如图,已知△ABC.(1)用直尺和圆规,作出边AC的垂直平分线,交AC于点E,BC于点D,(不写作法,保留作图痕迹)(2)在(1)的基础上,连接AD,若AE=5,△ABD的周长为20,则△ABC的周长是_______.20.已知a、b、c是三角形的三边长,①化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|;②若a+b=11,b+c=9,a+c=10,求这个三角形的各边.21.如图,在△ABC中,∠ACB=90°,D是AC上的一点,且AD=BC,DE⊥AC于D,AB=AE.求证:(1)AE⊥AB;(2)CD=DE﹣BC.22.如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.(1)判断△DBC的形状并证明你的结论.(2)求证:BF=AC.(3)试说明CE=12 BF.23.如图,在△ABC中,AB=AC,∠BAC=90°,点D、E分别在AB、BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.(1)求证:DE=EF.(2)判断BD和CF的数量关系,并说明理由.24.如图,点D在△ABC的AB边上,且∠ACD=∠A.(1)作△BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).25.如图1,在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,4),A(4,4),过C点作∠ECF分别交线段AB、OB于E、F两点.(1)若OF+BE=AB,求证:CF=CE.(2)如图2,∠ECF=45°,S△ECF=6,求S△BEF的值.参考答案1.A【解析】根据轴对称图形的定义:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,就可得到答案。
人教版八年级上册数学期中考试试题含答案详解

人教版八年级上册数学期中考试试卷一、选择题。
(每小题只有一个正确答案,每小题3分)1.下列图形中,是轴对称图形的是()A.B.C.D.2.已知等腰三角形的两边长分别为6和1,则这个等腰三角形的周长为()A.13B.8C.10D.8或133.若一个多边形的内角和为720°,则这个多边形是()A.三角形B.四边形C.五边形D.六边形4.如图,用尺规作图作已知角∠AOB的平分线OC,其根据是构造两个三角形全等,它所用到的识别方法是()A.SAS B.SSS C.ASA D.AAS5.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=()A.50°B.60°C.85°D.80°6.如图,∠A=50°,P是等腰△ABC内一点,AB=AC,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数为()A.100°B.115°C.130°D.140°7.如图,△ABC≌△DEF,若BC=12cm,BF=16cm,则下列判断错误的是()A.AB=DE B.BE=CF C.AB//DE D.EC=4cm8.如图,△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于E,测得BC=9,BD=5,则DE的长为()A.3B.4C.5D.69.如图,AB=AC,AD=AE,BE、CD交于点O,则图中全等的三角形共有( )A.四对B.三对C.二对D.一对10.如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM//BC交∠ABC的外角平分线于M,交AB、AC于F、E,下列结论:①MB⊥BD;②FD=FB;③MD=2CE,其中一定正确的有()A.0个B.1个C.2个D.3个二、填空题11.已知△ABC中,AB=6,BC=4,那么边AC的长可以是(填一个满足题意的即可). 12.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是_____________.13.点M与点N(-2,-3)关于y轴对称,则点M的坐标为.14.如图,D是AB边上的中点,将△ABC沿过点D的直线折叠,DE为折痕,使点A 落在BC上F处,若∠B=40°,则∠EDF=_____度.15.已知△ABC中,∠A=12∠B=13∠C,则△ABC是_____三角形.16.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,AB=18,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则BP+EP的最小值是____.三、解答题17.如图,A、F、B、D在一条直线上,AF=DB,BC=EF,AC=DE.求证:∠A=∠D.18.一个多边形,它的内角和比外角和还多180°,求这个多边形的边数.19.如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹).(2)连接AD,若∠B=35°,则∠CAD=°.20.△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.(1)作出△ABC关于原点O对称的△A1B1C1,并写出点C1的坐标;(2)求△ABC的面积.21.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.22.如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.(1)求证:AD平分∠BAC;(2)连接EF ,求证:AD 垂直平分EF .23.如图,AD 为△ABC 的中线,BE 为△ABD 的中线.(1)∠ABE=15°,∠BED=55°,求∠BAD 的度数;(2)作△BED 的边BD 边上的高;(3)若△ABC 的面积为20,BD=2.5,求△BDE 中BD 边上的高.24.如图,在△ABC 中,∠BAC=120°,AB=AC=4,AD ⊥BC ,AD 到E ,使AE=2AD ,连接BE .(1)求证:△ABE 为等边三角形;(2)将一块含60°角的直角三角板PMN 如图放置,其中点P 与点E 重合,且∠NEM=60°,边NE 与AB 交于点G ,边ME 与AC 交于点F .求证:BG=AF ;(3)在(2)的条件下,求四边形AGEF 的面积.25.已知,如图,BD 是ABC ∠的平分线,AB BC =,点P 在BD 上,PM AD ⊥,PN CD ⊥,垂足分别是M 、N .试说明:PM PN =.参考答案1.B【详解】分析:根据轴对称图形的概念求解.详解:A、不是轴对称图形,故此选项不合题意;B、是轴对称图形,故此选项符合题意;C、不是轴对称图形,故此选项不合题意;D、不是轴对称图形,故此选项不合题意;故选B.点睛:本题考查了轴对称图形,轴对称图形的判断方法:把某个图象沿某条直线折叠,如果图形的两部分能够重合,那么这个是轴对称图形.2.A【分析】分1是腰长和底边两种情况,利用三角形的三边关系判断,然后根据三角形的周长的定义列式计算即可得解.【详解】①1是腰长时,三角形的三边分别为1、1、6,不能组成三角形,②1是底边时,三角形的三边分别为6、6、1,能组成三角形,周长=6+6+1=13,综上所述,三角形的周长为13.故选A.【点睛】本题考查了等腰三角形的性质,三角形的三边关系,难点在于分情况讨论.3.D【分析】利用n边形的内角和可以表示成(n-2)•180°,结合方程即可求出答案.【详解】设这个多边形的边数为n,由题意,得(n-2)180°=720°,解得:n=6,则这个多边形是六边形.故选D.【点睛】本题主要考查多边形的内角和公式,比较容易,熟记n边形的内角和为(n-2)•180°是解题的关键.4.B【分析】根据作图的过程知道:OA=OB,OC=OC,AC=CB,所以由全等三角形的判定定理SSS可以证得△OAC≌△OBC.【详解】连接AC、BC,根据作图方法可得:OA=OB,AC=CB,在△OAC和△OBC中,OA OB OC OC AC CB =⎧⎪=⎨⎪=⎩,∴△OAC ≌△OBC (SSS ).故选:B .【点睛】本题考查了作图-基本作图及全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS .5.C【分析】根据三角形角平分线的性质求出∠ACD ,根据三角形外角性质求出∠A 即可.【详解】∵CE 是△ABC 的外角∠ACD 的平分线,∠ACE=60°,∴∠ACD=2∠ACE=120°,∵∠ACD=∠B+∠A ,∴∠A=∠ACD-∠B=120°-35°=85°,故选C .【点睛】本题考查了三角形外角性质,角平分线定义的应用,注意:三角形的一个外角等于和它不相邻的两个内角的和.6.B【分析】根据等腰三角形两底角相等求出∠ACB ,然后求出∠PCB+∠PBC=∠ACB ,再根据三角形的内角和定理列式计算即可得解.【详解】∵∠A=50°,△ABC 是等腰三角形,∴∠ACB=12(180°-∠A )=12(180°-50)=65°,∵∠PBC=∠PCA ,∴∠PCB+∠PBC=∠PCB+∠PCA=∠ACB=65°,∴∠BPC=180°-(∠PCB+∠PBC )=180°-65°=115°.【点睛】本题考查了等腰三角形两底角相等的性质,三角形的内角和定理,准确识图并求出∠PCB+∠PBC是解题的关键.7.D【分析】根据全等三角形的性质得出AB=DE,BC=EF,∠ACB=∠F,求出AC∥DF,BE=CF,即可判断各个选项.【详解】∵△ABC≌△DEF,∴AB=DE,BC=EF,∠ACB=∠F,∴AC∥DF,BC-EC=EF-EC,∴BE=CF,∵BC=12cm,BF=16cm,∴CF=BE=4cm,∴EC=12cm-4cm=8cm,即只有选项D错误;故选D.【点睛】本题考查了全等三角形的性质,平行线的判定的应用,能正确运用性质进行推理是解此题的关键,注意:全等三角形的对应边相等,对应角相等.8.B【分析】先根据角平分线的性质,得出DE=DC,再根据BC=9,BD=5,得出DC=9-5=4,即可得到DE=4.【详解】∵∠C=90°,AD平分∠BAC,DE⊥AB于E,∴DE=DC,∵BC=9,BD=5,∴DC=9-5=4,故选B.【点睛】本题主要考查了角平分线的性质的运用,解题时注意:角的平分线上的点到角的两边的距离相等.9.B【分析】找出全等的三角形即可得出选项.【详解】1、因为AB=AC,AD=AE,∠A=∠A,所以△ABE≌△ACD;2、因为BD=AB-AD,CE=AC-AE,所以BD=CE,又因为AB=AC,BC=BC,所以∠B=∠C,所以△BCD≌△CBE;3、当△ABE≌△ACD时,∠ABE=∠ACD,∠OBC=∠OCB,所以OB=OC,又因为BD=CE,所以△OBD≌△OCE,所以答案选择B项.【点睛】本题考查了全等的证明,熟悉掌握SAS,SSS,ASA是解决本题的关键.10.D【分析】如图,由BD分别是∠ABC及其外角的平分线,得到∠MBD=12×180°=90°,故①成立;证明BF=CE、BF=DF,得到FD=FB,故②成立;证明BF为直角△BDM的斜边上的中线,故③成立.【详解】如图,∵BD分别是∠ABC及其外角的平分线,∴∠MBD=12×180°=90°,故MB⊥BD,①成立;∵DF∥BC,∴∠FDB=∠DBC;∵∠FBD=∠DBC,∴∠FBD=∠FDB,∴FD=BF,②成立;∵∠DBM=90°,MF=DF,∴BF=12DM,而CE=BF,∴CE=12DM,即MD=2CE,故③成立.故选D.【点睛】该题主要考查了等腰三角形的判定及其性质、直角三角形的性质等几何知识点及其应用问题;应牢固掌握等腰三角形的判定及其性质、直角三角形的性质11.3,4,···(2到10之间的任意一个数)【解析】【分析】直接利用三角形三边关系得出AC的取值范围,进而得出答案.【详解】根据三角形的三边关系可得:AB-BC<AC<AB+BC,∵AB=6,BC=4,∴6-4<AC<6+4,即2<AC<10,∴AC的长可以是3,4,•••(2到10之间的任意一个数).故答案为3,4,•••(2到10之间的任意一个数).【点睛】此题主要考查了三角形三边关系,正确得出AC的取值范围是解题关键.12.60°【分析】连接BE,则BE的长度即为PE与PC和的最小值.再利用等边三角形的性质可得∠PBC=∠PCB=30°,即可解决问题.【详解】如图,连接BE,与AD交于点P,此时PE+PC最小,∵△ABC是等边三角形,AD⊥BC,∴PC=PB,∴PE+PC=PB+PE=BE,即BE就是PE+PC的最小值,∵△ABC是等边三角形,∴∠BCE=60°,∵BA=BC,AE=EC,∴BE⊥AC,∴∠BEC=90°,∴∠EBC=30°,∵PB=PC,∴∠PCB=∠PBC=30°,∴∠CPE=∠PBC+∠PCB=60°.【点睛】本题考查等边三角形的性质和动点问题,解题的关键是知道当三点共线时PE+PC最小. 13.(2,-3).【分析】根据平面直角坐标系中任意一点P(x,y),关于y轴对称的点的坐标为(-x,y),将M的坐标代入从而得出答案.【详解】根据关于x轴、y轴对称的点的坐标的特点,∴点N(-2,-3)关于y轴对称的点的坐标是(2,-3).故答案为(2,-3).【点睛】本题主要考查了平面直角坐标系中关于y轴对称的点的坐标的特点,注意掌握任意一点P(x,y),关于x轴的对称点的坐标是(x,-y),关于y轴对称的点的坐标为(-x,y),比较简单.14.40【分析】先根据图形翻折不变的性质可得AD=DF,根据等边对等角的性质可得∠B=∠BFD,再根据三角形的内角和定理列式计算可得∠BDF的解,再根据平角的定义和折叠的性质即可求解.【详解】∵△DEF是△DEA沿直线DE翻折变换而来,∴AD=DF,∵D是AB边的中点,∴AD=BD,∴BD=DF,∴∠B=∠BFD,∵∠B=50°,∴∠BDF=180°-∠B-∠BFD=180°-40°-40°=100°,∴∠EDF=(180°-∠BDF)÷2=40°.故答案为40.【点睛】本题考查的是图形翻折变换的图形能够重合的性质,以及等边对等角的性质,熟知折叠的性质是解答此题的关键.15.直角【分析】设∠A=x°,则∠B=2x°,∠C=3x°,利用三角形内角和为180°求的x,进而求出∠C为90°,即可得出答案.【详解】设∠A=x°,则∠B=2x°,∠C=3x°,∵∠A+∠B+∠C=180°∴x°+2x°+3x°=180°∴x°=30°∴∠C=3x°=90°∴△ABC是直角三角形故答案为直角【点睛】本题考查三角形内角和定理的运用以及三角形形状的判定,熟练掌握三角形内角和定理是解题关键.16.9【分析】根据翻折变换的性质可得点C、E关于AD对称,再根据轴对称确定最短路线问题,BC与AD的交点D即为使PB+PE的最小值的点P的位置,然后根据直角三角形两锐角互余求出∠BAC=60°,再求出∠CAD=30°,然后解直角三角形求解即可.【详解】∵将△ACD沿直线AD翻折,点C落在AB边上的点E处,∴点C、E关于AD对称,∴点D即为使PB+PE的最小值的点P的位置,PB+PE=BC,∵∠C=90°,∠BAC=30°,∴BC=12 AB,∴BC=9.∴PB+PE的最小值为9.故答案为9.【点睛】本题考查了轴对称确定最短路线问题,翻折变换的性质,解直角三角形,难点在于判断出PB+PE取得最小值时点P与点D重合.17.详见解析.【分析】已知AF=DB,则AF+FB=DB+FB,可得AB=DF,结合已知AC=DE,BC=FE可证明△ABC≌△DFE,利用全等三角形的性质证明结论.【详解】证明:∵AF=DB,∴AF+FB=DB+FB ,即AB=DF在△ABC 和△DFE 中,AC DE BC FE AB DF =⎧⎪=⎨⎪=⎩∴△ABC ≌△DEF (SSS ),∴∠A=∠D【点睛】本题考查了全等三角形的判定与性质.关键是由已知边相等,结合公共线段求对应边相等,证明全等三角形.18.多边形的边数为5【解析】【分析】根据多边形的外角和均为360°,已知该多边形的内角和比外角和还多180°,可以得出内角和为540°,再根据计算多边形内角和的公式(n-2)×180°,即可得出该多边形的边数.【详解】设多边形的边数为n ,则(n-2)×180°=360°+180°解得n=5答:多边形的边数为5【点睛】本题主要考查多边形的内角和和多边形的外角和.19.(1)详见解析;(2)20°.【解析】【分析】(1)线段垂直平分线的尺规作图;(2)通过线段垂直平分线的性质易得AD=BD ,从而∠BAD=∠B ,再求解即可.【详解】(1)如图,点D 即为所求.(2)在Rt△ABC中,∠B=35°,∴∠CAB=55°,又∵AD=BD,∴∠BAD=∠B=35°,∴∠CAD=∠CAB-∠DAB=55°-35°=20°.【点睛】本题主要考查了尺规作图,线段垂直平分线的作法;线段垂直平分线的性质. 20.(1)(-3,2);(2)2.5【解析】试题分析:(1)根据关于与原点对称的点横、纵坐标均为相反数求解即可;(2)△ABC的面积等于矩形的面积减去三个三角形的面积.(1)如图,C1坐标为(-3,2);(2)11123212131222 ABCS=⨯-⨯⨯-⨯⨯-⨯⨯3611 2.52=---=. 21.BE=0.8cm先证明△ACD ≌△CBE ,再求出EC 的长,解决问题.【详解】解:∵BE ⊥CE 于E ,AD ⊥CE 于D∴∠E =∠ADC =90°∵∠BCE +∠ACE =∠DAC +∠ACE =90°∴∠BCE =∠DAC∵AC =BC∴△ACD ≌△CBE∴CE =AD ,BE =CD =2.5﹣1.7=0.8(cm ).【点睛】本题考查全等三角形的性质和判定,准确找到全等条件是解题的关键.22.见解析【解析】【分析】(1)由于D 是BC 的中点,那么BD =CD ,而BE =CF ,DE ⊥AB ,DF ⊥AC ,利用HL 易证Rt Rt BDE CDF ≌,,可得DE =DF ,利用角平分线的判定定理可知点点D 在∠BAC 的平分线上,即AD 平分∠BAC ;(2)根据全等三角形的性质即可得到结论.【详解】(1)∵D 是BC 的中点∴BD =CD ,又∵BE =CF ,DE ⊥AB ,DF ⊥AC ,Rt Rt BDE CDF ≌,∴DE =DF ,∴点D 在∠BAC 的平分线上,∴AD 平分∠BAC ;(2)Rt Rt BDE CDF ≌,∴∠B =∠C ,∴AB =AC ,∴AB−BE=AC−CF,∴AE=AF,∵DE=DF,∴AD垂直平分EF.【点睛】本题考查了角平分线的性质定理:角的内部到角的两边距离相等的点在角平分线上. 23.(1)∠BAD=40°;(2)详见解析;(3)BD=2.5.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解;(2)根据高线的定义,过点E作BD的垂线即可得解;(3)根据三角形的中线把三角形分成的两个三角形面积相等,先求出△BDE的面积,再根据三角形的面积公式计算即可.【详解】(1)在△ABE中,∵∠ABE=15°,∠BAD=40°,∴∠BED=∠ABE+∠BAD=15°+40°=55°;(2)如图,EF为BD边上的高;(3)∵AD为△ABC的中线,BE为△ABD的中线,∴S△ABD =12S△ABC,S△BDE=12S△ABD,S△BDE=14S△ABC,∵△ABC的面积为20,BD=2.5,∴S△BDE =12BD•EF=12×5•EF=14×20,解得EF=2.【点睛】本题考查了三角形的外角性质,三角形的面积,利用三角形的中线把三角形分成两个面积相等的三角形是解题的关键.24.(1)见解析;(2)见解析;(3)【解析】【分析】(1)先证明9030ABD BAE ∠=-∠= ,,可知AB =2AD ,因为AE =2AD ,所以AB =AE ,从而可知△ABE 是等边三角形.(2)由(1)可知:60ABE AEB ∠=∠= ,AE =BE ,然后求证BEG AEF ≌,即可得出BG =AF ;(3)由于S 四边形AGEF AEG AEF AEG BEG ABE S S S S S =+=+= 故只需求出△ABE 的面积即可.【详解】(1)AB =AC ,AD ⊥BC ,160,902BAE CAE BAC ADB ∴∠=∠=∠=∠= ,9030ABD BAE ∴∠=-∠= ,∴AB =2AD ,∵AE =2AD ,∴AB =AE ,60BAE ∠= ,∴△ABE 是等边三角形.(2)∵△ABE 是等边三角形,60ABE AEB ∴∠=∠= ,AE =BE ,由(1)60,CAE ∠= ∴∠ABE =∠CAE ,60NEM BEA ∠=∠= ,∴∠NEM −∠AEN =∠BEA −∠AEN ,∴∠AEF =∠BEG ,在△BEG 与△AEF 中,,GBE FAE BE AE BEG AEF ∠=∠⎧⎪=⎨⎪∠=∠⎩(ASA).BEG AEF ∴ ≌∴BG =AF ;(3)由(2)可知:BEG AEF ≌,S BEG S AEF ∴= ,∴S 四边形AGEF AEG AEF AEG BEG ABES S S S S =+=+= ∵△ABE 是等边三角形,∴AE =AB =4,11422ABE S AE BD ∴=⋅=⨯⨯= ∴S四边形AGEF =25.见详解【分析】根据角平分线的定义可得∠ABD=∠CBD ,然后利用“边角边”证明△ABD 和△CBD 全等,根据全等三角形对应角相等可得∠ADB=∠CDB ,然后根据角平分线上的点到角的两边的距离相等证明即可.【详解】证明:∵BD 为∠ABC 的平分线,∴∠ABD=∠CBD ,在△ABD 和△CBD 中,AB BC ABD CBD BD BD ⎪∠⎪⎩∠⎧⎨===∴△ABD ≌△CBD (SAS ),∴∠ADB=∠CDB ,∵点P 在BD 上,PM ⊥AD ,PN ⊥CD ,∴PM=PN .【点睛】本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,确定出全等三角形并得到∠ADB=∠CDB 是解题的关键.。
八年级数学上学期期中试题(B卷)新人教版

内蒙古呼和浩特市实验教育集团2016-2017学年八年级数学上学期期中试题(B卷)、选择题(30 分)1.下列长度的三条线段中, 能组成三角形的是A 3 cm4 cm)8 cmB 3 cm)4 cm,7cm2.下列四个图形中,线段BE是厶ABC高的是(C 5 cm6cm10cmD 5 cm,6cm,11cm)3.使两个直角三角形全等的条件是(A 一个锐角对应相等两个锐角对应相等C 一条边对应相等斜边及一条直角边对应相等4.平面直角坐标系中,点A(m , —2 )、B(1,n —m厌于x轴对称,则mn的值为()A m =1 , n=1B m = —1 , n=1C m =1 , n=3 —1 , n=35.如图,△ ABC中,AC=25cm DE垂直平分AB,垂足为E,交AC于则BC边的长为()A 5 cmB 10 cmC 15 cmD 17.5 cmD,若厶DBC的周长是35cm6.等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为30°,则这个等腰三角形的顶角为A 60 或120°B 30 或150 °C 30 。
或120 °D 607. 占八、、P是锐角△ ABC内一点,PE丄AB于E, PF 丄BC于F, PH 丄CA于H,若PE=PF=PH则点P >△ABC三条中线的交点三条高线的交点三条角平分线的交点三边垂直平分线的交点8. 一个多边形的内角和是1440° ,且这个多边形的每一个内角都相等,则这个多边形的一个外角是A 60B 45C 36D 309.如图,将长方形ABCD沿直线BD折叠,使点C落在点E处,BE交AD于F,连接CE,下列结论① AB=ED②FA=FE ③BD平分/ FBC ④EC垂直平分BD 正确的有()A 1 个B 2 个C 3 个D 4 个10.如图,△ ABC中,点D在BC上,E是AC的中点, =2,S △ BFD = 0.5,则四边形FDCE的面积为()A 1.5B 2.5C 3D 6 BC=3BD,BE与AD相交于F,S A ABD、填空题(18分)11. △ ABC中,/ B=Z A+10°,Z C=Z B+10°则/ B=12. 如图,四边形ABCD中, AD// BC,添加一个条件使得△ ADB^A CBD,添加的条件是__________________13. 用18cm长的细绳围成一个边长4cm的等腰三角形,则这个等腰三角形腰长为cm14. 如图,/ CAE>^ ABC的外角,且AD// BC,AD平分/ EAC,若/ B = 63 ° ,则/ BAC= ______15. 若a、b、c为三角形的三边,化简l a—b+c | + | a —b—c | = ________16.如图,点P在/ AOB内,点M N分别是点P关于直线OA OB的对称点,线段交OA OB于E、卩,若厶PEF的周长是18cm,则MN的长是____________三解答题(52 分)17. (6 分)如图,AC和BD相交于点O, OA=OC,OB=OD,求证:AB// CD18. (6 分)如果a、b、c是厶ABC的三边,满足(b —3)7 MN(a—5) 2+ | c—4 | = 0,求厶ABC的周长求证:△ EBD^A EFD19. (6分) 如图,△ ABC 在平面直角坐标系的坐标分别为 A( — 1,5) , B( — 1, 0) , C( — 4,3),按要求完成(1) 在同一坐标系中,画出△ ABC 关于y 轴对称的图形△ A B C 20. (6分)如图,一艘轮船从 A 处向正北方向航行,达到21. ( 8 分)如图,AB=AC,DB=DC, (1) 求证:AD 平分/ BAC(2) 延长CD 与 AB 的延长线交于 E ,延长AD 到F ,使DF=DC 连接EF ,若/ C=100°,Z BAC=40 ,(2)六边形 ACBB C A ,的面积S= ___________C 恰好在正西方向,从 A 处、B 处望灯塔C 的角度分别是/ A=30° , / DBC=60 ,若 DB 等于 36 海里,求B 到CA 的距离B 处后,继续航行到达 D 处时发现,灯塔22. (8分)如图,△ AB3A A B C , AD A D 分别是△ ABC △ A B C 的对应边上的中线, 判断AD与AC T有怎样的数量关系?证明你的结论23. (12分)(1)如图1 , D是等边三角形△ ABC的边BA上任意一点(D与A、B不重合),连接DC 以DC为边在BC边上方作等边三角形△ DCE连接AE,/ ABC与/ EAC有怎样数量关系直接写出结论(2)如图2, D是等边三角形△ ABC边BA延长线上一点,连接DC,以DC为边在BC边上方作等边三角形△ DCE连接AE,求证:/ ABC=/ EAC(3)如图3 , D是等边三角形△ ABC边AB延长线上一点,连接DC,以DC为边在BC边上方作等边三角形△ DCE连接AE,探究/ ABC与/ EAC的数量关系,直接写出结论__________________实验中学2016-2017学年度第一学期八年级数学期中试卷答案(2016、11)(B)、选择题(30 分)1.C2.D3.D4.C5.B6.A7.C8.C9.C 10.B二、填空题(18分)11.60 ° 12. AD=BC(符合要求的其它条件均可以)13. 7cm 或4cm 14. 5415. 2c 16. 18cm三、解答题(52 分)17. 证明:在厶AOB^D^ COD中OA=OCAOB=/ CODOB=OD••• AOB^A CODAB // CD2 218. 解:•••( b —3) > 0 , (a—5) > 0 , | C- 4 | > 0且(b —3) 2 + ( a —5) 2+ | c —4 | = 0,(b —3) 2 =0 (a—5) 2 =0 | c —4 | = 0,b=3 a=5 c=4 .............................. 3 分• △ ABC的周长为a+b+c=5+3+4=12 ...................... 6 分19. (1)图略画图正确 ........... 3分(2)不要求画图写出25即可............ 6分20. 解:•/ C在D的正西方向北•••/ CDB==90......................... 1 分•••/ DBC =/ BCA +Z A•••/ BCA =Z DBC — Z A=60°—30°=30°在Rt △ BCD中,Z BCD+Z CBD=90• Z BCD= 90°—Z CBD=90 —60°=30• Z BCA = Z BCD• CB 平分Z ACD••• B到CA的距离等于BD=36海里21. (1)证明:在厶ABD^D^ ACD中AB=ACDB=DC■—AD=AD•△ABD^A ACD•/ 仁/ 2•AD平分/ BAC ....................... 3分F(2)由(1 )知△ ABD^A ACD•/ ADB2 ADC , / 仁/2在厶ACE中,/ C=100°/ BAC=40• / 仁/2 =20 °•/ ADB玄ADC=180 — / 2 -Z C = 60 °•/ 3=180 °— Z ADB-Z ADC=60vZ 4=Z ADC=60 ....................... 6 分又DF=DC, DB=DC• DB=DF在厶BED和△ EFD中DB=DFL Z 3=Z 4DE=DE•••△BED^A EFD ....................... 8 分22. AD=A / D,证明如下 ............ 1分证明:•/△ ABC^A A B C• AB=A B z BC=B / C Z Z B=Z B z........................................ 3 分••• AD A D/分别是BC与B z C 边上的中线• BD=B D在厶ABD和△ A B D中AB=A [ / B z/ B=Z B zBD=B / D z• △ABD^A A B / D z• AD=A / D z23. (1) ①/ ABC=Z EAC②证明:•••△ ABC^DA DCE均为等边三角形• CA=CB CD=CE / ACB玄DCE =60• / ACB+Z DCA=/ DCE+/ DCA即/ DCB=ECA ................在厶DCB和厶ECA中CB=CA/ DCB/ ECACD=CE△DCB^A EAC/ ABC=Z EAC10分内蒙古呼和浩特市实验教育集团2016-2017 学年八年级数学上学期期中试题( B 卷)新人教版③/ ABC +/ EAC=180 或 / EAC=2/ ABC 12 分。
人教版八年级数学上册期中检测B卷

人教版八年级数学上学期期中检测B卷考试范围:第十一章-第十三章;考试时间:120分钟;总分:120分一、选择题(本大题共6小题,每小题3分,共18分)1.(2022·广东·铁一中学八年级阶段练习)在下列长度的三条线段中,不能组成三角形的是( )A.2,3,4B.3,6,6C.2,2,6D.5,6,7【答案】C【分析】利用三角形的三边关系:三角形两边之和大于第三边,三角形的两边差小于第三边进行分析即可.【详解】解:A、2+3>4,能构成三角形,故此选项不符合题意;B、3+6>6,能构成三角形,故此选项不符合题意;C、2+2<6,不能构成三角形,故此选项符合题意;D、5+6>7,能构成三角形,故此选项不符合题意;故选:C.【点睛】此题主要考查了三角形的三边关系,关键是掌握在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.2.(山东省聊城市水城慧德学校、博雅学校等2022-2023学年八年级上学期第一次学情调查数学试题)如图,图案中不是轴对称图形的是()A.B.C.D.【答案】A【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【详解】解:A、不是轴对称图形,故此选项正确;B、是轴对称图形,故此选项错误;C、是轴对称图形,故此选项错误;D、是轴对称图形,故此选项错误;故选:A.【点睛】此题主要考查了轴对称图形,关键是掌握轴对称图形的概念.3.(2022·江苏·沭阳县怀文中学八年级阶段练习)如图,△ACB≌△A'CB',∠A'CB=30°,∠A'CB'=70°,则∠ACA'的度数是( )A .2B .3【答案】D 【分析】过点D 作DF AC ^Δ=4ABD S ,根据=9ABC S V ,求出Δ22×5===5ACD S AC .∵AD 平分∠BAC ,DE AB ^∴=DE DF ,∵2DE =,∴2DF =,∵=4AB ,A.8个B.7个C.6个D.5个【答案】A【分析】当AB为底时,作AB的垂直平分线,当AB为腰时,分别以A、B点为顶点,以AB为半径作弧,分别找到格点即可求解.【详解】解:当AB为底时,作AB的垂直平分线,可找出格点C的个数有5个,当AB为腰时,分别以A、B点为顶点,以AB为半径作弧,可找出格点C的个数有3个;\这样的顶点C有8个.故选:A.【点睛】本题考查了等腰三角形的性质,垂直平分线的性质,掌握等腰三角形的性质是解题的关键.二、填空题(本大题共6小题,每小题3分,共18分)7.(2022·湖北·鄂州市华容区庙岭中学八年级阶段练习)如图,AB=DB,∠1=∠2,添加_____________能判断△ABC≌△DBE【答案】EB=BC(答案不唯一)【分析】根据全等三角形的判定解答.【详解】解:∵∠1=∠2,∴∠1+∠ABE =∠2+∠ABE,即∠DBE =∠ABC ,若EB =BC ,则在△ABC 和△DBE 中,AB DB DBE ABCEB BC ìïÐ=Ðíï=î=∴△ABC ≌△DBE (SAS ),故答案为:EB =BC .【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解题关键.8.(2022·湖北·公安县教学研究中心八年级阶段练习)如图,四边形ABCD ≌四边形A B C D ¢¢¢¢,若90°60°105°B C D ÐÐÐ==¢=,,,则A Т=______°.【答案】105【分析】根据全等图形的性质:对应角相等,以及四边形的内角和进行计算即可;【详解】解:∵四边形ABCD ≌四边形A B C D ¢¢¢¢∴90°=60°B B C C ÐÐÐТ===¢,,∴=360°=360°90°60°105°=105°A B C D Ð-Ð-Ð-Т---¢¢¢ ,故答案为:105.【点睛】本题考查全等形的性质.熟记全等形的性质以及四边形的内角和为360°是解题的关键.9.(甘肃省庆阳市2021-2022学年八年级上学期期中数学试题)彩虹桥(庆阳雨洪集蓄保塬生态项目),位于庆阳市南区入口处,以世纪大道为中轴线,北起石油路,向南600米,占地1046亩,如图是彩虹桥中的双向飞虹斜拉桥,那么你能推断出斜拉桥中运用的数学原理是_____.(填“三角形的稳定性”或“四边形的不稳定性”)【答案】三角形的稳定性【分析】根据三角形的三边一旦确定,则形状大小完全确定,即三角形的稳定.【详解】解:虹桥(庆阳雨洪集蓄保塬生态项目),位于庆阳市南区入口处,以世纪大道为中轴线,北起石油路,向南600米,占地1046亩,如图是彩虹桥中的双向飞虹斜拉桥,那么你能推断出斜拉桥中运用的数学原理是是三角形的稳定性.故答案为:三角形的稳定性.【点睛】本题考查三角形的稳定性在实际生活中的应用本题.10.(2023·广东·高州市第一中学附属实验中学八年级开学考试)已知ABC V 三边长分别为3,5,7,DEF V 三边长分别为3,32x -,21x -,若这两个三角形全等,则x 为______ .【答案】3【分析】根据全等三角形的对应边相等分两种情况求解即可.【详解】ABC Q V 三边长分别为3,5,7,DEF V 三边长分别为3,32x -,21x -,这两个三角形全等,\分为两种情况:①当532x =-,721x =-时,x =3,4x =,此时x 的值不等,舍去;②当732x =-,521x =-时,3x =,3x =,此时x 的值相等,3x \=.故答案为:3.【点睛】本题考查全等三角形的性质和解一元一次方程,全等三角形的对应边相等,对应角相等,注意分情况讨论.11.(浙江省绣湖中学教育集团2022-2023学年八年级上学期10月月考数学试题)如图,在△ABC 中,AB =5,AC =7,AB ⊥AC ,EF 垂直平分BC ,点P 为直线EF 上一动点,则△ABP 周长的最小值是_____.【答案】12【分析】根据题意知点B 关于直线EF 的对称点为点C ,故当点P 与点D 重合时,AP +BP 的最小值,求出AC 长度即可得到结论.【详解】解:∵EF 垂直平分BC ,∴B 、C 关于EF 对称,设AC 交EF 于点D ,∴当P 和D 重合时,AP +BP 的值最小,最小值等于AC 的长,∴△ABP 周长的最小值是5+7=12.故答案为:12.【点睛】本题考查了轴对称-最短路线问题的应用,解此题的关键是找出P 的位置.凡是涉及最短距离的问在△ACD中可得出∠ADC=∠ACD,【点睛】本题考查等腰三角形存在问题,如果题中没有说明等腰三角形的腰或者底分别是哪条线段,都要进行分类讨论,让三条线段分别两两相等,得出三种情况,再根据题意看有没有需要排除的情况,然后再一一分析符合条件的图形.三、(本大题共5小题,每小题6分,共30分)(1)点B到AC的距离是______(2)画出表示点C到AB的距离的线段,并求这个距离.解题的关键.15.(2022·江苏·姜堰区实验初中八年级)如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.(1)若∠A=40°,求∠DBC的度数;(2)若AE=6,△CBD的周长为20,求△ABC的周长.【答案】(1)30°(2)32【分析】(1)由在△ABC中,AB=AC,∠A=40°,利用等腰三角形的性质,即可求得∠ABC的度数,然后由AB的垂直平分线MN交AC于点D,根据线段垂直平分线的性质,可求得AD=BD,继而求得∠ABD的度数,则可求得∠DBC的度数.(2)由△CBD的周长为20,推出AC+BC=20,根据AB=2AE=12,由此即可解决问题.(1)解:∵在△ABC中,AB=AC,∠A=40°,∴∠ABC=∠C=70°,∵AB的垂直平分线MN交AC于点D,∴AD=BD,∴∠ABD=∠A=40°,∴∠DBC=∠ABC-∠ABD=30°.(2)∵MN垂直平分AB,∴AD=DB,∵BC+BD+DC=20,∴AD+DC+BC=20,∴AC+BC=20,∵AB=2AE=12,∴△ABC的周长=AB+AC+BC=12+20=32.【点睛】此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.16.(2021·广东·梅华中学八年级期中)如图,在△ABC和△ADE中,AB = AD,AC = AE,∠1 = ∠2,AD、BC 相交于点F.(1)求证:△ABC≌△ADE;(2)若AB∥DE,AE = 3,BC = 4,求△ACF的周长.【答案】(1)见解析(2)7【分析】(1)根据∠1 = ∠2,得到∠1+ ∠CAF= ∠2+ ∠CAF即∠EAD = ∠CAB,利用SAS证明即可.(2)根据AB P DE,得到∠1=∠D,根据△ABC≌△ADE,得到∠D = ∠B,AE=AC,得到∠1=∠B,从而得到AF=BF,故AF+CF=BF+CF=BC,计算周长即可.(1)证明:因为∠1 = ∠2,所以∠1+ ∠CAF= ∠2+ ∠CAF,即∠EAD = ∠CAB,因为AB = AD,AC = AE,所以△ABC≌△ADE.(2)解:因为AB P DE,所以∠1=∠D,因为△ABC≌△ADE,AE=3,BC=4,所以∠D = ∠B,AE=AC,所以∠1=∠B,所以AF=BF,所以AF+CF=BF+CF=BC,所以△ACF的周长为:AC+AF+CF=AE+BF+CF=AE+BC=3+4=7.【点睛】本题考查了三角形全等的判定和性质,平行线的性质,等腰三角形的判定,熟练掌握三角形全等的判定和性质,等腰三角形的判定定理是解题的关键.17.(2022·吉林省第二实验学校八年级阶段练习)图①中所示的遮阳伞,伞柄垂直于地面,其示意图如图②.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米.(1)求AP长的取值范围;(2)当∠CPN=60°时,求AP的值.【答案】(1)0≤AP≤10;(2)6分米【分析】(1)根据题意,得AC=CN+PN,进一步求得AB的长,即可求得AP的取值范围;(2)由等边三角形的判定和性质得出∆CPN为等边三角形,CP=CN=PN=6分米,再结合图形求解即可.(1)解:∵BC=2分米,AC=CN+PN=12分米,∴AB=AC﹣BC=10分米.∴AP的取值范围是:0≤AP≤10;(2)根据题意得CN=PN,∠CPN=60°,∴∆CPN为等边三角形,∴CP=CN=PN=6分米,∵AC=CN+PN=12分米,∴AP=AC-CP=6分米.【点睛】题目主要考查线段间的数量关系,等边三角形的判定和性质,熟练掌握等边三角形的判定和性质是解题关键.四、(本大题共3小题,每小题8分,共24分)18.(2022·江苏·八年级单元测试)如图,已知△ABC,AD是∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.(1)求证:AD垂直平分EF;(1)如图1,若AE⊥BC于E,∠C=35°,求∠DAE的大小;(2)如图2,P为CB延长线上一点,过点P作PF⊥AD于F,求证:(1)若点Q 运动的速度与点P 运动的速度相等,当1t =时,求证:(2)在(1)的条件下,求PCQ Ð的度数;(3)如图②,若70CAB DBA Ð=Ð=°,9AB =,AC BD =V,ACPQ V≌BPQ=,ACP BPQ\Ð=Ð,PC PQ\Ð+Ð=Ð+ÐAPC BPQ APC ACP等三角形的判定定理和性质定理、注意分类讨论思想的灵活运用是解题的关键.22.(2022·江苏·南京市竹山中学八年级阶段练习)在△ABC 中,90BAC Ð=°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交射线BC 于点F .(1)如图①,当AE ⊥BC 时,求证:DE ∥AC ;(2)若10C B Ð-Ð=°,BAD x Ð=°.①如图②,当DE ⊥BC 时,求x 的值;②是否存在这样的x 的值,使得△DEF 是等腰三角形?若存在,求x 的值;若不存在,请说明理由.【答案】(1)证明见解析(2)①5;②存在;15x =或30【分析】(1)由翻折的性质可得∠E =∠B ,由等角代换可得∠B =∠CAF ,进而得出∠E =∠CAF ,即可证明DE ∥AC ;(2)①由三角形内角和定理可得90B C Ð+Ð=°,结合10C B Ð-Ð=°可得∠C ,∠B 的度数.由翻折的性质可得∠EDA =∠BDA ,求出∠BDA ,进而利用三角形内角和定理求出BAD Ð;②根据翻折的性质和三角形外角及三角形内角和定理,用含x 的代数式表示出∠FDE 、∠DFE 的度数,分三种情况讨论求出符合题意的x 值即可.(1)解:∵∠BAC =90°,∴90B C Ð+Ð=°,∵AE ⊥BC ,∴90AFC Ð=°,∴90CAF C Ð+Ð=°,∴CAF B Ð=Ð,由翻折的性质可得:∠E =∠B ,∴CAF E Ð=Ð,∴DE ∥AC ;(2)解:∵∠BAC =90°,23.(2022·江苏·姜堰区实验初中八年级)如图1,在边长为4cm的等边△ABC中,点P从点A出发沿着AB 以2cm/s的速度向点B运动,点Q从B点出发沿着BC以相同的速度向点C运动,P、Q两点同时出发,设运动时间为t秒.(1)当t=1时,试判断△PBQ的形状,并说明理由;(2)当PQ⊥BC时,求t的值;(3)如图2,过点P作PH⊥BC,垂足为H,连接PQ,以PQ为边向左作等边△PQE,连接BE.当PQ BC ^时,∵=60°B Ð∴=30°BPQ Ð∴2BP BQ=即42=2×2t t -设=EPB Ða ,∵PEQ V 是等边三角形,∴==60°EPQ PQE ÐÐ,EP =∴=60°BPQ Ð-a ,又=60°PBQ Ð,。
新人教版八年级数学上册期中试卷及答案解析

大集中学八年级数学上册期中阶段达标检测试卷一、选择题1、下列交通标志图案是轴对称图形的是()A.B.C.D.2、点A(﹣2,-3)关于x轴的对称点A′的坐标为()A.(2,﹣3)B.(﹣2,﹣3)C.(﹣2,3)D.( 2,3)3、已知等腰三角形的其中二边长分别为4,9,则这个等腰三角形的周长为()A.17 B.22 C.17或22 D.无法确定4、正多边形的每一个内角都为 135°,则该多边形的边数为()A.5 B.6 C.7 D.85、如图,点D,E分别在AB,AC上,AB=AC,∠B=∠C,若AD=2,BD=3,则CE的长为()A.2 B.3 C.5 D.无法确定6、已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形()A. 一定有一个内角为45°B. 一定有一个内角为60°C. 一定是直角三角形D. 一定是钝角三角形7、如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是()A.SSS B.SASC.AAS D.ASA8、如图,△ABC≌△CDA,则下列结论错误的是()A.AC=CA B.AB=ADC.∠ACB=∠CAD D.∠B=∠D9、在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )A.∠A=40°,∠B=50°B.∠A=40°,∠B=60°C.∠A=40°,∠B=80°D.∠A=20°,∠B=80°二、填空题10、点P(-3, 4)关于y轴的对称点P′的坐标是_____。
11、如图,AC=DC,BC=EC,请你添加一个适当的条件:___________,使得△ABC≌△DEC。
12、已知△ABC 的两条边长分别为 5 和 8,那么第三边长 x 的取值范围____________。
【期中测试AB卷】人教版数学八年级上册-B培优测试试题试卷含答案

【期中测试AB卷】人教版八年级上册数学·B培优测试学校:_____________班级:____________ 姓名:____________(时间:120分钟分值:120分)一、选择题(共10小题,满分30分,每小题3分)1.(3分)下面图形中,为轴对称图形的是( )A.B.C.D.2.(3分)若三角形的两边长分别为3和6,则第三边的长不可能是( )A.3B.4C.5D.6.3.(3分)如图,若∠B=35°,∠ACD=120°,则∠A=( )A.35°B.75°C.85°D.95°4.(3分)如图所示,在△ABC中,∠C=90°,EF∥AB,∠B=39°,则∠1的度数为( )A.38°B.39°C.51°D.52°5.(3分)如图,已知∠DAB=∠CAB,添加下列条件不能判定△DAB≌△CAB的是( )A.∠DBE=∠CBE B.∠D=∠C C.DA=CA D.DB=CB 6.(3分)如图,在△ABC中,BC=12cm,DE垂直平分AB,△BCE的周长为30cm,则AC的长为( )A.18 cm B.12 cm C.10 cm D.8 cm 7.(3分)如图,△ABC中,AD为BC边上中线,DM,DN分别∠ADB,∠ADC的角平分线,试比较BM+CN与MN的大小关系( )A.BM+CN=MN B.BM+CN<MN C.BM+CN>MN D.无法确定8.(3分)如图,已知∠1+2+∠3+∠4=280°,那么∠5的度数为( )A.70°B.80°C.90°D.100°9.(3分)矩形ABCD沿对角线AC折叠,使点B落在点B'处,若∠1=58°,则∠2=( )A.44°B.58°C.64°D.84°10.(3分)如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )A.60°B.75°C.90°D.120°二、填空题(共5小题,满分15分,每小题3分)11.(3分)室内墙壁上挂一平面镜,小明在平面镜内看到他背后的时钟如图,则这时的实际时间是 .(按12小时制填写)12.(3分)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图∠MON=40°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<60°).当△ABC为“灵动三角形”时,∠OAC的度数为 .13.(3分)如图,在△ABC中,BE平分∠ABC交AC于点E,点D在BC上,连接AD 交BE于点H,且∠DAB=∠C,BH=BD,过点H作HF∥BC交AC于点F,BG⊥AD 交AC于点G,若AE=6,EF=2,则GF= .14.(3分)如图,四边形ABCD的两个外角∠CBE,∠CDF的平分线交于点G.若∠A=52°,∠DGB=28°,则∠DCB的度数是 .15.(3分)如图,在Rt△ABC中,∠C=90°,两锐角的角平分线交于点P,点E、F 分别在边BC、AC上,且都不与点C重合,若∠EPF=45°,连接EF,当AC=6,BC=8,AB=10时,则△CEF的周长为 .三、解答题(共10小题,满分75分)16.(7分)如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点F,∠CAD=30°,∠B=50°,求∠ADC和∠AFC的度数.17.(7分)如图,已知在四边形ABCD中,∠A=70°,∠B=140°.(1)∠BCD+∠D的度数为 ;(2)若∠BCD的平分线交边AD于点E,且CE∥AB,求∠D的度数.18.(7分)如图,△ABC三个顶点坐标分别为A(﹣4,4)、B(﹣3,1)、C(﹣1,2).(1)画出将△ABC向右平移5个单位长度得到的图形△A1B1C1;(2)画出△A1B1C1关于x轴的对称图形△A2B2C2,并写出B2的坐标.19.(7分)等腰三角形ABC中,一腰AC上的中线BD把三角形的周长分为12cm和15cm 两部分,求此三角形的腰和底边的长.20.(7分)如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,求证:(1)△DFB≌△DAC;(2)CE=12 BF.21.(7分)如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC 于点F,连接AD.(1)求证:AD平分∠GAC;(2)若AB=AD,请判断△ABC的形状,并证明你的结论.22.(7分)如图,在△ABC中,∠ABC=3∠C,AD平分∠BAC,BE⊥AD于E,(1)若∠BAC=60°,求∠ADB的度数;(2)求证:BE=12(AC﹣AB).23.(8分)如图,在△ABC中,AB=AC,D是BC的中点,EF垂直平分AC,交AC 于点E,交AB于点F,M是直线EF上的动点.(1)当MD⊥BC时.①若ME=1,则点M到AB的距离为 ;②若∠CMD=30°,CD=3,求△BCM的周长;(2)若BC=8,且△ABC的面积为40,则△CDM的周长的最小值为 .24.(9分)综合与探究如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.(1)求证:△ACE≌△ABD.(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.25.(9分)如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1图形称之为“8字形”,易知∠A+∠C=∠B+∠D.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图2中,若∠B=96°,∠C=100°,求∠P的度数;(2)在图2中,若∠CAP=13∠BAC,∠CDP=13∠BDC,试问∠P与∠C、∠B之间的数量关系为 ;(3)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .参考答案一、选择题(共10小题,满分30分,每小题3分)1.A;2.A;3.C;4.C;5.D;6.A;7.C;8.B;9.C;10.C;二、填空题(共5小题,满分15分,每小题3分)11.1:3012.57.5°13.10 714.108°15.4三、解答题(共10小题,满分75分)16.解:∵AD是△ABC的角平分线,且∠CAD=30°,∴∠BAD=30°.又∵∠B=50°,∴∠ADC=∠BAD+∠B=30°+50°=80°.∵CE是△ABC的高,∴∠AEF=90°.∴∠AFC=∠BAD+∠AEF=30°+90°=120°.故答案为:80°,120°.17.解:(1)∵四边形ABCD的内角和为360°,∠A=70°,∠B=140°,∴∠BCD+∠D=360°﹣70°﹣140°=150°.故答案为:150°;(2)∵CE∥AB,∴∠ABC+∠BCE=180°,∠A=∠CED,∵∠A=70°,∠B=140°,∴∠BCE=40°,∠CED=70°,∵CE平分∠BCD,∴∠BCE=∠DCE=40°,∴∠D=180°﹣∠DCE﹣∠CED=180°﹣40°﹣70°=70°.18.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求,B2的坐标为(2,﹣1).19.解:设腰长为xcm,①腰长与腰长的一半是12cm时,x+12x=12,解得x=8,所以,底边=15―12×8=11,所以8cm、8cm、11cm能组成三角形;②腰长与腰长的一半是15cm时,x+12x=15,解得x=10,所以,底边=12―12×10=7,所以,三角形的三边为10cm、10cm、7cm,能组成三角形,综上所述,此三角形的腰和底边的长分别为8cm、11cm或10cm、7cm.20.证明:(1)∵∠ABC=45°,CD⊥AB,∴△BCD是等腰直角三角形,∠BDF=∠CDA=90°,∠BCD=45°,∴BD=CD,∠DCA+∠A=90°,∵BE⊥AC,∴∠DBF+∠A=90°,∴∠DBF=∠DCA,在△DFB和△DAC中,∠BDF=∠CDA BD=CD∠DBF=∠DCA,∴△DFB≌△DAC(ASA);(2)∵△DFB≌△DAC,∴BF=AC,∵∠ABC=45°,BE平分∠ABC,∴∠DBF=∠DCA=22.5°,∴∠A=90°﹣22.5°=67.5°,∠ACB=45°+22.5°=67.5°,∴∠A=∠ACB,∴AB=CB,∵BE⊥AC,∴CE=AE=12 AC,∴CE=12 BF.21.(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,∴DM=DN=DK,∴AD平分∠GAC,∠ABD=∠DBC,∴∠GAD=∠DAC,∴AD平分∠GAC.(2)解:△ABC是等腰三角形,证明:∵AB=AD,∴∠ABD=∠ADB,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠CBD,∴AD∥BC,∴∠GAD=∠ABC,∠DAC=∠ACB,∵AD平分∠GAC,∴∠GAD=∠CAD,∴∠ABC=∠ACB,∴△ABC是等腰三角形.22.(1)解:如图:延长BE交AC于点F,∵BF⊥AD,∴∠AEB=∠AEF.∵AD平分∠BAC,∴∠BAE=∠FAE,在△ABE和△AFE中,∠AEB=∠AEFAE=AE∠BAE=∠FAE,∴△ABE≌△AFE(ASA),∴∠ABF=∠AFB,AB=AF,BE=EF.∵∠C+∠CBF=∠AFB=∠ABF,∠ABF+∠CBF=∠ABC=3∠C,∴∠C+2∠CBF=3∠C,∴∠CBF=∠C.∵∠BAC=60°,∴△ABF是等边三角形,∴∠AFB=60°,∴∠CBF=∠C=30°.∴∠ADB=90°﹣30°=60°;(2)证明:由(1)知:∠CBF=∠C.∴BF=CF,∴BE=12BF=12CF.∵CF=AC﹣AF=AC﹣AB,∴BE=12(AC﹣AB).23.解:(1)①∵MD⊥BC,AB=AC,D是BC的中点,∴A、M、D共线,∴AD是△ABC的对称轴,∵ME=1,∴点M到AB的距离为1,故答案为:1;②∵D是BC的中点,MD⊥BC,∴MB=MC,∴MD平分∠BMC,∴∠BMC=2∠CMD=60°,∴△BCM是等边三角形,∴BC=BM=MC,∵D是BC的中点,∴BC=2CD=6,∴BM=MC=BC=6,∴△BCM的周长为BC+BM+MC=18;(2)连接AD交EF于点M,∵EF是AC的垂直平分线,∴AM=CM,∴CM+MD=AM+MD=AD,此时△CMD的值最小,最小值为AD+CD,∵BC=8,△ABC的面积为40,∴AD=10,∵D是BC的中点,∴CD=4,∴AD+CD=14,∴△CMD的周长最小值为14,故答案为:14.24.(1)证明:∵∠BAC =∠DAE .∴∠CAE =∠BAD .在△ACE 和△ABD 中,AC =AB∠CAE =∠BAD AE =AD,∴△ACE ≌△ABD (SAS );(2)解:∵△ACE ≌△ABD ,∴∠AEC =∠ADB ,∴∠AEF +∠AEC =∠AEF +∠ADB =180°.∴∠DAE +∠DFE =180°,∵∠BFC +∠DFE =180°,∴∠BFC =∠DAE =∠BAC =50°;(3)证明:如图,连接AF ,过点A 作AJ ⊥CF 于点J .∵△ACE ≌△ABD ,∴S △ACE =S △ABD ,CE =BD ,∵AJ ⊥CE ,AH ⊥BD .∴12CE ⋅AJ =12BD ⋅AH ,∴AJ =AH .在Rt △AFJ 和Rt △AFH 中,AF =AFAJ =AH ,∴Rt △AFJ ≌Rt △AFH (HL ),∴FJ =FH .在Rt △AJE 和Rt △AHD 中,AE =ADAJ =AH ,∴Rt △AJE ≌Rt △AHD (HL ),∴EJ =DH ,∴EF+DH=EF+EJ=FJ=FH.25.解:(1)∠CAB和∠BDC的平分线AP和DP相交于点P,∴∠CAP=∠BAP,∠BDP=∠CDP,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=∠P﹣∠B,即∠p=12(∠B+∠C),∵∠B=96°,∠C=100°,∴∠p=12(96°+100°)=98°.(2)∵∠CAP=13∠BAC,∠CDP=13∠BDC,∴∠BAP=23∠BAC,∠BDP=23∠BDC,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C―∠P=13∠BDC―13∠BAC,,∠P―∠B=23∠BDC―23∠BAC,∴2(∠C﹣∠P)=∠P﹣∠B∴∠p=13(∠B+∠C).故答案为:∠p=13(∠B+∠C);(3)如图:∵∠B+∠A=∠1,∠C+∠D=∠2,∴∠A+∠B+∠C+∠D=∠1+∠2,∵∠1+∠2+∠F+∠E=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°,故答案为:360°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省禹州市2017-2018学年八年级数学上学期期中试题
八年级数学期中考试参考答案B
一、1-10 CBABBDDABC
二、11、2020;12、4;13、8;14、25;15、①②③④.
三、16、解:设多边形的一个外角为x,则一个内角为4x,由题意得x+4x=180°,解得
x=36°.360°÷(36°)=10,(10-2)×180°=1440°.答略.
17、解:∵AD是BC上的高,∴∠ADC=90°,又∵∠C=50°,
∴∠DAC=90°﹣∠C=40°,∵∠BAC=70°,AE平分∠BAC,
∴∠ABC=180°﹣∠BAC﹣∠C=60°,∠BAO=∠BAC=35°,
∵BF平分∠ABC,∴∠ABO=∠ABC=30°,
∴∠AOB=180°﹣∠ABO﹣∠BAO=180°﹣30°﹣35°=115°.
18、解:(1)、(2)如图所示:
(3)由图可知,△A1B1C1与△A2B2C2关于直线x=﹣1对称.
19、解:(1)图略;(2)∵BD平分∠ABC,∠ABD=23°,∴∠ABC=46°,
∠DBC=23°,∵EF垂直平分BC,∴BF=CE,∴∠DBC=∠FCE=23°.
在△ABC中,∠A=100°,∠ABC=46°,∴∠ACB=180°-100°-46°=34°,∴∠ACF=34°
-23°=11°
20、解:(1)BE=DF,理由是:∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,
在△AFD和△CEB中,,∴△AFD≌△CEB(SAS),∴BE=DF.
(2)BE∥DF,∵△AFD≌△CEB,∴∠AFD=∠CEB,∴BE∥DF.
21、证明:(1)∵AB∥CD,∴∠CDA+∠DAB=180°.∵AM平分∠DAB,DM平分∠ADC,∴∠ADM=
∠ADC,∠DAM=∠DAB,∴∠ADM+∠DAM=(∠CDA+∠DAB)=×180°=90°,∴
∠AMD=90°,∴AM⊥DM;
(2)AD=CD+AB.理由:如图,延长DM、AB相交于点F,
∵M是BC的中点,∴CM=BM.∵AB∥CD,∴∠C=∠B,
∠CDM=∠F.在△DCM和△FBM中,,
∴△DCM≌△FBM(AAS),∴CD=BF,DM=FM.∵AM⊥DM,
∴AD=AF.∵AF=AB+BF,∴AF=AB+CD,∴AD=AB+CD.
22、解:∵∠DEN=105°,∴∠AED=75°,∵CD=DE,∴∠ECD=∠AED=75°,
∴∠CDE=30°,∵AB=BC,∴∠A=∠ACB,∴∠CBD=2∠A,
∵BC=CD,∴∠CDB=∠CBD=2∠A,∴∠DEN=∠CDE+3∠A,
即105°=30°+3∠A,解得∠A=25°.故答案为:25°.
23、解:①BP=6t,则PC=BC﹣BP=16﹣6t;
②当t=1时,BP=CQ=6×1=6厘米,∵AB=20厘米,点D为AB的中点,
∴BD=10厘米.又∵PC=BC﹣BP,BC=16厘米,∴PC=16﹣6=10厘米,
∴PC=BD,又∵AB=AC,∴∠B=∠C,在△BPD和△CQP中,,
∴△BPD≌△CQP(SAS);
③∵v P≠v Q,∴BP≠CQ,又∵△BPD≌△CPQ,∠B=∠C,
∴BP=PC=8cm,CQ=BD=10cm,∴点P,点Q运动的时间t==秒,
∴V Q===7.5厘米/秒.。
