“德瑞教育发展基金会” 2010年奖学金测试数学卷及答案
小学奥数之分数问题

第 一 讲 小 升 初· 竞 赛 中 的 分 数 问 题知识 导 航在分数式的计算应用问题中,主要包括以下几个方面的题型。
①和(差)倍问题。
具体表现为“已知分数的分子与分母的和(差),和约分过后的结果,求原分数。
②变化类。
具体表现为“已知分数的分子与分母和(差)的关系,再告诉分子或分母变化后的结果,求原分数。
”③因数分解类。
具体表现为“已知最简真分数的分子与分母的积,求原分数的可能值。
” ④中间分数计算类。
具体表现为“已知某分数在两个分数之间,求该分数的分子与分母的和的最小值。
”……精 典 例 题例1:一个分数约分后是37,若约分前分子与分母的和是40,那么约分前的分数是多少?思路 点 拨想一想:约分后是37 ,你可以想到什么你有几种方法来解答这个问题(友情提示:从方程与算术两个角度来思考。
)模 仿 练 习一个分数的分子与分母和是40,约分后是35,那么这个分数原来是多少例2:一个分数的分子与分母的和是19,加上这个分数的分数单位就是14 ,这个分数是多少(2006年成都外国语学校奖学金考试数学试题)3/16思路 点 拨想一想:加上这个分数的分数单位实际是分数中谁发生了变化想明白后,再结合例1方法来思考一下,相信你能自己解答的!模 仿 练 习一个分数的分子与分母之和是37,若分子减去1,分数值是12 ,原分数是多少(2007年成都外国语学校小语种数学试卷)例3:分子、分母相乘的积是2002的最简真分数共有多少个(2005年成都七中育才东区衔接班招生考试题)思 路 点 拨想一想:满足什么条件的分数才是最简真分数再想一想对“分子、分母相乘的积是2002”的信息又应该怎样去理解模 仿 练 习一个最简真分数,分子与分母的积是24,这个真分数是多少(成都外国语学校2011年“德瑞杯”知识竞赛数学试题)学以 致 用A 级1.一个分数分子与分母的和是72,约分后是27 ,这个原分数是多少(2005年成都七中育才东区衔接班招生考试题)2.将分数711 的分子增加77后,如果要求分数的大小不变,分母应变为多少(2010年成都七中嘉祥外国语学校6年级衔接班试题2)3.一个分数,分子、分母的和是2010,约成最简分数后是760,这个分数是多少(嘉祥外国语学校2011年5升6招生数学试题)B 级4.某分数分子分母的和为23,若分母增加17,此分数值为14 ,原分数为多少(成都实验外国语学校“德瑞教育发展基金会”2010年奖学金测试数学A 卷) 5.分子与分母的乘积是156的最简真分数有多少个(2008年成都嘉祥外国语衔接班招生考试题2)6. 一个分数,分子与分母的和是75,若分子加上3,则可约简成58 ,原来的分数是多少? (2007年成都七中育才东区衔接班招生考试题2)C 级7.m,n 为自然数,若34 <n m <45 ,则m+n 的最小值是多少(2007年成都七中育才东区衔接班招生考试题2)第 二 讲 分 数 计 算 中 的 拆 分)()())(()()()(103219321104321321432121321121+⋯+++⨯+⋯+++-⋯-+++++-++⨯+-+⨯-知 识 导 航分数计算中的拆分,又叫裂项计算。
【数学】初二年奖学金考试数学考卷

【数学】初二年奖学金考试数学考卷一、选择题(每题1分,共5分)1. 已知两个数相乘,其中一个数为5,另一个数为未知数x,那么x的值为:A. 5B. 1C. 2D. 10答案:A2. 一个三角形的两边之和等于第三边,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 任意三角形答案:D3. 已知一个等差数列的前两项分别为3和5,那么这个等差数列的公差是:A. 2B. 3C. 4D. 5答案:B4. 一个圆的直径为10cm,那么这个圆的周长是:A. 10π cmB. 20cmC. 20π cmD. 50cm答案:C5. 已知一个二次函数的图像是一个开口向上的抛物线,那么这个二次函数的系数a是:A. 负数B. 正数C. 0D. 无法确定答案:B二、判断题(每题1分,共5分)1. 一个数的平方根有两个值,一个是正数,另一个是负数。
()答案:×2. 一个三角形的内角和等于180度。
()答案:√3. 一个等差数列的前三项分别为2、4、6,那么这个等差数列的公差是2。
()答案:√4. 一个圆的直径是半径的两倍。
()答案:√5. 一个二次函数的图像是一个开口向下的抛物线,那么这个二次函数的系数a是负数。
()答案:√三、填空题(每题1分,共5分)1. 三角形内角和的公式是180°。
答案:180°2. 圆的周长公式是C = πd 或C = 2πr。
答案:C = πd 或C = 2πr3. 勾股定理表达式是 a^2 + b^2 = c^2。
答案:a^2 + b^2 = c^24. 函数 f(x) = ax^2 + bx + c 的顶点坐标是 (b/2a, c b^2/4a)。
答案:(b/2a, c b^2/4a)5. 直线 l 的方程是 y = mx + b。
答案:y = mx + b四、简答题(每题2分,共10分)1. 简述三角形的内角和公式。
答案:三角形内角和的公式是180°。
【数学】初二年奖学金考试数学考卷

专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数是质数?()A. 21B. 39C. 41D. 672. 已知一个等差数列的首项为3,公差为2,则第五项为()A. 7B. 9C. 11D. 133. 下列哪个图形是平行四边形?()A. 矩形B. 梯形C. 正方形D. 三角形4. 下列哪个单位是面积单位?()A. 米B. 平方米C. 立方米D. 千克5. 已知a=3,b=4,则a²+b²的值为()A. 7B. 12C. 25D. 9二、判断题(每题1分,共5分)1. 1的倒数是1。
()2. 0是自然数。
()3. 两条平行线之间的距离处处相等。
()4. 等腰梯形的两个底角相等。
()5. 相似三角形的面积比等于边长比的平方。
()三、填空题(每题1分,共5分)1. 已知一个正方形的边长为a,则它的面积为______。
2. 2的平方根是______。
3. 已知一个等差数列的首项为5,公差为3,则第四项为______。
4. 下列数中,______是最小的合数。
5. 一条直线的斜率为2,它在y轴上的截距为3,则该直线的方程为______。
四、简答题(每题2分,共10分)1. 简述等差数列的定义及通项公式。
2. 请写出勾股定理的内容。
3. 什么是三角形的外心?4. 请举例说明两种不同的概率求解方法。
5. 简述平行线的性质。
五、应用题(每题2分,共10分)1. 小明家离学校3公里,他以每小时4公里的速度步行去学校,需要多长时间?2. 某商店举行打折活动,原价120元的商品打8折,现价是多少?3. 一个长方形的长是10厘米,宽是6厘米,求它的面积。
4. 某班有50名学生,其中男生占60%,女生有多少人?5. 一个数加上60后乘以2,再减去30,结果为150,求这个数。
六、分析题(每题5分,共10分)1. 已知一个等差数列的前三项分别为2,5,8,求该数列的通项公式,并求出第10项的值。
2010年高等数学参考答案及评分标准

《高等数学》参考答案及评分标准一、选择题:(每小题3分,共15分)1B ,2A ,3D ,4C ,5C二、填空题:(每小题3分,共15分)1、118- 2、5,3⎡⎫+∞⎪⎢⎣⎭31)x + 4、24231x y z --==- 5、2sec 304()d f r rdr πθπθ⎰⎰ 三、计算题(要求写出主要计算步骤及结果,每小题7分,共91分)1、1x →2、tan 01lim ()x x x +→解:1x →解:原式0ln lim cot x x x e +→-=……2分1x →=……3分 201lim csc x x x e +→--= ………4分x →=………5分 20sin lim x x x e +→= ………6分 12= …………………………7分 01e == ………7分3、设2ln y x x = ,求y ''.解: 212ln y x x x x'=+⋅………………3分 2ln x x x =+ …………………4分12ln 21y x x x''=+⋅+ …………6分 2ln 3x =+ …………7分4、求由方程x y xy e +=所确定的隐函数()y y x =的微分dy .解: 方程两边分别对x 求导,得:………………………1分(1)x y dy dy y xe dx dx++=+……………………………4分 于是 x y x y dy e y dx x e ++-=- ……………………………5分所以 x y x ye y dy dx x e ++-=- ………………………7分 5、求由参数方程(1sin )cos x t t y t t=-⎧⎨=⎩所确定的函数的导数dy dx . 解: dydy dt dx dxdt= ……………………3分 cos (sin )(1sin )(cos )t t t t t t +-=-+- …………………6分 cos sin 1sin cos t t t t t t-=--…………………………7分 6、求函数(,)x y w f y z=(其中f 具有一阶连续偏导数)的一阶偏导数. 解: 1()x w y f x x∂∂'=⋅∂∂ ……………………………2分 11f y'= ………………………………………3分 12()()x y w y z f f y y y∂∂∂''=⋅+⋅∂∂∂……………………4分 1221x f f y z''=-+……………………………5分 2()y w z f z z∂∂'=⋅∂∂ ……………………………6分 22y f z'=- ……………………………………7分7、求函数y x z e =的全微分dz . 解:2()y x z y e x x ∂=⋅-∂……2分 , 1yx z e y x ∂=⋅∂……4分 z z dz dx dy x y∂∂=+∂∂ …………………………………6分 21()yx y e dx dy x x=-+ ………………………7分8、计算反常积分20x xe dx +∞-⎰ 9、已知2sec x 是()f x 的一个原函数,求()xf x dx ⎰. 解:20x xe dx +∞-⎰ 解:原式2sec xd x =⎰ …………2分2201()2x e d x +∞-=--⎰……3分 22sec sec x x xdx =-⎰…5分 2012x e +∞-=- …………6分 2sec tan x x x C =-+……7分 12= ……………………7分10、计算二重积分cos()D x x y dxdy +⎰⎰,其中D 是顶点分别为(0,0),(,0),(,)πππ的三角形闭区域.解:区域D 可表示为:00x y x π≤≤⎧⎨≤≤⎩ ………………3分 00cos()cos()xD x x y dxdy xdx x y dy π+=+⎰⎰⎰⎰ ………………4分 0(sin 2sin )x x x dx π=-⎰ ………………6分32π=- . ………………7分11、计算曲线积分22()(sin )L x y dx x y dy --+⎰,其中L是圆周y =自点(0,0)到(1,1)的一段弧.解: 22(,),(,)sin P x y x y Q x y x y =-=--…………………1分因为1Q P x y∂∂=-=∂∂,所以该曲线积分与路径无关;……2分 取从(0,0)O 经过(1,0)A 到(1,1)B 的折线段积分 ……3分 原式112200(sin )x dx x y dy =+--⎰⎰ ………5分 1021cos 232y dy -=--⎰ …………6分sin 2746=- …………7分 12、求幂级数2012n n n n x ∞=+∑的收敛域.解: 22211()22lim lim ()2(1)2nn n n n n n n x u x n x u x n x +++→∞→∞+=⋅=+ …………2分 当 212x <,即x <时,幂级数绝对收敛 ……4分 当x =2001((1)2n n n n n n ∞∞==+=+∑∑发散……6分所以该幂级数的收敛域为(. …………7分13、将函数21()(2)f x x =-展开为x 的幂级数,并指出收敛区间. 解: 1112212x x =⋅-- ………1分 1001()222nn n n n x x ∞∞+====∑∑ …………3分 逐项求导得: 12111(2)2n n n nx x -∞+==-∑ …………5分 由12x <得收敛区间为(2,2)- …………7分 四、综合题与应用题(本大题共3个小题,共29分)1、 求微分方程369(1)xy y y x e '''-+=+的通解. (10分)解:先求对应的齐次方程的通解Y由2690r r -+=,得123r r == ………2分于是,对应的齐次方程的通解为3312x x Y C e C xe =+ ………4分 3λ=是特征方程的二重根∴设原方程的特解为23()x y x ax b e *=+ ………6分代入原方程得:621ax b x +=+ ………7分 比较同类项的系数,解得:11,62a b == ………8分所以原方程的通解为:333231211()62x x x y C e C xe x x e =+++ ………10分 2、求曲线22,y x x y ==所围成的平面图形绕y 轴旋转一周所成的旋转体体积.(10分) 解:取y 作积分变量, 01y ≤≤ …………2分体积元素222()]dv y dy π=- …………5分140()V y y dy π=-⎰ …………8分12501132510y y ππ⎡⎤=-=⎢⎥⎣⎦ …………10分 3、设函数()y f x =由微分方程120x xy y x y ='+=⎧⎨=⎩所确定,(1)求函数()f x 的表达式。
2010年小学毕业测试数学试卷参考答案

2010年小学毕业测试数学试卷参考答案一、填空题1、52000803100,五百二十亿零八十万三千一百,520.008031亿,520亿。
2、.476647,或657 3、b a b a b a :==÷ 4、 b d ac ÷-=)( 5、5451, 6、3:4 ,43或0.75 7、25 8、反,正9、2,3,7 10、22785041a a .或π 11、9,64,37.5% 12、10二、选择题1、③2、②④3、①4、③5、② 三、判断题1、×2、√3、×4、√5、√ 四、计算1、直接写出得数109;21;1.9;32;90;3;90;2,600;0.15;160,16000002、解方程,求未知数x3、用简便方法计算。
).( ).(41)( %分分分504050101104121102521===-=-x x x x x x )( )1( 分分115135913554===+x x x x 分)分)=分)0.5( 0.5( 52 ( 158345243524315314353431=⨯=÷=-==-x x x x x x 分))(或分)(分)(分)(0.5536( 0.5 0.565 0.5 ::51756665669326596532=⨯=÷==⨯==x x x x x x分)(=-=分)(-=分))(-(=0.554455555000.555100551110055 ⨯⨯⨯9955五、只列式不计算1、3560÷⨯或设甲数为x ,则3560::=x2、h r h r V 22331ππ=⨯=六、解决实际问题1、⑴比例尺是 1:10×1000×100=1:1000000⑵要求不需太严格,图上距离量在4~ 5厘米范围内皆可。
在算实际直线距离时,可以有多种方法,结果在4×10=40(千米)到5×10=50(千米)范围内皆可。
2010数学真题卷及答案
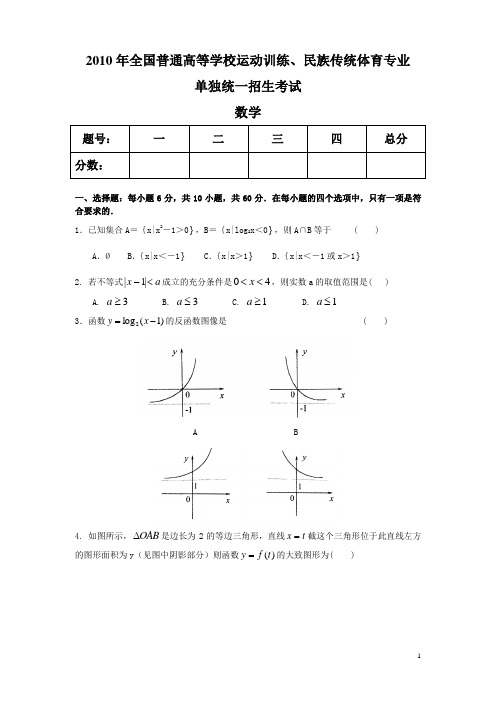
2010年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学一、选择题:每小题6分,共10小题,共60分.在每小题的四个选项中,只有一项是符合要求的.1.已知集合A ={x|x 2―1>0},B ={x|log 2x <0},则A ∩B 等于 ( )A .ØB .{x|x <-1}C .{x|x >1}D .{x|x <-1或x >1}2. 若不等式||x a -<1成立的充分条件是04<<x ,则实数a 的取值范围是( ) A. a ≥3B. a ≤3C. a ≥1D. a ≤13.函数)1(log 2-=x y 的反函数图像是 ( )A B4. 如图所示,∆OAB 是边长为2的等边三角形,直线x t =截这个三角形位于此直线左方的图形面积为y (见图中阴影部分)则函数y f t =()的大致图形为( )5.已知a 、b 是非零向量且满足(a -2b )⊥a ,(b -2a )⊥b ,则a 与b 的夹角是( )A .6π B .3π C .32π D .65π6椭圆22143x y +=的右焦点到直线y x =的距离是 ( )A.127. 过圆锥曲线C 的一个焦点F 的直线l 交曲线C 于A 、B 两点,且以AB 为直径的圆与F 相应的准线相交,则曲线C 为A. 双曲线B. 抛物线C. 椭圆D. 以上都有可能 8.若αααααcos sin cos 3sin ,2tan +-=则的值是( )A .31-B .-35C .31 D .35 9.直线052)3(057)3()1(2=-+-=-+-++y x m m y m x m 与直线垂直的充要条件是( )A .2-=mB .3=mC .31=-=m m 或D .23-==m m 或10.已知1(2)2x f x x ++=+,则1(2)f x -+= ( ) A.12x x -+ B.11x -+ C.211x x +-- D.21x x +-+二、填空题:每小题5分,共8小题,共计40分.将答案填在题中的横线上。
成都外国语学校2010年“德瑞杯”知识竞赛数学试卷-S版

成都外国语学校2010年“德瑞杯”知识竞赛数学试卷(100分钟完卷)一、 判断。
10分1. 1/2006是无限循环小数。
( )2. 大于0的任何数乘以一个分数都比原来的数小。
( ) 3. 两个整数的最小公倍数与最大公约数之积等于这两个数之积。
( ) 4. 一个正方形只有两条对称轴。
( ) 5. 两个三角形的周长不同,面积就一定不同。
( ) 二、 选择。
15分1. 如果3432÷=⨯b a ,那么a 和b 的大小关系为( ) A a >b B a <b C a 不小于b2.同样周长的圆、正方形、长方形中,面积最大的是( ) A 圆 B 正方形 C 长方形3.用三刀最多可把一个正方体蛋糕切成( ) A 6块 B 7块 C 8块4.从早晨6时整到次日早晨6时整,一个时钟的时针和分针将重合( ) A 22次 B 23次 C 24次 1 1 1 15.—— + —— + —— + …… + ————( ) 1×3 3×5 5×7 99×101A 大于0.5B 等于0.5C 小于0.5 三、填空。
30分1.一个大于10的整数除以5余1,除以7余1,这个整数最小为 。
2.一个等腰直角三角形的面积是100平方厘米,这个三角形最长边等于 3.61< ()3 < 112(括号里填整数) 4.将6个“优秀少先队员”的名额分给六年级一、二、三班,每个班至少1个名额,共有 种不同分法。
5.一个三角形三边长度之比分别为2:3:4,则相应的三条高之比分别为 。
6.小明和爸爸到电器商场买一种家用电器,发现甲品牌售价1200元,使用中,每小时用电0.5度,使用寿命5000小时;而乙品牌售价1300元,使用中,每小时用电0.4度,使用寿命5000小时。
每度电价格为0.4元,在相同的使用寿命期限内,你认为小明爸爸买 种品牌电器最省钱。
7.31减去41的21的差等于 。
“德瑞教育发展基金会”2010年奖学金测试数学试题

17、直角三角形的两直角边的长都是整厘米数,面积为 59.5 平方厘米.每次取四个同样的三角形围 成(不重叠,不剪裁)含有两个正方形图案的图形(如图),在围成的所有正方形图案中,最小的 正方形的面积是_____平方厘米. 18、一辆公共汽车由起点站到终点站(这两站在内)共途经 8 个车站.已知前 6 个车站共上车 100 人, 除终点站外前面各站共下车 80 人,则从前六站上车而在终点站下车的乘客共有____人. 四、计算下列各题,能用简便方法的用简便方法,要求写出主要步骤(每小题 5 分,共 30 分) 得分____________ 19、1.25? 17.6 阅卷人____________ 20、3-5+7-9+11-13+…+2007-2009+2011;
29、一天,师、徒二人接到一项加工零件的任务,先由师傅单独做 6 小时,剩下的任务由徒弟单独 做,4 小时做完.第二天,他们又接到一项加工任务,工作量是第一天接受任务的 2 倍.这项任务 先由师、徒二人合做 10 小时,剩下的全部由徒弟做完.已知徒弟的工作效率是师傅的 二天比徒弟多做 32 个零件.问: (1)第二天徒弟一共做了多少小时;(2)师徒二人两天共加工零件多少个.
2 2
2
1 100% = 25% 10
4 ,说明师傅四小时所加工的工作量等于徒弟五小时所加工的工作量. 5
5/4
这样,第一天加工零件总数,由师傅单独加工需要 6+4×
4 1 =9 (小时)完成;由徒弟单独加工需 5 5
要 6×1
1 1 +4=11 (小时)完成.假设第一天加工零件总数为单位“1”,可知第二天徒弟加工时间 2 4
36.1? 0.8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
600+500+300=1400
26. 解:跑一圈时:560÷(8+6)×2=80(秒) 以 8 米/秒的速度跑完半程用时: 280÷8=35 ( 秒 ) ∴跑完后半程用时: 80-35=45 (秒 ) 27、解:连 BD,设 BE 与 CD 交于点 H.则 S△BDG=S△BDE ∴S△BDG-S△BDH=S△BDE-S△BDH 即 S△DHG=S△BEH ∴S 阴=S△BEG=
26、小刚在 560 米的环形跑道上跑了一圈,前半时每秒跑 8 米,后半时每秒跑 6 米.小刚跑 后半程用了多少秒?
27、 如图, 是大小两个正方形组成的图形, 大正方形边长是 8 厘米, 小正方形边长为 6 厘米 ,
D
8
C G F
3
6
求阴影部分的面积.
28、某钟表,在 4 月 26 日零点比标准时间慢 6 分钟,它按此速度走到 5 月 3 日 8 时,比标 准时间快 4 分钟.这只表所指时间恰好为正确的时刻是几月几日几时几分?
1 2 × 6 = 18cm 2 2
28、解:7×24+8=176(小时)
5
176 ×
6 = 105.6 (小时) 6+4
105.6÷24=4.4(天) 0.4×24=9.6(小时) 0.6×60=36(分) ∴是 5 月 1 日 9 时 36 分. 29.解:设乙速为 xm / s ,则甲速为 3 xm / s ,车速为 30 xm / s ① 若开始甲乙同向,则后来甲乙相向 ∴ 50(30 x − x ) = ( x + 3 x ) • t
2 千米/时 3
C、675 千米/时
D、650 千米/时
9、现在弟弟的年龄是哥哥的一半,而 3 年前弟弟的年龄是哥哥的
1 ,则弟弟今年的岁数为 3
------------------------------------------------------------------------- ( ) A、6 B、15 C、12 D、9 10、有两个圆柱形水桶,甲桶比乙桶高 2 倍,而乙桶的直径是甲桶的 2 倍,则甲乙两桶容积 大的是谁?比另一桶大多少倍?---------------------------------------------( ) A、甲 ,
t =362.5(秒)
② 若经过身旁时,甲乙背向,则 50(30 x + x ) = (3 x − x )t
t =775(秒)
30.解:设一个出水管 1 小时排水量为“1”份, 则 9 根出水管 2 小时排水:9×3=18(份) 5 根出水管 6 小时排水:5×6=30(份) 6-2=4 小时 ∴4 小时内进水管进的水:30-18=12(份) ∴进水管每小时进水:12÷4=3(份) ∴池中原有水:18-3×2=12(份) 4 小时内,池中原有水加上进水管放入的水:12+4×3=24(份) 同时打开出水管的根数:24÷4=6(根)
2 3 + 4 3 + 6 3 + 8 3 + ...... + 30 3 =
和相等.
五、解答题﹙每小题 6 分,共 36 分﹚ 得分 25、实外初一年级四个班为希望工程捐款.一班捐了总数的 阅卷人
2 ,二班捐了 600 元,三班是一 、 7
二班总和的一半,四班捐了 500 元.问四个班共捐了多少元?
4 2 16 16 25 , , , ,1 , ( 67 15 53 23 39
) .若这个 13 7
22、一个三位数,被 43 除余 27,被 42 除余 5.那么,这个三位数是 数是四位数,则最小的四位数是 . 23﹑若 13 + 2 3 + 33 + 4 3 + ....... + 15 3 = 14400 ,则 . 24﹑如右上图,填方阵图,使每行、每列和对角线上三个数之 5 9
答案:一、﹙1﹚1.6 ;﹙2﹚
13 60
;﹙3﹚
1 2
;﹙4﹚5 ; ﹙5﹚
6 11
;﹙6﹚0.4
4
二、7.A
8.B
9.A10.BFra bibliotek11.B
三、计算 12.原式=371(539+248+213)=371000 13.原式=2009×2010×100010001-2010×2009×1000110001=0 14.
有盐水( )克. A、 480 B、360 C、300 D、440 8、甲乙两地相距 1500 千米.飞机从甲地到乙地是顺风,需 2 小时.从乙地返回甲地需 2.5 小时,则飞机往返的平均速度为 ------------------------------------------ ( ) A、700 千米/时 B、 666
﹙15﹚
﹙
1 1 1 1 1 1 1 1 1 1 1 1 + + ﹚﹙ + + ﹚—﹙ + + + ﹚﹙ + ﹚ 11 21 31 21 31 41 11 21 31 41 21 31
﹙16﹚
1 1 1 1 1 1 + + + + + 4 28 70 130 208 304
﹙17﹚
2010 −
3 5 9 17 33 65 129 257 − − − − − − − 2 4 8 16 32 64 128 256
阅卷人
(3)
3 ⎛ 1⎞ ÷ ⎜1 ⎟ = 4 ⎝ 2⎠ 1+ 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 +1 = 66
7、一个玻璃瓶内原有盐水,盐是水的
(4)
(5)
(6)
二、选择题﹙选择唯一正确答案,每小题 3 分,共 15 分﹚得分
1 1 ,加入 15 克盐后,盐占盐水的 ,瓶内原 11 9
2007 + 2006 × 2008 2007 + 2006 × 2008 2007 + 2006 × 2008 = = =1 2007 × 2008 − 1 (2006 + 1) × 2008 − 1 2006 × 2008 + 2007 1 451 1 1 1 1 1 1 1⎛ 1⎞ 6 + + + + + = ⎜1 − ⎟ = 1 × 4 4 × 7 7 × 10 10 × 13 13 × 16 16 × 19 3 ⎝ 19 ⎠ 19 1 1 1 1 1 1 1 1 1 + + + + + + + ﹚= 2001 2 4 8 16 32 64 128 256 256
29、 有甲乙二人, 乙在路上一直朝前行走, 甲乘车在同一条直路上经过乙的身旁.50 秒钟后 , 甲下车向乙走去.甲行走的速度比车慢 90%,但甲行走的速度是乙行走速度的 3 倍.问甲下车 后需多长的时间能和乙在一起?
30、有一蓄水池装有 10 根水管,其中一根为进水管,其余 9 根为相同的出水管.进水管以均 匀的速度不停地注水,到一定水位时,有人想打开出水管,使池内的水全部排完.如果把 9 根出水管全部打开,需 2 小时把池内的水排光.如果只打开 5 根出水管,需 6 小时把池内的 水排光.若要想 4 小时把水排光,至少需同时打开几根出水管?
2
四、填空题﹙每小题 3 分,共 21 分﹚
得分
阅卷人
18、 某分数, 分子分母之和为 23, 若把分母增加 17, 此分数值为
1 , 则原分数为 4
.
19、四个连续自然数的积是 24024,那么这四个自然数的和为 . 20、一根竹笋从发芽到长大,如果每天的高度是前一天的一倍,经过 6 天长到 2 米.则当它 长到 2.5 分米时,经过了 天. 21、按规律在括号内填上适当的数:
﹙20﹚3 ﹙21﹚ ﹙24﹚ 5 19 9 15 11 7 13 3 17
∴原式=1+1+1=3 15.
16. 原式=
17. 原式=2010-8-﹙ 四、 ﹙18﹚
8 15
﹙19﹚50
128 =4 32
﹙22﹚887,2693
﹙23﹚115200
五、 25. 解:
2 1 1 × = 7 2 7 1 600 × = 300 2 ⎛1 2⎞ 1400 ÷ ⎜ + ⎟ = 2450 (元) ⎝7 7⎠
﹙13﹚ 2009×201020102010-2010×200920092009
1
﹙14﹚
2007 + 2006 × 2008 2008 + 2007 × 2009 2009 + 2008 × 2010 + + 2007 × 2008 − 1 2008 × 2009 − 1 2009 × 2010 − 1
1 4
B、乙,
1 3
C、乙, 1
D、甲 ,
1 3
)
11、有四个自然数,任三个数相加,其和分别为 24,30,33,36.那么这四个数的和为( A、40 B、41 C、42 D、43 三、计算(每小题 5 分,共 30 分.要求写出主要步骤) 得分 阅卷人 ﹙12﹚ 371×539+248000×0.371+2130×37.1
6
“德瑞教育发展基金会” 2010 年奖学金测试 数学卷
测试时间:90 分钟 题号 得分 一、直接写得数﹙每小题 3 分,共 18 分﹚得分 (1) 1.28+32%= (2) 阅卷人 一 二 三 四 总分:120 分 五 总分 总分人
4 7 − = 5 12 ⎛1 1 1⎞ ⎜ + − ⎟ × 12 = ⎝3 4 6⎠ ̇ − 0.6 = 0.9
