2015-2016年河南省漯河市召陵区八年级(上)数学期中试卷及参考答案
河南省漯河市八年级上学期数学期中考试试卷
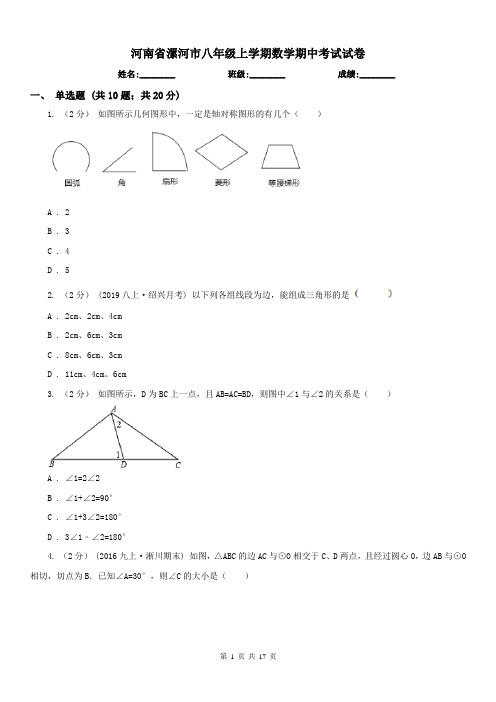
河南省漯河市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)如图所示几何图形中,一定是轴对称图形的有几个()A . 2B . 3C . 4D . 52. (2分) (2019八上·绍兴月考) 以下列各组线段为边,能组成三角形的是A . 2cm、2cm、4cmB . 2cm、6cm、3cmC . 8cm、6cm、3cmD . 11cm、4cm、6cm3. (2分)如图所示,D为BC上一点,且AB=AC=BD,则图中∠1与∠2的关系是()A . ∠1=2∠2B . ∠1+∠2=90°C . ∠1+3∠2=180°D . 3∠1﹣∠2=180°4. (2分) (2016九上·淅川期末) 如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O 相切,切点为B.已知∠A=30°,则∠C的大小是()A . 30°B . 45°C . 60°D . 40°5. (2分) (2018八上·泗阳期中) 用直尺和圆规作一角的平分线的依据是()A . SSSB . SASC . ASAD . AAS6. (2分)如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是()A . AB=ACB . ∠BAC=90°C . BD=ACD . ∠B=45°7. (2分)(2019·遵义模拟) 如图,点P是四边形ABCD内的一点,AP平分∠DAB,BP平分∠ABC,设∠C+∠D 的大小为x,∠P的大小为y,则x,y的关系是()A .B .C .D .8. (2分) (2019八上·渝中期中) 下面是作角等于已知角的尺规作图过程,要说明∠A′O′B′=∠AOB,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是()A . 边边边B . 边角边C . 角边角D . 角角边9. (2分)如图,在△ABC中,已知AB=AC,DE垂直平分AC,且AC=8,BC=6,则△BDC的周长为()A . 20B . 22C . 10D . 1410. (2分)(2018·龙东模拟) 如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DAE,其中结论正确的个数有()A . 1个B . 2个C . 3个D . 4个二、填空题 (共10题;共10分)11. (1分)一个三角形的三边长分别为4、8、x,那么x的取值范围是________.12. (1分)一个正常的人能活1 000 000分钟吗?答:________ (填“能”或“不能”)13. (1分)如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为________ 度(用关于α的代数式表示).14. (1分)如图,△ABC≌△ADE,∠EAC=25°,则∠BAD=________15. (1分)(2017·河东模拟) 如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF= AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有________条.16. (1分) (2016八上·西昌期末) △ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于D,△ABC的面积18,AB=6,AC=8,OD=2,则BC的长是________.17. (1分) (2018八上·天台期中) 若一个多边形每个内角为140°,则这个多边形的边数是________.18. (1分) (2017八下·富顺竞赛) 如图,已知 ,则的度数是 ________ .19. (1分)(2017·姑苏模拟) 如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.20. (1分)(2020·北京模拟) 在中,,,点在边上,连接,若为直角三角形,则的度数为________度.三、解答题 (共7题;共41分)21. (5分) (2018八上·嵊州期末) 在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC (顶点是网格线交点的三角形)的顶点A,B的坐标分别是(﹣6,7),(﹣4,3).(1)请你根据题意在图中的网格平面内作出平面直角坐标系.(2)请画出△ABC关于y轴对称的△A1B1C122. (5分)如图,一个三角形的纸片ABC ,其中∠A=∠C .①把△ABC纸片按(如图1)所示折叠,使点A落在BC边上的点F处,DE是折痕.说明BC//DF;________②把△ABC纸片沿DE折叠,当点A落在四边形BCED内时(如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;________③当点A落在四边形BCED外时(如图3),∠C与∠1、∠2的关系是________.(直接写出结论)23. (5分)(2019·北京模拟) 对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB=∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.(1)当⊙O的半径为1时①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是________;②点T在直线y=﹣ x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;(2)⊙C的圆心在x轴上,半径为1,直线y=﹣2x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,请求出圆心C的横坐标n的取值范围.24. (5分)如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,FG⊥BC 于G,请猜测AE与FG之间有怎样的数量关系,并说明理由.25. (5分) (2019九上·淅川期末) 观察发现:如图(1),⊙O是△ADC的外接圆,点B是边CD上的一点,且△ABC是等边三角形.OD与AB交于点E,以O为圆心、OE为半径的圆交AB于点F,连接CF、OF.(1)求∠AOD的度数;(2)线段AE、CF有何大小关系?证明你的猜想.拓展应用:如图(2),△HJI是等边三角形,点K是IH延长线上的一点.点O是△JKI的外接圆圆心,OK与JH相交于点E.如果等边三角形△JHI的边长为2,请直接写出JE的最小值和此时∠JEO的度数.26. (5分)已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.(1)如图1,当点P与点G分别在线段BC与线段AD上时.①求证:DG=2PC;②求证:四边形PEFD是菱形;(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.27. (11分) (2019九上·西城期中) 在Rt△ABC中,∠ACB=90°,AC=BC,CD为AB边上的中线.在Rt△AEF 中,∠AEF=90°,AE=EF,AF<AC.连接BF,M,N分别为线段AF,BF的中点,连接MN.(1)如图1,点F在△ABC内,求证:CD=MN;(2)如图2,点F在△ABC外,依题意补全图2,连接CN,EN,判断CN与EN的数量关系与位置关系,并加以证明;(3)将图1中的△AEF绕点A旋转,若AC=a,AF=b(b<a),直接写出EN的最大值与最小值.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7、答案:略8-1、9-1、10、答案:略二、填空题 (共10题;共10分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共7题;共41分)21-1、21-2、22-1、23-1、24-1、25-1、25-2、27-1、27-2、27-3、。
河南省漯河市召陵镇第二初级中学2015-2016学年八年级上学期期中考试(8套)(图片版)(河南省漯

八年级历史参考答案
1—5 BABAB 6—10 ADABC 11—15 DCABB 16—20 ADDBC
21.①为扭转对华贸易逆差,英国无耻地向中国走私鸦片。
鸦片的输入,已经严重危害了清朝的统治。
②道光皇帝。
③道光帝深受震动,任命林则徐为钦差大臣赴广东查禁鸦片。
④禁烟运动的措施有派人暗访密查,缉拿烟贩,收缴鸦片和虎门销烟22. (1)名称:甲午中日战争人物:邓世昌(2)原因:对中国进行掠夺理由:因发生战争的时间1894年是农历甲午年(分)(3)条约:《马关条约》影响:中国半殖民地化程度大大加深 23.(1)洋务运动。
目的:利用西方先进技术维护清朝统治或“师夷长技以自强”(2)作用客观上刺激了中国资本主义的发展,为中国的近代化开辟了道路,对外国经济势力的扩张也起到了一定抵制作用。
24.(1)五四爱国运动.(2)材料一中的口号最能说明五四爱国运动的性质.(3)曹汝霖、陆宗舆、章宗祥.(4)罢免了曹汝霖等卖国贼的职务;拒绝在对德和约上签字.25.(1)1927年8月1日;南昌起义。
(2)打响了武装反抗国民党反动统治的第一枪。
(3)1927年,蒋介石、汪精卫背叛革命,发动政变,疯狂屠杀革命者。
要推翻帝国主义和反动政权,必须要有革命的武装力量。
2015-2016学年八年级数学上册期中检测试卷参考答案及评分标准201510

12015—2016学年度第一学期期中检测八 年 级 数 学 试 题(友情提醒:全卷满分100分,考试时间90分钟,请你掌握好时间.)一、选择题(每小题3分,共30分)(请将正确答案序号填入以下表格相应的题号下,否则不得分)1. 下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为轴对称图形的是( ☆ )A .B .C .D .2. 以下列各组线段为边,能组成三角形的是( ☆ )A . 2cm ,3cm ,5cmB . 5cm ,6cm ,10cmC . 1cm ,1cm ,3cmD . 3cm ,4cm ,9cm3. 已知点M (a ,3),点N (2,b )关于y 轴对称,则(a+b )2015的值( ☆ )A .-3B . -1C .1D . 34. 如图1,∠B=∠D=90°,CB=CD ,∠1=30°,则∠2=( ☆ )A . 30°B . 40°C . 50°D . 60°5. 十二边形的外角和是( ☆ )A. 180°B. 360°C.1800 ° D2160°6. 已知等腰三角形一边长为4,一边的长为6,则等腰三角形的周长为( ☆)A .14 B . 16 C . 10 D . 14或16 7. 如图2,△ABC 中,AB=AC ,D 为BC 的中点,以下结论:(1)△ABD ≌△ACD ; (2)AD ⊥BC ;(3)∠B=∠C ; (4)AD 是△ABC 的角平分线.其中正确的有( ☆ ) A . 1个 B . 2个 C . 3个 D . 4个8. 已知△DEF ≌△ABC ,AB=AC ,且△ABC 的周长是23cm ,BC=4cm ,则△DEF 的边长中必有一边等于( ☆ )A . 9.5cmB . 9.5cm 或9cmC . 4cm 或9.5cmD . 9cm 9. 下列条件中,能判定△ABC ≌△DEF 的是( ☆ ) AC=,∠10. 如图3,BE 、CF 是△ABC 的角平分线,∠ABC=80°,∠ACB=60°,BE 、CF 相交于D ,则∠CDE 的度数是( ☆ )(图1)(图2)(图3)2A 、110°B 、70°C 、80°D 、75°二、填空题(每小题3分,共30分)11. 三角形的三边长分别为5,x ,8,则x 的取值范围是 .12. 已知如图4,△ABC ≌△FED ,且BC=DE ,∠A=30°,∠B=80°,则∠FDE= . 13. 如图5,则∠A+∠B+∠C+∠D+∠E+∠F 的度数为 .(图6)(图5)(图4)14. 如图6,已知AD 平分∠BAC ,要使△ABD ≌△ACD ,根据“AAS ”需要添加条件 _________ . 15. 如图7,在生活中,我们经常会看见在电线杆上拉两条钢线,来加固电线杆,这是利用了三角形的 .16. 如果一个多边形的每个内角都相等,且内角和为1800°,那么该多边形的一个外角 度. 17. 在直角坐标系中,如果点A 沿x 轴翻折后能够与点B (-1,4)重合,那么A ,B 两点之间的距离等于 .18. 如图8,在△ABC 中,AB =AC ,AF 是BC 边上的高,点E 、D 是AF 的三等分点,若△ABC 的面积为12cm 2,则图中全部阴影部分的面积是 ___cm 2.19. 如图9,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC= .20. 如图10,△ABC 和△FED 中,BD=EC ,∠B=∠E .当添加条件 时,就可得到△ABC ≌△FED ,依据是 (只需填写一个你认为正确的条件).三、解答题(共40分)21. (7分) 完成下列证明过程.如图11,已知AB ∥DE ,AB=DE ,D ,C 在AF 上,且AD =CF ,求证:△ABC ≌△DEF .证明: ∵ AB ∥DE∴∠_________=∠_________( )∵ AD=CF ∴AD+DC=CF+DC 即_____________ 在△ABC 和△DEF 中AB DCEF( 图11 )( 图10 )( 图9 )A( 图8 )E3AB=DE__________________________∴△ABC ≌△DEF ()22.(8分)如图12,四边形ABCD 中,E 点在AD 上,其中∠BAE =∠BCE =∠ACD =90°, 且BC =CE .请完整说明为何△ABC 与△DEC 全等的理由.23.(5分)如图13,已知△ABC 的三个顶点分别为A (2,3)、B (3,1)、C (-2,-2)。
河南省漯河市临颍县2015-2016学年八年级上学期期中考

2015-----2016学年上学期八年数学参考答案一、B D A D C B D C二、(9).17或19 (10).1800 (11).8㎝ (12).-4 (13).22.5 (14).1 (15).4 (16).2(17).15三、18.(1)证明过程正确.推理依据:①等边对等角.② AAS.③全等三角形的对应边相等.……3分(2)证明:连接AD,∵AB=AC,D是底边BC的中点,∴AD平分∠BAC(三线合一) .……………6分又∵DE⊥AB于E,DF⊥AC于F.∴DE=DF(角平分线上的点到角两边的距离相等).……………10分19.(1)AB=DC-----------------------------------1分∵BE=CF∴BE+EF=CF+FE即BF=CE---------------------------------2分在ABF和DCE中∠A=∠D∠B=∠CBF=CE∴ABF≌DCE(AAS)∴AB=DC(全等三角形对应边相等) -----------4分(2)CEF是等腰三角形 -----------------------6分∵ABF≌DCE∴∠AFE=∠DEC ----------------------------8分∴OE=CF(等角对等边)∴0EF是等腰三角形 ---------------------10分20.(1)△ACD≌△CBE ------------------------2分证明过程略----------------------6分(2)AD=CE=CD+DE=BE+DE=3+5=8 ---------------10分21.(1)“ASA”证全等………………5分;(2)∠ADE=10°………………10分。
22.(1)20°;……………2分(2)当DC=2时,△ABD≌△DCE.……………3分证明:∵∠ADE=40°,∠B=40°,又∵∠ADC=∠B+∠BAD ,∠ADC=∠ADE+∠EDC.∴∠BAD=∠EDC .……………5分在△ABD和△DCE中,∠B=∠C,AB=DC,∠BAD=∠EDC .∴△ABD≌△DCE.……………8分(3)当∠BAD= 30°时,DA=DE,这时△ADE为等腰三角形;……………10分当∠BAD= 60°时,EA=ED,这时△ADE为等腰三角形.……………12分。
2015-2016年河南省漯河市召陵区八年级(上)期末数学试卷含参考答案

2015-2016学年河南省漯河市召陵区八年级(上)期末数学试卷一、选择题(本题共8小题,每小题3分,共24分)1.(3分)下列关系成立的是()A.a0=1B.a3n÷a n=a3C.(﹣a)3÷(﹣a2)=a D.a+a n﹣1=a n2.(3分)把a2﹣4a多项式分解因式,结果正确的是()A.a(a﹣4)B.(a+2)(a﹣2)C.a(a+2)(a﹣2)D.(a﹣2)2﹣43.(3分)下列等式成立的是()A.(﹣3)﹣2=﹣9B.(﹣3)﹣2=C.a﹣2×b﹣2=a2×b2D.4.(3分)在△ABC和△FED中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件()A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F 5.(3分)化简的结果是()A.B.a C.D.6.(3分)甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是()A.B.C.D.7.(3分)把14cm长的铁丝截成三段,围成不是等边三角形的三角形,并且使三边均为整数,那么()A.有1种截法B.有2种截法C.有3种截法D.有4种截法8.(3分)把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是()A.B.C.D.二、填空题(本题共10小题,每小题3分,共21分)9.(3分)把0.0000007用科学记数法表示为.10.(3分)多项式4x2﹣12x2y+12x3y2分解因式时,应提取的公因式是.11.(3分)若9n=38,则n=.12.(3分)当x=时,分式值为零.13.(3分)若多项式x2+ax+b分解因式的结果为(x+1)(x﹣5),则a+b的值为.14.(3分)已知,则代数式的值为.15.(3分)如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=3cm,则AC=cm.16.(3分)如图,CP、BP分别平分△ABC的外角∠ECB,∠DBC,若∠A=50°,那么∠P=.17.(3分)某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x套,则根据题意可得方程为.18.(3分)李明同学从家到学校的速度是每小时a千米,沿原路从学校返回家(用的速度是每小时b千米,则李明同学来回的平均速度是千米/小时.含a,b的式子表示)三、解答题(本题共7小题,共66分)19.(12分)用乘法公式计算:(1)(2﹣3x)2﹣(3x+2)2(2)(2x+y+z)(2x﹣y﹣z)20.(7分)解方程:﹣=.21.(7分)先化简,再求值:(a﹣3﹣)÷,其中a=﹣2.22.(8分)已知a,b为实数,且ab=1,M=+,N=+,试确定M、N的大小关系.23.(9分)如图,给出五个等量关系:①AD=BC ②AC=BD ③CE=DE ④∠D=∠C ⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.24.(10分)某次地震后,政府为安置灾民,准备从某厂调拨用于搭建板房的板材5600m2和铝材2210m,该厂现有板材4600m2和铝材810m,不足部分计划安排110人进行生产,若每人每天能生产板材50m2或铝材30m,则应分别安排多少人生产板材和铝材,才能确保同时完成各自的生产任务?25.(13分)如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.(1)点D在边AB上时,试探究线段BD,AB和AF的数量关系,并证明你的结论;(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.2015-2016学年河南省漯河市召陵区八年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共8小题,每小题3分,共24分)1.(3分)下列关系成立的是()A.a0=1B.a3n÷a n=a3C.(﹣a)3÷(﹣a2)=a D.a+a n﹣1=a n【分析】分别根据0指数幂的运算法则、同底数幂的除法法则对各选项进行逐一判断即可.【解答】解:A、当a=0时,a0无意义,故本选项错误;B、a3n÷a n=a2n,故本选项错误;C、(﹣a)3÷(﹣a2)=a,故本选项正确;D、a与a n﹣1不是同类项,不能合并,故本选项错误.故选:C.2.(3分)把a2﹣4a多项式分解因式,结果正确的是()A.a(a﹣4)B.(a+2)(a﹣2)C.a(a+2)(a﹣2)D.(a﹣2)2﹣4【分析】直接提取公因式a即可.【解答】解:a2﹣4a=a(a﹣4),故选:A.3.(3分)下列等式成立的是()A.(﹣3)﹣2=﹣9B.(﹣3)﹣2=C.a﹣2×b﹣2=a2×b2D.【分析】分别根据负整数指数幂、分式的基本性质分别进行计算.【解答】解:A、错误,(﹣3)﹣2=;B、正确;C、错误,a﹣2×b﹣2=;D、错误,.故选:B.4.(3分)在△ABC和△FED中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件()A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F【分析】考查三角形全等的判定定理,有AAS,SSS,SAS,ASA四种.根据题目给出的两个已知条件,要证明△ABC≌△FED,需要已知一对对应边相等即可.【解答】解:∵∠C=∠D,∠B=∠E,说明:点C与D,B与E,A与F是对应顶点,AC的对应边应是FD,根据三角形全等的判定,当AC=FD时,有△ABC≌△FED.故选:C.5.(3分)化简的结果是()A.B.a C.D.【分析】将原式变形后,约分即可得到结果.【解答】解:原式==a.故选:B.6.(3分)甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是()A.B.C.D.【分析】题中等量关系:甲车行驶30千米与乙车行驶40千米所用时间相同,据此列出关系式.【解答】解:设甲车的速度为x千米/时,则乙车的速度为(x+15)千米/时,根据题意,得=.故选:C.7.(3分)把14cm长的铁丝截成三段,围成不是等边三角形的三角形,并且使三边均为整数,那么()A.有1种截法B.有2种截法C.有3种截法D.有4种截法【分析】根据题目要求,根据构成三角形的条件,周长为14,可逐步分析,将每个符合题意的三角形写出即可.【解答】解:根据三角形的三边关系,两边之和大于第三边,最短的边是1时,不成立;当最短的边是2时,三边长是:2,6,6;当最短的边是3时,三边长是:3,5,6;当最短的边是4时,三边长是:4,4,6和4,5,5.最短的边一定不能大于4.综上,有2,6,6;3,5,6;4,4,6和4,5,5共4种截法.故选:D.8.(3分)把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是()A.B.C.D.【分析】把一个正方形的纸片向上对折,向右对折,向右下方对折,从上部剪去一个等腰直角三角形,展开,看得到的图形为选项中的哪个即可.【解答】解:从折叠的图形中剪去8个等腰直角三角形,易得将从正方形纸片中剪去4个小正方形,故选C.二、填空题(本题共10小题,每小题3分,共21分)9.(3分)把0.0000007用科学记数法表示为7×10﹣7.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.0000007=7×10﹣7,故答案为:7×10﹣7.10.(3分)多项式4x2﹣12x2y+12x3y2分解因式时,应提取的公因式是4x2.【分析】直接找出公因式,进而提取公因式得出答案.【解答】解:4x2﹣12x2y+12x3y2=4x2(1﹣3y+3xy2).故答案为:4x2.11.(3分)若9n=38,则n=4.【分析】根据幂的乘方和积的乘方的运算法则求解.【解答】解:∵9n=32n=38,∴2n=8,∴n=4.故答案为:4.12.(3分)当x=﹣2时,分式值为零.【分析】分式的值为零:分子为0,分母不为0.【解答】解:当|x|﹣2=0,且x﹣2≠0,即x=﹣2时,分式值为零.故答案是:﹣2.13.(3分)若多项式x2+ax+b分解因式的结果为(x+1)(x﹣5),则a+b的值为﹣9.【分析】因式分解的结果利用多项式乘多项式法则计算,利用多项式相等的条件求出a与b的值,即可求出a+b的值.【解答】解:根据题意得:x2+ax+b=(x+1)(x﹣5)=x2﹣4x﹣5,∴a=﹣4,b=﹣5,则a+b=﹣4﹣5=﹣9.故答案为:﹣9.14.(3分)已知,则代数式的值为7.【分析】根据完全平方公式把已知条件两边平方,然后整理即可求解.【解答】解:∵x+=3,∴(x+)2=9,即x2+2+=9,∴x2+=9﹣2=7.15.(3分)如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=3cm,则AC=9cm.【分析】先根据直角三角形的性质得出∠ABC的度数,再由线段垂直平分线的性质得出AD=BD,故可得出∠A=∠ABD=30°,故BD是∠ABC的角平分线,由此可得出DE的长,根据直角三角形的性质求出AD的长,进而可得出结论.【解答】解:∵在△ABC中,∠C=90°,∠A=30°,∴∠ABC=90°﹣30°=60°.∵DE是线段AB的垂直平分线,∴AD=BD,∴∠A=∠ABD=30°,∴BD是∠ABC的角平分线,∴CD=DE=3cm,∴AD=2DE=6cm,∴AC=AD+CD=6+3=9cm.故答案为:9.16.(3分)如图,CP、BP分别平分△ABC的外角∠ECB,∠DBC,若∠A=50°,那么∠P=65°.【分析】运用三角形的内角和定理及外角的性质求出∠PBC+∠PCB的值,即可解决问题.【解答】解∵∠A=50°,∴∠ABC+∠ACB=130°,∴∠DBC+∠BCE=230°;∵BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线,∴∠PBC+∠PCB=115°,∴∠P=180°﹣115°=65°,故答案为:65°17.(3分)某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x套,则根据题意可得方程为+=18.【分析】关键描述语为:“共用了18天完成任务”,那么等量关系为:采用新技术前所用时间+采用新技术后所用时间=18天.【解答】解:采用新技术前所用时间为:,采用新技术后所用时间为:,∴所列方程为:+=18.18.(3分)李明同学从家到学校的速度是每小时a千米,沿原路从学校返回家的速度是每小时b千米,则李明同学来回的平均速度是千米/小时.(用含a,b的式子表示)【分析】设出从家到学校的路程为x千米,可表示出从家到学校和从学校返回家的时间,再求平均速度即可.【解答】解:设从家到学校的路程为x千米,则从家到学校的时间时,从学校返回家的时间时,李明同学来回的平均速度是:=千米/时,故答案为.三、解答题(本题共7小题,共66分)19.(12分)用乘法公式计算:(1)(2﹣3x)2﹣(3x+2)2(2)(2x+y+z)(2x﹣y﹣z)【分析】(1)利用完全平方公式,即可解答;(2)利用平方差公式,即可解答.【解答】解:(1)原式=4﹣12x+9x2﹣9x2﹣12x﹣4=﹣24x.(2)原式=[2x+(y+z)][2x﹣(y+z)]=(2x)2﹣(y+z)2=4x2﹣y2﹣z2﹣2yz.20.(7分)解方程:﹣=.【分析】观察可得最简公分母是x(x+2)(x﹣2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:两边乘x(x+2)(x﹣2)得到:5(x+2)﹣4(x﹣2)=3X5x+10﹣4x+8=3x﹣2x=﹣18x=9检验:x=9时,x(x+2)(x﹣2)≠0∴x=9的分式方程的根.21.(7分)先化简,再求值:(a﹣3﹣)÷,其中a=﹣2.【分析】先根据分式的化简法则把原式进行化简,再把a=﹣2代入进行计算即可.【解答】解:原式=•=•=2(a+4),当a=﹣2时,原式=2×(﹣2+4)=4.22.(8分)已知a,b为实数,且ab=1,M=+,N=+,试确定M、N的大小关系.【分析】利用作差法比较M与N大小即可.【解答】解:∵ab=1,∴M﹣N=+﹣(+)=﹣=﹣=0,则M=N.23.(9分)如图,给出五个等量关系:①AD=BC ②AC=BD ③CE=DE ④∠D=∠C ⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.【分析】本题主要考学生的创新思维能力.自己找条件和结论,自己证明.由于①②⑤中所给的条件都属于两个全等三角形里的边和角,可任选其中两个当条件,第三个当结论比较简便.【解答】解:已知:AD=BC,AC=BD,求证:∠DAB=∠CBA.证明:∵AD=BC,AC=BD,AB=AB,∴△ADB≌△BCA.∴∠DAB=∠CBA.24.(10分)某次地震后,政府为安置灾民,准备从某厂调拨用于搭建板房的板材5600m2和铝材2210m,该厂现有板材4600m2和铝材810m,不足部分计划安排110人进行生产,若每人每天能生产板材50m2或铝材30m,则应分别安排多少人生产板材和铝材,才能确保同时完成各自的生产任务?【分析】先设x人生产板材,则(110﹣x)人生产铝材,根据生产时间相等得列出方程,再解方程即可.【解答】解:设x人生产板材,则(110﹣x)人生产铝材,由题意得=,解得x=33,则110﹣x=77.答:分别安排33人生产板材,77人生产铝材,才能确保同时完成各自的生产任务.25.(13分)如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.(1)点D在边AB上时,试探究线段BD,AB和AF的数量关系,并证明你的结论;(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.【分析】(1)易证∠FBA=∠FCE,结合条件容易证到△FAB≌△DAC,从而有FA=DA,就可得到AB=AD+BD=FA+BD.(2)由于点D的位置在变化,因此线段AF、BD、AB之间的大小关系也会相应地发生变化,只需画出图象并借鉴(1)中的证明思路就可解决问题.【解答】解:(1)AB=FA+BD.证明:如图1,∵BE⊥CD即∠BEC=90°,∠BAC=90°,∴∠F+∠FBA=90°,∠F+∠FCE=90°.∴∠FBA=∠FCE.∵∠FAB=180°﹣∠DAC=90°,∴∠FAB=∠DAC.在△FAB和△DAC中,.∴△FAB≌△DAC(ASA).∴FA=DA.∴AB=AD+BD=FA+BD.(2)(1)中的结论不成立.点D在AB的延长线上时,AB=AF﹣BD;点D在AB的反向延长线上时,AB=BD ﹣AF.理由如下:①当点D在AB的延长线上时,如图2.同理可得:FA=DA.则AB=AD﹣BD=AF﹣BD.②点D在AB的反向延长线上时,如图3.同理可得:FA=DA.则AB=BD﹣AD=BD﹣AF.。
河南省漯河市召陵镇第二初级中学2015-2016学年八年级

八年级数学参考答案一、1——5 ADDCA 6——8 CCB二、9.50°或80° 10.(3,2) 11.4cm 12.40°13.∠C=∠E或AB=FD或AD=FB 14.15 15.2.516.68° 17.6 18.13cm三、19.略20.(1)画图略;(2)A1(-1,-1)、B1(-2,2)、C1(2,3) (3)S△ABC=6.521.(1)10°(2)∠ECD=(∠B-∠A)22.先证明△ABE≌△DCE(AAS),得出AE=DE,BE=CE,∴AE+CE=DE+BE 即BD=CA,又∵BC=BC,所以△ABC≌△DCB (SSS).(本题还可以用其它方法,只要合理即可得分)23.(1)∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC, 即∠BAD=∠CAE,又∵AB=AC,AD=AE, ∴△ABD≌△ACE, ∴BD=EC.(2) ∵△ABD≌△ACE, ∴∠BDA=∠E,又∵∠E+∠ADE=90°,∴∠BDA+∠ADE=90°,即∠BDE=90°,∴BD⊥DE24.(1) ∵△ABC是等边三角形,∴AB=AC, ∠BAE=∠ACD,又∵AE=CD, ∴△ABE≌△CAD(SAS).(2) ∵△ABE≌△CAD, ∴∠ABE=∠CAD,AD=BE,又∵∠BFP=∠BAD+∠ABE, ∴∠BFP=∠BAD+∠CAD,又∵∠BAD+∠CAD=60°,∴∠BFP=60°,又∵BP⊥AD, ∴∠BPF=90°,∴∠FBP=30°,∴BF=2PF=18,∴BE=18+3=21,∴AD=2125. (1)∵AD是∠BAC的角平分线,AB=AC,∴∠BDP=90°,BD=CD∵BE⊥AC, ∴∠AEP=∠BEC=90°,在△BPD和△APE中,∠AEP=∠BDP=90°,∠BPD=∠APE∴∠EBC=∠EAP,在△BCE和△APE中, ∵∠AEP=∠BEC, BE=AE, ∠EBC=∠EAP,∴△BCE≌△APE.(2)∵△BCE≌△APE,∴BC=AP,∵BD=CD, ∴BD=BC, ∴BD=AP.(3) △BDQ是等腰直角三角形.∵BE=AE,F是AB的中点,∴EF是线段AB的垂直平分线,∴AQ=BQ, ∴∠BAQ=∠ABQ, ,∵BE=AE, ∠BEA=90°,∴∠BAE=45°,∵AD是∠BAC的角平分线,∴∠BAD=∠CAD=22.5°, ∵∠BAD=∠ABQ, ∴∠BAD=∠ABQ=22.5°,∴∠BQD=22.5°×2=45°,∵∠ADB=90°,∴△BDQ是等腰直角三角形.。
漯河市召陵区2015-2016学年八年级上期中数学试卷(有答案)AKqPlH

2015-2016学年河南省漯河市召陵区八年级(上)期中数学试卷一、选择题(本题共8小题,每小题3分,共24分)1.下面所给的交通标志是轴对称图形的是()A.B.C.D.2.将一副三角板按图中方式叠放,则角α等于()A.30°B.45°C.60°D.75°3.下列说法错误的是()A.全等三角形的三条边相等,三个角也相等B.判定两个三角形全等的条件中至少有一个是边C.面积相等的两个图形是全等形D.全等三角形的面积和周长都相等4.某等腰三角形的两条边长分别为3cm和6cm,则它的周长为()A.9cm B.12cm C.15cm D.12cm或15cm5.若一个多边形的内角和为900°,则从这个多边形的其中一个顶点出发引的对角线的条数为()A.4 B.5 C.6 D.76.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于()A.46°B.60°C.68°D.77°7.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为()A.3 B.5 C.6 D.不能确定8.如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为()A.36°B.45°C.60°D.75°二、填空题(本题共10小题,每小题3分,共30分)9.等腰三角形中,如果一个外角为130°,那么这个等腰三角形的顶角的度数为.10.如果点P关于x轴的对称点为(﹣3,﹣2),那么点P关于y轴的对称点的坐标为.11.一个三角形的周长为48cm,最大边与最小边的差为14cm,另一边与最小边之和为25cm,那么这个三角形最小边的长为.12.如图,将△ABC绕点C顺时针方向旋转50°得到△A′CB′,若AC⊥A′B′,连接AA′,则∠BAC 等于.13.如图,已知AC=FE,BC=DE,点A、D、B、F在一条直线上,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是.14.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是.15.如图,在△ABC中,E是BC上一点,EC=2BE,点D是AC的中点,若S△ABC=15,则S△ADF =.﹣S△BEF16.如图,在△ABC中,按以下步骤作图:①分别以点A、C为圆心,以大于AC的长为半径画弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD,若∠C=28°,AB=BD,则∠B的度数为.17.如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB的平分线,且交AD于P点.如果AP=2,则AB的长为.18.如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=.三、解答题(本大题共7小题,共66分)19.如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹).20.如图,完成下列各题:(1)画出△ABC关于x轴的对称△A1B1C1,并写出点A1、B1、C1的坐标;(2)写出△ABC的面积(不要求过程).21.如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.(1)若∠A=30°,∠B=50°,求∠ECD的度数;(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)22.如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.23.如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.(1)求证:BD=EC;(2)BD与CE有何位置关系?请证你的猜想.24.如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.(1)求证:△ABE≌△CAD;(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.25.如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.(1)求证:△BCE≌△APE;(2)求证:BD=AP;(3)判断△BDQ的形状,并证明你的结论.2015-2016学年河南省漯河市召陵区八年级(上)期中数学试卷参考答案与试题解析一、选择题(本题共8小题,每小题3分,共24分)1.下面所给的交通标志是轴对称图形的是()A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:A、是轴对称图形,故正确;B、不是轴对称图形,故错误;C、不是轴对称图形,故错误;D、不是轴对称图形,故错误.故选A.2.将一副三角板按图中方式叠放,则角α等于()A.30°B.45°C.60°D.75°【考点】三角形的外角性质;平行线的性质.【分析】利用两直线平行,内错角相等和三角形的一个外角等于与它不相邻的两个内角的和计算.【解答】解:如图,根据两直线平行,内错角相等,∴∠1=45°,根据三角形的一个外角等于与它不相邻的两个内角的和,∴∠α=∠1+30°=75°.故选D.3.下列说法错误的是()A.全等三角形的三条边相等,三个角也相等B.判定两个三角形全等的条件中至少有一个是边C.面积相等的两个图形是全等形D.全等三角形的面积和周长都相等【考点】全等图形.【分析】根据全等图形概念和性质对各个选项进行判断即可.【解答】解:全等三角形的三条边相等,三个角也相等,A正确;判定两个三角形全等的条件中至少有一个是边,B正确;面积相等的两个图形不一定是全等形,C错误;全等三角形的面积和周长都相等,D正确,故选:C.4.某等腰三角形的两条边长分别为3cm和6cm,则它的周长为()A.9cm B.12cm C.15cm D.12cm或15cm【考点】等腰三角形的性质;三角形三边关系.【分析】题中没有指明哪个是底哪个是腰,则应该分两种情况进行分析,从而得到答案.【解答】解:(1)当3cm为腰时,因为3+3=6cm,不能构成三角形,故舍去;(2)当6cm为腰时,符合三角形三边关系,所以其周长=6+6+3=15cm.故选C.5.若一个多边形的内角和为900°,则从这个多边形的其中一个顶点出发引的对角线的条数为()A.4 B.5 C.6 D.7【考点】多边形内角与外角;多边形的对角线.【分析】根据题意和多边形内角和公式求出多边形的边数,根据多边形的对角线的条数的计算公式计算即可.【解答】解:设这个多边形的边数为n,则(n﹣2)×180°=900°,解得,n=7,从七边形的其中一个顶点出发引的对角线的条数:7﹣3=4,故选:A.6.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于()A.46°B.60°C.68°D.77°【考点】翻折变换(折叠问题).【分析】在△ABC中,先求得∠B=67°,由翻折的性质可知∠DEC=67°,由∠A+∠ADE=∠DEC可求得∠ADE=44°,然后根据∠BDC=求解即可.【解答】解:∵∠A+∠B=90°,∴∠B=90°﹣23°=67°.由翻折的性质可知:∠B=∠DEC=67°,∠BDC=∠EDC.∵∠A+∠ADE=∠DEC,∴∠EDA=67°﹣23°=44°.∴∠BDC===68°.故选:C.7.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为()A.3 B.5 C.6 D.不能确定【考点】角平分线的性质;平行线之间的距离.【分析】作PF⊥AD于F,PG⊥BC于G,根据角平分线的性质得到PF=PE=3,PG=PE=3,根据平行线间的距离的求法计算即可.【解答】解:作PF⊥AD于F,PG⊥BC于G,∵AP是∠BAD的角平分线,PF⊥AD,PE⊥AB,∴PF=PE=3,∵BP是∠ABC的角平分线,PE⊥AB,PG⊥BC,∴PG=PE=3,∵AD∥BC,∴两平行线AD与BC间的距离为PF+PG=6,故选:C.8.如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为()A.36°B.45°C.60°D.75°【考点】等腰三角形的性质.【分析】根据DE=BE,得到∠EBD=∠EDB=α,根据外角的性质得到∠AED=∠EBD+∠EDB=2α,根据等腰三角形的性质得到∠A=∠AED=2α,于是得到∠BDC=∠A+∠ABD=3α,由于∠ABC=∠C=∠BDC=3α,根据三角形的内角和列方程即可得到结论.【解答】解:∵DE=BE,∴∠EBD=∠EDB,设∠EBD=∠EDB=α,∴∠AED=∠EBD+∠EDB=2α,∵AD=DE,∴∠A=∠AED=2α,∴∠BDC=∠A+∠ABD=3α,∵BD=BC,AB=AB,∴∠ABC=∠C=∠BDC=3α,∴3α+3α+2α=180°,∴α=22.5°,∴∠A=45°.故选:B.二、填空题(本题共10小题,每小题3分,共30分)9.等腰三角形中,如果一个外角为130°,那么这个等腰三角形的顶角的度数为50°或80°.【考点】等腰三角形的性质.【分析】等腰三角形的一个外角等于130°,则等腰三角形的一个内角为50°,但已知没有明确此角是顶角还是底角,所以应分两种情况进行分类讨论.【解答】解:∵一个外角为130°,∴三角形的一个内角为50°,当50°为顶角时,其他两角都为65°、65°,当50°为底角时,其他两角为50°、80°,所以等腰三角形的顶角为50°或80°.故答案为:50°或80°.10.如果点P关于x轴的对称点为(﹣3,﹣2),那么点P关于y轴的对称点的坐标为(3,2).【考点】关于x轴、y轴对称的点的坐标.【分析】分别利用关于x,y轴对称点的性质得出点的坐标即可.【解答】解:∵点P关于x轴的对称点为(﹣3,﹣2),∴P(﹣3,2),∴点P关于y轴的对称点的坐标为:(3,2).故答案为:(3,2).11.一个三角形的周长为48cm,最大边与最小边的差为14cm,另一边与最小边之和为25cm,那么这个三角形最小边的长为9cm.【考点】三元一次方程组的应用;三角形三边关系.【分析】设三角形的最长边为a,最小边为b,另一边为c,根据三角形的周长为48cm,得出a+b+c=48,再根据最大边与最小边的差为14cm,得出a﹣b=14,最后根据另一边与最小边之和为25cm,得出c+b=25,然后组成方程组求解即可.【解答】解:设三角形的最长边为a,最小边为b,另一边为c,根据题意得:,②+③得:a+c=39④,把④代入①得:b=9,则这个三角形最小边的长为9cm;故答案为:9cm.12.如图,将△ABC绕点C顺时针方向旋转50°得到△A′CB′,若AC⊥A′B′,连接AA′,则∠BAC 等于40°.【考点】旋转的性质.【分析】先利用旋转的性质得到∠ACA′=50°,∠A=∠A′,则根据AC⊥A′B′,利用互余可计算出∠A′=40°,从而得到∠BAC的度数.【解答】解:∵△ABC绕点C顺时针方向旋转50°得到△A′CB′,∴∠ACA′=50°,∠A=∠A′,∵AC⊥A′B′,∴∠A′=90°﹣50°=40°,∴∠BAC=40°.故答案为40°.13.如图,已知AC=FE,BC=DE,点A、D、B、F在一条直线上,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是∠C=∠E(答案不惟一,也可以是AB=FD或AD=FB).【考点】全等三角形的判定.【分析】要判定△ABC≌△FDE,已知AC=FE,BC=DE,具备了两组边对应相等,故添加∠C=∠E,利用SAS可证全等.(也可添加其它条件).【解答】解:增加一个条件:∠C=∠E,显然能看出,在△ABC和△FDE中,利用SAS可证三角形全等.(答案不唯一).故填:∠C=∠E.14.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是15.【考点】角平分线的性质.【分析】过D作DE⊥BC于E,根据角平分线性质求出DE=3,根据三角形的面积求出即可.【解答】解:过D作DE⊥BC于E,∵∠A=90°,∴DA⊥AB,∵BD平分∠ABC,∴AD=DE=3,∴△BDC的面积是×DE×BC=×10×3=15,故答案为:15.15.如图,在△ABC中,E是BC上一点,EC=2BE,点D是AC的中点,若S△ABC=15,则S△ADF = 2.5.﹣S△BEF【考点】三角形的面积.【分析】根据题意先分别求出S △ABD ,S △ABE ,再根据S △ADF ﹣S △BEF =S △ABD ﹣S △ABE 即可求出结果.【解答】解:∵点D 是AC 的中点,∴AD=AC ,∵S △ABC =15,∴S △ABD =S △ABC =×15=7.5.∵EC=2BE ,S △ABC =15,∴S △ABE =S △ABC =×15=5,∵S △ABD ﹣S △ABE =(S △ADF +S △ABF )﹣(S △ABF +S △BEF )=S △ADF ﹣S △BEF ,即S △ADF ﹣S △BEF =S △ABD ﹣S △ABE =7.5﹣5=2.5.故答案为:2.5.16.如图,在△ABC 中,按以下步骤作图:①分别以点A 、C 为圆心,以大于AC 的长为半径画弧,两弧相交于M 、N 两点;②作直线MN 交BC 于点D ,连接AD ,若∠C=28°,AB=BD ,则∠B 的度数为 68° .【考点】作图—基本作图;线段垂直平分线的性质.【分析】利用线段垂直平分线的性质得出AD=DC ,再利用等腰三角形的性质结合三角形内角和定理得出答案.【解答】解:由题意可得:MN 是AC 的垂直平分线,则AD=DC,故∠C=∠DAC,∵∠C=28°,∴∠DAC=28°,∴∠ADB=56°,∵AB=BD,∴∠BAD=∠BDA=56°,∴∠B=180°﹣56°﹣56°=68°.故答案为:68°.17.如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB的平分线,且交AD于P点.如果AP=2,则AB的长为6.【考点】含30度角的直角三角形;角平分线的性质;等边三角形的判定与性质.【分析】易得△AEP的等边三角形,则AE=AP=2,在直角△AEC中,利用含30度角的直角三角形的性质来求EC的长度,然后在等腰△BEC中得到BE的长度,则易求AB的长度.【解答】解:∵△ABC中,∠BAC=90°,∠B=30°,∴∠ACB=60°.又∵CE是∠ACB的平分线,∴∠ECB=30°,∴∠AEC=∠B+∠ECB=60°,∠B=∠ECB∴∠AEP=60°,BE=EC.又AD⊥BC,∴∠BAD=∠EAP=60°,则∠AEP=∠EAP=60°,∴△AEP的等边三角形,则AE=AP=2,在直角△AEC中,∠ACE=30°,则EC=2AE=4,∴BE=EC=4,∴AB=BE+AE=6.故答案是:6.18.如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.【考点】全等三角形的判定与性质;角平分线的性质.【分析】作PF⊥OB于F,根据角平分线的性质就可以得出PC=PF,根据HL可以判断Rt△PCO ≌Rt△PFO,从而可得OC=OF,然后根据AAS就可以得出△CDP≌△EFP,从而得到CD=EF,进而得出DO+E0=13cm.【解答】证明:过P作PF⊥OB于F,∴∠PFO=90°,∵P为∠AOB的平分线OP上一点,PC⊥OA,∴PC=PF,∠PCA=90°,∴∠PCA=∠PFO,在Rt△PCO和RtPFO中,,∴Rt△PCO≌Rt△PFO(HL),∴OC=OF.∵∠ODP+∠OEP=180°,且∠OEP+∠PEB=180°,∴∠ODP=∠FEP,在△CDP和△EFP中,,∴△CDP≌△EFP(AAS),∴CD=EF,∵DO+EO=DC+CO+EO,∴DO+EO=EF+EO+CO,∴DO+EO=FO+CO,∴DO+EO=2CO,∵CO=6.5cm,∴DO+E0=13cm.故答案为:13cm.三、解答题(本大题共7小题,共66分)19.如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹).【考点】作图—复杂作图;角平分线的性质;线段垂直平分线的性质.【分析】作AB的垂直平分线和∠ABC的角平分线,两线相交于点P,则根据垂直平分线的性质定理有PA=PB,根据角平分线的性质定理得到点P到边AB、BC的距离相等,所以点P为满足条件的点.【解答】解:如图,20.如图,完成下列各题:(1)画出△ABC关于x轴的对称△A1B1C1,并写出点A1、B1、C1的坐标;(2)写出△ABC的面积(不要求过程).【考点】作图﹣轴对称变换.【分析】(1)分别作出点A、B、C关于x轴的对称点,然后顺次连接,并写出点A1、B1、C1的坐标;(2)用三角形ABC所在的矩形的面积减去三个小三角形的面积即可求解.【解答】解:(1)所作图形如图所示:A1(﹣1,﹣1)、B1(﹣2,2)、C1(2,3);=4×4﹣×1×3﹣×1×4﹣×3×4(3)S△ABC=6.5.21.如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.(1)若∠A=30°,∠B=50°,求∠ECD的度数;(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)【考点】三角形内角和定理;三角形的外角性质.【分析】(1)利用高的定义和互余得到∠BCD=90°﹣∠B,再根据角平分线定义得到∠BCE=∠ACB,接着根据三角形内角和定理得到∠ACB=180°﹣∠A﹣∠B,于是得到∠BCE=90°﹣(∠A+∠B),然后计算∠BCE﹣∠BCD得到∠ECD=(∠B﹣∠A),再把∠A=30°,∠B=50°代入计算即可;(2)直接由(1)得到结论.【解答】解:(1)∵CD为高,∴∠CDB=90°,∴∠BCD=90°﹣∠B,∵CE为角平分线,∴∠BCE=∠ACB,而∠ACB=180°﹣∠A﹣∠B,∴∠BCE==90°﹣(∠A+∠B),∴∠ECD=∠BCE﹣∠BCD=90°﹣(∠A+∠B)﹣(90°﹣∠B)=(∠B﹣∠A),当∠A=30°,∠B=50°时,∠ECD=×(50°﹣30°)=10°;(2)由(1)得∠ECD=(∠B﹣∠A).22.如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.【考点】全等三角形的判定.【分析】先证明△ABE≌△DCE可得出AE=DE,BE=CE,根据等式的性质可得AE+CE=DE+BE 即BD=CA,再加上公共边BC=BC,可证明△ABC≌△DCB.【解答】证明:∵在△ABE和△DCE中,∴△ABE≌△DCE(AAS),∴AE=ED,BE=CE,∴AC=DB,在△ABC和△DCB中,,∴△ABC≌△DCB(SSS).23.如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.(1)求证:BD=EC;(2)BD与CE有何位置关系?请证你的猜想.【考点】全等三角形的判定与性质.【分析】(1)求出∠BAD=∠CAE,根据SAS推出△ABD≌△ACE,根据全等三角形的性质推出即可;(2)根据全等三角形的性质得出∠BDA=∠E,根据∠E+∠ADE=90°求出∠BDA+∠ADE=90°即可.【解答】(1)证明:∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=EC;(2)BD⊥CE,证明:∵△ABD≌△ACE,∴∠BDA=∠E,又∵∠E+∠ADE=90°,∴∠BDA+∠ADE=90°,即∠BDE=90°,∴BD⊥DE.24.如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.(1)求证:△ABE≌△CAD;(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.【考点】全等三角形的判定与性质;等边三角形的性质.【分析】(1)根据等边三角形的三条边都相等可得AB=CA,每一个角都是60°可得,∠BAE=∠ACD=60°,然后利用“边角边”证明△ABE和△CAD全等.(2)根据全等三角形对应角相等可得∠CAD=∠ABE,然后求出∠BFP=60°,再根据直角三角形两锐角互余求出∠FBP=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出BF=2FP,再根据AD=BE=BF+FE代入数据进行计算即可得解.【解答】(1)证明:∵△ABC是等边三角形,∴AB=AC,∠BAE=∠ACD,又∵AE=CD,在△ABE与△CAD中,,∴△ABE≌△CAD(SAS).(2)解:∵△ABE≌△CAD,∴∠ABE=∠CAD,AD=BE,又∵∠BFP=∠BAD+∠ABE,∴∠BFP=∠BAD+∠CAD,又∵∠BAD+∠CAD=60°,∴∠BFP=60°,又∵BP⊥AD,∴∠BPF=90°,∴∠FBP=30°,∴BF=2PF=18,∴BE=18+3=21,∴AD=21.25.如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.(1)求证:△BCE≌△APE;(2)求证:BD=AP;(3)判断△BDQ的形状,并证明你的结论.【考点】全等三角形的判定与性质;等腰直角三角形.【分析】(1)求出∠AEP=∠BEC=90°,根据三角形内角和定理求出∠EBC=∠EAP,根据ASA推出△BCE≌△APE即可;(2)根据全等得出BC=AP,根据等腰三角形的性质得出BD=BC,即可求出答案;(3)根据线段垂直平分线的性质求出AQ=BQ,求出∠BAE=45°,根据角平分线的定义求出∠BAD=∠ABQ=22.5°,根据三角形外角性质求出∠BQD=45°,即可得出答案.【解答】证明:(1)如图:∵AD是∠BAC的角平分线,AB=AC,∴∠BDP=90°,BD=CD,∵BE⊥AC,∴∠AEP=∠BEC=90°,∵在△BPD和△APE中,∠AEP=∠BDP=90°,∠BPD=∠APE,∠PAE+∠PEA+∠APE=180°,∠BDP+∠BPD+∠EBC=180°,∴∠EBC=∠EAP,在△BCE和△APE中,,∴△BCE≌△APE;(2)∵△BCE≌△APE,∴BC=AP,∵BD=CD,∴BD=BC,∴BD=AP;(3)△BDQ是等腰直角三角形,证明:∵BE=AE,F是AB的中点,∴EF是线段AB的垂直平分线,∴AQ=BQ,∴∠BAQ=∠ABQ,∵BE=AE,∠BEA=90°,∴∠BAE=45°,∵AD是∠BAC的角平分线,∴∠BAD=∠CAD=22.5°,∵∠BAD=∠ABQ,∴∠BAD=∠ABQ=22.5°,∴∠BQD=22.5°×2=45°,∵∠ADB=90°,∴△BDQ是等腰直角三角形.2017年3月2日。
漯河市召陵区2015-2016学年八年级上期末数学试卷含答案解析

一、选择题(本题共 8 小题,每小题 3 分,共 24 分) 1.下列关系成立的是( ) A.a0=1 B.a3n÷an=a3 C.(﹣ a)3÷(﹣ a2)=a D.a+ann﹣ 1=a
2.把多項式 a2﹣ 4a 分解因式,结果正确的是( ) A.a(a+2)(a﹣ 2) B.a(a﹣ 4) C.(a+2)(a﹣ 2) D.(a﹣ 2)2﹣ 4
22.已知 a,b 为实数,且 ab=1,M= + ,N= + ,试确定 M、N 的大小关 系.
23.如图,给出五个等量关系:①AD=BC ②AC=BD ③CE=DE ④∠D=∠C ⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论 (只需写出一种情况),并加以证明.
第 3 页(共 15 页)
第 4 页(共 15 页)
2015-2016 学年河南省漯河市召陵区八年级(上)期末
数学试卷
参考答案与试题解析
一、选择题(本题共 8 小题,每小题 3 分,共 24 分) 1.下列关系成立的是( ) A.a0=1 B.a3n÷an=a3 C.(﹣ a)3÷(﹣ a2)=a D.﹣a+1ann =a 【考点】同底数幂的除法;合并同类项;幂的乘方与积的乘方;零指数幂. 【分析】分别根据 0 指数幂的运算法则、同底数幂的除法法则对各选项进行逐一判断即 可. 【解答】解:A、当 a=0 时,a0 无意义,故本选项错误; B、a3n÷an=a2n,故本选项错误; C、(﹣ a)3÷(﹣ a2)=a,故本选项正确; D、a 与 an﹣ 1 不是同类项,不能合并,故本选项错误. 故选 C. 【点评】本题考查的是同底数幂的除法,熟知同底数幂的除法法则是底数不变,指数相减 是解答此题的关键.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年河南省漯河市召陵区八年级(上)期中数学试卷一、选择题(本题共8小题,每小题3分,共24分)1.(3分)下面所给的交通标志是轴对称图形的是()A.B.C.D.2.(3分)将一副三角板按图中方式叠放,则角α等于()A.30°B.45°C.60°D.75°3.(3分)下列说法错误的是()A.全等三角形的三条边相等,三个角也相等B.判定两个三角形全等的条件中至少有一个是边C.面积相等的两个图形是全等形D.全等三角形的面积和周长都相等4.(3分)某等腰三角形的两条边长分别为3cm和6cm,则它的周长为()A.9cm B.12cm C.15cm D.12cm或15cm5.(3分)若一个多边形的内角和为900°,则从这个多边形的其中一个顶点出发引的对角线的条数为()A.4 B.5 C.6 D.76.(3分)如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC 边上的E处.若∠A=23°,则∠BDC等于()A.46°B.60°C.68°D.77°7.(3分)如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为()A.3 B.5 C.6 D.不能确定8.(3分)如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为()A.36°B.45°C.60°D.75°二、填空题(本题共10小题,每小题3分,共30分)9.(3分)等腰三角形中,如果一个外角为130°,那么这个等腰三角形的顶角的度数为.10.(3分)如果点P关于x轴的对称点为(﹣3,﹣2),那么点P关于y轴的对称点的坐标为.11.(3分)一个三角形的周长为48cm,最大边与最小边的差为14cm,另一边与最小边之和为25cm,那么这个三角形最小边的长为.12.(3分)如图,将△ABC绕点C顺时针方向旋转50°得到△A′CB′,若AC⊥A′B′,连接AA′,则∠BAC等于.13.(3分)如图,已知AC=FE,BC=DE,点A、D、B、F在一条直线上,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是.14.(3分)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是.15.(3分)如图,在△ABC中,E是BC上一点,EC=2BE,点D是AC的中点,若S=15,则S△ADF﹣S△BEF=.△ABC16.(3分)如图,在△ABC中,按以下步骤作图:①分别以点A、C为圆心,以大于AC的长为半径画弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD,若∠C=28°,AB=BD,则∠B的度数为.17.(3分)如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB 的平分线,且交AD于P点.如果AP=2,则AB的长为.18.(3分)如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=.三、解答题(本大题共7小题,共66分)19.(8分)如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹).20.(8分)如图,完成下列各题:(1)画出△ABC关于x轴的对称△A1B1C1,并写出点A1、B1、C1的坐标;(2)写出△ABC的面积(不要求过程).21.(8分)如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.(1)若∠A=30°,∠B=50°,求∠ECD的度数;(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)22.(8分)如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.23.(10分)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.(1)求证:BD=EC;(2)BD与CE有何位置关系?请证你的猜想.24.(11分)如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.(1)求证:△ABE≌△CAD;(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.25.(13分)如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC 的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.(1)求证:△BCE≌△APE;(2)求证:BD=AP;(3)判断△BDQ的形状,并证明你的结论.2015-2016学年河南省漯河市召陵区八年级(上)期中数学试卷参考答案与试题解析一、选择题(本题共8小题,每小题3分,共24分)1.(3分)下面所给的交通标志是轴对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,故正确;B、不是轴对称图形,故错误;C、不是轴对称图形,故错误;D、不是轴对称图形,故错误.故选:A.2.(3分)将一副三角板按图中方式叠放,则角α等于()A.30°B.45°C.60°D.75°【解答】解:如图,根据两直线平行,内错角相等,∴∠1=45°,根据三角形的一个外角等于与它不相邻的两个内角的和,∴∠α=∠1+30°=75°.故选:D.3.(3分)下列说法错误的是()A.全等三角形的三条边相等,三个角也相等B.判定两个三角形全等的条件中至少有一个是边C.面积相等的两个图形是全等形D.全等三角形的面积和周长都相等【解答】解:全等三角形的三条边相等,三个角也相等,A正确;判定两个三角形全等的条件中至少有一个是边,B正确;面积相等的两个图形不一定是全等形,C错误;全等三角形的面积和周长都相等,D正确,故选:C.4.(3分)某等腰三角形的两条边长分别为3cm和6cm,则它的周长为()A.9cm B.12cm C.15cm D.12cm或15cm【解答】解:(1)当3cm为腰时,因为3+3=6cm,不能构成三角形,故舍去;(2)当6cm为腰时,符合三角形三边关系,所以其周长=6+6+3=15cm.故选:C.5.(3分)若一个多边形的内角和为900°,则从这个多边形的其中一个顶点出发引的对角线的条数为()A.4 B.5 C.6 D.7【解答】解:设这个多边形的边数为n,则(n﹣2)×180°=900°,解得,n=7,从七边形的其中一个顶点出发引的对角线的条数:7﹣3=4,故选:A.6.(3分)如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC 边上的E处.若∠A=23°,则∠BDC等于()A.46°B.60°C.68°D.77°【解答】解:∵∠A+∠B=90°,∴∠B=90°﹣23°=67°.由翻折的性质可知:∠B=∠DEC=67°,∠BDC=∠EDC.∵∠A+∠ADE=∠DEC,∴∠EDA=67°﹣23°=44°.∴∠BDC===68°.故选:C.7.(3分)如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为()A.3 B.5 C.6 D.不能确定【解答】解:作PF⊥AD于F,PG⊥BC于G,∵AP是∠BAD的角平分线,PF⊥AD,PE⊥AB,∴PF=PE=3,∵BP是∠ABC的角平分线,PE⊥AB,PG⊥BC,∴PG=PE=3,∵AD∥BC,∴两平行线AD与BC间的距离为PF+PG=6,故选:C.8.(3分)如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为()A.36°B.45°C.60°D.75°【解答】解:∵DE=BE,∴∠EBD=∠EDB,设∠EBD=∠EDB=α,∴∠AED=∠EBD+∠EDB=2α,∵AD=DE,∴∠A=∠AED=2α,∴∠BDC=∠A+∠ABD=3α,∵BD=BC,AB=AB,∴∠ABC=∠C=∠BDC=3α,∴3α+3α+2α=180°,∴α=22.5°,∴∠A=45°.故选:B.二、填空题(本题共10小题,每小题3分,共30分)9.(3分)等腰三角形中,如果一个外角为130°,那么这个等腰三角形的顶角的度数为50°或80°.【解答】解:∵一个外角为130°,∴三角形的一个内角为50°,当50°为顶角时,其他两角都为65°、65°,当50°为底角时,其他两角为50°、80°,所以等腰三角形的顶角为50°或80°.故答案为:50°或80°.10.(3分)如果点P关于x轴的对称点为(﹣3,﹣2),那么点P关于y轴的对称点的坐标为(3,2).【解答】解:∵点P关于x轴的对称点为(﹣3,﹣2),∴P(﹣3,2),∴点P关于y轴的对称点的坐标为:(3,2).故答案为:(3,2).11.(3分)一个三角形的周长为48cm,最大边与最小边的差为14cm,另一边与最小边之和为25cm,那么这个三角形最小边的长为9cm.【解答】解:设三角形的最长边为a,最小边为b,另一边为c,根据题意得:,②+③得:a+c=39④,把④代入①得:b=9,则这个三角形最小边的长为9cm;故答案为:9cm.12.(3分)如图,将△ABC绕点C顺时针方向旋转50°得到△A′CB′,若AC⊥A′B′,连接AA′,则∠BAC等于40°.【解答】解:∵△ABC绕点C顺时针方向旋转50°得到△A′CB′,∴∠ACA′=50°,∠A=∠A′,∵AC⊥A′B′,∴∠A′=90°﹣50°=40°,∴∠BAC=40°.故答案为40°.13.(3分)如图,已知AC=FE,BC=DE,点A、D、B、F在一条直线上,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是∠C=∠E(答案不惟一,也可以是AB=FD或AD=FB).【解答】解:增加一个条件:∠C=∠E,显然能看出,在△ABC和△FDE中,利用SAS可证三角形全等.(答案不唯一).故填:∠C=∠E.14.(3分)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是15.【解答】解:过D作DE⊥BC于E,∵∠A=90°,∴DA⊥AB,∵BD平分∠ABC,∴AD=DE=3,∴△BDC的面积是×DE×BC=×10×3=15,故答案为:15.15.(3分)如图,在△ABC中,E是BC上一点,EC=2BE,点D是AC的中点,=15,则S△ADF﹣S△BEF= 2.5.若S△ABC【解答】解:∵点D 是AC 的中点,∴AD=AC ,∵S △ABC =15,∴S △ABD =S △ABC =×15=7.5.∵EC=2BE ,S △ABC =15,∴S △ABE =S △ABC =×15=5,∵S △ABD ﹣S △ABE =(S △ADF +S △ABF )﹣(S △ABF +S △BEF )=S △ADF ﹣S △BEF ,即S △ADF ﹣S △BEF =S △ABD ﹣S △ABE =7.5﹣5=2.5.故答案为:2.5.16.(3分)如图,在△ABC 中,按以下步骤作图:①分别以点A 、C 为圆心,以大于AC 的长为半径画弧,两弧相交于M 、N 两点; ②作直线MN 交BC 于点D ,连接AD ,若∠C=28°,AB=BD ,则∠B 的度数为 68° .【解答】解:由题意可得:MN 是AC 的垂直平分线,则AD=DC ,故∠C=∠DAC ,∵∠C=28°,∴∠DAC=28°,∴∠ADB=56°,∵AB=BD ,∴∠BAD=∠BDA=56°,∴∠B=180°﹣56°﹣56°=68°.故答案为:68°.17.(3分)如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB 的平分线,且交AD于P点.如果AP=2,则AB的长为6.【解答】解:∵△ABC中,∠BAC=90°,∠B=30°,∴∠ACB=60°.又∵CE是∠ACB的平分线,∴∠ECB=30°,∴∠AEC=∠B+∠ECB=60°,∠B=∠ECB∴∠AEP=60°,BE=EC.又AD⊥BC,∴∠BAD=∠EAP=60°,则∠AEP=∠EAP=60°,∴△AEP的等边三角形,则AE=AP=2,在直角△AEC中,∠ACE=30°,则EC=2AE=4,∴BE=EC=4,∴AB=BE+AE=6.故答案是:6.18.(3分)如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.【解答】证明:过P作PF⊥OB于F,∴∠PFO=90°,∵P为∠AOB的平分线OP上一点,PC⊥OA,∴PC=PF,∠PCA=90°,∴∠PCA=∠PFO,在Rt△PCO和RtPFO中,,∴Rt△PCO≌Rt△PFO(HL),∴OC=OF.∵∠ODP+∠OEP=180°,且∠OEP+∠PEB=180°,∴∠ODP=∠FEP,在△CDP和△EFP中,,∴△CDP≌△EFP(AAS),∴CD=EF,∵DO+EO=DC+CO+EO,∴DO+EO=EF+EO+CO,∴DO+EO=FO+CO,∴DO+EO=2CO,∵CO=6.5cm,∴DO+E0=13cm.故答案为:13cm.三、解答题(本大题共7小题,共66分)19.(8分)如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹).【解答】解:如图,20.(8分)如图,完成下列各题:(1)画出△ABC关于x轴的对称△A1B1C1,并写出点A1、B1、C1的坐标;(2)写出△ABC的面积(不要求过程).【解答】解:(1)所作图形如图所示:A1(﹣1,﹣1)、B1(﹣2,2)、C1(2,3);=4×4﹣×1×3﹣×1×4﹣×3×4(3)S△ABC=6.5.21.(8分)如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.(1)若∠A=30°,∠B=50°,求∠ECD的度数;(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)【解答】解:(1)∵CD为高,∴∠CDB=90°,∴∠BCD=90°﹣∠B,∵CE为角平分线,∴∠BCE=∠ACB,而∠ACB=180°﹣∠A﹣∠B,∴∠BCE=(180°﹣∠A﹣∠B)=90°﹣(∠A+∠B),∴∠ECD=∠BCE﹣∠BCD=90°﹣(∠A+∠B)﹣(90°﹣∠B)=(∠B﹣∠A),当∠A=30°,∠B=50°时,∠ECD=×(50°﹣30°)=10°;(2)由(1)得∠ECD=(∠B﹣∠A).22.(8分)如图,已知AB=CD,∠A=∠D,求证:△ABC≌△DCB.【解答】证明:∵在△ABE和△DCE中,∴△ABE≌△DCE(AAS),∴AE=ED,BE=CE,∴AC=DB,在△ABC和△DCB中,,∴△ABC≌△DCB(SSS).23.(10分)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连结BD.(1)求证:BD=EC;(2)BD与CE有何位置关系?请证你的猜想.【解答】(1)证明:∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=EC;(2)BD⊥CE,证明:∵△ABD≌△ACE,∴∠BDA=∠E,又∵∠E+∠ADE=90°,∴∠BDA+∠ADE=90°,即∠BDE=90°,∴BD⊥DE.24.(11分)如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.(1)求证:△ABE≌△CAD;(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.【解答】(1)证明:∵△ABC是等边三角形,∴AB=AC,∠BAE=∠ACD,又∵AE=CD,在△ABE与△CAD中,,∴△ABE≌△CAD(SAS).(2)解:∵△ABE≌△CAD,∴∠ABE=∠CAD,AD=BE,又∵∠BFP=∠BAD+∠ABE,∴∠BFP=∠BAD+∠CAD,又∵∠BAD+∠CAD=60°,∴∠BFP=60°,又∵BP⊥AD,∴∠BPF=90°,∴∠FBP=30°,∴BF=2PF=18,∴BE=18+3=21,∴AD=21.25.(13分)如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC 的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.(1)求证:△BCE≌△APE;(2)求证:BD=AP;(3)判断△BDQ的形状,并证明你的结论.【解答】证明:(1)如图:∵AD是∠BAC的角平分线,AB=AC,∴∠BDP=90°,BD=CD,∵BE⊥AC,∴∠AEP=∠BEC=90°,∵在△BPD和△APE中,∠AEP=∠BDP=90°,∠BPD=∠APE,∠PAE+∠PEA+∠APE=180°,∠BDP+∠BPD+∠EBC=180°,∴∠EBC=∠EAP,在△BCE和△APE中,,∴△BCE≌△APE;(2)∵△BCE≌△APE,∴BC=AP,∵BD=CD,∴BD=BC,∴BD=AP;(3)△BDQ是等腰直角三角形,证明:∵BE=AE,F是AB的中点,∴EF是线段AB的垂直平分线,∴AQ=BQ,∴∠BAQ=∠ABQ,∵BE=AE,∠BEA=90°,∴∠BAE=45°,∵AD是∠BAC的角平分线,∴∠BAD=∠CAD=22.5°,∵∠BAD=∠ABQ,∴∠BAD=∠ABQ=22.5°,∴∠BQD=22.5°×2=45°,∵∠ADB=90°,∴△BDQ是等腰直角三角形.。
