chapter2-foundations of individual behavior(1)
远大前程第二部分中英双语介绍

the Great Expectation story is divided into three phases of Pip's life expectations. Now i will introduce you the second phase and then have a brief study of the Bible’s influence on the characterization of two people in the book - havisham and Joe gargery.The second stage of Pip's expectations has Pip in London, learning the details of being a gentlemen, having tutors, fine clothing, and joining cultured society. Whereas he always engaged in honest labour when he was younger, he now is supported by a generous allowance given by the attorney Mr.Jaggers, which he frequently lives beyond. He learns to fit in this new milieu, and experiences not only friendship but rivalry as he finds himself in the same circles as Estella, who is also pursued by many other men, especially Bentley Drummle, whom she favours.As he adopts the physical and cultural norms of his new status, he also adopts the class attitudes that go with it, and when Joe comes to visit Pip and his friend and roommate Herbert to deliver an important message, Pip is embarrassed to the point of hostility by Joe's unlearned ways, despite his protestations of love and friendship for Joe.During this time, He learns that 20 years ago, havisham was swindled a large amount of money by brother Arthur and her fiance compeyson, thus became dispirited and dwell on the past memories. Pip asks why the fiance didn’t marry her to get the assets instead of choosing to obtain the half wealth sharing with her brother,Herbert explains that it is perhaps because the fiance was a married man,if he married havisham,his wife and arthur would conspire to expose his deceit,which would make him lose the trust and assets from havisham,so he has to give in.At the end of this stage, Pip is introduced to his benefactor, again changing his world.He turns out to be the outlaw who pip once helped and offers the story from a different perspective:he is another accomplice of the tragedy.under the guidance of compeyson,he and compeyson’s wife killed arthur and grabbed his assets to do some illegal trade. Later they got arrested imprisoned. The outlaw’s wife who was charged with a murder just delivered the daughter estella, the attorney of miss havisham helped her to escape the imprisonment , in return , estella was sent to havisham.threatened with the future of the outlaw and their daughter ,the wife had to be the attorney’s slave for over 20 years.在希伯来圣经中所讲述的早期的以色列文化中,“女性从属”的普遍性已经是一个不争的事实。
高等意识手册.txt

HANDBOOK TO HIGHER CONSCIOUSNESSKen Keyes Jr.ForewordMillions of years ago when our animal ancestors had to survive in the jungle,it was necessary to have an instantly effective fight or flight mechanism.When a tiger was about to spring, an automatic emotional response was a lifesaver. A nervous shock was needed to squirt adrenalin into the blood so thatmuscles became jet powered. Emotional alarms were needed to commandfull attention. When a tiger was ready to jump, there was no time to admirethe beautiful sunset. As a jungle survival mechanism, our animal ancestorswere programmed for automatic duality -- automatic feelings of otherness,threat, and paranoia. Survival required instant domination of consciousnessto meet the perils of the jungle.We are the pioneers in the evolution of human consciousness. It was onlyabout 10,000 years ago that our ancestors built the first cities. As civilizationgrew, survival no longer depended on the instant fight or flight of the jungle.Survival and happiness now depend on tuning in to the overall situationinvolving ourselves, the people around us, and the total environment of thehere and now. Perceptiveness, wisdom, and oneness are now the ingredientsof effective and happy living. But our biocomputers are still programmed forjungle fight or flight -- for a fast release of adrenalin into the blood stream,and for rapid heartbeat -- for automatic anger and fear. In our socialinteractions, our consciousness magnifies molehills and makes them intomountains -- and this constant distortion destroys our energy, our insight, andour ability to love.Thus survival in the jungle meant that we had to be programmed for instantparanoia -- instant fear -- instant anger -- instant perception of duality.Survival in our world today means that we must have instant perceptions ofoneness -- of love -- of compassion with everyone and understanding ofeverything around us. When we learn to cut through our paranoid jungleprogramming, we are on our way to higher consciousness and happiness.Evolution is now working to remedy this primitive jungle alarm wiring in ourbrain that tends to hold us on lower consciousness levels. Paranoid, dualisticindividuals who cannot love themselves and others tend to get heart trouble,ulcers, other psychosomatic diseases, are accident-prone, etc. Perhaps in100,000 years, through the ruthless survival of the fittest, humans may havenervous systems that are automatically structured to produce instant insightsthat facilitate love and oneness. But that doesn¡¯t help you and me. We needthe Living Love Way to show us how to live in higherconsciousness as soonas possible -- to override our jungle programming so that we can enjoy livinghere and now.We have escaped from the domination of instincts (inflexible unlearnedbehavior) that guides animals through their daily life situations. Since theyoung human is not provided with a full repertoire of automatic fixedresponses, we are unable to independently cope with life for a number ofyears after birth. This long period of plasticity and openness to learningcomplex life guidance patterns helps us avoid fixed preprogrammed behavior.For example, this long nurturing period lets us learn complex languagesystems -- and our flexibility is such that we can learn to communicate inSwahili as easily as in English or any other language.Instead of a complete pattern of animal-type instincts to provide survivalresponses to life situations, the young child uses ego mechanisms backed byhair-trigger emotions to develop security, sensation, and power magnificationof the moment-to-moment sensory inputs. Our personal development intofulfilling, happy lives (as well as the progression ofcivilization beyond thedangerous power consciousness) depends on our getting free of our egobacked,subject-object, me-them, security-sensation-power hang-ups.It may be helpful to see this progression of consciousness in outline form asfollows:ORGANISM METHOD OFPROTECTING ANDENHANCING THEORGANISMAnimal Relatively fixed lifestyle based on instinctor unlearnedpreprogrammedbehavior.LowerConsciousnessHumanEgo-directed, subjectobject,emotion-backedsecurity, sensation, andpower consciousness(increasingly involvingthe rational mind) thatmakes us inflexiblyguard and protecthabitual folkways andpersonal patterns.HigherConsciousnessHumanThe ego-driven negativeemotions have beenreplaced by wideranginginsight and deepintuitive understandinggiving full flexibility toflow in mutuallysupportive and lovingways with no inflexiblefolkways and personalpatterns.The biocomputer with which you are equipped is the mostremarkableinstrument in the universe. Your only problem is to learn to use it properly. Itis capable of handling two million visual inputs and one hundred thousandauditory inputs at any one time. Your biocomputer operates continuallythroughout all of its parts and is capable of making millions of simultaneouscomputations. It operates with enormous power primarily on unconsciouslevels -- with only a tiny proportion of its activity rising to the level ofconsciousness. The conscious level of your biocomputer is analogous to theprint-out of the man-made computers. Your journey into higher consciousness is a matter of your learning how to properly program yourremarkable biocomputer. When you really learn to operate your exquisitemechanism, you will be able to fully realize your potential for a happy life.A wonderful thing about life is that it is naturally good. Lifeis set up to work-- to produce love, fulfillment, and happiness continuously. However, varioussituations during your first years of life conditioned you in the methods ofconsciousness which continually generate unhappiness in your life. Yet everycurrent experience can aid you in your growth toward higher consciousness ifyou know how to use it.This Handbook will explain how you have been creating the experiences thatyou have. It will show you exactly what to do to break out of the traps inyour mind that are the cause of all the unhappiness that you have experiencedin your life! When you apply the Methods in the Handbook you will be ableto turn your life around. The continuous experience of love, serenity,happiness, joy, effectiveness, perceptiveness, and wisdom thatyou have hadonly in bits and pieces can now be available to you all of the time.You will learn how to experience the world as a friendly, loving place that hasbeen designed to give you everything that you need. You will develop a¡°miraculous¡± quality in your life. Beautiful things will happen socontinuously that you can no longer ascribe it to mere¡°coincidence.¡± Youwill experience that you can create more love, happiness, and serenity thanyou need for living a thoroughly fulfilled and enjoyable life. While this was certainly not your intention, you will becomeaware of howyou have been turning yourself off to the energies of the world around you.Your mind has been programmed to process incoming visual, auditory, andother information in ways that continuously alienate and separate you frompeople. You will realize that you have been unconscious of what you havebeen doing to yourself. it is as though you have been born with eyes that seeonly with great distortion -- but which give the illusion of seeing sharply andclearly. This handbook will help you become aware that the only realproblem in your life involves how consciously you use your mind -- and itgives you clear instructions for carrying out the inner work necessary tobecome an energetic, perceptive, loving being.Living Love is a positive cure for all of the suffering and unhappiness in yourlife and that of all humanity. The Living Love Way offers mankind one of themost powerful tools for emerging victorious in the race between higherconsciousness and the suffering of atomic annihilation,ecologicaldegradation, prejudice, and the thousand-fold ways we separate ourselvesfrom each other.Chapter 1Why This Book Was Written For Us¡°Most of us,¡± said the cosmic humorist, ¡°go through life not knowing whatwe want, but feeling damned sure this isn¡¯t it.¡±Over 99% of the people in the western world live on lower consciousnesslevels characterized by trying to find enough security, sex,¡°groovy¡±sensations, ego rushes, prestige, money, power, and status. This endlessstruggle yields lives of constant resentment, worry, suspicion, anger, jealousy,shyness, and fear. Everything people tell themselves they must do to behappy ends up yielding more frustration than joy. The more successful aperson is in making money, collecting skills and possessions, developingexciting sexual relationships, acquiring knowledge and degrees, and achievingpositions of status, power, and prestige, the less loving, peaceful, andcontented he may find himself or herself.And yet it is not these things in and of themselves that create an unhappy life-- it is the internal mental addiction or desire for them that minute-by-minutekeeps one from enjoying life. Addictions (or emotion-backed demands) bringfear of non-fulfillment; jealousy that someone may steal our source offulfillment; anger when someone thwarts us; cynicism ifconstantlyundersupplied; paranoia if constantly threatened; boredom ifwe¡¯re making noprogress toward satisfying our addictions; worry if we can¡¯t see a steadysupply; anxiety if we¡¯re worried about being worried; and unhappiness whenthe outside world does not supply us with whatever it is we are addicted to.Since the nature of life is such that we win some and lose some, an addictedperson has no chance of living a happy, loving, peaceful, conscious, wise andeffective life. And the addictive programming is not necessary to find andenjoy that which we prefer in life.You are ready for growth into the happiness of higher consciousness whenyou realize the utter futility of trying to live a beautiful life by your efforts torearrange or change the world of people and things outside of you to fit youraddictions and desires. You will find you have only to rearrange your ownpersonal, automatically programmed responses to life situations -- most ofwhich are childhood hangups.As you work toward higher levels of consciousness, you will find that youhave always had enough to be happy. It is the patterns in your head thatmake you unhappy, although you usually blame the people and conditionsoutside you for your unhappiness. Your journey into higher consciousnesscan enable you to be loving, peaceful, wise, and free of a constant barrage ofunpleasant emotional feelings.Living Love offers you four advantages in your adventure into higherconsciousness:1.For many people it can be one of the most powerful and rapidways forgrowth into higher consciousness that has ever been available to mankind.2.It does not require you to detach yourself from your presentlife. LivingLove can be used most effectively if you stay with your present business,personal life, and other conditions until you have grown to ahigh enoughstate of consciousness to be fully perceptive of the arbitrary mores,folkways, and social roles you are guarding and living out.3.Once you thoroughly understand the system, it is notessential to have ateacher for continuing your growth. Your life will be your best teacher, foryou will discover that you are always putting yourself into learningsituations that are ideal for your growth. The programming that you mostneed to change has an unerring way of putting you into life situations thatcan make you aware of the exact inner work you should be doing. 4.When you use the Living Love Way to find the love, innerpeace, wisdom,and effectiveness of higher consciousness, your inner work on yourselfimmediately adds to your enjoyment of life. With the Living Love Way,happiness is not a distant goal -- it is an ever-growing part of your hereand now.Think of the energy you now put into the up-and-down hour-by-hour copingwith your feelings while you continually try to rearrange the people andsituations in your life so that you can then be loving, serene, effective, andhappy. And yet year by year your quest for happiness is aselusive as findingthe pot of gold at the end of the rainbow. Since almost everyone around youseems to be having similar trouble in becoming a happy, loving being, youmay have lowered your standards and decided that continuous happiness isprobably not realistic.The Living Love Way invites you to set the highest imaginable standards oflove, serenity, peace, wisdom, effectiveness, and continuous happiness foryour life. and then you are ready to begin your journey into higherconsciousness.Chapter 2Secrets of HappinessWhy do we have lives filled with turmoil, desperation, and anxiety? Why arewe always pushing ourselves and others? Why do we have only small dribbles of peace, love, and happiness? Why is it that human beings arecharacterized by bickering and turmoil that make animals¡¯ relationships withtheir own species seem peaceful in comparison? The answer is so simple --but it is sometimes difficult for us to really understand because almost everyway we were taught to work toward happiness only reinforces the feelingsand activities that make us unhappy.This is a central point that must be understood. The ways we were taught tobe happy can¡¯t possibly work. Unless we see this point clearly, we cannotprogress to higher consciousness. Here¡¯s why.Most of us assume that our desires (backed up by our emotional feelings) arethe true guides to doing the things that will make us happy. But no one hasyet found happiness by using emotion-backed desires as guides. Flashes ofpleasure, yes; happiness, no.Our wants and desires are so seductive . . . They masquerade as ¡°needs¡± thatmust be satisfied so we can be happy at last. They lead us from one illusionof happiness to another. Some of us tell ourselves, ¡°if I can just get to bepresident of this corporation, I will be happy.¡± But have you ever seen areally happy president? His outside drama may feature beautiful yachts,Cadillacs, Playboy bunnies -- but is he really happy inside? Has his ulcergone away yet?We constantly tell ourselves such things as, ¡°If I could just go back to schooland acquire more knowledge -- perhaps get a Master¡¯s degree -- then I willbe happy.¡± But are people with Master¡¯s degrees or Ph.D.¡¯s any happier thanthe rest of us? It is beautiful to acquire knowledge but it is misleading toexpect it to bring us peace, love, and happiness. We tell ourselves, ¡°If I couldonly find the right person to love, then I would be happy.¡± So we search forsomeone who our addictions tell us is the right person -- and we experiencesome pleasurable moments. But since we don¡¯t know how to love, therelationship gradually deteriorates. Then we decide we didn¡¯t have the rightperson after all! As we grow into higher consciousness, we discover that it ismore important to be the right person than to find the right person.We must deeply understand why all of our negative emotions are misleadingguides to effective action in life situations. Our negative emotions are simplythe result of an extensive pattern of scars and wounds that we haveexperienced. And these emotional wounds lead us to perceive differencesthat make us uptight instead of similarities that enable us to understand andlove. The present programming of our emotions makes us perceive otherpeople (and the conditions of the world around us) as threats -- potentiallydangerous to our well-being. We then respond with adrenalin, fasterheartbeat, increased blood sugar, and other jungle survival responses thatprepare us for fight or flight. We are trapped in our ways of perceiving theworld around us.But no one (or no situation) need be felt as an emotional threat or dangerwhen we see things with the clearer perception of higher consciousness.Think of the most threatening situation you have felt in the last day or two.Are you about to lose your job? Is the person for whom you feel the mostlove paying more attention to someone else than to you? Do you have unpaidbills that you cannot take care of? Do you have a pain that could be cancer?Now, these problems either have solutions -- or they don¡¯t. Either you can dosomething about them here and now -- or you can¡¯t. If you can do somethinghere and now about them, then do it -- even if it¡¯s just a first step. It sapsyour energy to be worried or anxious about a problem. Do what you can do-- but don¡¯t be addicted to the results or you will create more worry foryourself. If you can¡¯t do anything about a problem here and now, then whymake yourself uncomfortable and drain your energy by worrying about it? Itis part of the here and nowness of your life. That¡¯s what is -- here and now.Worry, anxiety, or other unpleasant emotions are absolutely unnecessary --and simply lower your insight and the effectiveness of your actions.You must absolutely convince yourself of the lack of utility of these drainingemotions. You must see your unnecessary worrying as depriving you of theflowing effectiveness and joyousness that you should have in your life. Aslong as you think that these negative emotions have any function whatsoever,you will retard your growth into higher consciousness. If you do not hassleyourself emotionally when the outside world does not conform with yourinside programming (your desires, expectations, demands, or models of howthe world should treat you) you will have so much energy that you probablywill sleep fifty per cent less. You will be joyous and loving, and reallyappreciate each moment of your life -- no matter what¡¯s happening in theworld of people and situations outside you.Where and how did we get this emotional programming? Almost allof it wasacquired in the first few years of life. For example, when we were veryyoung, we had the experience of mother forcefully taking a perfume bottlefrom our tiny fingers and at the same time sending out bad vibrations basedon her desire not to have her perfume bottle broken. We cried. Throughbeing painfully pushed around, dominated, told what to do, and controlledwhen we were babies, we developed our emotionally intense security,sensation, and power programs. Many of our emotion-backed programscame from repeated moral directives or statements about howthings ¡°should¡±be. We developed a ¡°self¡± consciousness with robot-like emotionalresponses to protect the ¡°survival¡± of this separate self.So we become emotionally programmed to feel that we must have power tocontrol and manipulate people in order to be happy. We eventually becomevery finely attuned to the actions or vibrations of any person or situation thateven remotely threatens our power addictions -- our ability to manipulate andcontrol people and things around us.As we reach physical maturity and our biocomputer (or brain) is able tofunction more perceptively, we have all the power we need. Butourbiocomputer (backed up by the full repertory of our emotions) is stillprogrammed to compensate for the power deficiency we experienced whenwe were infants and young children. We now need to learn to flow with thepeople and things around us. But our power addiction keeps usfrom lovingpeople because we perceive them as objects that may threaten our power,prestige, or pecking order. If we want to love and be loved, we can¡¯t beaddicted to power -- or to anything else.As conscious beings the only thing we need to find happiness in life is toperceive clearly who we are (we are pure consciousness and notthe socialroles we are acting out), and exactly what are the real conditions, here andnow, of our lives. How basically simple is our problem! But to achieve thisclear perception of ourselves and the world around us takes constant innerwork. And this means developing the habit of emotionallyacceptingwhatever is here and now in our lives. For only an emotionally calmbiocomputer can see clearly and wisely, and come up witheffective ways tointeract with people and situations.Our power addiction is only one example of the happiness-destroyingprogramming that we put into our biocomputers when we were too young toperceive the realities of the world in which we lived. Although we now havethe basic capacity for clear perception, the operatinginstructions we gave ourbiocomputer anchor us to the lower levels. And so we¡¯re unconsciouslytrapped.Here and now is the reality in our lives -- and it is only from the conditions ofthe present that our future can be generated. But our present addictions,demands, and expectations (the programming of our biocomputer) dominateour consciousness and force us to spend most of the time we are awake (andmost of the time we are dreaming) in protesting and pouting about the hereand now situation in our lives. This lowers our perceptiveness and keeps usfrom finding effective solutions to our problems. The Living Love Way toHigher Consciousness shows us how to break through this trap, to freeourselves, and to find our full potential as human beings.Chapter 3The Law of Higher ConsciousnessYour growth into higher consciousness should begin by fully understandingthe importance of becoming one with the Law of Higher Consciousness :Love everyone unconditionally -- including yourself.This law can enable you to find the hidden splendor withinyourself andothers. Unfortunately, we have never been taught how to love unconditionally. Almost all of our loving has been motivated by emotionaldesires programmed into us at an early age. Most of our love experienceshave taught us we must earn or deserve love before we can have it -- and thatothers must deserve our love. This is conditional love -- it is like a barter or abusiness transaction. It is no wonder that our well-meaning but unskilledattempts to love usually end up in separation and alienation. We have beentaught to place conditions on our love : ¡°If you really loved me you would . ..¡± -- and then we use one of our addictions to finish the sentence. This is anexchange -- it is not unconditional love.What is unconditional love? It is not, ¡°I can love you if you do what myemotional programming -- my addictions -- says I want you todo.¡± It is justlove. Just, ¡°I love you because you are there. I love you because you arepart of the nowness of my life. I love you because although our bodies andminds may be on different trips, on the consciousness level allof us are alikein our humanness. We are one.¡±Real love is simply accepting another person. Completely and unconditionally! We experience things from his or her psychic space. It islike seeing the world through his or her eyes. Whatever he or she is goingthrough -- whatever he or she is feeling -- we have been there, too -- at sometime in our lives.When we love, we view others as unfolding beings in their journey towardhigher consciousness. We realize that no matter how intensely we strive forworldly attainments, we all seek love and oneness on the consciousnesslevel. We are all on the journey to higher consciousness. Some of us arehearing the messages life offers us and are working consciouslyto eliminateour addictions. Others are not progressing rapidly because they do not yetknow how to consciously work on themselves.We must also learn to love ourselves -- right here and now. We need to feelthat no matter how horrible we have judged our past actions, each day our lifebegins anew. We have at all times been lovable. A child may be naughty, buthe is always lovable. And so we are all children as long as weareprogrammed with our lower consciousness addictions. So we must acceptthe melodramas we get involved in as we live out our current crop ofaddictions. This, too, is a part of life and growth.Every part of the system of Living Love is designed to help you learn to loveeveryone unconditionally -- including yourself. You only need to plant theliving Love seeds in your consciousness and they willautomatically sprout.Do not berate yourself because you are not enlightened by thethird Tuesdayof next month. The more you learn to love and accept yourself,the more youwill realize that you are doing exactly what you need to do to provideyourself with experiences to grow into higher consciousness.How can you love others if you do not love yourself? The love you have foryourself and the love you have for ¡°another¡± are buildingblocks joiningtogether within you to create the beautiful edifice of real love. Learning to love unconditionally means getting free ofinterference from ourprogrammed addictions -- those emotion-backed demandinginstructions toour biocomputer. This enables us to perceive clearly what is here and now --to evaluate wisely -- and to act effectively to do whatever we want to doabout it. They key to this is the instant emotional acceptance of the here andnow -- the emotional acceptance of the previously unacceptable. When our emotions are triggered, we cannot perceive clearly our actual lifesituation. Our biocomputer then sends a flow of information toourconsciousness in which separation and alienation are emphasized. We createa horribly warped evaluation of the here and now based on our addictiveprogramming. When this happens, we magnify differences and suppresssimilarities between ourselves and ¡°others.¡± And this destroys our ability tolove unconditionally.We all know that just having the desire to love is not enough. As far back aswe can remember we have been aware of the importance of love in our lives.We know that lack of love is responsible for most of the unhappiness in theworld -- for difficulties in getting along with other people, for pollution,prejudice, wars, and other individual and group crimes against humanity. butwhat can we do about it?The Law of Higher Consciousness suggests a practical guide forthe AquarianAge :You add suffering to the worldjust as much when you take offenseas when you give offense.。
Mechanizing set theory cardinal arithmetic and the axiom of choice

Mechanizing Set TheoryCardinal Arithmetic and the Axiom of ChoiceLawrence C.PaulsonComputer Laboratory,University of Cambridgeemail:lcp@Krzysztof GrabczewskiNicholas Copernicus University,Toru´n,Polandemail:kgrabcze@mat.uni.torun.plJanuary1996Minor revisions,November2000Abstract.Fairly deep results of Zermelo-Frænkel(ZF)set theory have been mechanized using the proof assistant Isabelle.The results concern cardinal arithmetic and the Axiom of Choice (AC).A key result about cardinal multiplication isκ⊗κ=κ,whereκis any infinite cardinal. Proving this result required developing theories of orders,order-isomorphisms,order types, ordinal arithmetic,cardinals,etc.;this covers most of Kunen,Set Theory,Chapter I.Further-more,we have proved the equivalence of7formulations of the Well-ordering Theorem and20 formulations of AC;this covers thefirst two chapters of Rubin and Rubin,Equivalents of the Axiom of Choice,and involves highly technical material.The definitions used in the proofs are largely faithful in style to the original mathematics.Key words:Isabelle,cardinal arithmetic,Axiom of Choice,set theory,QED projectContents1Introduction1 2Isabelle and ZF Set Theory2 3The Cardinal Proofs:Motivation and Discussion33.1Infinite Branching Trees33.2Overview of Kunen,Chapter I5 4Foundations of Cardinal Arithmetic74.1Well-orderings74.2Order Types84.3Combining Well-orderings84.4Cardinal Numbers94.5Cardinal Arithmetic10 5Provingκ⊗κ=κ105.1Kunen’s Proof105.2Mechanizing the Proof12 6The Axiom of Choice and the Well-Ordering Theorem15 7Rubin and Rubin’s AC Proofs177.1The Well-Ordering Theorem177.2The Axiom of Choice187.3Difficulties with the Definitions207.4General Comments on the Proofs217.5Consolidating Some Proofs227.6The Axiom of Dependent Choice24 8Proving WO6=⇒WO1248.1The idea of the proof258.2Preliminaries to the Mechanization268.3Mechanizing the Proof27 9Conclusions302Lawrence C.Paulson and Krzysztof GrabczewskiMechanizing Set Theory11.IntroductionA growing corpus of mathematics has been checked by machine.Researchers have constructed computer proofs of results in logic[26],number theory[25], group theory[28],λ-calculus[10],etc.An especially wide variety of results have been mechanized using the Mizar Proof Checker,including the theorem κ⊗κ=κdiscussed below[2].However,the problem of mechanizing mathe-matics is far from solved.The Boyer/Moore Theorem Prover[3,4]has yielded the most impressive results[25,26].It has been successful because of its exceptionally strong sup-port for recursive definitions and inductive reasoning.But its lack of quantifiers forces mathematical statements to undergo serious contortions when they are formalized.Most automated reasoning systems arefirst-order at best,while mathematics makes heavy use of higher-order notations.We have conducted our work in Isabelle[20],which provides for higher-order syntax.Other recent systems that have been used for mechanizing mathematics include IMPS[6], HOL[8]and Coq[5].We describe below machine proofs concerning cardinal arithmetic and the Axiom of Choice(AC).Paulson has mechanized most of thefirst chapter of Kunen[12]and a paper by Abrial and Laffitte[1].Gra¸bczewski has mech-anized thefirst two chapters of Rubin and Rubin’s famous monograph[24], proving equivalent eight forms of the Well-ordering Theorem and twenty forms of AC.We have conducted these proofs using an implementation of Zermelo-Frænkel(ZF)set theory in pared with other Isabelle/ZF proofs [15,18,21]and other automated set theory proofs[23],these are deep,abstract and highly technical results.We have tried to reproduce the mathematics faithfully.This does not mean slavishly adhering to every detail of the text,but attempting to preserve its spirit.Mathematicians write in a mixture of natural language and symbols; they devise all manner of conventions to express their ideas succinctly.Their proofs make great intuitive leaps,whose detailed justification requires much additional work.We have been careful to note passages that seem unusually hard to mechanize,and discuss some of them below.In conducting these proofs,particularly from Rubin and Rubin,we have tried to follow the footsteps of Jutting[11].During the1970s,Jutting mech-anized a mathematics textbook using the AUTOMATH system[14].He paid close attention to the text—which described the construction of the real and complex numbers starting from the Peano axioms—and listed any deviations from pared with Jutting,we have worked in a more abstractfield,and with source material containing larger gaps.But we have had the advantage of much more powerful hardware and software.We have relied upon Isabelle’s reasoning tools(see§2below)tofill some of the gaps for us.2Lawrence C.Paulson and Krzysztof GrabczewskiWe have done this work in the spirit of the QED Project[22],which aims “to build a computer system that effectively represents all important mathe-matical knowledge and techniques.”Our results provide evidence,both posi-tive and negative,regarding the feasibility of QED.On the positive side,we are able to mechanize difficult mathematics.On the negative side,the cost of doing so is hard to predict:a short passage can cause immense difficulties. Overview.Section2is a brief introduction to Isabelle/ZF.The remaining sections reportfirst Paulson’s work and then Gra¸bczewski’s.Sections3–5dis-cuss the foundations of cardinal arithmetic in increasing detail,culminating in the machine proof of a key result about cardinal multiplication,κ⊗κ=κwhereκis infinite.Section6introduces the Axiom of Choice and describes the mechanization of Abrial and Laffitte.Sections7and8are devoted to the mechanization of parts of Rubin and Rubin.Section9presents some conclu-sions.2.Isabelle and ZF Set TheoryIsabelle[20]is a generic proof assistant.It supports proofs in higher-order log-ic,various modal logics,linear logic,etc.Our work is based upon Isabelle’s implementation of Zermelo-Frænkel(ZF)set theory,itself based upon an imple-mentation offirst-order logic.Isabelle/ZF arose from early work by Paul-son[17]and No¨e l[15];it is described in detail elsewhere[18,21].There are two key ideas behind Isabelle:−Expressions are typedλ-terms.Thus the syntax is higher-order,giving a uniform treatment of quantifiers,descriptions and other binding operators.In Isabelle/ZF,all sets have the same type.But other important objects, such as classes,class relations and class functions,can be expressed using higher types.−Theorems are schematic inference rules.Isabelle’s basic inference mech-anism is to join two schematic rules,in a sort of Horn clause resolution.A typical step in a backward proof consists of joining one rule(typicallya lemma)to another rule(representing the proof state).Thus,theoremsare proved by referring to previous theorems.Proof states may contain unknowns:placeholders for terms that have been left unspecified.Unifica-tion can incrementally instantiate unknowns,which may be shared among several subgoals.Built around these key ideas are various facilities intended to ease the user’s task.Notations can be defined using a general mixfix format,with precedences; variable-binding operators are easily specified.Isabelle manages a database ofMechanizing Set Theory 3theories and theorems;when asked to load a theory,it automatically loads any other theories that it depends upon.Although Isabelle supports proof checking,users will be more productive if they are provided with automatic tools.−The classical reasoner solves subgoals using methods borrowed from tab-leau provers.It employs user-supplied rules,typically about logical con-nectives or set operators,to break down assertions.−The simplifier employs user-supplied conditional equalities to rewrite a subgoal.It can make use of contextual information and handles commuta-tive operators using a simple method borrowed from Boyer and Moore [3,page 104].We have found these tools indispensable.But there is much room for improve-ment;mechanizing a page of text can take a week or more.We discuss some reasons for this below.A lengthier introduction to Isabelle and Isabelle/ZF appears elsewhere [18].The Isabelle documentation has been published as a book [20].Figure 1sum-marizes the Isabelle/ZF notation for set theory.Note.Application of the function f to the argument x is formally written f ‘x .In informal mathematics we use the more familiar f (x )for clarity.But a set-theoretic function is just another set,and Isabelle allows the notation f (x )only if f is a meta-level function.This usually corresponds to subscripting in informal mathematics,for example f x .For the Isabelle/ZF development of functions,see Paulson [18,§7.5].3.The Cardinal Proofs:Motivation and DiscussionThe original reason for mechanizing the theory of cardinals was to general-ize Paulson’s treatment of recursive data structures in ZF.The original treat-ment [21]permitted only finite branching,as in n -ary trees.Countable branch-ing required defining an uncountable ordinal.We are thus led to consider branching of any cardinality.3.1.I NFINITE B RANCHING T REESLet κstand for an infinite cardinal and κ+for its successor cardinal.Branching by an arbitrarily large index set I requires proving the theorem|I |≤κ∀i ∈I αi <κ+( i ∈I αi )<κ+(1)4Lawrence C.Paulson and Krzysztof Grabczewskisyntaxdescription {a 1,...,a n }finite set <a ,b >ordered pair {x :A.P [x ]}Separation {y .x :A ,Q [x,y ]}Replacement {b [x ].x :A }functional Replacement INT x :A.B [x ]x ∈A .B [x ],general intersection UN x :A.B [x ]x ∈A .B [x ],general union A Int BA ∩B ,intersection A Un BA ∪B ,union A ->BA →B ,function space A *BA ×B ,Cartesian product PROD x :A.B [x ]Πx ∈A .B [x ],general product SUM x :A.B [x ]Σx ∈A .B [x ],general sum THE x.P [x ]ιx.P [x ],definite description lam x :A.b [x ]λx ∈A .b [x ],abstraction f ‘xf ‘x or f (x ),function application a :Aa ∈A ,membership A <=BA ⊆B ,subset relation ALL x :A.P [x ]∀x ∈A .P [x ],bounded quantifierEX x :A.P [x ]∃x ∈A .P [x ],bounded quantifierFigure 1.ASCII notation for ZFYou need not understand the details of how this is used in order to follow the paper.1Not many set theory texts cover such material well.Elementary texts [9,27]never get far enough,while advanced texts such as Kunen [12]race through it.But Kunen’s rapid treatment is nonetheless clear,and mentions all the essen-tial elements.The desired result (1)follows fairly easily from Kunen’s Lem-ma 10.21[12,page 30]:∀α<κ|X α|≤κ| α<κX α|≤κThis,in turn,relies on the Axiom of Choice and its consequence the Well-ordering Theorem,which are discussed at length below.It also relies on a fundamental result about multiplication of infinite cardinals:κ⊗κ=κ.This is Theorem 10.12of Kunen.(In this paper,we refer only to his Chapter I.)The proof presents a challenging example of formalization,as we shall see.Mechanizing Set Theory5 We could prove A×A≈A,for all infinite sets A,by appealing to AC in the form of Zorn’s Lemma;see Halmos[9,pages97–8].Thenκ⊗κ=κwould follow immediately.But we need to proveκ⊗κ=κwithout AC in order to use it in later proofs about equivalences of AC.In fact,the law A×A≈A is known to be equivalent to the Axiom of Choice.Paulson hoped to proveκ⊗κ=κdirectly,but could notfind a suitable proof.He therefore decided to mechanize the whole of Kunen’s Chapter I, up to that theorem.We suggest this as a principle:theorems do not exist in isolation,but are part of a framework of supporting theorems.It is easier in the long run to build the entire framework,not just the parts thought to be relevant. The latter approach requires frequent,ad-hoc extensions to the framework.3.2.O VERVIEW OF K UNEN,C HAPTER IKunen’sfirst chapter is entitled,“Foundations of Set Theory.”Kunen remarks on page1that the chapter is merely a review for a reader who has already stud-ied basic set theory.This explains why the chapter is so succinct,as compared say with Halmos[9].Thefirst four sections are largely expository.Section5introduces a few axioms while§6describes the operations of Cartesian product,relations,func-tions,domain and range.Already,§6goes beyond the large Isabelle/ZF the-ory described in earlier papers[18,21].That theory emphasized computa-tional notions,such as recursive data structures,at the expense of traditional set theory.Now it was time to develop some of the missing material.Paul-son introduced some definitions about relations,orderings,well-orderings and order-isomorphisms,and proved thefirst two lemmas by well-founded induc-tion.The main theorem required a surprising amount of further work;see§4.3 below.Kunen’s§7covers ordinals.Much of this material had already been formal-ized in Isabelle/ZF[21,§3.2],but using a different definition of ordinal.A set A is transitive if A⊆P(A):every element of A is a subset of A.Kunen defines an ordinal to be a transitive set that is well-ordered by∈,while Isabelle/ZF defines an ordinal to be a transitive set of transitive sets.The two definitions are equivalent provided we assume,as we do,the Axiom of Foundation.Our work required formalizing some material from§7concerning order types and ordinal addition.We have also formalized ordinal multiplication.But we have ignored what Kunen calls A<ωbecause Isabelle/ZF provides list(A), the set offinite lists over A[21,§4.3]for the same purpose.Kunen’s§8and§13address the legitimacy of introducing new notations in axiomatic set theory.His discussion is more precise and comprehensive than Paulson’s defence of the notation of Isabelle/ZF[18,page361].Kunen’s§9concerns classes and recursion.The main theorems of this sec-tion,justifying transfinite induction and recursion over the class of ordinals,6Lawrence C.Paulson and Krzysztof Grabczewskiwere already in the Isabelle/ZF library[21,§3.2,§3.4].Kunen discusses here (and with some irony in§12)the difficulties of formalizing properties of class-es.Variables in ZF range over only sets;classes are essentially predicates,so a theorem about classes must be formalized as a theorem scheme.Many statements about classes are easily expressed in Isabelle/ZF.An ordi-nary class is a unary predicate,in Isabelle/ZF an object of type i⇒o,where i is the type of sets and o is the type of truth values.A class relation is a binary predicate and has the Isabelle type i⇒(i⇒o).A class function is tradition-ally represented by its graph,a single-valued class predicate[12,page25];it is more easily formalized in Isabelle as a meta-level function,an object of type i⇒i.See Paulson[18,§6]for an example involving the Replacement Axiom.Because Isabelle/ZF is built uponfirst-order logic,quantification over vari-ables of types i⇒o,i⇒i,etc.,is forbidden.(And it should be;allowing such quantification in uses of the Replacement Axiom would be illegitimate.)How-ever,schematic definitions and theorems may contain free variables of such types.Isabelle/ZF’s transfinite recursion operator[21,§3.4]satisfies an equa-tion similar to Kunen’s Theorem9.3,expressed in terms of class functions.Isabelle/ZF does not overload set operators such as∩,∪,domain and list to apply to classes.Overloading is possible in Isabelle,but is probably not worth the trouble in this case.And the class-oriented definitions might be cumber-some.Serious reasoning about classes might be easier in some other axiomatic framework,where classes formally exist.Kunen’s§10concerns cardinals.Some of these results presented great dif-ficulties and form one of the main subjects of this paper.But the Schr¨o der-Bernstein Theorem was already formalized in Isabelle/ZF[21,§2.6],and the first few lemmas were straightforward.An embarrassment was proving that the natural numbers are cardinals.This boils down to showing that if there is a bijection between an m-element set and an n-element set then m=n.Proving this obvious fact is most tiresome.Rea-soning about bijections is complicated;a helpful simplification(due to M.P. Fourman)is to reason about injections instead.Prove that if there is an injec-tion from an m-element set to an n-element set then m≤n.Applying this implication twice yields the desired result.Many intuitively obvious facts are hard to justify formally.This came up repeatedly in our proofs,and slowed our progress considerably.It is a funda-mental obstacle that will probably not yield to improved reasoning tools.Kunen proves(Theorem10.16)that for every ordinalαthere is a larger car-dinal,κ.Under AC this is an easy consequence of Cantor’s Theorem;without AC more work is required.Paulson slightly modified Kunen’s construction, lettingκbe the union of the order types of all well-orderings of subsets ofα, and found a pleasingly short machine proof.Our main concern,as mentioned above,is Kunen’s proof ofκ⊗κ=κ.We shall examine the machine proof in great detail.The other theorems of Kunen’sMechanizing Set Theory7§10concern such matters as cardinal exponentiation and cofinality.We havenot mechanized these,but the only obstacle to doing so is time.The rest of Kunen’s Chapter I is mainly discussion.4.Foundations of Cardinal ArithmeticLet us examine the cardinal proofs in detail.We begin by reviewing the neces-sary definitions and theorems.Then we look at the corresponding Isabelle/ZF theories leading up to the main result,κ⊗κ=κ.Throughout we shall con-centrate on unusual aspects of the formalization,since much of it is routine.4.1.W ELL-ORDERINGSA relation<is well-founded over a set A provided every non-empty subset of A has a<-minimal element.(This implies that<admits no infinite decreas-ing chains···<x n<···<x2<x1within A.)If furthermore A,< is a linear ordering then we say that<well-orders A.A function f is an order-isomorphism(or just an isomorphism)between two ordered sets A,< and A ,< if f is a bijection between A and A that preserves the orderings in both directions:x<y if and only if f(x)< f(y) for all x,y∈A.Write A,< ∼= A ,< if there exists an order-isomorphism between A,< and A ,< .If A,< is an ordered set and x∈A then pred(A,x,<)def={y∈A|y< x}is called the(proper)initial segment determined by x.We also speak of A itself as an initial segment of A,< .Kunen develops the theory of relations in his§6and proves three funda-mental properties of well-orderings:−There can be no isomorphism between a well-ordered set and a proper initial segment of itself.A useful corollary is that if two initial segments are isomorphic to each other,then they are equal.−There can be at most one isomorphism between two well-ordered sets.This result sounds important,but we have never used it.2−Any two well-orderings are either isomorphic to each other,or else one of them is isomorphic to a proper initial segment of the other.Kunen’s proof of the last property consists of a single sentence:Let f={ v,w |v∈A∧w∈B∧ pred(A,v,<A) ∼= pred(B,w,<B) };note that f is an isomorphism from some initial segment of A onto some initial segment of B,and that these initial segments cannot both be proper. This gives the central idea concisely;Suppes[27,pages233–4]gives a much longer proof that is arguably less clear.However,the assertions Kunen makes are not trivial and Paulson needed two days and a half to mechanize the proof.4.2.O RDER T YPESThe ordinals may be viewed as representatives of the well-ordered sets.Every ordinal is well-ordered by the membership relation∈.What is more important, every well-ordered set is isomorphic to a unique ordinal,called its order type and written type(A,<).Kunen[12,page17]proves this by a direct construc-tion.But to mechanize the result in Isabelle/ZF,it is easier to use well-founded recursion[21,§3.4].If A,< is a well-ordering,define a function f on A by the recursionf(x)={f(y)|y<x}for all x∈A.Thentype(A,<)def={f(x)|x∈A}.It is straightforward to show that f is an isomorphism between A,< and type(A,<),which is indeed an ordinal.Our work has required proving many properties of order types,such as methods for calculating them in particular cases.Our source material contains few such proofs;we have spent much time re-discovering them.4.3.C OMBINING W ELL-ORDERINGSLet A+B def=({0}×A)∪({1}×B)stand for the disjoint sum of A and B, which is formalized in Isabelle/ZF[21,§4.1].Let A,<A and B,<B be well-ordered sets.The order types of certain well-orderings of A+B and A×B are of key importance.The sum A+B is well-ordered by a relation<that combines<A and<B, putting the elements of A before those of B.It satisfies the following rules:a <A aInl(a )<Inl(a)b <B bInr(b )<Inr(b)a∈A b∈BInl(a)<Inr(b)The product A×B is well-ordered by a relation<that combines<A and<B,lexicographically:a <A ab ,b∈B,b a∈A b <B bCardinal=OrderType+Fixedpt+Nat+Sum+constsLeast::(i=>o)=>i(binder"LEAST"10)eqpoll,lepoll,lesspoll::[i,i]=>o(infixl50)cardinal::i=>i("|_|")Finite,Card::i=>odefsLeast_def"Least(P)==THE i.Ord(i)&P(i)&(ALL j.j<i-->˜P(j))"eqpoll_def"A eqpoll B==EX f.f:bij(A,B)"lepoll_def"A lepoll B==EX f.f:inj(A,B)"lesspoll_def"A lesspoll B==A lepoll B&˜(A eqpoll B)"Finite_def"Finite(A)==EX n:nat.A eqpoll n"cardinal_def"|A|==LEAST i.i eqpoll A"Card_def"Card(i)==(i=|i|)"endFigure2.Isabelle/ZF Theory Defining the Cardinal Numbers The well-orderings of A+B and A×B are traditionally used to define the ordinal sum and product.We do not require ordinal arithmetic until we come to the proofs from Rubin and Rubin.But we require the well-orderings themselves in order to proveκ⊗κ=κ.That proof requires yet another well-ordering construction:inverse image.If B,<B is an ordered set and f is a function from A to B then define <A byx<A y⇐⇒f(x)<B f(y).Clearly<A is well-founded if<B is.If f is injective and<B is a well-ordering then<A is also a well-ordering.If f is bijective then obviously f is an isomor-phism between the orders A,<A and B,<B ;it follows that their order types are equal.Sum,product and inverse image are useful for expressing well-orderings; this follows Paulson’s earlier work[16]within Constructive Type Theory.4.4.C ARDINAL N UMBERSFigure2presents the Isabelle/ZF definitions of cardinal numbers,following Kunen’s§10.The Isabelle theoryfile extends some Isabelle theories(Order-Type and others)with constants,which stand for operators or predicates.The constants are defined essentially as follows:−The least ordinalαsuch that P(α)is defined by a unique description[18, pages366–7]and may be written LEASTα.P(α).−Two sets A and B are equipollent if there exists a bijection between them.Write A≈B or,in Isabelle,A eqpoll B.−B dominates A if there exists an injection from A into B.Write A B or A lepoll B.−B strictly dominates A if A B and A≈B.Write A≺B orA lesspoll B.−A set isfinite if it is equipollent to a natural number.−The cardinality of A,written|A|,is the least ordinal equipollent to A.Without AC,no such ordinal has to exist;we might then regard|A|as undefined.But everything is defined in Isabelle/ZF.The operator THE returns0unless the description identifies an object uniquely.Thus,an “undefined”cardinality equals0;this conveniently ensures that|A|is always an ordinal.−A set i is a cardinal if i=|i|;write Card(i).Reasoning from these definitions is entirely straightforward except for the “obvious”facts aboutfinite cardinals mentioned above.4.5.C ARDINAL A RITHMETICLetκ,λ,µrange overfinite or infinite cardinals.Cardinal sum and product are defined in terms of disjoint sum and Cartesian product:κ⊕λdef=|κ+λ|κ⊗λdef=|κ×λ|These satisfy the familiar commutative,associative and distributive laws.The proofs are uninteresting but non-trivial,especially as we work without AC.We do so in order to use the results in proving various forms of AC to be equivalent (see below);but frequently this forces us to construct well-orderings explicitly.5.Provingκ⊗κ=κWe begin with an extended discussion of Kunen’s proof and then examine its formalization.5.1.K UNEN’S P ROOFKunen calls this result Theorem10.12.His proof is admirably concise.0,κκ,0α,00,α0,0Figure 3.Predecessors of α,β ,with β≤αTheorem.If κis an infinite cardinal then κ⊗κ=κ.Proof.By transfinite induction on κ.Assume this holds for smaller cardi-nals.Then for α<κ,|α×α|=|α|⊗|α|<κ(applying Lemma 10.10when αis finite).3Define a well-ordering on κ×κby α,β γ,δ iff max(α,β)<max(γ,δ)∨[max(α,β)=max(γ,δ)∧α,β precedes γ,δ lexicographically ].Each α,β ∈κ×κhas no more than|succ(max(α,β))×succ(max(α,β))|<κpredecessors in ,so type(κ×κ, )≤κ,whence |κ×κ|≤κ.Since clearly |κ×κ|≥κ,|κ×κ|=κ.The key to the proof is the ordering ,whose structure may be likened to that of a square onion.Let αand βbe ordinals such that β≤α<κ.The predecessors of α,β include all pairs of the form α,β for β <β,and all pairs of the form α ,α for α <α;these pairs constitute the αth layer of the onion.The other predecessors of α,β are pairs of the form γ,δ such that γ,δ<α;these pairs constitute the inner layers of the onion.(See Figure 3.)The set of all -predecessors of α,β is a subset of succ(α)×succ(α), which gives an upper bound on its cardinality.Kunen expresses this upper bound in terms of max(α,β)to avoid having to assumeβ≤α.To simplify the formal proofs,Paulson used the more generous upper bound |succ(succ(max(α,β)))×succ(succ(max(α,β)))|.This is still a cardinal belowκ.As Kunen notes,there are two cases.Ifαorβis infinite then succ(succ(max(α,β)))<κbecause max(α,β)<κand because infinite cardinals are closed under successor;therefore,the inductive hypothesis realizes our claim.On the other hand,ifαandβare bothfinite, then so is succ(succ(max(α,β))),whileκis infinite by assumption.To complete the proof,we must examine the second half of Kunen’s sen-tence:“so type(κ×κ, )≤κ,whence|κ×κ|≤κ.”Recall from§4.2that there is an isomorphismf:κ×κ→type(κ×κ, )such thatf(α,β)={f(γ,δ)| γ,δ α,β }.Thus,f(α,β)is an ordinal with the same cardinality as the set of predecessors of α,β .This implies f(α,β)<κfor allα,β<κ,and therefore type(κ×κ, )≤κ.Because f is a bijection betweenκ×κand type(κ×κ, ),we obtain|κ×κ|≤κ.The opposite inequality is trivial.5.2.M ECHANIZING THE P ROOFProvingκ⊗κ=κrequires formalizing the relation .Kunen’s definition looks complicated,but we can get the same effect using our well-ordering constructors(recall§4.3).Note that is an inverse image of the lexicographic well-ordering ofκ×κ×κ,under the function g:κ×κ→κ×κ×κdefined byg(α,β)= max(α,β),α,β ;this function is trivially injective.Figure4presents part of the Isabelle theoryfile for cardinal arithmetic.It defines as the constant csquare rel.Here is a summary of the operators appearing in its definition:−rvimage(A,f,<)is the inverse image ordering on A derived from< by f.−lam<x,y>:K*K.<x Un y,x,y>is the function called g above.The pattern-matching in the abstraction expands internally to the con-stant split,which takes apart ordered pairs[18,page367].Finally Un denotes union;note that max(α,β)=α∪βfor ordinalsαandβ.。
《月亮与六便士》chapter 2

Chapter 1I confess that when first I made acquaintance with Charles Strickland I never for a moment discerned that there was in him anything out of the ordinary. Yet now few will be found to deny his greatness. I do not speak of that greatness which is achieved by the fortunate politician or the successful soldier; that is a quality which belongs to the place he occupies rather than to the man; and a change of circumstances reduces it to very discreet proportions. The Prime Minister out of office is seen, too often, to have been but a pompous rhetorician, and the General without an army is but the tame hero of a market town. The greatness of Charles Strickland was authentic. It may be that you do not like his art, but at all events you can hardly refuse it the tribute of your interest. He disturbs and arrests. The time has passed when he was an object of ridicule, and it is no longer a mark of eccentricity to defend or of perversity to extol him. His faults are accepted as the necessary complement to his merits. It is still possible to discuss his place in art, and the adulation of his admirers is perhaps no less capricious than the disparagement of his detractors; but one thing can never be doubtful, and that is that he had genius. To my mind the most interesting thing in art is the personality of the artist; and if that is singular, I am willing to excuse a thousand faults. I suppose Velasquez was a better painter than El Greco, but custom stales one's admiration for him: the Cretan, sensual and tragic, proffers the mystery of his soul like a standing sacrifice. The artist, painter, poet, or musician, by his decoration, sublime or beautiful, satisfies the aesthetic sense; but that is akin to the sexual instinct, and shares its barbarity: he lays before you also the greater gift of himself. To pursue his secret has something of the fascination of a detective story. It is a riddle which shares with the universe the merit of having no answer. The most insignificant of Strickland's works suggests a personality which is strange, tormented, and complex; and it is this surely which prevents even those who do not like his pictures from being indifferent to them; it is this which has excited so curious an interest in his life and character.It was not till four years after Strickland's death that Maurice Huret wrote that article in the Mercure de France which rescued the unknown painter from oblivion and blazed the trail which succeeding writers, with more or less docility, have followed. For a long time no critic has enjoyed in France a more incontestable authority, and it was impossible not to be impressed by the claims he made; they seemed extravagant; but later judgments have confirmed his estimate, and the reputation of Charles Strickland is now firmly established on the lines which he laid down. The rise of this reputation is one of the most romantic incidents in the history of art. But I do not propose to deal with Charles Strickland's work except in so far as it touches upon his character. I cannot agree with the painters who claim superciliously that the layman can understand nothing of painting, and that he can best show his appreciation of their works by silence and a cheque-book. It is a grotesque misapprehension which sees in art no more than a craft comprehensible perfectly only to the craftsman: art is a manifestation of emotion, and emotion speaks a language that all may understand. But I will allow that the critic who has not a practical knowledge of technique is seldom able to say anything on the subject of real value, and my ignorance of painting is extreme. Fortunately, there is no need for me to risk the adventure, since my friend, Mr. Edward Leggatt, an able writer as well as an admirable painter, has exhaustively discussed Charles Strickland's work in a little book(1) which is a charming example of a style, for the most part, less happily cultivated in England than in France.(1) "A Modern Artist: Notes on the Work of Charles Strickland, " by Edward Leggatt, A. R. H. A. Martin Secker, 1917.Maurice Huret in his famous article gave an outline of Charles Strickland's life which was well calculated to whet the appetites of the inquiring. With his disinterested passion for art, he had a real desire to call the attention of the wise to a talent which was in the highest degree original; but he was too good a journalist to be unaware that the "human interest" would enable him more easily to effect his purpose. And when such as had come in contact with Strickland in the past, writers who had known him in London, painters who had met him in the cafes of Montmartre, discovered to their amazement that where they had seen but an unsuccessful artist, like another, authentic genius had rubbed shoulders with them there began to appear in the magazines of France and America a succession of articles, the reminiscences of one, the appreciation of another, which added to Strickland's notoriety, and fed without satisfying the curiosity of the public. The subject was grateful, and the industrious Weitbrecht-Rotholz in his imposing monograph(2) has been able to give a remarkable list of authorities.(2) "Karl Strickland: sein Leben und seine Kunst, " by Hugo Weitbrecht-Rotholz, Ph. D. Schwingel und Hanisch. Leipzig, 1914.The faculty for myth is innate in the human race. It seizes with avidity upon any incidents, surprising or mysterious, in the career of those who have at all distinguished themselves from their fellows, and invents a legend to which it then attaches a fanatical belief. It is the protest of romance against the commonplace of life. The incidents of the legend become the hero's surest passport to immortality. The ironic philosopher reflects with a smile that Sir Walter Raleigh is more safely inshrined in the memory of mankind because he set his cloak for the Virgin Queen to walk on than because he carried the English name to undiscovered countries. Charles Strickland lived obscurely. He made enemies rather than friends. It is not strange, then, that those who wrote of him should have eked out their scanty recollections with a lively fancy, and it is evident that there was enough in the little that was known of him to give opportunity to the romantic scribe; there was much in his life which was strange and terrible, in his character something outrageous, and in his fate not a little that was pathetic. In due course a legend arose of such circumstantiality that the wise historian would hesitate to attack it.But a wise historian is precisely what the Rev. Robert Strickland is not. He wrote his biography(3) avowedly to "remove certain misconceptions which had gained currency" in regard to the later part of his father's life, and which had "caused considerable pain to persons still living. " It is obvious that there was much in the commonly received account of Strickland's life to embarrass a respectable family. I have read this work with a good deal of amusement, and upon this I congratulate myself, since it is colourless and dull. Mr. Strickland has drawn the portrait of an excellent husband and father, a man of kindly temper, industrious habits, and moral disposition. The modern clergyman has acquired in his study of the science which I believe is called exegesis an astonishing facility for explaining things away, but the subtlety with which the Rev. Robert Strickland has "interpreted" all the facts in his father's life which a dutiful son might find it inconvenient to remember must surely lead him in the fullness of time to the highest dignities of the Church. I see already his muscular calves encased in the gaiters episcopal. It was a hazardous, though maybe a gallant thing to do, since it is probable that the legend commonly received has had no small share in the growth of Strickland's reputation; for there are many who have been attracted to his art by the detestation in which they held his character or the compassion withwhich they regarded his death; and the son's well-meaning efforts threw a singular chill upon the father's admirers. It is due to no accident that when one of his most important works, The Woman of Samaria, (4) was sold at Christie's shortly after the discussion which followed the publication of Mr. Strickland's biography, it fetched POUNDS 235 less than it had done nine months before when it was bought by the distinguished collector whose sudden death had brought it once more under the hammer. Perhaps Charles Strickland's power and originality would scarcely have sufficed to turn the scale if the remarkable mythopoeic faculty of mankind had not brushed aside with impatience a story which disappointed all its craving for the extraordinary. And presently Dr. Weitbrecht-Rotholz produced the work which finally set at rest the misgivings of all lovers of art.(3) "Strickland: The Man and His Work, " by his son, Robert Strickland. Wm. Heinemann, 1913.(4) This was described in Christie's catalogue as follows: "A nude woman, a native of the Society Islands, is lying on the ground beside a brook. Behind is a tropical Landscape with palm-trees, bananas, etc. 60 in. x 48 in. "Dr. Weitbrecht-Rotholz belongs to that school of historians which believes that human nature is not only about as bad as it can be, but a great deal worse; and certainly the reader is safer of entertainment in their hands than in those of the writers who take a malicious pleasure in representing the great figures of romance as patterns of the domestic virtues. For my part, I should be sorry to think that there was nothing between Anthony and Cleopatra but an economic situation; and it will require a great deal more evidence than is ever likely to be available, thank God, to persuade me that Tiberius was as blameless a monarch as King George V. Dr. Weitbrecht-Rotholz has dealt in such terms with the Rev. Robert Strickland's innocent biography that it is difficult to avoid feeling a certain sympathy for the unlucky parson. His decent reticence is branded as hypocrisy, his circumlocutions are roundly called lies, and his silence is vilified as treachery. And on the strength of peccadillos, reprehensible in an author, but excusable in a son, the Anglo-Saxon race is accused of prudishness, humbug, pretentiousness, deceit, cunning, and bad cooking. Personally I think it was rash of Mr. Strickland, in refuting the account which had gained belief of a certain "unpleasantness" between his father and mother, to state that Charles Strickland in a letter written from Paris had described her as "an excellent woman, " since Dr. Weitbrecht-Rotholz was able to print the letter in facsimile, and it appears that the passage referred to ran in fact as follows: God damn my wife. She is an excellent woman. I wish she was in hell. It is not thus that the Church in its great days dealt with evidence that was unwelcome. Dr. Weitbrecht-Rotholz was an enthusiastic admirer of Charles Strickland, and there was no danger that he would whitewash him. He had an unerring eye for the despicable motive in actions that had all the appearance of innocence. He was a psycho-pathologist, as well as a student of art, and the subconscious had few secrets from him. No mystic ever saw deeper meaning in common things. The mystic sees the ineffable, and the psycho-pathologist the unspeakable. There is a singular fascination in watching the eagerness with which the learned author ferrets out every circumstance which may throw discredit on his hero. His heart warms to him when he can bring forward some example of cruelty or meanness, and he exults like an inquisitor at the auto da fe of an heretic when with some forgotten story he can confound the filial piety of the Rev. Robert Strickland. His industry has been amazing. Nothing has been too small to escape him, and you may be sure that if Charles Strickland left a laundry bill unpaid it will be given you in extenso, and if he forebore to return a borrowed half-crown no detail of thetransaction will be omitted.老实说,我刚刚认识查理斯·思特里克兰德的时候,从来没注意到这个人有什么与众不同的地方,但是今天却很少有人不承认他的伟大了。
Foundations of Entrepreneurship

Ch. 1: The Foundations of Entrepreneurship
Copyright © 2011 Pearson Education
1-4
What is an Entrepreneur?
One who creates a new business in the face of risk and uncertainty for the purpose of achieving profit and growth by identifying opportunities and assembling the necessary resources to capitalize on them.
Copyright © 2011 Pearson Education
Ch. 1: The Foundations of Entrepreneurship
1 - 11
The Cultural Diversity of Entrepreneurship
Young entrepreneurs
Ch. 1: The Foundations of Entrepreneurship
Ch. 1: The Foundations of Entrepreneurship
Copyright © 2011 Pearson Education
1 - 10
Feeding the Entrepreneurial Fire
(continued)
Entrepreneurs as heroes Entrepreneurial education Demographic and economic factors Shift to a service economy Technology advancements Independent lifestyles E-commerce and the Internet International opportunities
987, Chapter 2
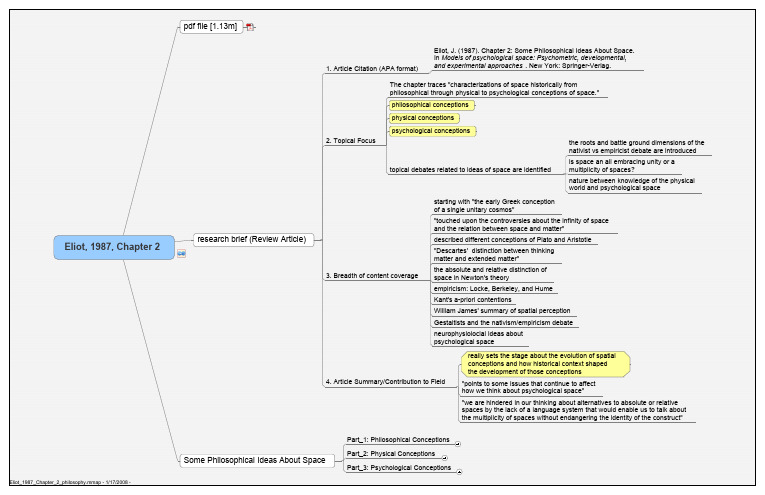
Eliot, 1987, Chapter 2pdf file [1.13m]research brief (Review Article)1. Article Citation (APA format)Eliot, J. (1987). Chapter 2: Some Philosophical Ideas About Space.In Models of psychological space: Psychometric, developmental,and experimental approaches. New York: Springer-Verlag.2. Topical FocusThe chapter traces "characterizations of space historically fromphilosophical through physical to psychological conceptions of space."philosophical conceptionsphysical conceptionspsychological conceptionstopical debates related to ideas of space are identifiedthe roots and battle ground dimensions of thenativist vs empiricist debate are introducedis space an all embracing unity or amultiplicity of spaces?nature between knowledge of the physicalworld and psychological space3. Breadth of content coveragestarting with "the early Greek conceptionof a single unitary cosmos""touched upon the controversies about the infinity of spaceand the relation between space and matter"described different conceptions of Plato and Aristotle"Descartes' distinction between thinkingmatter and extended matter"the absolute and relative distinction ofspace in Newton's theoryempiricism: Locke, Berkeley, and HumeKant's a-priori contentionsWilliam James' summary of spatial perceptionGestaltists and the nativism/empiricism debateneurophysiolocial ideas aboutpsychological space4. Article Summary/Contribution to Fieldreally sets the stage about the evolution of spatialconceptions and how historical context shapedthe development of those conceptions"points to some issues that continue to affecthow we think about psychological space""we are hindered in our thinking about alternatives to absolute or relativespaces by the lack of a language system that would enable us to talk aboutthe multiplicity of spaces without endangering the identity of the construct" Some Philosophical Ideas About SpacePart_1: Philosophical ConceptionsPart_2: Physical ConceptionsPart_3: Psychological ConceptionsEliot, 1987, Chapter 2pdf file [1.13m]research brief (Review Article)Some Philosophical Ideas About SpacePart_1: Philosophical Conceptions(1) Pre-Socratic(2) Plato(3) Aristotle(4) Middle Ages(5) Four Prominent Views(6) Scholasticism; Augustine (354-340)(7) Early Arab Philosophy(8) Mediaeval(9) 14th Century Scholastics(10) 15th and 16th Century(11) Renaissance philosophers(12) Rene Descartes (1596-1650)Part_2: Physical Conceptions(13) Line of Development 1: space mainly as anobject of physics --Isaac Newton (1643-1727)Line of Development 2: space as anGNOSEOLOGICAL concept (works ofBritish empiricists)(14) Locke (1632-1704)(15) Berkeley (1685-1753)(16) Hume, Lambert (1728-1777), Leibniz (1646-1716)(17) Kant (1724-1804)Part_3: Psychological Conceptions(18) Transition(19) Consequences of Newtonianconception (19th century)(20) William James (1890)(21) Nativism; Hochberg (1962)Eliot, 1987, Chapter 2pdf file [1.13m]research brief (Review Article)Some Philosophical Ideas About SpacePart_1: Philosophical Conceptions(1) Pre-SocraticPre-Socratic Philosopherscosmos or "structured order" a single unitary world"the assumption that the whole universewas incorporated in one all-embracing orunified space (Gosztonyi, 1976, pp.55-57)""unity of space"finite or infinite?concept of infinity: Anaximandros(610-547 B.C.)"Space, still conceived as a unity,nonetheless, could contain an infinitenumber of worlds like our own.""the borders of our world did notnecessarily coincide with the border ofspace"Archytasplace (topos)"is would be possible at the end of theworld to stretch out one's hand...""one must agree that space is unlimited"Atomistsconcentrated on the problem of matter.The distinction between space and matterwas unclearPythagoreans...the existence of the void...Anaxagoras (c. 488-428 B.C.)tried to disprove the possibility of the voidby physical observationsmany pre-Socratic philosopherscontributed important ideas to ourunderstanding of space,ideas that have great influence over the centuries(2) PlatoThe Timaeusdescribed space (chora) as somethingwhich, in its potential form, alreadyexisted before our world.space is opposed to the real thingnamely the ideas (or forms)and provides a place in which faint copiesof the eternal ideas form our world ofbecoming and perishingdistinguishes betweenthinking (noesis)sensation (aisthesis)space (triton genos)in its potential form, provides thepossibility of rthe real being, the ideas, tocome together with the nonbeing and thusfrom the things of our world of becomingthings do not emerge OUT OF SPACE,but only IN space as faint copies of the ideasthe process of becoming in our world can(in part) be characterized as aspatialization of ideas.both in its potential and its actual form,space is not directly accessible to ourperception.we can only infer space from the spatiality of the objectsthe atoms are composed of triangles, and theelements differ in the number of triangles buildingup their respective atomsatmos of fire have the form of pyramids(composed of four triangle)atoms of water are composed of 20triangles, and therefore can roll easily see SACHS, 1917it applied geometric concepts to spatial phenomenaconcept of three-dimensionality(3) Aristotledid not use the term "space" (chora), butrather "place" (topos)place as the fifth of ten categoriesplace is a quantitydistinguishes between discrete andcontinuous quantities place is continuousin his Physics (especially Book IV)treated space as a category and as a physical realityfinal definition implied that the place of an object is theadjacentimmovableboundary of the containing bodyintroduced space as a categoryan accident of substanceplace is the boundary of the bodycan be viewed as the totality of all placesor as the boundary of all bodiesoccupying placesand thus as the boundary of our cosmosall places are relative to that boundarydescribed space as having three extensions andthus being three-dimensional thus space is unisotropichis doctrine of the "natural places" of theelements further implies that space is also inhomogeneousspace itself is immovablehis definition tied space to corporealityappears to be the first Greek philosopherwho dealt with spatial perception(4) Middle AgesWilliam of Occamstill treated space within the framework ofsubstance and accidentTheophrastus and Stratton denied the existence of the vacuum(5) Four Prominent Viewsclassic pre-Socratic philosophy of natureidentified the borders of the cosmos and spaceby postulating the unity of the cosmosintroducing the important idea of the unity of spaceAtomistic theoryclearly distinguished matter and spaceintroduced space as somethingimmaterial but realalso implied the importance ofhomogeneity of spaceimplicitly raised the problem of whetherspace is to be thought of asisotropicor unisotropicinitiated longstanding debates aboutthe infinity of spaceand the possibility of an empty space or vacuumPlatonic theorystressed the distinction betweenthe ideal worldand our (spatial) world of becomingand the distinction between space inits potentialand its actual form (the spatiality of things)elaborated on the Pythagorean thought of ananalysis of matter and space by geometric conceptsdeveloped the notion that we cannotperceive space directly,but can only know about it by inferenceAristotlehis view dominated the greater part ofmedieval philosophyimplied the view of space as a category which was later reinterpreted as a form of our experiencethe definition of place as the adjacentboundary of the containing bodyand the interpretation of space asthe totality of placesimmovableand limited by the outer spacehis theory denied the existence of a vacuumimplied the doctrine of "natural places"and of forces inherent in spaceassumed three-dimensionalityand regarded space as bothunisotropicand inhomogeneousregarded space as an accidentintroducing the tradition of treating spacewithin the categorical framework ofsubstanceaccidenthis interpretation of space as dependenton the physical bodies, as finite andimmovable as a wholehas been regarded by some authors as a hindrancefor the development of theorizing about space up tothe end of the Middle Ages and even later(6) Scholasticism; Augustine (354-340)space interpreted more and moremetaphysically and theologicallyargued that space could not be infinite since this wouldconflict with the concept of an almighty God(7) Early Arab Philosophy(8) Mediaeval(9) 14th Century Scholastics(10) 15th and 16th Century(11) Renaissance philosophers(12) Rene Descartes (1596-1650)Part_2: Physical Conceptions(13) Line of Development 1: space mainly as anobject of physics --Isaac Newton (1643-1727)Line of Development 2: space as anGNOSEOLOGICAL concept (works ofBritish empiricists)(14) Locke (1632-1704)(15) Berkeley (1685-1753)(16) Hume, Lambert (1728-1777), Leibniz (1646-1716)(17) Kant (1724-1804)Part_3: Psychological Conceptions(18) Transition(19) Consequences of Newtonianconception (19th century)(20) William James (1890)(21) Nativism; Hochberg (1962)Eliot, 1987, Chapter 2pdf file [1.13m]research brief (Review Article)Some Philosophical Ideas About SpacePart_1: Philosophical Conceptions(1) Pre-Socratic(2) Plato(3) Aristotle(4) Middle Ages(5) Four Prominent Views(6) Scholasticism; Augustine (354-340)(7) Early Arab Philosophyalso dominated by theological interestsgreatly influenced by aristotletheir theory of space, however, differedfrom the doctrine of the Greek Atomists inthatthe atoms were held to have no extensionand were thought of as points in space.three-dimensionality of space and of thebodies in space was thus explained bythe relationsh of many atoms occupyingdifferent locaitons(8) MediaevalAquinas (1225-1274)added theological ideas to Aristotles viewsuch as the notion that God is spacelessand beyond any spatialitybut that space--like the whole cosmos--isnonetheless under his powerCouncil of the Doctors of the Sorbonne (1277)debates concluded by authoritarian verdictsdeclared the Aristotelian view that there isan absolutely immovable body in spaceto be heretical because this viewcontradicted the doctrine of an almightyGod.God could move the whole universeSilesian philosopher, Witelo (1220-1277)analyzed the sense of sight and decidedthat it is directed only at the perception oflight and colorthought that spatial perception could notrely on sight alonebut must involve an association andcombination of sensory elements(9) 14th Century ScholasticsHugh of St. Victor (1096-1141)tried to revive the Atomistic DoctrineNicholas of Autrecourt (died after 1350)tried to revive the Atomistic DoctrineJewish thinker, Hasdai Crescas (1340-1412)criticized Aristotle's view directlydescribed space as an empty dimensionalextension that is capable of taking up matterspace is a unity, homogeneous, immaterial,infinite, immovable and without "inner powers"thought to have contributed greatly to our modernview of physical space as being free ofmetaphysical forces and as being independent ofsubstanceformmatterand physical qualitieshis theory is central to the modern idea ofabstracting space from physical processesand his view on an immovable, "absolute"space reoccurs later in Newton(10) 15th and 16th CenturyItialian and German philosophersBernhardino Telesio (1508-1588)described space as a container of beingspace is incorporeal, immaterial,formless, free of inherent forces, andimmovable in its entirety(11) Renaissance philosophersGerman, Nicholas of Cusa (1401-1464)Franciscus Patritius (1529-1597)developed a metaphysical theory of lightexplicity refused to treat space within thetraditional Aristotelian scheme ofsubstance and accident.space exists before matterthe study of space was fundamental to all natural scienceGiordano Bruno (1548-1600)appears to have been influenced by Crescasbut went far beyond empirically orientedconceptions by asserting the existence ofa countless number of worlds like our ownin endless spaceeventually sentenced to death for refusingto retract these ideasCopernicusassumed the existence of a system ofspheres (if a heliocentric one), not ofsingle planets.held a homocentric view by insisting thatthe earth has a special status as thehome of manKeplerheld a homocentric view by insisting thatthe earth has a special status as thehome of manGalileoarrived at a conclusion about space whichis evident in modern thoughtnoted that there is the space in oureveryday experience and our scientificobservations:the space of intuitionthe idea of an infinite space forces us totranscent intuitive space by mathematicaland geometrical constructioninto the concept of abstract orconstructive spacewhich is no longer fully accessible to oursense and experience(12) Rene Descartes (1596-1650)Meditations (1641)struggling against skepticismargued that a special subjective evidence isboth certain and fundamental to knowledgeeach one of us is a "thinking matter" andtherefore must existspatial extension is an innate idea (ideae innatae)space must be involved when the objectsof the outer world are percieved"extended matter" in opposition to the"thinking matter"analytic geometry proceeds byCONSTRUCTING its elementary objectslikecircletriangleplaneetcout of such innate ideas as spatialextension or shaperather than by abstracting them fromphysical objectsbelieved in the existence of innate ideasideas not derived from experiencebut which come to mind with suchcertainty that they cannot be ignored ordisputedthe famous "wax example" of his secondMEDITATION (1641)argued that our knowledge of all qualitiesof a piece of wax can be doubted, up tothe principle that it has spatial extensionspatial extension is a principle whichcannot be broken down into severalspecifications by our mind any attempt to do so would be an "idle abstraction"spatial extension is a necessary, basicpredicate of the physical worldAristotle's philosophy of space also had asimilar double aspectspace introduced as a category and, yet,it was also conceived of as a property ofphysical objectsnote to self: does this have anyconnections with Artaud's "Theatre and itsdouble?"Descartes' theory may be considered as the starting pointof the longstanding debate as to whether spaceis best considered as an ideaor as something real,that is, the discussion of ideality versus reality of spacePart_2: Physical Conceptions(13) Line of Development 1: space mainly as anobject of physics --Isaac Newton (1643-1727)Line of Development 2: space as anGNOSEOLOGICAL concept (works ofBritish empiricists)(14) Locke (1632-1704)(15) Berkeley (1685-1753)(16) Hume, Lambert (1728-1777), Leibniz (1646-1716)(17) Kant (1724-1804)Part_3: Psychological Conceptions(18) Transition(19) Consequences of Newtonianconception (19th century)(20) William James (1890)(21) Nativism; Hochberg (1962)Eliot, 1987, Chapter 2pdf file [1.13m]research brief (Review Article)Some Philosophical Ideas About SpacePart_1: Philosophical Conceptions(1) Pre-Socratic(2) Plato(3) Aristotle(4) Middle Ages(5) Four Prominent Views(6) Scholasticism; Augustine (354-340)(7) Early Arab Philosophy(8) Mediaeval(9) 14th Century Scholastics(10) 15th and 16th Century(11) Renaissance philosophers(12) Rene Descartes (1596-1650)Part_2: Physical Conceptions(13) Line of Development 1: space mainly as anobject of physics --Isaac Newton (1643-1727)culminated in Newton's Principia (1687)distinguishes between two types of space,absolute and relative:absolute space"in its own nature, without relation toanything external, remains always similarand immovable"relative spaceis some moveable dimension or measureof the absolute space, which our sensesdetermine by its position to bodies"and Newton's Optics (1704)Newtons conception of space becamefundamental for classical physicsas a theory of physical space it marks theend of a tradition in natural philosophyphysical world consisted oftimespaceforcemasswith "space made up of points, timecomposed of instances, and both existingindependently of the bodies and eventswhich occupy them"in modern physics coordinate systems arenothing but a useful fiction not so for NewtonNewton argued that relative space as wellis accessible to us only via the relations ofthe objects in it.by contrast, absolute space is conceivedas immovable and homogenous.it was conceived as a container orframework which, like the Cheshire Cat'sgringwas something that remained after thecontents had been removed.Line of Development 2: space as anGNOSEOLOGICAL concept (works ofBritish empiricists)(14) Locke (1632-1704)if there were innate ideas, then everyonewould agree on themour mindis like "white paper void of all characters"into which all ideas enter "from experience;in that all our knowledge is founded,and from that it ultimately derives itself"the idea of space, is a simple one arrivedat by sight and touchspace differs from the body in that is itwithout soliditywithout resistance against moving bodiescontinuousimmovablespatial perception is not directed at spaceitself, but at the spatiality of the bodiesand at spatial relations(15) Berkeley (1685-1753)impression of spatiality, provided bysense of touch and spatial visionis only possible through the association ofthe impressions of vision with impressionsof touchfor our experience, we learn to associatecertain optic impressions with haptic orkinaesthetic ones,and thus arrive at spatial perceptionwhen discussing spatial vision, alluded to sensationsof tension when we adjust the muscles of our eyesto view distant objectsappears to have been the first to mentionboth the phenomenon of convergence inbinocular vision and the phenomenon ofaccommodationdenied the existence of absolute physicalspace and by asserting that nothing existsoutside our own thoughts.extended matter exists only in theperception and the imaginations of themindfor the outer world to exist means onlythat it is perceived (esse est percipi)the psychological treatment of traditional gnoseological problems byLocke and the further development of his theories by Berkeley thusprovided an empirical foundation to several of our modernpsychological theories of spatial perception.(16) Hume, Lambert (1728-1777), Leibniz (1646-1716)the empiricists claimed (especially Hume)their theory of knowledge to be valid both asa philosophical theoryand a psychological theoryGerman Mathematician Lambertinsisted the problem of a-priori conceptswas a logical and not a psychological oneLeibnizgenerally wrote of "virtually innate ideas"meaning that they were implied in thefunctions of mind but were not necessarily conscious in every caseHumewidened significantly the cleavage between empiricistsand nativists philosophers with respect to the questionof how we obtain our knowledge of the world(17) Kant (1724-1804)introduced a clear distinction between thephilosophical and the psychologicalinterpretations of the doctrine of innateideas.began his CRITIQUE OF PURE REASONwith an empiricist statement:"There is no doubt whatsoever that all ourknowledge begins with experience"However, he went on to add that"nevertheless, it does not necessarily allspring from experience."experience has temporal priority in ourknowledge, the bases of our knowledgehave logical a-priority over experiencesince without certain prerequisites ofknowledge, our experience would beimpossible.the only thing that can be said about these problems within aKantian framework is that the world is of indefinite magnitudePart_3: Psychological Conceptions(18) Transition(19) Consequences of Newtonianconception (19th century)(20) William James (1890)(21) Nativism; Hochberg (1962)Eliot, 1987, Chapter 2pdf file [1.13m]research brief (Review Article)Some Philosophical Ideas About SpacePart_1: Philosophical Conceptions(1) Pre-Socratic(2) Plato(3) Aristotle(4) Middle Ages(5) Four Prominent Views(6) Scholasticism; Augustine (354-340)(7) Early Arab Philosophy(8) Mediaeval(9) 14th Century Scholastics(10) 15th and 16th Century(11) Renaissance philosophers(12) Rene Descartes (1596-1650)Part_2: Physical Conceptions(13) Line of Development 1: space mainly as anobject of physics --Isaac Newton (1643-1727)Line of Development 2: space as anGNOSEOLOGICAL concept (works ofBritish empiricists)Part_3: Psychological Conceptions(18) TransitionLocke, Berkeley, and Hume introduced the psychological point of viewKantdelineating the philosophical point of view against itwas an a-priorist, not a nativistKantian doctrine was not designed as an empirical modelthus reaching the point historically wherepsychological theories of spaceseparate from the more generalphilosophical traditionsand become important fields of researchin their own right(19) Consequences of Newtonianconception (19th century)Gibson (1950)Extensity, shape, and distance: thesewere the primary constituents of spacethe problem of how we apprehendthe Newtonian universebecame essentially the problem of howwe apprehend geometric spacethe question that confronted philosophersof the 19th century waswhether every point in the visual field wasintrinsically connected at birthor whether points in the visual field weredifferentiated through experienceand then associated with an appropriateretinal point in the eye.Allport (1955)"spatiality" as a capacity of mind--i.e. nativistsnativist doctrinelocal signs were intrinsically spatial in characterthe points of sensory stimulation were "directly labeled"in phenomenological experience as to their lociHering (1861-1864)signs were attached to the visualexperiences arising from each retinal pointthere were three such signs for each point,one for each of the three dimensionsto account for spatial perception it was notnecessary to bring in eye movement becausethe spatial aspect was immediately givenLotze, Helmholtz, and Wundt (allempiricists) held a different viewLotzethe signs which were connected withsensations, or were properties of them, werenot originally endowed with a spatial character but had to acquire itthe process of acquisition involved muscularsensations and the associative combination orfusion of sensory componentsEvery tactile and retinal point had its local label.the aspect of sensory experience whichcarried the spatial quality was, for Lotze,the attribute of intensityspecifically, it was the intensity ofmuscular sensation, and intensity patternfor the spot touched...with the continuous movement of thereceptor in relation to the surfacethe successive local signs areexperienced in proper sequenceof the two positions, empiricism appearedthe stronger for two reasonsno anatomical structures were found thatwere sensitive todepthformsdistanceobjectsnativists had difficulty explaining size invariancejust as empiricists had difficulty in explaining therelationship between sensation and perceptionwith respect to our understanding of illusionsor the fact that the distance of an object canvary without change in its perceived size shape/size constancy(20) William James (1890)(21) Nativism; Hochberg (1962)Eliot, 1987, Chapter 2pdf file [1.13m]research brief (Review Article)Some Philosophical Ideas About SpacePart_1: Philosophical Conceptions(1) Pre-Socratic(2) Plato(3) Aristotle(4) Middle Ages(5) Four Prominent Views(6) Scholasticism; Augustine (354-340)(7) Early Arab Philosophy(8) Mediaeval(9) 14th Century Scholastics(10) 15th and 16th Century(11) Renaissance philosophers(12) Rene Descartes (1596-1650)Part_2: Physical Conceptions(13) Line of Development 1: space mainly as anobject of physics --Isaac Newton (1643-1727)Line of Development 2: space as anGNOSEOLOGICAL concept (works ofBritish empiricists)Part_3: Psychological Conceptions(18) Transition(19) Consequences of Newtonianconception (19th century)(20) William James (1890)commented on long history of interest inspatial perceptionsuggested it could be summarized interms of three main theoriesHelmholtz and Wundtspatial attributes reside in objects, notsensations, and are learned through inferenceswe use clues revealed through various sensorymodalities to form inferences about the natureof objects and object relationssenses respond directly to spatial stimuliand that spatial senses for vision, audition,and movement operate as distinctlydifferentiated modalitieswe use the various sensory excitations ascues to bring a given perceptioninto the stage of consciousnessour senses cooperate quite successfullyin giving us knowledge of the spatialcharacteristics of objects, such as theirlocationsizeshapestabilitymobilityfavored by Jamesspace is an innate form of all perception, neitherlearned nor inferred from experience not favored by James(21) Nativism; Hochberg (1962)Gestalt theory proposedthe ability to perceive spatialcharacteristics was inborn (nativist)spatial experiences are indeed as immediateas any of the so-called sensationsfixed relationships betweenstimulus and response do not exist and are not necessary for either (1) or (2) to be true.conceded that individual receptor organs couldnot be found for the experience of distanceGestalt movement in 1930s and1940s: Wertheimer, Kohler, and Koffkaall visual perception wasthree-dimensional becauseexperienced order in space is alwaysstructurally identical with a functionalorder in the distribution of underlyingbrain processes (Kohler, p. 39)concept of an underlying brain organization for all perceptionwas an interesting psychological analogue to Kant's earliernotion of an a-priori framework imposed by intuitionGibson (1950)those three guys were not as explicitabout the perception of space as theywere about form.for the Gestalt theorists, the perception ofform was organized according to recurringtendencies or laws ofsegmentationrelational groupingsimplicityunderlying brain processes weresaid to seek out "good form"see Pizlosee David N. Perkinsand to impose organization and meaning upon itby emphasizing organizationalproperties, Gestaltists indicated one way in whichperception was more than the sum of our sensationsO'Keefe and Nadaladvanced the notion that brainorganizaiton might be an a-priori basis forperceiving spatial informaitonthe hippocampus provides us with ana-priori Euclidian framework for ourperception of the external worldthis is a closer analog to the Kantiandoctrine of a-priori forms of intuition thanthose of the Gestalt viewpoint。
Contemporary American Culture and Society

Contemporary American Culture and SocietyIdentification of Key Terms, Ideas, and People(Be prepared not only to define key terms and recognize concepts or individuals but also to explain their significance and utilize the information in discussion of key points about American culture and society.)Chapter 1 –Introduction:Thomas Jefferson, Boston Tea Party, slavery, Civil War, Abraham Lincoln, Gilded Age, Depression Era, Franklin D. RooseveltChapter 2 –The Constitution and System of Governmen t: legislative article, executive article, judicial article, separation of powers, checks and balances, Federalist papers, James Madison, Alexander Hamilton, republicanism, federalism, two-chamber system.Chapter 3 – The Amendments: Bill of Rights, freedom of ideas, freedom of speech, freedom of religion, right to bear arms, symbolic speech, Miranda rights.Chapter 4 –Education: self-government, decentralization, universality, compulsory education (elementary & secondary), public taxation for schools, G.I. Bill of Rights. Chapter 5 –Immigration and Ethnicity: Hispanics, Asian Americans, Afro-Americans, Native Americans, melting pot, salad bowl, xenophobia, Immigrations Act (1965), affirmative action.Chapter 6 –Family and Personal Relationships: traditional family, heterosexual marriage, no fault divorce, no-family household, cohabitationChapter 7 – Domestic Economy: fiscal policy, GDP, federal budget, surplus, deficit, monetary policy, Federal Reserve System, NAFTA, WTO, Dow Jones Industrial Average, NASDAQ.Chapter 8 –Social Welfare: poverty line, welfare state, social insurance v. public assistance, unemployment compensation, Medicare, Medicaid, AFDC v. TANF. Chapter 9 –Political Parties and Interest Groups: two-party system, Republican Party, Democratic Party, the electoral college, traditional images of the two parities, lobbying, interest groupsChapter 10 –Work: minimum wage, unemployment rate, structural unemployment, telecommuting, graying workforce, structural change in the US labor market, employment trend, blue collar, white collarChapter 11 –Print Media: top five newspapers, freedom of the press, censorship, top ten consumer magazines, Watergate, concentration of ownership, online mediaChapter 12 –Electronic media: maturity of TV, TV’s influence on elections, three giant commercial TV networks, Public Broadcasting Service (PBS), invasion of privacy, copyright protection/infringement, obscenity and pornographyChapter 13 – Leisure and recreation: theme parks, Disneyland, family-oriented travel attractionsChapter 14 – Tourism and Holidays: official national holidays.Chapter 15 –Justice and the Law: Supreme Court, nine justices, judicial review, judicial independence, Courts of appeals (circuit courts), district courts, common law, public vs. private law, selection of Supreme Court JusticesChapter 16 –Crime and the Police: violent crimes, nonviolent/property crimes, Uniform Crime Report (UCR), National Crime Victimization Survey (NCVS), gun control, the Second Amendment, the Brady Act。
高考英语双文阅读与学习:了不起的盖茨比-Chapter 1-02

高考英语双文阅读与学习:了不起的盖茨比-Chapter 1-02Chapter 1第五段:My family have been prominent, well-to-do people in this Middle Western city for three generations.笔记:this Middle Western city:美国中西部的一个城市。
美国中西部具体指的是美国纵贯南北的阿巴拉契亚山脉以西、密西西比河盆地以北的地区, 那里集聚着许多来自北欧的移民。
这个地区包括美国北达科他州(North Dakota)、明尼苏达州(Minnesota)、俄亥俄州(Ohio)、密苏里州(Missouri)、印第安纳州(Indiana)等。
prominent /ˈprɑmənənt /重要的; 著名的 well-to-do富裕的(be better off经济状况较以前(或较大多数人)好)翻译:在这座中西部城市,我家连续三代都算是有头有脸的上流人士。
The Carraways are something of a clan, and we have a tradition that we're descended from the Dukes of Buccleuch, but the actual founder of my line was my grandfather's brother, who came here in fifty-one, sent a substitute to the Civil War, and started the wholesale hardware business that my father carries on today.笔记:something of a(an)既可与表物的名词连用,亦可与表人的名词连用。
它表示不确定的程度(多少,有点,在某种程度上): I'm something of a carpenter.我会点儿木工。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
你是否忠诚于组织愿意遵守规则,做你想要做的。
Chapter 2 Foundation of individual behavior
Job satisfaction工作满意度
Job satisfaction refers to an individual’s general attitude toward his or her job. Whether or not you like your job? Whether or not you feel satisfied with your job?工作 满意度是指个人对他或她的工作态度一 般。无论你是否喜欢你的工作吗?无论 你觉得你的工作满意吗?
What elements will influence individual behavior
哪些因素会影响个人的行为
Values 价值观
Perception 感觉
Attitude
Learning
Chapter 2 Foundation of individual behavior
1. Values (Happy employees create fortune.
Question
What elements do you think will lead to higher job satisfaction? 你认为哪些因素会导致更高的工作 满意度?
Chapter 2 Foundation of individual behavior
In an organization, we mainly focus on: commitment to the organization commitment to the organization indicate whether or not you are loyalty to the organization and willing to obey the rules and do what you are asked to do.在一个组织中,我们主要集中在: 组织承诺 对本组织的承诺表明
What do you see in these pictures?
Chapter 2 Foundation of individual behavior
(2) Attribution theory归因理论 Attribution theory has been proposed to develop explanations of how we judge people differently depending on what meaning we attribute to a given behavior.归因理论已提出要发展, 我们如何判断取决于什么意思,我 们归结到一个给定的行为的人有不 同的解释。
Chapter 2 Foundation of individual behavior (b) three factors that influence our judgment on causation三个因素影响我们的判断上 的因果关系 Distinctiveness(特殊性): refers to whether an individual displays different behaviors in different situations.是指一个 人是否显示在不同情况下的不同行为。
External Is everyone late today?
Internal
Chapter 2 Foundation of individual behavior
Consistency (一贯性) : refers to whether a person respond the same way over time.是 指一个人是否随着时间的推移同样的方 式回应。
Is attitude changeable? Guide the employees attitudes: provide information, communication, shape their behavior, define the role, provide feedback.
是态度的改变呢?
Chapter 2 Foundation of individual behavior
Why should we study individual behavior? 我们为什么要学习个体的行为
In order to manage people, you need to understand people. 为了管理的人,你 需要了解的人
Chapter 2 Foundation of individual behavior
情人眼里出西施。
(D) halo effect: we draw a general impression about an individual on the basis of a single characteristic.光环效应:我们画了一个关 于一个单一特点的基础上对个人的总体 印象。
No
External
Is he always late?
Yes
Internal
Chapter 2 Foundation of individual behavior
(3) shortcut to judging others快捷评判 他人
第一印象:我们选择我们观察到,加快阅 读别人的第一印象。
(A) First impression: we select the first impression we observe to speed read others.
Chapter 2 Foundation of individual behavior
2. Attitudes态度 (1) what is attitudes
Attitudes are evaluative statement-either favorable or unfavorable-concerning objects, people, or events.态度评价语 句无论是有利或不利的有关对象,人, 或事件。
Chapter 2 Foundation of individual behavior
The influence of job satisfaction工作满意度的影
响 positive积极 Suggestion, higher Exit, destructive behavior退出,破 productivity建议, 更高的生产力 destructive 坏性行为 constructive 破坏性 建设性的 neglect忽 Loyal忠诚 视 Negative消 极
No, she is External only polite to her boss.
Is she always polite?
Yes, she is Internal polite to everyone.
Chapter 2 Foundation of individual behavior
Consensus(一致性): refers to whether every one faced with a similar situation responds in the same way.是指是否面临着 类似的情况,每个人都在以同样的方式 回应。 Yes No
Chapter 2 Foundation of individual behavior
(C) Stereotype: we judge some one on the basis of our perception of the group to which he or she belongs.刻板印象:我们 判断我们的知觉,他或她所属的组的基 础上一些人
Values carry an individuals ideas as to what is right, good or desirable. 什么是正确的,良好的或可取的 值进行个人的想法
Chapter 2 Foundation of individual behavior
(2) The influence of individual values个人价 值的影响 (a) Values strongly influence a person’s attitudes and behavior.值强烈地影响一个 人的态度和行为。 (b) An employee’s performance and satisfaction are likely to higher if his or her values fit well with the organization. 如果适合他或她的价值观与组织以及雇 员的表现和满意度可能会更高。
Chapter 2 Foundation of individual behavior
个体行为的基础
(3) values vary among people人与人之间的 值的变化 (a) Descendiblity (b) Culture, parent’s behavior and your environment文化,父母的行为和你的环 境 (c) Occupation (d) Age
引导员工的态度:提供信息,通信,塑造他们 的行为,界定的作用,提供反馈。
Chapter 2 Foundation of individual behavior 3. Perception
Perception is a process by which individuals organize and interpret their sensory impressions in order to give meaning to their environment.认 知是一个过程,由个人组织和解释他们的感 官印象,为了给他们的环境意义。
