基于PID的倒立摆控制系统设计
基于PID控制的一级倒立摆系统的研究

本科生毕业设计(论文)论文题目:基于PID控制的一级倒立摆系统的研究姓名:学院:专业:班级、学号:指导教师:本文的研究对象为一级倒立摆系统,主要是基于PID控制的一级倒立摆控制系统的设计。
利用PID参数整定的多种方法对PID的三个参数进行调节,并对其优化,然后用利用Matlab对其进行仿真,并对最后仿真图的结果进行分析与比较。
倒立摆是一种典型的非线性、多变量、强耦合、快速的、自然不稳定的系统。
在实际生产生活中有很多类似的系统,故研究一级倒立摆系统的PID控制具有很大的实际意义。
本文介绍了多种PID参数整定算法,主要采用了的是Z-N整定法,并详细介绍了PID参数整定算法的相关理论和具体操作方法。
在本文中还建立了一级倒立摆的数学模型和物理模型。
本文着重讲述了Z-N整定法和试凑法对PID三个参数的进行优化的具体方法。
用Matlab对一级倒立摆系统进行了仿真,并且比较这些方法的优缺点,对最后的仿真图结果研究和分析。
得出PID参数整定方法的优缺点。
关键词:PID控制器参数整定一级倒立摆Matlab仿真Object of this paper is an inverted pendulum system is mainly based on PID control an inverted pendulum control system design. Use a variety of PID parameter tuning method to adjust the three parameters of PID, and its optimization, and then use them using matlab simulation, and the results of the last simulation diagram analysis and comparison.Inverted pendulum is a typical non-linear, multi-variable, strong coupling, fast, naturally unstable system. In real life there are a lot of similar production systems, it is of an inverted pendulum system PID control has great practical significance. This article describes a variety of PID parameter tuning algorithm, the main use of the Z-N entire titration, and details of the PID parameter tuning algorithms related theory and specific methods of operation. In this article, also established a mathematical model of the inverted pendulum and physical models. This paper focuses on the ZN Tuning Method for PID and genetic algorithms to optimize the three parameters of specific methods. Using Matlab on an inverted pendulum system is simulated, and compare the advantages and disadvantages of these methods, drawing on the final results of the simulation study and analysis. Draw two different PID parameter tuning method advantages and disadvantages.Key words: PID(Proportion Integration Differentiation)controller Parameter tuning An inverted pendulum Matlab simulation目录摘要 (I)Abstract (II)1 绪论 (1)1.1 课题的研究背景及意义 (1)1.2 国内外的研究现状 (2)1.3 本文的主要内容 (3)2 PID控制器参数整定法 (4)2.1 PID控制器的原理 (4)2.2 PID参数整定方法 (5)2.3 PID控制器的参数整定 (14)2.4 PID控制的特点 (15)3 直线一级倒立摆系统的建模 (17)3.1 倒立摆系统的简介 (17)3.2 一级倒立摆系统数学模型的建立 (18)3.3 倒立摆系统的的控制方法 (20)4 直线一级倒立摆的PID控制器设计及仿真 (22)4.1 基于Z-N整定法的PID控制器设计与仿真 (22)4.2 基于试凑法的PID控制器设计与仿真 (24)4.3 仿真结果的分析 (25)5 结论 (26)致谢................................... 错误!未定义书签。
基于PID和LQR算法的倒立摆控制设计

10.16638/ki.1671-7988.2017.05.001基于PID 和LQR 算法的倒立摆控制设计程明贺,陈仓(长安大学,陕西 西安 710064)摘 要:文章建立了一级倒立摆的数学模型,并在此基础上通过MA TLAB 仿真工具对一级倒立摆的PID (Proportion Integration Differentiation )及LQR (Linear Quadratic Regulator )控制算法进行了设计与仿真。
一般而言LQR 控制算法的控制性能要优于PID 控制算法。
关键词:倒立摆;PID ;LQR中图分类号:U462.1 文献标识码:A 文章编号:1671-7988 (2017)05-01-04Design of Single Inverted pendulum based on PID and LQRCheng Minghe, Chen Cang(Changan University, Shaanxi Xi'an 710064)Abstract: In this thesis single inverted pendulum model was built. And on this basis, through MA TLAB simulation tools, inverted pendulum PID and LQR control algorithm was carried on the design and simulation. In general, the LQR control algorithm is superior to the control performance of PID control algorithm. Key words: Single inverted pendulum; PID; LQRCLC NO.: U462.1 Document Code: A Article ID: 1671-7988 (2017)05-01-041、引言倒立摆是一种典型的快速多变量非线性绝对不稳定非最小相位系统。
基于双闭环PID控制的一阶倒立摆控制系统设计

基于双闭环PID控制的一阶倒立摆控制系统设计一阶倒立摆是一种常见的控制系统,它由一个旋转臂和一个悬挂在旋转臂末端的摆杆组成。
控制目标是使摆杆保持垂直位置并保持在指定的角度范围内。
本文将基于双闭环PID控制设计一阶倒立摆控制系统,并对其进行详细的分析和讨论。
首先,我们需要明确控制系统的结构。
一阶倒立摆控制系统可以分为两个闭环:内环和外环。
内环用于控制旋转臂的角度,并将输出作为外环的输入。
外环用于控制摆杆的角度,并根据测量的摆杆角度和设定的目标角度来调整内环的输入。
在进行控制系统设计之前,我们需要先建立一阶倒立摆的数学模型。
假设倒立摆的质量集中在摆杆的一端,摆杆的长度为L,质量为m,摩擦系数为b,重力加速度为g。
通过应用牛顿第二定律,可以得到如下动力学方程:mL²θ¨ + bLθ˙ + mgLsinθ = u其中,θ是旋转臂的角度,u是旋转臂的扭矩。
为了简化方程,我们进行恒定参数修正和线性化处理,得到线性方程:θ¨ + 2ξωnθ˙ + ωn²θ = kru其中,ξ是阻尼比,ωn是无阻尼自然频率,kr是旋转臂的增益。
接下来,我们将按照以下步骤设计基于双闭环PID控制的一阶倒立摆控制系统:1.内环设计:-选择合适的内环闭环控制器类型。
对于一阶倒立摆,可以选择PID控制器。
-根据倒立摆的特性和性能要求,选择合适的PID参数。
可以使用试错法、经验法、系统辨识等方法进行参数调整。
-将PID控制器的输入设置为旋转臂角度误差,输出为旋转臂的扭矩。
2.外环设计:-选择合适的外环闭环控制器类型。
对于一阶倒立摆,可以选择PID控制器。
-根据倒立摆的特性和性能要求,选择合适的PID参数。
-将PID控制器的输入设置为摆杆角度误差,输出为旋转臂的角度设定值。
3.进行系统仿真和调试:-使用MATLAB等仿真工具建立一阶倒立摆的数学模型,并将设计的控制器与模型进行集成。
-调整控制器的参数,以满足性能指标和系统稳定性的要求。
基于PID一阶倒立摆控制与仿真

目录0. 前言 (1)1 PID控制和编码器基本理论 (2)2 方案设计 (3)2.1 系统模型及分析 (3)2.2 比例(P)控制 (4)2.3 积分(I)控制 (4)2.4 微分(D)控制 (4)3 系统模型建立 (5)3.1 一阶倒立摆的微分方程模型 (5)3.2 传递函数 (7)3.3 状态空间方程 (7)4 软件编程与仿真 (8)4.1 实际系统参数 (8)4.2 PID控制设计分析 (8)4.3 PID参数的确定 (10)4.4 Simulink仿真 (11)4.5 单极倒立摆建模 (13)4.6 软件编程 (15)5 系统调试和结果分析 (18)6 结论及进一步设想 (19)课设体会 (21)基于PID一阶倒立摆控制与仿真亲摘要:本文主要研究目的是通过PID的调解实现对一阶倒立摆的控制,设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
首先对平面一级倒立摆系统进行分析,根据具体参数建立数学模型,通过对模型的分析判断,设计倒立摆PID控制器。
通过MATLAB软件进行仿真和实际系统实验,实现对倒立摆的稳定控制。
但是由于PID控制器为单输入单输出系统,所以只能控制摆杆的角度,并不能控制小车的位置,所以小车会往一个方向运动。
可以通过应用现代控制理论等单输入(小车加速度)多输出(摆杆角度和小车位置)的控制算法使系统更加的稳定。
关键词:倒立摆;PID控制;MATLAB仿真;0. 前言倒立摆是日常生活中许多重心在上、支点在下的控制问题的抽象模型,本身是一种自然不稳定体,它在控制过程中能有效地反映控制中许多抽象而关键的问题,如系统的非线性、可控性、鲁棒性等问题。
对倒立摆系统的控制就是使小车以及摆杆尽快地达到预期的平衡位置,而且还要使它们不会有太强的振荡幅度、速度以及角速度,当倒立摆系统达到期望位置后,系统能克服一定范围的扰动而保持平衡。
基于双闭环PID控制的一阶倒立摆控制系统设计

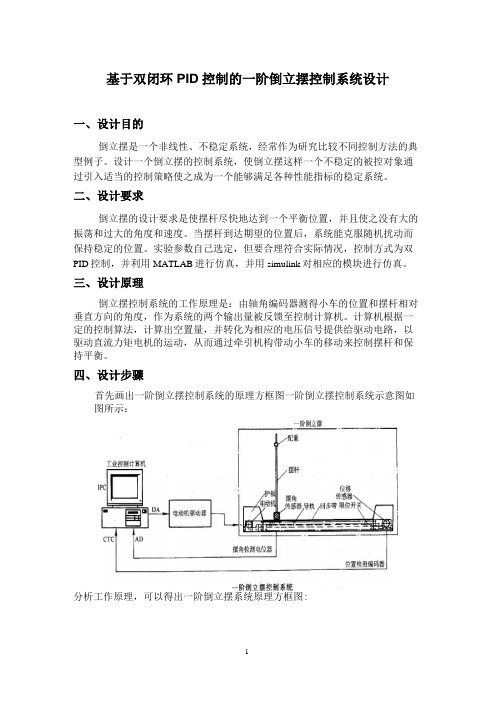
自动控制原理课程设计说明书基于双闭环PID控制的一阶倒立摆控制系统设计姓名:学号:学院:专业:指导教师:2018年 1月目录1 任务概述 (3)1.1设计概述 (3)1.2 要完成的设计任务: (4)2系统建模 (4)2.1 对象模型 (4)2.2 模型建立及封装 (5)3仿真验证 (9)3.1 实验设计 (9)3.2 建立M文件编制绘图子程序 (9)4 双闭环PID控制器设计 (12)4.1内环控制器的设计 (13)4.2外环控制器的设计 (13)5 仿真实验 (15)5.1简化模型 (15)5.2 仿真实验 (17)6 检验系统的鲁棒性 (18)6.1 编写程序求系统性能指标 (18)6.2 改变参数验证控制系统的鲁棒性 (19)7 结论 (22)附录 (22)1 任务概述1.1设计概述如图1 所示的“一阶倒立摆控制系统”中,通过检测小车位置与摆杆的摆动角,来适当控制驱动电动机拖动力的大小,控制器由一台工业控制计算机(IPC)完成。
图1 一阶倒立摆控制系统这是一个借助于“SIMULINK封装技术——子系统”,在模型验证的基础上,采用双闭环PID控制方案,实现倒立摆位置伺服控制的数字仿真实验。
1.2 要完成的设计任务:(1)通过理论分析建立对象模型(实际模型),并在原点进行线性化,得到线性化模型;将实际模型和线性化模型作为子系统,并进行封装,将倒立摆的振子质量m和倒摆长度L作为子系统的参数,可以由用户根据需要输入;(2)设计实验,进行模型验证;(3)一阶倒立摆系统为“自不稳定的非最小相位系统”。
将系统小车位置作为“外环”,而将摆杆摆角作为“内环”,设计内化与外环的PID控制器;(4)在单位阶跃输入下,进行SIMULINK仿真;(5)编写绘图程序,绘制阶跃响应曲线,并编程求解系统性能指标:最大超调量、调节时间、上升时间;(6)检验系统的鲁棒性:将对象的特性做如下变化后,同样在单位阶跃输入下,检验所设计控制系统的鲁棒性能,列表比较系统的性能指标(最大超调量、调节时间、上升时间)。
基于PID的倒立摆控制系统设计

基于PID的倒立摆控制系统设计摘要:倒立摆(Inverted Pendulum)控制系统设计是控制理论教学中的一种典型的实验对象,具有很高的教学和科研价值。
本文基于PID控制算法,设计一个倒立摆控制系统,对倒立摆进行控制。
首先介绍了倒立摆系统模型和其动力学方程,然后详细介绍PID控制算法的原理和设计方法,并将其应用于倒立摆系统中,进行控制器的设计。
最后,通过MATLAB/Simulink软件进行系统仿真,并对仿真结果进行分析和讨论。
研究结果表明,PID控制算法能够有效地控制倒立摆系统,并且具有良好的控制性能和稳定性。
一、引言倒立摆控制系统是一种实验教学中常见的控制对象,其模型简单、控制复杂度适中,具有很高的教学和科研价值。
倒立摆系统被广泛应用于控制理论教学、控制算法研究以及控制系统设计等领域。
PID控制是一种常用的控制算法,具有简单、易实现、稳定性好等特点。
因此,本文将基于PID控制算法设计一个倒立摆控制系统,对倒立摆进行控制。
二、倒立摆系统模型和动力学方程倒立摆系统由一个竖直放置的杆和一个可沿杆轴线做直线运动的摆组成。
根据杆的位置和速度,可以得到倒立摆的状态变量,进而得到系统的动力学方程。
本文采用小角度近似,假设杆的运动范围很小,可以将其近似为线性系统,动力学方程可以表示为:$$(M+m)l\ddot{\theta}-ml\ddot{x}\cos(\theta)+m\sin(\theta)g=0$$$$\ddot{x}-\ddot{\theta}l=0$$其中,M为杆的质量,m为摆的质量,l为杆的长度,g为重力加速度,x为摆的位置,$\theta$为杆的倾斜角度。
三、PID控制算法原理和设计方法PID控制算法是一种基于误差信号的反馈控制算法,由比例控制、积分控制和微分控制三部分组成。
比例控制根据当前误差的大小进行控制;积分控制用于消除系统的稳态误差;微分控制用于预测误差的变化趋势,提高系统的响应速度和稳定性。
PID控制的一阶倒立摆控制系统设计
基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。
设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
二、设计要求倒立摆的设计要求是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
实验参数自己选定,但要合理符合实际情况,控制方式为双PID控制,并利用MATLAB进行仿真,并用simulink对相应的模块进行仿真。
三、设计原理倒立摆控制系统的工作原理是:由轴角编码器测得小车的位置和摆杆相对垂直方向的角度,作为系统的两个输出量被反馈至控制计算机。
计算机根据一定的控制算法,计算出空置量,并转化为相应的电压信号提供给驱动电路,以驱动直流力矩电机的运动,从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。
四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示:分析工作原理,可以得出一阶倒立摆系统原理方框图:一阶倒立摆控制系统动态结构图 F 面的工作是根据结构框图,分析和解决各个环节的传递函数!1•一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和 匀质杆组成的系统,如下图所示, 其中:M :小车质量 m :为摆杆质量J :为摆杆惯量F :加在小车上的力 x :小车位置。
:摆杆与垂直向上方向的夹角l :摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律, (1) 摆杆绕其重心的转动方程为J 0=F/sin 0-F/cos 0(1)yx'/(2) 摆杆重心的运动方程为d 2=m-d 2t工业控制计算机电动机驰动器一阶倒立摆—Lb D 购*.—dl卜DI ⑸J bD I 即可知: (x +1sin 0)(l cos0)d 2t(3) 小车水平方向上的运动为d 2x d 2t联列上述4个方程,可以得出一阶倒立精确气模型:J +ml 2)F +mlG +ml 2)(M +m )-m 2/2cos 20+m )m lgsin 0ml 2)""若只考虑e 在其工作点附近e=0附近(-10°<0<10。
倒立摆的PID控制

S= -2.3635+20.43961 -2.3635-20.43961 -0.0001 -0.0001 系统的脉冲响应曲线如图(2)所示:
(2)
系统闭环极点均位于S平面左半部,系统稳定。系统 稳定时间约为2s,满足要求。由于此时稳态误差 为0,所以不需要改变积分环节(可以改变积分系 数,观察系统响应如何变化),系统响应的超调 亮比较大,威力较小超调,增加微分系数Kp,取 Kp=20,响应曲线如图(3)所示
• • • • • • • • •
M m b L I F x Φ θ
小车的质量 摆杆质量 小车摩擦系数 摆杆转动轴心到杆质心的长度 摆杆惯量 加在小车上的力 小车位置 摆杆与垂直向上的夹角 摆杆与垂直向下方向的夹角
矢量方向定义
应用Newton方法来建立系统的动力学方程过程如下。 .. .. (1)分析小车水平方向所受的合力,可以得到以下方 程如下。 Mx=F-bx-N (2) 由摆摊水平方向的受力进行分析可以得到下面等 式 N=md^2/(dt^2)*(x+l*sinθ)
G2(s)=(X(s)/U(s)=(I+m*l^2)/q*(s^2)-m*g*l/q)/ (S^4+b*(I+m*l^2)/q*(s^3)(M+m)*m*g*l/q*(s^2 )-b*m*g*l/q*s) 可以看出,den1=den2=den,小车的算式可以 简化成: X(s)=((num2)*(denPID)/(denPID)*(den)+k*(num PID)*(num1))*F(s)
由于输入信号r(s)=0,所以可以把结果图转换成如图2所示
(2)变换后的控制图
其中,反馈环代表我哦们面前设计的摆杆的控制器。 从此框图我们可以看出此处支队摆杆角度进行了控制, 并没有对小车位置进行控制。小车位置输出为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要倒立摆装置被公认为是自动控制理论中的典型实验设备,而一阶倒立摆系统为典型的多变量、非线性、自然不稳定系统。
对倒立摆的研究可归结为对非线性、高阶次、不稳定一类系统的研究,其控制方法和思路的研究对一般工业过程有广泛的用途。
本论文主要针对一阶倒立摆系统进行模糊PID控制器设计。
首先,对一阶倒立摆设备进行了系统分析,了解其工作机理,硬件结构,软件功能,并以垂直位置为动态稳定点得到这一位置的线性化方程。
其次,对模糊控制技术进行了分析,并对模糊PID控制器进行了详细的研究、设计和总结。
然后,以一阶倒立摆为被控对象,利用MATLAB软件的SIMULINK仿真功能先用常规PID控制算法进行控制;在常规PID控制的基础上设计了模糊参数自适应PID控制器。
模糊参数自适应PID控制器是在PID控制器的基础上对PID参数进行在线修改,增强了PID 控制器的自适应性。
当系统受到干扰,模型发生改变时,仿真结果表明了对于一阶倒立摆这一复杂非线性系统,模糊PID控制器比常规PID控制有较强的控制能力。
最后,在仿真设计的基础上,采用MATLAB软件的FUZZY控制工具箱生成模糊PID控制器并将其应用于一阶倒立摆系统的控制上,进行了可行性验证,调试顺利,效果良好。
实验结果表明,对于倒立摆这一较复杂的系统,采用模糊PID 控制算法有效。
关键词:一阶倒立摆;模糊控制;模糊PID控制;PID控制AbstractSingle inverted pendulum is the typical multi-variable, nonlinear, instable, naturally system. The studies of single inverted pendulum can be referred as investigating a classific non-linearity and instability system, the way of control and the thoughts are useful to general industrial process. Inverted pendulum device is considered as traditional tester of automation.In this paper, it investigated how to devise a fuzzy PID controller to insure single inverted pendulum operate right. First, the equipment of single inverted pendulum is studied, which help to understand the mechanism, the structure of hardware and the performance of software. We liner the system at balance position and get linear state equation. Second, the principle of FC is analyzed, and detail research of fuzzy PID controller is made. Then, in order to apply fuzzy PID to the single inverted pendulum system, which is a typical, highly nonlinear and absolutely unstable dynamic system, we observe the position and angles of the pendulum in order to get the right control rule sheet. Fuzzy PID which is able to control single inverted pendulum at a wider range than LQR, especially when is disturbed, or when model is changed, the result of simulation indicate that the fuzzy PID controller still has better ability of control.Last, software is compiled to apply fuzzy PID on single inverted pendulum. The tests on single inverted pendulum system indicate that fuzzy PID is a simple and easy way for nonlinear multi-variability system.Key words: single inverted pendulum;fuzzy control;fuzzy PID control;PI D control目录引言 (1)第1章绪论 (2)1.1倒立摆分类 (2)1.2倒立摆的特性 (5)1.3倒立摆系统的控制方法综述 (5)第2章系统数学模型的建立 (8)第3章PID控制 (12)3.1PID的原理和特点 (12)3.2PID控制参数设定及仿真 (13)3.3PID控制实验 (16)第4章模糊控制在倒立摆系统中的应用 (19)4.1模糊控制的特点及发展 (20)4.2模糊控制的基本原理 (22)4.3模糊控制器的组成 (23)4.4模糊PID控制 (25)第5章倒立摆控制系统的仿真 (30)5.1模糊控制器的设计 (30)5.2倒立摆控制系统的仿真 (34)结论 (37)参考文献 (38)致谢 (38)引言对倒立摆系统进行研究,不仅可以解决控制中的理论问题,还能将控制理论所涉及的三个基础学科:力学、数学和电学(含计算机)有机的结合起来,在倒立摆系统中进行综合应用。
而且倒立摆系统与双足机器人、火箭飞行控制和各类伺服云台的稳定有很大相似性,因此对倒立摆控制机理的研究具有重要的理论和实践意义。
倒立摆系统为典型的多变量、非线性、自然不稳定系统。
对倒立摆的研究可归结为对非线性、高阶次、不稳定一类系统的研究,其控制方法和思路的研究对一般工业过程有广泛的用途。
本文将模糊PID控制成功地引入到一阶倒立摆的控制中,并利用MATLAB软件的SIMULINK仿真功能进行控制,其控制性能有了很大的提高。
本文首先引入PID控制,由于PID控制器的整定需要依靠精确的数学模型而且PID参数是固定的,不能在线修改,所以,参数整定时间长且控制效果也不理想,不是控制时间长,就是超调量大,不能统一。
为了解决这个矛盾,改善控制性能,引入了模糊控制。
模糊控制不需要精确的数学模型而且动态性能好,完全弥补了传统PID控制器的不足。
但是,模糊控制的输出是不连续的,所以,其静态性能不好。
为了达到前期动态性能和后期静态性能的完美结合,引入了模糊PID控制。
模糊PID 控制器具有传统PID控制和模糊控制的全部优点,所以将模糊PID控制用于倒立摆,控制性能有了极大提高。
并采用MATLAB软件的FUZZY控制工具箱生成模糊PID控制器并将其应用于一阶倒立摆系统的控制上,进行了可行性验证,调试顺利,效果良好。
第1章绪论倒立摆的研究具有重要的工程背景[1]:(1) 机器人的站立与行走类似双倒立摆系统,尽管第一台机器人在美国问世至今已有三十年的历史,机器人的关键技术——机器人的行走控制至今仍未能很好解决。
(2) 在火箭等飞行器的飞行过程中,为了保持其正确的姿态,要不断进行实时控制。
(3) 通信卫星在预先计算好的轨道和确定的位置上运行的同时,要保持其稳定的姿态,使卫星天线一直指向地球,使它的太阳能电池板一直指向太阳。
(4) 侦察卫星中摄像机的轻微抖动会对摄像的图像质量产生很大的影响,为了提高摄像的质量,必须能自动地保持伺服云台的稳定,消除震动。
(5) 为防止单级火箭在拐弯时断裂而诞生的柔性火箭(多级火箭),其飞行姿态的控制也可以用多级倒立摆系统进行研究。
由于倒立摆系统与双足机器人、火箭飞行控制和各类伺服云台的稳定有很大相似性,因此对倒立摆控制机理的研究具有重要的理论和实践意义。
1.1 倒立摆分类倒立摆已经由原来的直线一级倒立摆扩展出很多种类,典型的有直线倒立摆,环形倒立摆,平面倒立摆和复合倒立摆等,倒立摆系统是在运动模块上装有倒立摆装置,由于在相同的运动模块上可以装载不同的倒立摆装置,倒立摆的种类由此而丰富很多,按倒立摆的结构来分,有以下类型的倒立摆:1) 直线倒立摆系列直线倒立摆是在直线运动模块上装有摆体组件,直线运动模块有一个自由度,小车可以沿导轨水平运动,在小车上装载不同的摆体组件,可以组成很多类别的倒立摆,直线柔性倒立摆和一般直线倒立摆的不同之处在于,柔性倒立摆有两个可以沿导轨滑动的小车,并且在主动小车和从动小车之间增加了一个弹簧,作为柔性关节。
直线倒立摆系列产品如图1-1 所示。
2) 环形倒立摆系列环形倒立摆是在圆周运动模块上装有摆体组件,圆周运动模块有一个自由度,可以围绕齿轮中心做圆周运动,在运动手臂末端装有摆体组件,根据摆体组件的级数和串连或并联的方式,可以组成很多形式的倒立摆。
如图1-2所示。
3) 平面倒立摆系列平面倒立摆是在可以做平面运动的运动模块上装有摆杆组件,平面运动模块主要有两类:一类是XY 运动平台,另一类是两自由度SCARA 机械臂;摆体组件也有一级、二级、三级和四级很多种。
如图1-3 所示4) 复合倒立摆系列复合倒立摆为一类新型倒立摆,由运动本体和摆杆组件组成,其运动本体可以很方便的调整成三种模式,一是2)中所述的环形倒立摆,还可以把本体翻转90 度,连杆竖直向下和竖直向上组成托摆和顶摆两种形式的倒立摆。
按倒立摆的级数来分:有一级倒立摆、两级倒立摆、三级倒立摆和四级倒立摆,一级倒立摆常用于控制理论的基础实验,多级倒立摆常用于控制算法的研究,倒立摆的级数越高,其控制难度更大,目前,可以实现的倒立摆控制最高为四级倒立摆。
图1-1 直线倒立摆系列图1-2 环形倒立摆系列图1-3 平面倒立摆系列图1-4 复合倒立摆1.2 倒立摆的特性虽然倒立摆的形式和结构各异,但所有的倒立摆都具有以下的特性:1) 非线性倒立摆是一个典型的非线性复杂系统,实际中可以通过线性化得到系统的近似模型,线性化处理后再进行控制。
