重庆市第一中学2021届高三上学期第四次月考数学测试试题
2021届重庆市第一中学高三上学期第一次月考数学试题(解析版)

2021届重庆市第一中学高三上学期第一次月考数学试题一、单选题1.设集合(){}ln 1A y y x ==-,{B y y ==,则A B =( )A .[)0,2B .()0,2C .[]0,2D .[)0,1【答案】A【解析】先分别利用对数型函数以及指数型函数求值域的方法求出集合,A B ,注意集合中的代表元素,再利用集合的交集运算求解即可. 【详解】∵(){}ln 1A y y x R ==-=,{[)0,2B y y ===,∴[)0,2AB =.故选:A. 【点睛】本题主要考查了集合间的运算以及对数函数和指数函数.属于较易题.2.设a ,()0,b ∈+∞,A =,B =,则A ,B 的大小关系是( )A .AB < B .A B >C .A B ≤D .A B ≥【答案】B【解析】根据题意计算做差可得22A B >,得到答案. 【详解】由a ,()0,b ∈+∞,得0A =>,0B =>22220A B -=-=>,∴22A B >,故A B >, 故选:B. 【点睛】本题考查了做差法比较大小,意在考查学生的计算能力和推断能力.3.已知直线l 是曲线2y x =的切线,则l 的方程不可能是( )A .5210x y -+=B .4210x y -+=C .13690x y -+=D .9440x y -+=【答案】B【解析】利用导数求出曲线2y x =的切线的斜率的取值范围,然后利用导数的几何意义判断各选项中的直线是否为曲线2y x =的切线,由此可得出结论.【详解】对于函数2y x =,定义域为[)0,+∞,则22y '=+>,所以,曲线2y x =的切线l 的斜率的取值范围是()2,+∞.对于A 选项,直线5210x y -+=的斜率为52,令522y '=+=,解得1x =,此时3y =,点()1,3在直线5210x y -+=上,则直线5210x y -+=与曲线2y x =相切;对于B 选项,直线4210x y -+=的斜率为2,该直线不是曲线2y x =的切线;对于C 选项,直线13690x y -+=的斜率为1326>, 令1326y '=+=,解得9x =,此时21y =,点()9,21在直线13690x y -+=上,所以,直线13690x y -+=与曲线2y x=相切;对于D 选项,直线9440x y -+=的斜率为924>, 令924y '==,解得4x =,此时10y =,点()4,10在直线9440x y -+=上,所以,直线9440x y -+=与曲线2y x =相切. 故选:B. 【点睛】本题考查利用导数的几何意义验证函数的切线方程,考查计算能力,属于中等题. 4.中国传统扇文化有着极其深厚的底蕴.一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形的面积为1S,圆面中剩余部分的面积为2S,当1S与2S的比值为512-时,扇面看上去形状较为美观,那么此时扇形的圆心角的弧度数为()A.(35)π-B.(51)πC.51)πD.52)π【答案】A【解析】根据扇形与圆面积公式,可知面积比即为圆心角之比,再根据圆心角和的关系,求解出扇形的圆心角.【详解】1S与2S所在扇形圆心角的比即为它们的面积比,设1S与2S所在扇形圆心角分别为,αβ,则512αβ=,又2αβπ+=,解得(35)απ=-故选:A【点睛】本题考查圆与扇形的面积计算,难度较易.扇形的面积公式:21122S r lrα==,其中α是扇形圆心角的弧度数,l是扇形的弧长.5.若函数()(),2log2,xaa x af xx x a⎧<<⎪=⎨->⎪⎩(其中0a>,1a≠)存在零点,则实数a的取值范围是()A.()1,11,32⎛⎫⋃⎪⎝⎭B.(]1,3C.()2,3D.(]2,3【答案】C【解析】根据题中所给的函数有零点,结合解析式的特征,求得函数的零点,再根据分段函数的意义再结合式子的特征求得结果.【详解】因为x a>时,()log(2)af x x=-,所以2a>,若函数若有零点,则()log 20a x -=,解得3x =, 故3a >,又2a >,∴实数a 的取值范围是()2,3. 故选:C. 【点睛】该题考查的是有关函数的问题,涉及到的知识点有根据分段函数有零点求参数的取值范围,属于简单题目.6.已知02ω<≤,函数()sin f x x x ωω=,对任意R x ∈,都有()3f x f x π⎛⎫-=- ⎪⎝⎭,则ω的值为( ) A .12B .1C .32D .2【答案】D【解析】化简函数()y f x =的解析式为()2sin 3f x x πω⎛⎫=- ⎪⎝⎭,由题意可知,点,06π⎛⎫⎪⎝⎭是函数()y f x =的一个对称中心,结合02ω<≤可求得ω的值. 【详解】()sin 2sin 3f x x x x πωωω⎛⎫==- ⎪⎝⎭,根据()3f x f x π⎛⎫-=-⎪⎝⎭,得,06π⎛⎫⎪⎝⎭是函数()y f x =的一个对称中心,则2sin 0663f ππωπ⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭,可得sin 063πωπ⎛⎫-= ⎪⎝⎭, 02ω<≤,0363ππωπ∴-<-≤,所以063πωπ-=,解得2ω=.故选:D. 【点睛】本题考查利用正弦型函数的对称性求参数值,同时也考查了辅助角公式的应用,考查计算能力,属于中等题.7.函数()2cos sin 2f x x x =+的一个单调减区间是( )A .,42ππ⎛⎫ ⎪⎝⎭B .0,6π⎛⎫ ⎪⎝⎭C .,2ππ⎛⎫ ⎪⎝⎭D .5,6ππ⎛⎫⎪⎝⎭【答案】A【解析】利用导数求得函数()y f x =的单调递减区间,利用赋值法可得出结果. 【详解】()2cos sin 2f x x x =+,该函数的定义域为R ,()()()222sin 2cos2212sin 2sin 22sin sin 1f x x x x x x x '=-+=--=-+-()()2sin 12sin 1x x =-+-,1sin 1x -≤≤,可得sin 10x +≥,令()0f x '<,可得2sin 10x ->,即1sin 2x >,解得()52266k x k k Z ππππ+<<+∈. 所以,函数()y f x =的单调递减区间为()52,266k k k Z ππππ⎛⎫++∈ ⎪⎝⎭. 当0k =时,函数()y f x =的一个单调递减区间为5,66ππ⎛⎫⎪⎝⎭, 5,,4266ππππ⎛⎫⎛⎫⊆ ⎪ ⎪⎝⎭⎝⎭, 对任意的k Z ∈,50,2,2666k k πππππ⎛⎫⎛⎫⊄++ ⎪ ⎪⎝⎭⎝⎭,5,2,2266k k ππππππ⎛⎫⎛⎫⊄++ ⎪ ⎪⎝⎭⎝⎭,55,2,2666k k ππππππ⎛⎫⎛⎫⊄++ ⎪ ⎪⎝⎭⎝⎭,故函数()y f x =的一个单调递减区间为,42ππ⎛⎫⎪⎝⎭. 故选:A. 【点睛】本题考查利用导数求解函数的单调区间,考查计算能力,属于中等题. 8.设函数()f x 在R 上存在导数()f x ',对任意的R x ∈,有()()2cos f x f x x +-=,且在[)0,+∞上有()sin f x x '>-,则不等式()cos sin 2f x f x x x π⎛⎫--≥- ⎪⎝⎭的解集是( )A .,4π⎛⎤-∞ ⎥⎝⎦B .,4π⎡⎫+∞⎪⎢⎣⎭C .,6π⎛⎤-∞ ⎥⎝⎦D .,6π⎡⎫+∞⎪⎢⎣⎭【答案】B【解析】构造函数,由已知得出所构造的函数的单调性,再利用其单调性解抽象不等式,可得选项. 【详解】设()()cos F x f x x =-,∵()()2cos f x f x x +-=,即()()cos cos f x x x f x -=--,即()()F x F x =--,故()F x 是奇函数,由于函数()f x 在R 上存在导函数()f x ',所以,函数()f x 在R 上连续,则函数()F x 在R 上连续.∵在[)0,+∞上有()sin f x x '>-,∴()()sin 0F x f x x ''=+>, 故()F x 在[)0,+∞单调递增,又∵()F x 是奇函数,且()F x 在R 上连续,∴()F x 在R 上单调递增, ∵()cos sin 2f x f x x x π⎛⎫--≥-⎪⎝⎭, ∴()cos sin cos 222f x x f x x f x x πππ⎛⎫⎛⎫⎛⎫-≥--=---⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 即()2F x F x π⎛⎫≥- ⎪⎝⎭,∴2x x π≥-,故4x π≥,故选:B . 【点睛】本题考查运用导函数分析函数的单调性,从而求解抽象不等式的问题,构造合适的函数是解决问题的关键,属于较难题.二、多选题9.已知ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2sin sin sin B A C =,则角B 的值不可能是( )A .45°B .60°C .75°D .90°【答案】CD【解析】先利用正弦定理得到2b ac =,再利用余弦定理和基本不等式得到0,3B π⎛⎤∈ ⎥⎝⎦,即可判断. 【详解】∵2sin sin sin B A C =, 由正弦定理得: ∴2b ac =,∴2222221cos 2222a cb ac ac ac ac B ac ac ac +-+--==≥=,当且仅当a c =时取等号, 又0B π<<,故0,3B π⎛⎤∈ ⎥⎝⎦.故选:CD. 【点睛】本题主要考查了正弦定理以及余弦定理,考查了基本不等式.属于较易题. 10.下列说法正确的是( ) A .“4x π=”是“tan 1x =”的充分不必要条件B .命题:p “若a b >,则22am bm >”的否定是真命题C .命题“0R x ∃∈,0012x x +≥”的否定形式是“R x ∀∈,12x x+>” D .将函数()cos2f x x x =+的图象向左平移4π个单位长度得到()g x 的图象,则()g x 的图象关于点0,4π⎛⎫⎪⎝⎭对称【答案】ABD【解析】解方程tan 1x =,利用集合的包含关系可判断A 选项的正误;判断命题p 的真假,可判断出该命题的否定的真假,进而可判断B 选项的正误;利用特称命题的否定可判断C 选项的正误;利用图象平移得出函数()y g x =的解析式,利用对称性的定义可判断D 选项的正误. 【详解】对于A 选项,解方程tan 1x =,可得()4x k k Z ππ=+∈,4π⎧⎫⎨⎬⎩⎭ ,4x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭,所以,“4x π=”是“tan 1x =”的充分不必要条件, A 选项正确;对于B 选项,当0m =时,22am bm =,则命题p 为假命题,它的否定为真命题,B 选项正确;对于C 选项,命题“0R x ∃∈,0012x x +≥”的否定形式是“R x ∀∈,12x x+<”,C 选项错误;对于D 选项,将函数()cos2f x x x =+的图象向左平移4π个单位长度, 得到()cos 2sin 2444g x x x x x πππ⎛⎫=+++=-++ ⎪⎝⎭, ()()sin 2sin 244g x x x x x ππ-=---+=-+,则()()2g x g x π+-=,故函数()y g x =的图象关于点0,4π⎛⎫⎪⎝⎭对称,D 选项正确; 故选:ABD. 【点睛】本题考查命题真假的判断,考查了充分不必要条件、命题的否定的真假、特称命题的否定的判断,同时也考查了函数对称性的验证,考查推理能力,属于中等题.11.在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间,并构成一般不动点定理的基石,布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L.E.J.Brouwer ),简单的讲就是对于满足一定条件的连续函数()f x ,存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )A .()2xf x x =+B .()23g x x x =--C .()21,12,1x x f x x x ⎧-≤⎪=⎨->⎪⎩D .()ln 1f x x =-【答案】BC【解析】只要解方程00()f x x =,观察它有没有实解即可得, 【详解】选项A ,若()00f x x =,则020x =,该方程无解,故A 中函数不是“不动点”函数;选项B ,若()00g x x =,则200230x x --=,解得03x =或-1,故B 中函数是“不动点”函数;选项C ,若()00f x x =,则01x ≤,0021xx -=,或01x >,002x x -=,解得01x =,故C 中函数是:“不动点”函数;选项D ,若()00f x x =,则00ln 1x x -=,该方程无解,故D 中函数不是“不动点”函数. 故选:BC. 【点睛】本题考查新定义“不动点”,解题关键是根据新定义把问题转化为方程有无实数解. 12.已知函数()[][]sin cos cos sin f x x x =+,其中[]x 表示不超过实数x 的最大整数,关于()f x 有下述四个结论,正确的是( ) A .()f x 的一个周期是2π B .()f x 是非奇非偶函数C .()f x 在(0,)π单调递减D .()f x【答案】ABD【解析】先根据周期函数定义判断选项A ,再根据[]y x =函数的意义,转化()f x 为分段函数判断B 选项,结合三角函数的图象与性质判断C ,D 选项. 【详解】[][]()2sin co (cos in )s s f x x x f x π+=+=,()f x ∴的一个周期是2π,故A 正确;sin11,01,0,2cos1,21sin1,,2()3cos1sin1,,23cos1,,22cos1,,02x x x x f x x x x πππππππππ+=⎧⎪⎛⎫⎪∈ ⎪⎪⎝⎭⎪⎪=⎪⎪⎛⎤⎪-∈ ⎪⎥=⎝⎦⎨⎪⎛⎫⎪-∈ ⎪⎝⎭⎪⎪⎡⎫⎪∈⎪⎢⎪⎣⎭⎪⎛⎫⎪∈- ⎪⎪⎝⎭⎩,()f x ∴是非奇非偶函数,B 正确;对于C ,(0,)2x π∈时,()1f x =,不增不减,所以C 错误;对于D ,[0,)2x π∈,()sin11sin11 1.742f x π=+>+=+>>D 正确. 故选:ABD 【点睛】本题主要考查了函数的周期性,单调性,奇偶性,考查了特例法求解选择题,属于中档题.三、填空题13.若幂函数()f x 过点()2,8,则满足不等式(3)(1)f a f a -≤-的实数a 的取值范围是______. 【答案】(,2]-∞【解析】先求得幂函数()f x 的解析式,在根据()f x 的单调性求得不等式(3)(1)f a f a -≤-的解集.【详解】设()f x x α=,代入点()2,8,得28,3αα==,所以()3f x x =,所以()f x 在R 上递增,所以(3)(1)31f a f a a a -≤-⇒-≤-,解得2a ≤,所以实数a 的取值范围是(,2]-∞.故答案为:(,2]-∞ 【点睛】本小题主要考查幂函数解析式的求法,考查幂函数的单调性,属于基础题. 14.已知1a >,1b >,则log log 216a b b a +的最小值是______. 【答案】8【解析】利用换底公式可得log log 1a b b a ⨯=,再利用基本不等式可得答案. 【详解】因为1a >,1b >,所以log 0,log 0b a a b >>,因为lg log lg log log 1lg log lg aa b bb b a b a a a b ⎧=⎪⎪⇒⨯=⎨⎪=⎪⎩,所以,log log 2168a b b a +≥==,当log 2a b =时取“=”. 故答案为:8. 【点睛】本题主要考查指数式的运算、考查了换底公式与基本不等式的应用,属于中档题. 15.4cos50tan40-=______.【解析】【详解】4sin 40cos40sin 404cos50tan 40cos 40--=2cos10sin 30cos10sin10cos30cos 40--=,1cos10sin1022cos 40⎫-⎪⎝⎭=403cos 40==【考点】三角函数诱导公式、切割化弦思想.16.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若2b =,()cos25cos 3A B C ++=-,点P 是ABC 的重心,且27AP =,则c =______.【答案】4【解析】首先根据余弦二倍角公式得到1cos 2A =,设BC 边上的中线为AD ,得到7AD =,从而得到()12AD AB AC =+,再平方解方程即可得到答案. 【详解】因为()cos25cos 3A B C +-+=,所以22cos 5cos 20A A -+=, 所以1cos 2A =或cos 2A =(舍去). 设BC 边上的中线为AD ,如图所示:因为27AP =,所以7AD = 又因为()12AD AB AC =+, 所以()222124AD AB AC AB AC =++⋅, 所以()22172cos 4c b bc A =++,2211722242⎛⎫=++⨯⨯ ⎪⎝⎭c c ,化简得22240c c +-=,解得4c =或6c =-(舍去). 故答案为:4 【点睛】本题主要平面向量数量积的应用,同时考查了余弦二倍角公式,属于简单题.四、解答题17.已知点()2,1P -在角α的终边上,且02απ≤< .(1)求值:2sin cos 4sin cos αααα-+;(2)若32ππβ<<,且sin 210αβ⎛⎫-= ⎪⎝⎭,求2αβ+的值.【答案】(1)2;(2)724απβ+=. 【解析】先利用同角三角函数的基本关系得到sin ,cos ,tan ααα;(1)原式分子分母同除cos α得到正切,代入已知量即可得出结果;(2)先利用已知角的范围求得5224παπβ<-<,求出cos 2αβ⎛⎫- ⎪⎝⎭,再利用22ααββα⎛⎫+=-+ ⎪⎝⎭,最后利用两角和的余弦公式求解即可得出结果. 【详解】由题意:sin α=,cos α=, 1tan 2α=-,且2παπ<<,(1)2sin cos 2tan 124sin cos 4tan 1αααααα--==++;(2)∵32ππβ<<,224παπ-<-<-,∴5224παπβ<-<,∴cos 2αβ⎛⎫-= ⎪⎝⎭ ∴cos cos cos cos sin sin 2222ααααββαβαβα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=--- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,5521010⎛⎫=-⨯- ⎪ ⎪⎭=⎝-, ∵5242παβπ<+<, ∴724απβ+=. 【点睛】本题主要考查了同角三角函数的基本关系以及两角和的余弦公式.属于中档题.18.已知函数()22sin 24f x x x π⎛⎫=+- ⎪⎝⎭.(1)当,42x ππ⎡⎤∈⎢⎥⎣⎦时,求()f x 的值域; (2)是否存在实数()2,t ∈+∞,使得()f x 在()2,t 上单调递增?若存在,求出t 的取值范围,若不存在,说明理由.【答案】(1)()[]2,3f x ∈;(2)不存在,理由见解析.【解析】(1)由二倍角公式降幂,再由两角差的正弦公式化函数为一个角的一个三角函数形式,然后由正弦函数性质求得值域;(2)求出函数的单调区间,由2在减区间内部,得结论. 【详解】解:(1)∵()22sin 24f x x x π⎛⎫=+- ⎪⎝⎭1cos 21sin 212sin 223x x x x x ππ⎡⎤⎛⎫⎛⎫=-+-=+-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.又∵,42x ππ⎡⎤∈⎢⎥⎣⎦,∴22633x πππ≤-≤,即212sin 233π⎛⎫≤+-≤ ⎪⎝⎭x , ∴()[]2,3f x ∈; (2)由222232k x k πππππ-+≤-≤+()k Z ∈得51212k x ππππ-+≤≤+()k Z ∈, 所以()f x 的递增区间是5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦()k Z ∈,递减区间是511,1212k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈,令0k =,函数在511,1212ππ⎡⎤⎢⎥⎣⎦上递减,而5112,1212ππ⎡⎤∈⎢⎥⎣⎦,即函数在112,12π⎛⎫⎪⎝⎭上是递减的,故不存在实数()2,t ∈+∞,使得()f x 在()2,t 上递增. 【点睛】本题考查正弦型函数的值域,考查正弦型函数的单调性,解题方法由二倍角公式,两角和与差的正弦公式化函数为一个角的一个三角函数形式,然后由正弦函数性质求解. 19.已知R a ∈,函数()1ln f x ax x =--在1x =处取得极值.(1)求函数()f x 的单调区间;(2)若对()0,x ∀∈+∞,()2f x bx ≥-恒成立,求实数b 的最大值. 【答案】(1)函数()f x 在0,1上单调递减,在1,上单调递增;(2)211e -. 【解析】(1)首先对函数求导,根据函数()1ln f x ax x =--在1x =处取得极值,得到()110f a '=-=,求得1a =,根据导数的符号求得其单调区间; (2)将不等式转化为1ln 1x b x x +-≥,之后构造新函数()1ln 1xg x x x=+-,利用导数求得其最小值,进而求得最值,得到结果. 【详解】()11ax f x a x x-'=-=,由()110f a '=-=得1a =,()1ln =--f x x x , (1)()1x f x x-'=,由0f x 得1x >,由0f x 得01x <<,故函数()f x 在0,1上单调递减,在1,上单调递增.(2)()1ln 21x f x bx b x x≥-⇒+-≥, 令()1ln 1x g x x x =+-,则()2ln 2x g x x -'=,由0g x,得2x e >,由0g x ,得20x e <<,故()g x 在()20,e上递减,在()2e ,+∞上递增,∴()()22min 1e1eg x g ==-,即211e b ≤-, 故实数b 的最大值是211e-.【点睛】该题考查的是有关应用导数研究函数的问题,涉及到的知识点有根据极值点求参数的值,利用导数求函数的单调区间,利用导数求参数的取值范围,属于中档题目. 20.已知函数()1f x x ax =-,其中0a >. (1)求关于x 的不等式()2f x a>的解集; (2)若12a =,求[]0,x m ∈时,函数()f x 的最大值.【答案】(1)2,a ⎛⎫+∞⎪⎝⎭;(2)2max 2,0121,1212,212m m m y m m m m ⎧-<<⎪⎪⎪=≤≤+⎨⎪⎪->+⎪⎩. 【解析】(1)根据分段函数定义域解不等式可求得答案; (2)画出函数()f x 的图象,数形结合可求得()f x 的最大值 【详解】(1)()()()11,11,x ax x af x x x x a α⎧-≥⎪⎪=⎨⎪-<⎪⎩,(0)a >当1x a ≥时,由()2>f x a ,得(12)x ax a ->,1(2)()0ax x a-+>,20ax ->,2x a>, 当1x a <时,由()2>f x a ,即(1)2x ax a ->,220ax x a -+<,令220ax x a-+=,180∆=-<,方程无解,而0a >,所以220ax x a-+<无解,综上所述,2x a >,所以不等式()2f x a >的解集为2,a ⎛⎫+∞ ⎪⎝⎭. (2)12a =时()22,21212,22x x x f x x x x x x ⎧-≤⎪⎪=-=⎨⎪->⎪⎩,∵()112f =,由1122x x -=得另一个根21x =,由()f x 的图像可知,当01m <<时,函数的最大值为()2122m m f m m m ⎛⎫=-=- ⎪⎝⎭;当121m ≤≤+时,函数的最大值为12; 当21m >+时,函数的最大值为()22m f m m =-综上所述,函数的最大值为2max2,0121,1212,212m m m y m m m m ⎧-<<⎪⎪⎪=≤≤+⎨⎪⎪->+⎪⎩. 【点睛】本题考查了解分段函数不等式的问题,分段函数求最值的问题,考查了数形结合的思想. 21.重庆、武汉、南京并称为三大“火炉”城市,而重庆比武汉、南京更厉害,堪称三大“火炉”之首.某人在歌乐山修建了一座避暑山庄O (如图).为吸引游客,准备在门前两条夹角为6π(即AOB ∠)的小路之间修建一处弓形花园,使之有着类似“冰淇淋”般的凉爽感,已知弓形花园的弦长23AB =且点A ,B 落在小路上,记弓形花园的顶点为M ,且6MAB MBA π∠=∠=,设OBA θ∠=.(1)将OA ,OB 用含有θ的关系式表示出来;(2)该山庄准备在M 点处修建喷泉,为获取更好的观景视野,如何规划花园(即OA ,OB 长度),才使得喷泉M 与山庄O 距离即值OM 最大? 【答案】(1)43OA θ=;436OB πθ⎛⎫=+ ⎪⎝⎭;(2)当632OB OA ==时,OM 取最大值.【解析】(1)在OAB 中,利用正弦定理即可将OA ,OB 用含有θ的关系式表示出来; (2)在OMB △中,由余弦定理得出2OM 21632283πθ⎛⎫=-++ ⎪⎝⎭,结合三角函数的性质,即可得出OM 的最大值,再求出,OA OB 的长度即可. 【详解】(1)在ABC 中,由正弦定理可知sin sin 6OA ABπθ=,则OA θ=;同理由正弦定理可得sin sin 6OB ABOABπ=∠,则6OB OAB πθ⎛⎫=∠=+⎪⎝⎭, (2)∵AB =6MAB MBA π∠=∠=,∴2AM BM ==,在OMB △中,由余弦定理可知2222cos 6OM OB BM OB BM πθ⎛⎫=+-⋅+ ⎪⎝⎭248sin 4cos 666πππθθθ⎛⎫⎛⎫⎛⎫=++-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭241cos 24233ππθθ⎛⎫⎛⎫⎛⎫=-++-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2823cos 228228333πππθθθ⎤⎛⎫⎛⎫⎛⎫=-++++=-++ ⎪ ⎪ ⎪⎥⎝⎭⎝⎭⎝⎭⎦, ∵50,6πθ⎛⎫∈ ⎪⎝⎭, ∴2272,333πππθ⎛⎫+∈ ⎪⎝⎭,∴2sin 21,32πθ⎡⎫⎛⎫+=-⎪⎢⎪⎪⎝⎭⎣⎭, 当2sin 213πθ⎛⎫+=- ⎪⎝⎭时,即512πθ=时, OM4=+,此时5sin cos cos sin 124646OA πππππ⎫==+=⎪⎭,5551261212OB πππππ⎛⎫⎛⎫=+=-== ⎪ ⎪⎝⎭⎝⎭即当OB OA ==OM 取最大值.【点睛】本题主要考查了正弦定理和余弦定理的实际应用,涉及了三角函数求值域,属于中档题. 22.已知函数()sin ln()f x x a x b =++,()g x 是()f x 的导函数.(1)若0a >,当1b =时,函数()g x 在(,4)π内有唯一的极小值,求a 的取值范围; (2)若1a =-,1e 2b π<<-,试研究()f x 的零点个数.【答案】(1)(0,25sin 4)a ∈-;(2)()f x 有3个零点. 【解析】(1)先求导得2sin )(1)(ag x x x '=--+,求出2()0(1)a g ππ'=-<+()4sin 425a g '=--,再由sin 4025a --≤和sin 4025a-->两种情况讨论求得a 的取值范围;(2)分析可知,只需研究(,)b π-时零点的个数情况,再分(,),(,)22x b x πππ∈-∈两种情形讨论即可. 【详解】解:(1)当1b =时,si ()(l )n 1n f x a x x =++,cos 1()()x x ag f x x '==++, 2sin )(1)(a g x x x '=--+()0a >在(),4π是增函数,2()0(1)ag ππ'=-<+,(4)sin 425ag '=--, 当(4)sin 4025ag '=--≤时,()g x 在(,4)π是减函数,无极值; 当(4)sin 4025ag '=-->时,0(,4)x π∃∈,使得00()g x '=, 从而()g x 在0(,)x π单调递减,在0(,4)x 单调递增,0x 为()g x 唯一的极小值点,所以()0,25sin 4a ∈-(2)当1a =-时,()sin ln()f x x x b =-+,(1,)2b e π∈-,可知,(i )(),x π∈+∞时,()0f x <,无零点;所以只需研究(,)b π-,1()cos f x x x b'=-+,(ii )(,)2x ππ∈时,1()cos 0f x x x b'=-<+,可知()f x 单调递减, ()1ln()1ln()02222f b e ππππ=-+>-+-=,()0f π<,存在唯一的(,)2s ππ∈,()0f s =;(iii )当(,)2x b π∈-,21()sin ()f x x x b ''=-++是减函数,且21(0)00f b ''=+>,21()102()2f b ππ''=-+<+ 则1(0,)2x π∃∈,1()0f x ''=,()f x '在1(,)b x -是增函数,1()2x π,是减函数,并且 lim ()0x b f x +→-'<,()1010f b'=->,1()022f b ππ'=-<+, 所以2(,0)x b ∃∈-,2()0f x '=;3(0,)2x π∃∈,3()0f x '=,且知()f x()f x 在()2,b x -减,在()23,x x 增,在3(,)2x π减,又因为()lim 0x b x f +→->,()00ln 0f b =-<,()02f π>,(,0)m b ∃∈-,()0f m =, (0,)2n π∃∈,()0f n =,综上所述,由(i )(ii )(iii )可知,()f x 有3个零点. 【点睛】本题主要考查利用导数研究函数的极值和零点问题,意在考查学生对这些知识的理解掌握水平和分析推理能力.。
精品解析:重庆市第一中学校2022-2023学年高三下学期4月月考地理试题(解析版)

A.类型1-产业园区-类型2-农村村落区-类型3-城市居民区-类型4-综合功能区
B.类型1-城市居民区-类型2-综合功能区-类型3-产业园区-类型4-农村村落区
C.类型1-城市居民区-类型2-产业园区-类型3-农村村落区-类型4-综合功能区
D.类型1-综合功能区-类型2-城市居民区-类型3-产业园区-类型4-农村村落区
2023年4月5日清明节,是“二十四节气”中唯一一个既是节气又是传统节日的日子,下图示意二十四节气地球在公转轨道上的位置。读图,完成下面小题。
3.与清明节期间我国各地昼夜长短状况最相似的节气是( )
A.立春B.惊蛰C.霜降D.白露
4.清明时节,以下说法最准确的是( )
A.华南梅雨纷纷B.西北沙尘严重C.东北春耕繁忙D.西南道路结冰
【15题详解】
结合所学可知,河道回归旧河道,只有是由于河道弯曲,河流凹岸侵蚀,使得河流回到原位置,B正确;北半球地转偏向力向右,河流会远离城区,D错误;风力吹拂和降水条件对河道的影响较小,AC错误。故选B。
【点睛】引起地表形态变化的作用,按其能量来源分为内力作用和外力作用。内力作用的能量主要来自于地球内部的热能,表现为地壳运动、岩浆活动和变质作用等,它使地表变得高低起伏。外力作用的能量来源主要来自于地球外部的太阳能,以及地球重力能等,表现为地表物质的风化、侵蚀、搬运和堆积等作用。
【2题详解】
根据所学知识,为应对人口老龄化,应适当鼓励生育,进一步完善养老保障体系,②④正确;老龄化和劳动力密集型产业没有必然关系,排除①;提倡晚婚晚育,少生优生不利于缓解人口老龄化,排除③。因此D正确,排除ABC。故选D。
【点睛】人口增长分为自然增长和机械增长。自然增长主要在于本地区人口自然增长率的高低,当本地出生率大于死亡率时,人口自然增长较多,反之则较少。机械增长一般指的是人口迁移,影响人口迁移的因素包括气候、文化教育、政治、经济等因素,其中,目前影响人口迁移最主要的因素在于经济因素。
高三试卷语文-重庆市第一中学2024届高三上学期摸底考试语文试卷及参考答案

2023年重庆一中高2024届高三上学期开学语文测试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号码填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将答题卡交回。
一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成下面小题。
材料一:在我国传统美学和文论中,“意象”是个古老而又新鲜的话题,是出现得很早并富有深广文化底蕴的一个重要概念,是主观情志与外界客观物象相撞而契合的产物,是指有意味的具体形象,即“意”与“象”的融合。
其在文艺创作和文学鉴赏中的作用与地位都是不可忽视的。
“意”和“象”最早见于《周易·系辞》“书不尽言,言不尽意……圣人立象以尽意”之言。
东汉王充将“意”与“象”合成一个完整的概念。
其在《论衡·乱龙篇》说:“夫画布为熊、麋之象,名布为侯,礼贵意象,示义取名也。
”曹魏时代的王弼《周易略例·明象》“夫象者,出意者也;言者,明象者也。
尽意莫若象,尽象莫若言。
言生于象,故可以寻言以观象;象生于意,故可以寻象以观意。
意以象尽,象以言著”一段文字,阐明了意、象、言三者的关系。
从文学的创作来看,即从内心的“意”到关注的“象”,再至依托的“言”;从文学的欣赏来看,即从依托的“言”到关注的“象”,再至所传达的主观“意”。
将“意”“象”引进文学领域并实现其根本性语义转换的是晋代的挚虞,而南朝梁代的刘勰在《文心雕龙·神思》中则第一次将“意”“象”合为一词而又引进文学理论,使它具有了美学意义。
实际上,刘勰是将营构“意象”作为艺术构思的首要任务来看待的。
从此以后,对“意象”的认识及其在文艺美学上的地位就确定了下来,在文艺创作中,审美意象的营构是艺术家们必须要经过的一个步骤,是“眼中竹”至“胸中竹”的中间环节,即“意象”成为现实生活向艺术作品转化的必不可少的中介;而同样,在艺术欣赏活动之中,“意象”也起着一个读者从作品中获得审美感受的桥梁作用,亦是第二个中介。
2021届重庆市第一中学校高三上学期第三次月考数学试题(解析版)

2021届重庆市第一中学校高三上学期第三次月考数学试题一、单选题1.复数z 满足21iz i=-,则复数z 的虚部为()A .﹣1B .1C .iD .﹣i【答案】B【分析】利用复数的除法运算化简211ii i=-+-,再利用复数的代数形式求出结果.【详解】解:∵()()()()2121211112i i i i i z i i i i ++====-+--+,则复数z 的虚部为1.故选:B .【点睛】本题考查复数的除法运算.复数的除法运算关键是分母“实数化”,其一般步骤如下:(1)分子、分母同时乘分母的共轭复数;(2)对分子、分母分别进行乘法运算;(3)整理、化简成实部、虚部分开的标准形式.2.已知集合{}22,A xx x Z =<∈∣,则A 的真子集共有()个A .3B .4C .6D .7【答案】D【分析】写出集合{1,0,1}A =-,即可确定真子集的个数.【详解】因为{}22,{1,0,1}A xx x Z =<∈=-∣,所以其真子集个数为3217-=.故选:D.【点睛】本题考查集合的真子集个数问题,属于简单题.3.已知某圆锥的母线长为4,底面圆的半径为2,则圆锥的全面积为()A .10πB .12πC .14πD .16π【答案】B【分析】首先求得底面周长,即侧面展开图的扇形弧长,然后根据扇形的面积公式即可求得侧面积,即圆锥的侧面积,再求得圆锥的底面积,侧面积与底面积的和就是全面积.【详解】底面周长是:2×2π=4π,则侧面积是:14π48π2⨯⨯=,底面积是:π×22=4π,则全面积是:8π+4π=12π.故选B .【点睛】本题考查了圆锥的全面积计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.4.为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大它的光就越暗.到了1850年,由于光度计在天体光度测量的应用,英国天文学家普森又提出了亮度的概念,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足()12212.5lg lg m m E E -=-,其中星等为k m 的星的亮度为(1,2)k E k =.已知“心宿二”的星等是1.00,“天津四”的星等是1.25,则“心宿二”的亮度大约是“天津四”的()倍.(当||x 较小时,2101 2.3 2.7x x x ≈++)A .1.27B .1.26C .1.23D .1.22【答案】B【分析】把已知数据代入公式计算12E E .【详解】由题意211 1.25 2.5(lg lg )E E -=-,12lg0.1E E =,∴0.1212101 2.30.1 2.70.1 1.257 1.26E E =≈+⨯+⨯=≈.故选:B .【点睛】本题考查数学新文化,考查阅读理解能力.解题关键是在新环境中抽象出数学知识,用数学的思想解决问题.5.向量,a b 满足||1a = ,a 与b 的夹角为3π,则||a b - 的取值范围为()A .[1,)+∞B .[0,)+∞C .1,2⎡⎫+∞⎪⎢⎣⎭D .3,2⎫+∞⎪⎢⎪⎣⎭【答案】D【分析】把||a b -用数量积表示后结合函数的性质得出结论.【详解】22222||()2121cos 3a b a b a a b b b b π-=-=-⋅+=-⨯⨯+ 21b b -+= 2134423b ⎛⎫=+≥⎪⎝⎭- ,所以3||2a b -≥ .1||2b = 时取得最小值.故选:D .【点睛】本题考查平面向量的模,解题关键是把模用向量的数量积表示,然后结合二次函数性质得出结论.6.已知三棱锥P ABC -,过点P 作PO ⊥面,ABC O 为ABC ∆中的一点,,PA PB PB PC ⊥⊥,PC PA ⊥,则点O 为ABC ∆的()A .内心B .外心C .重心D .垂心【答案】D【分析】连接AO 并延长交BC 于一点E ,连接PO ,由于PA ,PB ,PC 两两垂直可以得到PA ⊥面PBC ,而BC ⊂面PBC ,可得BC ⊥PA ,由PO ⊥平面ABC 于O ,BC ⊂面ABC ,PO ⊥BC ,可得BC ⊥AE ,同理可以证明CO ⊥AB ,又BO ⊥AC .故O 是△ABC 的垂心.【详解】连接AO 并延长交BC 于一点E ,连接PO ,由于PA ,PB ,PC 两两垂直可以得到PA ⊥面PBC ,而BC ⊂面PBC ,∴BC ⊥PA ,∵PO ⊥平面ABC 于O ,BC ⊂面ABC ,∴PO ⊥BC ,∴BC ⊥平面APE ,∵AE ⊂面APE ,∴BC ⊥AE ;同理可以证明CO ⊥AB ,又BO ⊥AC .∴O 是△ABC 的垂心.故选D .【点睛】本题主要考查了直线与平面垂直的性质,解题时要注意数形结合,属于基本知识的考查.7.设sin5a π=,b =,2314c ⎛⎫= ⎪⎝⎭,则()A .a c b <<B .b a c <<C .c a b<<D .c b a<<【答案】C【分析】借助中间量1和12比较大小即可.【详解】解:由对数函数y x =在()0,∞+单调递增的性质得:1b =>=,由指数函数12xy ⎛⎫= ⎪⎝⎭在R 单调递减的性质得:2413311142212c ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=<=,由三角函数sin y x =在0,2π⎛⎫ ⎪⎝⎭上单调递增的性质得1sin sin 562a ππ=>=.所以c ab <<.故选:C.【点睛】本题考查利用函数的单调性比较大小,考查运算能力,化归转化思想,是中档题.本题解题的关键在于借助中间量1和12,尤其在比较a 与c 的大小时,将c 变形得24331142c ⎛⎫⎛⎫= ⎪ =⎪⎝⎭⎝⎭,进而与12比较大小是重中之核心步骤.8.已知三棱锥P ABC -的四个顶点均在同一个确定的球面上,且BA BC ==,2ABC π∠=,若三棱锥P ABC -体积的最大值为3,则其外接球的半径为()A .2B .3C .4D .5【答案】A【分析】由题意分析知三棱锥P ABC -体积的最大时,P ,O ,O '共线且O P '⊥面ABC ,P 在大于半球的的球面上,根据棱锥体积公式求得||O P ',进而应用勾股定理求外接球的半径.【详解】由题意知:AC 中点O '为面ABC 外接圆圆心,若外接球球心为O ,半径为R ,三棱锥P ABC -体积的最大时,P ,O ,O '共线且O 在P ,O '之间,∴1||33P ABC ABC V S O P -'=⋅⋅= ,1||||32ABC S BA BC =⋅⋅= ,即||3O P '=,||||32AC O C '==,所以()22222'|||'|33O C OC OO R R =-=--=,解得2R =,故选:A【点睛】关键点点睛:理解三棱锥P ABC -体积的最大时P 的位置及与球心、底面外接圆圆心的关系,结合棱锥体积公式、勾股定理求球体半径.二、多选题9.设m 、n 是两条不同的直线,α、β是两个不同的平面,下列命题中错误..的是()A .若,,//m n m n αβ⊂⊂,则//αβB .若,m n m α⊂⊥,则n α⊥C .若,m n αα^Ì,则m n ⊥D .若//,,m n αβαβ⊂⊂,则//m n【答案】ABD【分析】根据空间线、面关系,结合空间关系相关图例以及线线、线面、面面间的平行、垂直判定与性质,即可知选项的正误.【详解】A :,,//m n m n αβ⊂⊂,α、β不一定平行,错误.B :,m n m α⊂⊥,n 不一定垂直于α,错误.C :由线面垂直的性质:,m n αα^Ì,则必有m n ⊥,正确.D ://,,m n αβαβ⊂⊂,m 、n 不一定平行,错误.故选:ABD10.下列函数中,在(0,1)内是减函数的是()A .||12x y ⎛⎫= ⎪⎝⎭B .212log y x =C .121=+y x D .2log sin y x=【答案】ABC【分析】根据复合函数的单调性判断确定选项中各函数是否为减函数即可.【详解】A :1(2t y =为减函数,||t x =在(0,1)上为增函数,所以||12x y ⎛⎫= ⎪⎝⎭为减函数;B :12log y t =为减函数,2t x =在(0,1)上为增函数,所以212log y x =为减函数;C :1y t =为减函数,21t x =+在(0,1)上为增函数,所以121=+y x 为减函数;D :2log y t =为增函数,sin t x =在(0,1)上为增函数,所以2log sin y x =为增函数;故选:ABC【点睛】结论点睛:对于复合函数的单调性有如下结论1、内外层函数同增或同减为增函数;2、内外层函数一增一减为减函数;11.下列关于函数1()2sin 26f x x π⎛⎫=+⎪⎝⎭的图像或性质的说法中,正确的为()A .函数()f x 的图像关于直线83x π=对称B .将函数()f x 的图像向右平移3π个单位所得图像的函数为12sin 23y x π⎛⎫=+ ⎪⎝⎭C .函数()f x 在区间5,33ππ⎛⎫-⎪⎝⎭上单调递增D .若()f x a =,则1cos 232a x π⎛⎫-=⎪⎝⎭【答案】AD 【分析】令1262x k πππ+=+得到对称轴,即可判断A ;根据平移变换知识可判断B ;求出其单调增区间即可判断C ;利用配角法即可判断D.【详解】对于A ,令1262x k πππ+=+()k ∈Z ,解得22()3x k k Z ππ=+∈,当1k =时,得83x π=,故A 正确;对于B ,将函数()f x 的图像向右平移3π个单位,得112sin[()]2sin 2362y x x ππ=-+=,故B 错误;对于C ,令122()2262k x k k Z πππππ-+<+<+∈4244()33k x k k Z ππππ⇒-+<<+∈,故C 错误;对于D ,若12sin()26x a π+=,则11cos()sin[()]23223x x πππ-=+-=1sin()262ax π+=,故D 正确.故选:AD【点睛】方法点睛:函数()sin (0,0)y A x B A ωϕω=++>>的性质:(1)max min =+y A B y A B =-,.(2)周期2π.T ω=(3)由()ππ2x k k +=+∈Z ωϕ求对称轴(4)由()ππ2π2π22k x k k -+≤+≤+∈Z ωϕ求增区间;由()π3π2π2π22k x k k +≤+≤+∈Z ωϕ求减区间.12.定义在(0,)+∞上的函数()f x 的导函数为()'f x ,且()()f x f x x'<,则对任意1x 、2(0,)x ∈+∞,其中12x x ≠,则下列不等式中一定成立的有()A .()()()1212f x x f x f x +<+B .()()()()21121212x xf x f x f x f x x x +<+C .()1122(1)x x f f <D .()()()1212f x x f x f x <【答案】ABC【分析】构造()()f x g x x=,由()()f x f x x '<有()0g x '<,即()g x 在(0,)+∞上单调递减,根据各选项的不等式,结合()g x 的单调性即可判断正误.【详解】由()()f x f x x '<知:()()0xf x f x x'-<,令()()f x g x x =,则()()()20xf x f x g x x '-='<,∴()g x 在(0,)+∞上单调递减,即122112121212()()()()()g x g x x f x x f x x x x x x x --=<--当120x x ->时,2112()()x f x x f x <;当120x x -<时,2112()()x f x x f x >;A :121()()g x x g x +<,122()()g x x g x +<有112112()()x f x x f x x x +<+,212212()()x f x x f x x x +<+,所以()()()1212f x x f x f x +<+;B:由上得21121212()()()()x f x x x x f x x x -<-成立,整理有()()()()21121212x xf x f x f x f x x x +<+;C :由121x >,所以111(2)(1)(2)(1)21x x x f f g g =<=,整理得()1122(1)x x f f <;D :令121=x x 且121x x >>时,211x x =,12111()()()()g x g x f x f x =,12()(1)(1)g x x g f ==,有121()()g x x g x >,122()()g x x g x <,所以无法确定1212(),()()g x x g x g x 的大小.故选:ABC【点睛】思路点睛:由()()f x f x x '<形式得到()()0xf x f x x'-<,1、构造函数:()()f x g x x =,即()()()xf x f x g x x'-'=.2、确定单调性:由已知()0g x '<,即可知()g x 在(0,)+∞上单调递减.3、结合()g x 单调性,转化变形选项中的函数不等式,证明是否成立.三、填空题13.若一个球的体积为323π,则该球的表面积为_________.【答案】16π【解析】由题意,根据球的体积公式343V R π=,则343233R ππ=,解得2R =,又根据球的表面积公式24S R π=,所以该球的表面积为24216S ππ=⋅=.14.设向量a ,b 不平行,向量a b λ+ 与2a b + 平行,则实数λ=_________.【答案】12【解析】因为向量a b λ+ 与2a b + 平行,所以2a b k a b λ+=+ (),则{12,k k λ==,所以12λ=.【解析】向量共线.15.一般把数字出现的规律满足如图的模型称为蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,则第21行从左至右的第4个数字应是____________.【答案】228【分析】由题知,第n 行有n 个数字,奇数行从右至左由小变大,偶数行从左至右由小变大,则前20行共有20(120)123202102+++++==L 个数字,第21行最左端的数为21021231+=,从左到右第4个数字为228.【详解】观察数据可知,第n 行有n 个数字,奇数行从右至左由小变大,偶数行从左至右由小变大,则前20行共有20(120)123202102+++++==L 个数字,第21行最左端的数为21021231+=,所以第21行从左到右第4个数字为228.故答案为:228.【点睛】关键点睛:本题考查合情推理、数列的前n 项和,解题关键要善于观察发现数据特征,考查了学生的逻辑思维能力、数据处理能力、运算求解能力,综合性较强,属于较难题型.四、双空题16.已知等比数列{}n a 的公比为q ,且101a <<,20201a =,则q 的取值范围为______;能使不等式12121110m m a a a a a a ⎛⎫⎛⎫⎛⎫-+-++-≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 成立的最大正整数m =______.【答案】(1,)+∞4039【分析】根据已知求得1a 的表达式,由此求得q 的取值范围.根据12121110m m a a a a a a ⎛⎫⎛⎫⎛⎫-+-++-≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 成立列不等式,化简求得m 的取值范围,从而求得最大正整数m .【详解】由已知201911201911a qa q =⇒=,结合101a <<知2019101q <<,解得1q >,故q 的取值范围为(1,)+∞.由于{}n a 是等比数列,所以1n a ⎧⎫⎨⎬⎩⎭是首项为11a ,公比为1q 的等比数列.要使12121110m m a a a a a a ⎛⎫⎛⎫⎛⎫-+-++-≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 成立则1212111m ma a a a a a +++≤+++ 即()111111111m m a q a q q q⎛⎫-⎪-⎝⎭≤--,将120191a q=代入整理得:40394039m q q m ≤⇒≤故最大正整数4039m =.故答案为:(1,)+∞;4039【点睛】本小题主要考查等比数列的性质,考查等比数列前n 项和公式,属于中档题.五、解答题17.在四棱柱1111ABCD A B C D -中,底面ABCD 是等腰梯形,M 是线段AB 的中点,1160,22,2,DAB AB CD DD C M ∠=︒====(1)求证:1//C M 平面11A ADD ;(2)求异面直线 CM 与1DD 所成角的余弦值.【答案】(1)证明见解析;(2)14.【分析】(1)易得1111//,C D MA C D MA =,则四边形11AMC D 为平行四边形,得到11//C M D A ,再利用线面平行的判定定理证明.(2)由//CM DA ,将异面直线CM 与1DD 成的角,转化为 DA 与1DD 相交所成的角,然后在1ADD ,利用余弦定理求解.【详解】(1)因为四边形ABCD 是等腰梯形,且2AB CD =,所以//AB DC .又由M 是AB 的中点,因此//CD MA 且CD MA =.如图所示:连接1AD ,在四棱柱1111ABCD A B C D -中,因为1111//,CD C D CD C D =,可得1111//,C D MA C D MA =,所以四边形11AMC D 为平行四边形.因此11//C M D A ,又1C M ⊄平面11A ADD ,1D A ⊂平面11A ADD ,所以1//C M 平面11A ADD .(2)因为//CM DA ,所以异面直线CM 与1DD 成的角,即为 DA 与1DD 相交所成的直角或锐角,在1ADD中,1C M =,所以111,2AD AD DD ===,由余弦定理可得:22211111cos 24AD DD AD ADD AD DD +-∠==-⋅,所以异面直线CM 和1DD 余弦值为14.【点睛】方法点睛:判断或证明线面平行的常用方法:(1)利用线面平行的定义,一般用反证法;(2)利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;(3)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β);(4)利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β).18.已知数列{}n a 满足:13a =,且对任意的n *∈N ,都有1,1,n n a a +成等差数列.(1)证明数列{}1n a -等比数列;(2)已知数列{}n b 前n 和为n S ,条件①:()1(21)n n b a n =-+,条件②:11n n n b a +=-,请在条件①②中仅选择一个条件作为已知条件.............来求数列{}n b 前n 和n S .【答案】(1)证明见解析;(2)答案不唯一,具体见解析.【分析】(1)由条件得121n n a a +=-,利用等比数列定义可得证.(2)选条件①得(21)2nn b n =+,选条件②得1(1)()2nn b n =+⋅利用错位相减法可得解.【详解】(1)由条件可知112n n a a ++=,即121n n a a +=-,∴()1121n n a a +-=-,且112a -=∴{}1n a -是以112a -=为首项,2q =为公比的等比数列,∴12nn a -=,∴()21nn a n N*=+∈(2)条件①:()1(21)(21)2nn n b a n n =-+=+,123325272(21)2nn S n =⋅+⋅+⋅+++⋅ 23412325272(21)2n n S n +=⋅+⋅+⋅+++⋅利用错位相减法:123413222222222(21)2nn n S n +-=⋅+⋅+⋅+⋅++⋅+⋅- 118(12)6(21)212n n n S n -+--=++⋅--化简得()12(21)2n n S n n N +*=-+∈条件②:11(1)()12nn n n b n a +==+⋅-231111234(1)2222n nS n =⋅+⋅+⋅+++⋅ 234111111234(1)22222n n S n +=⋅+⋅+⋅+++⋅ 利用错位相减法:23411111111(1)222222n n n S n +=++++-+⋅ 1111[1()]11421(1)12212n n n S n -+-=+-+⋅-化简得()13(3)(2n n s n n N *=-+∈【点睛】错位相减法求和的方法:如果数列{}n a 是等差数列,{}n b 是等比数列,求数列{}n n a b 的前n 项和时,可采用错位相减法,一般是和式两边同乘以等比数列{}n b 的公比,然后作差求解;在写“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式19.已知椭圆C 的两个焦点分别为12(1,0),(1,0)F F -,短轴的两个端点分别为12,B B .且122B B =.(1)求椭圆C 的标准方程;(2)过点2F 的直线l 与椭圆C 相交于P ,Q 两点,且11F P FQ ⊥ ,求直线l 的方程.【答案】(1)2212x y +=;(2)10x +-=,或10x -=.【分析】(1)由题干条件可得c 和b 的值,进而求出2a 的值,从而求出椭圆方程;(2)首先考虑斜率不存在的情况,不符合题意;当斜率存在时,联立方程,可得()22121222214,2121k k x x x x k k -+=⋅=++,又110F P FQ ⋅= ,向量坐标化可得()()()2221212111110k x x k x x k F P FQ ⋅--==++++uuu r uuu r ,代入1212,x x x x +⋅,化简,即可求出k 的取值,从而求出直线方程.【详解】解(1)由条件可知:1c =,又122B B =,所以1b =,则22a =,所以椭圆C 的方程为2212x y +=(2)当直线l 的斜率不存在时,其方程为1x =,不符合题意;当直线l 的斜率存在时,设直线l 的方程为(1)y k x =-,22(1)12y k x x y =-⎧⎪⎨+=⎪⎩得()()2222214210k x k x k +-+-=,()2810k ∆=+>,设()()1122,,,P x y Q x y ,则()22121222214,2121k k x x x x k k -+=⋅=++,()()1111221,,1,F P x y F Q x y =+=+ ,∵110F P FQ ⋅= ,即()()()()()22212121212111110x x y y k x x k x x k +++=+--+++=,即()()()222222221411()102121k k kk k k k -+--++=++化简得:2201172k k =+-解得217,77k k ==±.故直线l的方程为10x +-=,或10x --=.【点睛】方法点睛:(1)将向量转化为坐标的关系;(2)联立直线和椭圆,求出两根之和,两根之积;(3)将两根之和和两根之积代入坐标关系中,解出k .20.已知()cossin 222x x x f x ⎛⎫=+ ⎪⎝⎭,记ABC 的内角,,A B C 的对边分别为,,a b c .(1)求()f B 的取值范围;(2)当4a =,433b =,且()f B 取(1)中的最大值时,求ABC 的面积.【答案】(1)30,12⎛+ ⎝⎦;(2)833或433【分析】(1)利用公式对函数化简,根据B 角的范围,求函数值域.(2)由(1)求出B 的大小,利用正弦定理和三角形面积公式即可求出结果.【详解】(1)2()cossin sin cos 222222x x x x x x f x ⎛⎫=+=+ ⎪⎝⎭13(cos 1)3sin sin 2232x x x π+⎛⎫=+=++ ⎪⎝⎭因为B 为三角形的内角,所以(0,)B π∈所以4,333B πππ⎛⎫+∈ ⎪⎝⎭,所以3()0,12f B ⎛∈+ ⎝⎦(2)34()11,,23333f B B B ππππ⎛⎫⎛⎫=++=+∈ ⎪ ⎝⎭⎝⎭,,326B B πππ∴+==,由正弦定理得:4343sin 1sin sin sin 22a b A A B A =⇒=⇒=()0,,3A A ππ∈∴=,或23A π=,若3A π=,则2C π=,183sin 23ABC S ab C ==若23π=A ,则6π=C,1sin 23==ABC S ab C 【点睛】本题考查了三角恒等变换、正弦定理和三角形面积公式等基本数学知识,考查了数学运算能力和逻辑推理能力,属于中档题目.21.在直三棱柱111ABC A B C -中,112,120,,AB AC AA BAC D D ==∠=分别是线段11,BC B C 的中点,过线段AD 的中点P 作BC 的平行线,分别交,AB AC 于点,M N .(1)证明:平面1A MN ⊥平面11ADD A ;(2)求二面角1A A M N --的余弦值.【答案】(1)证明见解析;(2)155.【分析】(1)根据线面垂直的判定定理即可证明MN ⊥平面ADD 1A 1;又MN ⊂平面A 1MN ,所以平面A 1MN ⊥平面ADD 1A 1;(2)建立空间坐标系,利用向量法求出平面的法向量,利用向量法进行求解即可.【详解】(1)证明:∵AB=AC ,D 是BC 的中点,∴BC ⊥AD ,∵M ,N 分别为AB ,AC 的中点,∴MN ∥BC ,∴MN ⊥AD ,∵AA 1⊥平面ABC,MN ⊂平面ABC ,∴AA 1⊥MN ,∵AD,AA 1⊂平面ADD 1A 1,且AD∩AA 1=A ,∴MN ⊥平面ADD 1A 1∴,又MN ⊂平面A 1MN ,所以平面A 1MN ⊥平面ADD 1A 1;(2)设AA 1=1,如图:过A 1作A 1E ∥BC ,建立以A 1为坐标原点,A 1E ,A 1D 1,A 1A 分别为x ,y ,z 轴的空间直角坐标系如图:则A 1(0,0,0),A(0,0,1),∵P 是AD 的中点,∴M ,N 分别为AB ,AC 的中点.则31,,122M ⎛⎫ ⎪ ⎪⎝⎭,31,,122N ⎛⎫- ⎪ ⎪⎝⎭,则131,,122A M ⎛⎫= ⎪ ⎪⎝⎭,()10,0,1A A =,)NM = ,设平面AA 1M 的法向量为(),,m x y z=,则100m AM m A A ⎧⋅=⎪⎨⋅=⎪⎩,得10220x y z z ++=⎨⎪=⎩,令1x =,则y =,则()1,m =,同理设平面A 1MN 的法向量为(),,n x y z=,则100n A M n NM ⎧⋅=⎨⋅=⎩,得310220x y z ++=⎪⎨⎪=⎩,令2y =,则1z =-,则()0,2,1n =-,则()15cos ,5m n m n m n ⋅===-⋅,∵二面角A-A 1M-N 是锐二面角,∴二面角A-A 1M-N 的余弦值是155.【点睛】本题主要考查直线垂直的判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.22.已知21()(1)2xf x e ax b x =---.其中常数 2.71828e ≈⋅⋅⋅⋅⋅⋅.(1)当2,4a b ==时,求()f x 在[1,2]上的最大值;(2)若对任意0,()a f x >均有两个极值点()1212,x x x x <,(ⅰ)求实数b 的取值范围;(ⅱ)当a e =时,证明:()()12f x f x e +>.【答案】(1)max ()1f x e =-;(2)(ⅰ)1b >;(ⅱ)证明见解析.【分析】(1)由题得2()4(1)x f x e x x =---,()24x f x e x '=--,()2x f x e ''=-,由[1,2]x ∈,可得()0f x ''>,即()'f x 在[1,2]上单增,且2(2)80f e -'=<,即()0f x '<,可知()f x 在[1,2]上单减,求得max ()(1)1f x f e ==-.(2)(ⅰ)利用两次求导可得(,ln )x a ∈-∞时,()'f x 单减;(ln ,)x a ∈+∞时,()'f x 单增,再由()f x 有两个极值点,知(ln )ln 0f a a a a b =--<',即ln b a a a >-恒成立,构造函数()ln g a a a a =-,利用导数求其最大值,可得实数b 的取值范围;(ⅱ)设()()(2),(1)h x f x f x x ''=--<,求导可得()h x 在(,1)-∞单增,得到()(2)f x f x ''<-,可得()()112f x f x ''<-,()()122f x f x ''->,结合()'f x 在(1,)+∞上单增,可得()()122f x f x >-,得到()()()()2222122222222x x f x f x f x f x e e ex ex e -+>-+=+-+-,构造22()22x x M x e e ex ex e -=+-+-,(1)x >,再利用导数证明()2(1)M x M e >=,即可得到()()12f x f x e+>【详解】(1)由2,4a b ==得,2()4(1)x f x e x x =---,求导()24x f x e x '=--,()2x f x e ''=-,[1,2]x ∈ ,2[,]x e e e ∴∈,20x e ∴->,即()0f x ''>()f x '∴在[1,2]上单增,且2(2)80f e -'=<,即[1,2]x ∀∈,()0f x '<,()f x ∴在[1,2]上单减,max ()(1)1f x f e ∴==-.(2)(ⅰ)求导()x f x e ax b '=--,因为对任意0,()a f x >均有两个极值点12,x x ,所以()0f x '=有两个根,求二阶导()x f x e a ''=-,令()0f x ''=,得ln x a=当(,ln )x a ∈-∞时,()0f x ''<,()'f x 单减;当(ln ,)x a ∈+∞时,()0f x ''>,()'f x 单增,由()0f x '=有两个根12,x x ,知(ln )ln 0f a a a a b =--<',即ln b a a a >-对任意0a >都成立,设()ln g a a a a =-,求导()ln g a a '=-,令()0g a '=,得1a =,当(0,1)x ∈时,()0g a '>,()g a 单增;当(1,)x ∈+∞时,()0g a '<,()g a 单减,max (()1)1g g a =∴=,1b ∴>又0,,()ba b f e x f x a -⎛⎫''-=>→+∞→+∞ ⎪⎝⎭Q ,所以实数b 的取值范围是:1b >.(ⅱ)当a e =时,()x f x e ex b '=--,()x f x e e ''=-,令()0f x ''=,得1x =当(,1)x ∈-∞时,()0f x ''<,()'f x 单减;当(1,)x ∈+∞时,()0f x ''>,()'f x 单增,又12,x x 是()0f x '=的两根,且12x x <,121,1x x <∴>,121x ∴->设()()(2),(1)h x f x f x x ''=--<,即22(2)2()2,(1)xxx xe ex b ee x b e e ex e x h x --⎡⎤=-=-------+<⎣⎦,则2()2220x x h x e e e e e -=+->-='()h x ∴在(,1)-∞单增,()(1)0h x h ∴<=,即()(2)f x f x ''<-又11,x <,()()112f x f x ''∴<-,()()122f x f x ''∴->又()f x ' 在(1,)+∞上单增,122x x ∴->,即1222x x x <-<,又()f x 在()12,x x 上单减,()()122f x f x ∴>-()()()()2222122222222x x f x f x f x f x e e ex ex e-∴+>-+=+-+-令22()22x x M x e e ex ex e -=+-+-,(1)x >则2()22x x M x e e ex e -'=--+,2()20x x M x e e e -''=+-≥()M x '∴在(1,)+∞单增,且(1)0M '=,()0M x '∴>,故()M x 在(1,)+∞单增又21x > ,()2(1)M x M e ∴>=,即()()12f x f x e+>【点睛】方法点睛:本题考查利用导数研究函数的单调性,求极值,最值,以及证明不等式,证明不等式的方法:若证明()()f x g x <,(,)x a b ∈,可以构造函数()()()F x f x g x =-,如果()0F x '<,则()F x 在(,)a b 上是减函数,同时若()0F a ≤,由减函数的定义可知(,)x a b ∈时,有()0F x <,即证明了()()f x g x <,考查学生的函数与方程思想,化归与转化思想,考查逻辑思维能力与推理论证能力,属于难题.。
重庆市第一中学2023-2024学年高三上学期开学考试物理试题及答案

2023年重庆一中高2024届高三开学考试物理测试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号码填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将答题卡交回。
一、单项选择题:本题共7小题,每小题4分,共28分。
在每小题给出的四个选项中,只有一项符合题目要求,选对得4分,选错得0分。
1.日本政府拟向太平洋排放核废水引发国际社会的广泛关注与谴责。
辐射的危害程度常用“当量剂量”这一物理量衡量,其国际单位是希沃特,记作Sv。
每千克(kg)人体组织吸收1焦耳(J)为1希沃特。
下列选项中用国际单位制的基本单位表达希沃特,正确的是A.m2/s2B.kg2·m2/s2C.J/kg D.m2/s2.下列关于物理学发展过程的说法中,正确的是A.伽利略有关自由落体运动规律的结论是完全通过实验得到的B.牛顿最早通过理想斜面实验提出力不是维持物体运动的原因C.“月—地检验”表明地面物体所受地球的引力与月球所受地球的引力遵从相同的规律D.牛顿力学适用于宏观低速物体,无法研究人造地球卫星的运动3.一质量为m的乘客乘坐竖直电梯下楼,其位移s与时间t的关系图像如图所示,其中t1~t2时间段内图像为直线。
乘客所受支持力的大小用F N表示,速度大小用v表示。
重力加速度大小为g。
以下判断正确的是A.0~t1时间内,v增大,F N>mgB.t1~t2时间内,v减小,F N<mgC.t2~t3时间内,v增大,F N<mgD.t2~t3时间内,v减小,F N>mg4.宇宙中有两颗相距400 km的中子星,它们绕自身连线上的某点每秒转动12圈。
将两颗中子星都看作是质量均匀分布的球体,由这些数据和万有引力常量,利用牛顿力学知识,可以估算出这一时刻两颗中子星A.各自的质量B.质量之和C.各自的速度D.各自的自转角速度5.登陆火星的飞船需经历如图所示的变轨过程。
云南省玉溪第一中学2022届高三数学上学期第四次月考试题 文(含解析)
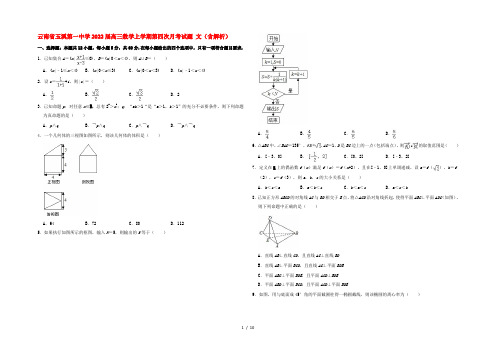
云南省玉溪第一中学2022届高三数学上学期第四次月考试题文(含解析)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求. 1.已知集合A={x |≤0},B={x|0<x<4},则A∪B=()A.{x|﹣1≤x<4} B.{x|0<x≤3} C.{x|0<x<3} D.{x|﹣1<x<4}2.设z =+i,则|z|=()A .B .C .D.23.已知命题p:对任意x∈R,总有2x>x2;q:“ab>1“是“a>1,b>1”的充分不必要条件,则下列命题为真命题的是()A.p∧q B.¬p∧q C.p∧¬q D.¬p∧¬q4.一个几何体的三视图如图所示,则该几何体的体积是()A.64 B.72 C.80 D.112 5.如果执行如图所示的框图,输入N=5,则输出的S等于()A .B .C .D .6.△ABC中,∠BAC=135°,,AC=1,D是BC边上的一点(包括端点),则的取值范围是()A.[﹣3,0] B .C.[0,2] D.[﹣3,2]7.定义在R上的偶函数f(x)满足f(x)=f(x+2),且在[﹣1,0]上单调递减,设a=f (),b=f (2),c=f(3),则a,b,c的大小关系是()A.b<c<a B.a<b<c C.b<a<c D.a<c<b8.已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是()A.直线AB⊥直线CD,且直线AC⊥直线BDB.直线AB⊥平面BCD,且直线AC⊥平面BDEC.平面ABC⊥平面BDE,且平面ACD⊥BDED.平面ABD⊥平面BCD,且平面ACD⊥平面BDE9.如图,用与底面成45°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为()A .B .C .D .10.某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x 件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均每件产品的生产准备费用与仓储费用之和最小,每批应生产产品()A.60件B.80件C.100件D.120件11.已知函数f(x)=a sin x ﹣cos x的一条对称轴为x =﹣,且f(x1)•f(x2)=﹣4,则|x1+x2|的最小值为()A .B .C .D .12.设等差数列{a n}满足a1=1,a n>0(n∈N*),其前n项和为S n,若数列{}也为等差数列,则的最大值是()A.310 B.212 C.180 D.121二、填空题:本题共4小题,每题5分,共20分.13.若直线ax﹣by﹣3=0(a>0,b>0)过点(1,﹣1),则+的最小值为.14.向量=(﹣1,1),=(1,0),若(﹣)⊥(2+λ),则λ=.15.在等差数列{a n}中,若a10=0,则有等式:a1+a2+…+a n=a1+a2+…+a19﹣n(n<19)成立,类比上述性质,相应地,在等比数列{b n}中,若b9=1,则有等式成立.16.已知在△ABC中,D为边AC上一点,AB=AD=4,AC=6,若△ABC的外心恰在线段BD上,则BC=.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.(一)必考题:共60分.第17-21题为必考题,每个试题考生都必须作答.17.已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.18.在等差数列{a n}中,a1=1,其前n项和为S n,等比数列{b n}的各项均为正数,b1=1,且b2+S3=11,S6=9b3.(1)求数列{a n}和{b n}的通项公式;(2)设c n=,求数列{c n}的前n项和T n.19.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,DC =6,AD=8,BC=10,PD=9,E为PA的中点.(1)求证:DE∥平面BPC;(2)线段AB上是否存在一点F,满足CF⊥DB?若存在,试求出此时三棱锥B﹣PCF的体积;若不存在,请说明理由.20.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A(1,0).(1)若l1与圆相切,求l1的方程;(2)若l1与圆相交于P,Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,判断AM•AN是否为定值,若是,则求出定值;若不是,请说明理由.21.已知函数f(x)=lnx﹣x+1.(1)证明f(x)≤0恒成立;(3)证明:(二)选考题:共10分.请考生在第22、23题中任选一题作答.作答时用2B铅笔在答题卡上把所选题目题号后的方框涂黑.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.已知直线l的参数方程为(t为参数),圆C的参数方程为(α为参数).(Ⅰ)若直线l与圆C的相交弦长不小于,求实数m的取值范围;(Ⅱ)若点A的坐标为(2,0),动点P在圆C上,试求线段PA的中点Q的轨迹方程..[选修4-5:不等式选讲]23.(1)求f(x)=+的最大值;(2)设a,b,c>0,且ab+bc+ca=1,求证:.2022云南省玉溪一中高三(上)第四次月考数学试卷(文科)参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求. 1.已知集合A={x |≤0},B={x|0<x<4},则A∪B=()A.{x|﹣1≤x<4} B.{x|0<x≤3} C.{x|0<x<3} D.{x|﹣1<x<4}【解答】解:A={x|﹣1≤x<3},B={x|0<x<4},∴A∪B={x|﹣1≤x<4}.故选:A.2.设z =+i,则|z|=()A .B .C .D.2【解答】解:z =+i =+i =.故|z|==.故选:B.3.已知命题p:对任意x∈R,总有2x>x2;q:“ab>1“是“a>1,b>1”的充分不必要条件,则下列命题为真命题的是()A.p∧q B.¬p∧q C.p∧¬q D.¬p∧¬q【解答】解:命题p:对任意x∈R,总有2x>x2;是假命题,例如取x=2时,2x与x2相等.q:由“a>1,b>1”⇒:“ab>1”;反之不成立,例如取a=10,b =.∴“ab>1“是“a>1,b>1”的必要不充分条件,是假命题.∴下列命题为真命题的是¬p∧(¬q),故选:D.4.一个几何体的三视图如图所示,则该几何体的体积是()A.64 B.72 C.80 D.112【解答】解:由三视图可知该几何体为上部是一四棱锥,下部为正方体的组合体.四棱锥的高h1=3,正方体棱长为4V正方体=Sh2=42×4=64,V四棱锥=Sh1==16,所以V=64+16=80.故选:C.5.如果执行如图所示的框图,输入N=5,则输出的S等于()A .B .C .D .【解答】解:n=5时,k=1,S=0,第一次运行:S=0+=,k=1<5,第二次运行:k=1+1=2,S ==,k=2<5,第三次运行:k=2+1=3,=,k=3<5,第四次运行:k=3+1=4,S ==,k=4<5,第五次运行:k=4+1=5,S ==,k=5,结束运行,输出S =.故选:D.6.△ABC中,∠BAC=135°,,AC=1,D是BC边上的一点(包括端点),则的取值范围是()A.[﹣3,0] B .C.[0,2] D.[﹣3,2]【解答】解:∵D是BC上的一点,(包括端点),∴设=,(0≤λ≤1),∵∠BAC=135°,,AC=1,D是BC边上的一点(包括端点),∴==﹣1,∴=[]•()=(2λ﹣1)﹣+(1﹣λ)=(2λ﹣1)﹣+(1﹣λ)=﹣(2λ﹣1)﹣2λ+(1﹣λ)=﹣5λ+2,∵0≤λ≤1,∴﹣5λ+2∈[﹣3,2],∴的取值范围是[﹣3,2].故选:D.7.定义在R上的偶函数f(x)满足f(x)=f(x+2),且在[﹣1,0]上单调递减,设a=f (),b=f (2),c=f(3),则a,b,c的大小关系是()A.b<c<a B.a<b<c C.b<a<c D.a<c<b【解答】解:∵偶函数f(x)满足f(x)=f(x+2),故周期T=2,∵在[﹣1,0]上单调递减,根据偶函数的对称性可知在[0,1]上单调递增,距对称轴越远,函数值越大,∵a=f ()=f (),=f(2﹣),b=f(2)=f(0),c=f(3)=f(1),则b<a<c.故选:C.8.已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是()A.直线AB⊥直线CD,且直线AC⊥直线BDB.直线AB⊥平面BCD,且直线AC⊥平面BDEC.平面ABC⊥平面BDE,且平面ACD⊥BDED.平面ABD⊥平面BCD,且平面ACD⊥平面BDE【解答】解:由题意知DC⊥BE,AB∩BE=E,∴直线AB⊥直线CD不成立,故A错误;∵AC⊥AB,∴AB与BC不垂直,∴直线AB⊥平面BCD不成立,故B错误;∵BE⊥DE,BE⊥AC,∴AC⊥平面BDE,∴平面ABC⊥平面BDE,且平面ACD⊥平面BDE,故C正确;∵平面ABD⊥平面BCD不成立,故D错误.故选:C.9.如图,用与底面成45°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为()A .B .C .D .【解答】解:设圆柱底面圆的方程为x2+y2=R2,∵与底面成45°角的平面截圆柱,∴椭圆的半长轴长是R,半短轴长是R,∴c=R,∴e ===.故选:A.10.某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x 件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均每件产品的生产准备费用与仓储费用之和最小,每批应生产产品()A.60件B.80件C.100件D.120件【解答】解:根据题意,该生产x 件产品的生产准备费用与仓储费用之和是=这样平均每件的生产准备费用与仓储费用之和为(x为正整数)由基本不等式,得当且仅当时,f(x)取得最小值、可得x=80时,每件产品的生产准备费用与仓储费用之和最小故选:B.11.已知函数f(x)=a sin x ﹣cos x的一条对称轴为x =﹣,且f(x1)•f(x2)=﹣4,则|x1+x2|的最小值为()A .B .C .D .【解答】解:f(x)=a sin x ﹣cos x=,由于函数的对称轴为:x =﹣,所以,则:,解得:a=1.所以:f(x)=2sin(x ﹣),由于:f(x1)•f(x2)=﹣4,所以函数必须取得最大值和最小值,所以:或所以:|x1+x2|=4k,当k=0时,最小值为.故选:C.12.设等差数列{a n}满足a1=1,a n>0(n∈N*),其前n项和为S n,若数列{}也为等差数列,则的最大值是()A.310 B.212 C.180 D.121【解答】解:设等差数列{a n}的公差为d,a1=1,a n>0(n∈N*),∴a n=1+(n﹣1)d,S n =.∴=1,=,=,∵数列{}也为等差数列,∴2=+,∴=1+,化为(d﹣2)2=0,解得d=2.∴a n=2n﹣1,S n=n2.∴==,∵数列单调递减,∴的最大值是=121.故选:D.二、填空题:本题共4小题,每题5分,共20分.13.若直线ax﹣by﹣3=0(a>0,b>0)过点(1,﹣1),则+的最小值为.【解答】解:∵ax﹣by﹣3=0(a>0,b>0)过点(1,﹣1),∴a+b=3,则+=(+)(a+b)==.故答案为:14.向量=(﹣1,1),=(1,0),若(﹣)⊥(2+λ),则λ= 3 .【解答】解:向量=(﹣1,1),=(1,0),∴=2,=1,=﹣1;又(﹣)⊥(2+λ),∴(﹣)•(2+λ)=2+(λ﹣2)•﹣λ=0,即2×2+(λ﹣2)•(﹣1)﹣λ•1=0,解得λ=3.故答案为:3.15.在等差数列{a n}中,若a 10=0,则有等式:a1+a2+…+a n=a1+a2+…+a19﹣n(n<19)成立,类比上述性质,相应地,在等比数列{b n}中,若b9=1,则有等式b1•b2•…•b n=b1•b2•…•b17﹣n(n<17)成立.【解答】解:在等差数列{a n}中,若a10=0,则有等式a1+a2+…+a n=a1+a2+…+a19﹣n(n<19,n∈N+)成立,故相应的在等比数列{b n}中,若b9=1,则有等式b1•b2•…•b n=b1•b2•…•b17﹣n(n<17)故答案为b1•b2•…•b n=b1•b2•…•b17﹣n(n<17)16.已知在△ABC中,D为边AC上一点,AB=AD=4,AC=6,若△ABC的外心恰在线段BD上,则BC=2.【解答】解:∵外心为三角形三边垂直平分线的交点,△ABC的外心恰在线段BD上,∴作线段AC的垂直平分线,交BD于点O,即为△ABC外心,∴OA=OB=OC,取AB的中点E,连接OE,则有OE⊥AB,可得∠BEO=∠OFD=90°,∵AB=AD,∴∠ABD=∠ADB,∴△BEO∽△DFO,∵AC=6,∴AF=3,∴DF=AD﹣AF=1,∵BE=2,∴==2,设OD=a,则有OB=OA=2a,OF2=OD2﹣FD2=a2﹣1,由AO2=AF2+OF2,得到4a2=9+a2﹣1,即a2=,由余弦定理得:cos A====,∴BC2=AB2+AC2﹣2AB•AC cos A=16+36﹣2×4×6×=40,则BC=2.故答案为:2三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.(一)必考题:共60分.第17-21题为必考题,每个试题考生都必须作答.17.已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.【解答】解:(1)由,解得,∴cos2α=;(2)由(1)得,sin2,则tan2α=.∵α,β∈(0,),∴α+β∈(0,π),∴sin(α+β)==.则tan(α+β)=.∴tan(α﹣β)=tan[2α﹣(α+β)]==.18.在等差数列{a n}中,a1=1,其前n项和为S n,等比数列{b n}的各项均为正数,b1=1,且b2+S3=11,S6=9b3.(1)求数列{a n}和{b n}的通项公式;(2)设c n =,求数列{c n}的前n项和T n.【解答】解:(1)设等差数列{a n}公差为d,等比数列{b n}的公比为q,则,解得d=2,q=2,所以a n=2n﹣1,b n=2n﹣1;(2)c n=(2n﹣1)()n﹣1.∴数列{c n}的前n项和T n=1×()0+3×()1+5×()2+…+(2n﹣1)•()n﹣1,T n=1×()1+3×()2+5×()3+…+(2n﹣1)•()n,∴T n =+2×()1+2×()2+2×()3+…+2×()n﹣1﹣(2n﹣1)•()n=1+2(1﹣()n﹣1)﹣(2n﹣1)•()n=3﹣(2n+3)×()n∴T n=6﹣(2n+3)•()n+119.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,PD=9,E为PA的中点.(1)求证:DE∥平面BPC;(2)线段AB上是否存在一点F,满足CF⊥DB?若存在,试求出此时三棱锥B﹣PCF的体积;若不存在,请说明理由.【解答】(1)证明:取PB的中点M,连接EM和CM,过点C作CN⊥AB,垂足为点N.∵CN⊥AB,DA⊥AB,∴CN∥DA,又AB∥CD,∴四边形CDAN为平行四边形,∴CN=AD=8,DC=AN=6,在Rt△BNC中,BN ==,∴AB=12,而E,M分别为PA,PB的中点,∴EM∥AB且EM=6,又DC∥AB,∴EM∥CD且EM=CD,则四边形CDEM为平行四边形,∴DE∥CM.∵CM⊂平面PBC,DE⊄平面PBC,∴DE∥平面BPC;(2)解:由题意可得DA,DC,DP两两互相垂直,如图,以D为原点,分别以DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系D﹣xyz,则D(0,0,0),B(8,12,0),C(0,6,0),假设AB上存在一点F使CF⊥BD,设点F坐标为(8,t,0),则=(8,t﹣6,0),=(8,12,0),由,得64+12(t﹣6)=12t﹣8=0,得t =,即AF =,则BF=12﹣=,又PD=9,∴=136.20.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A(1,0).(1)若l1与圆相切,求l1的方程;(2)若l1与圆相交于P,Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,判断AM•AN是否为定值,若是,则求出定值;若不是,请说明理由.【解答】解:(1)①若直线l1的斜率不存在,即直线x=1,符合题意.②若直线l1斜率存在,设直线l1为y=k(x﹣1),即kx﹣y﹣k=0.由题意知,圆心(3,4)到已知直线l1的距离等于半径2,即解之得.所求直线方程是x=1,3x﹣4y﹣3=0.(2)直线与圆相交,斜率必定存在,且不为0,可设直线方程为kx﹣y﹣k=0由得;又直线CM与l1垂直,得.∴AM•AN =为定值.21.已知函数f(x)=lnx﹣x+1.(1)证明f(x)≤0恒成立;(3)证明:【解答】解:(1)f(x)=lnx﹣x+1,f'(x )=,(x>0),当x∈(0,1),f'(x)>0,f(x)递增;当x∈(1,+∞),f'(x)<0,f(x)递减,故f(x)min=f(1)=0,所以f(x)≤0恒成立;(2)由(1)知,lnx≤x﹣1,x=1时取等号,n>1,则lnn<n﹣1=,故=,所以<.(二)选考题:共10分.请考生在第22、23题中任选一题作答.作答时用2B铅笔在答题卡上把所选题目题号后的方框涂黑.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.已知直线l 的参数方程为(t为参数),圆C 的参数方程为(α为参数).(Ⅰ)若直线l与圆C 的相交弦长不小于,求实数m的取值范围;(Ⅱ)若点A的坐标为(2,0),动点P在圆C上,试求线段PA的中点Q的轨迹方程..【解答】解:(Ⅰ)直线l 的参数方程为(t为参数),普通方程为y=mx,圆C 的参数方程为(a为参数),普通方程为x2+(y﹣1)2=1.圆心到直线l的距离d =,相交弦长=2,∴2≥,∴m≤﹣1或m≥1;(Ⅱ)设P(cosα,1+sinα),Q(x,y),则x =(cosα+2),y =(1+sinα),消去α,整理可得线段PA的中点Q的轨迹方程(x﹣1)2+(y ﹣)2=.[选修4-5:不等式选讲]23.(1)求f(x )=+的最大值;(2)设a,b,c>0,且ab+bc+ca=1,求证:.【解答】解:(1)由题意知:定义域为[0,4],由基本不等式,得=,当且仅当,即x=2,取等号;(2)因为ab+bc+ca=1,a,b,c>0,2(a+b+c)2=a2+b2+b2+c2+a2+4ab+4ac+4bc≥6(ab+bc+ac)=6,当且仅当a=b=c,取等号,故.。
重庆市第一中学2020-2021学年高三上期第三次月考英语试题及答案

2020年重庆一中高2021届高三上期第三次月考英语测试试题卷第一部分听力(共两节,满分20分)第一节(共5小题,每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选岀最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Where does the conversation probably take place?A. In a bank.B. In a restaurant.C. In a hospital.2. What will the woman most probably do this Friday?A. Do some shopping.B. Watch a movie.C. Organize a sales promotion.3. What does the woman think of the trip to Indonesia?A. Safe.B. Dangerous.C. Exciting.4. How much does the man make in a year?A. £49,000.B. £50,000.C. £ 60,000.5. What are the speakers mainly talking about?A. The man's travel experience.B. A flight to Romania.C. Family members.第二节听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听下面一段对话,回答第6和第7两个小题。
6. Who bought the Christmas tree?A. The woman's grandpa.B. The woman's mother.C. The woman’s father.7. How old is the tree?A. 40 years old.B. 75 years old.C. 80 years old.听下面一段对话,回答第8和第9两个小题。
重庆一中2021届高三上学期第一次月考生物试题含答案

秘密★启用前2020年重庆一中高2021届高三上期第一次月考生物试题卷答题前,考上先将自己的姓名、考号填写在相应位置,认真核对条形码上的考号、姓名,并将条形码贴在相应位置上。
1。
选择题答案用2B铅笔填涂在答题卡上。
2.非选择题答在答题卡规定的地方。
保持答题卡清洁,不折叠,不破损.一、选择题:本题共20小题,每小题2分,共40分。
每小题给出的四个选项中,只有一个选项是最符合题目要求的。
1。
系统是指彼此间相互作用,相互依赖的的组分有规律地结合而形成的整体。
下列有关系统的说法正确的是A.病毒是由核酸和蛋白质组成的生命系统B。
蓝藻和小麦的生命系统结构层次相同C.大肠杆菌和人体成熟红细胞都没有生物膜,也没有生物膜系统D。
动物园里的全部动物不是一个种群,也不是一个生态系统2.诗圣杜甫的《发秦州》有“充肠多薯蓣,崖蜜亦易求”的名句,薯蓣俗名山药,焦作的怀山药畅销全国,其块茎中平均含粗蛋白质14。
48%,粗纤维3. 48%,淀粉43。
7%及多种微量元素等.下列相关叙述不正确的是A。
山药中淀粉和纤维素的单体都是葡萄糖B。
山药细胞中的糖类都是其能源物质C。
山药细胞中的核酸的彻底水解产物有8种D.山药中蛋白质的药用功能由其结构直接决定3。
科学家最近发现了一种在低光照环境中能吸收光能并释放氧气的蓝细菌一一温泉拟甲色球藻。
下列相关叙述正确的是A.温泉拟甲色球藻细胞膜的主要成分是磷酸和蛋白质B。
温泉拟甲色球藻的拟核区能形成DNA--蛋白质复合物C。
温泉拟甲色球藻含有核糖体,核糖体中不含有元素PD。
温泉拟甲色球藻吸收光能是在类囊体薄膜上进行的4。
下列研究课题中,实验材料与试剂选择最合理的是5。
研究发现,V-ATPase 为溶酶体膜上的一种蛋白质,其形成过程类似于分泌蛋白。
V—ATPase具有ATP水解酶活性,能够利用水解ATP释放的能量逆浓度梯度将细胞质基质中的H+转运到溶酶体内。
溶酶体膜上的蛋白质是高度糖基化的,性质非常稳定,不易被水解酶水解.下列叙述中不合理的是A.溶酶体膜蛋白高度糖基化可能有利于防止溶酶体膜被自身水解酶分解B。
