高一必修二 第一二章周测
必修二第一、二章测试卷

优e学必修二一、二章检测(时间:90分钟,满分:100分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 关于“斜二测画法”,下列说法不正确的是()A.原图形中平行于x轴的线段,其对应线段平行于x′轴,长度不变B.原图形中平行于y轴的线段,其对应线段平行于y′轴,长度变为原来的1 2C.画与直角坐标系xOy对应的x′O′y′时,∠x′O′y′必须是45°D.在画直观图时,由于选轴的不同,所得的直观图可能不同2.下列推理错误的是()A.A∈l,A∈α,B∈l,B∈αlαB.A∈α,A∈β,B∈α,B∈βα∩β=ABC.l⊄α,A∈l A∉αD.A∈l,lαA∈α3.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是()A.6 B.C.D.12 4.对两条不相交的空间直线a与b,必存在平面α,使得()A.aα,bαB.aα,b∥αC.a⊥α,b⊥αD.aα,b⊥α5.下面四个命题:①若直线a,b异面,b,c异面,则a,c异面;②若直线a,b相交,b,c相交,则a,c相交;③若a∥b,则a,b与c所成的角相等;④若a⊥b,b⊥c,则a∥c.其中真命题的个数为()A.4 B.3C.2 D.16.在正方体ABCDA1B1C1D1中,E,F分别是线段A1B1,B1C1上的不与端点重合的动点,如果A1E=B1F,有下面四个结论:①EF⊥AA1; ②EF∥AC;③EF与AC异面;④EF∥平面ABCD.其中一定正确的是()A.①②B.②③C.②④D.①④7.设a,b为两条不重合的直线,α,β为两个不重合的平面,下列命题中为真命题的是() A.若a,b与α所成的角相等,则a∥bB.若a∥α,b∥β,α∥β,则a∥bC.若aα,bβ,a∥b,则α∥βD.若a⊥α,b⊥β,α⊥β,则a⊥b8.已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m ∥β,则下列四种位置关系中,不一定成立的是()A.AB∥m B.AC⊥mC.AB∥βD.AC⊥β9.若m,n为两条不重合的直线,α,β为两个不重合的平面,则下列命题中的真命题的个数是()①若m,n都平行于平面α,则m,n一定不是相交直线;②若m,n都垂直于平面α,则m,n一定是平行直线;③已知α,β互相垂直,m,n互相垂直,若m⊥α,则n⊥β;④m,n在平面α内的射影互相垂直,则m,n互相垂直.A.1 B.2C.3 D.410.已知某几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是()A .12cm 3 B .13cm 3 C .16cm 3 D .112cm 3 二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上) 11.下列图形可用符号表示为__________.12.若圆锥的母线长为2 cm ,底面圆的周长为2π cm ,则圆锥的体积为__________cm 3. 13.设平面α∥平面β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于点S ,且点S 位于平面α,β之间,AS =8,BS =6,CS =12,则SD =__________.14.如图,正方体ABCD A 1B 1C 1D 1中,若过A ,C ,B 1三点的平面与底面A 1B 1C 1D 1的交线为l ,则l 与AC 的关系是________.15.如图是一个几何体的三视图,若它的体积是a =____.16.(10分)如图,在三棱锥P-ABC中,P A⊥AB,P A⊥BC,AB⊥BC,P A=AB=BC=2,D 为线段AC的中点,E为线段PC上一点.(1)求证:P A⊥BD;(2)求证:平面BDE⊥平面P AC;(3)当P A∥平面BDE时,求三棱锥E-BCD的体积.17.(15分)如图,△ABC中,AC=BC AB,ABED是边长为1的正方形,平面ABED ⊥底面ABC,若G,F分别是EC,BD的中点.(1)求证:GF∥平面ABC;(2)求证:AC⊥平面EBC;(3)求几何体ADEBC的体积V.参考答案1.答案:C2.答案:C3.答案:D4.答案:B5.答案:D6.答案:D7.答案:D8.答案:D9.答案:A10. 答案:C11. 答案:α∩β=AB12.13. 答案:914.答案:平行15.16.[解析](1)证明:因为P A⊥AB,P A⊥BC,所以P A⊥平面ABC.又因为BD⊂平面ABC,所以P A⊥BD.(2)证明:因为AB=BC,D为AC的中点,所以BD⊥AC.由(1)知,P A⊥BD,所以BD⊥平面P AC,所以平面BDE⊥平面P AC.(3)解:因为P A∥平面BDE,平面P AC∩平面BDE=DE,所以P A∥DE.因为D为AC的中点,所以DE =12P A =1,BD =DC = 2.由(1)知,P A ⊥平面ABC , 所以DE ⊥平面ABC ,所以三棱锥E -BCD 的体积V =16BD ·DC ·DE =13.17. 解:(1)证明:连接AE ,如图所示,∵ADEB 为正方形,∴AE ∩BD =F ,且F 是AE 的中点. 又G 是EC 的中点, ∴GF ∥AC , 又AC平面ABC ,GF平面ABC ,∴GF ∥平面ABC .(2)证明:∵ADEB 为正方形, ∴EB ⊥AB ,又∵平面ABED ⊥平面ABC ,平面ABED ∩平面ABC =AB ,EB 平面ABED ,∴BE ⊥平面ABC ,∴BE ⊥AC .又∵AC =BC =2AB ,∴CA 2+CB 2=AB 2, ∴AC ⊥BC .又∵BC ∩BE =B , ∴AC ⊥平面BCE .(3)取AB 的中点N ,如图所示,∵AC=BC,∴CN⊥AB.又平面ABED⊥平面ABC,CN平面ABC,平面ABED∩平面ABC=AB,∴CN⊥平面ABED.∵△ABC是等腰直角三角形,∴CN=12AB=12,∴V CABED=13S ABED·CN=13×1×12=16.。
必修二1~2章测验参考答案及解析

假期作业二参考答案及解析1.解析:选D 。
同一元素的各种同位素的化学性质几乎相同,但物理性质有较大差异,如密度,熔、沸点等。
2.解析:选A 。
根据Na 、F 两种元素在周期表中的位置,结合“位—构—性”间的关系进行解答。
3.解析:选C 。
A 元素原子L 层比B 元素原子L 层少3个电子,即A 的L 层为5个电子,需得3个电子达到8电子的稳定结构。
B 元素原子核外电子总数比A 多5,说明B 元素原子的L 层已充满为8个电子,则B 元素原子核外共有7+5=12个电子,最外层为2个电子。
A 、B 形成化合物时,A 显-3价,B 显+2价,则化学式为B 3A 2。
4.解析:选C 。
同周期元素的非金属性逐渐增强,同主族元素的非金属性逐渐减弱。
非金属性越强,其最高价氧化物对应水化物的酸性越强。
5.解析:选C 。
元素周期表是按原子序数排列的,原子序数和核电荷数相等。
尽管目前只发现一百多种元素,但并不意味着元素只有这一百余种,还有很多种元素有待人们去发现;元素周期表中每个纵行叫做一族,但第8、9、10三个纵行合为一族,所以尽管表中共有18个纵行,但只有16个族。
6.解析:选A 。
E 原子核外有四个电子层,位于第四周期,A 、B 、C 、D 是前三周期元素。
从它们在周期表中的位置知它们位于周期表的右侧。
设B 的原子序数为x ,则有(x -1)+x +(x +1)+(x -8)+(x +18)=85,x =15,即为磷元素7.解析:选B 。
9.2 g 金属钠可以与重水反应生成0.2 mol 氢气,这样的0.2 mol 氢气含有0.4 mol 中子,0.4 mol 电子,0.4 mol 质子和0.2 mol 分子,故B 项正确。
8.解析:选D 。
离子键只存在于离子化合物中;NH 4Cl 是非金属原子间形成的离子化合物,稀有气体分子中不存在化学键;单质分子中同种原子吸引共用电子对能力相同,是非极性共价键,D 项正确。
9.解析:选D 。
必修2第一二章测试题

立体几何测试题姓名: 班级: 分数时间:120分钟 分值:150分一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下列说法不正确的是( ) A .圆柱的侧面展开图是一个矩形 B .圆锥过轴的截面是一个等腰三角形C .平行于圆台底面的平面截圆台截面是圆面D .直角三角形绕它的一边旋转一周形成的曲面围成的几何体是圆锥 2. 下列四个几何体中,每个几何体的三视图有且仅有两个视图相同的是( )A .①②B .①③C .①④D .②④3.如右图所示的直观图,其平面图形的面积为( )A . 3B . 223 C . 6 D .. 324、已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2是:( )A. 1:3B. 1:1C. 2:1D. 3:15、如果两个球的体积之比为8:27,那么两个球的表面积之比为 ( ) A.8:27 B. 2:3 C.4:9 D. 2:96、,a b 是异面直线,,b c 是异面直线,则,a c 的位置关系是( ) .A 相交、平行或异面 .B 相交或平行 .C 异面 .D 平行或异面7、下列四个命题中假命题的个数是( )① 两条直线都和同一个平面平行,则这两条直线平行。
② 两条直线没有公共点,则这两条直线平行。
③ 两条直线都和第三条直线垂直,则这两条直线平行。
④ //,,//a b a b αβαβ⊂⊂⇒。
①正方体 ②圆锥 ③三棱台 ④正四棱锥.4A .3B .2C .1D8. 如右图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为( ) .(不考虑接触点) A.π4πC. 32π+D. 18+π9.在正方体A 1B 1C 1D 1—ABCD 中,AC 与B 1D 所成的角的大小为 ( )A .6πB .4πC .3πD .2π10.如图,是一个无盖正方体盒子的表面展开图,A 、B 、C 为其上的三个点,则在正方体盒子中, ∠ABC 等于 ( )A .45°B .60°C .90°D .120° 11.某几何体的三视图如图所示,则它的体积是(A )283π-(B )83π-(C )82π- (D )23π12.正方形ABCD 的边长为6 cm ,点E 在AD 上,且AE =13 AD ,点F 在BC 上,且BF =13 BC ,把正方形沿对角线BD 折成直二面角A -BD -C 后,则EF = ( )A .27 cmB .215 cmC . 2 6 cmD .6 cm二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)13.一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为________cm 2.正 视 侧视俯视14.已知一个棱长为6cm 的正方体塑料盒子(无上盖),上口放着一个半径为5cm 的钢球,则球心到盒底的距离为_________cm.15、若圆锥的高是底面半径和母线的等比中项,则称此圆锥为“黄金圆锥”。
必修2第一、二章章节测试.docx

必修2 —、二章章节测试(总分120分,时间60分钟)班级 __________ 姓名 __________ 学号 ____________一、选择题(总分60,每小题5分)1.下列各组几何体中是多面体的一组是()A 三棱柱四棱台B 三棱柱四棱台C 三棱柱四棱台D 圆锥圆台球半球2、下列说法正确的是( )其余各面是三角形的多面体是棱锥 其余各面均为梯形的多面体是棱台 其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面互相平行,侧面均为平行四边形 3•如图中甲、乙、丙所示,下面是三个几何体的三视图,相应的标号是(① 长方体②圆锥③三棱锥④圆柱 A ②①③ B ①②③C ③②④D ④③② 4.如果两直线a // b ,且d 〃平面a,则方与a 的位置关系是( )。
A.相交B./? 〃平面aC. b u 平面aD. b //平面a 或bu 平面a5•在空间四边形ABCD 屮,E 、F 分别是AB 和BC 上的点,若AE : EB=CF : FB 二1: 3,则对角线AC 和平面DEF 的位置关系是( ) A 平行 B 相交 C 直线在平面内D 不能确定 6. 平面a 与平面0平行的条件可以是()A. a 内有无穷多条直线都与0平行B. 直线a // a , a // [5,且直线a 不在a 内,也不在0内C. 直线 a u a,直线 b u 0,且 G〃0, b // a D. a 内的任何直线都与0平行7、 过平面外一点,可作这个平面的平行线的条数是( )球 圆锥 正方体圆台 正方体六棱锥A 有一个面是多边形,B 有两个面互相平行,C 有两个面互相平行, 甲乙俯视图A 1条B 2条C无数条D有限条8、已知加,"表示两条直线Q,0,7表示平面,下列命题中止确的个数是((1)aC\y = m,/? A / = 7?, K mHn,则all(3(2)若加,兀相交且都在a,0外,mHa.mllp.nlla,nll/3.则a//0(3)若mH a. mil P,则all P(4)若mil a,nilp,且加//〃,则allPA. 1B. 2C. 3D. 49.如果直线a 〃平面a,贝ij ( )A.平面a内有且只有一条直线与。
高一数学周练必修二第一章

高一数学周练一.选择题(共8小题)1.同时具有性质 “周期为π,图象关于直线x =π3对称,在-π6,π3 上是增函数”的函数是( )A .y =sin x 2+π6 B .y =cos 2x +π3 C .y =cos 2x -π6 D .y =sin 2x -π6 2.若实数x 、y 满足x -2cos y =1,则x 2+cos y 的取值范围是( )A .[-1,+∞)B .[-1,10]C .-916,+∞D .-916,10 3.如果函数f (x )上存在两个不同点A 、B 关于原点对称,则称A 、B 两点为一对友好点,记作(A ,B ),规定(A ,B )和(B ,A )是同一对,已知f (x )=|cos x |x ≥0-lg (-x )x <0 ,则函数F (x )上共存在友好点( )A .1对B .3对C .5对D .7对4.记函数f (x )=sin ωx +π4(ω>0)的最小正周期为T .若π<T <2π,且y =f (x )的图象的一条对称轴为x =π6,关于该函数有下列四个说法:①2<ω<3;②f π2=0;③f (x )在-π6,π6上单调递增;④为了得到g (x )=sin ωx 的图象,只需将f (x )的图象向右平移π4个单位长度.以上四个说法中,正确的个数为( )A .1B .2C .3D .45.为了得到函数y =sin 2x +π3 的图象,可以将函数y =cos 2x +π4的图象( )A .向左平移5π24个单位B .向右平移5π24个单位C .向左平移π2个单位D .向右平移π2个单位6.阻尼器是一种以提供运动的阻力,从而达到减振效果的专业工程装置,深圳第一高楼平安金融中心的阻尼器减震装置,是亚洲最大的阻尼器,被称为“镇楼神器”,由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其离开平衡位置的位移s (cm )和时间t (s )的函数关系式为s =2sin (ωx +φ),其中ω>0,若该阻尼器模型在摆动过程中连续三次位移为s 0(-2<s 0<2)的时间分别为t 1,t 2,t 3,且t 3-t 1=2,则ω=( )A .π2B .πC .3π2D .2π7.将函数f (x )=3sin2x +2cos 2x -1的图象向右平移φ0<φ<π2个单位长度后得到函数g (x )的图像,对于满足|f (x 1)-g (x 2)|=4的x 1,x 2,当|x 1-x 2|最小值为π6时,φ=( )A .π3B .π4C .π2D .5π128.函数y =12-x 的图象与函数y =sin π2x (-4≤x ≤8)的图象所有交点的横坐标之和等于( )A .16B .12C .8D .4二.多选题(共4小题)9.在直角坐标系xOy 中,角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,终边经过点P (x ,-2),且tan α=2,则( )A .x =-1B .sin α=-255C .cos α=255D .tanα2<010.下列结论正确的是( )A .若x 1,x 2都是第一象限角,且x 1>x 2,则sin x 1>sin x 2B .函数f (x )=|sin x |的最小正周期是πC .函数y =12cos 2x +sin x 的最小值为-1D .已知函数f (x )的图象与x 轴有四个交点,且f (x +1)为偶函数,则方程f (x )=0的所有实根之和为411.已知函数f (x )=tan 2x -π3,则( )A .f (0)=3B .f (x )最小正周期为π2C .2π3,0为f (x )的一个对称中心D .f (x )在5π12,7π12上单调递增12.摩天轮常被当作一个城市的地标性建筑,如深圳前海的“湾区之光”摩天轮,如图所示,某摩天轮最高点离地面高度128米,转盘直径为120米,设置若干个座舱,游客从离地面最近的位置进舱,开启后按逆时针匀速旋转t 分钟,当t =15时,游客随舱旋转至距离地面最远处.以下关于摩天轮的说法中,正确的为( )A .摩天轮离地面最近的距离为4米B .若旋转t 分钟后,游客距离地面的高度为h 米,则h =-60cos π15t+68C .若在t 1,t 2时刻,游客距离地面的高度相等,则t 1+t 2的最小值为30D .ヨt 1,t 2∈[0,20],使得游客在该时刻距离地面的高度均为90米三.填空题(共4小题)13.若角α的终边在第四象限,且cos α=45,则tan (π-α)= .14.已知函数f (x )=sin x ,对于任意的x 1∈[0,a ],总存在x 2∈[a ,2a ],使得f (x 1)≤f (x 2)成立,则实数a 的取值范围是 .15.已知函数f (x )=2cos (ωx +φ)ω>0,|φ|<π2 的部分图象如图所示,则ω= ,f π2= .16.设函数f (x )=2sin π2x +π5.若对任意x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为 .四.解答题(共6小题)17.已知扇形的面积为π6,弧长为π6,设圆心角为α.(1)求α的弧度;(2)求cos π2+2α sin (-π-2α)cos 11π2-2α sin 9π2+2α 的值.18.函数f (x )=2sin ωx +π6(ω>0)的最小正周期为π.(1)求函数f (x )在[0,π]上的单调递增区间;(2)当x ∈-π6,π4时,求f (x )的值域.19.如图,某地一天从4~18时的温度变化曲线近似满足f (x )=A sin (ωx +φ)+b ,其中A >0,ω>0,0<φ<π.(1)求A ,b ,ω,φ;(2)求这一天4~12时的最大温差近似值.参考数据:2≈1.4,3≈1.7.20.如图,已知函数f (x )=A sin (ωx +φ)A >0,|φ|<π2的图象与y 轴交于点0,-12 ,且π3,1 为该图象的最高点.(Ⅰ)求函数y =f (x )在[0,π]上的零点;(Ⅱ)若函数y =f (λx )在0,π2内单调递增,求正实数λ的取值范围..21.设函数f(x)=sin2x+π4(1)在给出的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象;(2)求出函数y=f(x)在[0,π]上的单调区间和最值.22.海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天时间与水深(单位:米)的关系表:时刻0:003:006:009:0012:0015:0018:0021:0024:00水深10.013.09.97.010.013.010.17.010.0(1)请用一个函数来近似描述这个港口的水深y与时间t的函数关系;(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上认为是安全的(船舶停靠时,船底只要不碰海底即可).某船吃水深度(船底离水面的距离)为6.5米.Ⅰ)如果该船是旅游船,1:00进港希望在同一天内安全出港,它至多能在港内停留多长时间(忽略进出港所需时间)?Ⅱ)如果该船是货船,在2:00开始卸货,吃水深度以每小时0.5米的速度减少,由于台风等天气原因该船必须在10:00之前离开该港口,为了使卸下的货物尽可能多而且能安全驶离该港口,那么该船在什么整点时刻必须停止卸货(忽略出港所需时间)?高一数学周练参考答案与试题解析一.选择题(共8小题)1.D .2.D .3.D .4.B .5.B .6.B .7A .8.A .二.多选题(共4小题)9.ABD .10.BCD .11.BCD .12.BC .三.填空题(共4小题)13.34.140,π2 ∪5π4,+∞ .15.2;-3.16.2四.解答题(共6小题)17.【解答】解:(1)由扇形面积公式得12×π6r =π6,所以r =2,故α=l r =π12;(2)cos π2+2α sin (-π-2α)cos 11π2-2α sin 9π2+2α =-sin2α⋅sin2α-sin2αcos2α=tan2α=tan π6=33.18.【解答】解:(1)由函数的最小正周期为π,可得T =2πω=π,可得ω=2,所以函数f (x )=2sin 2x +π6 ,函数的单调递增区间满足-π2+2k π≤2x +π6≤π2+2k π,k ∈Z ,解得-π3+k π≤x ≤π6+k π,k ∈Z ,因为x ∈[0,π],当k =0时,x ∈0,π6,当k =1时,x ∈23π,π ,当k ≥2或k ≤1,x ∈∅,综上所述:函数的单调递增区间为0,π6 和23π,π ;(2)当x ∈-π6,π4 时,-π6≤2x +π6≤23π,当2x +π6=-π6时,(f (x ))min =2sin -π6 =-1,当2x +π6=π2时,[f (x )]max =2sin π2=2;所以f (x )的值域∈[-1,2].19.【解答】解:(1)由图象可知,A +b =30-A +b =10,解得A =10,b =20,12⋅2πω=14-6,解得ω=π8,再根据五点法作图可得,π8⋅6+φ=3π2+2k π,k ∈Z ,由0<φ<π,则φ=3π4.(2)由(1)可得,f (x )=10sin π8x +3π4+20,当x ∈[4,12]时,由图象可知,f (x )min =f (6)=10,f (x )max =f (12)=10sin 32π+3π4+20=10×22+20=20+52≈27,故这一天4~12时的最大温差近似值为27-10=17.20.【解答】解:(Ⅰ)由函数f (x )=A sin (ωx +φ)的图象知,A =1,f (0)=sin φ=-12,又|φ|<π2,所以φ=-π6,由f π3 =sin π3ω-π6 =1,结合图象知π3ω-π6=π2,解得ω=2,所以f (x )=sin 2x -π6 ,令f (x )=0,得sin 2x -π6=0,解得2x -π6=k π,k ∈Z ,所以x =12k π+π12,k ∈Z ;令k =0,得x =π12,令k =1,得x =7π12,所以函数y =f (x )在[0,π]上的零点是π12和7π12;(Ⅱ)函数y =f (λx )=sin 2λx -π6,λ>0,当x ∈0,π2 时,2λx -π6∈-π6,λπ-π6 ,令λπ-π6≤π2,解得λ≤23,所以正实数λ的取值范围是0,23.21.【解答】解:(1)列表:x 0π838π5π87π8π2x +π4π4π2π3π22π9π4sin 2x +π42210-122描点得图象:(2)由图象可知f (x )的单调增区间:0,π8 ,5π8,π ,单调减区间:π8,5π8 ,函数的最大值是:1,函数的最小值是:-1.22.【解答】(1)以时间为横坐标,水深为纵坐标,在直角坐标系中画出散点图.如图.根据图象,可考虑用函数y=A sin(ωt+φ)+h刻画水深与时间之间的对应关系.从数据和图象可以得出A=3,h=10,T=12,φ=0,由T=2πω=12,得ω=π6,所以这个港口水深与时间的关系可用y=3sinπ6t+10近似描述⋯(4分)(2)Ⅰ)由题意,y≥11.5就可以进出港,令sinπ6t=12,如图,在区间[0,12]内,函数y=3sin π6t+10与直线y=11.5有两个交点,由π6t=π6或56π,得t A=1,t B=5,由周期性得t C=13,t D=17,由于该船从1:00进港,可以17:00离港,所以在同一天安全出港,在港内停留的最多时间是16小时⋯(8分)Ⅱ)设在时刻t货船航行的安全水深为y,那么y=11.5-0.5(t-2)(t≥2).设f(t)=3sin π6t+10,t∈[2,10],g(t)=11.5-0.5(t-2)(t≥2)由f(6)=10>g(6)=9.5且f(7)=8.5<g(7)=9知,为了安全,货船最好在整点时刻6点之前停止卸货⋯(13分)。
最新人教版高中数学必修二第一、二章同步测试试卷及解析

单元形成性评价(一)(第一、二章)(120分钟150分)一、选择题(每小题5分,共60分)1.在空间四边形ABCD的边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF,HG交于一点P,则( )A.点P一定在直线BD上B.点P一定在直线AC上C.点P一定在直线AC或BD上D.点P既不在直线AC上,也不在直线BD上【解析】选B.如图,因为P∈HG,HG⊂平面ACD,所以P∈平面ACD.同理,P∈平面BAC.因为平面BAC∩平面ACD=AC,所以P∈AC.2.给定下列四个说法:①若一个平面内的两条直线与另一个平面都平行,则这两个平面相互平行;②若一个平面经过另一个平面的垂线,则这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,说法正确的是( )A.①和② B.②和③C.③和④ D.②和④【解析】选D.当两个平面相交时,一个平面内的两条直线也可以平行于另一个平面,故①错误;由平面与平面垂直的判定可知②正确;空间中垂直于同一条直线的两条直线还可以相交或者异面,故③错误;若两个平面垂直,只有在一个平面内与它们的交线垂直的直线才与另一个平面垂直,故④正确.3.一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:①长方形;②正方形;③圆.其中正确的是( )A.①② B.②③C.①③ D.①②③【解析】选B.根据画三视图的规则“长对正,高平齐,宽相等”可知,几何体的俯视图不可能是圆和正方形.4.《算数书》竹简于上世纪八十年代在湖北省张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“禾盖”的术:置如其周,令相乘也,又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈136L 2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈7264L 2h 相当于将圆锥体积公式中的圆周率π近似取为( )A .15750B .258C .237D .227【解析】选D.设圆锥的底面半径为r , 则圆锥的底面周长L =2πr ,所以r =L2π,所以V =13 πr 2h =L 2h12π.令L 2h 12π =7264L 2h , 得π=227.5.(2020·全国Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5-14B.5-12C.5+14D.5+12【解析】选C.如图,设CD=a,PE=b,则PO=PE2-OE2=b2-a42,由题意PO2=12ab,即b2-a24=12ab,化简得4⎝⎛⎭⎪⎫ba2-2·ba-1=0,解得ba=1+54(负值舍去).6.E,F,G分别是空间四边形ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是( )A.0 B.1C.2 D.3【解析】选C.在△ACD中,因为G,F分别为AD与CD的中点,所以GF∥AC.而GF⊂平面EFG,AC⊄平面EFG,所以AC∥平面EFG.同理,BD∥平面EFG.7.已知直三棱柱ABCA1B1C1中,M,N分别是A1B1,AB的中点,P点在线段B1C上,则NP与平面AMC1的位置关系是( )A.垂直B.平行C.相交但不垂直D.要依P点的位置而定【解析】选B.连接B1N,MN,CN.因为在直三棱柱ABCA1B1C1中,M,N分别是A1B1,AB的中点,所以MN B1B,又B1B C1C,所以四边形MC1CN为平行四边形,所以C1M∥NC.因为C1M⊄平面NCB1内,NC⊂平面NCB1,所以C1M∥平面NCB1.同理可得AM∥平面NCB1.又因为C1M∩AM=M,AM⊂平面C1AM,C1M⊂平面C1AM,所以平面C1AM∥平面NCB1.又因为P点在线段B1C上,所以NP∥平面C1AM.8.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15【解析】选D.由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分,如图所示,截去部分是一个三棱锥.设正方体的棱长为1,则三棱锥的体积为V1=13×12×1×1×1=16,剩余部分的体积V2=13-16=56.所以V1V2=1656=15.9.已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )A.AB∥m B.AC⊥mC.AB∥β D.AC⊥β【解析】选D.因为m∥α,m∥β,α∩β=l,所以m∥l.因为AB∥l,所以AB∥m.故A一定成立;因为AC⊥l,m∥l,所以AC⊥m.故B一定成立;因为A∈α,AB∥l,l⊂α,所以B∈α.所以AB⊄β,l⊂β,所以AB∥β.故C一定成立;因为AC⊥l,当点C在平面α内时,AC⊥β成立,当点C不在平面α内时,AC⊥β不成立.故D不一定成立.10.E,F,G分别为正方体ABCDA1B1C1D1中平面A1B1C1D1,平面B1BCC1,平面CC1D1D的对角线交点,则AE与FG所成的角为( )A.90°B.60°C.45°D.30°【解析】选A.如图,易得FG∥BD,B1D1∥BD,AE⊥B1D1.所以选A.11.(2021·全国甲卷)已如A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥OABC的体积为( )A.212B.312C.24D.34【解析】选A.因为AC⊥BC,AC=BC=1,所以AB = 2 ,所以OO ′=OA 2-AO ′2=12-⎝ ⎛⎭⎪⎫222 =22 .所以V O -ABC =13 ·S △ABC ·OO ′=13 ·12 ·1·1·22 =212.12.已知二面角αl β为60°,动点P ,Q 分别在平面α,β内,P 到β的距离为 3 ,Q 到α的距离为2 3 ,则P ,Q 两点之间距离的最小值为( )A . 3B .2C .2 3D .4【解析】选C.如图,分别作QA ⊥α于点A ,AC ⊥l 于点C ,PB ⊥β于点B ,PD ⊥l 于点D ,连接CQ ,BD ,则∠ACQ =∠PDB =60°,AQ =2 3 ,BP = 3 ,所以AC =PD =2.又因为PQ =AQ 2+AP 2=12+AP 2≥2 3 ,当且仅当AP =0,即点A 与点P 重合时取最小值.二、填空题(每小题5分,共20分)13.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的表面积为574π,则圆台较小的底面半径为________.【解析】设圆台较小的底面半径为r ,那么较大的底面半径为3r ,由已知得π(r +3r)×3+πr 2+9πr 2=574π,解得r =7. 答案:714.如图所示,在直四棱柱ABCD A 1B 1C 1D 1中,当底面四边形A 1B 1C 1D 1满足条件________时,有A 1C ⊥B 1D 1.(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).【解析】由直四棱柱可知CC 1⊥平面A 1B 1C 1D 1,又B 1D 1⊂平面A 1B 1C 1D 1,所以CC 1⊥B 1D 1,要使B 1D 1⊥A 1C ,只要B 1D 1⊥平面A 1CC 1,所以只要B 1D 1⊥A 1C 1,还可以填写四边形A 1B 1C 1D 1是菱形、正方形等条件.答案:B 1D 1⊥A 1C 1(答案不唯一)15.已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°.若△SAB的面积为8,则该圆锥的体积为________.【解析】由题意画出图形,如图,设AC是底面圆O的直径,连接SO,则SO是圆锥的高.设圆锥的母线长为l,则由SA⊥SB,△SAB的面积为8,得12l2=8,得l=4.在Rt△ASO中,由题意知∠SAO=30°,所以SO=12l=2,AO=32l=2 3 .故该圆锥的体积V=13π×AO2×SO=13π×(2 3 )2×2=8π.答案:8π16.已知四面体PABC中,PA=PB=4,PC=2,AC=2 5 ,PB⊥平面PAC,则四面体PABC 外接球的体积为________.【解析】因为PA=4,PC=2,AC=2 5 ,所以在△PAC中,PA2+PC2=20=AC2,可得AP⊥PC,又因为PB⊥平面PAC,PA,PC⊂平面PAC,所以PB⊥PA,PB⊥PC.以PA,PB,PC为长、宽、高,作长方体如图所示,则该长方体的外接球就是四面体PABC的外接球.因为长方体的体对角线长为42+42+22=6,所以长方体外接球的直径2R=6,则R=3,因此,四面体PABC的外接球体积为V=4π3R3=36π.答案:36π三、解答题(共70分)17.(10分)如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.(1)求证:AE⊥BE;(2)求三棱锥DAEC的体积.【解析】(1)因为AD⊥平面ABE,且AD∥BC,所以BC⊥平面ABE.因为AE⊂平面ABE,所以AE⊥BC.因为BF⊥平面ACE,且AE⊂平面ACE,所以BF⊥AE,又BC∩BF=B,所以AE⊥平面BCE,又因为BE⊂平面BCE,所以AE⊥BE.(2)在△ABE中,过点E作EH⊥AB于点H. 因为AD⊥平面ABE,且AD⊂平面ABCD,所以平面ABCD⊥平面ABE,又因为平面ABCD∩平面ABE=AB,EH⊂平面ABE,所以EH⊥平面ABCD.由已知及(1)得EH=12AB= 2 ,S△ADC=2 2 .故VDAEC =VEADC=13×2 2 × 2 =43.18.(12分)如图,四棱锥PABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=12 AD,∠BAD=∠ABC=90°.(1)证明:BC∥平面PAD;(2)若△PCD面积为27 ,求四棱锥PABCD的体积.【解析】(1)因为底面ABCD中,∠BAD=∠ABC=90°,所以BC∥AD,又AD⊂平面PAD,BC⊄平面PAD,所以BC∥平面PAD.(2)取AD的中点M,连接PM,CM,由AB=BC=12AD及BC∥AD,∠ABC=90°得四边形ABCM为正方形,则CM⊥AD.因为侧面PAD为等边三角形,所以PM⊥AD,又因为侧面PAD垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PM⊥底面ABCD.因为CM⊂底面ABCD,所以PM⊥CM.设BC=x,则CM=x,CD= 2 x,PM= 3 x,PC=PD=2x.取CD的中点N,连接PN,则PN⊥CD,所以PN=142x.因为△PCD的面积为27 ,所以12× 2 x×142x=27 ,解得x=-2(舍去),x=2.于是AB=BC=2,AD=4,PM=2 3 .所以四棱锥PABCD的体积V=13×2(2+4)2×2 3 =4 3 .19.(12分)如图,在直三棱柱ABCA1B1C1中,E,F分别为A1C1和BC的中点.(1)求证:EF∥平面AA1B1B;(2)若AA1=3,AB=2 3 ,求EF与平面ABC所成的角.【解析】(1)如图,取A1B1的中点D,连接DE,BD.因为E是A1C1的中点,所以DE12B1C1.又因为BC B1C1,BF=12BC,所以DE BF.所以四边形BDEF为平行四边形.所以BD∥EF.又因为BD⊂平面AA1B1 B,EF⊄平面AA1B1 B,所以EF∥平面AA1B1B.(2)如图,取AC的中点H,连接HF,EH. 因为EH∥AA1,AA1⊥平面ABC,所以EH⊥平面ABC.所以∠EFH就是EF与平面ABC所成的角.在Rt△EHF中,FH= 3 ,EH=AA1=3,所以tan ∠EFH=EHFH= 3 ,所以∠EFH=60°.故EF与平面ABC所成的角为60°.20.(12分)如图,在四棱锥PABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD 是边长为2的菱形,∠BAD=60°,N是PB的中点,E为AD的中点,过A,D,N的平面交PC 于点M.求证:(1)EN ∥平面PDC ; (2)BC ⊥平面PEB ; (3)平面PBC ⊥平面ADMN.【证明】(1)因为AD ∥BC ,BC ⊂平面PBC , AD ⊄平面PBC ,所以AD ∥平面PBC. 又平面ADMN ∩平面PBC =MN , 所以AD ∥MN.又因为AD ∥BC ,所以MN ∥BC. 又因为N 为PB 的中点, 所以M 为PC 的中点,所以MN =12 BC.因为E 为AD 的中点,所以DE =12 AD =12BC =MN ,所以DE MN ,所以四边形DENM 为平行四边形,所以EN ∥DM.又因为EN ⊄平面PDC ,DM ⊂平面PDC ,所以EN∥平面PDC.(2)因为四边形ABCD是边长为2的菱形,且∠BAD=60°,E为AD中点,所以BE⊥AD.又因为PE⊥AD,PE∩BE=E,所以AD⊥平面PEB.因为AD∥BC,所以BC⊥平面PEB.(3)由(2)知AD⊥PB.又因为PA=AB,且N为PB的中点,所以AN⊥PB.因为AD∩AN=A,所以PB⊥平面ADMN.又因为PB⊂平面PBC,所以平面PBC⊥平面ADMN.21.(12分)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2 3 ,∠BAD=90°.(1)求证:AD⊥BC;(2)求异面直线BC与MD所成角的余弦值;(3)求直线CD与平面ABD所成角的正弦值.【解析】(1)由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.(2) 如图,取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角.在Rt△DAM中,DM=AD2+AM2=13 .因为AD⊥平面ABC,故AD⊥AC.在Rt△DAN中,DN=AD2+AN2=13 .在等腰△DMN中,MN=1,可得cos ∠DMN=12MNDM=1326.所以,异面直线BC与MD所成角的余弦值为1326.(3)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM= 3 . 又因为平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,而CM⊂平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.在Rt△CAD中,CD=AC2+AD2=4.在Rt△CMD中,sin ∠CDM=CMCD=34.所以,直线CD与平面ABD所成角的正弦值为34 .22.(12分)如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面△PAD为等边三角形.(1)求证:AD⊥PB;(2)若E为BC边上的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD?并证明你的结论.【解析】(1)设G为AD的中点,连接PG,BG,如图.因为△PAD为等边三角形,所以PG⊥AD.在菱形ABCD中,∠DAB=60°,G为AD的中点,所以BG⊥AD.又因为BG∩PG=G,BG,PG⊂平面PGB,所以AD⊥平面PGB.因为PB⊂平面PGB,所以AD⊥PB.(2)当F为PC的中点时,满足平面DEF⊥平面ABCD.如图,设F为PC的中点,连接DF,EF,DE,则在△PBC中,EF∥PB. 在菱形ABCD中,GB∥DE,而EF,DE⊂平面DEF,PB,GB⊂平面PBG,EF∩DE=E,PB∩BG=B,所以平面DEF∥平面PGB.由(1)得AD⊥平面PGB,而AD⊂平面ABCD,所以平面PGB⊥平面ABCD,所以平面DEF⊥平面ABCD.。
高一数学必修二第一二章测试卷答案

高一数学必修二第一、二章测试卷一、选择题:(每题5分共40分)1.不共面的四点可以确定平面的个数为 ( ) A . 2个 B . 3个 C . 4个 D .无法确定 2.若直线a 和b 没有公共点,则a 与b 的位置关系是( )A .相交B .平行C .异面D .平行或异面3.长方体ABCD -A 1B 1C 1D 1中,异面直线AB ,A 1D 1所成的角等于( ) A .30° B .45° C .60° D .90° 4.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错.误.的是( ). A .BD ∥平面CB 1D 1 B .AC 1⊥BD C .AC 1⊥平面CB 1D 1D .异面直线AD 与CB 1角为60°5.关于直线m ,n 与平面 α,β,有下列四个命题:①m ∥α n ∥β 且 α∥β,则m ∥n ; ②m ⊥α n ⊥β 且 α⊥β,则m ⊥n ; ③m ⊥α n ∥β 且 α∥β,则m ⊥n ; ④m ∥α n ⊥β 且 α⊥β,则m ∥n .其中正确的序号是( ). A .①②B .③④C .①④D .②③6.给出下列四个命题:①垂直于同一直线的两条直线互相平行 ②垂直于同一平面的两个平面互相平行③若直线l 1,l 2与同一平面所成的角相等,则l 1,l 2互相平行 ④若直线l 1,l 2是异面直线,则与l 1,l 2都相交的两条直线是异面直线 其中错误的...命题的个数是( ). A .1B .2C .3D .47.下列命题中正确的个数是( )①若直线l 上有无数个点不在平面 α 内,则l ∥α②若直线l 与平面 α 平行,则l 与平面 α 内的任意一条直线都平行(第4题)③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行④若直线l 与平面 α 平行,则l 与平面 α 内的任意一条直线都没有公共点 A .0个B .1个C .2个D .3个8.如右图所示的直观图,其平面图形的面积为( )A . 3B . 223 C . 6 D .. 32二、填空题(每题5分共20分)1. (2010·南京三模)已知圆锥的母线长为2,高为3,则该圆锥的侧面积是_______ _2.一个长方体的长、宽、高之比为2:1:3,全面积为88cm 2,则它的体积为___________. 2、右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是4. 两个球的表面积之比是1:16,这两个球的体积之比为________三、解答题(共40分)1.(10分)如图,在三棱锥P ABC -中,PA ⊥底面,,60,90ABC PA AB ABC BCA ︒︒=∠=∠=, 点D ,E 分别在棱,PB PC 上, 求证:BC ⊥平面PAC ;俯视图正(主)视图 侧(左)视图2、(20分)如图,四棱锥P —ABCD 中, PA ⊥平面ABCD ,底面ABCD是直角梯形,AB ⊥AD ,CD ⊥AD ,CD=2AB ,E 为PC 中点.F 为PD 中点 (I) 求证:平面PDC ⊥平面PAD ;(II) 求证:BE//平面PAD .3、(10分)如图,四棱锥ABCD S -的底面是正方形,⊥SA 底面ABCD ,E 是SC 上一点.求证:平面⊥EBD 平面SAC ;高一数学必修二第一、二章测试卷答案一、选择题:(每题5分共40分)1.C2.D3.D4.D5.D6.D7.B8.C 二、填空题(每题5分共20分)1. 22. 483. 12π4. 1:64三、解答题(共40分)1. 证明:∵PA ⊥底面ABC ,∴PA ⊥BC .又90BCA ︒∠=,∴AC ⊥BC . ∴BC ⊥平面PAC .ED CBASA B CD E P F2.证明:(1)由PA ⊥平面ABCD ⇒⎪⎭⎪⎬⎫=⋂⊥⊥A AD PA CD PA )AD (CD 已知 ⇒⎭⎬⎫⊂⊥P A D CD PAD CD 面面 ⇒平面PDC ⊥平面PAD ;(2)由E 为PC 中点,得EF 为△PDC 的中位线,则EF//CD ,CD=2EF .又CD=2AB ,则EF=AB .由AB//CD ,则EF ∥AB . 所以四边形ABEF 为平行四边形,则EF//AF . 由AF ⊂面PAD ,则EF//面PAD . 3.证明: ⊥SA 底面ABCD BD SA ⊥∴且AC BD ⊥ ∴S A C 平面⊥BD∴平面⊥EBD 平面SACAB CD EP F。
高一数学必修二第一章检测试题(含答案)
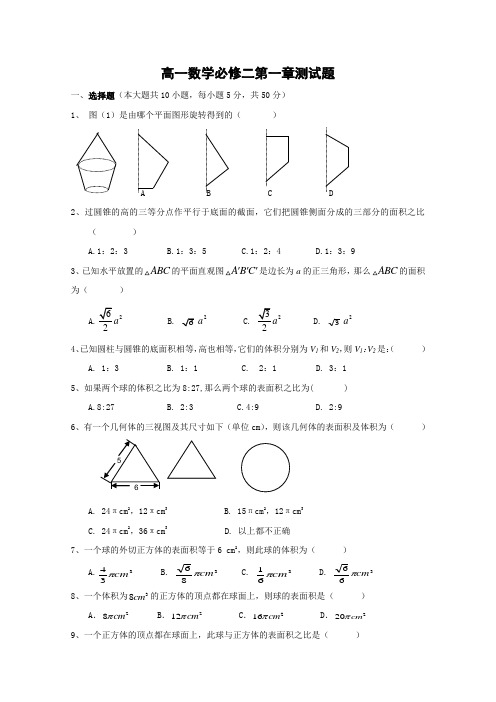
高一数学必修二第一章测试题一、选择题(本大题共10小题,每小题5分,共50分) 1、 图(1)是由哪个平面图形旋转得到的( )A B C D2、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比( )A.1:2:3B.1:3:5C.1:2:4D.1:3:93、已知水平放置的ABC 的平面直观图A B C '''是边长为a 的正三角形,那么ABC 的面积为( ) 22a C.22a D. 32a4、已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2是:( )A. 1:3B. 1:1C. 2:1D. 3:1 5、如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:96、有一个几何体的三视图及其尺寸如下(单位cm ),则该几何体的表面积及体积为( )A. 24πcm 2,12πcm 3B. 15πcm 2,12πcm 3C. 24πcm 2,36πcm3D. 以上都不正确7、一个球的外切正方体的表面积等于6 cm 2,则此球的体积为( )A.334cm π B.386cm π C. 361cm π D. 366cm π 8、一个体积为38cm 的正方体的顶点都在球面上,则球的表面积是( )A .28cm πB .212cm πC .216cm πD .220cm π 9、一个正方体的顶点都在球面上,此球与正方体的表面积之比是( )A. 3πB. 4πC. 2π D. π10、如右图为一个几何体的三视图,其中府视图为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为( )A. 6+3B. 24+3C. 24+23D. 32一、选择题答题表二、填空题(本大题共4小题,每小题5分,共20分)11. 长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为_______________. 12.一个半球的全面积为Q ,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 . 13、从长方体的一个顶点出发的三条棱上各取一点E 、F 、G ,过此三点作长方体的截面,那么截去的几何体是_________.14、一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.三、解答题(本大题共6小题,15、16、17、18每题13分,19、20每题14分,共80分) 15.将圆心角为1200,面积为3π的扇形,作为圆锥的侧面,求圆锥的表面积和体积.16. (如图)在底半径为2母线长为4的圆锥中内接一个高为3的圆柱,求圆柱 的表面积A B 1正视图侧视图府视图17、如图,在四边形ABCD中,,,,,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.18.已知长方体的全面积为11,十二条棱长度之和为24,求长方体的对角线的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一物理必修2
编写人:李嘉媛审核人:唐安祥编写时间:2015-4-2 -、单选题
1、雨滴由静止开始自由下落,中途遇到水平方向吹来的风,则下列说法正确的是()
A.雨滴落地时间与风速无关
B.风速越大,雨滴下落时间越长
C.雨滴下落速度与风速无关
D.雨滴运动轨迹与风速无关
2.关于竖直上抛运动,下列说法中正确的是( )
A.将物体以一定初速度竖直向上抛出,仅受重力,则物体的运动为竖直上抛运动
B.做竖直上抛运动的物体,其加速度与物体重力有关,重力越大的物体,加速度越大
C.竖直上抛运动只包括上升阶段
D.竖直上抛运动其速度和加速度的方向都可以改变
3、将甲、乙、丙三个小球同时水平抛出后落在同一水平面上,已知甲和乙抛射点的高度相同,乙和丙抛射速度相同。
下列判断中正确的是( )
A. 丙和甲一定同时落地
B. 乙和甲一定同时落地
C. 甲和乙水平射程一定相同
D. 乙和丙水平射程一定相同
4、物体受到几个外力的作用而作匀速直线运动,如果撤掉其中的一个力,它可能做( )
A.匀速直线运动
B.曲线运动
C.变加速曲线运动
D.变加速直线运动
二、双选题
5、图所示,以v0=10 m/s 的速度水平抛出的小球,飞行一段时间后垂直地撞在倾角α=30°的斜面上,g取10 m/s2,以下结论中正确的是( )
A.小球飞行时间是 3 s
B.小球飞行的时间是2 s
C.小球撞击斜面时的速度大小为20 m/s
D.小球下降的距离是10 m
6、地面以20 m/s的初速度竖直上抛一物体,当物体运动到距离地面15 m高时所经历的时间可能是( )
A.1 s B.2 s
C.3 s D.4 s
7、乙两个做圆周运动的质点,它们的角速度之比为3∶2,线速度之比为2∶3,那么下列说法正确的是( )
A.它们的半径之比为4∶9 B.它们的半径之比为1∶2
C.它们的周期之比为3∶2 D.它们的周期之比为2∶3
班级:_______ 姓名:_______ 得分:_______
三、计算题。
(解答时请写出必要的文字说明,方程式和重要的运算步骤,只写出答案的不得分,由数值计算的题,答案中必须写出数值和单位)(所有题目重力加速度g 取10 m/s 2 )
8、有A 、B 两小球,B 在地面,B 以初速度v 0= 20 m/s 做竖直上抛运动.问:
(1)B 球上升的最大高度是多少?上升到最大高度需要多少时间?
(2)若A 在B 球正上方.A 与B 相距s =10 m ,A 球做自由落体运动,AB 两球同时开始运动,请问需要多久时间相遇?
9、如图一辆质量为500kg 的汽车静止在一座半径为50m 的圆弧形拱桥顶部
(1)此时汽车对圆弧形拱桥的压力是多大?
(2)如果汽车以6m/s 的速度经过拱桥的顶部,则汽车对圆弧形拱桥的压力是多大?
(3)汽车以多大速度通过拱桥的顶部时,汽车对圆弧形拱桥的压力恰好为零?
单选题 双选题
1 2 3
4 5 6 7。
