江苏省南通市2015届高三第一次模拟考试
江苏省南通市2015年职业学校对口单招高三第一次调研考试数学试题Word版含..
南通市2015年职业学校对口单招高三年级第一次调研考试数学试卷注意事项：1．本试卷分选择题、填空题、解答题三部分．试卷满分150分．考试时间120分钟． 2．答题前，考生务必将自己的姓名、学校、考试号用0.5mm 黑色签字笔填写在答题卡规定区域．3．选择题作答：用2B 铅笔把答题卡上相应题号中正确答案的标号涂黑．4．非选择题作答：用0.5mm 黑色签字笔直接答在相应题号的答题区域内，否则无效． 一、选择题（本大题共10小题，每小题4分，共40分．在下列每小题中，选出一个正确答案，请在答题卡上将所选的字母标号涂黑）1．已知全集U={Z x x x Î<£,60 } }，，集合A={1,3,5},B={1,4},A={1,3,5},B={1,4},则则BC A C uuU等于 ( ( ▲▲ ) A. A.｛｛1,3,4,51,3,4,5｝｝B. B.｛｛0,20,2｝｝C.C.｛｛0,2,3,4,50,2,3,4,5｝｝D. D.｛｛1｝2. 2. 已知向量已知向量(1,2)a =，(2,3)b x =-，若a ⊥（a +b ），则x= ( x= ( ▲▲ ) A.3B.-21C.-3D.21 3. 3. 若点若点P )4,(m -是角a 终边上一点，且53cos -=a ，则m 的值为的值为( ( ▲▲ ) . A. 3 B. -3 C. 3± D.5 4. 81()x x-的二项展开式中，2x 的系数是的系数是 ( ( ▲▲ )A.70B.-70C.28D.-285. 5. 设设23 (1)() (12)3 (2)x x f x x x x x ---ìï=-<<íïî≤≥，若()9f x =，则x = ( ( ▲▲ ) A.-12B. B.±±3C.-12或±或±3 3D.-12或36.6.已知已知a ，b 为正实数，且a+b=1a+b=1，则，则ba 22log log +的最大值为的最大值为 ( ( ▲▲ ) A.2B.-2C.21D.-21 7.7.若函数若函数f （x+3x+3）的定义域为（）的定义域为（-1,1-1,1）），则函数f （x ）的定义域为）的定义域为( ( ▲▲ ) A.A.（（-4-4，，-2-2）） B. B. （（-1,1-1,1）） C. C.（（2,42,4）） D. D.（（0，1）8.8.已知抛物线已知抛物线221y x =上一点P 的横坐标为1，则点P 到该抛物线的焦点F 的距离为的距离为( ( ▲▲ )A.89 B.23C.2D.459.9.如图，在正方体如图，在正方体1111ABCD A B C D -中，1O 为底面的中心，则1O A 与上底面1111D C B A所成角的正切值是( ( ▲▲ ) A.1 B.22C.2D.22 10. ()3sin(2)3f x x p=-的图象为C ，以下结论不正确的是，以下结论不正确的是 （（ ▲ ） A ．图象C 关于直线1112x p =对称对称 B ．图象C 关于点2(,0)3p 对称对称 C ．函数()f x 在区间5(,)1212p p-上是增函数上是增函数D ．由3sin2y x =的图象向右平移3p个单位，就可以得到图象C二、填空题（本大题共5小题，每小题4分，共20分） 11.11.化简逻辑函数式化简逻辑函数式AB BC C B B A +++= ▲ .12.若某算法框图如图所示，则输出的结果为则输出的结果为 ▲ . 13.13. 某工程的工作明细表如下：某工程的工作明细表如下：工作代码工作代码 紧前工作紧前工作 紧后工作紧后工作工期工期//天 A B 、E --- 1 BC A 5 C --- B 、D 3 D CE 2 EDA1则完成这项工程的最短工期为则完成这项工程的最短工期为______▲▲________天天.14.14.某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，成绩某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，成绩(百分制)如下表：如下表：如果公司要求形体、口才、专业水平、创新能力按照5%、30%、35%、30%计算总分，那么候选人候选人 面试面试 笔试笔试 形体形体 口才口才 专业水平专业水平 创新能力创新能力 甲 86 90 96 92 乙92889593将录取将录取 ▲ .15.15.圆圆)(sin cos 1为参数a a a îíì=+=y x 上的点到直线)(1为参数t t y t x îíì+==的最大距离为的最大距离为▲▲ . 三、解答题（本大题共8小题，共90分）16.（本题满分6分）已知c bx ax ++2＜0的解集为1|{x ＜x ＜}2，求b ax -＞0的解集的解集. .17.17.（本题满分（本题满分10分）已知复数z 满足i z z 48+=+-， 其中i 为虚数单位为虚数单位. . (1)(1)求复数求复数z . . （（2）求复数1+z 的三角形式的三角形式. .18. 18. （本题满分（本题满分12分）已知函数21cos sin 3sin )(2-+=x x x x f （1）求函数)(x f 的最小正周期的最小正周期. .（2）已知c b a ,,分别为ABC D 的内角C B A 、、的对边，其中A 为锐角，1)(4,32===A f c a 且,求的面积及ABC b D .19. 19. （本题满分（本题满分12分）分） 已知数列{}n a 满足341=a ,132,n n a a n N ++=+Î.（1）求证）求证::数列{}1-na 为等比数列为等比数列. .（2）设13log (1)n nb a =-，求数列þýüîíì´+11n n b b 的前n 项和n S .20. 20. （本题满分（本题满分12分）已知二次函数()f x 满足(2)(2)f x f x -+=--，且()f x =x 有等根，()f x 的图像被x 轴截得的线段长为4. （1）求()f x 的解析式．的解析式．（2）若[]2,3-Îx ，求函数()f x 的最值21. 21. （本题满分（本题满分1212分）某工厂分）某工厂20142014年第一季度生产的年第一季度生产的A A 、B 、C 、D 四种型号的产品产量用条形图表示如图，现用分层抽样的方法从中选取形图表示如图，现用分层抽样的方法从中选取5050件样品参加四月份的一个展销会件样品参加四月份的一个展销会. . （1）问）问A A 、B 、C 、D 四种型号的产品中各应抽取多少件？四种型号的产品中各应抽取多少件？ （2）从）从5050件样品中随机地抽取件样品中随机地抽取22件，求这件，求这22件产品恰好是不同型号产品的概率；件产品恰好是不同型号产品的概率；20015010050DCBA（3）从）从A A 、C 型号的产品中随机地抽取型号的产品中随机地抽取33件，求抽取件，求抽取A A 种型号的产品２件的概率种型号的产品２件的概率..22. 22. （本题满分（本题满分12分）某工厂家具车间造A 、B 型两类桌子，每张桌子需木工和漆工两道工序完成道工序完成..已知木工做一张A 、B 型桌子分别需要1小时和2小时，漆工油漆一张A 、B 型桌子分别需要3小时和1小时；又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张A 、B 型桌子分别获利润2千元和3千元，试问工厂每天应生产A 、B 型桌子各多少张，才能获得利润最大？少张，才能获得利润最大？23. 23. （本题满分（本题满分14分）已知焦点在x 轴上的椭圆C 的离心率为36，短轴长为2. （1）求椭圆C 的方程；的方程；（2）若将坐标原点平移到'O （-1,1），求椭圆C 在新坐标系下的方程；在新坐标系下的方程； （3）斜率为1的直线l 与椭圆C 交于,P Q 两点，若6=PQ ，求直线l 的方程．的方程．全市中等职业学校对口单招 2015届高三年级第一轮复习调研测试数学试卷参考答案及评分标准一、选择题一、选择题1.C2.D3.A4.A5.D6.B7.C8.B9.C 10.D 二、填空题二、填空题11.A+B 12.63 13.9 14.甲 15.12+ 三、解答题三、解答题16.解：由题意得ïîïíì=-30ab a ＞ •………………………………………………•………………………………………………11分 ∴∴3-=ab∴由∴由b ax -＞0得abx ＞ (3)3分 ∴∴3-＞x ………………………………………………………………55分 ∴∴b ax -＞0的解集为（的解集为（-3-3，，+∞）………………………………∞）………………………………66分 17.解：（1）设),(R b a bi a z Î+= ………………………………………………………………11分 ∴∴i b a bi a z z 4822+=+++=+-………………………………………………………………33分∴∴ïîïíì==++4822b b a a 解得îíì==43b a ∴∴i z 43+= ........................................................................55分 （2）i i z 441431+=++=+ (6)6分 ∴∴24|1|=+z ，4)1arg(p=+z ………………………………………………………………99分∴∴)4sin 4(cos 241p p i z ++的三角形式为 (10)10分18.解：（1）)62sin(212sin 2322cos 121cos sin 3sin )(2p -=-+-=-+=x x x x x x x f ………………………………………………………………44分 ∴周期p p==22T ………………………………………………………………55分 （2）1)62sin()(=-=p A A f (6)6分 ∴Z k k A Î+=-,2262p p p∴∴Z k k A Î+=,3p p ∵为锐角A∴∴3p=A (8)8分 又由C Cc A a sin 43sin32,sin sin ==p 得 ………………………………………………………………99分解得2p=C (10)10分 ∴△∴△ABC ABC 为Rt Rt△△∴222=-=a c b 3221==D abSABC………………………………………………………………1212分19.（1）证明：311)1(31113231111=--=--+=--+n n n n n n a a a a a a (4)4分 ∴数列∴数列{}1-na 为等比数列为等比数列 ………………………………………………………………55分 （2）由（）由（11）得数列{}1-na 为等比数列，且公比为31 ∴∴nnn n n a a )31()31()1(1111=´-=-- (7)7分 ∴∴n a b nn n ==-=)31(log )1(log 3131 (8)8分 ∴∴111)1(111+-=+=´+nn n n b bn n ………………………………………………………………99分 ∴∴11111113121211+=+-=+-++-+-=n n n n nS n L (12)12分 20. 解：（1）∵()()x f x f --=+-22∴()x f 的图像的对称轴为x =-2 =-2 (2)2分 又∵()f x 的图像被x 轴截得的线段长为4. ∴图像过点（∴图像过点（-4-4，，0），（0,00,0）） ………………………………………………………………44分 ∴设()()x x a x f 4+==ax ax 42+ ………………………………………………………………55分 又()f x =x 有等根有等根 即ax ax 42+=xx a ax )14(2-+=0有等根有等根 ∴()0142=-=D a (7)7分 ∴41=a ∴∴()x x x f +=241 …………………………………………………………88分 （2）由（）由（11）得对称轴为x =-2[]2,3-Î∴当x =-2时()f x 取最小值－1 当x =2时()f x 取最大值3. ………………………………………………………………1212分 21.解：（1）由图可知A:B:C:D=100：200：50：150 =2：4：1：3 ∴A=1010250=´ B=2010450=´ C=510150=´D=1510350=´………………………………………………44分 （（2）设事件A=A=｛取得｛取得2件产品恰好是不同型号产品｝()250215252202101C C C C C A p +++-==75 ………………………………………………………………88分 （（3）设事件B=B=｛｛A 、C 中抽取3件抽到A 种型号的产品２件｝()315115210C C C B p ==9145........................................................................1212分 22. . 解：设每天生产解：设每天生产A 型桌子x 张，B 型桌子y 张. . (1)1分 则ïîïíì³³£+£+,09382y x y x y x ………………………………………………………………44分 目标函数为：z =2x +3y ………………………………………………………………55分 作出可行域：域：………………………………………………………………88分把直线l ：2x +3y =0向右上方平移至l ′的位置时，直线经过可行域上的点M ，且与原点距离最大，此时z =2x +3y 取最大值取最大值. .解方程îíì=+=+9382y x y x得M 的坐标为（的坐标为（22，3）. . ………………………………………………………………1111分 答：每天应生产A 型桌子2张，B 型桌子3张才能获得最大利润张才能获得最大利润. . …………………………1212分 23. 解：（1）∵22,36==b e∴3=a 又焦点在又焦点在x 轴上轴上 所以1322=+y x ………………………………3分（2）∵坐标原点平移到（-1,1）()ïîí+3x23-，433-= 又6=PQ ，所以6=2122124)(1x x x x k-++=433449222-´-m m。
三角函数模型
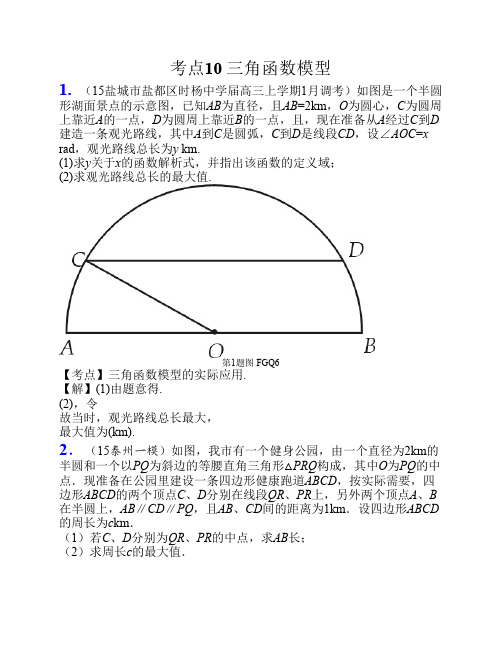
考点10 三角函数模型1.（15盐城市盐都区时杨中学届高三上学期1月调考）如图是一个半圆形湖面景点的示意图，已知AB为直径，且AB=2km，O为圆心，C为圆周上靠近A的一点，D为圆周上靠近B的一点，且，现在准备从A经过C到D 建造一条观光路线，其中A到C是圆弧，C到D是线段CD，设∠AOC=x rad，观光路线总长为y km.(1)求y关于x的函数解析式，并指出该函数的定义域；(2)求观光路线总长的最大值.第1题图 FGQ6【考点】三角函数模型的实际应用.【解】(1)由题意得.(2)，令故当时，观光路线总长最大，最大值为(km).2．（15泰州一模）如图，我市有一个健身公园，由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成，其中O为PQ的中点．现准备在公园里建设一条四边形健康跑道ABCD，按实际需要，四边形ABCD的两个顶点C、D分别在线段QR、PR上，另外两个顶点A、B 在半圆上，AB∥CD∥PQ，且AB、CD间的距离为1km．设四边形ABCD 的周长为c km．（1）若C、D分别为QR、PR的中点，求AB长；（2）求周长c的最大值．第2题图 JSY27【考点】三角函数的最值；在实际问题中建立三角函数模型．【解】（1）连结RO并延长分别交AB、CD于M、N，连结OB，∵C、D分别为QR、PR的中点，PQ=2，∴，∵△PRQ为等腰直角三角形，PQ为斜边，∴，．∵MN=1，∴．在Rt△BMO中，BO=1，∴，∴． （2）设∠BOM=θ，＜＜在Rt△BMO中，BO=1，∴BM=sinθ，OM=cosθ．∵MN=1，∴CN=RN=1－ON=OM=cosθ，∴，，当sinθ+cosθ=即有sin2θ=，即或时取等号．∴当或时，周长c的最大值为km．第2题图 JSY283．（15连云港赣榆海头9月调研）如图所示，某人想制造一个支架，它由四根金属杆PH，HA，HB，HC构成，其底端三点A，B，C均匀地固定在半径为3m的圆O上（圆O在地面上），P，H，O三点相异且共线，PO与地面垂直．现要求点P到地面的距离恰为3m，记用料总长为L=PH+HA+HB+HC，设∠HAO=．（1）试将L表示为的函数，并注明定义域；（2）当的正弦值是多少时，用料最省？第3题图 cqn003【考点】球的体积和表面积．【解】（1）因PO与地面垂直，且三点A，B，C均匀地固定在半径为3m 的圆O上，则△AOH，△BOH，△CO H是全等的直角三角形，又圆O的半径为3，所以OH=3tan，AH=BH=CH=，…（3分）又，所以，…（6分）若点P，H重合，则，即，所以，从而，．…（8分）（2）由（1）知，所以，当=0时，，…（12分）令，，当时，＞0；当时，＜0；所以函数L在（0，）上单调递减，在上单调递增，…（15分）所以当，即时，L有最小值，此时用料最省．…（16分）4．（15江苏模拟（三））如图，有一景区的平面图是一半圆形，其中AB长为2km，C、D两点在半圆弧上，满足BC=CD．设．（1）现要在景区内铺设一条观光道路，由线段AB、BC、CD和DA组成，则当θ为何值时，观光道路的总长l最长，并求l的最大值．（2）若要在景区内种植鲜花，其中在△AOD和△BOC内种满鲜花，在扇形COD内种一半面积的鲜花，则当θ为何值时，鲜花种植面积S最大．第4题图 cqn4【解】（1）由题，，取BC中点M，连结OM．则，．∴．同理可得，．∴．即．∴当，即时，有．第4题图 cqn10（2），，．∴．∴∵，∴解得，列表得＋0－递增极大值递减∴当时，有．答：（1）当时，观光道路的总长l最长，最长为5km；（2）当时，鲜花种植面积S最大．5．(江苏省南京市2015届高三上学期9月调考数学试卷)如图，公路AM、AN围成的是一块顶角为a的角形耕地，其中tan a=.在该块土地中P 处有一小型建筑，经测量，它到公路AM，AN的距离分别为km，km.现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用，问如何确定B点的位置，使得该工业园区的面积最小？并求最小面积.第5题图 FGQ19【考点】解三角形的实际应用.【解】过点P作PE⊥AM，PF⊥AN，垂足为E、F，连接PA.设AB=x，AC=y.因为P到AM，AN的距离分别为3，，即PE=3，PF=.由①因为tan a=，所以sin a=.所以②由①②可得. ③因为.当且仅当取“=”，结合③解得x=5，y=.所以有最小值15.答：当AB=5km时，该工业园区的面积最小，最小面积为.第5题图 FGQ206.(江苏省南通市2015届高三第一次模拟考试数学试题)在长为20m，宽为16m的长方形展厅正中央有一圆盘形展台(圆心为点C)，展厅入口位于长方形的长边的中间，在展厅一角B点处安装监控摄像头，使点B与圆C在同一水平面上，且展台与入口都在摄像头水平监控范围内(如图阴影所示 ).第6题图 FGQ50(1 )若圆盘半径为m，求监控摄像头最小水平视角的正切值；(2 )过监控摄像头最大水平视角为60°，求圆盘半径的最大值.(注：水平摄像视角指镜头中心点水平观察物体边缘的实现的夹角 )【考点】直线与圆的位置关系.【解】(1 )过B作圆C的切线BE，切点为E，设圆C所在平面上入口中点为A，连接CA，CE，CB，则CE⊥BE，CA⊥AB第6题图 FGQ15∴监控摄像头水平视角为∠ABE时，水平视角最小.在直角三角形ABC中，AB=10，AC=8，tan∠ABC=，在直角三角形BCE中，CE=，，tan∠CBE= ，∴tan∠ABE=tan(∠ABC+∠CBE )，∴监控摄像头最小水平视角的正切值为.(2 )当∠ABE=60°时，若直线BE与圆C相切，则圆C的半径最大.在平面ABC内，以B为坐标原点，BA为x轴建立平面直角坐标系，则直线BE方程为y=x，∴，∴圆C的半径最大为(m ).7.（15南通市如东县栟茶高级中学高三上学期第二次学情调研）某小区想利用一矩形空地ABCD建造市民健身广场，设计时决定保留空地边上的一个水塘(如图中阴影部分)，水塘可近似看作一个等腰直角三角形，其中AD=60m，AB=40m，且中，∠EGF=90°，经测量得到AE=10m，EF=20m．为保证安全同时考虑美观，健身广场周围准备加设一个保护栏．设计时经过点G作一条直线交AB，DF于M，N，从而得到五边形MBCDN的市民健身广场．(1)假设DN=x(m)，试将五边形MBCDN的面积y表示为x的函数，并注明函数的定义域；(2)问：应如何设计，可使市民健身广场的面积最大？并求出健身广场的最大面积．第7题图 FGQ59【考点】解三角形的实际应用．【解】 (1)作GH⊥EF，垂足为H∵DN=x，所以NH=40－x，NA=60－x，∵，∴，∴过M作交CD于T，则有，可解得，由于N与F重合时，AM=AF=30适合条件，故x∈(0，30].第7题图 FGQ60(2)，所以当且仅当，即x=20∈(0，30]时，y取得最大值2000，答：当DN=20m时，得到的市民健身广场面积最大，最大面积为2000m2．8.（15宿迁市沭阳县银河学校高三上学期开学试卷）某固定在墙上的广告金属支架如图所示，根据要求，AB至少长3米，C为AB的中点，B 到D的距离比CD的长小0.5米，∠BCD=60°（1）若CD=x，BC=y，将支架的总长度表示为y的函数，并写出函数的定义域．（注：支架的总长度为图中线段AB、BD和CD长度之和）（2）如何设计AB，CD的长，可使支架总长度最短．第8题 Abc13【考点】解三角形的实际应用．【解】（1）由CD=x，则BD=x－0.5，BC=y，则支架的总长度为AC+BC+BD+CD，在△BCD中，由余弦定理+－2xy cos60°=，化简得－xy+x－0.25=0，即x= ①记l=y+y+x－0.5+x=2y+2x－0.5=－0.5（y≥1.5）.（2）由题中条件得2y≥3，即y≥1.5，设y－1=t（t≥0.5）则原式l=4t++5.5∵t≥0.5，∴由基本不等式4t+当且仅当4t=，即t=时成立，∴y=+1，∴x=，∴当AB=，CD=时，金属支架总长度最短．9.（15无锡市高三上学期期中试卷）如图，ABC为一直角三角形草坪，其中∠C=90°，BC=2米，AB=4米，为了重建草坪，设计师准备了两套方案：方案一RNN-01 方案二RNN-02第9题图方案一：扩大为一个直角三角形，其中斜边DE过点B，且与AC平行，DF过点A，EF过点C；方案二：扩大为一个等边三角形，其中DE过点B，DF过点A，EF过点C．（1）求方案一中三角形DEF面积的最小值；（2）求方案二中三角形DEF面积的最大值．【考点】基本不等式在最值问题中的应用．【答案】（1）在方案一：在三角形AFC中，设∠ACF=α，α∈，则，…（2分）因为DE∥AC，所以∠E=α，，且，即，…（4分）°解得，…（6分）所以，所以当=1，即=45°时，有最小值．（2）在方案二：在三角形DBA中，设∠DBA=，∈，则，解得，三角形CBE中，有，解得，…则等边三角形的边长为，…（14分）所以边长的最大值为，所以面积的最大值为．…（16分）10.（15南京一中等五校联考）如图，某广场为一半径为80米的半圆形区域，现准备在其一扇形区域OAB内建两个圆形花坛，该扇形的圆心角为变量2（0＜2＜π），其中半径较大的花坛⊙P内切于该扇形，半径较小的花坛⊙Q与⊙P外切，且与OA、OB相切．（1）求⊙P的半径（用表示）；（2）求⊙Q的半径的最大值．第10题图 RNN-12【考点】三角函数的最值；三角函数中的恒等变换应用．【解】（1）设⊙P切OA于M，连PM，⊙Q切OA于N，连QN，记⊙P、⊙Q的半径分别为、．∵⊙P与⊙O内切，∴|OP|=80，∴，∴．（2）∵∴，∴令t=1+sin∈（1，2），∴=，令m=∈（，1），=80（），∴m=时，有最大值10．第10题图 RNN-0711．如图，中国渔民在中国南海黄岩岛附近捕鱼作业，中国海监船在A 地侦察发现，在南偏东方向的B地，有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶，企图抓捕正在C地捕鱼的中国渔民．此时，C地位于中国海监船的南偏东方向的10海里处，中国海监船以每小时30海里的距离赶往C地救援我国渔民，能不能及时赶到？(≈1.41，≈1.73，≈2.45)第17题图 FGQ79【解】 如图，过点A作AD⊥BC，交BC的延长线于点D.因为∠CAD＝，AC＝10海里，所以△ACD是等腰直角三角形．所以AD＝CD＝AC＝×10＝ (海里)．在中，因为∠DAB＝，所以BD＝AD×tan＝ (海里)．所以BC＝BD－CD＝(－)海里．因为中国海监船以每小时30海里的速度航行，某国军舰正以每小时13海里的速度航行，所以中国海监船到达C点所用的时间(小时)，某国军舰到达C点所用的时间 (小时)．因为，所以中国海监船能及时赶到．。
2015届江苏高考南通市高考模拟密卷(三)(南通市数学学科基地命题)
2015届江苏高考南通市高考模拟密卷（三）(南通市数学学科基地命题)南通市数学学科基地命题第Ⅰ卷（必做题，共160分） 一、填空题：本大题共14小题，每小题5分，共70分 ． 1．已知集合{}2|20M x x x =-≥,{}|1N x x =≤，则R M N （ ）ð= .2．如果1a bi -+与-b i +互为共轭复数（,a b ∈R ，i 为虚数单位）， 则||a bi += ．3．如右图，该程序运行后输出的结果为 .4．在△ABC 中，∠C ＝90°，M 是BC 的中点，1AC =．若sin B ＝13，则AM ＝________.5．某单位有,,A B C 三部门，其人数比例为3∶4∶5，现欲用分层抽样方法抽调n 名志愿者支援西部大开发 ．若在A 部门恰好选出了6名志愿者，那么n ＝________． 6．函数()2sin()(0,f x x ωϕω=+>且||)2πϕ<的部分图像如图所示,则(0)f 的值为 .7．连续抛掷两颗骰子得到的点数分别是a ，b ，则函数2()f x ax bx =-在1x =处取得最值的概率是 .8．在等差数列{}n a 和等比数列{}n b 中，已知12128,2,1,2a a b b =-=-==，那么满足n n a b =的n 的所有取值构成的集合是 .9．已知如图所示的多面体EF ABCD -中，四边形ABCD 是菱形，四边形BDEF 是矩形，ED ⊥平面ABCD ，∠BAD ＝3π.若BF ＝BD＝2，则多面体的体积 ．10．如果关于x 的方程23ax x +=有两个实数解，那么实数a 的值是 ． 11．设()()2,0,1,0.x a x f x x a x x⎧-⎪=⎨++>⎪⎩… 若()0f 是()f x 的最小值，则实数a 的取值范围为 .12．已知椭圆2221(3x y a a +=>的中心、右焦点、右顶点依次为,,,O F G直线2x =x 轴 交于H 点，则FG OH取得最大值时a 的值为 .FEDCBA13．在四边形ABCD 中，2AB =，AD BC =，BA BC BABC+3BD BD，则四边形ABCD 的面积是 ．14．()f x 是定义在R 上的奇函数，若当0x ≥时，[)[)12log (1),0,1()13,1,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩ ，则关于x 的函数()()(10)F x f x a a =+-<<的所有零点之和为 （用a 表示） 二、解答题：本大题共6小题，共90分.15．（本小题满分14分）如图，在xoy 平面上，点(1,0)A ，点B 在单位圆上，AOB θ∠=（0θπ<<）（1）若点34(,)55B -，求tan()4πθ+的值；（2）若OA OB OC +=，1813OB OC ⋅=，求cos()3πθ-.16．（本小题满分14分）在四棱锥P ABC D -中,PAC ⊥平面平面ABC D ,ABC ∆是边长为4的正三角形,AC 与BD 的交点M 恰好是AC 中点,又120ADC ∠=,点N 在线段PB 上,且13PN NB =. (1)求证：PA BD ⊥； (2)求证：//MN 平面PDC .17.（本小题满分14分）2014年8月以“分享青春，共筑未来”为口号的青奥会在江苏南京举行， 为此某商店经销一种青奥会纪念徽章，每枚徽章的成本为30元，并且每卖出一枚徽章需向相关部门上缴a 元（a 为常数，25a ≤≤），设每枚徽章的售价为x 元（3541x ≤≤）.根据市场调查，日销售量与x e （e 为自然对数的底数）成反比例.已知当每枚徽章的售价为40元时，日销售量为10枚. （1）求该商店的日利润()L x 与每枚徽章的售价x 的函数关系式；（2）当每枚徽章的售价为多少元时，该商店的日利润()L x 最大？并求出()L x 的最大值.CBP18．(本小题满分16分) 已知椭圆2222:1(0)x y E a b a b+=>>过点)． （1）若A 是椭圆E 的上顶点，12,F F 分别是左右焦点，直线12,AF AF 分别交椭圆于,B C ，直线BO 交AC于D ，求证:3:5ABD ABC S S ∆∆=；（2）若12,A A 分别是椭圆E 的左右顶点，动点M 满足212MA A A ⊥，且1MA 交椭圆E 于点P ．求证：OP OM ⋅为定值.19.（本小题满分16分）已知函数21()ln 2f x ax x =+，()g x bx =-，设()()()h x f x g x =-.（1）若()f x 在x =处取得极值，且(1)(1)2f g '=--，求函数h (x )的单调区间； （2）若0a =时函数h (x )有两个不同的零点x 1,x 2.①求b 的取值范围；②求证：1221x x e >.20.（本小题满分16分）若数列{}n C1n c +，②存在常数(M M 与n 无关），使n c M ≤.则称数列{}n c 是“和谐数列”.（1）设n S 为等比数列{}n a 的前n 项和，且442,30a S ==，求证：数列{}n S 是“和谐数列”； （2）设{}n a 是各项为正数，公比为q 的等比数列，n S 是{}n a 的前n 项和，求证：数列{}n S 是“和谐数列”的充要条件为01q <<.第Ⅱ卷（附加题，共40分）21．[选做题]本题包括A 、B 、C 、D 四小题，每小题10分；请选定其中两题，并在相应的答题区域内作答．．．．．．．．．．．．．．．．．．．．． A ．（选修４－１：几何证明选讲）如图，AB 是圆O 的直径，D 为圆O 上一点，过D 作圆O 的切线交AB 的延长线于点C ．若AB = 2 BC ， 求证：A C ∠=∠．B ．（选修４－２：矩阵与变换）已知矩阵21a M b ⎡⎤=⎢⎥⎣⎦，其中,a b 均为实数，若点(3,1)A -在矩阵M 的变换作用下得到点(3,5)B ，求矩阵M 的特征值.C ．（选修４－４：坐标系与参数方程）在直角坐标系中，以原点为极点，x 轴的正半轴为极轴建立极坐标系，两种坐标系取相同的单位长度．已知曲线1325: 45x t C y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数）和曲线22:sin 2cos C ρθθ=相交于A B 、两点，求AB 中点的直角坐标．D ．（选修４－５：不等式选讲）已知实数a ，b ，c ，d 满足3a b c d +++=，22222365a b c d +++=，求a 的取值范围．【必做题】第22题、第23题，每题10分，共计20分.22．（本小题满分10分）甲、乙、丙三位同学商量高考后外出旅游，甲提议去古都西安，乙提议去海上花园厦门，丙表示随意．最终，三人商定以抛硬币的方式决定结果．规则是：由丙抛掷硬币若干次，若正面朝上，则甲得一分、乙得零分；若反面朝上，则乙得一分、甲得零分，先得4分者获胜．三人均执行胜者的提议．若记所需抛掷硬币的次数为X ． （1）求6X =的概率；（2）求X 的分布列和数学期望．23．（本小题满分10分）在数学上，常用符号来表示算式，如记0ni i a =∑=0123n a a a a a +++++，其中i N ∈，n N +∈.（1）若0a ，1a ，2a ，…，n a 成等差数列，且00a =，求证：()0nii n i a C ==∑12n n a -⋅；（2）若22201221(1)nknn k x a a x a x a x =+=+++∑，20n n i i b a ==∑，记11[(1)]niin i n i d b C ==+-∑，且不等式(1)n nt d b ⋅-≤恒成立，求实数t 的取值范围.2015年高考模拟试卷(3)参考答案南通市数学学科基地命题 第Ⅰ卷（必做题，共160分）一、填空题1．(]0,1； 2； 3．1027； 由流程图，b 和a 的值依次为1,1;3,2;10,3;1027,4，结束循环. 45．24；6．7112； 8．{}3,5 ；【解析】 由已知得，1614,2n n n a n b -=-=，令n n a b =，可得16142n n --=，解得3n =或5，所以满足n n a b =的n 的所有取值构成的集合是{}3,5. 9【解析】如图，连接AC ，AC ∩BD ＝O .因为四边形ABCD 是菱形，所以，AC ⊥BD ，又因为ED ⊥平面ABCD ，AC ⊂平面ABCD ，所以，ED ⊥AC .因为，ED ，BD ⊂平面BDEF ，且ED ∩BD ＝D ，所以，AC ⊥平面BDEF ，所以，AO 为四棱锥A -BDEF 的高．又因为，四边形ABCD 是菱形，∠BAD ＝3π，所以，△ABD 为等边三角形．又因为，BF ＝BD ＝2，所以，AD ＝2，AOS四边形BDEF ＝4，所以，V 四棱锥A -BDEF＝10．2± ； 11．[]0,2； 12．2； 13．；【解析】 设BA a BA=，BC b BC=，BD c BD=，则|a |=|b |=|c |=1，a +b ，所以，得cos<a ,b >=12,又由AD BC =，所以，可得图形为有一个3π角的菱形，所以，其面积22S =⨯=. 14．112a⎛⎫- ⎪⎝⎭；【解析】 根据对称性，作出R 上的函数图象，由()()F x f x a =+，所以，零点就是()f x 与()0,1y a =-∈交点的横坐标，共有5个交点，根据对称性，函数()f x 的图象与()0,1y a =-∈的交点在()2,4之间的交点关于3x =对称，所以，126x x +=，在()()5,43,2----之间的两个交点关于3x =-对称，所以，346x x +=-，设(]1,0x ∈-，则[)0,1x -∈，所以，12()log (1)()f x x f x -=-+=-，即12()log (1)f x x =--+，由()0f x a +=，所以，12log (1)0x a --++=，即5112a x ⎛⎫=- ⎪⎝⎭，所以，12345112ax x x x x ⎛⎫++++=- ⎪⎝⎭.二、解答题OFEDCBA15. （1）由于34(,)55B -，AOB θ∠=，所以3cos 5θ=-，4sin 5θ= ，所以4tan 3θ=-， 所以1tan 1tan()41tan 7πθθθ++==-- ；（2）由于(1,0)OA =,(cos ,sin )OB θθ=,所以(1cos ,sin )OC OA OB θθ=+=+,22218cos (1cos )sin cos cos sin 13OC OB θθθθθθ⋅=⨯++=++=. 所以5cos 13θ=，所以12sin 13θ=，所以cos()coscos sinsin 333πππθθθ-=+=16．（1）因为ABC ∆是正三角形,M 是AC 中点, 所以BM AC ⊥,即BD AC ⊥, 又PAC ABCD ⊥平面平面,,PACABCD AC =平面平面BD ⊂平面ABCD ,,BD AC ⊥所以BD ⊥平面PAC .又PA ⊂平面PAC ,所以.PA BD ⊥.(2)在正三角形ABC 中,BM =在ACD 中，因为M 为AC 中点, DM AC ⊥，所以AD CD =, 因为120ADC ∠=,所以60ADM ∠=. 所以, DM =,所以:3:1BM MD =, 所以::BN NP BM MD =,所以//MN PD . 又MN ⊄平面PDC ,PD ⊂平面PDC ,所 以//MN 平面PDC . 17. （1）设日销售量为x k e ，则4010k e =， 所以4010k e =，则日销售量为4010x e e 枚.每枚徽章的售价为x 元时，每枚徽章的利润为(30)x a --元，则日利润40401030()(30)10(3541)x xe x aL x x a e x e e --=--=≤≤.（2）4031()10(3541)x a xL x e x e +-'=≤≤.①当24a ≤≤时，333135a ≤+≤，而3541x ≤≤， 所以()0,()L x L x '≤在[]35,41上单调递减，CBP则当35x =时，()L x 取得最大值为510(5)a e -. ②当45a <≤时，353136a <+≤，令()0L x '=，得31x a =+， 当[]35,31x a ∈+时，()0,()L x L x '>在[]35,31a +上单调递增； 当(]31,41x a ∈+时，()0,()L x L x '<在(]31,41a +上单调递减. 所以当31x a =+时，()L x 取得最大值为910a e -.综上，当24a ≤≤时，每枚徽章的售价为35元时，该商店的日利润()L x 最大,5max ()10(5)L x a e =-; 当45a <≤时，每枚徽章的售价为（31a +）元时，该商店的日利润()L x 最大，9max ()10a L x e -= . 18. （1）易得22211,a b c a⎧+=⎪⎪⎨⎪=⎪⎩且222c a b =-，解得224 2 a b ⎧=⎪⎨=⎪⎩，，所以,椭圆E 的方程为22142x y +=；所以，12(A F F ，所以，直线:AB y x =:AC y x =- 将y x =230x +=，所以(B，同理可得C ， 所以直线BO 为14y x =，联立12y xy x ⎧=⎪⎨⎪=-+⎩，得交点D ，所以，88,53AD AC ==，即:3:5AD AC =所以，:3:5ABDABCSS=；（2）设0(2 )M y ，，11( )P x y ，， 易得直线1MA 的方程为0042y yy x =+， 代入椭圆22142x y +=,得()2222000140822y y y x x +++-=，由()201204828y x y --=+得，()20120288y x y --=+，从而012088y y y =+， 所以()()2220000022220000284888 (2 )48888y y y y OP OM y y y y y ----⎛⎫⋅=⋅=+= ⎪++++⎝⎭，，. 19. (1)因为1()f x ax x'=+，所以(1)1f a '=+, 由(1)(1)2f g '=--可得a =b-3. 又因为()f x在x =处取得极值，所以0f '=， 所以a = -2,b =1 . 所以2()ln h x x x x =-++，其定义域为（0，+∞）2121(21)(1)()21=x x x x h x x x x x-++-+-'=-++=令()0h x '=得121,12x x =-=，当x ∈（0,1）时，()>0h x '，当x ∈（1,+∞）()<0h x '，所以函数h (x )在区间（0,1）上单调增；在区间（1,+∞）上单调减. （2）当0a =时，()ln h x x bx =+，其定义域为（0，+∞）. ①由()0h x =得ln -x b x =，记ln ()x x x ϕ=-，则2ln 1()x x x ϕ-'=, 所以ln ()xx xϕ=-在(0,)e 单调减，在(,)e +∞单调增， 所以当x e =时ln ()x x x ϕ=-取得最小值1e-. 又(1)0ϕ=，所以(0,1)x ∈时()0x ϕ>，而(1,)x ∈+∞时()0x ϕ<,所以b 的取值范围是（1e -，0）.②由题意得1122ln 0,ln 0x bx x bx +=+=,所以12122121ln ()0,ln ln ()0x x b x x x x b x x ++=-+-=, 所以12122121ln ln ln x x x x x x x x +=--，不妨设x 1<x 2,要证212x x e > , 只需要证12122121ln (ln ln )2x x x x x x x x +=->-.即证2121212()ln ln x x x x x x -->+，设21(1)xt t x =>,则2(1)4()ln ln 211t F t t t t t -=-=+-++, 所以22214(1)()0(1)(1)t F t t t t t -'=-=>++, 所以函数()F t 在（1，+∞）上单调增，而(1)0F =， 所以()0F t >即2(1)ln 1t t t ->+, 所以212x x e > .20. （1）设公比为q ，则3411414161(1)21a a q a a q q s q ⎧==⎧⎪⎪⇒⎨⎨-==⎪⎪⎩-⎩, 所以51322n n s -=-.(32s =532(22n n --+4223222n -≤+214411)322n n S +--=-=.且513232.2n n S -=-<即存在常数32,所以，数列{}n S 是“和谐数列” . （2）充分性设等比数列{}n a 的公比q ，且0 1.q << 则1111(1)1111n n n a q a a q aS q q q q-==-<----. 令11a M q=-，则.n S M < 因为222222112()(1)(1)()(1)11n n n n n n n a aS S q q q q q q q ++++=--=--+--21222122111()(12)()(1)11n n n n a aq q q S q q++++<-+=-=-- 所以{}n S 是“和谐数列” 必要性等比数列{}n a 各项为正，且n S 是“和谐数列”.C因为0.n a > 所以，0.q >下面用反证法证明，1q <（1）当1,q =则1,n S na =因为10,a >所以，不存在M ，使1na M <对1n N -∈恒成立;当1q >，则111(1)111n n n a q a a S q q q q -==---- 所以，对于给定的正数M ，若11,11n a a q M q q ->-- 因为，1q >，所以，11log (1).q q n M a ->+ 即当11log (1)q q n M a ->+时，有n S M >. 所以，不存在常数M ，使.n S M ≤ 所以，0 1.q <<综上,数列{}n S 是“和谐数列”的充要条件为其公比为01q <<.第Ⅱ卷（附加题，共40分）21. A. 连结OD ，BD ，因为AB 是圆O 的直径，所以902ADB AB OB ∠==o ，．由AB = 2 BC ，所以，AB OC =，因为DC 是圆O 的切线，所以90CDO ∠=o ．于是△ADB ≅△CDO ，所以，AD DC =所以，A C ∠=∠.B ．由条件可知233115a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦，所以233,315a b ⨯-=⎧⎨-=⎩， 则3,2a b ==．矩阵的特征多项式为223()(2)(1)(2)(3)3421f λλλλλλλ--==-----=---- 令()0f λ=,得两个特征值分别为121,4λλ=-=．C. 将1C 化为直角坐标方程为4380x y --=将2C 化为直角坐标方程为22y x =将直线方程代入22y x =可得22380y y --=解之可得1232y y +=，124y y =-，所以，2212124128y y x x ++== 所以，中点坐标为341,416⎛⎫ ⎪⎝⎭D. 由柯西不等式，得()2222111(236)()236b c d b c d ++++++≥， 即()2222236b c d b c d ++++≥．由条件，得()2253a a --≥，解得12a ≤≤== 时等号成立， 代入111,,36b c d ===时，max 2a =；211,,33b c d ===时，min 1a =， 所以a 的取值范围是[1,2]．22. （1）抛掷硬币正面向上、反面向上的概率都为12， ()323511156222216P X C ⎛⎫⎛⎫==⨯⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭ （2）X 的分布列为:所以，1155934567.84161616EX =⨯+⨯+⨯+⨯= 23. （1）设等差数列的通项公式为0n a a nd =+，其中d 为公差则()0n i i n i a C ==∑12012n n n n n a a C a C a C ++++01120()(2)n n n n n n n n a C C C d C C nC =++++++因为11k k n n kC nC --=所以122n nn n C C nC ++011111()n n n n n C C C ----=+++ 所以()0n i i n i a C ==∑1022n n a nd -⋅+⋅=12n n a -⋅.注：第（1）问也可以用倒序相加法证明.（2）令1x =，则223202(14)22222421n n n n i i a =-=++++==⋅--∑ 令1x =-，则20[(1)]0ni i i a =-=∑，所以20n n i i b a ==∑1(242)412n n =⋅-=- 根据已知条件可知，012233(41)(41)(41)(1)(41)n n n n n n n n nd C C C C C =--+---++-- 01223301234[(4)(4)(4)(4)][(1)]1n n n n n n n n n n n n n n n C C C C C C C C C C C =+-+-+-++---+-+++-+(14)(11)1(3)n n n =---+=-+，所以(3)1n n d =-+将41n n b =-、(3)1n n d =-+代入不等式(1)n n t d b ⋅-≤得，(3)41n n t ⋅-≤-当n 为偶数时，41()()33n n t ≤-，所以22415()()333t ≤-=； 当n 为奇数，41[()()]33n n t ≥--，所以1141[()()]133t ≥--=-； 综上所述，所以实数t 的取值范围是5[1,]3-.。
江苏省高邮市界首中学2015届高三高考模拟数学试题(1)参考答案(南通市数学学科基地命题)
2015年高考模拟试卷(1) 参考答案南通市数学学科基地命题第Ⅰ卷（必做题，共160分）一、填空题1. 6；2. [1,)+∞；3. 70；4. 1；5.20；6.3； 7. 5；8. ； 9. 516； 10. [,]62ππ； 11. 1(,6ln3]e ；【解析】当1[,1)3x ∈时，1(1,3]x∈，由条件得，11()2()2ln 2ln f x f x x x===-，函数()()(0g x f x a x a =->恰有一个零点⇔方程()f x ax =(0)a >有唯一解，在直角坐标系内分别作出()y f x =与y ax =(0)a >的图象，当直线y ax =经过点1(,2ln3)3时，6ln 3a = 6ln 3，当直线y ax =和曲线()ln f x x =相切时，切点为(,1)e ，此时1a e =，由图象可知，当16ln3a e<≤时，函数()y f x =与y ax =(0)a >的图象由唯一的交点．12. ；【解析】在四边形OAPB 中，60APB ∠=，90OAP OBP ∠=∠=，OA OB b ==，2OP b ∴=，由题意得，2b a ≤，即a ≤，化解得c a ≥，又在椭圆中1e <，1e ≤<． 13. {1，2，3}；【解析】由于数列{}n a 的通项公式为13()2n n a -=，所以数列{}n a 为等比数列，首项为132a =，公比132q =；数列1{}n a 也是等比数列，首项为23，公比223q =．不等式113nni i i i a a ==>∑∑等价于1113nni i i i a a ==>∑∑，即231()1()323231132n n--⋅>--，解之得22()193n<<，n N *∈，n ∴只能取1,2,3．14. (0,1)(2,)+∞；【解析】()3ln33ln32(33)ln322ln320x x x x f x --'=+-=+-≥->，∴函数()f x 在(,)-∞+∞上单调递增，且(0)0f =，112220(2)(log )0log 0x x f x x ->⎧⎪∴-<⇔⎨<⎪⎩或1220log 0x x -<⎧⎪⎨>⎪⎩，解得2x >或01x <<．二、解答题15. （1）tan (2)tan b A c b B =-， ∴由正弦定理，得sin sin sin (2sin sin )cos cos A BB C B A B⋅=-⋅, 又在ABC ∆中，sin 0B ≠， sin cos 2sin cos cos sin A B C A A B ∴=-，即sin()2sin cos A B C A +=， 又sin()sin 0A B C +=≠， 1cos 2A ∴=，又0A π<<，3A π∴=；（2） 由余弦定理，2222cos a b c bc A =+-，2b =，3c =，3A π=，a ∴=，11sin 22BC AD AB AC A ⋅=⋅⋅32AD =⋅，AD ∴=227cos 7AD AC AD AC C AD AD ⋅∠∴⋅===.16.（1）底面ABCD 为矩形，BC CD ∴⊥，又PD BC ⊥，,CD PD PCD ⊂平面，PD CD D =， BC ∴⊥平面PCD ， 又BC ABCD ⊂平面， ∴平面ABCD ⊥平面PCD ；（2）连接AC ，交BD 于O ，连接GO ， //PC 平面BDG ，平面PCA 平面BDG GO =， //PC GO ∴， PG COGA OA∴=，底面ABCD 为矩形， ∴O 是AC 的中点，即CO OA =， PG GA ∴=， ∴G 为PA 的中点.17. （1）在AOM ∆中，15AO =，AOM β∠=且cos β=OM =由余弦定理得，2222cos AMOA OM OA OM AOM=+-⋅⋅∠2215215=+-⨯ 13915152315372.=⨯+⨯-⨯⨯⨯=AM ∴=M 与站A 的距离AM 为；（2）cos β=，且β为锐角，sin β∴=在AOM ∆中，由正弦定理得，sin sin AM OMMAOβ=∠,，sin MAO ∴∠=，4MAO π∴∠=，4ABO πα∴∠=-， tan2α=，sin α∴=，cos α=，sin sin()4ABOπα∴∠=-=，又A O πα∠=-，sin sin()AOB πα∴∠=-=，在AOB ∆中，15AO =，由正弦定理得，sin sinAB AOAOB ABO=∠∠，即15AB =，AB ∴=AB 段的长AB 为．18. （1）圆O 的方程为222x y b +=，直线y x =O 相切，b =，即1b =，又3e =， =2a ∴=， ∴椭圆C 的方程为2214x y +=；（2）由题意，可得11((,22M N ， ∴圆D的半径r =AB ∴==， ∴ABD ∆的面积为1122S ==； （3）由题意可知1212(2,0),(2,0),(0,1),(0,1)A A B B --，2A P 的斜率为k ，∴直线2A P 的方程为(2)y k x =-， 由2214(2)x y y k x =+=-⎧⎪⎨⎪⎩，得2222(14)161640k x k x k +-+-=， 其中2A x =，228214P k x k -∴=+，222824(,)1414k kP k k --∴++，则直线2B P 的方程为211221)k y x k +=-+-（， 令0y =，则2(21)21k x k -=+， 即2(21)(,0)21k F k -+，直线12A B 的方程为220x y -+=，由220(2)x y y k x -+=⎧⎨=-⎩，解得4221421k x k k y k +⎧=⎪⎪-⎨⎪=⎪-⎩，424(,)2121k k E k k +∴--，∴EF 的斜率421212(21)4242121k k k m k k k k -+-==-+-+- ， ∴2112242k m k k +-=⋅-=（定值）． 19. （1）22()()ln g x f x ax bx x ax bx =++=++， 1()2g x ax b x'∴=++，由题意得(1)120g a b '=++=， 21b a ∴=--；（2）11(21)(1)()2221(0)ax x g x ax b ax a x x x x--'=++=+--=>，①当0a =时，(1)()(0)x g x x x--'=>，当1x >时，()0g x '<，∴函数()g x 在(1,)+∞单调减； 当01x <<时，()0g x '>，∴函数()g x 在(0,1)单调增；②当102a <<时，即112a>，12()(1)2()(0)a x x a g x x x --'=>， ∴函数()g x 在(11,)2a 上单调减；函数()g x 在(12,)a +∞和(0,1)单调增；③当12a =时，即21a =，2(1)()0(0)x g x x x -'=≥>，∴函数()g x 在(0,)+∞单调增；④当12a >时．即112a<，12()(1)2()(0)a x x a g x x x--'=>， ∴函数()g x 在(1,1)2a单调减区间；函数()g x 在(1,)+∞和(0,12)a单调增；（3）由题设210x x >>，21212211ln ln 1111x x k x x x x x x -∴<<⇔<<- 21212121ln ln x x x xx x x x --⇔<-<22211111ln 1x x x x x x ⇔-<<- ①令()ln 1(1)h x x x x =-+>，则11()1(1)xh x x x x-'=-=>，1x ∴>时，()0h x '<， ∴函数()g x 在(1,)+∞是减函数， 而(1)0h =，1x ∴>时，()(1)0h x h <=210x x >>，211x x ∴>， 222111()ln 10x x x h x x x ∴=-+<，即2211ln 1x xx x <-， ②令1()ln 1(1)H x x x x =+->，则22111()(1)x H x x x x x-'=-=>，1x ∴>时，()0H x '>， ∴()H x 在(1,)+∞是增函数，1x ∴>时，()(1)0H x H >=， 2221111()ln 10x x H x x x x ∴=+->，即221111ln x x x x -< ③由①②③得2111k x x <<．20.（1）1C =，21n n a S An Bn ∴+=++，①令1n =，可得121a A B =++，即2A B +=，令2n =，可得122421a a A B +=++，即425A B +=，13,22A B ∴==,213122n n a S n n ∴+=++， ①当2n ≥时，21113(1)(1)122n n a S n n --∴+=-+-+， ②①-②，得121n n a a n --=+(2)n ≥，11[(1)]2n n a n a n -∴-=--，即112n n b b -=，又111102b a =-=≠，0n b ≠，112n n b b -=∴， ∴数列{}n b 是等比数列； ②数列{}n a 是等差数列，∴设11(1)(1),2n n n n a a n d S na d -=+-=+，21n n a S An Bn +=++， 1221()221d dn a n a An B d n ∴++++=+-，*n N ∈ 11221d A d B a a d ⎧=⎪⎪⎪∴=+⎨⎪-=⎪⎪⎩，111122122223d d d a a d d d Ad B +--=++-∴===； （2）当0C =时，2n n a S An Bn +=+数列{}n a 是等差数列，11a =，∴(1)1(1),2n n n n a n d S n d -=+-=+， 22(1)122d dn n An Bn d ∴++=++-， 1d ∴=，n a n ∴=，21(1)11111(1)1n n a n n n n ++++=+-++， 1111ni n n =+-∴+， 13311111n i n n n n λλ=∴-≤-≤+-+++，即211n n λ≤+++， *n N ∴∀∈，211n n λ≤+++， 令2()f x x x =+， 22222()1x f x x x -'=-=，当2x ≥时，()0f x '>， ()f x ∴在[2,)+∞上是增函数，而12n +≥，min 2(1)31n n ∴++=+， 3λ∴≤．第Ⅱ卷（附加题，共40分）21. A ．连接BC ，,AB CD 相交于点E ．因为AB 是线段CD 的垂直平分线，所以AB 是圆的直径，∠ACB ＝90°．设AE x =，则6EB x =-，由射影定理得CE 2＝AE ·EB ，又CE =(6)5x x -=，解得1x =（舍）或5x = 所以，AC 2＝AE ·AB ＝5×6＝30，ACB ．2415⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦M ，即24215a b +⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦， ∴24,21 5.a b +=⎧⎨-=⎩ 解得2,3.a b =⎧⎨=⎩，∴1231M ⎡⎤=⎢⎥-⎣⎦， 解法一：12det()731M ∴==--， 11212777731317777M ---⎡⎤⎡⎤⎢⎥⎢⎥--==⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥--⎣⎦⎣⎦.解法二:设1c d M e f -⎡⎤=⎢⎥⎣⎦，由1M M -=1001⎡⎤⎢⎥⎣⎦，得32103201c d c d e fe f +-⎡⎤⎡⎤=⎢⎥⎢⎥+-⎣⎦⎣⎦∴31,30,20,2 1.c de f c d e f+=⎧⎪+=⎪⎨-=⎪⎪-=⎩ 解得1,72,73,71.7c d e f ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=-⎩112773177M -⎡⎤⎢⎥∴=⎢⎥⎢⎥-⎢⎥⎣⎦． C ．因为圆心为直线2sin()sin 33ππρθ-=与极轴的交点，所以令0θ=，得1ρ=，即圆心是(1,0)，又圆C 经过点6P π，）， ∴圆的半径1r =，∴圆过原点， ∴圆C 的极坐标方程是2cos ρθ=．（说明：化为普通方程去完成给相应的分数）D.由,,a b c为正数，根据平均值不等式，得11a b +≥11b c +≥，11a c +≥．将此三式相加，得1112()a b c ++≥+111a b c ++≥+．由1abc =1．所以，111a b c ++≥= 22.（1）令2n n a c n+=， 则11(33)4622(33)(2)23311(1)n n n n n n n a n a n a a n c n n nc n n ++++++++++====+++=， 11210c a =+=≠，0n c ∴≠，13n ncc +∴=，∴数列{}n c ，即2n a n +⎧⎫⎨⎬⎩⎭是等比数列；（2）由（1）得123n n a n-+=，132n n a n -∴=⋅-，1312n n n b a n -∴==+， 下面用数学归纳法证明当2n ≥，*n N ∈时，12241521n n n b b b n +++++<-+． ①当2n =时，不等式的左边341173412b b =+=+=，右边413555=-=，而73125<，∴2n =时，不等式成立；②假设当(2)n k k =≥时，不等式成立，即12241521k k k b b b k +++++<-+；当1n k =+时，11122(1)12221221()()k k k k k k k k k b b b b b b b b b +++++++++++++=+++++- 4111152121221k k k k <-++-++++41152214152(1)4152(1)1k k k k =+-++=-+<-++∴当1n k =+时，不等式也成立． 由①②可得，当2n ≥，*n N ∈时，12241521n n n b b b n +++++≤-+．23. （1）设(,)M x y ，则(,)N x p -，(0,)NM y p ∴=+，(,2)NF x p =-，(,)FM x y p =-，(,2)FN x p =-，NM NF FM FN ⋅=⋅，22()2()p y p x p y p ∴+=--，24x py ∴=，即动点M 的轨迹C 的方程为24x py =； 另解：设(,)M x y ，则(,)N x p -，NM NF FM FN ⋅=⋅，()0NF MN MF ∴⋅+=，∴以,MN MF 为邻边的平行四边形是菱形，MF MN ∴=，y p =+ ，24x py ∴=，即动点M 的轨迹C 的方程为24x py =； （2）①设0(,)Q x p -，211(,)4x A x p ，222(,)4x B x p，则切线QA 的方程2111(,)42x xy x x p p-=-， 21101()42x xp x x p p∴--=-，22101240x x x p ∴--=， ①同理22202240x x x p ∴--=， ② 方法1:①②得12120()(2)0x x x x x -+-=，12120,20x x x x x ≠∴+-=，1202x x x ∴+=，即A 、Q 、B 三点的横坐标成等差数列.方法2：由①②得12,x x 是方程220240x x x p --=的两根，1202x x x ∴+=，即A 、Q 、B 三点的横坐标成等差数列. ②由①②得12,x x 是方程220240x x x p --=的两根，12021224x x x x x p +=⎧∴⎨⋅=-⎩， (4,)Q p --，1221284x x x x p +=-⎧∴⎨⋅=-⎩， 20AB =，20=，20，20， 4217160p p ∴-+=，1p ∴=或4p =.。
空间几何体的概念、表面积和体积
考点1 空间几何体的概念、表面积和体积1. (2015高考冲刺压轴卷江苏试卷一)已知长方体1111ABCD A BC D -的各个顶点都在表面积为16π的球面上，且3AB AD =,12AA AD =，则四棱锥1D ABCD -的体积为________. 【考点】四棱锥的体积. 【答案】463【分析】3AB AD = ，12AA AD =，∴设AD a =，则3AB a =，12AA a = 又因为长方体的对角线是其外接球的直径，∴222221(2)8r AD AB AA a =++=∴222r a =，又∵24π16πr =，∴242r a =⇒= ∴1111462622333D ABCD ABCD V S AA -=⨯⨯=⨯⨯⨯=.第1题图 FGQ272．(江苏省南京市2015届高三上学期9月调考数学试卷)已知圆锥的侧面展开图是一个半径为2的半圆，则这个圆锥的高是______.【考点】圆锥的侧面展开图. 【答案】3【分析】∵圆锥的侧面展开图是一个半径为2的半圆，∴圆锥的轴截面为边长为2的正三角形，则圆锥的高h =2×sin60°=3.3．(江苏省南通市2015届高三第一次模拟考试数学试题)底面边长为2，高为1的正四棱锥的侧面积为________. 【考点】四棱锥的侧面积. 【答案】42【分析】正四棱锥底面边长为2，高为1，则侧面的高22112h =+=，故此正四棱锥的侧面积1422422S =⨯⨯⨯=. 4．(淮安都梁中学2015届高三10月调研)已知圆锥的高为4，底面半径为3，则圆锥的侧面积为 ．【考点】圆锥的侧面积． 【答案】15π【分析】圆锥的高为4，底面半径为3，所以圆锥的母线为5圆锥的侧面积：16π515π2⨯⨯=.s 5．（南通市2015届高三第三次调研）已知一个空间几何体的所有棱长均为1 cm ，其表面展开图如图所示，则该空间几何体的体积V = cm 3．zl073第5题图【考点】空间几何体，几何体的展开图，棱柱、棱锥的体积． 【答案】216+【分析】由该几何体的表面展开图只该几何体为一个正方体和一个正四棱锥的组合，则其体积V=3122111326+⨯⨯=+. 6．（2015江苏苏州市高三上调考）若圆柱的底面直径和高都与球的直径相等，圆柱、球的表面积分别记为1S 、2S ，则有1S ：2S = ．【考点】旋转体（圆柱、圆锥、圆台）． 【答案】3：2．【分析】由题意可得：圆柱的底面直径和高都与球的直径相等，设球的半径为1，所以等边圆柱的表面积为：1S =6π， 球的表面积为：2S =4π．所以圆柱的表面积与球的表面积之比为1S ：2S =3：2． 故答案为：3：2．7．（2015江苏高考冲刺压轴卷（三））正三角形ABC 的边长为2，将它沿高AD 翻折，使点B 与点C 间的距离为3，此时四面体ABCD 外接球表面积为 ． 【考点】立体几何中的边角关系和球的表面积公式. 【答案】7π【分析】正△ABC 中，AD BD ⊥，AD CD ⊥；2AB BC AC ===，3AD =，1BD CD ==；将四面体ABCD 还原成三棱柱，可以得到一个直棱柱。
江苏省南通市高级中学2015届高三一模数学试题 Word版
南通市高级中学2014-2015年高三数学一模试卷 试题Ⅰ注 意 事 项置上1． )B = ▲2． 若9z z ⋅=（其中z 表示复数z 的共轭复数），则复数z 的模为 ▲ ． 3． 已知函数()af x x =在1x =处的导数为2-，则实数a 的值是 ▲ ． 4． 根据国家质量监督检验检疫局发布的《车辆驾驶人员血液、呼气酒精含量阈值与检验》(GB19522—2004)中规定车辆驾驶人员血液酒精含量：“饮酒驾车”的临界值为20mg/100ml ； “醉酒驾车”的临界值为80mg/100ml ．某地区交通执法部门统计了5月份的执法记录数据：根据此数据，可估计该地区5月份“饮酒驾车” 发生的频率等于 ▲ ．5． 要得到函数sin 2y x =的函数图象，可将函数()πsin 23y x =+的图象向右至少平移 ▲ 个单位．6．在平面直角坐标系xOy 中，“直线y x b=+，b ∈R 与曲线x =切”的充要条件是 “ ▲ ”．7． 如图，i N 表示第i 个学生的学号，i G 表示第i 个学生的成绩，已知学号在1~10的学生的成绩依次为401、392、385、359、 372、327、354、361、345、337，则打印出的第5组数据是 ▲ ．8． 在△ABC 中，若tan :A tan :tan 1:2:3B C =，则A = ▲ ． 9． 已知()y f x =是R 上的奇函数，且0x >时，()1f x =，则不等（第7题）式2()(0)f x x f -<的解集为 ▲ ． 10．设正四棱锥的侧棱长为1，则其体积的最大值为 ▲ ． 11．已知平面向量a ，b ，c 满足1=a ，2=b ，a ，b 的夹角等于π3，且()()0-⋅-=a c b c ，则c的取值范围是 ▲ ．12．在平面直角坐标系xOy 中，过点11( 0)A x ，、22( 0)A x ，分别作x 轴的垂线与抛物线22x y =分别交于点12A A ''、，直线12A A ''与 x 轴交于点33( 0)A x ，，这样就称 12x x 、确定了3x ．同样，可由23x x 、确定4x ，…，若12x =，23x =，则5x = ▲ ． 13．定义：min {x ，y}为实数x ，y 中较小的数．已知{}22min 4b h a a b =+，，其中a ，b 均为正实数，则h 的最大值是 ▲ ．14．在平面直角坐标系xOy 中，直角三角形ABC 的三个顶点都在椭圆2221 (1)x y a a +=>上，其中0 1A （，）为直角顶点．若该三角形的面积的最大值为278，则实数a 的值为 ▲ ．二、解答题：本大题共6小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本题满分14分）已知函数()()2ππ()sin cos sin sin 44f x x x x x x x =+++-∈R，． （1）求()f x 的最小正周期和值域；（2）若x x =()0π02x ≤≤为()f x 的一个零点，求0sin 2x 的值．16．（本题满分14分）如图，在边长为1的菱形ABCD 中，将正三角形BCD 沿BD 向上折起，折起后的点C 记为C '，且CC a '=（0a <．（1）若a =C —BD —C '的大小； （2）当a 变化时，线段CC '上是否总存在一点 E ，使得A C '//平面BED ？请说明理由．（第16题）DC 'A B C17．（本题满分15分）在平面直角坐标系xOy 中，设A 、B 是双曲线2212y x -=上的两点，(12)M ，是线段AB 的中点，线段AB 的垂直平分线与双曲线相交于C 、D 两点． （1）求直线AB 与CD 的方程；（2）判断A 、B 、C 、D 四点是否共圆？若共圆，请求出圆的方程；若不共圆，请说明理由． 18．（本题满分15分）某省高考数学阅卷点共有400名阅卷老师，为了高效地完成文、理科数学卷的阅卷任务，需将400名阅卷老师分成两组同时展开阅卷工作，一组完成269捆文科卷，另一组完成475捆理科卷．根据历年阅卷经验，文科每捆卷需要一位阅卷老师工作3天完成，理科每捆卷需要一位阅卷老师工作4天完成．（假定每位阅卷老师工作一天的阅卷量相同，每捆卷的份数也相同）（1）如何安排文、理科阅卷老师的人数，使得全省数学阅卷时间最省？（2）由于今年理科阅卷任务较重，理科实际每捆卷需要一位阅卷老师工作4.5天完成，在按（1）分配的人数阅卷4天后，阅卷领导小组决定从文科组抽调20名阅卷老师去阅理科卷，试问完成全省数学阅卷任务至少需要多少天？（天数精确到小数点后第3位）（参考数据：807 6.782119≈，95 6.78614≈，331 3.34399≈，1013.5 3.367301≈）19．（本题满分16分）已知函数()f x 的导函数()f x '是二次函数，且()0f x '=的两根为1±．若()f x 的极大值与极小值之和为0，(2)2f -=． （1）求函数()f x 的解析式；（2）若函数在开区间(99)m m --, 上存在最大值与最小值，求实数m 的取值范围．（3）设函数()()f x x g x =⋅，正实数a ，b ，c 满足()()()0ag b bg c cg a ==>，证明：a b c ==． 20．（本题满分16分） 设首项为1的正项数列{}n a的前n 项和为n S ，数列{}2na 的前n 项和为n T ，且24()3n n S p T --=， 其中p 为常数.（1）求p 的值；（2）求证：数列{}n a为等比数列；（3）证明：“数列n a ，12x n a +，22yn a +成等差数列，其中x 、y 均为整数”的充要条件是“1x =，且2y =”．试题Ⅱ（附加题）21．【选做题】本题包括A 、B 、C 、D 四小题，请选定其中两题，并在相应的答题区域内作答．若 多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤． A ．（几何证明选讲）如图，AB 是半圆的直径，C 是AB 延长线上一点，CD 切半圆于点D ，CD=2，DE ⊥AB ，垂足为E ，且E 是OB 的 中点，求BC 的长．B ．（矩阵与变换） 已知矩阵122a ⎡⎤⎢⎥⎣⎦的属于特征值b 的一个特征向量为11⎡⎤⎢⎥⎣⎦，求实数a 、b 的值．C ．（极坐标与参数方程）在平面直角坐标系xOy 中，已知点(1 2)A -，在曲线22 2 x pt y pt ⎧=⎪⎨=⎪⎩，（t 为参数，p 为正常数），求p的值．D ．（不等式选讲）设123 a a a ，，均为正数，且1231a a a ++=，求证：1231119.++≥【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．22．已知函数2()2(1)ln(1)2f x x x x x =++--，[)0x ∈+∞，，求()f x 的最大值.23．（1）已知*k n ∈N 、，且k n ≤，求证：11C C k k n n k n --=；（2）设数列0a ，1a ，2a ，…满足01a a ≠，112i i i a a a -++=（i =1，2，3，…）．证明：对任意的正整数n ，011222012()C (1)C (1)C (1)C n n n n nn n n n n p x a x a x x a x x a x --=-+-+-+⋅⋅⋅+是关于x 的一次式．南通市数学一模试卷 参考答案1. {}5；2. 3；3. 2；4. 0.09；5. π6； 6. b =； 7. 8361，； 8. π4；9. (01)，； 10. ； 11. ⎣⎦； 12. 12； 13. 12； 14.3．答案解析 1．易得{}1 3 9A B A ==，，U ，则()U A B =U ð{}5；2.3z ==；3. 易得2()af x x '=-，则(1)2f a '=-=-，即2a =； 4. “饮酒驾车” 发生的频率等于11520.09200++=；5. 将()()πsin 2sin 23y x x π=+=+6向右至少平移π6个单位得sin 2y x =；6. 1=，且0b <，即b =；7. 打印出的第5组数据是学号为8号，且成绩为361，故结果是8361，； 8. 设tan A k =，则t a n 2B k =，tan 3C k =，且0k >，利用tan tan tan tan()A B C A B +=-+=-可求得1k =，所以A π=4； 9. 易得(0)0f =，20x x -<，故所求解集为(0 1)，；10. 法 1 设正四棱锥的底面边长为x ，则体积1V x =，记()22y t t=-，t>，利用导数可求得当43t=时，max3227y=，此时maxV=；法2 设正四棱锥的侧棱与底面所成角为θ，则()22122cos sin1sin sin 33Vθθθθ=⨯⨯=-⨯，0<θπ<2，记()2101y t t t=-<<，，利用导数可求得当t=时，maxy，此时maxV=；15．命题立意：本题主要考查三角函数的图像与性质、两角和与差的正、余弦公式，考查运算求解能力．（1）易得()2221()sin2sin cos2f x x x x x=++-1cos212cos222x x x-=-1s i n2c o s22x x=-+＝()π12sin262x-+，（5分）所以()f x周期π，值域为3522⎡⎤-⎢⎥⎣⎦，；（7分）（2）由()00π1()2sin2062f x x=-+=得()0π1sin2064x-=-<，（9分）又由0π2x≤≤得02ππ5π666x≤≤--，所以02ππ0x≤≤--，故()0πcos26x-=，（11分）此时，()00ππsin2sin266x x⎡⎤=-+⎢⎥⎣⎦()()00ππππsin2cos cos2sin6666x x=-+-1142=-=．（14分）16．命题立意：本题主要考查直线与平面、平面与平面的位置关系，考查空间想象、推理论证能力．解：（1）连结AC，交BD于点O，连结OC'，菱形ABCD中，CO BD⊥，因三角形BCD沿BD折起，所以C O BD'⊥，故C OC'∠为二面角C—BD—C'的平面角，（5分）（第16题图）D C'ABCOEO AB2CM1C（第11题图）易得C O CO '=CC '= 所以C OC π'∠=3，二面角C —BD —C '的大小为π3；（7分）（2）当a 变化时，线段CC '的中点E 总满足A C '//平面BED ，下证之：（9分） 因为E ，O 分别为线段CC '，AC 的中点， 所以//OE AC '，（11分） 又AC '⊄平面BED ，OE ⊂平面BED ， 所以A C '//平面BED. （14分）17．命题立意：本题主要考查求双曲线、直线、圆等基础知识，考查运算求解与探究能力． 解：（1）设A 11()x y ，，则11(24)B x y --，， 代入双曲线2212y x -=得2211221112(4)(2)12y x y x ⎧-=⎪⎪⎨-⎪--=⎪⎩，， 解得110x y ⎧⎨=⎩=-1，或1134x y =⎧⎨=⎩，， 即A B 、的坐标为10-（，）、34（，），所以AB ：1y x =+，CD ：3y x =-+；（7分） （2）A 、B 、C 、D 四点共圆，下证之：（9分）证明：由3y x =-+与2212y x -=联立方程组可得C D 、的坐标为(36--+、(36-+-，（11分）由三点A 、B 、C 可先确定一个圆22(3)(6)40x y ++-=①，（13分）经检验(36D -+-适合①式，所以A 、B 、C 、D 四点共圆．（15分）（注：本题亦可以利用圆的几何性质判断四点共圆）18．命题立意：本题主要考查数学建模和解决实际问题的能力，考查运算求解能力． 解：（1）设文科阅卷人数为x ，且x ∈*N ，则阅卷时间为2693119.246()4754119.246400x x f x x x ⨯⎧⎪=⎨⨯⎪>-⎩≤，，，，（5分）而(119) 6.782f =，(120) 6.786f =，故(119)(120)f f <，答：当文、理科阅卷人数分别是119,281时，全省阅卷时间最省；（8分）（2）文科阅卷时间为：1269311943347.34399⨯-⨯⨯⨯+=，（11分）理科阅卷时间为：1475 4.52814 4.54.547.367301⨯-⨯⨯⨯+=，（14分）答：全省阅卷时间最短为7.367天．（15分）19．命题立意：本题主要考查利用导数研究三次函数的图像与性质等基础知识，考查灵活运用数形解：（1）设()(1)(1)f x a x x'=+-，则可设()3()3xf x a x c=-+，其中c因为()f x的极大值与极小值之和为0，所以(1)(1)0f f-+=，即0c=，由(2)2f-=得3a=-，所以3()3f x x x=-；（5分）（2）由（1）得3()3f x x x=-，且()3(1)(1)f x x x'=-+-列表：由题意得，三次函数在开区间上存在的最大值与最小值必为极值（如图），（7分）又(2)2f-=，故(2)2f=-，所以192m<-≤，且291m--<-≤，解得78m<≤；（10分）（3）题设等价与222(3)(3)(3)a b b c c a-=-=-，且a，b，c>0，所以a，b，c假设在a，b，c中有两个不等，不妨设a≠b，则a>b或a<b．若a>b，则由22(3)(3)a b b c-=-得2233b c-<-即b c>，又由22(3)(3)b c c a-=-得c>a．于是a>b>c>a，出现矛盾．x(21)--,1-(11)-,1(12),y'-0 + 0 -y↘极小值2-↗极大值2↘同理，若a <b ，也必出现出矛盾． 故假设不成立，所以a b c ==．（16分）20．命题立意：本题主要考查等差、等比数列的定义与通项公式、求和公式等基础知识，考查灵活运用基本量进行探索求解、推理分析能力．解：（1）n = 1时，由24(1)13p --=得p = 0或2，（2分） 若p = 0时，243n n S T -=， 当2n =时，22224(1)1a a -++=，解得20a =或212a =-， 而0n a >，所以p = 0不符合题意，故p = 2；（5分）（2）当p = 2时，241(2)33n n T S =-- ①，则21141(2)33n n T S ++=--②，②-①并化简得1134n n n a S S ++=-- ③，则22134n n n a S S +++=-- ④， ④-③得211n n a a ++=（n *∈N ），又易得211a a =， 所以数列{an}是等比数列，且112n na -=；（10分）（3）充分性：若x = 1，y = 2，由112n n a -=知n a ，12x n a +，22y n a +依次为112n -，22n ，142n +，满足112142222n n n -+⨯=+，即an ，2xan +1，2yan +2成等差数列；（12分）必要性：假设n a ，12x n a +，22yn a +成等差数列，其中x 、y 均为整数，又112n n a -=，所以11111222222x y n nn -+⋅⋅=+⋅， 化简得2221x y --=显然2x y >-，设(2)k x y =--，因为x 、y 均为整数，所以当2k ≥时，2221x y -->或2221x y --<，故当1k =，且当1x =，且20y -=时上式成立，即证． （16分）21．A ．命题立意：本题主要考查三角形、圆的有关知识，考查推理论证、运算求解能力．解：连接OD ，则OD ⊥DC ， 在Rt △OED 中，1OE =OB 1=OD ， 所以∠ODE =30°，（5分）在Rt △ODC 中，∠DCO =30°，由DC =2得OD =DCtan30°=，所以BC =．（10分）B ．命题立意：本题主要考查二阶矩阵的特征值与特征向量，考查运算求解能力． 解：由二阶矩阵的特征值与特征向量的概念知122a ⎡⎤⎢⎥⎣⎦11⎡⎤⎢⎥⎣⎦=11b ⎡⎤⎢⎥⎣⎦，（5分） 所以3 2 b b a =⎧⎨=+⎩，，解得1 3a b ==，.（10分） C ．命题立意：本题主要考查参数方程，考查运算求解能力．解：由22 2 x pt y pt ⎧=⎪⎨=⎪⎩，，（t 为参数，p 为正常数），消去参数t 得22y px =，（8分）将点(1 2)A -，代入22y px =得2p =.（10分）D ．命题立意：本题主要考查证明不等式的基本方法，考查推理论证能力． 证明：因为a1，a2，a3均为正数，且12310a a a ++=>，所以123111a a a ++()123123111()a a a a a a =++++()()11123123111339a a a a a a ⋅=≥，（8分）当且仅当12313a a a ===时等号成立， 所以1239111a a a ++≥.（10分）22．命题立意：本题主要考查复合函数求导等知识，考查运算求解、推理论证能力．证明：由2()2(1)ln(1)2f x x x x x =++--得()2ln(1)2f x x x '=+-，（2分）令()2ln(1)2g x x x=+-，则22()2xg x -'=-=， 当10x -<<时，()0g x '>，()g x 在(1 0)-，上为增函数； 当x ＞0时，()0g x '<，()g x 在(0)+∞，上为减函数，所以()g x 在x=0处取得极大值，且(0)0g =，（6分） 故()0f x '≤（当且仅当0x =时取等号），所以函数()f x 为[)0+∞，上的减函数，（8分）则()(0)0f x f =≤，即()f x 的最大值为0．（10分）23．命题立意：本题主要考查组合数的性质、二项式定理，考查推理论证能力．（1）证明：左边!!C !()!(1)!()!k n n n k k k n k k n k ==⋅=---， 右边(1)!!(1)!()!(1)!()!n n n k n k k n k -=⋅=----，所以11C C k k n n k n --=；（3分）（2）证明：由题意得数列0a ，1a ，2a ，…为等差数列，且公差为100a a -≠.（5分）则011222012()C (1)C (1)C (1)C n n n n n n n n n n p x a x a x x a x x a x --=-+-+-+⋅⋅⋅+[][]0110010010C (1)+()C (1)+()C n n n n n n n a x a a a x x a n a a x -=-+--+⋅⋅⋅+-01111222010C (1)C (1)C ()C (1)+2C (1)C n n n n n n n n n n n n n n a x x x x a a x x x x n x ---⎡⎤⎡⎤=-+-+⋅⋅⋅++---+⋅⋅⋅+⎣⎦⎣⎦[]011211010111(1)()C (1)+C (1)C n n n n n n n n a x x a a nx x x x x -------⎡⎤=-++---+⋅⋅⋅+⎣⎦ []1010()(1)n a a a nx x x -=+-+-010()a a a nx =+-，所以对任意的正整数n ，()p x 是关于x 的一次式．（10分）。
2015届江苏高考南通市高考模拟密卷(一)(南通市数学学科基地命题)
2015届江苏高考南通市高考模拟密卷（一）(南通市数学学科基地命题)南通市数学学科基地命题第Ⅰ卷（必做题，共160分）一、填空题：本大题共14小题，每小题5分，共70分 ．1．设,a b R ∈，231a bii i+=+-，其中i 是虚数单位，则a b += ．2．已知集合{}P x x a =≤，{}sin ,Q y y R θθ==∈．若P Q ⊇，则实数a 的取值范围是 ． 3．为了了解一片经济林的生长情况，随机测量了其中100株树木 的底部周长（单位：cm )，所得数据如图．则在这100株树木 中，底部周长不小于100cm 的有 株．4．设向量(1,)a m =r ，(1,2)b m =-r ，且a b ≠r r ，若()a b a -⊥r r r，则实数m = ．5．如图所示的流程图的运行结果是 ．6．将边长为a 的正方形ABCD 沿对角线AC 折起，使BD a =， 则三棱锥D ABC -的体积为 ．7．设等差数列{}n a 的前n 项和为n S ，若19a =，462a a +=． 当n S 取最大值时，n = ． 8．已知44ππθ-≤≤，且1cos45θ=，则44cos sin θθ-= ． 9．若在区间(1,1)-内任取实数a ，在区间(0,1)内任取实数b ，则直线0ax by -=与圆22(1)(2)1x y -+-=相交的概率为 ．10．设函数()sin(2),[,]66f x x x a ππ=+∈-的值域是1[,1]2-，则实数a 的取值范围为 ．11．已知函数()f x 满足：当[]1,3x ∈时，()ln f x x =，当1[,1)3x ∈时，1()2()f x f x =．若在区间1[,3]3内，函数()()(0)g x f x ax a =->恰有一个零点，则实数a 的取值范围是 ．12．设椭圆2222:1(0)x y C a b a b+=>>和圆222:O x y b +=，若椭圆C 上存在点P ，使得过点P 引圆O 的两条切线，切点分别为A 、B ，满足60APB ∠=，则椭圆C 的离心率的取值范围是 ．13．设数列{}n a 的通项公式为13()2n n a -=，则满足不等式113n ni i i i a a ==>∑∑的正整数n 的集合为 ．14．设函数()332x x f x x -=--，则满足12(2)(log )0x f x -<的x 的取值范围是 ．二、解答题：本大题共6小题，共90分.请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程第5题图第3题图或演算步骤. 15．（本小题满分14分）在ABC ∆中，,,A B C 的对边分别为,,a b c ，且tan (2)tan b A c b B =-． （1）求角A 的大小；（2）设AD BC ⊥，D 为垂足，若2b =，3c =，求AD AC ⋅u u u r u u u r的值． 16．（本小题满分14分）如图，四棱锥P ABCD -中，底面ABCD 为矩形，PD BC ⊥，G 为PA 上一点． （1）求证：平面PCD ⊥平面ABCD ；（2）若PC ∥平面BDG ，求证：G 为PA 的中点．17．（本小题满分14分）如图，某城市有一条公路从正西方AO 通过市中心O 后转向东偏北α角方向的OB ．位于该 市的某大学M 与市中心O的距离OM =，且AOM β∠=．现要修筑一条铁路L ，L 在OA 上设一站A ，在OB 上设一站B ，铁路在AB 部分为直线段，且经过大学M ．其中tan 2α=，cos β=15AO km =．（1）求大学M 与站A 的距离AM ；（2）求铁路AB 段的长AB ．P B C D G18．（本小题满分16分）设椭圆:C 22221(0)x y a b a b+=>>的离心率为e =y x =+C的短半轴长为半径的圆O 相切． （1）求椭圆C 的方程；（2）设直线12x =与椭圆C 交于不同的两点,M N ，以线段MN 为直径作圆D ．若圆D 与y 轴相交于不同的两点,A B ，求ABD ∆的面积； （3）如图，1A 、2A 、1B 、2B 是椭圆C 的顶点，P 是椭圆C 上除顶点外的任意点，直线2B P 交x 轴于点F ，直线12A B 交2A P 于点E ．设2A P 的斜率为k ，EF 的斜率为m ，求证：2m k -为定值．19．（本小题满分16分）已知函数()ln f x x =，2()()g x f x ax bx =++，其中函数()y g x =的图象在点(1,(1))g 处的切线平行于x 轴．（1）确定a 与b 的关系；（2）若0a ≥，试讨论函数()g x 的单调性；（3）设斜率为k 的直线与函数()y f x =的图象交于两点1122(,),(,)A x y B x y 12()x x <，求证：2111k x x <<．20．（本小题满分16分）设数列{}n a 的前n 项和为n S ，满足2n n a S An Bn C +=++*(0,)A n N ≠∈． （1）当1C =时，①设n n b a n =-，若132a =，294a =．求实数,A B 的值，并判定数列{}nb 是否为等比数列；DCBA ②若数列{}n a 是等差数列，求1B A-的值； （2）当0C =时，若数列{}n a 是等差数列，11a =，且*n N ∀∈，131ni n λ=-≤+求实数λ的取值范围．第Ⅱ卷（附加题，共40分）21．[选做题]本题包括A 、B 、C 、D 四小题，每小题10分；请选定其中两题，并在相应的答题区域．．．．．．．．．．．．．．．．． 内作答．．．． A ．（选修４－１：几何证明选讲）如图，设AB 、CD 是圆O 的两条弦，直线AB 是线段CD的垂直平分线．已知6,AB CD ==AC 的长度．B ．（选修４－２：矩阵与变换）若点(2,1)A 在矩阵11a b ⎡⎤=⎢⎥-⎣⎦M 对应变换的作用下得到点(4,5)B ，求矩阵M 的逆矩阵． C ．（选修４－４：坐标系与参数方程）在极坐标系中，设圆C 经过点6P π，），圆心是直线sin()3πρθ-=C 的 极坐标方程．D ．（选修４－５：不等式选讲） 设,,a b c 均为正数，1abc =．求证：111a b c++≥．【必做题】第22题、第23题，每题10分，共计20分. 22．（本小题满分10分）已知数列{}n a 满足11a =-，*1(33)46,n n n a n a n N n++++=∈．（1）求证：数列2n a n +⎧⎫⎨⎬⎩⎭是等比数列；（2）设1*3,2n n n b n N a -=∈+，求证：当2n ≥，*n N ∈时，12241521n n n b b b n +++++<-+． 23．（本小题满分10分）如图，已知点(0,)F p ，直线:(0)l y p p p =->其中为常数且，M 为平面内的动点，过M 作l 的垂线，垂足为N ，且NM NF FM FN ⋅=⋅u u u u r u u u r u u u r u u u r． （1）求动点M 的轨迹C 的方程；（2）设Q 是l 上的任意一点，过Q 作轨迹C 的切线，切点为A 、B ． ①求证：A 、Q 、B 三点的横坐标成等差数列；②若(4,)Q p --，20AB =，求p 的值．2015年高考模拟试卷(1) 参考答案南通市数学学科基地命题第Ⅰ卷（必做题，共160分）一、填空题1. 6；2. [1,)+∞；3. 70；4. 1；5.20；6.3； 7. 5；8. ； 9. 516； 10. [,]62ππ； 11. 1(,6ln3]e ；【解析】当1[,1)3x ∈时，1(1,3]x∈，由条件得，11()2()2ln 2ln f x f x x x===-，函数()()(0)g x f x ax a =->恰有一个零点⇔方程()f x ax =(0)a >有唯一解，在直角坐标系内分别作出()y f x =与y ax =(0)a >的图象，当直线y ax =经过点1(,2ln3)3时，6ln 3a =6ln 3，当直线y ax =和曲线()ln f x x =相切时，切点为(,1)e ，此时1a e =，由图象可知，当16ln3a e<≤时，函数()y f x =与y ax =(0)a >的图象由唯一的交点．12. ；【解析】在四边形OAPB 中，60APB ∠=，90OAP OBP ∠=∠=，OA OB b ==，2OP b ∴=，由题意得，2b a ≤，即a ≤，化解得c a ≥，又在椭圆中1e <，1e ≤<． 13. {1，2，3}；【解析】由于数列{}n a 的通项公式为13()2n n a -=，所以数列{}n a 为等比数列，首项为132a =，公比132q =；数列1{}n a 也是等比数列，首项为23，公比223q =．不等式113n n i i i i a a ==>∑∑等价于1113n ni i i i a a ==>∑∑，即231()1()323231132n n--⋅>--，解之得22()193n <<，n N *∈，n ∴只能取1,2,3． 14. (0,1)(2,)+∞；【解析】()3ln33ln32(33)ln322ln320x xx x f x --'=+-=+-≥->，∴函数()f x 在(,)-∞+∞上单调递增，且(0)0f =，112220(2)(log )0log 0x x f x x ->⎧⎪∴-<⇔⎨<⎪⎩或1220log 0x x -<⎧⎪⎨>⎪⎩，解得2x >或01x <<．二、解答题15. （1）tan (2)tan b A c b B =-， ∴由正弦定理，得sin sin sin (2sin sin )cos cos A BB C B A B⋅=-⋅, 又在ABC ∆中，sin 0B ≠， sin cos 2sin cos cos sin A B C A A B ∴=-，即sin()2sin cos A B C A +=， 又sin()sin 0A B C +=≠， 1cos 2A ∴=，又0A π<<，3A π∴=；（2） 由余弦定理，2222cos a b c bc A =+-，2b =，3c =，A π=， a ∴11sin2BC AD AB AC A ⋅=⋅⋅32AD =⋅， AD ∴=227cos 7AD AC AD AC C AD AD ⋅∠∴⋅===.16.（1）底面ABCD 为矩形，BC CD ∴⊥，又PD BC ⊥，,CD PD PCD ⊂平面，PD CD D =， BC ∴⊥平面PCD ， 又BC ABCD ⊂平面， ∴平面ABCD ⊥平面PCD ；（2）连接AC ，交BD 于O ，连接GO ， //PC 平面BDG ，平面PCA 平面BDG GO =， //PC GO ∴， PG COGA OA∴=，底面ABCD 为矩形， ∴O 是AC 的中点，即CO OA =， PG GA ∴=， ∴G 为PA 的中点.17. （1）在AOM ∆中，15AO =，AOM β∠=且cos β=OM =由余弦定理得，2222cos AM OA OM OA OM AOM =+-⋅⋅∠2215215=+-⨯13915152315372.=⨯+⨯-⨯⨯⨯=AM ∴=M 与站A 的距离AM为；（2）cos β=，且β为锐角，sin β∴=在AOM ∆中，由正弦定理得，sin sin AM OMMAOβ=∠,=，sin MAO ∴∠=，4MAO π∴∠=， 4ABO πα∴∠=-， tan 2α=，sin α∴=，cos α=，sin sin()4ABO πα∴∠=-=AOB πα∠=-，sin sin()AOB πα∴∠=-=，在AOB ∆中，15AO =， 由正弦定理得，sin sin AB AOAOB ABO=∠∠，即15AB =，AB ∴=AB 段的长AB为． 18. （1）圆O 的方程为222x y b +=，直线y x =O 相切，b =，即1b =，又3e =，，2a ∴=， ∴椭圆C 的方程为221x y +=；（2）由题意，可得11((,22MN ， ∴圆D 的半径r =，AB ∴=， ∴ABD ∆的面积为1122S ==； （3）由题意可知1212(2,0),(2,0),(0,1),(0,1)A A B B --，2A P 的斜率为k ，∴直线2A P 的方程为(2)y k x =-， 由2214(2)x y y k x =+=-⎧⎪⎨⎪⎩，得2222(14)161640k x k x k +-+-=，其中2A x =，228214P k x k -∴=+，222824(,)1414k kP k k--∴++， 则直线2B P 的方程为211221)k y x k +=-+-（， 令0y =，则2(21)21k x k -=+， 即2(21)(,0)21k F k -+，直线12A B 的方程为220x y -+=，由220(2)x y y k x -+=⎧⎨=-⎩，解得4221421k x k k y k +⎧=⎪⎪-⎨⎪=⎪-⎩，424(,)2121k k E k k +∴--，∴EF 的斜率421212(21)4242121k k k m k k k k -+-==-+-+- ， ∴2112242k m k k +-=⋅-=（定值）． 19. （1）22()()ln g x f x ax bx x ax bx =++=++， 1()2g x ax b x'∴=++，由题意得(1)120g a b '=++=， 21b a ∴=--；（2）11(21)(1)()2221(0)ax x g x ax b ax a x x x x--'=++=+--=>，①当0a =时，(1)()(0)x g x x x--'=>，当1x >时，()0g x '<，∴函数()g x 在(1,)+∞单调减； 当01x <<时，()0g x '>，∴函数()g x 在(0,1)单调增；②当102a <<时，即112a>，12()(1)2()(0)a x x a g x x x --'=>， ∴函数()g x 在(11,)2a 上单调减；函数()g x 在(12,)a +∞和(0,1)单调增；③当12a =时，即21a =，2(1)()0(0)x g x x x -'=≥>，∴函数()g x 在(0,)+∞单调增；④当12a >时．即112a <，12()(1)2()(0)a x x a g x x x --'=>， ∴函数()g x 在(1,1)2a单调减区间；函数()g x 在(1,)+∞和(0,12)a单调增；（3）由题设210x x >>，21212211ln ln 1111x x k x x x x x x -∴<<⇔<<- 21212121ln ln x x x xx x x x --⇔<-<22211111ln 1x x x x x x ⇔-<<- ①令()ln 1(1)h x x x x =-+>，则11()1(1)x h x x x x-'=-=>， 1x ∴>时，()0h x '<， ∴函数()g x 在(1,)+∞是减函数， 而(1)0h =，1x ∴>时，()(1)0h x h <=210x x >>，211x x ∴>， 222111()ln 10x x x h x x x ∴=-+<，即2211ln 1x xx x <-， ②令1()ln 1(1)H x x x x =+->，则22111()(1)x H x x x x x-'=-=>，1x ∴>时，()0H x '>， ∴()H x 在(1,)+∞是增函数，1x ∴>时，()(1)0H x H >=， 2221111()ln 10x x H x x x x ∴=+->，即221111ln x x x -< ③由①②③得2111k x x <<．20.（1）1C =，21n n a S An Bn ∴+=++，①令1n =，可得121a A B =++，即2A B +=，令2n =，可得122421a a A B +=++，即425A B +=，13,22A B ∴==,213122n n a S n n ∴+=++， ①当2n ≥时，21113(1)(1)122n n a S n n --∴+=-+-+， ②①-②，得121n n a a n --=+(2)n ≥，11[(1)]2n n a n a n -∴-=--，即112n n b b -=，又111102b a =-=≠，0n b ≠，112n n b b -=∴， ∴数列{}n b 是等比数列； ②数列{}n a 是等差数列，∴设11(1)(1),2n n n n a a n d S na d -=+-=+， 21n n a S An Bn +=++， 1221()221d dn a n a An B d n ∴++++=+-，*n N ∈ 11221d A d B a a d ⎧=⎪⎪⎪∴=+⎨⎪-=⎪⎪⎩，111122122223d d d a a d AB +--=++-∴===； （2）当0C =时，2n n a S An Bn +=+数列{}n a 是等差数列，11a =，∴(1)1(1),2n n n n a n d S n d -=+-=+，22(1)122d dn n An Bn d ∴++=++-， 1d ∴=，n a n ∴=，21(1)11111(1)1n n a n n n n ++++==+-++， 1111ni n n =+-∴+， 13311111n i n n n n λλ=∴-≤-≤+-+++， 即211n n λ≤+++， *n N ∴∀∈，211n n λ≤+++， 令2()f x x x =+， 22222()1x f x x x -'=-=，当2x ≥时，()0f x '>， ()f x ∴在[2,)+∞上是增函数，而12n +≥，min 2(1)31n n ∴++=+，3λ∴≤．第Ⅱ卷（附加题，共40分）21. A ．连接BC ，,AB CD 相交于点E ．因为AB 是线段CD 的垂直平分线，所以AB 是圆的直径，∠ACB ＝90°．设AE x =，则6EB x =-，由射影定理得CE 2＝AE ·EB ，又CE(6)5x x -=，解得1x =（舍）或5x = 所以，AC 2＝AE ·AB ＝5×6＝30，ACB ．2415⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦M ，即24215a b +⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦， ∴24,21 5.a b +=⎧⎨-=⎩ 解得2,3.a b =⎧⎨=⎩，∴1231M ⎡⎤=⎢⎥-⎣⎦， 解法一：12det()731M ∴==--， 11212777731317777M ---⎡⎤⎡⎤⎢⎥⎢⎥--==⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥--⎣⎦⎣⎦. 解法二:设1c d M e f -⎡⎤=⎢⎥⎣⎦，由1M M -=1001⎡⎤⎢⎥⎣⎦，得32103201c d c d e f e f +-⎡⎤⎡⎤=⎢⎥⎢⎥+-⎣⎦⎣⎦∴31,30,20,2 1.c de f c d e f+=⎧⎪+=⎪⎨-=⎪⎪-=⎩ 解得1,72,73,71.7c d e f ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=-⎩112773177M -⎡⎤⎢⎥∴=⎢⎥⎢⎥-⎢⎥⎣⎦． C ．因为圆心为直线2sin()sin33ππρθ-=与极轴的交点，所以令0θ=，得1ρ=，即圆心是(1,0)，又圆C 经过点6P π，）， ∴圆的半径1r =，∴圆过原点， ∴圆C 的极坐标方程是2cos ρθ=．（说明：化为普通方程去完成给相应的分数）D.由,,a b c 为正数，根据平均值不等式，得11a b +≥11b c +≥，11a c +≥．将此三式相加，得1112()a b c ++≥111a b c ++≥．由1abc =1=．所以，111a b c ++≥= 22.（1）令2n n a c n+=， 则11(33)4622(33)(2)23311(1)n n n n n n n a n a n a a n c n n nc n n ++++++++++====+++=， 11210c a =+=≠，0n c ∴≠，13n ncc +∴=，∴数列{}n c ，即2n a n +⎧⎫⎨⎬⎩⎭是等比数列；（2）由（1）得123n n a n-+=，132n n a n -∴=⋅-，1312n n n b a n -∴==+， 下面用数学归纳法证明当2n ≥，*n N ∈时，12241521n n n b b b n +++++<-+． ①当2n =时，不等式的左边341173412b b =+=+=，右边413555=-=，而73125<，∴2n =时，不等式成立；②假设当(2)n k k =≥时，不等式成立，即12241521k k k b b b k +++++<-+；当1n k =+时，11122(1)12221221()()k k k k k k k k k b b b b b b b b b +++++++++++++=+++++- 4111152121221k k k k <-++-++++ 41152214152(1)4152(1)1k k k k =+-++=-+<-++∴当1n k =+时，不等式也成立． 由①②可得，当2n ≥，*n N ∈时，12241521n n n b b b n +++++≤-+．23. （1）设(,)M x y ，则(,)N x p -，(0,)NM y p ∴=+，(,2)NF x p =-，(,)FM x y p =-，(,2)FN x p =-，NM NF FM FN ⋅=⋅，22()2()p y p x p y p ∴+=--，24x py ∴=，即动点M 的轨迹C 的方程为24x py =； 另解：设(,)M x y ，则(,)N x p -，NM NF FM FN ⋅=⋅，()0NF MN MF ∴⋅+=，∴以,MN MF 为邻边的平行四边形是菱形，MF MN ∴=，y p + ，24x py ∴=，即动点M 的轨迹C 的方程为24x py =； （2）①设0(,)Q x p -，211(,)4x A x p ，222(,)4x B x p，则切线QA 的方程2111(,)42x xy x x p p-=-， 21101()42x xp x x p p∴--=-，22101240x x x p ∴--=， ①同理22202240x x x p ∴--=， ② 方法1:①②得12120()(2)0x x x x x -+-=，12120,20x x x x x ≠∴+-=，1202x x x ∴+=，即A 、Q 、B 三点的横坐标成等差数列.方法2：由①②得12,x x 是方程220240x x x p --=的两根，1202x x x ∴+=，即A 、Q 、B 三点的横坐标成等差数列. ②由①②得12,x x 是方程220240x x x p --=的两根，12021224x x x x x p +=⎧∴⎨⋅=-⎩， (4,)Q p --，1221284x x x x p +=-⎧∴⎨⋅=-⎩， 20AB =，20，20=，20， 4217160p p ∴-+=，1p ∴=或4p =.。
南通市高三数学一模试卷(20200910012431)
已知 a， b，c 均为正实数．求证：
a
b
c 111
≥
．
bc ca ab a b c
【必做题】第 22、23 题，每小题 10 分，共计 20 分．请在答．题．卡．指． 定．区．域． 内作答，解答时应写出 文字说明、证明过程或演算步骤．
22．（本小题满分 10 分） 如图，在四棱锥 A BCDE 中，底面 BCDE 为平行四边形， 平面 ABE 平面 BCDE ，AB AE ， DB DE ， BAE BDE 90°． A （1）求异面直线 AB 与 DE 所成角的大小； （2）求二面角 B AE C 的余弦值．
证明过程或演算步骤．
15． ( 本小题满分 14 分 )
在△ ABC中，角 A， B， C的对边分别为 a， b， c．已知 b cosC ccosB 2a cos A ．
（1）求 A 的大小； uuur uuur
（2）若 AB AC = 3 ，求△ ABC的面积．
16． ( 本小题满分 14 分 ) 如图，在直三棱柱 ABC A1B1C1 中， AC BC， CC1= 4 ， M 是棱 CC1 上的一点． （ 1）求证： BC AM；
的最大值为 ▲ ．
【答案】 200
12． 已知函数 y
ax
b (b
0) 的图象经过点 P(1，3) ，如下图所示，则
4 a1
1 的最小值 b
A
为▲．
y
【答案】
9 2
3P x
O1 x
?O
B
C M
（第 12 题）
（第 13 题）
uuur uuuur 13． 如上图，圆 O内接△ ABC中， M是 BC的中点， AC=3．若 AO AM 4 ，则 AB= ▲ ．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
江苏省南通市20XX届高三第一次模拟考试生物注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分120分,考试用时100分钟。
2. 答题前,考生务必将自己的学校、班级、姓名写在密封线内。
第Ⅰ卷(选择题共55分)一、单项选择题:本题包括20小题,每小题2分,共40分。
每小题只有一个选项最符合题意。
1. 下列有关唾液淀粉酶和ATP的叙述,正确的是( )A. 两种物质共有的元素是C、H、O、N、PB. 唾液腺细胞能同时合成这两种物质C. 两种物质的合成过程均需要模板D. 唾液淀粉酶的合成不需要消耗ATP2. 下列有关叙述不能体现“细胞结构与功能相适应”的是( )A. 磷脂双分子层构成细胞膜的基本骨架,有利于将细胞内外水环境隔开B. 靠近叶片背面的叶肉细胞中的叶绿体比较大,有利于观察叶绿体C. 精子细胞变形过程中线粒体聚集在尾的基部,有利于精子的灵活运动D. 胃腺细胞中附着核糖体的内质网比较发达,有利于胃蛋白酶的合成和加工3. 右图是甲、乙两种雄性高等动物的细胞分裂模式图,下列相关判断正确的是( )A. 甲、乙动物正常体细胞中的染色体数目分别是3个、4个B. 甲动物体细胞中没有同源染色体,乙动物体细胞中有同源染色体C. 图示两种细胞中染色单体数和DNA分子数之比均为1∶1D. 图示两种细胞都能在各自的精巢中找到4. 下列有关细胞凋亡和癌变的叙述,错误的是( )A. 细胞凋亡有利于维持人体内环境的稳态B. 癌变的细胞形态结构会发生显著变化C. 两者的发生都是遗传物质改变的结果D. 通过激活细胞凋亡机制可杀死癌细胞5. 向装有5 mL体积分数为3% H2O2溶液的密闭容器中,加入2滴新鲜肝脏研磨液,每隔一段时间测定容器中O2浓度,得到如右图中曲线a(实线)所示结果。
下列相关叙述错误的是( )A. 曲线a表明,随着时间的推移H2O2分解速率呈现由快转慢直到停止的特点B. 在t1时,向容器中再加入2滴新鲜肝脏研磨液,可以得到曲线b所示结果C. 在t1时,向容器中再加入2滴质量分数为3.5% FeCl3溶液,可以得到曲线c所示结果D. 在t2时,向容器中再加入5 mL 3% H2O2溶液,可以得到曲线d所示结果6. 研究人员用32P标记的T2噬菌体进行噬菌体侵染大肠杆菌的实验,下列相关说法正确的是( )A. T2噬菌体中含32P的成分是磷脂分子和DNA分子B. 经保温培养、搅拌、离心后,放射性全部集中在沉淀物中C. 在产生的子代噬菌体中不会检测到放射性D. 本实验可以证明T2噬菌体DNA可侵入大肠杆菌7. 人体细胞中的一个DNA分子( )A. 基本组成单位是核糖核苷酸B. 可转录形成多种mRNAC. 复制场所是细胞核或核糖体D. 存在控制相对性状的等位基因8. 已知小麦植株高茎(A)对矮茎(a)为显性,抗病(B)对感病(b)为显性,两对基因独立遗传。
研究人员以基因型为AaBb的高茎抗病小麦幼苗为材料,通过右下图三种途径获得矮茎抗病新品种。
下列相关叙述错误的是( )A. 途径①③依据的原理分别是基因重组、染色体变异B. 途径①获得的矮茎抗病植株中纯合子占1/3C. 途径②③获得的矮茎抗病植株均能稳定遗传D. 三种育种途径获得的矮茎抗病植株中a的基因频率均为19. 下列有关现代生物进化理论的叙述,正确的是( )A. 生物的进化与无机环境的变化相互影响B. 突变和基因重组不会导致种群基因频率的改变C. 进化一定导致生殖隔离,形成新物种D. 生物个体是进化的基本单位10. 下表中亲本在产生后代时表现出交叉遗传现象的是( )11. 下表是血浆、组织液和骨骼肌细胞内液某些成分的浓度及总渗透压的比较(浓度单位为mEq·L-1,渗透压单位为mOsm·L-1)。
下列相关叙述错误的是( )A. Na+、Cl-主要分布在细胞外液中B. 与组织液相比,血浆中蛋白质含量高C. HC有利于维持内环境pH相对稳定D. 血浆渗透压主要是由蛋白质的含量决定的12. 当HIV侵入人体后,不会发生( )A. 吞噬细胞吞噬、处理HIVB. HIV侵入T淋巴细胞并增殖C. T细胞增殖、分化形成记忆细胞D. 浆细胞迅速增殖、分泌抗体13. 右图为人体血糖调节模型,下列相关分析错误的是( )A. 图中胰岛细胞为胰岛B细胞B. 神经与胰岛细胞之间通过化学物质传递信号C. 胰岛素的主要功能是促进肝糖原和肌糖原水解D. 反馈调节有利于维持机体血糖平衡14. 下列关于生态学知识在生产中的应用,属于种群水平的是( )A. 利用玉米螟天敌赤眼蜂防治虫害B. “稻—藕—鱼”立体种养,充分利用了稻田的有限空间C. 依据年龄组成预测草原老鼠种群数量变化D. 建立人工防护林时注意适当增加植物种类多样性15. 某农田弃耕后发生了一系列的演替,演替过程中不同阶段优势植物和常见植物记录见右表。
下列相关判断错误的是( )A. 在演替过程中不断形成新物种,并取代原有的物种B. 随着时间的推移,群落的垂直结构变得复杂C. 群落演替使生态系统对光能的利用率提高D. 与草本植物阶段相比,木本植物阶段的演替比较缓慢16. 在利用动物细胞融合技术制备单克隆抗体时,不需要考虑( )A. 选择的小鼠必须是纯种B. 用同种抗原多次注射小鼠C. 细胞融合时加入促融剂D. 筛选时采用单细胞培养技术17. 科学家能利用胡萝卜组织在实验室中培育出完整的胡萝卜植株。
此过程中不需要( )A. 制备含蔗糖等有机营养物质的固体培养基B. 对离体的组织要进行快速消毒C. 使用胰蛋白酶处理制备细胞悬液D. 控制光照及培养基中植物激素的种类和含量18. 下列有关胚胎移植技术的叙述,错误的是( )A. 对供、受体母畜进行同期发情处理B. 受体母畜对移植胚胎不发生排斥C. 可快速扩大良种动物的种群数量D. 胚胎必须发育到原肠胚阶段才能移植19. 下列有关酶制剂应用的叙述,正确的是( )A. 纤维素酶可用于处理棉、麻制品,使其柔软B. 加酶洗衣粉的洗涤效果总比普通洗衣粉好C. 固定化葡萄糖异构酶可催化一系列化学反应D. 腐乳前期发酵主要依赖毛霉产生的淀粉酶20. 下列有关实验的分析,错误的是( )A. 对洋葱根尖解离不充分,会观察到细胞重叠B. 制作腐乳时加盐过多,会导致腐乳过硬、影响口味C. 利用血细胞计数板进行酵母菌计数时,统计值比实际活菌数多D. 固定化酵母细胞时,凝胶珠在CaCl2溶液中浸泡时间过长,会使固定细胞偏少二、多项选择题:本题包括5小题,每小题3分,共15分。
每小题有不止一个选项符合题意,全选对的得3分,选对但不全的得2分,错选或不答的得0分。
21. 下图是酵母细胞中的部分代谢过程,相关叙述正确的是( )A. 过程①发生在线粒体基质中B. 过程②需要含氮物质做原料C. 过程③合成ATP最多D. 过程④在氧充足和缺氧时都能发生22. 右图是某单基因遗传病的遗传系谱图。
下列相关分析正确的是( )A. 该遗传病是由一个基因控制的B. 该遗传病的致病基因不在性染色体上C. 若Ⅰ2不带致病基因,则该病为常染色体显性遗传D. 若Ⅱ4带致病基因,则Ⅱ5与Ⅱ6再生一个正常女孩的概率是1/423. 下列有关植物激素与动物激素的比较,正确的是( )A. 都具有微量、高效、作用于靶细胞(器官)等特点B. 激素受体的化学本质都是蛋白质,并且都分布在细胞膜上C. 植物激素的作用都具有两重性,即低浓度促进、高浓度抑制D. 动物激素调节往往受到神经系统的直接或间接控制24. 下列有关生物多样性的叙述,正确的是( )A. 生物多样性的形成经过了漫长的共同进化过程B. 与西双版纳热带雨林相比,大兴安岭针叶林的物种多样性较高C. 从裸岩到森林演替过程中,物种多样性增加D. 保护生物多样性就是保护生物种类和种群基因库25. 下列有关微生物实验室培养的叙述,正确的是( )A. 在熔化琼脂时,需要控制火力并不断搅拌,以免发生焦糊B. 灼烧、高压蒸汽灭菌、紫外线照射等都属于无菌技术C. 样品中活菌数量统计时,接种方法应采用划线法D. 用平板培养基培养微生物时,应将平板倒过来放置第Ⅱ卷(非选择题共65分)三、非选择题:本题包括8小题,共65分。
26. (8分)黑藻是一种常见的单子叶沉水植物,其叶片小而薄,叶肉细胞内有大而清晰的叶绿体,液泡无色。
某同学观察黑藻叶肉细胞的质壁分离和复原现象,实验步骤如下图所示。
请据图回答:(1)在制作黑藻叶片临时装片时,为了防止产生气泡,盖盖玻片的正确方法是。
(2)步骤①中,要将视野右上方的叶肉细胞移到中央,应将装片向(填方向)移动。
(3)若步骤②中使用的试剂是0.3 g·mL-1的蔗糖溶液,则在步骤③中观察到质壁分离现象,这是黑藻细胞通过作用失水的结果。
步骤④滴加清水后,步骤⑤观察到多数黑藻细胞不能发生质壁分离复原现象,最可能的原因是。
(4)某兴趣小组用右图装置探究光照强度对黑藻光合速率的影响。
①用多套图示装置进行实验时,控制自变量的方法是。
②黑藻培养液中加入适量NaHCO3目的是。
光源用荧光灯比白炽灯更好,这是因为。
③预期实验结果: 。
27. (8分)植物叶片在离体后,水分会迅速减少,叶片内的各种生理活动都会发生变化。
离体叶片净光合速率下降有两个主要因素:一是气孔导度(指单位时间、单位面积叶片通过气孔的气体量)的下降,阻止了CO2的供应;二是缺水引起叶肉细胞光合能力的下降,使叶肉细胞利用CO2的能力降低。
科研人员用茶树离体叶片作为研究材料,测定了气孔导度、净光合速率、蒸腾速率、胞间CO2浓度的变化,结果如下图所示。
请回答:(1)在叶肉细胞中,水光解的场所是叶绿体的;实验开始4 min时,水光解产生气体的去向有。
(2)实验开始大约min后叶片表现出从外界吸收O2放出CO2;实验8 min时,叶肉细胞中产生ATP的场所有。
(3)胞间CO2进入叶绿体后,与结合而被固定,再被还原生成有机物。
(4)在最初04 min内,叶肉细胞净光合速率下降的主要原因是;12 min后,胞间CO2浓度,净光合速率下降的主要原因是。
28. (8分)Notch信号途径是一种细胞间相互作用的基本途径,调控着细胞增殖、分化、凋亡等过程。
右图表示肝脏组织受损或部分切除后激活Notch信号途径实现再生的过程。
图中受损细胞A的膜上产生信号分子,与正常细胞B膜上的Notch分子(一种跨膜受体)结合,导致Notch的膜内部分水解成NICD,NICD再与RBP(一种核内转录因子)一起结合到靶基因的相应部位,激活靶基因,最终引起肝脏再生。
请分析回答:(1)信号分子与细胞膜上的Notch分子结合后引起肝细胞的一系列变化,这体现了细胞膜的功能。
(2)在Notch分子基因表达过程中,过程①需要的酶主要是;过程②除需要mRNA外,还需要(2分)。