最新中职数学基础模块上册教案:有理指数(二)
语文版中职数学基础模块上册4.1《有理数指数幂》word教案

有理数指数幂教案一、条件分析1.学情分析在上个单元中,学生学习了函数的概念、表示方法、单调性、奇偶性,对函数有了初步的认识,但是还远远不够,函数是个大家庭,需要我们继续深入学习已到达实际运用的目的。
对于这个章节的内容,学生在初中已经学过,加之初数内容的补充,学生对这方面的知识掌握起来比较容易,难点在于对八个公式的记忆可能混淆,因此在学习本章节的内容时应多做练习巩固所学知识。
2.教材分析本节内容由整数指数幂、n次根式、分数指数幂构成,这三个内容环环相扣,层层递进,所以,在学习这个章节的内容时,应注意知识的内在联系。
二、三维目标知识与技能目标A层:1. 理解有理数指数幂的概念;2. 识记正整数指数幂的运算法则;3. 识记分数指数幂的运算法则;4. 理解n次方根、n次算术根的概念。
B层:1. 理解有理数指数幂的概念;2. 识记正整数指数幂的运算法则;3. 识记分数指数幂的运算法则。
C层:1. 识记正整数指数幂的运算法则;2. 识记分数指数幂的运算法则。
过程与方法目标讲授法、练习法、游戏法。
在学习有理数指数运算时通过竞答游戏激发学生学习兴趣,通过练习加深学生对所学知识的巩固。
情感态度和价值观目标通过对有理数指数幂的探究,培养学生观察、归纳、抽象的能力和语言表达能力;通过学习有理数指数幂的知识,让学生明白,对于问题的解决,我们可以采用多种方法,其中有效的方法是转化,把不熟悉的问题转化成我们所熟悉的问题就能轻松解决。
三、教学重点有理数指数幂的运算法则四、教学难点n次方根与n次算术根的区别和联系五、主要参考资料:中等职业教育课程教材数学基础模块(上)、学生学习指导用书、教学参考书。
六、教学进程:故事导入:谣言的力量某人听到一则谣言后一小时内传给两人,以后他没有再传给别人.而那两人同样在一小时内每人又分别传给另外的两人。
如此下去,一昼夜能传遍一个千万人口的大城市吗?能?还是不能?请注意,一小时内,一个人只传给两个人,一昼夜只有24小时,一个千万人口的大城市能传遍吗?只凭直觉,是很难正确判断的。
中职数学有理数指数幂教案

中职数学有理数指数幂教案数学教案课题:有理数的指数幂教学目标:1. 了解有理数的指数幂的概念。
2. 掌握有理数的指数幂的运算规则和性质。
3. 能够应用有理数的指数幂解决实际问题。
教学内容与教学步骤:一、导入(5分钟)1. 引导学生回顾有理数的概念和性质。
2. 提问:什么是指数?什么是幂?在数学中有什么重要的应用?二、讲解(20分钟)1. 定义有理数的指数幂。
- 对于有理数a和正整数n,a的n次方(记作a^n)定义为n个a 的乘积,即a^n = a × a × ... × a (n个a)。
- 对于有理数a和正整数n,a的-n次方定义为1/a的n次方,即a^(-n) = 1/(a^n)。
2. 讲解有理数的指数幂的运算规则和性质。
- 同底数的幂相乘,指数相加。
- 同底数的幂相除,指数相减。
- 幂的幂,指数相乘。
- 幂的乘方,底数不变,指数相乘。
- 任何数的0次方等于1。
- 任何数的1次方等于它本身。
- 任何数的-1次方等于它的倒数。
3. 通过例题演示运用有理数的指数幂的运算规则。
三、练习(15分钟)1. 学生个别或小组进行练习,巩固运用有理数的指数幂的运算规则和性质。
2. 针对学生的不同水平,提供不同难度的练习题。
四、拓展与应用(10分钟)1. 引导学生将有理数的指数幂应用于实际问题。
2. 提问:在生活中有哪些场景可以运用有理数的指数幂?五、归纳总结(5分钟)1. 让学生总结有理数的指数幂的运算规则和性质。
2. 强调掌握和应用有理数的指数幂的重要性。
六、作业布置(5分钟)1. 布置课后作业,要求练习有理数的指数幂的运算。
2. 鼓励学生多做实际问题的应用题。
备注:本教案中没有包含任何网址、超链接和电话等外部信息。
中职数学(基础模块)上册教案

中职数学(基础模块)上册教案1.1集合的概念知识目标:(1)理解集合、元素及其关系;(2)掌握集合的列举法与描述法会用适当的方法表示集合.能力目标:通过集合语言的学习与运用,培养学生的数学思维能力.教学重点:集合的表示法.教学难点:集合表示法的选择与规范书写.课时安排:2课时.1.2集合之间的关系知识目标:(1)掌握子集、真子集的概念;(2)掌握两个集合相等的概念;(3)会判断集合之间的关系.能力目标:通过集合语言的学习与运用,培养学生的数学思维能力.教学重点:集合与集合间的关系及其相关符号表示.教学难点:真子集的概念.课时安排:2课时.1.3集合的运算(1)知识目标:(1)理解并集与交集的概念;(2)会求出两个集合的并集与交集.能力目标:(1)通过数形结合的方法处理问题,培养学生的观察能力;(2)通过交集与并集问题的研究,培养学生的数学思维能力.教学重点:交集与并集.教学难点:用描述法表示集合的交集与并集.课时安排:2课时.1.3集合的运算(2)知识目标:(1)理解全集与补集的概念;(2)会求集合的补集.能力目标:(1)通过数形结合的方法处理问题,培养学生的观察能力;(2)通过全集与补集问题的研究,培养学生的数学思维能力.教学重点:集合的补运算.教学难点:集合并、交、补的综合运算.课时安排:2课时.1.4充要条件知识目标:了解“充分条件”、“必要条件”及“充要条件”.能力目标:通过对条件与结论的研究与判断,培养思维能力.教学重点:(1)对“充分条件”、“必要条件”及“充要条件”的理解.(2)符号“”,“”,“”的正确使用.教学难点:“充分条件”、“必要条件”、“充要条件”的判定.课时安排:2课时.2.1不等式的基本性质知识目标:⑴理解不等式的基本性质;⑵了解不等式基本性质的应用.能力目标:⑴了解比较两个实数大小的方法;⑵培养学生的数学思维能力和计算技能.教学重点:⑴比较两个实数大小的方法;⑵不等式的基本性质.教学难点:比较两个实数大小的方法.课时安排:1课时.2.2区间知识目标:⑴掌握区间的概念;⑵用区间表示相关的集合.能力目标:通过数形结合的学习过程,培养学生的观察能力和数学思维能力.教学重点:区间的概念.教学难点:区间端点的取舍.课时安排:1课时.2.3一元二次不等式式的图像解法.观察能力与数学思维能力;⑵通过求解一元二次不等式,培养学生的计算技能.2.4含绝对值的不等式知识目标:(1)理解含绝对值不等式或的解法;(2)了解或的解法.能力目标:(1)通过含绝对值不等式的学习;培养学生的计算技能与数学思维能力;(2)通过数形结合的研究问题,培养学生的观察能力.教学重点:(1)不等式或的解法.(2)利用变量替换解不等式或.教学难点:利用变量替换解不等式或.课时安排:2课时.3.1函数的概念及其表示法知识目标:(1)理解函数的定义;(2)理解函数值的概念及表示;(3)理解函数的三种表示方法;(4)掌握利用“描点法”作函数图像的方法.能力目标:(1)通过函数概念的学习,培养学生的数学思维能力;(2)通过函数值的学习,培养学生的计算能力和计算工具使用技能;(3)会利用“描点法”作简单函数的图像,培养学生的观察能力和数学思维能力.教学重点:(1)函数的概念;(2)利用“描点法”描绘函数图像.教学难点:(1)对函数的概念及记号的理解;(2)利用“描点法”描绘函数图像.课时安排:2课时.3.2函数的性质知识目标:⑴理解函数的单调性与奇偶性的概念;⑵会借助于函数图像讨论函数的单调性;⑶理解具有奇偶性的函数的图像特征,会判断简单函数的奇偶性.能力目标:⑴通过利用函数图像研究函数性质,培养学生的观察能力;⑵通过函数奇偶性的判断,培养学生的数学思维能力.教学重点:⑴函数单调性与奇偶性的概念及其图像特征;⑵简单函数奇偶性的判定.教学难点:函数奇偶性的判断.(某函数单调性的判断)课时安排:2课时.3.3函数的实际应用举例知识目标:(1)理解分段函数的概念;(2)理解分段函数的图像;(3)了解实际问题中的分段函数问题.能力目标:(1)会求分段函数的定义域和分段函数在点处的函数值;(2)掌握分段函数的作图方法;(3)能建立简单实际问题的分段函数的关系式.教学重点:(1)分段函数的概念;(2)分段函数的图像.教学难点:(1)建立实际问题的分段函数关系;(2)分段函数的图像.课时安排:2课时.4.1实数指数幂(1)知识目标:⑴复习整数指数幂的知识;⑵了解n次根式的概念;⑶理解分数指数幂的定义.能力目标:⑴掌握根式与分数指数幂之间的转化;⑵会利用计算器求根式和分数指数幂的值;⑶培养计算工具使用技能.教学重点:分数指数幂的定义.教学难点:根式和分数指数幂的互化.课时安排:2课时.4.1实数指数幂(2)知识目标:⑴掌握实数指数幂的运算法则;⑵通过几个常见的幂函数,了解幂函数的图像特点.能力目标:⑴正确进行实数指数幂的运算;⑵培养学生的计算技能;⑶通过对幂函数图形的作图与观察,培养学生的计算工具使用能力与观察能力.教学重点:有理数指数幂的运算.教学难点:有理数指数幂的运算.课时安排:2课时.4.2指数函数知识目标:⑴理解指数函数的图像及性质;⑵了解指数模型,了解指数函数的应用.能力目标:⑴会画出指数函数的简图;⑵会判断指数函数的单调性;⑶了解指数函数在生活生产中的部分应用,从而培养学生分析与解决问题能力.教学重点:⑴指数函数的概念、图像和性质;⑵指数函数的应用实例.教学难点:指数函数的应用实例.课时安排:2课时.4.3对数知识目标:⑴理解对数的概念,理解常用对数和自然对数的概念;⑵掌握利用计算器求对数值的方法;⑶了解积、商、幂的对数.能力目标:⑴会进行指数式与对数式之间的互化;⑵会运用函数型计算器计算对数值;⑶培养计算工具的使用技能.教学重点:指数式与对数式的关系.教学难点:对数的概念.课时安排:2课时.4.4对数函数知识目标:⑴了解对数函数的图像及性质特征;⑵了解对数函数的实际应用.能力目标:⑴观察对数函数的图像,总结对数函数的性质,培养观察能力;⑵通过应用实例的介绍,培养学生数学思维能力和分析与解决问题能力.教学重点:对数函数的图像及性质.教学难点:对数函数的应用中实际问题的题意分析.课时安排:2课时.5.1角的概念推广知识目标:⑴了解角的概念推广的实际背景意义;⑵理解任意角、象限角、界限角、终边相同的角的概念.能力目标:(1)会判断角所在的象限;(2)会求指定范围内与已知角终边相同的角;(3)培养观察能力和计算技能.教学重点:终边相同角的概念.教学难点:终边相同角的表示和确定.课时安排:2课时.5.2弧度制知识目标:⑴理解弧度制的概念;⑵理解角度制与弧度制的换算关系.能力目标:(1)会进行角度制与弧度制的换算;(2)会利用计算器进行角度制与弧度制的换算;(3)培养学生的计算技能与计算工具使用技能.教学重点:弧度制的概念,弧度与角度的换算.教学难点:弧度制的概念.课时安排:2课时.5.3任意角的正弦函数、余弦函数和正切函数知识目标:⑴理解任意角的三角函数的定义及定义域;⑵理解三角函数在各象限的正负号;⑶掌握界限角的三角函数值.能力目标:⑴会利用定义求任意角的三角函数值;⑵会判断任意角三角函数的正负号;⑶培养学生的观察能力.教学重点:⑴任意角的三角函数的概念;⑵三角函数在各象限的符号;⑶特殊角的三角函数值.教学难点:任意角的三角函数值符号的确定.课时安排:2课时.5.4同角三角函数的基本关系知识目标:理解同角的三角函数基本关系式.能力目标:⑴已知一个三角函数值,会利用同角三角函数的基本关系式求其他的三角函数值;⑵会利用同角三角函数的基本关系式求三角式的值.教学重点:同角的三角函数基本关系式的应用.教学难点:应用平方关系求正弦或余弦值时,正负号的确定.课时安排:2课时.5.5诱导公式知识目标:了解“”、“”、“180°”的诱导公式.能力目标:(1)会利用简化公式将任意角的三角函数的转化为锐角的三角函数;(2)会利用计算器求任意角的三角函数值;(3)培养学生的数学思维能力及应用计算工具的能力.教学重点:三个诱导公式.教学难点:诱导公式的应用.课时安排:2课时.5.6三角函数的图像和性质知识目标:(1)理解正弦函数的图像和性质;(2)理解用“五点法”画正弦函数的简图的方法;(3)了解余弦函数的图像和性质.能力目标:(1)认识周期现象,以正弦函数、余弦函数为载体,理解周期函数;(2)会用“五点法”作出正弦函数、余弦函数的简图;(3)通过对照学习研究,使学生体验类比的方法,从而培养数学思维能力.教学重点:(1)正弦函数的图像及性质;(2)用“五点法”作出函数y=sin某在上的简图.教学难点:周期性的理解.课时安排:2课时.5.7已知三角函数值求角知识目标:(1)掌握利用计算器求角度的方法;(2)了解已知三角函数值,求指定范围内的角的方法.能力目标:(1)会利用计算器求角;(2)已知三角函数值会求指定范围内的角;(3)培养使用计算工具的技能.教学重点:已知三角函数值,利用计算器求角;利用诱导公式求出指定范围内的角.教学难点:已知三角函数值,利用计算器求指定范围内的角.。
教案 高教版《数学》(基础模块)——4.1有理数指数幂(2)

4.1有理数指数幂(2)——实数指数幂【教学目标】知识目标:1、掌握实数指数幂的运算法则;2、通过几个常见的幂函数,了解幂函数的图像特点。
能力目标:1、正确进行实数指数幂的运算;2、培养学生的计算技能;3、通过对幂函数图形的作图与观察,培养学生的计算工具使用能力与观察能力。
【教学重点】实数指数幂的运算法则,有理数指数幂的运算。
【教学难点】有理数指数幂的运算。
【教学设计】1、在复习整数指数幂的运算中,学习实数指数幂的运算;2、通过学生的动手计算,巩固知识,培养计算技能;3、通过“描点法”作图认识幂函数的图像,通过利用软件的大量作图,总结图像规律;4、通过知识应用巩固有理数指数幂的概念。
【课时安排】2课时。
(90分钟)【教学过程】一、实数指数幂 1、复习导入整数指数幂,当*n ∈N 时,na = ; 规定当0a ≠时,0a = ; n a -= ; 分数指数幂:mna = ;0a ≠时,m na-= 。
其中*m n n ∈N 、且>1。
当n 为奇数时,a ∈R ;当n 为偶数时,0a。
例1、将下列各根式写成分数指数幂:(2.例2、将下列各分数指数幂写成根式:(1)3465-;(2)232.3()2、扩展:整数指数幂的运算法则为: (1) m n a a ⋅= ; (2) ()nm a= ;(3) ()nab = 。
其中()m n ∈Ζ、运算法则同样适用于有理数指数幂的情况3、概念当p 、q 为有理数时,有p q p q a a a +⋅=; ()qp pq a a =; ()pp p ab a b =⋅运算法则成立的条件是,出现的每个有理数指数幂都有意义。
说明:可以证明,当p 、q 为实数时,上述指数幂运算法则也成立。
4、典型例题例1、计算下列各式的值:(1)130.125; (2分析 (1)题中的底为小数,需要首先将其化为分数,有利于运算法则的利用;(2)题中,首先要把根式化成分数指数幂,然后再进行化简与计算。
人教版中职数学4.1.1-2有理指数 (二)

求下列各式的值: 8 8; 33 ×3 ×3 √ √ √
3 6
3 5
2 5
8 ;
2 3 1 4
2 3
; (a b )3.
三、应用 例1 利用函数型计算器计算(精确到0.001).
(1)0.21.52;(2)3.14-2;(3)3.1 .
例2 利用函数型计算器计算函数值. 已知 f ( x ) = 2.71 x , 求:f (-3),f (-2) , f (-1) , f ( 1 ) , f ( 2 ) , f ( 3 )(精确到0.001).
我国农业科学家在研究某农作物的生长状况时, 得到该农作物生长时间 x 周(从第 1 周到第 12 周)与 植株高度 y cm 之间的关系: y=3
x 4
当该农作物生长了 4 周,8 周时, 植株高度分别是 3 cm,32 cm . 当该农作物生长了 1 周,5 周时, 植株的高度是多少呢?
一、根式 1.方根
一般地,若
x n = a( n > 1,n N ),
则 x 叫做 a 的 n 次方根.
例如: (1) 3 2 = 9 ,
则 3 是 9 的二次方根(平方根);
(-3) 2 = 9, 则 -3 也是 9 的二次方根(平方根); (2) (-5) 3 = -125, 则 -5 是 -125 的三次方根(立方根);
指数 指 数
对数
对数 4.1.1. a n = a×a×a×…×a a 0 = 1( a ≠ 0 ), a-n =
( n 个 a 连乘 )
1 ( a ≠ 0 ,n N+). an
2.运算法则 (1) a m a n = a m+n; (2)( a m ) n = a m n ; (3)( a b ) m = a m b m.
人教版中职数学基础上册《有理指数》2课时表格式教案

有理指数(一)【教学目标】1. 理解整数指数幂及其运算律,并会进行有关运算.2. 培养学生的观察、分析、归纳等逻辑思维能力.3. 培养学生勇于发现、勇于探索、勇于创新的精神;培养学生合作交流等良好品质.【教学重点】零指数幂、负整指数幂的定义.【教学难点】零指数幂及负整指数幂的定义过程,整数指数幂的运算.【教学方法】这节课主要采用问题解决法和分组教学法.在引入指数幂时,以在国际象棋棋盘上放米粒为导入素材,既体现数学的应用价值,也能引起学生的学习兴趣.从正整指数的运算法则中的a mm-n (m>n,a ≠ 0)a n=a这一法则出发,通过取消m>n的限制引入了零指数幂和负整指数幂的定义,从而把正整指数幂推广到整数指数幂.在本节教学中,要以取消m>n这一条件为出发点,让学生积极大胆地猜想,以此增强学生的参与意识,从而提高学生的学习兴趣.【教学过程】有理指数(二)【教学目标】1. 了解根式的概念和性质;理解分数指数幂的概念;掌握有理数指数幂的运算性质.2. 会对根式、分数指数幂进行互化.培养学生的观察、分析、归纳等逻辑思维能力.3. 培养学生用事物之间普遍联系的观点看问题.【教学重点】分数指数幂的概念以及分数指数幂的运算性质.【教学难点】对分数指数幂概念的理解.【教学方法】这节课主要采用问题解决教学法.在引入分数指数幂时,先讲方根的概念,根据方根的定义,得到根式具有的性质.在利用根式的运算性质对根式的化简过程中,引导学生注意发现并归纳其变形特点,进而由特殊情形归纳出一般规律.在对根式的性质进行练习以后,为了解决运算的合理性,引入了分数指数幂的概念,从而将指数幂推广到了有理数范围.在学生掌握了有理指数幂的运算性质后,将有理指数幂推广到实数指数幂.考虑到职校学生的实际情况,并没有给出严格的推证.【教学过程】。
最新中职数学基础模块上册教案:指数函数数学
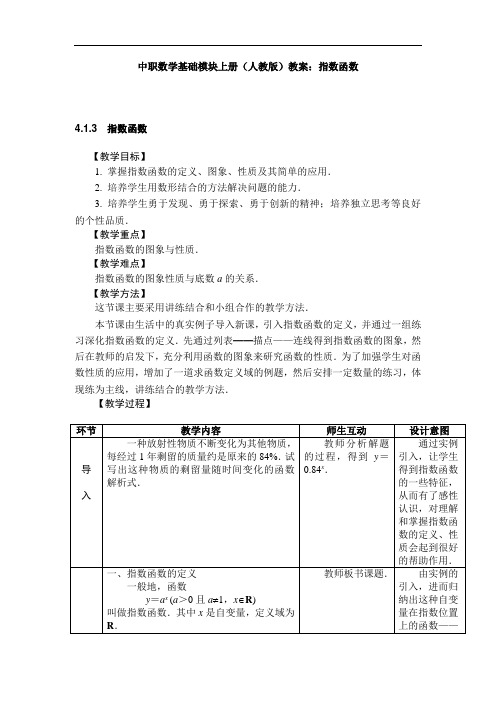
中职数学基础模块上册(人教版)教案:指数函数
4.1.3 指数函数
【教学目标】
1. 掌握指数函数的定义、图象、性质及其简单的应用.
2. 培养学生用数形结合的方法解决问题的能力.
3. 培养学生勇于发现、勇于探索、勇于创新的精神;培养独立思考等良好的个性品质.
【教学重点】
指数函数的图象与性质.
【教学难点】
指数函数的图象性质与底数a的关系.
【教学方法】
这节课主要采用讲练结合和小组合作的教学方法.
本节课由生活中的真实例子导入新课,引入指数函数的定义,并通过一组练习深化指数函数的定义.先通过列表——描点——连线得到指数函数的图象,然后在教师的启发下,充分利用函数的图象来研究函数的性质.为了加强学生对函数性质的应用,增加了一道求函数定义域的例题,然后安排一定数量的练习,体现练为主线,讲练结合的教学方法.
【教学过程】。
职教高中数学基础模块上册教案

职教高中数学基础模块上册教案学科:数学年级:高一教材版本:职教高中数学基础模块上册单元:基础数学概念教学目标:1. 了解基础数学概念的定义和性质;2. 掌握基础数学运算的方法;3. 能够应用基础数学知识解决实际问题。
教学重点:1. 数学基础概念的理解和掌握;2. 基础数学运算方法的学习和运用。
教学难点:1. 数学概念的抽象理解;2. 基础数学运算的灵活运用。
教学准备:1. 教材《职教高中数学基础模块上册》;2. 手绘板、教学PPT等教学工具;3. 课堂练习题、作业布置等辅助材料。
教学过程:一、导入(5分钟)教师引导学生回顾上节课学习内容,激发学生对数学的兴趣,引入本节课的话题。
二、讲解数学基础概念(15分钟)1. 教师讲解数学基础概念的定义和性质,例如整数、有理数等;2. 通过实例引导学生理解数学概念的抽象含义。
三、学习基础数学运算方法(20分钟)1. 教师讲解基础数学运算方法,包括加减乘除、分式运算等;2. 分步骤演示基础数学运算的解题方法,引导学生理解和掌握运算规则。
四、练习与讨论(15分钟)1. 分发练习题,让学生在课堂上独立完成;2. 学生之间互相交流讨论解题思路和方法;3. 教师及时指导学生解决问题,引导学生发现和分析解题中的问题。
五、作业布置(5分钟)布置课后作业,要求学生复习本节课所学内容,独立完成作业并做好错题订正。
六、课堂总结(5分钟)教师对本节课的重点难点进行总结,强调学生要掌握数学基础概念和运算方法,为下节课的学习做好准备。
教学反思:本节课注重引导学生深入理解数学基础概念,并通过实例演示和练习来提高学生的运算能力。
教学过程中要注意启发学生思考,激发学生对数学的兴趣,提高学生的数学学习积极性。
同时,要根据学生的实际情况调整教学策略,确保教学效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中职数学基础模块上册教案:有理指数(二)
4.1.1 有理指数(二)
【教学目标】
1. 了解根式的概念和性质;理解分数指数幂的概念;掌握有理数指数幂的运算性质.
2. 会对根式、分数指数幂进行互化.培养学生的观察、分析、归纳等逻辑思维能力.
3. 培养学生用事物之间普遍联系的观点看问题.
【教学重点】
分数指数幂的概念以及分数指数幂的运算性质.
【教学难点】
对分数指数幂概念的理解.
【教学方法】
这节课主要采用问题解决教学法.
在引入分数指数幂时,先讲方根的概念,根据方根的定义,得到根式具有的性质.在利用根式的运算性质对根式的化简过程中,引导学生注意发现并归纳其变形特点,进而由特殊情形归纳出一般规律.在对根式的性质进行练习以后,为了解决运算的合理性,引入了分数指数幂的概念,从而将指数幂推广到了有理数范围.在学生掌握了有理指数幂的运算性质后,将有理指数幂推广到实数指数幂.考虑到职校学生的实际情况,并没有给出严格的推证.
【教学过程】。
