全等三角形的判定SSS
11.2 三角形全等的判定(SSS)(含答案)

11.2 三角形全等的判定(SSS)题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
◆课堂测控测试点边边边1.如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF,∠A=•43°,求∠D的度数,下面是小红同学的求解过程,请你说明每一步的理由.解:因为BE=CF,所以BE+EC=CF+EC,即BC=EF.在△ABC与△DEF中,,,AB DEAC DFBC EF=⎧⎪=⎨⎪=⎩所以△ABC≌△DEF().所以∠D=∠A=43°().2.已知:如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE.◆课后测控3.如图,AC=BD,AB=DC,求证:∠B=∠C.4.已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.5.三月三放风筝,下图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你用所学知识给予证明.◆拓展测控6.有一块三角形的厚铁板(如图),根据实际生产需要,工人师傅要把∠MAN平分开,现在他手边只有一把尺子(没有刻度)和一根细绳,•你能帮助工人师傅想个办法吗?并说明你这样做的理由.答案:1.SSS 全等三角形对应角相等2.∵C是AB的中点,∴AC=BC.在△ACD与△CBE中,,,,AC CBAD CECD BE=⎧⎪=⎨⎪=⎩∴△ACD≌△CBE(SSS).[总结反思]三条边对应相等的两个三角形全等,•运用此结论可证明两个三角形全等.3.证明:在△ABD与△DCA中,,,,AB DCDB ACAD DA=⎧⎪=⎨⎪=⎩∴△ABD≌△DCA(SSS),∴∠B=∠C.[解题规律]证明线段相等或角相等时,常证明它们所在的两个三角形全等,本题中证明两个三角形全等已具备两个条件,运用公共边这个隐含条件是解题关键.4.∵AC=BD,∴AC+CB=BD+CB,即AB=CD.在△AMB和△CND中,,,,AM CNBM DNAB CD=⎧⎪=⎨⎪=⎩∴△AMB≌△CND(SSS).∴∠A=∠NCD,∴AM∥CN.[解题技巧]题目中条件AC=BD不能直接用来证明,可运用等式的性质变为AB=CD.5.证明:连结DH.在△DEH和△DFH中,,,.DE DFEH FHDH DH=⎧⎪=⎨⎪=⎩∴△DEH≌△DFH(SSS),∴∠DEH=∠DFH.[解题规律]连结EH即将原图形分成一对三角形,利用公共边运用SSS可得两个三角形全等.6.用绳子的一定长度在AM,AN边上截取AB=AC,再选取适当长度的绳子,将其对折,得绳子的中点D,把绳子的两端点固定在B,C两点,拽住绳子中点D,向外拉直BD和CD,•再在铁板上点出D的位置,作射线AD,则AD平分∠MAN.理由如下:如图,∵在△ABD和△ACD中,,,,AB ACBD CDAD AD=⎧⎪=⎨⎪=⎩∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD,即AD平分∠MAN.[解题技巧]这是一道实际应用问题,通过构造两个三角形全等将∠MAN平分,•解题关键是得到绳子的中点并拉直绳子,从而可知DB=DC.可以编辑的试卷(可以删除)This document is collected from the Internet, which is convenient for readers to use. If there is any infringement, please contact the author and delete it immediately.。
sss判定三角形全等定理

sss判定三角形全等定理
有两条边相等的三角形是等腰三角形;三边都相等的三角形是等边三角形,也叫正三
角形;有一个内角是直角的三角形叫做直角三角形。
其中,构成直角的两边叫做直角边,
直角边所对的边叫做斜边。
全等的条件:
1、两个三角形对应的'三条边成正比,两个三角形全系列等,缩写“边边边”或“sss"。
2、两个三角形对应的两边及其夹角相等,两个三角形全等,简称“边角边”或“sas”。
3、两个三角形对应的两角及其夹边成正比,两个三角形全系列等,缩写“角边角”
或“asa”。
4、两个三角形对应的两角及其一角的对边相等,两个三角形全等,简称“角角边”
或“aas”。
5、两个直角三角形对应的一条斜边和一条直角边成正比,两个直角三角形全系列等,缩写“直角边、斜边”或“hl”。
注意,证明三角形全等没有“ssa”或“边边角”的方法,即两边与其中一边的对角
相等无法证明这两个三角形全等,但从意义上来说,直角三角形的“hl”证明等同“ssa”。
全等三角形的判定(sss)

A
A’
B
C B’
C’
图一
图二
AB=A’B’
∠A=∠A’ ΔABC ≌ ∆A’ B’ C’ (SAS) AC=A’C’
A
A’
B
C
B’
C’
∠A=∠A’
AB=A’B’
ΔABC ≌ ∆A’ B’ C’
∠B=∠B’
(ASA)
A
A’
B
C
B’
C’
∠A=∠A’
∠B=∠B’ ΔABC ≌ ∆A’ B’ C’(AAS)
AD=AD(公共边)
∴ △ABD≌ACD(SAS)
总结 上题中应用了哪些性质及定理
性质一:等腰三角形的两底角相等 性质二:等腰三角形的中线、角平分线、高线互相重合。 定理三:在两个三角形中,如果有三条边相等,那么这两个三角形全等。 定理四:在两个三角形中,如果有两个角相等及一条边相等,那么这两个三角形 全等。 定理五:在两个三角形中,如果有两个角相等及所夹的边相等,那么这两个三角 形全等。 定理六:在两个三角形中,如果有两条边相等及所夹的角相等,那么这两个三角 形全等。
作业:课后习题
AC=A’C’
定理的引入 A
C
E
F
B
D
思考
已知:AC=DE AB=DF BC=FE 求证:△ABC≌ △DFE
定理的引入 A
C
D
已知:AC=DC AB=DB 求证:△ABC≌ △DBC
B
证明:连接AD, ∵AC=DC
∴∠CAD= ∠CDA
同理, ∠BAD= ∠BDA
∴ ∠BAC= ∠BDC
∵ AC=DC
答:图中有△ABE≌ACE,△BDE≌CDE △ABD≌ACD。
全等三角形的判定SSS
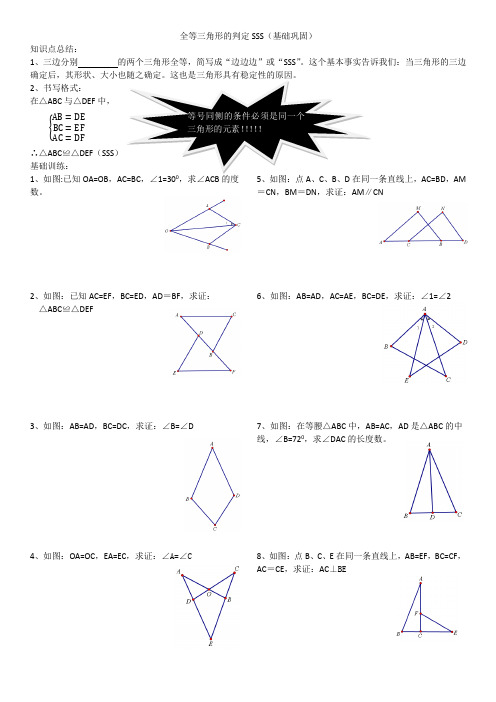
全等三角形的判定SSS (基础巩固)知识点总结:1、三边分别 的两个三角形全等,简写成“边边边”或“SSS ”。
这个基本事实告诉我们:当三角形的三边确定后,其形状、大小也随之确定。
这也是三角形具有稳定性的原因。
2、书写格式:在△ABC 与△DEF 中, {AB =DE BC =EF AC =DF∴△ABC ≌△DEF (SSS )基础训练:1、如图:已知OA=OB ,AC=BC ,∠1=300,求∠ACB 的度数。
2、如图:已知AC=EF ,BC=ED ,AD =BF ,求证: △ABC ≌△DEF3、如图:AB=AD ,BC=DC ,求证:∠B=∠D4、如图:OA=OC ,EA=EC ,求证:∠A=∠C5、如图:点A 、C 、B 、D 在同一条直线上,AC=BD ,AM =CN ,BM =DN ,求证:AM ∥CN6、如图:AB=AD ,AC=AE ,BC=DE ,求证:∠1=∠27、如图:在等腰△ABC 中,AB=AC ,AD 是△ABC 的中线,∠B=720,求∠DAC 的长度数。
8、如图:点B 、C 、E 在同一条直线上,AB=EF ,BC=CF ,AC =CE ,求证:AC ⊥BE等号同侧的条件必须是同一个三角形的元素!!!!!能力提升:1、如图:E在BC边上,AD=AB,AE=AC,DE=BC,求证:∠1=∠32、如图:已知△AOB≌△COD,△COE≌△AOF,求证:△BOF≌△DOE3、如图:AC与BD相交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF,求证:AE∥CF4、如图:AC=BD,AD=BC,AD与BC相交于点O,且CO=OD,过O点作△ABC的中线,交AB于点E,求证:DE⊥AB5、如图:已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠26、如图:在△ABC中,AB=AC,D是BC中点,E是AC上一点,且AE=AD,若∠EDC=180,求∠BAD的度数。
全等三角形的判定(SSS)说课稿

全等三角形的判定(SSS)第一课时一、教材分析:(一)本节内容在全书和章节的地位本节内容选自人教版初中数学八年级上册第十一章,本课是探索三角形全等条件的第一课时,是在学习了全等三角形的概念,全等三角形的性质后展开的。
对于全等三角形的研究,实际是平面几何对封闭的两个图形关系研究的第一步,它是两个三角形间最简单、最常见的关系,它不仅是下节课探索三角形全等其它条件的基础,还是证明线段相等、角相等的重要依据,同时也为今后探索直角三角形全等的条件以及三角形相似的条件提供很好的模式和方法。
因此,本节课的知识具有承前启后的作用,占有相当重要的地位。
(二)三维教案目标1.知识与能力目标因为是第一课时,本节课主要给学生讲解全等三角形的“SSS”判定公理,同时理解三角形的稳定性,能用三角形全等解决一些现实问题,熟悉掌握“SSS”|的判定方法,能够自主探索,动手操作,在过程中体会到自主学习索取知识的乐趣,从而启发学生学习数学的方式,为下节课打下基础。
2.过程与方法目标通过分解三角形的各个边和角,两个三角形做对比,用问题分解法求解,探索全等三角形的全等条件,经历认知探知过程,体会挖掘知识的过程。
通过两个三角形边与角的对比发现全等三角形的判定条件“SSS”,锻炼学生分析问题,解决问题的能力。
3.情感态度与价值观培养学生勇于探索、团结协作的精神,积累数学活动的经验。
(三)重点与难点1.教案难点认识三角形全等的发现过程以及边边边的辨析。
能够对运用三角形判定公理“SSS”解决三角形全等问题,对三角形其他定理的拓展与思考,了解三角形的稳定性。
2.教案重点利用性质和判定,关键是学会准确地找出两个全等三角形中的对应边与对应角。
准确理解“SSS”三角形判定的公理,规范书写全等三角形的证明;二、教法与学情分析1.教法分析数学是一门培养人的思维,发展人的思维的重要学科,因此在教案中,不仅要使学生知其然,而且还要使学生知其所以然。
针对初二年纪学生的认知结构和心理特征,和本节课的特色。
12.2.1三角形全等的判定(SSS)

C
• 例4.如图,AB=AD,BC=CD,求证: • (1)△ABC≌△ADC; (2)∠B=∠D.
课 本 P8 工人师傅常用角尺平分一个任意角. 做法如下:如图, AOB是一个任意角,在边OA,OB上分别取OM=ON,移动 角尺,使角尺两边相同的刻度分别与M,N重合. 过角尺顶点 C的射线OC便是AOB的平分线.为什么?
画法:1.画线段B'C'=BC;
2. 分别以B'、C'为圆心, 线段AB、AC为半径画弧, 两弧交于点A ';
3.连接线段A'B'、A'C' .
' ' 则ΔA'BC 为所求作的三角形.
你能得出什 么结论?
三边对应相等的两个三角形全等,简 写为“边边边”或“SSS”。 用上面的结论可以判定两个三角形全等. 判断两个三角形全等的推理过程,叫做证明 三角形全等.
O
C
A
应用所学,例题解析
用尺规作一个角等于已知角. 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 作法: (2)画一条射线O′A′,以点O′为圆心,OC 长为半 径画弧,交O′A′于点C′; B D
O
C
A
O′
C′
A′
应用所学,例题解析
用尺规作一个角等于已知角. 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 作法: (3)以点C′为圆心,CD 长为半径画弧,与第2 步中 所画的弧交于点D′; B D′ D
探究活动
你如 能果 说给 出出 有三 哪个 几条 种件 可画 能三 的角 情形 况, ?
三个条件呢?
1. 三个角;
2. 三条边; 3. 两边一角;
4. 两角一边。
【数学课件】三角形全等的判定(SSS)

如 何 用 符 号 语 言 来 表 达 呢
A
D
B
C
E
F
在△ABC与△DEF中 AB=DE AC=DF BC=EF ∴△ABC≌△DEF(SSS)
思考:你能 用“边边边” 解释三角形 具有稳定性 吗?
例1 已知:如图,AB=AD,BC=CD, 求证:△ABC≌ △ADC
A B D
证明:在△ABC和△ADC中 AB=AD (已知) BC=CD (已知) AC = AC (公共边)
失 败
(2)一个角 (1)两边 4cm
6cm 4cm 6cm
2.给定两个条件: (2)一边一角
30º 6cm
失 败
30º 6cm
(3)两角
30º 20º 30º 20º
俗话说:失败是成功之母! 我们继续探究: 千万别泄气哦! 探究二
(1)三边 给定三个条件: (2)两边一角 (3)一边两角 (4)三角 [动手画一画]
画出一个三角形,使它的三边长分别为3cm、 4cm、6cm , 把你画的三角形与小组内画的进 行比较,它们一定全等吗?
画法: 1.画线段AB=3㎝; 2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两 弧交于点C; 3. 连接线段AC、BC.
结论:三边对应相等的两个三角形全等. 可ቤተ መጻሕፍቲ ባይዱ写为”边边边”或SSS
课堂小测
2.如图,已知 AB DC,AC DB .求证: △ABC≌△DCB.
A
D
O B C
1.课本P15习题11.2的第1、2题(一号本)
能力提升题:
课本16页第9题(一号本)
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
三角形全等的判定(SSS)

A D B
C
E
F
证明三角形全等的步骤
1、准备条件:证全等时要用的间接条件
要先证好 2、证明三角形全等书写三步骤: (1)写出在哪两个三角形中
(2)摆出三个条件用大括号括起来
(3)写出全等结论
证:
A
B
E
D
C
A
D
B
E
C
F
A D 证:∵BE=CF ∴BE+EC=CF+EC 即 BC=EF B C E 在△ABC和△FDE中 AB=DE 欲证角相等,转化 BC=EF 为证三角形全等 AC=DF ∴△ABC ≌△DEF(SSS) ∴∠A=∠D(全等三角形对应角相 等)
8cm
8cm
满足下列条件的两个三角形是否一定 全等 (3)三个条件 三角 三边 两边一角 两角一边
画法
B
A
C
这个结果反映了什么规律
三边对应相等的两个三角形全等
(可以简写为“边边边”或“SSS”)
用数学语言表述:
A B D
C
E
F
A
B
D
C
证: A
B
D
C
A D
C
B
F
E
A D B
C
E
F
证:
F
小结
1、知道三角形三条边的长度怎样画三角形 2、三边对应相等的两个三角形全等 (边边边或SSS) (1)准备条件 3、书写格式: (2)三角形全等书写的三步骤
4、通过证明三角形全等证明三角形边相等角
相等
P103
复习巩固 1、 2
13.2三角形全 等的判定
1、全等三角形的定义: 能够完全重合的两个三角形叫做全等 三角形 对应顶点 对应边 对应角 2、全等三角形有什么性质? A B C E D F
