【配套K12】新版高中数学人教A版必修4习题：第三章三角恒等变换 3.2.1
新版高中数学人教A版必修4习题：第三章三角恒等变换 3-1-3 含解析-2019最新整理
答案:D
4若x
A
解析:当x,cos2x-sin2x=cos2x
=co
答案:D
5化
A.si
C.2si
答案:B
解析:原
答案:
7在△ABC中,cos A
解析:∵0<A<π,∴sinA
∴sin2A=2sinAcosA
cos2A=2cos2A-1=22A
答案:
8已知cos 2θ
解析:cos4θ+sin4θ=(cos2θ+sin2θ)2-2sin2θcos2θ
=1
=1
答案:
9已知函数f(x)=sin2x+2sin xcos x+3cos2x,x∈R,求f(x)的周期及值域.
解f(x)2x
=2+sin2x+cos2x=2
∴函数f(x)的周期为π,值域为[2
10在△ABC中,若sin Asin B=cos△ABC的形状.
解sinAsinB=cos
即2sinAsinB+cos(A+B)=1,
(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.
解(1)由|a|2=x)2+sin2x=4sin2x,
|b|2=cos2x+sin2x=1,
及|a|=|b|,得4sin2x=1.
又x∈sinx
所以x
(2)f(x)=a·bx·cosx+sin2x
2x2x
当x,si1.
∴sin10°sin30°sin50°sin70°
答案:
7已知函数f(x)=sin x-
(1)求f(x)的最小正周期;
(2)求f(x)在区
高中数学(人教A版,必修四) 第三章 三角恒等变换 3.2 课时作业(含答案)
§3.2 简单的三角恒等变换 课时目标 1.了解半角公式及推导过程.2.能利用两角和与差的公式进行简单的三角恒等变换.3.了解三角变换在解数学问题时所起的作用，进一步体会三角变换的规律．1．半角公式(1)S α2：sin α2＝____________________； (2)C α2：cos α2＝____________________________； (3)T α2：tan α2＝______________(无理形式)＝________________＝______________(有理形式)． 2．辅助角公式使a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)成立时，cos φ＝__________________，sin φ＝______，其中φ称为辅助角，它的终边所在象限由__________决定．一、选择题1．已知180°<α<360°，则cos α2的值等于( ) A ．－1－cos α2 B. 1－cos α2C ．－1＋cos α2 D. 1＋cos α22．函数y ＝sin ⎝⎛⎭⎫x ＋π3＋sin ⎝⎛⎭⎫x －π3的最大值是( ) A ．2 B ．1 C.12D. 3 3．函数f (x )＝sin x －cos x ，x ∈⎣⎡⎦⎤0，π2的最小值为( ) A ．－2 B ．－ 3 C ．－ 2 D ．－14．使函数f (x )＝sin(2x ＋θ)＋3cos(2x ＋θ)为奇函数的θ的一个值是( )A.π6B.π3C.π2D.2π35．函数f (x )＝sin x －3cos x (x ∈[－π，0])的单调递增区间是( )A.⎣⎡⎦⎤－π，－5π6B.⎣⎡⎦⎤－5π6，－π6 C.⎣⎡⎦⎤－π3，0 D.⎣⎡⎦⎤－π6，0 6．若cos α＝－45，α是第三象限的角，则1＋tan α21－tan α2等于( ) A ．－1 B.1 C ．2 D ．－27．函数f (x )＝sin(2x －π4)－22sin 2x 的最小正周期是______． 8．已知等腰三角形底角的余弦值为23，则顶角的正弦值是________． 9．已知等腰三角形顶角的余弦值为45，则底角的正切值为________． 10.2002年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成一个大正方形(如图所示)．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么cos 2θ的值等于____．三、解答题11．已知函数f (x )＝3sin ⎝⎛⎭⎫2x －π6＋2sin 2⎝⎛⎭⎫x －π12 (x ∈R )． (1)求函数f (x )的最小正周期；(2)求使函数f (x )取得最大值的x 的集合．12．已知向量m ＝(cos θ，sin θ)和n ＝(2－sin θ，cos θ)，θ∈(π，2π)，且|m ＋n |＝825，求cos ⎝⎛⎭⎫θ2＋π8的值．能力提升13．当y ＝2cos x －3sin x 取得最大值时，tan x 的值是( )A.32 B ．－32C.13 D ．4 14．求函数f (x )＝3sin(x ＋20°)＋5sin(x ＋80°)的最大值．§3.2 简单的三角恒等变换知识梳理1．(1)± 1－cos α2 (2)± 1＋cos α2(3)± 1－cos α1＋cos α sin α1＋cos α1－cos αsin α 2.a a 2＋b 2 b a 2＋b 2点(a ，b ) 作业设计1．C2．B [y ＝2sin x cos π3＝sin x ．] 3．D [f (x )＝2sin ⎝⎛⎭⎫x －π4，x ∈⎣⎡⎦⎤0，π2. ∵－π4≤x －π4≤π4， ∴f (x )min ＝2sin ⎝⎛⎭⎫－π4＝－1.] 4．D [f (x )＝sin(2x ＋θ)＋3cos(2x ＋θ)＝2sin ⎝⎛⎭⎫2x ＋π3＋θ. 当θ＝23π时，f (x )＝2sin(2x ＋π)＝－2sin 2x .] 5．D [f (x )＝2sin ⎝⎛⎭⎫x －π3，f (x )的单调递增区间为⎣⎡⎦⎤2k π－π6，2k π＋56π (k ∈Z )， 令k ＝0得增区间为⎣⎡⎦⎤－π6，56π.] 6．A [∵α是第三象限角，cos α＝－45， ∴sin α＝－35. ∴1＋tan α21－tan α2＝1＋sin α2cos α21－sin α2cos α2＝cos α2＋sin α2cos α2－sin α2＝cos α2＋sin α2cos α2－sin α2·cos α2＋sin α2cos α2＋sin α2＝1＋sin αcos α＝1－35－45＝－12.] 7．π解析 f (x )＝22sin 2x －22cos 2x －2(1－cos 2x )＝22sin 2x ＋22cos 2x － 2 ＝sin(2x ＋π4)－2，∴T ＝2π2＝π. 8.459解析 设α为该等腰三角形的一底角，则cos α＝23，顶角为180°－2α. ∴sin(180°－2α)＝sin 2α＝2sin αcos α＝21－⎝⎛⎭⎫232·23＝459. 9．3解析 设该等腰三角形的顶角为α，则cos α＝45， 底角大小为12(180°－α)．∴tan ⎣⎡⎦⎤12(180°－α)＝tan ⎝⎛⎭⎫90°－α2＝1tan α2＝1＋cos αsin α＝1＋4535＝3. 10.725解析 由题意，5cos θ－5sin θ＝1，θ∈⎝⎛⎭⎫0，π4. ∴cos θ－sin θ＝15. 由(cos θ＋sin θ)2＋(cos θ－sin θ)2＝2.∴cos θ＋sin θ＝75. ∴cos 2θ＝cos 2 θ－sin 2 θ＝(cos θ＋sin θ)(cos θ－sin θ)＝725. 11．解 (1)∵f (x )＝3sin2⎝⎛⎭⎫x －π12＋1－cos2⎝⎛⎭⎫x －π12 ＝2⎣⎡⎦⎤32sin2⎝⎛⎭⎫x －π12－12cos2⎝⎛⎭⎫x －π12＋1 ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π12－π6＋1 ＝2sin ⎝⎛⎭⎫2x －π3＋1，∴T ＝2π2＝π. (2)当f (x )取得最大值时，sin ⎝⎛⎭⎫2x －π3＝1， 有2x －π3＝2k π＋π2， 即x ＝k π＋5π12(k ∈Z )， ∴所求x 的集合为{x |x ＝k π＋5π12，k ∈Z }． 12．解 m ＋n ＝(cos θ－sin θ＋2，cos θ＋sin θ)， |m ＋n |＝(cos θ－sin θ＋2)2＋(cos θ＋sin θ)2＝4＋22(cos θ－sin θ)＝4＋4cos ⎝⎛⎭⎫θ＋π4 ＝21＋cos ⎝⎛⎭⎫θ＋π4. 由已知|m ＋n |＝825，得cos ⎝⎛⎭⎫θ＋π4＝725. 又cos ⎝⎛⎭⎫θ＋π4＝2cos 2⎝⎛⎭⎫θ2＋π8－1， 所以cos 2⎝⎛⎭⎫θ2＋π8＝1625.∵π<θ<2π，∴5π8<θ2＋π8<9π8. ∴cos ⎝⎛⎭⎫θ2＋π8<0.∴cos ⎝⎛⎭⎫θ2＋π8＝－45. 13．B [y ＝2cos x －3sin x ＝13⎝⎛⎭⎫213cos x －313sin x ＝13(sin φcos x －cos φsin x )＝13sin(φ－x )，当sin(φ－x )＝1，φ－x ＝2k π＋π2时，y 取到最大值． ∴φ＝2k π＋π2＋x ，(k ∈Z ) ∴sin φ＝cos x ，cos φ＝－sin x ，∴cos x ＝sin φ＝213，sin x ＝－cos φ＝－313. ∴tan x ＝－32.] 14．解 3sin(x ＋20°)＋5sin(x ＋80°)＝3sin(x ＋20°)＋5sin(x ＋20°)cos 60°＋5cos(x ＋20°)sin 60°＝112sin(x ＋20°)＋532cos(x ＋20°)＝⎝⎛⎭⎫1122＋⎝⎛⎭⎫5322sin(x ＋20°＋φ)＝7sin ()x ＋20°＋φ 其中cos φ＝1114，sin φ＝5314.所以f (x )max ＝7.。
【配套K12】高中数学第三章三角恒等变换3.2倍角公式和半角公式3.2.2半角的正弦余弦和正切课堂导
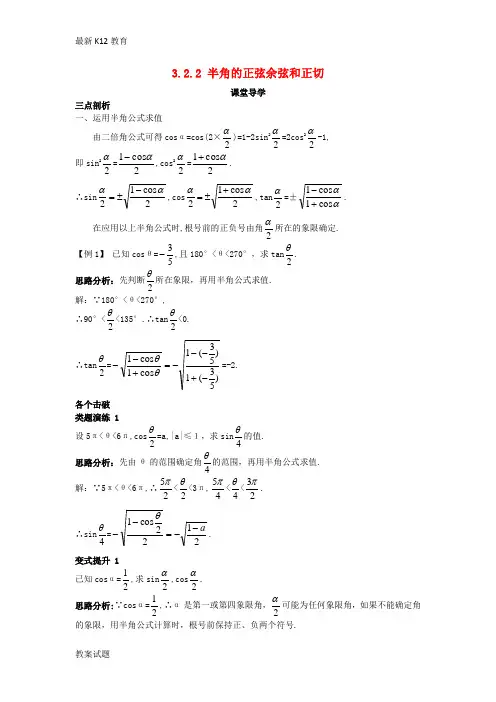
3.2.2 半角的正弦余弦和正切课堂导学三点剖析一、运用半角公式求值由二倍角公式可得cos α=cos(2×2α)=1-2sin 22α=2cos 22α-1, 即sin 22α=2cos 1α-,cos 22α=2cos 1α+. ∴sin 2cos 12αα-±=,cos 2cos 12αα+±=,tan 2α=±ααcos 1cos 1+-. 在应用以上半角公式时,根号前的正负号由角2α所在的象限确定. 【例1】 已知cos θ=53-,且180°<θ<270°，求tan 2θ. 思路分析：先判断2θ所在象限，再用半角公式求值. 解：∵180°<θ<270°, ∴90°<2θ<135°.∴tan 2θ<0. ∴tan 2θ=)53(1)53(1cos 1cos 1-+---=+--θθ=-2. 各个击破类题演练 1设5π<θ<6π,cos2θ=a,|a|≤１，求sin 4θ的值. 思路分析：先由θ的范围确定角4θ的范围，再用半角公式求值. 解：∵5π<θ<6π,∴25π<2θ<3π,45π<4θ<23π. ∴sin 4θ=2122cos 1a --=--θ. 变式提升 1已知cos α=21,求sin 2α,cos 2α. 思路分析:∵cos α=21,∴α是第一或第四象限角，2α可能为任何象限角，如果不能确定角的象限，用半角公式计算时，根号前保持正、负两个符号.解:sin 2α=±22112cos 1-±=-α=±21. cos 2α=±2322112cos 1±=+±=+α. 二、运用公式化简三角函数式在三角恒等变形中,所涉及的三角公式要求做到灵活运用,既要会正用,又要会逆用,更要会变用.特别要注意根号前正负号的选择,要由2α所在的象限来确定. 【例2】 若23π<α<2π,化简:α2cos 21212121++. 思路分析:在逐层去根号时,要根据角的范围确定被开方数的符号. 解：∵23π<α<2π,∴43π<2α<π. ∴原式=αααcos 2121cos 212122cos 121212+=+=++ 2cos )cos 1(212αα=+==-cos 2α. 类题演练 2化简:8cos 228sin 12+=+等于( )A.2sin4B.2sin4-4cos4C.-2sin4-4cos4D.4cos4-2sin4解析:原式=)14cos 2(22)4cos 4(sin 222-+++-2(sin4+cos4)-2cos4=-2sin4-4cos4.答案:C变式提升 2 化简:cos α·cos2α·cos 22α·…·cos 12-n α. 解:原式=1112sin 22sin 22cos 2cos cos ---∙∙∙∙n n n ααααα 12222sin 22sin 2cos 2cos 2cos cos ---∙∙∙∙∙=n n n αααααα=11112322sin 22sin 2sin 2sin cos 2sin 22sin 2cos 2coscos -----=∙∙=∙∙∙∙n n n n n n αααααααααα .。
高中数学第三章三角恒等变换3.2简单的三角恒等变换课后习题新人教A版必修4(2021年整理)
2018-2019学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换课后习题新人教A版必修4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换课后习题新人教A版必修4）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年高中数学第三章三角恒等变换 3.2 简单的三角恒等变换课后习题新人教A 版必修4的全部内容。
3。
2简单的三角恒等变换课后篇巩固探究1。
cos2的值为（)A.B。
C.D。
解析cos2.答案B2.已知α为第一象限角,且tan α=,则sin 的值为（）A。
B.—C。
± D。
解析因为α为第一象限角，且tan α=，所以cos α=，而是第一或第三象限角.当是第一象限角时，sin ；当是第三象限角时,sin =—=-,故sin =±.答案C3.若函数f(x）=(1+tan x）cos x，则f=（)A。
B.-C。
1 D.解析∵f(x）=cos x=cos x+sin x=2sin,∴f=2sin=2sin.答案D4。
设a=cos 7°+sin 7°,b=,c=,则有(）A.b〉a>c B。
a〉b>c C。
a〉c>b D.c>b>a解析因为a=cos 7°+sin 7°=sin 30°·cos 7°+cos 30°·sin 7°=sin 37°，b==tan 38°,c==sin 36°,又tan 38°〉sin 38°>sin 37°>sin 36°.所以b〉a〉c.答案A5。
高中数学必修4第3章课后习题解答
新课程标准数学必修4第三章课后习题解答（第1页共12页）新课程标准数学必修4第三章课后习题解答第三章三角恒等变换3．1两角和与差的正弦、余弦和正切公式练习（P127）1、cos()coscossinsin0cos 1sin sin222.cos(2)cos2cos sin2sin 1cos0sincos .2、解：由3cos ,(,)52，得2234sin1cos1()55；所以23242cos()coscos sinsin()444252510.3、解：由15sin17，是第二象限角，得22158cos1sin1()1717；所以811538153cos()cos cossin sin33317217234.4、解：由23sin ,(,)32，得2225cos1sin1()33；又由33cos,(,2)42，得2237sin1cos 1()44.所以35723527cos()cos cos sin sin ()()()434312.练习（P131）1、（1）624；（2）624；（3）624；（4）23.2、解：由3cos,(,)52，得2234sin1cos1()55；所以4133433sin()sin coscos sin()333525210.3、解：由12sin13，是第三象限角，得22125cos1sin1()1313；所以351125312cos()coscos sinsin ()()66621321326.4、解：tantan314tan()241311tantan4.5、（1）1；（2）12；（3）1；（4）32；新课程标准数学必修4第三章课后习题解答（第2页共12页）（5）原式=1(cos34cos26sin34sin 26)cos(3426)cos602；（6）原式=sin 20cos70cos20sin 70(sin 20cos70cos20sin 70)sin 901.6、（1）原式=cos cos sinsin cos()333x xx ；（2）原式=312(sin cos )2(sin coscos sin)2sin()22666x x x x x ；（3）原式=222(sin cos )2(sin cos cos sin )2sin()22444x x x x x；（4）原式=1322(cos sin )22(coscos sinsin )22cos()22333x x x x x .7、解：由已知得3sin()cos cos()sin5，即3sin[()]5，3sin()5所以3sin 5.又是第三象限角，于是2234cos1sin 1()55.因此555324272sin()sincoscos sin()()()()444525210.练习（P135）1、解：因为812，所以382又由4cos85，得243sin 1()855，3sin 385tan 484cos 85所以3424sinsin(2)2sin cos2()()488855252222437coscos(2)cossin()()488855252232tan23162484tantan(2)3482771tan1()842、解：由3sin()5，得3sin5，所以222316cos1sin1()525所以2221637cos2cos sin()255253、解：由sin 2sin且sin 0可得1cos2，又由(,)2，得2213sin 1cos1()22，所以sin 3tan (2)3cos2.新课程标准数学必修4第三章课后习题解答（第3页共12页）4、解：由1tan23，得22tan 11tan3.所以2tan6tan 10，所以tan 3105、（1）11sin15cos15sin 3024；（2）222cossincos 8842；（3）原式=212tan22.511tan4521tan 22.522；（4）原式=2cos452.习题3.1A 组（P137）1、（1）333cos()cos cos sin sin 0cos (1)sin sin 222；（2）333sin()sincoscossin1cos 0sincos222；（3）cos()cos cos sin sin 1cos 0sin cos ；（4）sin()sin coscos sin0cos(1)sinsin .2、解：由3cos,05，得2234sin1cos1()55，所以4331433cos()cos cossin sin666525210.3、解：由2sin,(,)32，得2225cos 1sin1()33，又由33cos ,(,)42，得2237sin1cos 1()44，所以53273527cos()cos cos sin sin ()()343412.4、解：由1cos7，是锐角，得22143sin1cos1()77因为,是锐角，所以(0,)，又因为11cos()14，所以221153sin()1cos ()1()1414所以coscos[()]cos()cos sin()sin11153431()14714725、解：由60150，得9030180又由3sin(30)5，得2234cos(30)1sin (30)1()55所以coscos[(30)30]cos(30)cos30sin(30)sin 30新课程标准数学必修4第三章课后习题解答（第4页共12页）43314335252106、（1）624；（2）264；（3）23.7、解：由2sin ,(,)32，得2225cos 1sin1()33.又由3cos 4，是第三象限角，得2237sin1cos 1()44.所以cos()cos cos sin sin 5327()()3434352712sin()sin cos cos sin 2357()()()3434635128、解：∵53sin ,cos 135AB且,A B 为ABC 的内角∴0,02AB，124cos ,sin 135AB当12cos 13A时，sin()sin cos cos sin A B A B A B5312433()013513565A B ，不合题意，舍去∴124cos ,sin 135A B∴cos cos()(cos cos sin sin )CA B A B A B 1235416()135135659、解：由3sin,(,)52，得2234cos 1sin1()55.∴sin 353tan()cos544.∴31tan tan 242tan()311tantan111()42.新课程标准数学必修4第三章课后习题解答（第5页共12页）31tan tan 42tan()2311tantan1()42.10、解：∵tan ,tan是22370xx 的两个实数根.∴3tantan2，7tantan2.∴3tantan 12tan()71tantan31()2.11、解：∵tan()3,tan()5∴tan()tan()tan 2tan[()()]1tan()tan()3541357tan()tan()tan2tan[()()]1tan()tan()351135812、解：∵::2:3:6BD DC AD∴11tan,tan32BD DC ADAD ∴tantan tan tan()1tan tan BAC1132111132又∵0180BAC ，∴45BAC 13、（1）65sin()6x；（2）3sin()3x ；（3）2sin()26x ；（4）27sin()212x ；（5）22；（6）12；（7）sin()；（8）cos()；（9）3；（10）tan().14、解：由sin0.8,(0,)2，得22cos 1sin10.80.6∴sin 22sin cos 20.80.60.962222cos2cossin0.60.80.2815、解：由3cos,1802703，得2236sin1cos 1()33∴6322sin 22sin cos 2()()3332222361cos2cossin()()333sin 222tan2(3)22cos2316、解：设5sin sin 13BC，且090B，所以12cos 13B.βαDACB（第12题）新课程标准数学必修4第三章课后习题解答（第6页共12页）∴512120sin sin(1802)sin 22sin cos 21313169A B B B B2222125119cos cos(1802)cos2(cos sin )(()())1313169A B BB B sin 120169120tan ()cos 169119119A AA17、解：22122tan33tan 211tan41()3，13tan tan274tan(2)1131tan tan 2174.18、解：1cos()cos sin()sin 31cos[()]3，即1cos 3又3(,2)2，所以22122sin1cos 1()33∴22142sin 22sin cos 2()33922221227cos2cossin()()339∴72422728cos(2)cos2cossin2sin()44492921819、（1）1sin 2；（2）cos2；（3）1sin 44x ；（4）tan2.习题3.1B 组（P138）1、略.2、解：∵tan ,tan A B 是x 的方程2(1)10xp x ，即210x px p 的两个实根∴tan tan A B p ，tan tan 1A B p ∴tan tan[()]tan()CAB A B tan tan 11tan tan 1(1)ABp A Bp 由于0C ，所以34C.3、反应一般的规律的等式是（表述形式不唯一）223sincos (30)sin cos(30)4（证明略）本题是开放型问题，反映一般规律的等式的表述形式还可以是：223sin (30)cossin(30)cos 4223sin (15)cos (15)sin(15)cos(15)4223sincossin cos4，其中30，等等思考过程要求从角，三角函数种类，式子结构形式三个方面寻找共同特点，从而作出归纳.对认识三角函数式特点有帮助，证明过程也会促进推理能力、运算能力的提高.4、因为12PAPP ，则2222(cos()1)sin ()(cos cos )(sin sin )新课程标准数学必修4第三章课后习题解答（第7页共12页）即22cos()22cos cos 2sin sin所以cos()cos cossin sin3．2简单的三角恒等变换练习（P142）1、略.2、略.3、略.4、（1）1sin 42y x .最小正周期为2，递增区间为[,],8282k k kZ ，最大值为12；（2）cos 2y x.最小正周期为2，递增区间为[2,22],k k k Z ，最大值为3；（3）2sin(4)3yx.最小正周期为2，递增区间为5[,],242242kk kZ ，最大值为 2.习题3.2A 组（P143）1、（1）略；（2）提示：左式通分后分子分母同乘以2；（3）略；（4）提示：用22sincos代替1，用2sin cos 代替sin 2；（5）略；（6）提示：用22cos 代替1cos2；（7）提示：用22sin 代替1cos2，用22cos 代替1cos2；（8）略.2、由已知可有1sincoscos sin2……①，1sin coscos sin3……②（1）②×3－①×2可得sin cos 5cos sin（2）把（1）所得的两边同除以cos cos 得tan 5tan注意：这里cos cos0隐含与①、②之中3、由已知可解得1tan2.于是2212()2tan 42tan211tan31()21tantan1142tan()1431tantan1()142∴tan24tan()44、由已知可解得sinx ，cos y，于是2222sincos 1xy.5、()2sin(4)3f x x，最小正周期是2，递减区间为7[,],242242k k kZ .习题3.2B 组（P143）1、略.2、由于762790，所以sin 76sin(9014)cos14m新课程标准数学必修4第三章课后习题解答（第8页共12页）即22cos 71m ，得1cos72m 3、设存在锐角,使223，所以23，tan()32，又tantan 232，又因为tantan2tan()21tan tan2，所以tantan tan()(1tantan )33222由此可解得tan 1，4，所以6.经检验6，4是符合题意的两锐角.4、线段AB 的中点M 的坐标为11((cos cos ),(sinsin ))22.过M 作1MM 垂直于x 轴，交x 轴于1M ，111()()22MOM .在Rt OMA 中，coscos22OMOA .在1Rt OM M 中，11cos cos cos 22OM OM MOM ，11sin sincos22M MOM MOM .于是有1(cos cos )cos cos 222，1(sin sin )sin cos2225、当2x时，22()sin cos 1f ；当4x时，4422222()sin cos(sincos )2sincosf 211sin 22，此时有1()12f ≤≤；当6x 时，662232222()sincos(sincos)3sincos(sincos)f 231sin 24，此时有1()14f ≤≤；由此猜想，当2,x k k N 时，11()12k f ≤≤6、（1）345(sin cos )5sin()55yxx x，其中34cos,sin55所以，y 的最大值为5，最小值为﹣5；（第4题）新课程标准数学必修4第三章课后习题解答（第9页共12页）（2）22sin()yab x，其中2222cos,sina b abab所以，y 的最大值为22ab ，最小值为22ab ；第三章复习参考题A 组（P146）1、1665.提示：()2、5665.提示：5sin()sin[()]sin[()()]443、1.4、（1）提示：把公式tantantan()1tan tan变形；（2）3；（3）2；（4）3.提示：利用（1）的恒等式.5、（1）原式=cos103sin104sin(3010)4sin10cos10sin 20；（2）原式=sin10sin103cos10sin 40(3)sin 40cos10cos10=2sin 40cos40sin801cos10cos10；（3）原式=3sin 203sin 20cos20tan70cos10(1)tan70cos10cos20cos20=sin 702sin10sin 20cos101cos70cos20cos70；（4）原式=3sin10cos103sin10sin50(1)sin 50cos10cos102cos50sin100sin501cos10cos106、（1）95；（2）2425；（3）223.提示：4422222sincos(sincos)2sincos；（4）1725.7、由已知可求得2cos cos 5，1sin sin5，于是sin sin 1tan tancos cos2.8、（1）左边=222cos 214cos232(cos 22cos 21)22242(cos21)2(2cos )8cos=右边（2）左边=2222sincos2sincos (sincos )2cos 2sin cos 2cos (cos sin )新课程标准数学必修4第三章课后习题解答（第10页共12页）（第12（2）题）sincos 11tan2cos 22=右边（3）左边=sin(2)2cos()sin sin[()]2cos()sinsin2cos (cos sin )sin()coscos()sinsinsinsin=右边（4）左边=222234cos 22cos 212(cos 22cos 21)34cos 22cos 212(cos 22cos 21)A A A A A A A A 2224222(1cos2)(2sin )tan (1cos2)(2cos )A A A A A =右边9、（1）1sin 21cos2sin 2cos222sin(2)24y x xx x x递减区间为5[,],88k k kZ （2）最大值为22，最小值为22.10、2222()(cos sin )(cos sin )2sin cos cos2sin 22cos(2)4f x x x x x x xx x x（1）最小正周期是；（2）由[0,]2x 得52[,]444x，所以当24x ，即38x时，()f x 的最小值为2.()f x 取最小值时x 的集合为3{}8.11、2()2sin 2sin cos 1cos2sin 22sin(2)14f x xx xx xx（1）最小正周期是，最大值为21；（2）()f x 在[,]22上的图象如右图：12、()3sin cos 2sin()6f x xxa xa .（1）由21a 得1a ；（2）2{22,}3x k x k kZ ≤≤.13、如图，设ABD ，则CAE ，2sin h AB，1cos h AC所以1212sin 2ABCh h S AB AC，(0)2当22，即4时，ABCS的最小值为12h h .第三章复习参考题B 组（P147）h 1h 2l 2l 1BDE AC（第13题）新课程标准数学必修4第三章课后习题解答（第11页共12页）1、解法一：由221sin cos 5sincos1，及0≤≤，可解得4sin5，13cos sin 55，所以24sin 225，7cos225，312sin(2)sin 2cos cos2sin 44450.解法二：由1sincos5得21(sincos )25，24sin 225，所以249cos 2625.又由1sin cos5，得2sin()410.因为[0,]，所以3[,]444.而当[,0]44时，sin()04≤；当3[,]444时，22sin()4210≥.所以(0,)44，即(,)42所以2(,)2，7cos225.312sin(2)4502、把1coscos 2两边分别平方得221coscos 2cos cos 4把1sinsin3两边分别平方得221sin sin2sin sin9把所得两式相加，得1322(cos cos sin sin )36，即1322cos()36，所以59cos()723、由43sin()sin 35可得3343sincos225，4sin()65.又02，所以366，于是3cos()65.所以334cos cos[()]66104、22sin 22sin 2sin cos 2sin 2sin cos (cos sin )sin 1tan cos sin 1cos xxx x xx x xx x xx xx 1tan sin2sin2tan()1tan 4x xx x x由177124x得5234x，又3cos()45x ，所以4sin()45x ，4tan()43x新课程标准数学必修4第三章课后习题解答（第12页共12页）所以2cos cos[()]cos()cossin()sin44444410xx x x ，72sin 10x，7sin 22sin cos 25xx x所以2sin 22sin 281tan 75xx x，5、把已知代入222sin cos(sincos )2sin cos1，得22(2sin )2sin1.变形得2(1cos2)(1cos2)1，2cos 2cos2，224cos 24cos 2本题从对比已知条件和所证等式开始，可发现应消去已知条件中含的三角函数.考虑sin cos ，sin cos 这两者又有什么关系？及得上解法.5、6两题上述解法称为消去法6、()3sin 21cos22sin(2)16f x x x m xm .由[0,]2x 得72[,]666x，于是有216m .解得3m.()2sin(2)4()6f x xxR 的最小值为242，此时x 的取值集合由322()62x k kZ ，求得为2()3xk kZ 7、设APx ，AQy ，BCP ，DCQ ，则tan 1x ，tan1y于是2()tan()()x y xy xy又APQ 的周长为2，即222x yxy，变形可得2()2xy x y 于是2()tan()1()[2()2]x y xy x y .又02，所以4，()24PCQ.8、（1）由221sin cos 5sincos 1，可得225sin5sin 120解得4sin 5或3sin 5（由(0,)，舍去）所以13cossin 55，于是4tan 3（2）根据所给条件，可求得仅由sin ,cos ,tan 表示的三角函数式的值，例如，sin()3，cos22，sincos 2tan，sincos 3sin2cos，等等.。
【配套K12】高中数学第三章三角恒等变换3.1.3二倍角的正弦余弦正切公式课时作业新人教版必修4
【创新设计】（浙江专用）2016-2017高中数学 第三章 三角恒等变换 3.1.3 二倍角的正弦、余弦、正切公式课时作业 新人教版必修41.如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数f (x )，则y ＝f (x )在[0，π]的图象大致为( )解析 如图所示，当x ∈⎝⎛⎭⎪⎫0，π2时，则P (cos x ，sin x )，M (cos x ，0)，作MM ′⊥OP ，M ′为垂足，则|MM ′||OM |＝sin x ，∴f （x ）cos x＝sin x ，∴f (x )＝sin x cos x ＝12sin 2x ，则当x ＝π4时，f (x )max ＝12；当x ∈⎝ ⎛⎭⎪⎫π2，π时，有f （x ）|cos x |＝sin(π－x )，f (x )＝－sin x cos x ＝－12sin 2x ，当x ＝3π4时，f (x )max ＝12.只有B 选项的图象符合. 答案 B 2.3－sin 70°2－cos 210°的值是( ) A.12B.22C.2D.32解析 原式＝3－sin 70°2－12（1＋cos 20°）＝2（3－cos 20°）3－cos 20°＝2.答案 C3.若sin ⎝ ⎛⎭⎪⎫π6－α＝13，则cos ⎝ ⎛⎭⎪⎫2π3＋2α的值为( ) A.－13B.－79C.13D.79解析 cos ⎝⎛⎭⎪⎫2π3＋2α＝－cos ⎝ ⎛⎭⎪⎫π3－2α＝－cos[2⎝ ⎛⎭⎪⎫π6－α]＝－[1－2sin 2⎝ ⎛⎭⎪⎫π6－α]＝2sin 2⎝ ⎛⎭⎪⎫π6－α－1＝－79.答案 B4.设sin 2α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，则tan 2α的值是________.解析 因为sin 2α＝2sin αcos α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，所以cos α＝－12，sin α＝1－cos 2α＝32，所以tan α＝－3，则tan 2α＝2tan α1－tan 2α＝－231－（－3）2＝ 3. 答案35.若α∈⎝⎛⎭⎪⎫0，π2，且sin 2α＋cos 2α＝14，则tan α的值等于________.解析 由sin 2 α＋cos 2α＝14得sin 2 α＋1－2sin 2 α＝1－sin 2 α＝cos 2α＝14.∵α∈⎝⎛⎭⎪⎫0，π2，∴cos α＝12，∴α＝π3，∴tan α＝tan π3＝ 3.答案36.已知函数f (x )＝2cos ⎝ ⎛⎭⎪⎫x －π12，x ∈R .(1)求f ⎝ ⎛⎭⎪⎫－π6的值； (2)若cos θ＝35，θ∈⎝ ⎛⎭⎪⎫3π2，2π，求f ⎝⎛⎭⎪⎫2θ＋π3. 解 (1)f ⎝ ⎛⎭⎪⎫－π6＝2cos ⎝ ⎛⎭⎪⎫－π6－π12＝2cos ⎝ ⎛⎭⎪⎫－π4＝2cos π4＝1； (2)f ⎝ ⎛⎭⎪⎫2θ＋π3＝2cos ⎝ ⎛⎭⎪⎫2θ＋π3－π12＝2cos ⎝⎛⎭⎪⎫2θ＋π4＝cos 2θ－sin 2θ因为cos θ＝35，θ∈⎝ ⎛⎭⎪⎫3π2，2π，所以sin θ＝－45，所以sin 2θ＝2sin θcos θ＝－2425，cos 2θ＝cos 2 θ－sin 2θ＝－725，所以f ⎝ ⎛⎭⎪⎫2θ＋π3＝cos 2θ－sin 2θ＝－725－⎝ ⎛⎭⎪⎫－2425＝1725. 7.求值：(1)sin 6°sin 42°sin 66°sin 78°. (2)sin 50°（1＋3tan 10°）－cos 20°cos 80°1－cos 20°.解 (1)原式＝sin 6°cos 48°cos 24°cos 12° ＝sin 6°cos 6°cos 12°cos 24°cos 48°cos 6°＝sin 96°16cos 6°＝cos 6°16cos 6°＝116. (2)∵sin 50°(1＋3tan 10°) ＝sin 50°·cos 10°＋3sin 10°cos 10°＝sin 50°·2sin 40°cos 10°＝sin 80°cos 10°＝1，cos 80°1－cos 20°＝sin 10°2sin 210°＝2sin 210°， ∴sin 50°（1＋3tan 10°）－cos 20°cos 80°1－cos 20°＝1－cos 20°2sin 210°＝2sin 210°2sin 210°＝ 2. 8.已知cos ⎝ ⎛⎭⎪⎫x －π4＝210，x ∈⎝ ⎛⎭⎪⎫π2，3π4.(1)求sin x 的值. (2)求sin ⎝⎛⎭⎪⎫2x ＋π3的值.解 (1)因为x ∈⎝ ⎛⎭⎪⎫π2，3π4，所以x －π4∈⎝ ⎛⎭⎪⎫π4，π2，于是sin ⎝ ⎛⎭⎪⎫x －π4＝1－cos 2⎝⎛⎭⎪⎫x －π4＝7210，则sin x ＝sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫x －π4＋π4＝sin ⎝ ⎛⎭⎪⎫x －π4cos π4＋cos ⎝⎛⎭⎪⎫x －π4sin π4＝7210×22＋210×22＝45.(2)因为x ∈⎝ ⎛⎭⎪⎫π2，3π4，故cos x ＝－1－sin 2x ＝－1－⎝ ⎛⎭⎪⎫452＝－35， sin 2x ＝2sin x cos x ＝－2425，cos 2x ＝2cos 2x －1＝－725，所以sin ⎝⎛⎭⎪⎫2x ＋π3 ＝sin 2x cos π3＋cos 2x sin π3＝－24＋7350.能 力 提 升9.4cos 50°－tan 40°＝( ) A. 2 B.2＋32C. 3D.22－1解析 4cos 50°－tan 40°＝4cos 50°－sin 40°cos 40°＝4cos 50°cos 40°－sin 40°cos 40°＝4sin 40°cos 40°－sin 40°cos 40°＝2sin 80°－sin 40°cos 40°＝2sin （60°＋20°）－sin （60°－20°）cos 40°＝32cos 20°＋32sin 20°cos 40°＝3cos 40°cos 40°＝3，选C.答案 C10.若1－tan θ2＋tan θ＝1，则cos 2θ1＋sin 2θ的值为( )A.3B.－3C.－2D.－12解析 ∵1－tan θ2＋tan θ＝1，∴tan θ＝－12.∴cos 2θ1＋sin 2θ＝cos 2θ－sin 2θ（sin θ＋cos θ）2＝cos θ－sin θcos θ＋sin θ＝1－tan θ1＋tan θ＝1－⎝ ⎛⎭⎪⎫－121＋⎝ ⎛⎭⎪⎫－12＝3. 答案 A11.函数y ＝sin 2x ＋23sin 2x 的最小正周期T 为________. 解析 y ＝sin 2x ＋23sin 2 x ＝sin 2x ＋23×1－cos 2x2＝sin 2x －3cos 2x ＋ 3 ＝2sin ⎝ ⎛⎭⎪⎫2x －π3＋3， 所以周期T ＝2π2＝π.答案 π12.已知tan θ2＝3，则1－cos θ＋sin θ1＋cos θ＋sin θ＝______.解析 1－cos θ＋sin θ1＋cos θ＋sin θ＝2sin 2θ2＋2sin θ2cosθ22cos 2θ2＋2sin θ2cosθ2＝2sin θ2⎝ ⎛⎭⎪⎫sin θ2＋cos θ22cos θ2⎝ ⎛⎭⎪⎫cos θ2＋sin θ2＝tan θ2＝3.答案 313.设f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π6＋2m sin x cos x ，x ∈R .(1)当m ＝0时，求f (x )在⎣⎢⎡⎦⎥⎤0，π3内的最小值及相应的x 的值；(2)若f (x )的最大值为12，求m 的值.解 (1)因为x ∈⎣⎢⎡⎦⎥⎤0，π3，则2x ＋π6∈⎣⎢⎡⎦⎥⎤16π，56π，所以f (x )min＝12，此时x ＝0或π3.(2)令f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6＋2m sin x cos x ＝⎝⎛⎭⎪⎫m ＋32·sin 2x ＋12cos 2x ＝⎝⎛⎭⎪⎫m ＋322＋14sin(2x ＋φ)，其中tan φ＝12m ＋32，于是f (x )max ＝⎝⎛⎭⎪⎫m ＋322＋14，令⎝⎛⎭⎪⎫m ＋322＋14＝12，得m ＝－32. 探 究 创 新14.已知向量a ＝⎝ ⎛⎭⎪⎫cos x ，－12，b ＝(3sin x ，cos 2x )，x ∈R ，设函数f (x )＝a ·b .(1)求f (x )的最小正周期.(2)求f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值.解 (1)f (x )＝a ·b ＝cos x ·3sin x －12cos 2x＝32sin 2x －12cos 2x ＝sin ⎝⎛⎭⎪⎫2x －π6. 最小正周期T ＝2π2＝π.所以f (x )＝sin ⎝⎛⎭⎪⎫2x －π6的最小正周期为π. (2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，⎝ ⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－π6，5π6，由正弦函数y ＝sin x 在⎣⎢⎡⎦⎥⎤－π6，5π6上的图象知，f (x )＝sin ⎝⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫－π6，f ⎝ ⎛⎭⎪⎫π2＝⎣⎢⎡⎦⎥⎤－12，1. 所以，f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值分别为1，－12.。
[配套k12学习]新版高中数学人教A版必修4习题：第三章三角恒等变换 检测B
![[配套k12学习]新版高中数学人教A版必修4习题：第三章三角恒等变换 检测B](https://img.taocdn.com/s3/m/0dae586ebe1e650e52ea99df.png)
第三章检测(B)(时间:90分钟满分:120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1已知taA.C.解析:tanα=taC.答案:C2已知sin 2αAC解析:由半角公式可得,cos答案:A3A≤a≤C.a≤a≤解析:由x+cos x=2si则-2≤2a-3≤2,≤a≤答案:A4函数y=siA.π,1B.πC.2π,1D.2π解析:∵y=sin2x·2x·2x·2x·2x, ∴T=π,y max=1.答案:A5设aA.a>b>cB.a<b<cC.b<c<aD.a<c<b解析:a6°6°=sin24°,b=2sin13°cos13°=sin26°,c25°,所以a<c<b.答案:D6若函数f(x)=(1≤xA.1B.2C解析:f(x)=cos x x==2si∴当x,f(x)取最大值2.答案:B7已知cos2α-cos2β=a,那么sin(α+β)sin(α-β)=()A.C.-aD.a解析:sin(α+β)sin(α-β)=(sinαcosβ+cosαsinβ)·(sinαcosβ-cosαsinβ)=sin2αcos2β-cos2αsin2β=(1-cos2α)cos2β-cos2α(1-cos2β)=cos2β-cos2α=-a.故选C.答案:C8已知coA.C.解析:∵coα+sinα∴si∴si答案:C94cos 50°-tan 40°=()ABCD.解析:4cos50°-tan40°答案:C10已知角α,β满AC解析:设sin(α-β)=x,即sinαcosβ-cosαsinβ=x.①又sin(α+β)即sinαcosβ+cosαsinβ由①②得,sinαcosβαsinβ解得x=答案:B二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)11化简解析:原=cosα.答案:cos α12已知(sin x-2cos x)(3+2sin x+2cos x)=0,解析:∵3+2sin x+2cos x=3+≥3-∴3+2sin x+2cos x≠0,∴sin x-2cos x=0,即sin x=2cos x,∴(2cos x)2+cos2x=1,cos2x=2cos2x答案:13已知函数f(x)=sin ωx+cos ωx(ω>0),x∈R.若函数f(x)在区间(-ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为.答案:14已知α,β∈解析:∴tanα∵3sinβ=sin(2α+β),∴3sin[(α+β)-α]=sin[(α+β)+α],即3sin(α+β)cosα-3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα, 化简得sin(α+β)cosα=2cos(α+β)sinα,即tan(α+β)=2tanα=1.又α,β∈∴α+β∈∴α+β答案:15已知α为第二象限角,函数f(x)=2cos解析:因为f(x)=2cos x=1+cos x x=1+2co所以1+2cosα即cosα=又α为第二象限角,所以sinα所答案:三、解答题(本大题共5小题,共45分.解答时应写出必要的文字说明、证明过程或演算步骤)16(8分)已知tan α=2.(1)求ta(2)解(1)ta(217(8分)已知tan α=∈(0,π).求:(1)tan(α+β)的值;(2分析(1)先求出tanβ,再用两角和的正切公式求解;(2)求出sinα,cosα,sinβ代入公式可得.解(1)由cosβ∈(0,π),得sinββ=2.所以tan(α+β)(2)因为tanα=∈(0,π),所以sinαα=.所以原式=18(9分)已知函数f(x)∈R.(1)求(2)若cos θ解(1)(2)=cos2θ-sin2θ.因为cosθ所以sinθ=sin2θ=2sinθcosθ=2θ=cos2θ-sin2θ=所2θ-sin2θ=19(10分)已知函数f(x)=2si(1)求函数f(x)的最小正周期及最值;(2)令g(x)=解(1)∵f(x)=si=si=2si∴f(x)的最小正周期为T当si,f(x)取得最小值-2;当si,f(x)取得最大值2.(2)g(x)是偶函数,理由如下:由(1)知f(x)=2si∴g(x)==2si=2si∵g(-x)=2co∴函数g(x)是偶函数.20(10分)已知函数f(x)=si(1)求f(x)的单调递增区间;(2)若α是第二象限角,解(1)因为函数y=sin x的单调递增区间∈Z,≤3x∈Z,≤x≤∈Z.所以,函数f(x)的单调递增区间∈Z.(2)由已知,有si·(cos2α-sin2α),所以sinαcoαsi即sinα+cosαα-sinα)2(sinα+cosα).当sinα+cosα=0时,由α是第二象限角,知α∈Z.此时,cosα-sinα=当sinα+cosα≠0时,有(cosα-sinα)2由α是第二象限角,知cosα-sinα<0,此时cosα-sinα=综上所述,cosα-sinα=。
(精编)人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单
人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换同步测试B卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题；共30分)1. （2分）若2sinx=1+cosx，则的值等于（）A .B . 或不存在C . 2D . 2或2. （2分）设A、B、C为三角形的三内角，且方程（sinB﹣sinA）x2+（sinA﹣sinC）x+（sinC﹣sinB）=0有等根，那么角B（）A . B＞60°B . B≥60°C . B＜60°D . B≤60°3. （2分）设均为锐角，且，则（）A .B .C . 或D . 或4. （2分）若则的值为（）A .B .C .D . -25. （2分）设f(x)=cosx-sinx把y=f(x)的图象按向量(>0)平移后，恰好得到函数y=(x)的图象，则的值可以为（）A .B .C . πD .6. （2分） (2018高一下·濮阳期末) 若将函数的图形向右平移个单位，所得图象关于轴对称，则的最小正值是（）A .B .C .D .7. （2分）(2018·全国Ⅰ卷文) 已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α= ,则|a-b|=（）A .B .C .D . 18. （2分） (2020高一下·宁波期中) 已知，则的值为（）A .B . -3C .D . 39. （2分）将函数的图像向右平移个单位，再将图像上每一点横坐标缩短到原来的倍，所得图像关于直线对称，则的最小正值为（）A .B .C .D .10. （2分） (2018高一下·平顶山期末) 设，则下列式子正确的是（）A .B .C .D .11. （2分） (2019高一下·上高月考) 已知，，，则（）A .B .C .D .12. （2分）函数y＝12sin＋5sin的最大值为（）A . 6＋B . 17C . 13D . 1213. （2分） (2017高一下·沈阳期末) 设都是锐角，且，，则等于（）A .B .C . 或D . 或14. （2分）计算A .B .C .D .15. （2分）为了得到函数的图像,可以将函数y=2sin2x的图像（）A . 向右平移个单位长度B . 向右平移个单位长度C . 向左平移个单位长度D . 向左平移个单位长度二、填空题 (共5题；共5分)16. （1分） (2020高二上·重庆月考) 已知a，b，c分别为三个内角A、B、C的对边，，，则的面积为________.17. （1分）已知，且，则的值为________．18. （1分） (2016高一下·岳阳期末) 已知tanα=cosα，那么sinα=________．19. （1分） (2016高三上·盐城期中) 已知sinα= ，且α为钝角，则cos =________．20. （1分）若，，则cos2α=________．三、解答题 (共5题；共25分)21. （5分）已知sinx=，角x终边在第一象限，求tan的值．22. （5分）若，，且，，求（1）sin2β的值．（2）cosα的值．23. （5分） (2018高一下·威远期中) 已知(Ⅰ)求的值.(Ⅱ)求的值24. （5分） (2019高三上·中山月考) 已知函数 , .（Ⅰ）求函数的最大正周期与单调增区间值;（Ⅱ）求函数在区间上的最大值与最小值.25. （5分）已知关于x的方程sinxsin5x=a在x∈[0，π）上有唯一解，求实数a的取值范围．参考答案一、单选题 (共15题；共30分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：二、填空题 (共5题；共5分)答案：16-1、考点：解析：答案：17-1、解析：答案：18-1、考点：解析：答案：19-1、考点：解析：答案：20-1、解析：三、解答题 (共5题；共25分)答案：21-1、考点：解析：答案：22-1、解析：答案：23-1、考点：解析：答案：24-1、考点：解析：答案：25-1、考点：解析：。
人教A版高一数学必修4 练习--第三章 三角恒等变换3.2--含解析
(本栏目内容，在学生用书中以独立形式分册装订！)一、选择题(每小题5分，共20分)1．已知cos θ＝－14(－180°＜θ＜－90°)，则cos θ2＝( )A ．－64B.64C ．－38D.38解析： 因为－180°＜θ＜－90°，所以－90°＜θ2＜－45°.又cos θ＝－14，所以cosθ2＝1＋cos θ2＝ 1－142＝64，故选B. 答案： B2．已知α∈⎝⎛⎭⎫－π2，0，cos α＝45，则tan α2＝( )A ．3B ．－3 C.13D ．－13解析： 因为α∈⎝⎛⎭⎫－π2，0，且cos α＝45，所以α2∈⎝⎛⎭⎫－π4，0，tan α2＝－1－cos α1＋cos α＝－1－451＋45＝－13，故选D.3．若α∈⎣⎡⎦⎤7π4，2π，则 1＋cos 2α2－1－cos 2α2等于( ) A ．cos α－sin α B ．cos α＋sin α C ．－cos α＋sin α D ．－cos α－sin α解析： ∵α∈⎣⎡⎦⎤7π4，2π， ∴sin α＜0，cos α＞0，则1＋cos 2α2－1－cos 2α2＝cos 2α－sin 2α ＝|cos α|－|sin α|＝cos α－(－sin α)＝cos α＋sin α. 答案： B4．已知sin α＋cos α＝13，则2cos 2⎝⎛⎭⎫π4－α－1＝( )A.89 B.1718 C ．－89D ．－23解析： ∵sin α＋cos α＝13，平方可得1＋sin 2α＝19，可得sin 2α＝－89.2cos 2⎝⎛⎭⎫π4－α－1＝cos ⎝⎛⎭⎫π2－2α＝sin 2α＝－89. 答案： C二、填空题(每小题5分，共15分)5．已知tanα2＝3，则cos α＝________．解析： cos α＝cos 2α2－sin 2α2＝cos 2α2－sin 2α2cos 2α2＋sin 2α2＝1－tan 2α21＋tan 2α2＝1－321＋32＝－45.答案： －456．若sin α＋cos αsin α－cos α＝12，则tan 2α等于________．解析： 由sin α＋cos αsin α－cos α＝12，得2(sin α＋cos α)＝sin α－cos α， 即tan α＝－3.又tan 2α＝2tan α1－tan 2α＝－61－9＝68＝34.答案： 347．函数y ＝32sin 2x ＋cos 2x 的最小正周期为________． 解析： y ＝32sin 2x ＋cos 2x ＝32sin 2x ＋cos2x ＋12＝32sin 2x ＋12cos 2x ＋12＝sin ⎝⎛⎭⎫2x ＋π6＋12，所以该函数的最小正周期为π.三、解答题(每小题10分，共20分)8．化简：(1)sin ⎝⎛⎭⎫α＋π42cos 2α2＋2sin α2cos α2－1. (2)已知π<α<3π2，化简：1＋sin α1＋cos α－1－cos α＋1－sin α1＋cos α＋1－cos α.解析： (1)原式＝sin αcos π4＋cos αsinπ4cos α＋sin α＝22（sin α＋cos α）cos α＋sin α＝22.(2)原式＝⎝⎛⎭⎫sin α2＋cos α222⎪⎪⎪⎪cosα2－2⎪⎪⎪⎪sin α2＋⎝⎛⎭⎫sin α2－cos α222⎪⎪⎪⎪cos α2＋2⎪⎪⎪⎪sin α2，∵π<α<3π2，∴π2<α2<3π4.∴cos α2<0，sin α2>0. ∴原式＝⎝⎛⎭⎫sin α2＋cos α22－2⎝⎛⎭⎫sin α2＋cosα2＋⎝⎛⎭⎫sin α2－cos α222⎝⎛⎭⎫sin α2－cosα2＝－sin α2＋cos α22＋sin α2－cosα22。
高中数学第三章三角恒等变换教材习题本新人教A版必修4
第三章 三角恒等变换P1461， 已知βα,都是锐角，()135cos ,54sin =+=βαα，求βsin 的值,2， 已知⎪⎭⎫⎝⎛∈⎪⎭⎫ ⎝⎛∈-=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛-4,0,43,4,131245sin ,534cos πβππαβπαπ，求()s i n αβ+=3， 已知βα,都是锐角，1010sin ,71tan ==βα，求()=+βα2tan4， 证明()()βαβαβαβα+-+=+tan tan tan tan tan tan 求000040tan 20tan 340tan 20tan ++的值 若43πβα=+，求()()βαtan 1tan 1--的值 求000040tan 20tan 120tan 40tan 20tan 0++的值5， 化简0010cos 310sin 1-()()310tan 40sin 00-()120tan 310cos 70tan 000-()0010tan 3150sin +6， 已知23,53cos πθπθ<<-=，求22cos 2sin ⎪⎭⎫⎝⎛-θθ的值 已知512cos 2sin =-θθ，求θsin 的值 已知95cos sin 44=+θθ，求θ2sin 的值 已知532cos =θ，=+θθ44cos sin7已知()()53cos ,51cos =-=+βαβα，求tan tan αβ的值 8证明 ()()A AA A A 424tan 4cos 2cos 434cos 2cos 43sin sin cos 2sin 2sin 21tan 212sin cos 22sin 1cos 832cos 44cos =+++-=+-++=++=++αββααβαααααααα 9，已知函数()x x x y 22cos 2cos sin ++= 求它的递减区间求它的最大值和最小值10.已知函数x x x x y 44sin cos sin 2cos --=求y 的最小正周期 当⎥⎦⎤⎢⎣⎡∈2,0πx 时，求y 的最小值以及取得最小值时的x 的集合 11，已知函数)cos (sin sin 2x x x y +=求y 的最小正周期和最大值画出函数y 在区.2,2⎥⎦⎤⎢⎣⎡-ππ上的图形 12已知函数a x x x y ++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=cos 6sin 6sin ππ的最大值为1 求常数a 的值 求使y ≥0成立的x 的取值范围13已知直线21//l l ，A 是21,l l 之间的一个定点，且A 点到21,l l 的距离分别为21,h h ，B 是直线2l 上一动点，作AB AC ⊥，且使AC 与直线1l 交于点C ，求三角形ABC 面积的最小值B 组 已知πααα≤≤=-051cos sin ，求⎪⎭⎫ ⎝⎛-42sin πα的值 已知11sin sin ,cos cos 23αβαβ+=+=，求()βα-cos 的值 已知02,534sin 3sin <<--=+⎪⎭⎫ ⎝⎛+απαπα，求αcos 的值 已知471217,534cos πππ<<=⎪⎭⎫ ⎝⎛+x x ，求x x x tan 1sin 22sin 2-+的值 已知βθθαθθ2sin cos sin ,sin 2cos sin ==+，求证βα2cos 2cos 422= 若函数m x x y ++=2cos 22sin 3在区间⎥⎦⎥⎢⎣⎢2.0π的最大值为6，求常数m 的值及函数当R x ∈时的最小值，并求相应的x 的值的集合在正方形ABCD 的边长为1，P,Q 分别为边AB,DA 上的点，当三角形APQ 的周长为2时，求角PCO 的大小已知()π,0,51cos sin ∈=+x x x ，求=x tan P139用αcos 表示2tan 2cos ,2sin222ααα 求证P A Q DCBA P C Q D OB ()()[]2cos 2sin 2sin sin sin sin 21sin sin φθφθφθβαβαβα++=+-++=求函数x x y cos 3sin +=的周期及最大值和最小值例题4、如图，已知OPQ 是半径为1，圆心角为3π的扇形，C 是扇形弧上的动点，ABCD 是扇形的内接矩形。
[k12精品]高中数学第三章三角恒等变换3.2倍角公式和半角公式3.2.1倍角公式示范教案新人教B版必修4
![[k12精品]高中数学第三章三角恒等变换3.2倍角公式和半角公式3.2.1倍角公式示范教案新人教B版必修4](https://img.taocdn.com/s3/m/6c020a36eff9aef8941e0660.png)
3.2.1 倍角公式示范教案 整体设计教学分析倍角公式是在研究了两角和与差的三角函数的基础上，进一步研究具有“二倍角”关系的正弦、余弦、正切公式的，它既是两角和与差的正弦、余弦、正切公式的特殊化，又为以后求三角函数值、化简、证明提供了非常有用的理论工具，通过对二倍角的推导知道，二倍角的内涵是：揭示具有倍数关系的两个三角函数的运算规律，通过推导还让学生加深理解了高中数学由一般到特殊的化归思想．因此本节内容也是培养学生运算和逻辑推理能力的重要内容，对培养学生的探索精神和创新能力、发现问题和解决问题的能力都有着十分重要的意义．本节课通过教师提出问题、设置情境及对和角公式中α、β关系的特殊情形α＝β时的简化，让学生在探究中既感到自然、易于接受，还可清晰知道和角的三角函数与倍角公式的联系，同时也让学生学会怎样发现规律及体会由一般到特殊的化归思想．这一切教师要引导学生自己去做，因为，《数学课程标准》提出：“要让学生在参与特定的数学活动，在具体情境中初步认识对象的特征，获得一些体验．”在实际教学过程中不要过多地补充一些高技巧、高难度的练习，否则就违背了新课标在这一节的编写意图和新课改精神．三维目标1．通过让学生探索、发现并推导二倍角公式，了解它们之间、以及它们与和角公式之间的内在联系，并通过强化题目的训练，加深对二倍角公式的理解，培养运算能力及逻辑推理能力．2．通过二倍角的正弦、余弦、正切公式的运用，会进行简单的求值、化简、恒等证明．体会化归这一基本数学思想在发现中和求值、化简、恒等证明中所起的作用．3．通过本节学习，引导学生领悟寻找数学规律的方法，培养学生的创新意识，以及善于发现和勇于探索的科学精神．重点难点教学重点：二倍角公式推导及其应用．教学难点：灵活应用和、差、倍角公式进行三角式化简、求值、证明恒等式． 课时安排 1课时教学过程 导入新课思路1.(复习导入)请学生回忆上两节共同探讨的和角公式、差角公式，并回忆这组公式的来龙去脉，然后让学生默写这六个公式．教师引导学生：和角公式与差角公式是可以互相化归的．当两角相等时，两角之和便为此角的二倍，那么是否可把和角公式化归为二倍角公式呢？今天，我们进一步探讨一下二倍角的问题，请同学们思考一下，应解决哪些问题呢？由此展开新课．思路2.(问题导入)出示问题，让学生计算，若sin α＝35，α∈(π2，π)，求sin2α，cos2α的值．学生会很容易看出：sin2α＝sin(α＋α)＝sin αcos α＋cos αsin α＝2sin αcos α的，以此展开新课，并由此展开联想推出其他公式．推进新课新知探究 提出问题还记得和角的正弦、余弦、正切公式吗？请学生默写出来，并由一名学生到黑板默写你写的这三个公式中角α、β会有特殊关系α＝β吗？此时公式变成什么形式？ 在得到的C 2α公式中，还有其他表示形式吗？ 细心观察二倍角公式结构，有什么特征呢？能看出公式中角的含义吗？思考过公式成立的条件吗？让学生填空：老师随机给出等号一边括号内的角，学生回答等号另一边括号内的角，稍后两人为一组，做填数游戏：＝，＝cos 2 －sin2思考过公式的逆用吗？想一想C 2α还有哪些变形？请思考以下问题：sin2α＝2sin α吗？cos2α＝2cos α吗？tan2α＝2tan α吗 活动：本节总的指导思想是教师引导学生自己推导倍角公式．学生默写完问题(1)后，教师打出课件，然后引导学生观察正弦、余弦的和角公式，提醒学生注意公式中的α，β，既然可以是任意角，怎么任意的？你会有些什么样的奇妙想法呢？并鼓励学生大胆试一试．如果学生想到α，β会有相等这个特殊情况，教师就此进入下一个问题，如果学生没想到这种特殊情况，教师适当点拨进入问题(2)，然后找一名学生到黑板进行简化，其他学生在自己的座位上简化，教师再与学生一起集体订正黑板的书写，最后学生都不难得出以下式子，鼓励学生尝试一下，对得出的结论给出解释．这个过程教师要舍得花时间，充分地让学生去思考、去探究，并初步地感受二倍角的意义．同时开拓学生的思维空间，为学生将来遇到的3α或3β等角的探究附设类比联想的源泉．sin(α＋β)＝sin αcos β＋cos αsin β⇒sin2α＝2sin αcos α(S 2α)；cos(α＋β)＝cos αcos β－sin αsin β⇒cos2α＝cos 2α－sin 2α(C 2α)；tan(α＋β)＝tan α＋tan β1－tan αtan β ⇒tan2α＝2tan α1－tan 2α(T 2α)． 这时教师适时地向学生指出，我们把这三个公式分别叫做二倍角的正弦，余弦，正切公式，并指导学生阅读教科书，确切明了二倍角的含义，以后的“倍角”专指“二倍角”．教师适时提出问题(3)，点拨学生结合sin 2α＋cos 2α＝1思考，因此二倍角的余弦公式又可表示为以下右表中的公式．sin2α＝2sin αcos α2αcos2α＝cos 2α－sin 2α2αtan2α＝2tan α1－tan 2α2αcos2α＝2cos 2α－1cos2α＝1－2sin 2α这时教师点出，这些公式都叫做倍角公式(用多媒体演示)．倍角公式给出了α的三角函数与2α的三角函数之间的关系．问题(4)，教师指导学生，这组公式用途很广，并与学生一起观察公式的特征与记忆，首先公式左边角是右边角的2倍；左边是2α的三角函数的一次式，右边是α的三角函数的二次式，即左到右→升幂缩角，右到左→降幂扩角、二倍角的正弦是单项式，余弦是多项式，正切是分式．问题(5)，因为还没有应用，对公式中的含义学生可能还理解不到位，教师要引导学生观察思考并初步感性认识到：(Ⅰ)这里的“倍角”专指“二倍角”，遇到“三倍角”等名词时，“三”字等不可省去；(Ⅱ)通过二倍角公式，可以用单角的三角函数表示二倍角的三角函数；(Ⅲ)二倍角公式是两角和的三角函数公式的特殊情况；(Ⅳ)公式(S 2α)，(C 2α)中的角α没有限制，都是α∈R ，但公式(T 2α)需在α≠12k π＋π4和α≠k π＋π2(k∈Z )时才成立，这一条件限制要引起学生的注意．但是当α＝k π＋π2，k∈Z 时，虽然tan α不存在，此时不能用此公式，但tan2α是存在的，故可改用诱导公式．问题(6)，填空是为了让学生明了二倍角的相对性，即二倍角公式不仅限于2α是α的二倍的形式，其他如4α是2α的二倍，α2是α4的二倍，3α是3α2的二倍，α3是α6的二倍，π2－α是π4－α2的二倍等，所有这些都可以应用二倍角公式． 例如：sin α2＝2sin α4cos α4，cos α3＝cos 2α6－sin 2α6等等．问题(7)，本组公式的灵活运用还在于它的逆用以及它的变形用，这点教师更要提醒学生引起足够的注意．如：sin3αcos3α＝12sin6α，4sin α4cos α4＝2(2sin α4cos α4)＝2sin α2，2tan40°1－tan 240°＝tan80°，cos 22α－sin 22α＝cos4α，tan2α＝2tan α(1－tan 2α)等等． 问题(8)，一般情况下：sin2α≠2sin α，cos2α≠2cos α，tan2α≠2tan α.若sin2α＝2sin α，则2sin αcos α＝2sin α，即sin α＝0或cos α＝1，此时α＝k π(k∈Z )．若cos2α＝2cos α，则2cos 2α－2cos α－1＝0，即cos α＝1－32(cos α＝1＋32舍去)．若tan2α＝2tan α，则2tan α1－tan 2α＝2tan α，∴tan α＝0，即α＝k π(k∈Z )． 讨论结果：(1)～(8)略． 应用示例思路1例 1已知sin α＝513，α∈(π2，π)，求sin2α，cos2α，tan2α的值．活动：教师引导学生分析题目中角的关系，观察所给条件与结论的结构，注意二倍角公式的选用，领悟“倍角”是相对的这一换元思想．让学生体会“倍”的深刻含义，它是描述两个数量之间关系的．本题中的已知条件给出了α的正弦值．由于2α是α的二倍角，因此可以考虑用倍角公式．本例是直接应用二倍角公式解题，目的是为了让学生初步熟悉二倍角的应用，理解二倍角的相对性，教师大胆放手，可让学生自己独立探究完成．解：因为sin α＝513，α∈(π2，π)，所以cos α＝－1－sin 2α＝－1－5132＝－1213， sin2α＝2sin αcos α＝2×513×(－1213)＝－120169， cos2α＝cos 2α－sin 2α＝(－1213)2－(513)2＝119169，tan2α＝sin2αcos2α＝－120169÷119169＝－120119.点评：学生由问题中条件与结论的结构不难想象出解法，但要提醒学生注意，在解题时注意优化问题的解答过程，使问题的解答简捷、巧妙、规范，并达到熟练掌握的程度．本节变式训练1．y ＝(sinx －cosx)2－1是( )A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数 答案：D 2．若cos2αα－π4＝－22，则cos α＋sin α的值为( ) A ．－72 B ．－12 C.12 D.72 答案：C 3．下列各式中，值为32的是( ) A ．2sin15°－cos15° B ．cos 215°－sin 215°C ．2sin 215°－1D ．sin 215°＋cos 215° 答案：B例 2证明1＋sin2θ－cos2θ1＋sin2θ＋cos2θ＝tan θ.活动：教师可点拨学生想一想，到现在为止，所学的证明三角恒等式的方法大致有几种：从复杂一端化向简单一端；两边化简，中间碰头；化切为弦；还可以利用分析综合法解决，有时几种方法会同时使用等．对找不到思考方向的学生，教师点出：可否再添加一种，化倍角为单角？这可否成为证明三角恒等式的一种方法？再适时引导，前面学习同角三角函数的基本关系时曾用到“1”的代换，对“1”的妙用大家深有体会，这里可否在“1”上做做文章？待学生探究解决方法后，可找几个学生到黑板书写解答过程，以便对照点评及给学生以启发．点评时对能够善于运用所学的新知识解决问题的学生给予赞扬；对暂时找不到思路的学生给予点拨、鼓励．强调“1”的妙用很妙，妙在它在三角恒等式中一旦出现，在证明过程中就会起到至关重要的作用，在今后的证题中，万万不要忽视它．证明：方法一：左＝sin2θ＋－cos2θsin2θ＋＋cos2θ＝2sin θcos θ＋＋1－2cos 2θ2sin θcos θ＋＋2cos 2θ－＝sin θcos θ＋1－cos 2θsin θcos θ＋cos 2θ＝sin θcos θ＋sin 2θsin θcos θ＋cos 2θ ＝sin θθ＋sin θcos θθ＋cos θ＝tan θ＝右，所以，原式成立． 方法二：左＝sin 2θ＋cos 2θ＋sin2θ＋sin 2θ－cos 2θsin 2θ＋cos 2θ＋sin2θ＋cos 2θ－sin 2θ＝sin2θ＋2sin 2θsin2θ＋2cos 2θ＝2sin θθ＋cos θ2cos θθ＋cos θ＝tan θ＝右．方法三： 左＝＋sin2θ－cos2θ＋sin2θ＋cos2θ＝2θ＋cos 2θ＋2sin θ·cos θ－2θ－sin 2θ2θ＋cos 2θ＋2sin θ·cos θ＋2θ－sin 2θ＝θ＋cos θ2－θ＋sin θθ－sinθθ＋cos θ2＋θ＋sin θθ－sinθ＝θ＋cos θθ＋cos θ＋sin θ－cos θθ＋cos θθ＋cos θ＋cos θ－sin θ＝θ＋cos θθθ＋cos θθ＝tan θ＝右．点评：以上几种方法大致遵循以下规律：首先从复杂端化向简单端；第二，化倍角为单角，这是我们今天刚刚学习的；第三，证题中注意对数字的处理，尤其“1”的代换的妙用，请同学们在探究中仔细体会这点．在这道题中通常用的几种方法都用到了，不论用哪一种方法，都要思路清晰，书写规范才是.变式训练1．若角α的终边经过点P(1，－2)，则tan2α的值为__________． 答案：432．证明恒等式：sin2θ＋sin θ2cos2θ＋2sin 2θ＋cos θ＝tan θ. 证明：左边＝2sin θcos θ＋sin θ2θ－sin 2θ＋2sin 2θ＋cos θ ＝sin θθ＋cos θθ＋＝tan θ＝右边.思路2例 1求sin10°sin30°sin50°sin70°的值．活动：本例是一道灵活应用二倍角公式的经典例题，有一定难度，但也是训练学生思维能力的一道好题．本题需要公式的逆用，逆用公式的先决条件是认识公式的本质，要善于把表象的东西拿开，正确捕捉公式的本质属性，以便合理运用公式．教学中教师可让学生充分进行讨论探究，不要轻易告诉学生解法，可适时点拨学生需要做怎样的变化，又需怎样应用二倍角公式．并点拨学生结合诱导公式思考．学生经过探索发现，如果用诱导公式把10°，30°，50°，70°正弦的积化为20°，40°，60°，80°余弦的积，其中60°是特殊角，很容易发现40°是20°的2倍，80°是40°的2倍，故可考虑逆用二倍角公式．解：原式＝cos80°cos60°cos40°cos20°＝23·sin20°cos20°cos40°cos80°23·2sin20°＝sin160°16sin20°＝sin20°16sin20°＝116.例 2在△ABC 中，cosA ＝45，tanB ＝2，求tan(2A ＋2B)的值．活动：这是本节课本上最后一个例题，结合三角形，具有一定的综合性，同时也是和与差公式的应用问题．教师可引导学生注意在三角形的背景下研究问题，会带来一些隐含的条件，如A ＋B ＋C ＝π，0<A<π，0<B<π，0<C<π，就是其中的一个隐含条件．可先让学生讨论探究，教师适时点拨．学生探究解法时教师进一步启发学生思考由条件到结果的函数及角的联系．由于对2A ＋2B 与A ，B 之间关系的看法不同会产生不同的解题思路，所以学生会产生不同的解法，不过它们都是对倍角公式、和角公式的联合运用，本质上没有区别．不论学生的解答正确与否，教师都不要直接干预．在学生自己尝试解决问题后，教师可与学生一起比较各种不同的解法，并引导学生进行解题方法的归纳总结．基础较好的班级还可以把求tan(2A ＋2B)的值改为求tan2C 的值．解法一：在△ABC 中，由cosA ＝45，0<A<π，得sinA ＝1－cos 2A ＝1－452＝35. 所以tanA ＝sinA cosA ＝35×54＝34，tan2A ＝2tanA1－tan 2A ＝2×341－342＝247. 又tanB ＝2，所以tan2B ＝2tanB 1－tan 2B ＝2×21－22＝－43.于是tan(2A ＋2B)＝tan2A ＋tan2B1－tan2Atan2B ＝247－431－247－43＝44117. 解法二：在△ABC 中，由cosA ＝45，0<A<π，得sinA ＝1－cos 2A ＝1－452＝35. 所以tanA ＝sinA cosA ＝35×54＝34.又tanB ＝2，所以tan(A ＋B)＝tanA ＋tanB 1－tanAtanB ＝34＋21－34×2＝－112.于是tan(2A ＋2B)＝tan[2(A ＋B)]＝＋1－tan2＋＝－1121－－1122＝44117. 变式训练化简：1＋cos4α＋sin4α1－cos4α＋sin4α.解：原式＝2cos 22α＋2sin2αcos2α2sin 22α＋2sin2αcos2α＝2cos2αα＋sin2α2sin2αα＋cos2α＝1tan2α. 课堂小结1．先由学生回顾本节课都学到了什么？有哪些收获？对前面学过的两角和公式有什么新的认识？对三角函数式子的变化有什么新的认识？怎样用二倍角公式进行简单三角函数式的化简、求值与恒等式证明．2．教师画龙点睛：本节课要理解并掌握二倍角公式及其推导，明白从一般到特殊的思想，并要正确熟练地运用二倍角公式解题．在解题时要注意分析三角函数名称、角的关系，一个题目能给出多种解法，从中比较最佳解决问题的途径，以达到优化解题过程，规范解题步骤，领悟变换思路，强化数学思想方法之目的．作业课本本节练习B 组1～4.设计感想 1．新课改的核心理念是：以学生发展为本．本节课的设计流程从回顾→探索→应用，充分体现了“学生主体、主动探索、培养能力”的新课改理念，体现“活动、开放、综合”的创新教学模式．本节在学生探究和角公式的特殊情形中得到了二倍角公式，在这个活动过程中，由一般化归为特殊的基本数学思想方法就深深的留在了学生记忆中．本节课的教学设计流程还是比较流畅的．2．纵观本教案的设计，学生发现二倍角后就是应用，至于如何训练二倍角公式正用，逆用，变形用倒成了次要的了．而学生从探究活动过程中学会了怎样去发现数学规律，又发现了怎样逆用公式及活用公式，那才是深层的，那才是我们中学数学教育的最终目的．3．教学矛盾的主要方面是学生的学，学是中心，会学是目的，根据高中三角函数的推理特点，本节主要是教给学生“回顾公式、探索特殊情形、发现规律、推导公式、学习应用”的探索创新式学习方法．这样做增加了学生温故知新的空间，增强了学生的参与意识，教给了学生发现规律、探索推导、获取新知的途径，让学生真正尝试到探索的喜悦，真正成为教学的主体．备课资料 一、三角变换中的“一致代换”法在三角变换中，“一致代换”法是一种重要的方法，所谓“一致代换”法，即在三角变换中，化“异角”“异名”“异次”为“同角”“同名”“同次”的方法．它主要包括：在三角函数式中，①如果只含同角三角函数，一般应从变化函数名称入手，尽量化为同名函数，常用“化弦法”；②如果含有异角，一般应从变化角入手，尽量化不同角为同角，变复角为单角；③如果含有异次幂，一般利用升幂或降幂公式化异次幂为同次幂．二、备用习题1．求值：1sin10°－3cos10°.2．化简：cos36°cos72°.3．化简：cos αcos α2cos α22cos α23·…·cos α2n －1.4．求值：sin6°sin42°sin66°sin78°.5．已知向量m ＝(sinA ，cosA)，n ＝(1，－2)，且m·n ＝0. (1)求tanA 的值；(2)求函数f(x)＝cos2x ＋tanAsinx(x∈R )的值域．6．已知cos(α－β2)＝－19，sin(α2－β)＝23，且π2<α<π，0<β<π2，求cos(α＋β)的值．7．已知cos(x －π4)＝210，x∈(π2，3π4)．(1)求sinx 的值； (2)求sin(2x ＋π3)的值．参考答案：1．解：原式＝cos10°－3sin10°sin10°cos10°＝12cos10°－32sin10°cos10° ＝－cos30°sin2sin10°cos10°＝－sin20°＝4.2．解：原式＝2sin36°cos36°·cos72°2sin36°＝2sin72°cos72°4sin36°＝sin144°4sin36°＝14.3．解：先将原式同乘除因式sin α2n －1，然后逐次使用倍角公式，则原式＝sin2α2nsin α2n －1.4．解：原式＝sin6°cos48°cos24°cos12°＝sin6°cos12°cos24°cos48° ＝24cos6°sin6°cos12°cos24°cos48°24cos6°＝sin96°24cos6°＝cos6°16cos6°＝116. 5．解：(1)由题意，得m·n ＝sinA －2cosA ＝0，因为cosA≠0，所以tanA ＝2.(2)由(1)知tanA ＝2，得f(x)＝cos2x ＋2sinx ＝1－2sin 2x ＋2sinx ＝－2(sinx －12)2＋32，因为x∈R ，所以sinx∈[－1,1]．当sinx ＝12时，f(x)有最大值32；当sinx ＝－1时，f(x)有最小值－3，所以所求函数f(x)的值域是[－3，32]．6．∵cos(α－β2)＝－19，π2<α<π，0<β<π2，∴π2<α－β2<π. ∴sin(α－β2)＝459.∵sin(α2－β)＝23，π2<α<π，0<β<π2，∴0<α2－β<π2.∴cos(α2－β)＝53.∵cosα＋β2＝cos[(α－β2)－(α2－β)]＝cos(α－β2)cos(α2－β)＋sin(α－β2)sin(α2－β) ＝(－19)×53＋459×23＝7275，∴cos(α＋β)＝2cos2α＋β2－1＝－239729. 7．解：(1)因为x∈(π2，3π4)，所以x －π4∈(π4，π2)．于是sin(x －π4)＝1－cos2－π4＝7210， sinx ＝sin[(x －π4)＋π4]＝sin(x －π4)cos π4＋cos(x －π4)sin π4＝7210×22＋210×22＝45. (2)因为x∈(π2，3π4)，故cosx ＝－1－sin 2x ＝－1－452＝－35，sin2x ＝2sinxcosx ＝－2425，cos2x ＝2cos 2x －1＝－725.所以sin(2x ＋π3)＝sin2xcos π3＋cos2xsin π3＝－24＋7350.。
高中数学第三章三角恒等变换3.2简单的三角恒等变换练习新人教A版必修4(2021年整理)
2017-2018学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换练习新人教A版必修4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017-2018学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换练习新人教A版必修4）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017-2018学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换练习新人教A版必修4的全部内容。
3.2 简单的三角恒等变换题号1234567891011得分答案一、选择题(本大题共7小题，每小题5分，共35分）1．函数y＝错误!的最小正周期等于( )A.错误! B．πC．2π D．3π2。
错误!＝（）A．1 B．2C. 2 D。
错误!3．函数y＝3sin 4x＋错误!cos 4x的最大值是( )A. 3 B．2 错误!C．3 D．64．函数f(x）＝(1＋tan x)cos x的最小正周期为（）A．2π B.错误!C．π D.错误!5．函数y＝cos2错误!＋sin2错误!－1是（)A．最小正周期为2π的奇函数B．最小正周期为π的偶函数C．最小正周期为π的奇函数D．最小正周期为2π的偶函数6．如果函数f(x)＝sin 2x＋acos 2x的图像关于直线x＝－错误!对称，则实数a的值为（)A．2 B．－2C．1 D．－17．已知函数f(x)＝错误!sin ωx＋cos ωx(ω〉0)，y＝f(x)的图像与直线y＝2的两个相邻交点的距离等于π，则f(x)的单调递增区间是( )A.错误!，k∈ZB。
错误!，k∈ZC.错误!,k∈ZD。
错误!，k∈Z二、填空题（本大题共4小题，每小题5分，共20分)8．函数f(x）＝sin x－cos x的单调递增区间是____________________．9．已知sin（α＋错误!)＋sin α＝－错误!，－错误!<α<0，则cos α＝________．10．函数y＝sin 2x3＋cos（错误!＋错误!）的图像中相邻的两条对称轴之间的距离是________．11．已知函数f（x）＝cos 2x－2 3sin xcos x，给出下列结论:①存在x1，x2，当x1－x2＝π时，f(x1)＝f(x2)成立；②f(x）在区间[－错误!，错误!］上单调递增;③函数f(x）的图像关于点(错误!，0)中心对称;④将函数f（x）的图像向左平移错误!个单位后所得图像与g（x）＝2sin 2x的图像重合．其中正确结论的序号为________．三、解答题（本大题共2小题，共25分)得分12．(12分）已知函数f（x）＝4cos xsin 错误!－1.(1）求f（x）的最小正周期；（2）求f（x)在区间错误!上的最大值和最小值．13。
数学必修四人教版全国通用版讲义：第三章 三角恒等变换3.2.1 Word版含答案
§3.2倍角公式和半角公式3．2.1 倍角公式学习目标1.会从两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.2.能熟练运用二倍角的公式进行简单的恒等变换并能灵活地将公式变形运用．知识点一二倍角公式的推导思考1二倍角的正弦、余弦、正切公式就是用α的三角函数表示2α的三角函数的公式．根据前面学过的两角和与差的正弦、余弦、正切公式，你能推导出二倍角的正弦、余弦、正切公式吗？答案sin 2α＝sin(α＋α)＝sin αcos α＋cos αsin α＝2sin αcos α；cos 2α＝cos(α＋α)＝cos αcos α－sin αsin α＝cos2α－sin2α；tan 2α＝tan(α＋α)＝2tan α1－tan2α.思考2根据同角三角函数的基本关系式sin2α＋cos2α＝1，你能否只用sin α或cos α表示cos 2α？答案cos 2α＝cos2α－sin2α＝cos2α－(1－cos2α)＝2cos2α－1；或cos 2α＝cos2α－sin2α＝(1－sin2α)－sin2α＝1－2sin2α.梳理二倍角的正弦、余弦、正切公式sin2α＝2sin αcos α，(S2α)cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α，(C2α)tan 2α＝2tan α1－tan2α. (T2α) 知识点二二倍角公式的变形(1)公式的逆用2sin αcos α＝sin 2α，sin αcos α＝12sin 2α， cos 2α－sin 2α＝cos 2α，2tan α1－tan 2α＝tan 2α. (2)二倍角公式的重要变形——升幂公式和降幂公式升幂公式1＋cos 2α＝2cos 2α，1－cos 2α＝2sin 2α，1＋cos α＝2cos 2α2,1－cos α＝2sin 2α2. 降幂公式cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2.1．sin α＝2sin α2cos α2.( √ ) 2．cos 4α＝cos 22α－sin 22α.( √ )3．对任意角α，tan 2α＝2tan α1－tan 2α.( × ) 提示 公式中所含各角应使三角函数有意义．如α＝π4及α＝π2，上式均无意义.类型一 给角求值例1 求下列各式的值．(1)cos 72°cos 36°；(2)13－23cos 215°； (3)1－tan 275°tan 75°；(4)1sin 10°－3cos 10°. 解 (1)cos 36°cos 72°＝2sin 36°cos 36°cos 72°2sin 36° ＝2sin 72°cos 72°4sin 36°＝sin 144°4sin 36°＝14. (2)13－23cos 215°＝－13(2cos 215°－1)＝－13cos 30° ＝－36. (3)1－tan 275°tan 75°＝2·1－tan 275°2tan 75°＝2·1tan 150°＝－2 3. (4)1sin 10°－3cos 10°＝cos 10°－3sin 10°sin 10°cos 10°＝2⎝⎛⎭⎫12cos 10°－32sin 10°sin 10°cos 10°＝4(sin 30°cos 10°－cos 30°sin 10°)2sin 10°cos 10°＝4sin 20°sin 20°＝4. 反思与感悟 对于给角求值问题，一般有两类：(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式子进行转化，一般可以化为特殊角．(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现可以连用二倍角的正弦公式的形式．跟踪训练1 求下列各式的值：(1)cos 2π7cos 4π7cos 6π7； (2)1sin 50°＋3cos 50°. 解 (1)原式＝2sin 2π7cos 2π7cos 4π7cos 6π72sin 2π7＝sin 4π7cos 4π7cos 6π72sin 2π7＝sin 8π7cos 6π74sin 2π7＝sin π7cos π74sin 2π7＝sin 2π78sin 2π7＝18. (2)原式＝cos 50°＋3sin 50°sin 50°cos 50°＝2⎝⎛⎭⎫12cos 50°＋32sin 50°12×2sin 50°cos 50°＝2sin 80°12sin 100°＝2sin 80°12sin 80°＝4. 类型二 给值求值例2 (1)若sin α－cos α＝13，则sin 2α＝________. 答案 89解析 (sin α－cos α)2＝sin 2α＋cos 2α－2sin αcos α＝1－sin 2α＝⎝⎛⎭⎫132⇒sin 2α＝1－⎝⎛⎭⎫132＝89.(2)若tan α＝34，则cos 2α＋2sin 2α等于( ) A.6425 B.4825 C ．1 D.1625答案 A解析 cos 2α＋2sin 2α＝cos 2α＋4sin αcos αcos 2α＋sin 2α＝1＋4tan α1＋tan 2α. 把tan α＝34代入，得 cos 2α＋2sin 2α＝1＋4×341＋⎝⎛⎭⎫342＝42516＝6425.故选A. 引申探究 在本例(1)中，若改为sin α＋cos α＝13，求sin 2α. 解 由题意，得(sin α＋cos α)2＝19， ∴1＋2sin αcos α＝19，即1＋sin 2α＝19. ∴sin 2α＝－89. 反思与感悟 (1)条件求值问题常有两种解题途径：①对题设条件变形，把条件中的角、函数名向结论中的角、函数名靠拢．②对结论变形，将结论中的角、函数名向题设条件中的角、函数名靠拢，以便将题设条件代入结论．(2)一个重要结论：(sin θ±cos θ)2＝1±sin 2θ.跟踪训练2 已知tan α＝2.(1)求tan ⎝⎛⎭⎫α＋π4的值； (2)求sin 2αsin 2α＋sin αcos α－cos 2α－1的值． 解 (1)tan ⎝⎛⎭⎫α＋π4＝tan α＋tan π41－tan αtan π4＝2＋11－2×1＝－3. (2)sin 2αsin 2α＋sin αcos α－cos 2α－1＝2sin αcos αsin 2α＋sin αcos α－2cos 2α ＝2tan αtan 2α＋tan α－2＝2×24＋2－2＝1.类型三 利用倍角公式化简例3 化简2cos 2α－12tan ⎝⎛⎭⎫π4－αsin 2⎝⎛⎭⎫π4＋α. 解 方法一 原式＝2cos 2α－12·sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－αsin 2⎝⎛⎭⎫π4＋α ＝2cos 2α－12·sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π4－α＝2cos 2α－1sin ⎝⎛⎭⎫π2－2α ＝cos 2αcos 2α＝1. 方法二 原式＝cos 2α2·1－tan α1＋tan α⎝⎛⎭⎫22sin α＋22cos α2 ＝cos 2αcos α－sin αcos α＋sin α(sin α＋cos α)2＝cos 2α(cos α－sin α)(cos α＋sin α)＝cos 2αcos 2α－sin 2α＝1. 反思与感悟 (1)对于三角函数式的化简有下面的要求：①能求出值的应求出值．②使三角函数种数尽量少．③使三角函数式中的项数尽量少．④尽量使分母不含有三角函数．⑤尽量使被开方数不含三角函数．(2)化简的方法：①弦切互化，异名化同名，异角化同角．②降幂或升幂．跟踪训练3 化简下列各式：(1)若π4＜α＜π2，则1－sin 2α＝________； (2)若α为第三象限角，则1＋cos 2αcos α－1－cos 2αsin α＝________. 答案 (1)sin α－cos α (2)0解析 (1)∵α∈⎝⎛⎭⎫π4，π2，∴sin α＞cos α， ∴1－sin 2α＝1－2sin αcos α ＝sin 2α－2sin αcos α＋cos 2α ＝(sin α－cos α)2＝sin α－cos α.(2)∵α为第三象限角，∴cos α＜0，sin α＜0， ∴1＋cos 2αcos α－ 1－cos 2αsin α＝2cos 2αcos α－2sin 2αsin α ＝－2cos αcos α－－2sin αsin α＝0.1.12sin π12cos π12的值等于( ) A.14 B.18 C.116 D.12答案 B解析 原式＝14sin π6＝18. 2．sin 4π12－cos 4π12等于( ) A ．－12 B ．－32 C.12 D.32答案 B解析 原式＝⎝⎛⎭⎫sin 2π12＋cos 2π12·⎝⎛⎭⎫sin 2π12－cos 2π12＝－⎝⎛⎭⎫cos 2π12－sin 2π12＝－cos π6＝－32. 3.tan 7.5°1－tan 27.5°＝________. 答案 1－32 解析 tan 7.5°1－tan 27.5°＝12·2tan 7.5°1－tan 27.5°＝12tan 15°＝12·tan 45°－tan 30°1＋tan 45°·tan 30°＝1－32. 4．设sin 2α＝－sin α，α∈⎝⎛⎭⎫π2，π，则tan 2α的值是________． 答案 3解析 ∵sin 2α＝－sin α，∴sin α(2cos α＋1)＝0，又α∈⎝⎛⎭⎫π2，π，∴sin α≠0，∴2cos α＋1＝0，即cos α＝－12，sin α＝32，tan α＝－3， ∴tan 2α＝2tan α1－tan 2α＝－231－(－3)2＝ 3. 5．已知sin ⎝⎛⎭⎫π4－x ＝513，0<x <π4，求cos 2x cos ⎝⎛⎭⎫π4＋x 的值． 解 原式＝sin ⎝⎛⎭⎫π2＋2x cos ⎝⎛⎭⎫π4＋x ＝2sin ⎝⎛⎭⎫π4＋x cos ⎝⎛⎭⎫π4＋x cos ⎝⎛⎭⎫π4＋x ＝2sin ⎝⎛⎭⎫π4＋x . ∵sin ⎝⎛⎭⎫π4－x ＝cos ⎝⎛⎭⎫π4＋x ＝513，且0<x <π4， ∴π4＋x ∈⎝⎛⎭⎫π4，π2， ∴sin ⎝⎛⎭⎫π4＋x ＝ 1－cos 2⎝⎛⎭⎫π4＋x ＝1213，∴原式＝2×1213＝2413.1．对于“二倍角”应该有广义上的理解，如：8α是4α的二倍；6α是3α的二倍；4α是2α的二倍；3α是32α的二倍；α2是α4的二倍； α3是α6的二倍；α2n ＝2·α2n ＋1(n ∈N ＋)． 2．二倍角余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛．二倍角的常用形式： ①1＋cos 2α＝2cos 2α；②cos 2α＝1＋cos 2α2； ③1－cos 2α＝2sin 2α；④sin 2α＝1－cos 2α2.一、选择题1．已知α是第三象限角，cos α＝－513，则sin 2α等于( ) A ．－1213 B.1213 C ．－120169 D.120169答案 D解析 由α是第三象限角，且cos α＝－513， 得sin α＝－1213，所以sin 2α＝2sin αcos α＝2×⎝⎛⎭⎫－1213×⎝⎛⎭⎫－513＝120169.故选D. 2．已知x ∈⎝⎛⎭⎫－π2，0，cos x ＝45，则tan 2x 等于( ) A.724 B ．－724 C.247 D ．－247答案 D解析 由cos x ＝45，x ∈⎝⎛⎭⎫－π2，0， 得sin x ＝－35， 所以tan x ＝－34， 所以tan 2x ＝2tan x 1－tan 2x ＝2×⎝⎛⎭⎫－341－⎝⎛⎭⎫－342＝－247，故选D. 3．已知sin 2α＝23，则cos 2⎝⎛⎭⎫α＋π4等于( )A.16B.13C.12D.23答案 A解析 因为cos 2⎝⎛⎭⎫α＋π4＝1＋cos ⎣⎡⎦⎤2⎝⎛⎭⎫α＋π42＝1＋cos ⎝⎛⎭⎫2α＋π22＝1－sin 2α2，所以cos 2⎝⎛⎭⎫α＋π4＝1－sin 2α2＝1－232＝16.故选A.4．如果|cos θ|＝15，5π2<θ<3π，则sin θ2的值是( )A ．－105 B.105 C ．－155 D.155答案 C解析 ∵5π2<θ<3π，|cos θ|＝15，∴cos θ<0，cos θ＝－15.又∵5π4<θ2<3π2，∴sin θ2<0.∴sin 2θ2＝1－cos θ2＝35，sin θ2＝－155.5．已知α为第二象限角，sin α＋cos α＝33，则cos 2α等于() A ．－53 B ．－59 C.59 D.53答案 A解析 由题意，得(sin α＋cos α)2＝13，∴1＋sin 2α＝13，sin 2α＝－23.∵α为第二象限角，∴cos α－sin α<0.又∵sin α＋cos α>0，∴cos α<0，sin α>0，且|cos α|<|sin α|，∴cos 2α＝cos 2α－sin 2α<0，∴cos 2α＝－1－sin 22α＝－1－⎝⎛⎭⎫－232＝－1－49＝－53，故选A. 6．若f (x )＝2tan x －2sin 2x 2－1sin x 2cos x 2，则f ⎝⎛⎭⎫π12的值为( ) A ．4 3 B.833C ．4D ．8 答案 D解析 ∵f (x )＝2sin x cos x ＋2cos x 2sin x 2cos x 2＝2⎝⎛⎭⎫sin x cos x ＋cos x sin x ＝42sin x cos x ＝4sin 2x ， ∴f ⎝⎛⎭⎫π12＝4sin π6＝412＝8.故选D. 二、填空题7．2sin 222.5°－1＝________.答案 －22 解析 原式＝－cos 45°＝－22. 8．若tan θ＝－13，则cos 2θ＝________. 答案 45解析 tan θ＝－13，则cos 2θ＝cos 2θ－sin 2θ ＝cos 2θ－sin 2θcos 2θ＋sin 2θ＝1－tan 2θ1＋tan 2θ＝45. 9．若cos ⎝⎛⎭⎫π4－α＝35，则sin 2α＝________. 答案 －725解析 因为sin 2α＝cos ⎝⎛⎭⎫π2－2α＝2cos 2⎝⎛⎭⎫π4－α－1，又因为cos ⎝⎛⎭⎫π4－α＝35，所以sin 2α＝2×925－1＝－725. 10．sin 6°sin 42°sin 66°sin 78°＝________.答案 116解析 原式＝sin 6°cos 48°cos 24°cos 12°＝sin 6°cos 6°cos 12°cos 24°cos 48°cos 6° ＝sin 96°16cos 6°＝cos 6°16cos 6°＝116. 三、解答题11．若tan α＋1tan α＝103，α∈⎝⎛⎭⎫π4，π2，求sin ⎝⎛⎭⎫2α＋π4＋2cos π4cos 2α的值． 解 由tan α＋1tan α＝103，得tan α＝13或tan α＝3. 又∵α∈⎝⎛⎭⎫π4，π2，∴tan α＝3.∴sin α＝31010，cos α＝1010. ∴sin ⎝⎛⎭⎫2α＋π4＋2cos π4cos 2α ＝sin 2αcos π4＋cos 2αsin π4＋2cos π4cos 2α ＝22×2sin αcos α＋22(2cos 2α－1)＋2cos 2α ＝2sin αcos α＋22cos 2α－22 ＝2×31010×1010＋22×⎝⎛⎭⎫10102－22＝5210－22＝0. 12．已知π<α<32π，化简： 1＋sin α1＋cos α－1－cos α＋1－sin α1＋cos α＋1－cos α . 解 ∵π<α<32π， ∴π2<α2<34π， ∴1＋cos α＝2⎪⎪⎪⎪cos α2＝－2cos α2， 1－cos α＝2⎪⎪⎪⎪sin α2＝2sin α2.∴1＋sin α1＋cos α－1－cos α＋1－sin α1＋cos α＋1－cos α＝1＋sin α－2⎝⎛⎭⎫cos α2＋sin α2＋1－sin α2⎝⎛⎭⎫sin α2－cos α2 ＝⎝⎛⎭⎫cos α2＋sin α22－2⎝⎛⎭⎫cos α2＋sin α2＋⎝⎛⎭⎫sin α2－cos α222⎝⎛⎭⎫sin α2－cos α2 ＝－2cos α2. 13．已知函数f (x )＝2cos ⎝⎛⎭⎫x －π6，x ∈R . (1)求f (π)的值；(2)若f ⎝⎛⎭⎫α＋2π3＝65，α∈⎝⎛⎭⎫－π2，0，求f (2α)的值． 解 (1)f (π)＝2cos ⎝⎛⎭⎫π－π6＝－2cos π6＝－2×32＝－ 3. (2)因为f ⎝⎛⎭⎫α＋2π3＝2cos ⎝⎛⎭⎫α＋2π3－π6＝2cos ⎝⎛⎭⎫α＋π2 ＝－2sin α＝65，所以sin α＝－35. 又α∈⎝⎛⎭⎫－π2，0， 故cos α＝1－sin 2α＝1－⎝⎛⎭⎫－352＝45. 所以sin 2α＝2sin αcos α＝2×⎝⎛⎭⎫－35×45＝－2425， cos 2α＝2cos 2α－1＝2×⎝⎛⎭⎫452－1＝725. 所以f (2α)＝2cos ⎝⎛⎭⎫2α－π6 ＝2cos 2αcos π6＋2sin 2αsin π6＝2×725×32＋2×⎝⎛⎭⎫－2425×12＝73－2425. 四、探究与拓展14．设α是第二象限角，P (x,4)为其终边上的一点，且cos α＝x 5，则tan 2α＝________.答案 247解析 cos α＝x x 2＋42＝x 5， ∴x 2＝9或x ＝0.∴x ＝±3或x ＝0.又∵α是第二象限角，∴x ＝－3，∴cos α＝－35，sin α＝45， ∴tan α＝－43，tan 2α＝2×⎝⎛⎭⎫－431－⎝⎛⎭⎫－432＝－831－169＝－83－79 ＝7221＝247. 15.如图，在矩形ABCD 中，AB ＝2，AD ＝3，P 是AB 的中点．该矩形有一内接Rt △PQR ，P 为直角顶点，点Q ，R 分别落在线段BC 和线段AD 上，记Rt △PQR 的面积为S .设∠BPQ 为α，求S ＝f (α)及f (α)的最大值．解 由题图知，在Rt △PBQ 中，PQ ＝1cos α； 在Rt △P AR 中，RP ＝1sin α. 因为∠RPQ 为直角，所以S ＝12PR ·PQ ＝12·1cos α·1sin α＝1sin 2α. 又因为R ，Q 分别在线段AD ，BC 上，所以π6≤α≤π3，所以π3≤2α≤2π3. 所以sin 2α∈⎣⎡⎦⎤32，1， 所以当2α＝π3或2π3时，(sin 2α)min ＝32， 所以S max ＝233. 所以S ＝f (α)＝1sin 2α⎝⎛⎭⎫π6≤α≤π3，其最大值为233.。
高中数学第三章三角恒等变换3.2简单的三角恒等变换课后习题新人教A版必修4
高中数学第三章三角恒等变换3.2简单的三角恒等变换课后习题新人教A 版必修4解析：cos 2 ■讣〔 琲 答案:B答案:A3. 已知 2sin a=+cos a ,则 tan1B.2或不存在 D.2或不存在解析：由 2sin a = 1 +cos a ,得 4sin a 1 时,tan $ 2.答案:Ba4. 已知 tan =3,则 cos a= )1. cos的值为（2.已知cos©3 B. C.- D.-,540 ° <a<720° ,则 sin 世等于( )a a 270°<:<360° ,135 ° < <180° A. 解析：••• 540° <a<720°. X 21'卩+ 1斗B. 4C. 4等于（a a2不存在，当cos 》工0A.Tl1 + COS —KTT 1 _4 1 _+ 1of 一2S OC当4 4 3A .5B.-5C.-5D. 35解析:cos -tan 2；2 1-3=-5.若函数 ps- f (x )=(1+\?tan x )cosx ,则f U 勿=()A. 2B.-花C.1D皿i f-sin X i解析：••• f(x)=：cos x=cos x+斜sin ■ n nJ12 + 6 2i=2sin答案：Da 1 + tan-6.右 cosa 是第三象限的角，a tan-—等于(A.-2B.?C.2D.-2斗解析：Ta 是第三象限角,cos a=-,sin a=-.2a=COS答案:Bna Sin 2 1 +aa1 + tan — 8 迈cicos21 + sincr 3 l -5cosa —45 —答案:A7.设 5 n < 0<6 n ,cos ^=a ,贝U sin 5= ___________5TT5TT93n2 < - — <-< 2解■/ 5 n <9<6 n, /. V <3n, 4 4答案:--解析：T 在厶 ABC 中 , B+C=t -A ,a sin 2a acos — - sin-a a cos —+sin —又cos9 =a ,二 sin8.在△ABC答案：--202cos"— - sin^ - 1L - sinfl sinff + cosO ~ sin0 + cosOcos X) 3si nm _ 46 +4)答案：； 10.已知函数f (x )上sin [(1 -a )x ]+cos [(1 -a )x ]的最大值为2,则f (x )的最小正周期 为 __________ .解析：••• f (x )=E + Isin [(1 -a )x+0 ](其中怙门卩= R 由已知得金+1=2「a=3.王/• f (x )=2sin( -2x+0 ) . /-T= - = n .答案：nv 'l + COS ZOJM11. 求 '1' -sin 10sin 1 + COSJ 4B +C22+cos 2A=COS (fi + C)2A=1 - cos (IT - A)+cos 2 A=+cos2 1 1+2COS 2A-1=2COS 2A +COS A-29 十 6 2=-9i眄40 + =542CO 4 -血9 - 1ITL4,贝ysin0 + cos?的值等于r K.4= —解析：T sinI 4lh,o<e LTT,3〃 + _cos l4丿 5的值•,0 <e 9.已知sinTT4coslO D cos z5°- sin250解：原式=_.、二1」-sin 10 ° x $肿|j + a|12. 已知2sin ' =sin 9 +cos 9 ,2sin 23 =sin 2 9 ,求证:sin 2 a- (sin a +cos a ) =sin 9 +cos 9 .两边平方得2(1 +sin 2 a )=1 +sin 2 9 ,/• sin 2 9 =1 +2sin 2 a .2又sin 2 9 =2sin 3 ,/• sin 2 9 =1- cos 2 卩./• 1- cos 2 3 =1+2sin 2 a ./• 2sin 2 a +cos 2 3 =0,1sin 2 a +」cos 2 3 =0. + ' cos 2 (3 =0.证明：■/ 2sin -sin 9 +cos 9 ,。
高中数学 第三章 三角恒等变换测试题(含解析)新人教A版必修4(2021年最新整理)
高中数学第三章三角恒等变换测试题（含解析）新人教A版必修4 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章三角恒等变换测试题（含解析）新人教A版必修4）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章三角恒等变换测试题（含解析）新人教A版必修4的全部内容。
第三章三角恒等变换一．选择题（本大题共12小题，每小题5分,共60分.在每小题给出的四个选项中，只有一个是符合题目要求的） 1.15sin 951852-等于 （ ） A 。
185 B.365C 。
3635 D.18352。
已知m A A =+tan 1tan ，则A 2sin 的值为 ( ） A 。
21mB.m 1C.m 2 D 。
m 23．sin 12π—3cos 12π的值是 （ ）A ．0B ． —2C ． 2D ． 2 sin 125π4.已知3cos ()52x x ππ=-<<，则sin 2x =（ ）A.55B.55-C.255- D.2555．若△ABC 中，sin B·sin C＝cos 2错误!，则△ABC 的形状为( ）A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰直角三角形6。
函数sin 3cos 22x xy =+的图象的一条对称轴方程是 （ ）A 。
x =113π B.x =53π C 。
53x π=- D 。
3x π=-7.已知α为锐角，且cos 错误!＝错误!，则cos α的值为( )A 。
错误! B.错误! C 。
错误! D.错误!8。
函数22()cos ()sin ()11212f x x x ππ=-++-是（ )A 。
高中数学必修4(人教A版)第三章三角恒等变换3.1知识点总结含同步练习及答案
α 1 − cos α = 2 2 α 1 + cos α = cos2 2 2 α 1 − cos α = tan2 2 1 + cos α α sin α 1 − cos α tan = = 2 1 + cos α sin α sin 2 12 3 例题： 已知 ，α ∈ (π, π) ，求sin 2α ，cos 2α，tan 2α的值． cos α = − 13 2 12 3 解：因为cos α = − ，α ∈ (π, π) ．所以 13 2 − − − − − − − − − − 5 12 2 − − − − − − − − ． sin α = −√1 − cos2 α = −√1 − (− ) =− 13 13 5 12 120
)
C．
1 9
D．
√5 3
答案： B
因为 sin α =
2 1 ，所以 cos (π − 2α) = − cos 2α = − (1 − 2sin 2 α) = − ． 3 9 )
B．−
3. 化简 A．
sin 2 35∘ − sin 20∘
1 2 = (
答案： B
1 2
1 2
C．−1
D．1
4. 如图，正方形 ABCD 的边长为 1 ，延长 BA 至 E，使 AE = 1 ，连接 EC , ED，则 sin ∠CED =
（1）已知 sin α =
= (− cos 83∘ )(− cos 23∘ ) + sin 83∘ sin 23∘ = cos(83∘ − 23∘ ) 1 = cos 60∘ = . 2
sin(
π π π + α) = sin cos α + cos sin α 3 3 3 4 1 3 √3 = × + × 2 5 2 5 4√3 + 3 = 10 π π π − α) = sin cos α − cos cos α 3 3 3 4 1 3 √3 = × − × 2 5 2 5 3 − 4√3 = 10
新版高中数学人教A版必修4习题：第三章三角恒等变换 3.2.1
精心整理提升自我3.2简单的三角恒等变换第1课时三角恒等变换课时过关·能力提升基础巩固1设5π<θ<6π,co那么等于-A.C.-解析:若5π<θ<6π,则--则si答案:D2y=sin x cos x+sin2x可化为()A.y-B.yC.y=si-D.y=2si解析:y2x-2x2x精心整理提升自我答案:A3已知cos α=则等于A.C.解析:则si-答案:D等于A.tan αB.tan 2αC.1 D解析:原式2α.答案:B5化简A.sin αB.cos αC.1+sin 2αD.1-sin 2α解析:原式=2si=2cos=1+co2α.答案:D6已知sin θ则解析:∵θ∈∴cosθ=-∴co答案:7若-则的值为解析:由已知得--α+cosα答案:8已知ta则解析:∵ta---解得cosα答案:9已知sin θ+cos θ=2sin α,sin2β=sin θcos θ,求证:2cos 2α=cos 2β.分析观察已知条件和要证的结论,发现要证的等式中不含角θ,因此从已知条件中消去角θ,问题即可得证.证明由题意,得①②①2-②×2,得4sin2α-2sin2β=1.∴1-2sin2β=2-4sin2α,则有cos2β=2cos2α.10已知函数f(x)=2sin(π-x)cos x.(1)将f(x)化为A sin(ωx+φ)的形式(A>0,ω>0);(2)求f(x)的最小正周期;(3)求f(x)在区间-上的最大值和最小值解(1)f(x)=2sin(π-x)cos x=2sin x cos x=sin2x.(2)由(1)知函数f(x)的最小正周期为T(3)由≤x≤得≤2x≤π,所以≤sin2x≤1,即f(x)的最大值为1,最小值为能力提升1已知θ为锐角,sin 2θ=则A.解析:∵θ是锐角,∴si∵sin2θ=-co∴sin∴si答案:B2函数f(x)=co则可化为AC.1解析:f(x)=cos2x co2x si2x2x2x2x2x.答案:A3已知向量m=(sin x,1),n函数m·n的最大值为6,则A的值为()A.6B.3C.解析:f(x)=m·n x cos x2x==A si因为A>0,所以A=6.答案:A4若si-则解析:si-2x=sin2x-cos2x解得tan2x=4.答案:4★5若co-则解析:co-2θ∴cos2θ∴sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ=1=1-答案:6已知函数f(x)=sin x+si∈R.(1)将f(x)化为A sin(ωx+φ)(A>0,ω>0)的形式;(2)求f(x)的最小正周期;(3)求f(x)的最大值和最小值.解(1)f(x)=sin x+si x+cos x(2)f(x)的最小正周期为2π.(3)∵si的最大值、最小值分别为1,-1,∴f(x)的最大值为最小值为7在△ABC中,已知ta求的值解∵A+B+C=π,∴ta- C.∴2si·co又C∈(0,π),∴co≠0.∴2si∴sin又0★8设2si求证:sin 2α证明将2siθ+cosθ两边平方,得2sinθcosθ=4sin 即sin2θ=4sin将sin2θ=2sin2β代入,得2sin2β=4sin∴1-cos2β=4sin∴-2β.∴-2sin2α=cos2β,即sin2α2β=0.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.2简单的三角恒等变换第1课时三角恒等变换课时过关·能力提升基础巩固1设5π<θ<6π,co sθ2=a,那么sinθ4等于()A.−√1+a2B.−√1-a2C.−√1+a2D.−√1-a2解析:若5π<θ<6π,则5π2<θ2<3π,5π4<θ4<3π2,则si nθ4=−√1-cosθ22=−√1-a2.答案:D2y=sin x cos x+sin2x可化为()A.y=√22sin(2x-π4)+12B.y=√2sin(2x+π4)−12C.y=si n(2x-π4)+12D.y=2si n(2x+3π4)+1解析:y=12sin2x+1-cos2x2=12sin2x−12cos2x+12=√22(√22sin2x-√22cos2x)+12=√22sin(2x-π4)+12.答案:A3已知cos α=−15,π<α<3π2,则sinα2等于()A.−√105B.√105C.−√155D.√155解析:∵π2<α<π,∴π4<α2<π2,则si nα2=√1-cosα2=√155.答案:D42sin2αsin2α·2cos2αcos2α等于()A.tan αB.tan 2αC.1D.12解析:原式=(2sinαcosα)2sin2αcos2α=sin22αsin2αcos2α=sin2αcos2α=tan2α.答案:B5化简cos2αtan(π4+α)=() A.sin α B.cos αC.1+sin 2α D.1-sin 2α解析:原式=sin(π2+2α)tan(π4+α)=sin2(π4+α)tan(π4+α)=2si n(π4+α)cos(π4+α)·cos(π4+α)sin(π4+α)=2cos2(π4+α)=1+cos2(π4+α)=1+co s(π2+2α)=1−sin2α.答案:D6已知sin θ=45,θ∈(π2,π),则cosθ2=.解析:∵θ∈(π2,π),∴θ2∈(π4,π2).∴cosθ=−√1-sin2θ=−35.∴co sθ2=√1+cosθ2=√55.答案:√557若sin(α-π4)cos2α=−√2,则sin α+cos α的值为.解析:由已知得sinαcosπ4-cosαsinπ4cos2α-sin2α=√22(sinα-cosα)(cosα+sinα)(cosα-sinα)=√2(sinα+cosα)=−√2.∴sin α+cos α=12. 答案:128已知ta n α2=13,则cos α= .解析:∵ta n α2=±√1-cosα1+cosα,∴tan2α2=1-cosα1+cosα.∴1-cosα1+cosα=19,解得cos α=45.答案:459已知sin θ+cos θ=2sin α,sin 2β=sin θcos θ,求证:2cos 2α=cos 2β.分析观察已知条件和要证的结论,发现要证的等式中不含角θ,因此从已知条件中消去角θ,问题即可得证.证明由题意,得{2sinα=sinθ+cosθ,sin 2β=sinθcosθ.①②①2-②×2,得4sin 2α-2sin 2β=1.∴1-2sin 2β=2-4sin 2α,则有cos2β=2cos2α.10已知函数f (x )=2sin(π-x )cos x.(1)将f (x )化为A sin(ωx+φ)的形式(A>0,ω>0);(2)求f (x )的最小正周期;(3)求f (x )在区间[-π6,π2]上的最大值和最小值.解(1)f (x )=2sin(π-x )cos x=2sin x cos x=sin2x.(2)由(1)知函数f (x )的最小正周期为T =2π2=π. (3)由−π6≤x ≤π2,得−π3≤2x ≤π,所以−√32≤sin2x ≤1,即f (x )的最大值为1,最小值为−√32.能力提升1已知θ为锐角,sin 2θ=−79,则sin (π4+θ)=( )A.±13B.13C.−13D.±√23解析:∵θ是锐角,∴π4+θ<π,∴si n (π4+θ)>0. ∵sin2θ=-co s (π2+2θ)=2sin2(θ+π4)−1=−79,∴sin 2(θ+π4)=19, ∴si n (θ+π4)=13.答案:B2函数f (x )=co s (2x +π3)+12−12cos 2x,则f(x)可化为( ) A .12−√32sin 2xB.12+√32sin 2xC.1−√3sin 2xD.−√32sin 2x解析:f(x)=cos2x co s π3−sin2x si nπ3+12−12cos2x=12cos2x−√32sin2x+12−12cos2x=12−√32sin2x.答案:A3已知向量m=(sin x,1),n=(√3Acosx,A2cos2x)(A>0),函数f(x)=m·n的最大值为6,则A的值为()A.6B.3C.3√2D.12解析:f(x)=m·n=√3Asin x cos x+A2cos2x=A(√32sin2x+12cos2x)=A si n(2x+π6).因为A>0,所以A=6.答案:A4若si n(3π2-2x)=35,则tan2x=.解析:si n(3π2-2x)=−cos2x=sin2x-cos2x=sin2x-cos2xsin2x+cos2x=tan2x-1tan2x+1=35,解得tan2x=4.答案:4★5若co s(π4+θ)cos(π4-θ)=14,则sin4θ+cos4θ=.解析:co s(π4+θ)cos(π4-θ)=cos(π4+θ)sin(π4+θ)=12sin2(π4+θ)=12sin (π2+2θ)=12cos 2θ=14,∴cos2θ=12.∴sin 4θ+cos 4θ=(sin 2θ+cos 2θ)2-2sin 2θcos 2θ =1−12sin22θ=1−12(1−cos22θ) =1−12×(1-14)=58. 答案:586已知函数f (x )=sin x+si n (x +π2),x ∈R .(1)将f (x )化为A sin(ωx+φ)(A>0,ω>0)的形式;(2)求f (x )的最小正周期;(3)求f (x )的最大值和最小值.解(1)f (x )=sin x+si n (x +π2)=sin x+cos x =√2(√22sinx +√22cosx)=√2sin (x +π4). (2)f (x )的最小正周期为2π.(3)∵si n (x +π4)的最大值、最小值分别为1,-1, ∴f (x )的最大值为√2,最小值为−√2.7在△ABC 中,已知ta n A+B 2=sin C,求sin C 2的值.解∵A+B+C=π,∴A+B 2=π2−C 2.∴ta n A+B 2=tan (π2-C 2)=cos C 2sin C 2=sin C. ∴2si n C 2·co s C 2=cos C 2sin C 2.又C ∈(0,π),∴C 2∈(0,π2).∴co s C 2≠0.∴2si n C 2=1sin C 2, ∴sin 2C 2=12.又0<C 2<π2,∴sin C 2>0.∴sin C 2=√22.★8设2si n (π4+α)=sin θ+cos θ,2sin2β=sin 2θ.求证:sin 2α+12cos 2β=0.证明将2si n (π4+α)=sin θ+cos θ两边平方,得2sin θcos θ=4sin 2(π4+α)−1,即sin2θ=4sin 2(π4+α)−1,将sin2θ=2sin 2β代入,得2sin 2β=4sin 2(π4+α)−1,∴1-cos2β=4sin 2(π4+α)−1.∴2[1-2sin 2(π4+α)]=cos 2β. ∴-2sin2α=cos2β,即sin2α+12cos 2β=0.。