《平行线分线段成比例》习题1
平行线分线段成比例定理的_典型例题

平行线分线段成比例的一些学习技巧平行线分线段成比例是相似三角形学习的基础,但学习的策略是相同的,我认为需要掌握一定数量的基本图形,需要有学习者个单独的独特的解答策略。
而很多同学往往都只是用原有的方法解决后来学习的内容,这对几何学习,尤其是相似三角形的学习是相当不利的。
下面介绍一些平行线分线段成比例的基本习题。
例1(1)已知,则=(2)如果,那么的值是()A.7 B.8 C.9 D.10分析本考题主要考查比与代数式比的互换.第(1)小题可将代数式比的形式转化成积的形式:,整理后再转化成比的形式,便有对于第(2)小题,可连续运用两次等比定理,得出,即,其比的比值为9,故选C,但这里需要注意的是:第一,等比定理本身隐含着一个约束条件——分母为零;第二,“比”与“比值”是两个不同的概念,比是一种运算,而比的比值是运算的结果.例2、已知:1、、2三个数,请你再添上个数,写出一个比例式 .分析这是一道开放型试题,旨在考查学生的发散思维能力,由于题中没有明确告知求1、、2的第四比例项,因此,所添的数可能是前三数的第四比例项,也可能不是前三数的第四比例项,这样本考题便有多种确定方法,如从可求出,便有比例式或,从,又能求出,也得到比例式等等.例3如下图,BD=5:3,E为AD的中点,求BE:EF的值.分析应设法在已知比例式BD:DC与未知比例式BE:EF之间架设桥梁,即添平行线辅助线.解过D作DG∥CA交BF于G,则中点,DG∥AF,例 4如下图,AC∥BD,AD、BC相交于E,EF∥BD,求证:分析待证式可变形为.依AC∥EF∥BD,可将线段的比例式与化归为同一直线AB上的线段比而证得.证明AC∥EF∥BD,.说明证明线段倒数和的关系的常见方法是先变形为证线段比的和为一定值,然后化归为同一直线上的线段比.例5、已知a、b、c均为非零的实数,且满足求的值.解设则三式相加,得当时,有时,则,这时原式=例6如下图,中,D是AB上一点,E是内一点,DE∥BC,过D作AC的平行线交CE的处长线于F,CF与AB交于P,求证BF∥AE.证明DE∥AC,∥,..BF∥AE.。
初三数学平行线分线段成比例专题练习试题

平行线分线段成比率专题练习题1.如图,若 DE//BC,则以下式子不建立的是()A.AD AEB.AD ECC.AD AE DED.BD ECBD EC AB AC AB AC BC AB AC2.如图,在△ ABC中,DE∥BC,DE分别与 AB、AC订交于点 D、E,若 AD=4,DB=2,则AE︰EC的值为A. 0.5B. 2C.2D.3323.如图, l 1∥l 2∥l 3,依据“平行线分线段成比率定理” ,以下比率式中正确的是()A.AD CEB.AD BCC.AB CDD.AD DFBC DF BE AF CD EF BC CEAD EBC4.以以下图,△ABC中若 DE∥ BC, EF∥ AB,则以下比率式正确的选项是()A.B.C.D.5.如图,已知AB // CD // EF,AD : AF 3 : 5 , BE 12 ,那么CE的长等于().A.36B. 24C.15D.9 55226.如图,直线 l 1//l 2// l 3,直线 AC分别交 l 1, l 2, l 3于点 A, B, C;直线 DF分别交 l 1, l 2, l 3于点D, E, F .AC与 DF相较于点 H,且 AH=2, HB=1, BC=5,则的值为()( A)1(B)2(C)2(D)257.如图, AD∥ BE∥ CF,直线 l 1、l 2这与三条平行线分别交于点A、B、C 和点 D、E、F.已知 AB=l ,BC=3,DE =2,则 EF' 的长为()A. 4B.5C.6D.88.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点AB3DE A、B、C 和 D、E、F.已知2,则BC DF的值为()A.3B .2C .2D .3 23559.以以下图,△ ABC中, DE∥ BC,若AD1,则以下结论中正确的选项是()DB2A.AE1B. DE1 EC2BC2△ ADE的周长1△ ADE 的面积1C.= D .=△ ABC的周长3△ ABC的面积310.如图,直线 l 1∥ l 2∥ l 3,直线 AC分别交 l 1,l 2,l 3于点 A,B,C;直线 DF分别交 l 1,l 2,l 3于点 D,E,F. AC与 DF订交于点H,且 AH=2, HB=1, BC=5,则DE的值为EF11.如图,已知:△ABC中, DE∥ BC, AD=3, DB=6, AE=2,则 EC=_______.12.如图,在△ ABC中, DE∥ BC,分别交 AB,AC于点 D、E.若 AD=3,DB=2,BC=6,则 DE的长为.13.如图,在△ABC中, DE∥BC,分别交A B, AC于点 D,E.若 AD =3, DB =2, BC =6,则 DE的长为.14.在平行四边形ABCD中, E 为 BC边上的一点.连结AE.A DBE C(1)若 AB=AE,求证:∠ DAE=∠ D;(2)若点 E 为 BC的中点,连结 BD,交 AE于 F,求 EF︰ FA的值.15.(本小题满分10 分)如图,已知B、C、E 三点在同一条直线上,△ABC与△ DCE都是等边三角形 . 此中线段 BD交 AC于点 G,线段 AE交 CD于点 F.DAG FB C E求证:( 1)△ ACE≌△ BCD;(2)AG AF. GC FE16.如图,在△ABC中,已知DE∥ BC, AD=4, DB=8, DE=3.( 1)求的值;( 2)求 BC的长.17.如图, a∥ b∥ c,(1)若 AC=6cm, EC=4cm, BD=8cm,则线段 DF 的长度是多少厘米?(2)若 AE: EC=5:2, DB=5cm,则线段 DF的长度是多少厘米?18.请阅读下边资料,并回答所提出的问题.三角形内角均分线定理:三角形的内角均分线分对边所得的两条线段和这个角的两边对应成比率.已知:如图,△ABC中, AD 是角均分线.求证:AB BD.AC DC证明:过 C 作 CE ∥ DA ,交 BA 的延伸线于 E .∴ D1 = DE,D2 = D3. ①AD 是角均分线,∴D1= D 2.3E .AC AE .②又AD // CE ,ABBD ③AE .DCAB BD . ACDC( 1)上述证明过程中,步骤①②③处的原因是什么?(写出两条即可)( 2)用三角形内角均分线定理解答:已知,△ABC 中, AD 是角均分线, AB=7cm ,AC=4cm ,BC=6cm ,求 BD的长;ACDB( 3)我们知道假如两个三角形的高相等,那么它们面积的比就等于底的比.请你经过研究△ ABD 和△ ACD面积的比来证明三角形内角均分线定理.19.如图,梯形ABCD中, DC//EF//AB , AC交 EF于 G.若 AE=2ED,CF=2cm,那么 CB的长是多少?20.如图,在△ ABC中, D, E,F 分别是边A B,AC,BC上的点,且DE∥ BC,EF∥ AB,AD:DB=3:2,BC=20㎝,求 FC的长.。
(完整版)平行线分线段成比例经典例题与变式练习(含标准答案)

平行线分线段成比例知识梳理1. 平行线分线段成比例定理2. 平行线分线段成比例定理的推论:如图,在三角形中,如果 AD AE DE3. 平行的判定定理:如上图,如果有 A A D B A A C E B D C E ,那么DE ∥ BC专题讲解专题一、平行线分线段成比例定理及其推论基本应用【例1】如图, DE ∥ BC ,且 DB AE ,若AB 5,AC 10,求 AE 的长。
如下图,如果 l 1∥ l 2∥ l 3,则BC ACAB DEAC DFABDE AC 1 2DFEFDFDE ∥ BC ,则A A DB A A EC BD C E例2】如图,已知 AB / /EF //CD ,若 AB a ,CD b ,EF c ,求证:1 1ca【巩固】如图, AB BD ,CD BD ,垂足分别为 B 、 D ,AC 和 BD 相交于点 E ,EFBD ,垂足为 F .证明: A 1B C 1D E 1F .【例3】如图,在梯形 ABCD 中, AB ∥CD , AB 12,CD 9 ,过对角线交点 O 作EF ∥ CD 交AD ,BC 于E ,F ,求 EF 的长。
AE巩固】如图,找出 S ABDS BEDS BCD 之间的关系,并证明你的结论1 b【巩固】(上海市数学竞赛题)如图,在梯形 ABCD 中, AD ∥BC , AD a ,BC b ,E ,F 分别 是AD ,BC 的中点, AF 交 BE 于 P , CE 交 DF 于 Q ,求 PQ 的长。
专题二、定理及推论与中点有关的问题 【例4】( 2007 年北师大附中期末试卷)1(1)如图( 1),在 ABC 中, M 是 AC 的中点, E 是 AB 上一点,且 AE 1AB ,4的值为( )5A. B.1 C.2 【例5】( 2001 年河北省中考试卷)如图,在 AC 边上的任意一点, BE 交 AD 于点O . (1)当 AE 1时,求 AO的值;AC 2 AD3 / 14连接 EM 并延长, 交 BC 的延长线于 D ,则 BCCD2)如图( 2),已知 ABC 中, AE : EB 1:3 , B D :DC 2:1 , AD 与CE 相交于 F ,则 EF FC AFFDD.2A2)当AE 1、1时,求AO的值;AC 3 4 AD3)试猜想AE 1时AO的值,并证明你的猜想AC n 1 AD【例6】(2003年湖北恩施中考题)如图,AD是ABC的中线,点E在AD上,F是BE 延长线与AC 的交点.(1)如果E是AD的中点,求证:AF 1;FC 2(2)由(1)知,当E是AD中点时,AF 1 AE成立,若E是AD上任意一点(E与A、D FC 2 ED 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.【巩固】(天津市竞赛题)如图,已知ABC中,AD是BC边上的中线,E是AD 上的一点,且BE AC ,延长BE 交AC 于 F 。
初三数学平行线分线段成比例专题练习题
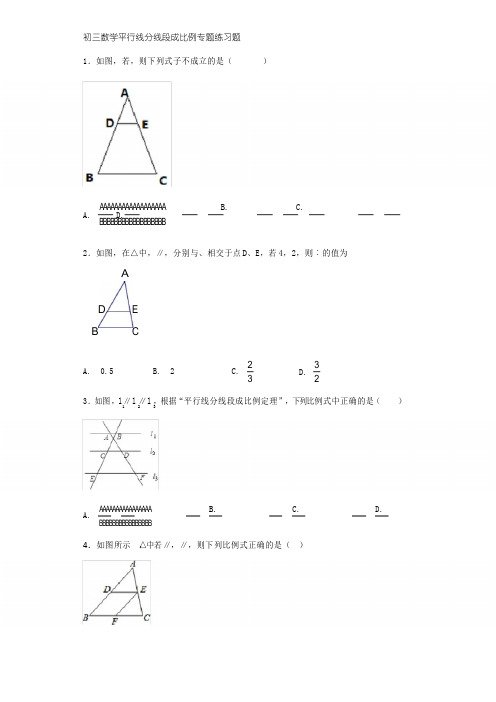
初三数学平行线分线段成比例专题练习题1.如图,若,则下列式子不成立的是()A.AAAAAAAAAAAAAAAAAAB.C.D.BBBBBBBBBBBBBBBBBB2.如图,在△中,∥,分别与、相交于点D、E,若4,2,则︰的值为AD BE CA.0.5B.2C.23D. 323.如图,l∥l∥l,根据“平行线分线段成比例定理”,下列比例式中正确的是()1 2 3A.AAAAAAAAAAAAAAAAB.C.D. BBBBBBBBBBBBBBBB4.如图所示△,中若∥,∥,则下列比例式正确的是()A .5.如图,已知 B .C .AB // CD // EF ,AD : AF 3 : 5 D .,BE 12,那么 C E 的长等于().A .36 5B .24 15 9 C .D .5226.如图,直线 l l l ,直线分别交 l , l , l 于点 A ,B ,C ;直线分别交 l , l , 12312312l 于点 D ,E ,F .与相较于点 H ,且 2,1,5,则 的值为( )3(A )1 2(B )2(C )25(D )7.如图,∥∥,直线 l 、l 这与三条平行线分别交于点 A 、B 、C 和点 D 、E 、F .已知, 123, =2,则'的长为()A .4B .5C .6D .88.如图, l 1∥ l 2∥ l 3,两条直线与这三条平行线分别交于点 A 、B 、C 和 D 、E 、F .已知AB 3 DE,则 的值为( ) BC 2 DFA .3 2 23 B .C .D .23559.如图所示,△中△ ,∥,若AD 1 DB 2,则下列结论中正确的是( )A .AE 1 DE 1B .EC 2BC 2C .△ADE 的周长 1= △ABC 的周长 3D .△ADE 的面积 1= △ABC 的面积 310.如图,直线 l ∥l ∥l ,直线分别交 l ,l ,l 于点 A ,B ,C ;直线分别交 l ,l ,1 2 3 1 2 3 12l 于点 D ,E ,F .与相交于点 H ,且 2,1,5,则 3DD EE的值为11.如图,已知:△中△ ,∥,3,6,2,则.12.如图,在△中△,∥,分别交,于点D、E.若3,2,6,则的长为.13.如图,在△中△,∥,分别交,于点D,E.若=3,=2,=6,则的长为.14.在平行四边形中,E为边上的一点.连结.A DB E C(1)若,求证:∠∠D;(2)若点E为的中点,连接,交于F,求︰的值.15.(本小题满分10分)如图,已知B、C、E三点在同一条直线上△,△△与都是等边三角形.其中线段交于点G,线段交于点F.求证:(1)△≌△;(2)AG AF GC FE.16.如图,在△中△,已知∥,4,8,3.(1)求 的值;(2)求的长.17.如图,a ∥b ∥c,(1)若 6,4,8,则线段的长度是多少厘米?(2)若:5:2,5,则线段的长度是多少厘米?18.请阅读下面材料,并回答所提出的问题.三角形内角平分线定理:三角形的内角平 分线分对边所得的两条线段和这个角的两边对应成比例.已知:如图,△中, 是角平分线.求证:AB BD AC DC.证明:过 C 作∥,交的延长线于 E .∴1 = E ,2 = 3. ①是角平分线,∴1=2.3 E AC AE ..②又A D//CE,AB BD.③AE DCAB BDAC DC.(1)上述证明过程中,步骤①②③处的理由是什么?(写出两条即可)(2)用三角形内角平分线定理解答:已知,△中△,是角平分线,7,4,6,求的长;ACBD(3)我们知道如果两个三角形的高相等,那么它们面积的比就等于底的比.请你通过研究△和△面积的比来证明三角形内角平分线定理.19.如图,梯形中,交于G.若2,2,那么的长是多少?20.如图,在△中△,D,E,F分别是边,上的点,且∥,∥,:3:2,20㎝,求的长.参考答案1.B【解析】试题分析:根据平行线段分线段成比例的性质,可△知△△∽,然后可知A、C、D正确,B答案的线段不对应,故错误.故选B考点:1.平行线的性质,2.相似三角形2.B【解析】试题分析:因为∥,所以︰:4:2=2,故选:B.考点:平行线分线段成比例定理.3.D.【解析】试题解析:∵直线l∥l∥l,1 2 3∴AD BCDF CE,故A错误;AD BC AF BEAF BE DF CECE BC DF AD ,故B错误;故C错误;,故D正确;故选D.考点:平行线分线段成比例定理.4.C【解析】试题分析:用平行线分线段成比例定理以及比例的性质进行变形即可得到答案.解:∵∥,∥,∴四边形是平行四边形,∴,;∵∥,∴,,∵∥,∴=,=,∴,故选C.考点:平行线分线段成比例.5.B【解析】试题分析:根据平行线分线段成比例得到:行计算.AD BC3BC即,可计算出,然后利用进AF BE512∵∴AB//CD//EFAD BC3BC,即AF BE512∴∴36BC5CE BE BC 12362455,故选B考点:平行线分线段成比例.6.D【解析】试题分析:解:∵2,1,∴3,∵l∥l∥l,1 2 3∴,故选:D.考点:平行线分线段成比例.7.C.【解析】试题分析:∵∥∥,∴A A A A12,∵1,3,2,∴B B B B3EF,解得6,故选C.考点:平行线分线段成比例.8.D.【解析】试题分析:∵l1∥l2∥l3,A A3DE AB33,∴B B2DF AC325,故选D.考点:平行线分线段成比例.9.C.【解析】试题分析:∵∥,∴△∽△,∵:1:2,∴:1:3,∴两相似三角形的相似比为1:3,∵周长的比等于相似比,面积的比等于相似比的平方,∴C正确.故选C.考点:相似三角形的判定与性质.10.3 5【解析】试题解析:∵2,1,∴3,∵l∥l∥l,1 2 3∴DE AB3 EF BC5考点:平行线分线段成比例.11.4.【解析】试题解析:∵△中,∥,∴AD AE BD EC,∵3,6,2,∴326EC,∴4.考点:平行线分线段成比例.12.18 5.【解析】试题解析:∵∥∴AD DE AB BC即:AD DE AD DB BC又:3,2,6,3DE ∴326∴DE 18 5.考点:平行线分线段成比例.13.185.【解析】试题分析:由∥可得△∽△,根据相似三角形的性质可得AD DE3DE,即=AB BC56,解得DE 18 5.考点:相似三角形的判定与性质.14.(1)详见解析;(2)︰1︰2,解题过程见解析.【解析】试题分析:(1)由平行四边形的性质可得∠∠;由平行线的性质可得∠∠;由等腰三角形的性质可得∠∠;再由等量代换即可得∠∠;(2)易证△△∽,根据相似三角形对应边的比相等即可得︰的值.A DFB E C试题解析:(1)证明:∵四边形为平行四边形,∴∠∠∥.∴∠∠.又∵∴∠∠.∴∠∠.∴∠∠.(2)∵∥,∴∠∠,∠∠,∴△∽△.︰︰︰1︰2考点:平行四边形的性质;平行线的性质;等腰三角形的性质;相似三角形的判定及性质.15.【解析】试题分析:(1)根据等边三角形的性质可得,,∠=∠60°,且由等量代换得∠ =∠,然后根据全等三角形的判定可得证;(2)根据等边三角形的性质可得,,∠=∠60°,因此可得AB ACCD ED和∥;再由平行线的性质可得∠ =∠,∠∠,然后根据两角相等的两三角形相似,证得△∽△,再由相似三角形的性质得AG AB AF AC,同理证得,从而的证结论. GC CD FE ED试题解析:证明:(1)∵△与△都是等边三角形,∴,,∠=∠60°,∴∠∠=∠∠,即∠=∠,∴△≌△().(2)∵△与△都是等边三角形,∴,,∠=∠60°∴AB ACCD ED,∥,∴∠=∠,∠∠,∴△∽△,∴AG AB GC CD.AF AC同理,FE ED.∴AG AF GC FE.考点:三角形全等,三角形相似的判定与性质16.(1);(2)9.【解析】试题分析:(1)由已知条件求得的值,再求:即可;(2)已知∥,可证△∽△,可得出,把,的值代入,即可求得的值.解:(1)∵4,8∴4+8=12∴=;(2)∵∥∴△∽△∴∵3∴∴9.考点:平行线分线段成比例;相似三角形的判定与性质.17.(1);(2).【解析】试题分析:(1)由平行线分线段成比例定理得出,即可得出结果;(2)由平行线分线段成比例定理得出=,即可得出结果.解:(1)∵a∥b∥c,∴,即,解得:;(2)∵a∥b∥c,∴=,即,解得:.考点:平行线分线段成比例.18.(1)①平行线的性质定理;②等腰三角形的判定定理;③平行线分线段成比例定理;(2)4211.(3)证明见解析.【解析】试题分析:(1)由比例式AB BDAE DC,想到作平行线,用到了平行线的性质定理;只要证明即可,用到了等腰三角形的判定定理;由∥,写出比例式AB BDAC DC,用到了平行线分线段成比例定理(推论);(2)利用三角形内角平分线性质定理,列出比例式,代入数据计算出结果.(3)根据三角形的面积公式进行证明即可.试题解析:(1)证明过程中用到的定理有:①平行线的性质定理;②等腰三角形的判定定理;③平行线分线段成比例定理;(2)∵是角平分线,∴BD ABDC AC,又∵7,4,6,∴BD 76 BD 442,∴().(3)∵△和△的高相等,可得:△和△面积的比=12 1 2BD hDC h1AB hDC 12AB AC,可得:BD ABDC AC .考点:相似形综合题.19.6.【解析】试题分析:由平行线的性质可得 的长.AE AG CF CG,ED GC BC AG,进而再由题中条件即可求解与试题解析:∵∥∥,∴AE AG CF CG =2,又 5,∴2.5.ED GC BC AG,2,∴6.的长是 6.考点:平行线分线段成比例. 20.8.【解析】11 BD 2AC h试题分析:由∥,:3:2,得到AD AE3AE BF3,再由∥,DB EC2EC FC2,可设3k,2k,得到520,解出k的值即可得到的长.试题解析:∵∥,:3:2,∴AD AE3AE BF3,∵∥,,设3k,2k,∴325k,DB EC2EC FC 2又20,∴520,4,∴28.考点:平行线分线段成比例.。
九年级数学下册《第二十七章-平行线分线段成比例》练习题附答案解析-人教版

九年级数学下册《第二十七章 平行线分线段成比例》练习题附答案解析-人教版班级:___________姓名:___________考号:____________一、单选题1.如图,在ABCD 中AB=10,AD=6,E 是AD 的中点,在CD 上取一点F ,使CBF ∽ABE △,则DF 的长是( )A .8.2 B.6.4 C .5 D .1.82.如图,在ABC 中DE ∥BC ,57AD AB 记ADE 的面积为s 1,四边形DBCE 的面积为s 2,则12s s 的值是( )A .57B .2549C .2425D .25243.如图,△ABC 与△DEF 位似,点O 是它们的位似中心,其中OD =2OA ,△ABC 的周长为10,则△DEF 的周长是( )A .20B .30C .40D .904.如图,在ABC 中D 、E 分别是边AB 、AC 上的点,且∥DE BC ,连接CD ,过点E 作EF CD ∥,交AB 于点F ,则下列比例式不成立的是( )A .AF AD AD AB = B .EF DE CD BC = C .AF AD FD BD = D .AF EF FD BC= 5.如图,直线123l l l ∥∥,直线a ,b 与1l ,2l 和3l 分别交于点A ,B ,C 和点D ,E ,F .若:2:3AB BC =和10DF = 则DE 的长是( )A .2B .3C .4D .66.如图,AD 是△ABC 的边BC 上的中线,点E 是AD 的中点,连接BE 并延长交AC 于点F ,则AF :FC =( )A .1:2B .1:3C .1:4D .2:57.如图,两条直线被第三条平行所截,则DE 的长为( )A .4.2B .3.2C .4D .3.68.如图,四边形ABCD 中P 为对角线BD 上一点,过点P 作//PE AB ,交AD 于点E ,过点P 作//PF CD 交BC 于点F ,则下列所给的结论中不一定正确的是( ).A .PE PF AB CD = B .AE BF DE CF =C .1CF AE BC AD += D .1PE PF AB CD+= 9.如图,在菱形ABCD 中点E ,F 分别在AB ,CD 上,且BE =2AE ,DF =2CF ,点G ,H 分别是AC 的三等分点,则S 四边形EHFG ÷S 菱形ABCD 的值为( )A .19B .16C .13D .29二、填空题10.如图,已知AB ∥CD ∥EF ,AD :AF =3:5,BC =6,则CE 的长为______.11.已知ABC ∽A B C ''',分别为ABC 与A B C '''的中线,下列结论中:①:4:3AD A D ''=;②ABD △∽A B D '''△;③ABD △∽A B C ''';④ABC 与A B C ''''对应边上的高之比为4:3.其中结论正确的序号是______.12.如图,△ABC中DE∥BC,G为BC上一点,连结AG交DE于点F,若AF=2,AG=6,EC=5,则AC=________.13.如图,AB∥CD∥EF,若AC=2,CE=5,BD=3则DF=___.三、解答题14.如图在△ABC中D为AB边上一点,且△CBD∽△ACD.(1)求∠ADC度数;(2)如果AC=4,BD=6,求CD的长.15.如图,在△ABC中点D,F,E分别在AB,BC,AC边上,DF∥AC,EF∥AB.(1)求证:△BDF ∽△FEC .(2)设12AE EC =. ①若BC =15,求线段BF 的长;②若△FEC 的面积是16,求△ABC 的面积.16.(1)[基础巩固]如图①,在三角形纸片ABC 中90ACB ∠=︒,将ABC 折叠,使点B 与点C 重合,折痕为MN ,则AM 与BM 的数量关系为______;(2)[思维提高]如图②,在三角形纸片ABC 中将ABC 折叠,使点B 与点C 重合,折痕为MN ,求AM BM 的值; (3)[拓展延伸]如图③,在三角形纸片ABC 中将ABC 沿过顶点C 的直线折叠,使点B 落在边AC 上的点B '处,折痕为CM .求线段AC 的长; 参考答案与解析1.A【分析】E 是AD 的中点可求得AE ,根据三角形相似的性质可得CF BC AE BA=,可得CF 的长即可求解. 【详解】解:∵E 是AD 的中点,6AD =∴132AE AD == 又∵CBF ∽ABE △CF BC AE BA ∴=,即6310CF =解得 1.8CF =10 1.88.2DF DC CF ∴=-=-=故选:A .【点睛】本题考查了三角形相似的性质,掌握三角形相似的性质对应边的比相等是解题的关键.2.D【分析】根据ADE ABC ∆∆∽,通过相似三角形的面积等于相似比的平方,求出ABC ∆与ADE ∆的面积比,再根据21ABC S S S =-得到12s s 的值. 【详解】解:∵DE ∥BC∴ADE ABC ∆∆∽ ∴22549ADE ABC AD A S S B ∆∆⎛⎫== ⎪⎝⎭ ∴14925ABC S S ∆= ∵21ABC S S S =- ∴212425S S = ∴122524S S =故选:D .【点睛】本题考查相似三角形的性质,解题的关键是熟知相似三角形的面积等于相似比的平方.3.A【分析】利用位似的性质得△ABC ∽△DEF ,OD =2OA ,然后根据相似三角形的性质解决问题【详解】解:∵△ABC 与△DEF 位似,点O 为位似中心.∴△ABC ∽△DEF ,OD =2OA∴△ABC 与△DEF 的周长比是:1:2.∴△ABC 的周长为10,则△DEF 的周长是20故选:A .【点睛】本题主要考查了位似变换,正确掌握位似图形的性质是解题关键.4.D【分析】根据平行线分线段成比例和相似三角形的性质可求解.∴成立的是ABC ,不成立的是D故选:D.【点睛】本题考查了平行线分线段成比例,相似三角形的判定和性质,熟练运用相似三角形的性质是本题的关键.5.C【分析】根据平行线分线段定理得到::AB BC DE EF =,设2DE x =,根据10DF =,列方程求解即可.【详解】解:∵123l l l ∥∥∴::2:3AB BC DE EF ==设2DE x =,则3EF x =∵10DF =∴2310x x +=,解得2x =∴4DE =故选:C .【点睛】本题主要考查了平行线分线段定理,熟练掌握平行线分线段定理是解答本题的关键.6.A【分析】作DH ∥AC 交BF 于H ,如图,先证明△EDH ≌△EAF 得到DH =AF ,然后判断DH 为△BCF 的中位线,从而得到CF =2DH .【详解】解:作DH ∥AC 交BF 于H ,如图∵DH ∥AF∴∠EDH =∠EAF ,∠EHD =∠EFA∵DE =AE∴△EDH ≌△EAF (AAS )∴DH =AF∵点D 为BC 的中点,DH ∥CF∴DH 为△BCF 的中位线∴CF =2DH =2AF∴AF :FC =1:2故选:A .【点睛】本题考查平行线分线段成比例定理,三角形的中位线定理,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.7.D 【分析】根据平行线分线段成比例得到AB DE AC DF =,将数据代入即可求出答案. 【详解】解:////AD BE CF ∴AB DE AC DF= 4AB =,6BC =和9DF =∴4610AC AB BC =+=+= ∴4109DE = ∴ 3.6DE =.故选:D .【点睛】本题考查了平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.8.A【分析】根据//PE AB ,可证△EPD ∽△ABD ,△BFP ∽△BCD ,即可判断A ;由//PE AB ,//PF CD 可得AE BP ED PD = BF BP FC PD =可判断B ;由//PE AB ,//PF CD 可得AE BP AD BD =,FC PD BC BD= 可判断C ,由 //PE AB ,可证△EPD ∽△ABD ,△BFP ∽△BCD ,可判定D .【详解】解:A .∵//PE AB∴∠DEP =∠A ,∠DPE =∠DBA∴△EPD ∽△ABD∴ EP DPAB DB =∵//PF CD∴∠BPF =∠BDC ,∠BFP =∠C∴△BFP ∽△BCD∴ PF BPCD DB = ∵DPBPDB DB ≠ ∴PEPFAB CD ≠故选项A 不正确;B .∵//PE AB //PF CD ∴AEBP ED PD = BFBPFC PD = ∴AE BFDE CF =故选项B 正确;C .∵//PE AB //PF CD ∴AE BP AD BD = FCPDBC BD = ∴1AEFCBPPDAD BC BD BD +=+=故选项C 正确1CFAEBC AD +=D .∵//PE AB∴∠DEP =∠A ,∠DPE =∠DBA∴△EPD ∽△ABD∴ EP DPAB DB =∵//PF CD∴∠BPF =∠BDC ,∠BFP =∠C∴△BFP ∽△BCD∴ PF BPCD DB =∴ 1EP PF DP PB DP PB AB CD DB BD BD ++=+==故选项D 正确.故选择A .【点睛】本题考查平行线截线段比例,和三角形相似判定与性质,掌握平行线截线段长比例,和三角形相似判定与性质是解题关键.9.A【分析】由题意可证EG ∥BC ,EG =2,HF ∥AD ,HF =2,可得四边形EHFG 为平行四边形,即可求解.【详解】解:∵BE =2AE ,DF =2FC ∴12AE BC = 12CF DF = ∵G 、H 分别是AC 的三等分点 ∴12AG GC =12CH AH = ∴AE AG BE GC = ∴EG ∥BC ∴13EG AE BC AB == 同理可得HF ∥AD ,13HF AD = ∴111339EHFGABCD S S =⨯=四边形菱形故选:A .【点睛】本题考查了菱形的性质,由题意可证EG ∥BC ,HF ∥AD 是本题的关键.10.4【分析】由AB CD EF ∥∥,推出AD BC AF BE =,推出365BE=,可得结论. 【详解】∵AB CD EF ∥∥ ∴AD BC AF BE = ∴365BE = ∴BE =10∴CE =BE -BD =10-6=4故答案为:4.【点睛】本题考查平行线分线段成比例定理等知识,解题的关键是掌握平行线分线段成比例定理.11.①②④【分析】根据相似三角形的性质,对每个选项进行判断,即可得到答案.【详解】解:∵ABC ∽A B C ''',AD 、A D ''分别为ABC 与A B C '''的中线 ∴4''''3AB AD A B A D ==,故①正确; ∵'B B ∠=∠ 121''''''''2BC BD BC AB B D B C A B B C === ∴ABD △∽A B D '''△,故②正确;∴ABC 与A B C '''对应边上的高之比为4:3,故④正确;而ABD △与A B C '''不相似,故③错误;∴正确的结论有:①②④;故答案为:①②④.【点睛】本题考查了相似三角形的性质,解题的关键是熟练掌握相似三角形对应中线,对应边上的高的比等于相似比.12.7.5【分析】由DE ∥BC ,得AF AE AG AC=,代入已知量即可求得答案. 【详解】解:∵DE ∥BC ∴AF AE AG AC = ∵AE =AC -EC =AC -5,AF =2,AG =6 ∴256AC AC -= 解得AC =7.5故答案为:7.5【点睛】此题主要考查了平行线分线段成比例定理,利用平行线分线段成比例列出比例式是解题的关键. 13.7.5【分析】直接根据平行线分线段成比例定理即可得出结论.【详解】解:∵直线AB ∥CD ∥EF ,AC =2,CE =5,BD =3∴AC BDCE DF=,即235DF=,解得DF=7.5.故答案为:7.5.【点睛】本题考查的是平行线分线段成比例定理,熟知三条平行线截两条直线,所得的对应线段成比例是解答此题的关键.14.(1)∠ADC=90°(2)CD=【分析】(1))由相似三角形的性质及邻补角可进行求解;(2)先证明△ACD∽△ABC,然后根据相似三角形的性质可得ACAB=ADAC,然后代入数值问题可求解.(1)解:∵△CBD∽△ACD ∴∠CDB=∠ADC∵∠CDB+∠ADC=180°∴∠ADC=90°;(2)如图∵△CBD∽△ACD∴∠ACD=∠B∵∠A=∠A∴△ACD∽△ABC∴ACAB=ADAC,即ACAD BD+=ADAC∴46AD+=4AD∴AD=2(负根已经舍弃)∴CD【点睛】本题主要考查相似三角形的判定与性质,熟练掌握相似三角形的性质是解题的关键.15.(1)证明见详解(2)①BF=5;②S△ABC=16×94=36【分析】(1)由平行线的性质得出∠BFD=∠C,∠B=∠EFC,即可得出结论;(2)①由平行线的性质得出12BF AEFC EC==,即可得出结果;②先求出2,3ECAC=易证△EFC∽△ABC,由相似三角形的面积比等于相似比的平方即可得出结果.(1)证明:∵DF∥AC∴∠BFD=∠C∵EF∥AB∴∠B=∠EFC∵∠BFD=∠C,∠B=∠EFC ∴△BDF∽△FEC;(2)解:①∵EF∥AB∴12 BF AEFC EC==∴12 BFBC BF=-∵BC=15∴1 152 BFBF=-∴BF=5;②∵12 AE EC=∴2EC AE=∴2223 EC EC AEAC AE EC AE AE===++∵EF∥AB∴∠CEF=∠B∵∠C=∠C.∠CEF=∠B∴△EFC∽△ABC∴249 EFCABCS ECS AC∆∆⎛⎫==⎪⎝⎭∵S△EFC=16∴S△ABC=94×16=36.【点睛】本题考查了相似三角形的判定与性质、平行线的性质等知识;熟练掌握相似三角形的判定与性质是解题的关键.16.(1)AM=BM(2)16 9(3)152 AC=【分析】(1)利用平行线分线段成比例定理解决问题即可;(2)利用相似三角形的性质求出BM,AM即可;(3)证明△BCM∽△BAC,推出BC BM CMAB BC AC==,由此即可解决问题.(1)解:如图①中∵△ABC折叠,使点B与点C重合,折痕为MN ∴MN垂直平分线段BC∴CN=BN∵∠MNB=∠ACB=90°∴MN∥AC∵CN=BN∴AM=BM.故答案为AM=BM.(2)如图②中∵CA=CB=6∴∠A=∠B由题意MN垂直平分线段BC ∴BM=CM∴∠B=∠MCB∴∠BCM=∠A∵∠B=∠B∴△BCM∽△BAC∴BC BM BA BC=∴6106BM=∴185 BM=∴18321055 AM AB BM=-=-=∴321651895AMBM==.(3)如图③中由折叠的性质可知,CB=CB′=6,∠BCM=∠ACM ∵∠ACB=2∠A∴∠BCM=∠A∵∠B=∠B∴△BCM∽△BAC∴BC BM CM AB BC AC ==∴696BM =∴BM=4∴AM=CM=5∴65 9AC =∴152 AC=.【点睛】本题属于几何变换综合题,考查了相似三角形的判定和性质,等腰三角形的性质,平行线分线段成比例定理等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.。
初三数学平行线分线段成比例专题习题
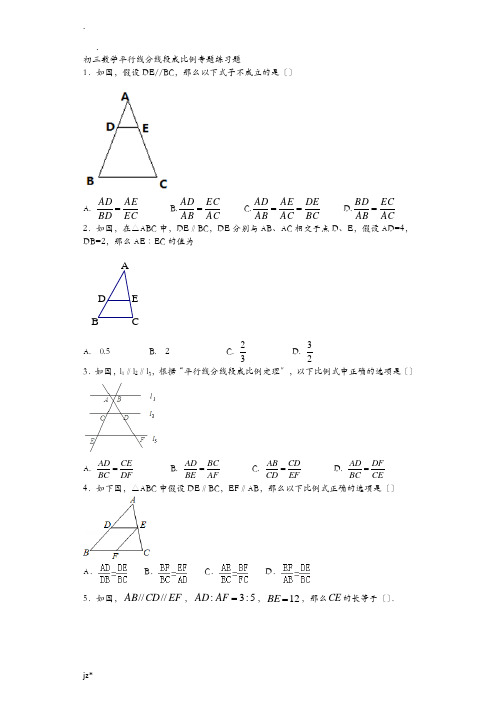
7.如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.AB=l,BC=3,DE =2,那么EF'的长为〔〕
A.4 B.5 C.6 D.8
8.如图, ∥ ∥ ,两条直线与这三条平行线分别交于点A、B、C和D、E、F. ,那么 的值为〔〕
考点:平行线分线段成比例.
20.8.
【解析】
试题分析:由DE∥BC,AD:DB=3:2,得到 ,再由EF∥AB, ,可设BF=3k,FC=2k,得到BC=BF+FC=5k=20cm,解出k的值即可得到FC的长.
试题解析:∵DE∥BC,AD:DB=3:2,∴ ,∵EF∥AB, ,设BF=3k,FC=2k,∴BC=BF+FC=3k+2k=5k,又BC=20cm,∴5k=20,k=4,∴FC=2k=8.
求证:〔1〕△ACE≌△BCD;
〔2〕 .
16.如图,在△ABC中,DE∥BC,AD=4,DB=8,DE=3.
〔1〕求 的值;
〔2〕求BC的长.
17.如图,a∥b∥c,
〔1〕假设AC=6cm,EC=4cm,BD=8cm,那么线段DF的长度是多少厘米?
〔2〕假设AE:EC=5:2,DB=5cm,那么线段DF的长度是多少厘米?
〔3〕∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面积的比= ,
可得: .
考点:相似形综合题.
19.6cm.
【解析】
试题分析:由平行线的性质可得 , ,进而再由题中条件即可求解BC与GC的长.
试题解析:∵DC∥EF∥AB,∴ =2,又AG=5cm,∴GC=2.5cm. ,CF=2cm,
∴BC=6cm.CB的长是6cm.
平行线分线段成比例定理优生课后训练题(附答案)

平行线分线段成比例定理专项练习题1.如图,在Rt △ABC 中,∠C =90°,AC =3,BC =4,点D 是AB 的中点,点P 是直线BC 上一点,将△BDP 沿DP 所在的直线翻折后,点B 落在B 1处,若B 1D ⊥BC ,则点P 与点B 之间的距离为( )A .1B .54C .1或 3D .54或5 2.在平行四边形ABCD 中,E 是AD 上一点,连接CE 并延长交BA 的延长线于点F ,则下列结论错误的是( )A .AEF DEC ∠=∠B .::FA CD AE EC = C .::FA AB EF EC =D .AB DC =3.如图,已知////AB CD EF ,:3:5AD AF =,6BC =,CE 的长为( )A .2B .4C .3D .54.AD 是△ABC 的中线,E 是AD 上一点,AE :ED=1:3,BE 的延长线交AC 于F ,AF :FC=A .1:3B .1:4C .1:5D .1:6 5.如图,已知一组平行线a ∥b ∥c ,被直线m 、n 所截,交点分别为A 、B 、C 和D 、E 、F ,且AB =1.5,BC =2,DE =1.8,则EF =( )A .4.4B .4C .3.4D .2.4 6.如图,已知点D 、E 分别在ABC ∆的边AB 、AC 上,//DE BC ,点F 在CD 延长线上,//BC AF ,则下列结论错误的是( )A .DE AF AF BC =B .FD DC AE EC = C .AD AE AB AC = D .BD DE AB AF = 7.已知在ABC 中,点D 为AB 上一点,过点D 作BC 的平行线交AC 于点E ,过点E 作AB 的平行线交BC 于点F .则下列说法不正确的是( )A .AD AE AB AC = B .DE AE BC AC = C .BF AD BC AB = D .AD BF AB FC = 8.如图,已知E 是平行四边形ABCD 中DA 边的延长线上一点,且AD =2AE ,连接EC 分别交AB ,BD 于点F ,G .(1)求证:BF =2AF ;(2)若BD =20cm ,求DG 的长.9.如图,已知DE ∥BC ,FE ∥CD ,AF =3,AD =5,AE =4.(1)求CE 的长;(2)求AB 的长.10.如图,在ABC △中,D 为AC 上一点,E 为CB 的延长线上一点,连接BD 交AB 于点F ,且AC EF BC FD=,DG AB ∥.求证:AD EB =.11.如图,一组等距的平行线,点A 、B 、C 分别在直线l 1、l 6、l 4上,AB 交l 3于点D ,AC 交l 3于点E ,BC 交于l 5点F ,若△DEF 的面积为1,则△ABC 的面积为_____.12.如图,D E 、分别是ABC ∆的边BC AB 、上的点,AD CE 、相交于点F ,15AE EB =,13BD BC =,则:CF EF =__________.13.如图,在▱ABCD 中,E 为AD 的三等分点,AE=AD ,连结BE ,交AC 于点F ,AC=15,则AF 为_____.参考答案1.D解:如图,若点B1在BC左侧,∵∠C=90°,AC=3,BC=4,∴AB=225AC BC+=∵点D是AB的中点,∴BD=12BA=52∵B1D⊥BC,∠C=90°∴B1D∥AC∴12BD BE DEAB BC AC===∴BE=EC=12BC=2,DE=12AC=32∵折叠∴B1D=BD=52,B1P=BP∴B1E=B1D-DE=1∴在Rt△B1PE中,B1P2=B1E2+PE2,∴BP2=1+(2-BP)2,∴BP=5 4如图,若点B1在BC右侧,∵B1E=DE+B1D=32+52,∴B1E=4在Rt△EB1P中,B1P2=B1E2+EP2,∴BP2=16+(BP-2)2,∴BP=5 故选:D.2.B解:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,AB=CD,∴FA:CD=EF:EC,即FA:AB=EF:EC,∴FA:CD=AE:DE,并不等于AE:EC,又∠AEF与∠DEC是对顶角,所以∠AEF=∠DEC.故选:B.3.B解:∵AD:AF=3:5,∴AD:DF=3:2,∵AB∥CD∥EF,∴AD BCDF CE=,即362CE=,解得,CE=4,故选B.4.D解:作DH∥BF交AC于H.∵AD是△ABC的中线,∴BD=DC.∵DH∥BF,∴CH:FH=CD:BD,∴FH=HC.∵DH∥BF,∴13AF AEFH ED==,∴AF:FC=1:6.故选D.5.D解:∵a∥b∥c,∴AB DEBC EF=,∵AB=1.5,BC=2,DE=1.8,∴1.5 1.82EF=, ∴EF=2.4故选:D.6.A解:∵AF∥BC,DE∥BC,∴AF∥DE,∴DE CDAF CF=,,AF DFBC CD=∴DE AFAF BC≠故A错误,∵AF∥DE,∴FD DCAE EC=,故B正确,∵DE∥BC,∴AD AEAB AC=,故C正确,∵AF∥DE,∴DE CD AF CF=,∵AF∥BC,∴BD CD AB CF=,∴BD DEAB AF=,故D正确,故选:A.7.D解:∵DE∥BC,EF∥AB,∴AD AE DEAB AC BC==,A、B选项正确;∵四边形BDEF是平行四边形,∴DE=BF,∴AD DE BFAB BC BC==,故C选项正确,D选项错误;故选:D.8.解:(1)∵四边形ABCD为平行四边形,∴AB∥CD,AD∥BC,∵AF∥CD,∴AEAD=EFCF=12,∵AE∥BC,∴AFBF=EFCF=12,∴BF=2AF;(2)解:∵四边形ABCD为平行四边形,∴AB=CD,而BF=2AF,∴BF=23AB=23CD,∵BF∥CD,∴BFCD=BGDG=23,∴BDDG=53,∴DG=35BD=35×20=12cm.9.(1)CE=83;(2)AB=253.解:(1)∵FE∥CD,∴AEAC=AFAD,即4AC=35,解得,AC=203,则CE=AC﹣AE=203﹣4=83;(2)∵DE∥BC,∴ADAB=AEAC,即5AB=4203,解得,AB=253.10.解:∵DG AB∥,∴AC ADBC BG=,=EF EBFD BG,∵AC EFBC FD=,∴AD EBBG BG=,∴AD EB=.11.15 4解:连接DC,设平行线间的距离为h,AD=2a,如图所示:∵122DEFS DE h DE h=⋅=⋅,122ADES DE h DE h=⋅=⋅,∴S△DEF=S△DEA,又∵S△DEF=1,∴S△DEA=1,同理可得:12DECS=,又∵S△ADC=S△ADE+S△DEC,∴32ADCS=,又∵平行线是一组等距的,AD=2a,∴23 AD h BD h=,∴BD=3a,设C到AB的距离为k,∴12ADCS AD k=⋅=ak,1322BDCS BD k ak=⋅=,∴339224BDCS=⨯=,又∵S△ABC=S△ADC+S△BDC,∴9315424ABCS=+=.故答案为:154.12.12 解:过点E 作//EG BC 交AD 于点G,∵//EG BC ,∴EGAEBD AB = ∵15AE EB =,13BD BC =,∴11,62AE AB BD CD ==1162EGCD ∴=112EGCD ∴=∵//EG BC ,∴12CF CDEF EG ==故答案为:12.13.6解:故答案为6.。
平行线分线段成比例练习题

平行线分线段成比例练习题平行线分线段成比例练习题在几何学中,平行线是一种非常重要的概念。
当两条直线在同一平面上且永远不相交时,我们称它们为平行线。
平行线具有许多有趣的性质和特点,其中之一是平行线分线段成比例。
在这篇文章中,我们将通过一些练习题来加深对平行线分线段成比例的理解和应用。
练习题1:已知AB和CD是两条平行线,E是AB上的一点,F是CD上的一点。
如果AE 与CF的比例为2:3,求BE与DF的比例。
解答:根据平行线分线段成比例的性质,我们可以得出以下等式:AE/CF = BE/DF由已知条件AE/CF = 2/3,代入得:2/3 = BE/DF通过交叉相乘得:2DF = 3BE因此,BE与DF的比例为3:2。
练习题2:在平行线AB和CD上,分别取两个点E和F。
如果AE与CF的比例为4:5,且BE与DF的比例为3:2,求AE与DE的比例。
解答:首先,根据平行线分线段成比例的性质,我们可以得到以下等式:AE/CF = BE/DF代入已知条件得:AE/5 = 3/2通过交叉相乘得:2AE = 15因此,AE = 15/2 = 7.5接下来,我们需要求出DE的长度。
根据平行线分线段成比例的性质,我们可以得到以下等式:AE/DE = BE/DF代入已知条件得:7.5/DE = 3/2通过交叉相乘得:2DE = 22.5因此,DE = 22.5/2 = 11.25最后,我们可以求得AE与DE的比例:AE/DE = 7.5/11.25 = 2/3练习题3:在平行线AB和CD上,分别取两个点E和F。
如果AE与CF的比例为3:4,且BE与DF的比例为5:6,求AE与DE的比例。
解答:根据平行线分线段成比例的性质,我们可以得到以下等式:AE/CF = BE/DF代入已知条件得:AE/4 = 5/6通过交叉相乘得:6AE = 20因此,AE = 20/6 = 10/3接下来,我们需要求出DE的长度。
根据平行线分线段成比例的性质,我们可以得到以下等式:AE/DE = BE/DF代入已知条件得:(10/3)/DE = 5/6通过交叉相乘得:6DE = 50/3因此,DE = (50/3)/6 = 25/9最后,我们可以求得AE与DE的比例:AE/DE = (10/3)/(25/9) = 30/25 = 6/5通过以上练习题的解答,我们可以看到平行线分线段成比例的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.填空题: 1.如图,梯形 ABCD,AD//BC,延长两腰交于点 E,若 AD 2,BC 6,AB 4 ,则
ED EC
,
DE DC
E A D
B
C
ቤተ መጻሕፍቲ ባይዱ
2. 如图, ABC 中, EF//BC , AD 交 EF 于 G ,已知 EG 2,GF 3,BD 5 ,则
A
E
D
B
F
C
DC
A
E B
G D
F C
3. 如 图 , 梯 形 ABCD 中 , DC / / AB,DC 2,AB 35 . , 且 MN//PQ//AB ,
DM MP PA ,则 MN=________,PQ=________
D M P A C N Q B
4.如图,菱形 ADEF, AB 7,AC 5,BC 6 ,则 BE=________ A
D F
B
E
C
二.选择题 1.如图,H 为平行四边形 ABCD 中 AD 边上一点,且 AH 则 AK:KC 等于( A. 1:2 B. 1:1 ) C. 1:3
1 DH ,AC 和 BH 交于点 K, 2
D. 2:3
A K
H
D
B
C
2.如图, ABC 中,D 在 AB 上,E 在 AC 上,下列条件中,能判定 DE//BC 的是( A. AD AC AE AB B. AD AE EC DB C. AD AB AE AC D. BD AC AE AB A
)
D
E
B
C
3.如图, ABC 中,DE//BC,BE 与 CD 交于点 O,AO 与 DE、BC 交于 N、M,则下列式 子中错误的是( )
DN AD BM AB DO DE C. OC BC
A.
AD DE AB BC AE AO D. EC OM
B.
三.计算题: 1. 如图,已知菱形 BEDF 内接于 ABC ,点 E、D、F 分别在 AB、AC 和 BC 上,若 AB 15,BC 12 ,求菱形边长.
