河南省信阳高级中学2017-2018学年高一下学期开学考试数学---精校解析Word版
河南省信阳市2017_2018学年高一英语下学期开学考试试题(附答案)

河南省信阳市2017-2018学年高一下学期开学考试英语试题第Ⅰ卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题。
从题中所给的A,B,C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例: How much is the shirt?A.£ 19.15B.£ 9.18C.£ 9.15答案是C。
1.How much will the man pay for what he is buying?A. Two dollars.B. Four dollars.C. Six dollars.2.Why can't the man go to the west coast?A. He is looking for a new job.B. He is training his workers.C. He is busy with his new job training.3.What does the man tell the woman?A. There is another cat like his.B. She has mistaken another dog for his.C. He seldom goes out with his dog.4.What is the most probable relationship between the two speakers?A. Doctor and patient.B. Professor and student.C. Manager and secretary.5.Why does the woman ask the man to go to the airport?A. To meet a girl.B. To buy a ticketC. To see a girl off. 第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话。
河南省信阳高级中学2017-2018学年高一4月月考数学试题
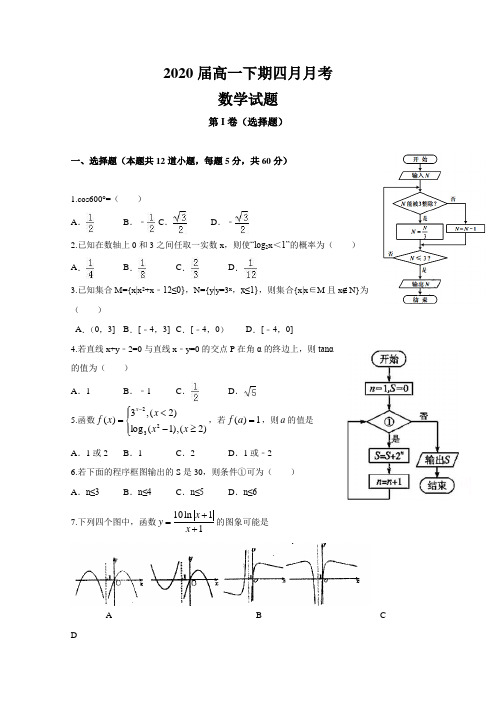
2020届高一下期四月月考数学试题第I 卷(选择题)一、选择题(本题共12道小题,每题5分,共60分)1.cos600°=( ) A.B.﹣ C.D.﹣2.已知在数轴上0和3之间任取一实数x ,则使“log 2x <1”的概率为( ) A.B.C.D.3.已知集合M={x|x 2+x ﹣12≤0},N={y|y=3x ,x≤1},则集合{x|x ∈M 且x ∉N}为( )A .(0,3]B .[﹣4,3]C .[﹣4,0)D .[﹣4,0]4.若直线x+y ﹣2=0与直线x ﹣y=0的交点P 在角α的终边上,则tanα的值为( ) A .1B .﹣1C.D.5.函数⎪⎩⎪⎨⎧≥-<=-)2(),1(log )2(,3)(232x x x x f x ,若1)(=a f ,则a 的值是 A .1或2 B .1 C .2 D .1或﹣26.若下面的程序框图输出的S 是30,则条件①可为( ) A .n≤3B .n≤4C .n≤5D .n≤67.下列四个图中,函数10ln 11x y x +=+的图象可能是A B CD8.已知直线m x y l +=:与曲线21x y -=有两个公共点,则实数m 的取值范围是 A .(-2,2) B .(-1,1) C .D .]22[,-9.阅读右面的程序框图,运行相应的程序,若输入N 的值为19,则输出N 的值为 ( )A.0B.1C.2D.310.已知直线12:210,:(21)10l x ay l a x ay +-=---=与平行,则a 的值是( )A.0或1B.1或14 C.0或14D.1411. 如图,网格纸上小正方形的边长为1,粗线画出的是 某几何体的三视图,则该几何体的体积为( )A .23B .2C .43D .4 12.已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ,若关于的不等式()||2x f x a ≥+在R 上恒成立,则a 的取值范围是 A.[2,2]-B.[-C.[-D.[-第II 卷(非选择题)二、填空题(本题共4道小题,每题5分,共20分)13.某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。
河南省信阳高级中学2017-2018学年高一下学期开学考试数学试题+Word版含答案

2020届高一寒假开学考试数学试题第I 卷(选择题)一、单选题1.设集合{|01}M x x =≤≤, 2{|1}N x x =≥,则()R M C N ⋃=()A. []0,1B. ()1,1-C. (]1,1-D. ()0,12.若直线:3l y kx =-及直线30x y +-=相11交,且交点在第一象限,则直线l 的倾斜角的取值范围是()A. ()000,60B. ()0030,60C. ()0030,90D. ()0060,903.若()()0.2422,log 3.2,log 0.5a b c ===,则( )A. b c a >>B. b a c >>C. c a b >>D. a b c >>4.下列函数中,既是偶函数又在区间()0,∞+上递增的函数为A. 3y x =B. 2log y x =C. y x =D. 2y x =-5.方程21x -=x +k 有惟一解,则实数k 的范围是 ( )A. k =-2B. k ∈(-2, 2)C. k ∈[-1,1)D. k =或-1≤k <16.网格纸上的小正方形边长为1,粗实线画出的是最某几何体的三视图,则该几何体的表面积为( )A. 843+B. 823+C. 443+D. 423+7.函数()()ln 1f x x x =-+的零点所在的大致区间是( )A. B. C. ()2,e D. (),e +∞8.设m n 、是不同的直线, αβγ、、是不同的平面,有以下四个命题:①若//,//αβαγ,则//βγ②若,//m αβα⊥,则m β⊥③若,//m m αβ⊥,则αβ⊥ ④若//,m n n α⊂,则//m α其中正确命题的序号是( )A. ②③B. ①④C. ①③D. ②④9.圆221:2880C x y x y +++-=及圆222:4410C x y x y +---=的位置关系是( )A. 内含B. 外离C. 外切D. 相交10.函数()()23ln f x x x =-⋅的大致图象为A. B. C. D.11..如图,在三棱锥V-ABC 中,VO ⊥平面ABC ,O ∈CD ,VA=VB ,AD=BD ,则下列结论中不一定成立的是 ( )A. AC=BCB. VC ⊥VDC. AB ⊥VCD. S △VCD ·AB=S △ABC ·VO12.已知函数()21,21{ 14,15x x f x x x x+-≤≤=+-<≤,若关于x 的方程()0f x ax -=有两个解,则实数a 的取值范围是( )A. B. C. {}56,,0,2225⎛⎫⎡⎫-∞-⋃+∞⋃- ⎪⎪⎢⎝⎭⎣⎭D. 第II 卷(非选择题)二、填空题13.若幂函数()()223m m f x x m Z --=∈为偶函数,且在区间(),0-∞上递增,则的值是______.14.已知直线1l 及直线2:4310l x y -+=垂直,且及圆22:230C x y y ++-=相切,则直线1l 的一般方程为__________.15.,,,A B C D 是同一球面上的四个点, ABC ∆中, , AB AC =, AD ⊥平面ABC , 6AD =,AB =__________.16.符号[]x 表示不超过x 的最大整数,如[][]3, 1.082π=-=-,定义函数{}[]x x x =-.给出下列四个结论:①函数{}x 的定义域是R ,值域为[]0,1;②方程{}0x x +=有2个解;③函数{}x 是增函数;④函数{}x 对于定义域内任意x ,都有{}{}1x x =+,其中正确结论的序号有_________.三、解答题17.(本小题共10分)求值.(1)3log 169log log 273+;(2)10328110.25lg162lg52722--⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭+--+.18.(本小题共12分)设全集U R =,集合{}|1 3 A x x =-<<, (]{}|2,,2 x B y y x ==∈-∞, {}| 1 C x a x a =+<<(1)求()()U U C A C B ⋂;(2)若()C A B ⊆⋂,求实数a 的取值范围.19.(本小题共12分)已知直线l 经过点()6,4P ,斜率为k(Ⅰ)若l的纵截距是横截距的两倍,求直线l的方程;(Ⅱ)若1k=-,一条光线从点()M出发,遇到直线l反射,反射6,0光线遇到y轴再次反射回点M,求光线所经过的路程。
河南省信阳市信阳高级中学2018届高三普通高等学校招生全国统一考试模拟测试数学(理)试题(一)(解析版)

【答案】C
【解析】
设等比数列{an}的公比为q,
则a2·a3=a·q3=a1·a4=2a1,
解得a4=2,
∵a4与2a7的等差中项为 ,
∴a4+2a7=a4+2a4q3=2+4q3=5,
解得 。
∴ 。
∴ 。选C。
视频
8.根据如下程序框图,运行相应程序,则输出S的值为
A. B. C. D.3
分别与前面括号中 、 相乘后求和可得: .
【点睛】本题考查二项展开式的公式以及系数的求法,注意区分二项式系数与各项系数的区别,掌握其不同的求法,合并同类项时注意其系数.
11.已知直三棱柱ABC—A1B1C1的底面为等边三角形,且底面积为 ,体积为 ,点P,Q分别为线段A1B,B1C上的动点,若直线PQ∩平面ACC1A1= ,点M为线段PQ的中点,则点M的轨迹长度为
【点睛】本题考查数列的通项以及前n项和的求法,结合函数的恒成立问题,考查数列的最值,可根据函数特点进行推理求得最值.
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.已知函数 .
(1)求函数 图象的对称轴方程;
(2)将函数 图象向右平移 个单位,所得图象对应的函数为 .当 时,求函数 的值域.
原式= .
故选C.
【点睛】本题考查向量的线性运算及数量积,数量积问题一般要将两个向量转化为已知边长和夹角的两向量,但本题经化简能得到共线的两向量所以直接根据模的大小计算即可.
6.已知函数 ,则f(x)的大致图象为
A. B.
C. D.
【答案】A
【解析】
【分析】
由函数奇偶性定义判断函数的奇偶性,再给函数求导判断单调性,最后代入特殊点判断.
河南省信阳市高一下学期开学数学试卷

河南省信阳市高一下学期开学数学试卷姓名:________ 班级:________ 成绩:________一、填空题: (共14题;共14分)1. (1分)满足{1,2,3}⊆A⊆{1,2,3,4,5}的集合A的个数为________.2. (1分) (2017高一上·如东月考) 已知角的顶点在坐标原点,始边与轴正半轴重合,终边在直线,则 ________.3. (1分) (2018高一上·江苏月考) 若的定义域为,则实数的取值范围是________.4. (1分)(2020·南昌模拟) 一百馒头,一百和尚,大和尚每人每餐a个馒头,小和尚每餐每a人吃1个馒头.若大和尚的人数用表示,则 ________.5. (1分) (2016高一上·绍兴期中) 函数的最大值为________.6. (1分)设,,,则a,b,c由小到大的顺序为________.7. (1分) (2019高一上·无锡期中) 若平面直角坐标系内两点P,Q满足条件:①P,Q都在函数f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数f(x)的图象上的一个“友好点对”(点对(P,Q)与点对(Q,P)看作同一个“友好点对”).已知函数,若此函数的“友好点对”有且只有一对,则实数的取值范围是________.8. (1分) (2016高一上·宿迁期末) 函数f(x)=cos2x,x∈[ , ]的值域是________.9. (1分) (2016高二下·衡阳期中) 将函数y=sin2x(x∈R)图象上所有的点向左平移个单位长度,所得图象的函数解析式为________.10. (1分)(2017·成安模拟) 在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2﹣a2=bc,,,则b+c的取值范围是________.11. (1分)关于函数有下列命题:①f(x)的表达式可改写为;②f(x)的图象关于点对称;③f(x)的图象关于直线x=对称;④f(x)在区间上是减函数;其中正确的是________ (请将所有正确命题的序号都填上)12. (1分)已知奇函数f(x)是R上的减函数,且f(3)=﹣2,设P={x||f(x+t)﹣1|<1},Q={x|f(x)<﹣2},若“x∈Q”是“x∈P”的必要不充分条件,则实数t的取值范围是________.13. (1分) (2016高一上·宿迁期末) 已知方程3x+x=5的根在区间[k,k+1)(k∈Z),则k的值为________14. (1分) (2018高一上·寻乌期末) 已知偶函数是区间上单调递增,则满足的取值集合是________.二、解答题 (共6题;共55分)15. (10分) (2017高一下·上饶期中) 设向量,的夹角为60°且| |=| |=1,如果,,.(1)证明:A、B、D三点共线.(2)试确定实数k的值,使k的取值满足向量与向量垂直.16. (10分) (2016高一下·衡水期末) 在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2 cosB ﹣sin(A﹣B)sinB+cos(A+C)=﹣.(1)求cosA的值;(2)若a=4 ,b=5,求向量在方向上的投影.17. (5分)下表给出的是某港口在某季节每天几个时刻的水深.时刻0:003:006:009:0012:0015:0018:0021:0024:00水深/m 5.08.0 5.0 2.0 5.08.0 5.0 2.0 5.0(1)若该港口的水深y(m)和时刻t(0≤t≤24)的关系可用函数y=Asin(ωt)+b(其中A>0,ω>0,b∈R)来近似描述,求A,ω,b的值;(2)若一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有2.5m的安全间隙(船底与海底的距离),试用(1)中的函数关系判断该船何时能进入港口?18. (10分)(2019·泉州模拟) 已知函数, .(1)证明:函数的极小值点为1;(2)若函数在有两个零点,证明: .19. (10分) (2019高一上·吉林期中) 设函数, .(1)求的定义域;(2)是否存在最大值或最小值?如果存在,请把它求出来;若不存在,请说明理由.20. (10分) (2016高三上·江苏期中) 设n∈N* , f(n)=3n+7n﹣2.(1)求f(1),f(2),f(3)的值;(2)证明:对任意正整数n,f(n)是8的倍数.参考答案一、填空题: (共14题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共55分)15-1、15-2、16-1、16-2、17-1、18-1、18-2、19-1、19-2、20-1、20-2、。
河南省信阳高级中学2018届高三下学期开学考试数学(文)试卷(含答案)

信阳高中2018届高三第十次大考文数试题一、选择题1.知集合, ,则A. B. C. D.A. B. C D.4.“”是“”的5.设函数,若,则实数A. B. C. 或 D. 或6.已知函数,在区间上有最小值,则函数在区间上一定A. 是减函数B. 是增函数C. 有最小值D. 有最大值7.设实数x,y 满足约束条件,则则的取值范围是A. B. C.D. 8.如图三棱锥ABC V -,VC VA ⊥,BC AB ⊥,030=∠=∠ACB VAC 若侧面底面,则其主视图与左视图面积之比为。
A:B:C:D:9.若实数α满足ααtan cos =,则+==A.-1B.1C.-2D.210.知函数 的定义域为R,,对任意,都有成立,则不等式 的解集为A.B.C.D.11.已知圆C :(a<0)的圆心在直线上,且圆C上的点到直线的距离的最大值为,则的值为A. 1B. 2C. 3D. 412.对于集合{}12,,,n a a a 和常数0a ,定义:)(cos ....)(cos )(cos )(sin ....)(sin )(sin 0202201202022012a a a a a a a a a a a a t n n -++-+--++-+-= 为集合{}12,,,n a a a 相对于0a 的“类正切平方”.则集合57,,266πππ⎧⎫⎨⎬⎩⎭相对于0a 的“类正切平方”t =A.12B.2C.1二、填空题 13.已知是R 上的奇函数,则的值为_______14. 在公比为q且各项均为正数的等比数列 中,为 的前n 项和.若 ,且,则q 的值为__________15. 在平面直角坐标系中,已知圆上有四个点到直线的距离为1,则实数的取值范围是_____。
16.若函数()y f x =对定义域D 内的每一个x 1,都存在唯一的x 2∈D ,使得12()()1f x f x ⋅=成立,则称f (x )为“自倒函数”.给出下列命题:①()sin [])22f x x x ππ=∈-,是自倒函数; ②自倒函数f (x )可以是奇函数; ③自倒函数f (x )的值域可以是R ;④若()()y f x y g x ==,都是自倒函数,且定义域相同,则()()y f x g x =⋅也是自倒函数. 则以上命题正确的是 (写出所有正确命题的序号). 三、解答题17.(本小题满分10分) 已知函数.(1)若不等式的解集为,求实数的值;(2)若不等式,对任意的实数都成立,求正实数的最小值.18.(本小题满分12分)在中,角A,B,C的对边分别是a,b,c,且(1)求角A的大小;(2)已知等差数列的公差不为零,若,且, , 成等比数列,求的前n项和19.(本小题满分12分)如图,四棱锥的底面是边长为a的菱形,,平面ABCD,,E为PA中点, (1)求证:平面平面ABCD; (2)求点E到平面PBC的距离.(2)将函数f(x)的图象向右平移个单位长度后得到函数g(x)的图象,求函数g(x)在区间[0,]上的取值范围.21. (本小题满分12分)在平面直角坐标系xoy 中,曲线Γ:22()y x mx m m R =-+∈与x 轴交于不同的两点,A B , 曲线Γ与y 轴交于点C .(1)是否存在以AB 为直径的圆过点C ?若存在,求出该圆的方程;若不存在,请说明理由 (2)求证:过,,A B C 三点的圆过定点22. (本小题满分12分) 已知函数ln ()xm x nf x e +=(m 、n 为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x )在点(1,f (1))处的切线方程是2y e=. (1)求m 、n 的值; (2)求f (x )的最大值;(3)设ln(1)()()2x e x g x f x +'=⋅(其中()f x '为f (x )的导函数),证明:对任意x >0,都有2()1g x e -<+.(注:1[ln(1)]1x x '+=+)信阳高中2018届高三第十次大考文数答案一.选择题CABBA BCADC CC 二.填空题 13.67 14.215- 15.)13,13(- 16.①②17.解;(1)由题意知,不等式,解集为.由,得,所以,由,解得.(2)由题意,,从而,,又,故正实数的最小值为18.解:(1),可得,由正弦定理可得,即有,,可得;(2)等差数列的公差d不为零, 若,可得,,,成等比数列,可得,即有, 化简可得,则,,则前n项和19.(1)证明:连接AC与BD相交于O,连接EO,则,因为平面ABCD,所以平面ABCD,又平面EDB,所以平面平面ABCD;(2)解:在底面作,垂足为H,因为平面平面ABCD,所以平面PCB,又因为,所以平面PBC,所以点E到平面PBC的距离就是点O到平面PBC的距离OH,计算得出.20.解:(1)f(x)=cos(2x+)+2cos2x=-cos2x-sin2x+1+cos2x=cos2x-sin2x+1=cos(2x+)+1,∴函数f(x)的最小正周期为π. 由2kπ≤2x+≤(2k+1)π,解得kπ-≤x≤kπ+,∴单调减区间是[kπ-,kπ+],k ∈Z.(2)由(1)得g(x)=cos(2(x-)+)+1=cos(2x-)+1.∵0≤x≤, ∴-≤2x -≤, ∴-≤cos(2x -)≤1,∴≤cos(2x -)+1≤2,即f(x)的取值范围为[,2].21.解:由曲线22()y x mx m m R =-+∈ ,令0y =得220x mx m -+=设12(,0)(,0)A x B x ,则可得21212=80,,2m m x x m x x m ∆->+== 令0x =得2y m =,(0,2)C m ∴Ⅰ.若存在以AB 为直径的圆过点C ,则0AC BC ∙=得21240x x m +=,即2124002m m m m +=∴==-或 由10082m m m ∆><>∴=-得或此时(0,1)C -. AB 的中点1(,0)4M -即圆心. 半径||r CM ==故所求圆的方程为22117()416x y ++=Ⅱ.设过AB 两点的圆的方程为2220x y mx Ey m +-++= 将点(0,2)C m 代入可得12E m =--∴过,,A B C 三点的圆的方程为22(12)20x y mx m y m +--++=整理得22(22)0x y y m x y +--+-=令220220x y y x y ⎧+-=⎨+-=⎩ 可得205145x x y y ⎧=⎪=⎧⎪⎨⎨=⎩⎪=⎪⎩或22.Ⅰ.解:由ln ()xm x n f x e +=,得ln ()(0)x m nx mx xf x x xe --'=>由已知得(1)0m nf e-'==,解得m = n又2(1)n f ==,∴n = 2,m = 2. Ⅱ.解:由(Ⅰ)得:2(1ln )()xx x x f x xe--'=当x ∈(0,1)时,1ln 0x x x -->;当x ∈(1,+∞)时,1ln 0x x x --< ∴当x ∈(0,1)时,()0f x '>;当x ∈(1,+∞)时,()0f x '<∴f (x )的单调递增区间是 (0,1),单调递减区间是(1,+∞) ∴x = 1时,max 2()f x e=.Ⅲ.证:ln(1)(1ln )ln(1)()()(0)2x e x x x x x g x f x x x+--+'=⋅=> 对任意x > 0,2()1g x e -<+等价于2(1)1ln x e x x x -+--<令()1ln (0)p x x x x x =-->,则()ln 2p x x '=-- 由()ln 20p x x '=--=得:2x e -=∴当x ∈(0,2e -)时,()0p x '>,p (x )单调递增当x ∈(2e -,+∞)时,()0p x '<,p (x )单调递减所以p (x )的最大值为22()1p e e --=+,即21ln 1x x x e ---+≤ 设()ln(1)q x x x =-+,则()01xq x x '=>+ ∴当x ∈(0,+∞)时,q (x )单调递增,q (x ) >q (0) = 0 故当x ∈(0,+∞)时,()ln(1)0q x x x =-+>,即1ln(1)xx >+ ∴22(1)1ln 1ln(1)x e x x x e x --+--+<+≤∴对任意x > 0,都有2()1g x e -<+.。
2017-2018学年河南省信阳市高一(下)期末数学试卷 Word版含解析

2017-2018学年河南省信阳市高一(下)期末数学试卷一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.sin(﹣)的值是()A.B.﹣C.D.﹣2.若a,b,c为实数,则下列正确的是()A.若a>b,则ac2>bc2B.若a<b<0,则C.若a<b<0,则a2>ab>b2D.若a<b<0,则3.在等差数列{a n}中,3(a3+a5)+2(a7+a10+a13)=24,则此数列前13项的和是()A.13 B.26 C.52 D.564.在△ABC中,若∠C=90°,角A,B,C的对边分别为a,b,c,则的取值范围是()A.(0,]B.[]C.()D.(1,]5.已知扇形的圆心角为,半径为4,则扇形的面积S为()A.3πB.4πC.6πD.2π6.已知向量的最小值为()A.B.6 C.12 D.7.设等比数列{a n}的前n项和为S n,满足a n>0,q>1,且a3+a5=20,a2a6=64,则S6=()A.63 B.48 C.42 D.368.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,下列说法正确的是()A.f(x)的图象关于直线对称B.f(x)的图象关于点对称C.若方程f(x)=m在上有两个不相等的实数根,则实数m的取值范围是D.将函数的图象向左平移个单位得到函数f(x)的图象9.在△ABC中,若(+)•=||2,则()A.△ABC是锐角三角形B.△ABC是直角三角形C.△ABC是钝角三角形D.△ABC的形状不能确定10.设S n为等差数列{a n}的前n项的和,a1=﹣2014,,则S2014的值为()A.﹣2013 B.﹣2014 C.2013 D.2014 11.设变量x,y满足约束条件,则s=的取值范围是()A.[1,]B.[,1]C.[1,2]D.[,2] 12.定义为n个正数p1,p2,…,p n的“均倒数”.若已知数列{a n}的前n项的“均倒数”为,又b n=,则=()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.把答案直接填在题中的横线上)13.已知向量,,.若λ为实数,(),则λ=.14.不等式≥2的解集是.15.已知向量,满足(+2)•(﹣)=﹣6,且||=1,||=2,则在上的投影为.16.已知正项等比数列{a n}满足a7=a6+2a5,若存在两项a m,a n使得=4a1,则+的最小值为.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.已知函数f(x)=x2+2x+a(1)当时,求不等式f(x)>1的解集;(2)若对于任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.18.已知cos(+x)=,.(Ⅰ)求sin2x的值.(Ⅱ)求tanx的值.19.已知函数f(x)=sin2x﹣2sin2x.(1)求函数f(x)的最小正周期;(2)求函数y=f(x)在[﹣,]上的值域.20.在等差数列{a n}中,a1=3,其前n项和为S n,等比数列{b n}的各项均为正数,b1=1,公比为q,且b2+S2=12.q=(Ⅰ)求a n与b n;(Ⅱ)设数列{c n}满足c n=,求的{c n}的前n项和T n.21.已知向量=(2sinx,﹣1),=(sinx﹣cosx,﹣2),函数f(x)=(﹣)•.(Ⅰ)求f(x)在区间上的零点;(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,a=4,f(A)=2,△ABC的面积S=,求b+c的值.22.已知数列{a n}中,a1=1,a n+1=(n∈N*)(1)求证:{}是等比数列,并求{a n}的通项公式a n;(2)数列{b n}满足b n=(3n﹣1)•,数列{b n}的前n项和为T n,若不等式(﹣1)对一切n∈N*恒成立,求λ的取值范围.2014-2015学年河南省信阳市高一(下)期末数学试卷参考答案与试题解析一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.sin(﹣)的值是()A.B.﹣C.D.﹣考点:运用诱导公式化简求值.专题:三角函数的求值.分析:直接利用诱导公式化简求值即可.解答:解:sin(﹣)=﹣sin(2π+)=﹣sin=﹣.故选:D.点评:本题考查三角函数的化简求值,特殊角的三角函数以及诱导公式的应用,考查计算能力.2.若a,b,c为实数,则下列正确的是()A.若a>b,则ac2>bc2B.若a<b<0,则C.若a<b<0,则a2>ab>b2D.若a<b<0,则考点:不等式的基本性质.专题:不等式的解法及应用.分析:根据不等式的基本性质,逐一分析四个答案中的不等式是否一定成立,可得答案.解答:解:当c=0时,若a>b,则ac2=bc2,故A错误;若a<b<0,ab>0,则,即,故B错误;若a<b<0,则a2>ab且ab>b2,即a2>ab>b2,故C正确;若a<b<0,则,,故,故D错误;故选:C.点评:本题考查的知识点是不等式的基本性质,熟练掌握不等式的基本性质,是解答的关键.3.在等差数列{a n}中,3(a3+a5)+2(a7+a10+a13)=24,则此数列前13项的和是()A.13 B.26 C.52 D.56考点:等差数列的性质;等差数列的前n项和.专题:等差数列与等比数列.分析:可得a3+a5=2a4,a7+a13=2a10,代入已知可得a4+a10=4,而S13==,代入计算可得.解答:解:由等差数列的性质可得:a3+a5=2a4,a7+a13=2a10,代入已知可得3×2a4+2×3a10=24,即a4+a10=4,故数列的前13项之和S13====26故选B点评:本题考查等差数列的性质和求和公式,涉及整体代入的思想,属中档题.4.在△ABC中,若∠C=90°,角A,B,C的对边分别为a,b,c,则的取值范围是()A.(0,]B.[]C.()D.(1,]考点:正弦定理.专题:解三角形.分析:根据正弦定理进行化简,结合两角和差的正弦公式进行化简即可.解答:解:由正弦定理得a=csinA,b=ccosA,则=sinA+cosA=sin(A+),∵0<A<,∴<A+<,∴1<sin(A+≤,即的取值范围是(1,],故选:D.点评:本题主要考查正弦定理的应用,利用两角和差的正弦公式以及三角函数的性质是解决本题的关键.5.已知扇形的圆心角为,半径为4,则扇形的面积S为()A.3πB.4πC.6πD.2π考点:扇形面积公式.专题:三角函数的求值.分析:利用S=S==,即可求得结论.解答:解:∵扇形的圆心角为,半径为4,∴S====6π.故选:C.点评:本题考查扇形面积的计算,考查学生的计算能力,属于基础题.6.已知向量的最小值为()A.B.6 C.12 D.考点:基本不等式;数量积判断两个平面向量的垂直关系.专题:计算题.分析:利用向量垂直的充要条件列出方程求出x,y满足的方程;利用基本不等式得到函数的最值,检验等号何时取得.解答:解:由已知⊥⇒=0⇒(x﹣1,2)•(4,y)=0⇒2x+y=2则9x+3y=,当且仅当32x=3y,即时取得等号.故选B.点评:本题考查向量垂直的充要条件:坐标交叉相乘相等、考查利用基本不等式求函数的最值需满足的条件:一正、二定、三相等.7.设等比数列{a n}的前n项和为S n,满足a n>0,q>1,且a3+a5=20,a2a6=64,则S6=()A.63 B.48 C.42 D.36考点:等比数列的前n项和.专题:等差数列与等比数列.分析:由已知结合等比数列的性质求得首项和公比,代入等比数列的前n项和得答案.解答:解:在等比数列{a n}中,∵a2a6=64,∴a3a5=a2a6=64,又a3+a5=20,∴a3和a5为方程x2﹣20x+64=0的两根,∵a n>0,q>1,∴a3<a5,∴a5=16,a3=4,∴q=,∴a1=,∴S6==63.故选:A.点评:本题考查了等比数列的性质,考查了等比数列的前n项和,是基础的计算题.8.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,下列说法正确的是()A.f(x)的图象关于直线对称B.f(x)的图象关于点对称C.若方程f(x)=m在上有两个不相等的实数根,则实数m的取值范围是D.将函数的图象向左平移个单位得到函数f(x)的图象考点:正弦函数的图象.专题:三角函数的图像与性质.分析:由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得f (x)的解析式,结合图象,可得结论.解答:解:由函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象可得A=2,==﹣,求得ω=2,再根据五点法作图可得2×+φ=π,∴φ=,∴f(x)=2sin(2x+),在上,2x+∈[﹣,],当实数m的取值范围是时,函数f(x)的图象和直线y=m有2个交点,故选:C.点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的定义域和值域,属于中档题.9.在△ABC中,若(+)•=||2,则()A.△ABC是锐角三角形B.△ABC是直角三角形C.△ABC是钝角三角形D.△ABC的形状不能确定考点:平面向量数量积的运算.专题:平面向量及应用.分析:由(+)•=||2,可得(+)•=||2,进而得到,利用勾股定理的逆定理即可判断出.解答:解:∵(+)•=||2,∴(+)•=||2,∴,即,∴∠A=90°.∴△ABC是直角三角形.故选:B.点评:本题考查了向量的三角形法则和数量积运算法则、勾股定理的逆定理,属于基础题.10.设S n为等差数列{a n}的前n项的和,a1=﹣2014,,则S2014的值为()A.﹣2013 B.﹣2014 C.2013 D.2014考点:等差数列的性质.专题:等差数列与等比数列.分析:写出等差数列的前n项和,代入求得公差,然后再代入等差数列的前n项和得答案.解答:解:∵数列{a n}为等差数列,且a1=﹣2014,则,∴=﹣2014+1003d+2014﹣1002d=2,即d=2.∴=﹣2014.故选:B.点评:本题考查了等差数列的性质,考查了等差数列的前n项和,是基础的计算题.11.设变量x,y满足约束条件,则s=的取值范围是()A.[1,]B.[,1]C.[1,2]D.[,2]考点:简单线性规划.专题:计算题.分析:先根据已知中,变量x,y满足约束条件,画出满足约束条件的可行域,进而分析s=的几何意义,我们结合图象,利用角点法,即可求出答案.解答:解:满足约束条件的可行域如下图所示:根据题意,s=可以看作是可行域中的一点与点(﹣1,﹣1)连线的斜率,由图分析易得:当x=1,y=O时,其斜率最小,即s=取最小值当x=0,y=1时,其斜率最大,即s=取最大值2故s=的取值范围是[,2]故选D点评:本题考查的知识点是简单线性规划,其中解答的关键是画出满足约束条件的可行域,“角点法”是解答此类问题的常用方法.12.定义为n个正数p1,p2,…,p n的“均倒数”.若已知数列{a n}的前n项的“均倒数”为,又b n=,则=()A.B.C.D.考点:数列的求和.专题:等差数列与等比数列.分析:首先根据信息建立等量关系,进一步求出数列的通项公式,最后利用裂项相消法求出结果.解答:解:定义为n个正数p1,p2,…,p n的“均倒数”.所以:已知数列{a n}的前n项的“均倒数”为,即:=所以:S n=n(2n+1)则:a n=S n﹣S n﹣1=4n﹣1,当n=1时,也成立.则:a n=4n﹣1.由于:b n==n,所以:则:=(1﹣)+()+…+()=1﹣故选:B点评:本题考查的知识要点:信息题型的应用,数列通项公式的求法,利用裂项相消法求数列的和.二、填空题(本大题共4小题,每小题5分,共20分.把答案直接填在题中的横线上)13.已知向量,,.若λ为实数,(),则λ=.考点:平面向量共线(平行)的坐标表示.专题:平面向量及应用.分析:由题意可得的坐标,由向量平行的充要条件可得关于λ的方程,解之即可.解答:解:由题意可得=(1,2)+λ(1,0)=(1+λ,2),因为(),所以4(1+λ)﹣3×2=0,解得λ=故答案为:点评:本题是对于向量平行的考查,正确利用向量平行的充要条件是解决问题的关键,属基础题.14.不等式≥2的解集是[,1)∪(1,3].考点:其他不等式的解法.分析:注意到分母恒大于或等于0,直接转化为整式不等式求解,注意x≠1解答:解:⇔x+5≥2(x﹣1)2且x≠1⇔2x2﹣5x﹣3≤0且x≠1⇔[,1)∪(1,3]故答案为:[,1)∪(1,3]点评:本题考查解分式不等式,在解题过程中,注意等价转化.15.已知向量,满足(+2)•(﹣)=﹣6,且||=1,||=2,则在上的投影为.考点:平面向量数量积的运算.专题:平面向量及应用.分析:先求出•=1,从而得到在上的投影为,代入求出即可.解答:解:∵向量,满足(+2)•(﹣)=﹣6,且||=1,||=2,∴+•﹣2=1+•﹣8=﹣6,∴•=1,∴在上的投影为=,故答案为:.点评:本题考查了平面向量的运算性质,是一道基础题.16.已知正项等比数列{a n}满足a7=a6+2a5,若存在两项a m,a n使得=4a1,则+的最小值为.考点:等比数列的性质;基本不等式.专题:等差数列与等比数列.分析:由已知中正项等比数列{a n}满足:a7=a6+2a5,我们易求出数列的公比,再结合存在两项a m、a n使得,我们可以求出正整数m,n的和,再结合基本不等式中“1”的活用,即可得到答案.解答:解:设等比数列{a n}的首项为a1,公比为q,∵a7=a6+2a5,则a1•q6=a1•q5+2a1•q4即q2﹣q﹣2=0,解得q=2或q=﹣1(舍去)若,则m+n=6则6()=(m+n)()=5+()≥5+4=9则故答案为点评:本题考查的知识点是等比数列的性质,基本不等式,其中根据已知中正项等比数列{a n}满足:a 7=a6+2a5若存在两项a m、a n使得,将问题转化为用基本不等式求最值是解答本题的关键.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.已知函数f(x)=x2+2x+a(1)当时,求不等式f(x)>1的解集;(2)若对于任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.考点:函数恒成立问题;一元二次不等式的解法.专题:综合题;不等式的解法及应用.分析:(1)a=时,化简不等式,根据二次不等式的求解方法可得结果;(2)f(x)>0即x2+2x+a>0对∀x∈[1,+∞)恒成立,分离出参数a后转化为二次函数的最值问题可求;解答:解:(1)当a=时,f(x)>1即,化简得2x2+4x﹣1>0,解得x>﹣1+或x<﹣1﹣,∴不等式f(x)>1的解集为:;(2)f(x)>0即x2+2x+a>0对∀x∈[1,+∞)恒成立,可化为a>﹣x2﹣2x对∀x∈[1,+∞)恒成立,令g(x)=﹣x2﹣2x,可知g(x)在[1,+∞)上单调递减,∴当x=1时,g max(x)=﹣3,∴a>﹣3.点评:本题考查一元二次不等式的求解、函数恒成立问题,考查转化思想,恒成立问题常转化为函数最值问题解决.18.已知cos(+x)=,.(Ⅰ)求sin2x的值.(Ⅱ)求tanx的值.考点:二倍角的正弦.专题:计算题;三角函数的求值.分析:(Ⅰ)由诱导公式可求cos2(+x)=﹣sin2x,又利用二倍角公式可得cos2(+x)=2cos2(+x)﹣1=﹣,即可解得sin2x的值.(Ⅱ)由已知可求范围,利用同角三角函数关系式可求sin(+x),可得tan(+x)===﹣,即可得解.解答:解:(Ⅰ)∵cos2(+x)=cos(+2x)=﹣sin2x,又cos2(+x)=2cos2(+x)﹣1=2×=﹣.∴sin2x=.(Ⅱ)∵.∴,∴sin(+x)=﹣=﹣,∴tan(+x)===﹣,∴tanx=7.点评:本题主要考查了诱导公式,二倍角公式,同角三角函数关系式的应用,属于基础题.19.已知函数f(x)=sin2x﹣2sin2x.(1)求函数f(x)的最小正周期;(2)求函数y=f(x)在[﹣,]上的值域.考点:三角函数中的恒等变换应用;三角函数的周期性及其求法.专题:三角函数的图像与性质.分析:(1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x+)﹣1,由三角函数的周期性及其求法即可求得函数f(x)的最小正周期.(2)由x∈[﹣,],可求2x+的范围,根据正弦函数的图象和性质可得sin(2x+)的范围,从而可求函数y=f(x)在[﹣,]上的值域.解答:解:(1)∵f(x)=sin2x﹣2sin2x=sin2x﹣(1﹣cos2x)=sin(2x+)﹣1,∴由三角函数的周期性及其求法可得函数f(x)的最小正周期T=.(2)∵x∈[﹣,],∴2x+∈[﹣,π],∴sin(2x+)∈[﹣,1],∴y=f(x)=sin(2x+)﹣1∈[﹣2,],∴函数y=f(x)在[﹣,]上的值域是:[﹣2,].点评:本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质,属于基本知识的考查.20.在等差数列{a n}中,a1=3,其前n项和为S n,等比数列{b n}的各项均为正数,b1=1,公比为q,且b2+S2=12.q=(Ⅰ)求a n与b n;(Ⅱ)设数列{c n}满足c n=,求的{c n}的前n项和T n.考点:等差数列与等比数列的综合;数列的求和.专题:计算题.分析:(Ⅰ)根据条件列出关于公差和公比的方程组,解方程即可求出公差和公比,进而求出通项;(Ⅱ)对通项化简,利用裂项法求和,即可得到数列的前n项和.解答:解:(Ⅰ)设{a n}的公差为d,因为所以b2+b2q=12,即q+q2=12,∴q=3或q=﹣4(舍),b2=3,s2=9,a2=6,d=3.故a n=3+3(n﹣1)=3n,.(Ⅱ)因为=,所以:c n=,故T n=.点评:本题考查数列的通项与求和,考查等差数列与等比数列的综合,考查裂项法求数列的和,属于中档题.21.已知向量=(2sinx,﹣1),=(sinx﹣cosx,﹣2),函数f(x)=(﹣)•.(Ⅰ)求f(x)在区间上的零点;(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,a=4,f(A)=2,△ABC的面积S=,求b+c的值.考点:平面向量数量积的运算;正弦定理.专题:函数的性质及应用.分析:根据向量的数量积得出f(x)=.再运用三角函数性质求解在区间上的零点;(Ⅱ)由f(A)=2,得出.根据面积公式得出,化简得出bc=4,根据余弦定理,再运用配方求解即可.解答:解:(Ⅰ)f(x)=(m﹣n)•m====.由f(x)=0,得(k∈Z),则(k∈Z),因为,所以f(x)在区间上的零点是,.(Ⅱ)由f(A)=2,得,所以(k∈Z),因为0<A<π,所以.因为根据余弦定理a2=b2+c2﹣2bccosA,得16=b2+c2﹣bc,所以(b+c)2=16+3bc=28,所以.点评:本题考查了平面向量数量积的运用及应用,正弦定理在三角形中的应用,综合性较大,关键是结合三角函数的图象性质求解.22.已知数列{a n}中,a1=1,a n+1=(n∈N*)(1)求证:{}是等比数列,并求{a n}的通项公式a n;(2)数列{b n}满足b n=(3n﹣1)•,数列{b n}的前n项和为T n,若不等式(﹣1)对一切n∈N*恒成立,求λ的取值范围.考点:数列与不等式的综合;等比关系的确定.专题:等差数列与等比数列.分析:(1)由数列{a n}中,a1=1,a n+1=(n∈N*),可得=1+.变形为,利用等比数列的通项公式即可得出.(2)由(1)可知:b n,利用“错位相减法”即可得出T n,利用不等式(﹣1),通过对n分为偶数与奇数讨论即可.解答:解:(1)由数列{a n}中,a1=1,a n+1=(n∈N*),可得=1+.∴,∴{}是首项为,公比为3的等比数列,∴,化为.(2)由(1)可知:=,T n=+…+.…++,两式相减得﹣==.∴.∴(﹣1)n•λ<+=4﹣.若n为偶数,则,∴λ<3.若n为奇数,则,∴﹣λ<2,解得λ>﹣2.综上可得﹣2<λ<3.点评:熟练掌握等比数列的通项公式和前n项和公式、“错位相减法”、分类讨论的思想方法等是解题的关键.。
河南省信阳高级中学2017-2018学年普通高等学校招生全国统一考试模拟测试数学(文)试题(一)(含解析)

2018年普通高等学校招生全国统一考试模拟卷文科数学一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若集合,,则A. B. C. D.【答案】C【解析】试题分析:由题意,,,故选C。
考点:集合的运算2. 已知复数,若,则复数z的共轭复数A. B. C. D.【答案】B【解析】试题分析:,选B.考点:复数概念【名师点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如. 其次要熟悉复数相关基本概念,如复数的实部为、虚部为、模为、对应点为、共轭为3. 设等差数列的前项和为,若,则A. 27B. 36C. 45D. 54【答案】D【解析】由题意,可得:∴,即∴故选:D4. 已知命题:“”是“”的充要条件;:,,则A. ¬∨为真命题B. ∧¬为假命题C. ∧为真命题D. ∨为真命题【答案】D【解析】函数是增函数,所以,所以是充要条件,所以命题使正确的,为真命题,由图像可知和关于直线对称,没有交点,所以不存在,使,所以命题使错误的,为假命题,根据复合命题的真假可知是真命题,故选D.5. 已知角的终边经过点,则的值等于A. B. C. D.【答案】C【解析】分析:利用任意角的三角函数的定义和诱导公式,即可求解的值.详解:因为角的终边经过点,由三角函数的定义可知,又由诱导公式可得,故选C.点睛:本题主要考查了任意角的三角函数的定义,诱导公式的化简求值问题,其中解答中熟记三角函数的定义和诱导公式是解答的关键,着重考查了推理与运算能力.6. 某几何体的三视图如图所示,图中每一个小方格均为正方形,且边长为1,则该几何体的体积为A. 8πB.C.D. 12π【答案】B【解析】几何体为半个圆锥与半个圆柱的组合体,如图,体积为选B.7. 若程序框图如图所示,则该程序运行后输出的值是A. 5B. 6C. 7D. 8【答案】A【解析】试题分析:当输入的值为时,第一次循环,;第二次循环,;第三次循环,;第四次循环,;第五次循环,;退出循环输出结果为,故选A.考点:1、程序框图;2、条件结果及循环结构.8. 一组数据共有7个数,记得其中有10、2、5、2、4、2,还有一个数没记清,但知道这组数的平均值、中位数、众数依次成等差数列,这个数的所有可能值的和为A. B. 3 C. 9 D. 17【答案】C【解析】设没记清的数为,若,则这列数:,2,2,2,4,5,10,平均数为,中位数为2,众数为2,所以,,若,则这列数为2,2,2,,4,5,10,则平均数为,中位数为,众数为2,所以,若,则这列数为2,2,2,4,5,,10,或2,2,2,4,5,10,,则平均数为,中位数4,众数2,所以,所以-11+3+17=9点睛:仔细审题,回想平均数、中位数、众数的定义及等差数列的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设集合,则()
B. C. D.
∵集合
故选C.
若直线与直线交,且交点在第一象限,则直线的倾斜角的取值范围是()
B. C. D.
【答案】C
【解析】联立方程得交点,由交点在第一象限知:解得是锐角,故
3. 若
B.
D.
【解析】∵
,即
题,常见思路有两个:一是判断出各个数值所在区间(一般是看三个区间
既是偶函数又在区间
B. C. D.
=
=- B. ,
或-1≤
B. C. D.
,其中底面和侧面是底边为
均为以为底边的等腰三角形,取的中点,连接
.
的零点所在的大致区间是(
B. C. D.
【答案】
在
的零点所在的大致区间是
是不同的直线,
,则②若,则
,则,则
【解析】
与圆的位置关系是(内含 B. 外离 C. 外切 D. 相交
【解析】圆的标准方程即:,
的标准方程即:,
两圆的圆心距为:
,满足
.
函数
B.
D.
∴函数为偶函数,排除
点睛:根据函数的解析式判断函数图象的大体形状时,一般运用排除的方法,具体如下:
=
AB⊥平面
·BD+S
·(BD+AD)
所以·VO=
△VCD△ABC
已知函数,若关于的方程有两个解,则实数
B.
D.
【答案】A
........................
若幂函数为偶函数,且在区间上递增,则
【解析】∵幂函数为偶函数,且在区间
在单调递减
,即
又∵
,,
时,是奇函数,不满足题意;
时,且在区间上递增,在
时,是奇函数,不满足题意
.
故答案为.
递减,得,则,,为偶函数,依次验证
已知直线与直线垂直,且与圆相切,则直线【答案】或(和)
或
3x+4y-14=0.
,平面,【答案】
【解析】
,则的外接圆的直径,即,则,所以由球心距、外接圆半径、球半径可得,解之
,所以球的表面积,应填答案
16. 符号表示不超过的最大整数,如定义函数
,值域为个解;③函数
,都有,其中正确结论的序号有
【解析】画出函数
的定义域是,故函数由图象可得函数
的图象与的图象有两个交点,所以方程有两个解,即方程
因为所以
;
(1)18;(2)
(1)利用对数的运算法则,,化简求值;
,
==
18. 设全集,集合,
;
,求实数
,;
利用指数函数的单调性即可得集合,由补集的定义知,根据交集的运算得,再根据的取值范围.
或或
2)∵集合
,解得
∴实数的取值范围是
已知直线经过点,斜率为
(Ⅰ)若的纵截距是横截距的两倍,求直线的方程;
(Ⅱ)若,一条光线从点出发,遇到直线反射,反射光线遇到轴再次反射回点
或
试题解析:
(Ⅰ)由题意得。
直线的方程为,
的纵截距是横截距的两倍
解得或
∴直线或,
或
(Ⅱ)当时,直线,
关于的对称点为
解得,
关于轴的对称点为
光线所经过的路程为
是正方形,平面
的中点,且
平面;
平面;
与四棱锥的体积之比
平面,根据面面垂直的判定定理可知在平面垂直,而根据线面垂直的判定定理可知平面平面,满足定理条件;
,利用线面平行的判定定理,即可证明平面)不妨设,求出
,根据面,所以即为点到平面的距离,根据三棱锥的体积公式求出体积得到
分别为
又∵四边形
,∴,
在平面外,在平面
平面,平面
都在平面
平面.
平面,
平面.
∵四边形,
,∴平面,
中,∵分别为
,∴平面
,∴平面平面
解:∵平面,四边形为正方形,不妨设,则.
平面,且,
即为点到平面的距离,
21. 已知圆C:x2+y2-2x+4y-4=0,
关于直线对称的圆的方程;
为直径的圆经过点
()
【解析】试题分析:(1)关键求圆心关于直线的对称点,根据垂直平分条件列方程组,解方程组可得圆
为直径的圆过
方程,利用韦达定理代入解得的方程
,
圆的方程
,
又
解得
经检验
∴存在这样的直线为
已知,函数.
的定义域及其零点;
)讨论并用函数单调性定义证明函数在定义域上的单调性;
,当时,若对任意,使得,求实数
定义域,的零点为;(3) .
,解不等式可得定义域,可得解析式,易得零点;)设,是
内的任意两个不相等的实数,且,可得
,易得,由二次函数分类讨论可得,解关于
,,解得
定义域.
,解得,故函数的零点为
,是内的任意两个不相等的实数,且,则,
∵
,即
,故
,存在,使得成立,只需)知当时,在上单调递增,则.
时,,成立;
时,在,由,解得
时,在,由,解得综上,满足条件的的范围是。
