大学物理练习题十七
江苏大学 物理练习17
班级______________学号____________姓名________________知识点:简谐振动及其合成练习 十七一、选择题1. 一弹簧振子,水平放置时,它作简谐振动。
若把它竖直放置或放在光滑斜面上,试判断下列情况正确的是 ( )(A )竖直放置作简谐振动,在光滑斜面上不作简谐振动; (B )竖直放置不作简谐振动,在光滑斜面上作简谐振动; (C )两种情况都作简谐振动;(D )两种情况都不作简谐振动。
2. 两个简谐振动的振动曲线如图所示,则有( )(A )A 超前2π; (B )A 落后2π; (C )A 超前π; (D )A 落后π。
3. 一个质点作简谐振动,周期为T ,当质点由平衡位置向x 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的最短时间为: ( )(A )4T ; (B )12T ; (C )6T ; (D )8T 。
4. 当一个弹簧振子的振幅增大时,分析下列物理量哪个不受影响:(A )振动的周期; ( ) (B )振动的最大速度;(C )振动的最大加速度;(D )振动系统的总能量。
5. 一轻弹簧,上端固定,下端挂有质量为m 的重物,其自由振动的周期为T .今已知振子离开平衡位置为x 时,其振动速度为v ,加速度为a 。
则下列计算该振子劲度系数的公式中,错误的是: ( ) (A) 2m ax 2m ax /x m k v =; (B) x mg k /=;(C) 22/4T m k π=; (D) x ma k /=。
6. 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动表式为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处。
则第二个质点的振动表式为 ( ) (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ;(C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
大学物理规范作业17-33PPT课件

P 3
2 1
0
V1
V2
A
P1 (V2
V1 )
RT1
V1
(V2
V1 )
19944
J
21
福州大学大学物理规范作业B 19
22
一、选择题:
1.一定量的某种理想气体起始温度为T ,体积为V, 该气 体在下面的循环过程中经过三个平衡过程:(1)绝热 膨胀到体积2V , (2)等体变化使温度恢复为T,(3)等温压 缩到原来的体积V,则这整个循环过程中 【 A 】
V1 1T1 Vc 1Tc V2 1Tc
得:
Tc
V1 V2
1
T1
V1 V2
2/3
T1
对单原子分V子1 i=3V2
1 (i 2)R / 2 1 2
iR / 2
3
5
3
26
再由绝热方程: 得到:
P1V1 PCV2
PC
P1
V1 V2
RT1 V1
V1 V2
RT1V 1 V2
1
RT1 V2
4P1V1
8
混合后气体温度为T,
T
4
3 / 2T1 5 / 2T2
284K
9
2.有N个粒子,其速率分布函数为:
f (v) av / v0 (v0 v 0)
f (v) a (2v0 v v0 )
f (v) 0 (v 2v0 )
1.画速率分布曲线并求常数a;(2)分别求速率大于v 0
中气体(1)从外界吸收的热量Q=______A_1______;(2)内能增加了 E _____A__2______。
解:等温过程 ET 0 QT AT QTa A1 放热
大学物理习题课答案课件

E
M M mol
CJ
根 据 根 据 热 力 学 定 律 Q =E+A 可 知 A=-E 623J
(负 号 表 示 外 界 做 功 )
练习十八 热力学基础(二)
1. 用公式 ECVT
(式中CV为定体摩尔热容量,视为常量,v为气体摩尔数)计算理想气体内能增量
时,此式
[(A) ]
所以Q2
1 n
Q1
4.已知1 mol的某种理想气体(其分子可视为刚性分子),在等压过程中温度上升1 K,内
能增加了20.78 J,则气体对外作功为_____8_._3__1_J_____, 气体吸收热量为_____2_9__.0__9_J_____.
等压过程:E=n i RT i R 20.78J ,
2
2
Cp
Cv
R
i 2
R
R
20.78
8.31
29.09
Qp nC pT 29.09J
Qp E A p
A p 8.31J
6.一定量的某种理想气体进行如图所示的循环过程.已知气体在状态A的温度为TA= 300 K,求
(1) 气体在状态B、C的温度; (2) 各过程中气体对外所作的功; (3) 经过整个循环过程,气体从外界吸收的总热量(各过程吸热的代数和).
Q =A+ΔE =200 J.
1
2
B
V (m 3) 3
2. 热力学第二定律表明:
(A) 不可能从单一热源吸收热量使之全部变为有用的功.
(B) 在一个可逆过程中,工作物质净吸热等于对外作的功.
(C) 摩擦生热的过程是不可逆的.
(D) 热量不可能从温度低的物体传到温度高的物体.
[C ]
大学物理下第17章习题详解

第17章习题解答【17-1】解 首先写出S 点的振动方程若选向上为正方向,则有:-=0 21cos 0-=ϕ 0=-A sin 0>0, sin 0<0即 πϕ320-= 初始位相 πϕ320-= 则 m t y s )32cos(02.0πω-= 再建立如图题17-1(a )所示坐标系,坐标原点选在S 点,沿x 轴正向取任一P 点,该点振动位相将落后于S 点,滞后时间为:ux t =∆ 则该波的波动方程为:m u x t y ⎥⎦⎤⎢⎣⎡--=πω32)(cos 02.0 若坐标原点不选在S 点,如图题17-1(b )所示,P 点仍选在S 点右方,则P 点振动落后于S 点的时间为:uL x t -=∆ 则该波的波动方程为:m u L x t y ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0 若P 点选在S 点左侧,如图题17-1(c )所示,则m u L x t y ⎥⎦⎤⎢⎣⎡--+=πω32)(cos 02.0 【17-2】解(1)由图题17-2可知,波长 =0.8m振幅 A=0.5m频率 Hz Hz u v 1258.0100===λ 周期 s vT 31081-⨯== (2)平面简谐波标准动方程为:⎥⎦⎤⎢⎣⎡+-=ϕω)(cos u x t A y 由图可知,当t=0,x=0时,y=A=,故=0。
将A 、(v)、u 、代入波动方程,得: m x t y ⎥⎦⎤⎢⎣⎡-=)100(250cos 5.0π 【17-3】解 (1)由图题17-3可知,对于O 点,t=0时,y=0,故2πϕ±= 再由该列波的传播方向可知,0<0取 2πϕ= 由图题17-3可知,m OP 40.0==λ,且u=0.08m/s ,则s rrad s rad uv /52/40.008.0222ππλππω==== 可得O 点振动表达式为:m t y )252cos(04.00ππ+= (2)已知该波沿x 轴正方向传播,u=0.08m/s ,以及O 点振动表达式,波动方程为: m x t y ⎥⎦⎤⎢⎣⎡+-=2)08.0(52cos 04.0ππ (3)将x==代入上式,即为P 点振动方程:m t y p ⎥⎦⎤⎢⎣⎡-=ππ3252cos 04.0 (4)图题17-3中虚线为下一时刻波形,由图可知,a 点向下运动,b 点向上运动。
大学物理下17章习题参考答案中国石油大学

17章习题参考答案17-3 如图所示,通过回路的磁场与线圈平面垂直且指出纸里,磁通量按如下规律变化()Wb 1017632-⨯++=Φt t式中t 的单位为s 。
问s 0.2=t 时,回路中感应电动势的大小是多少? R 上的电流方向如何?[解] ()310712d d -⨯+=Φ-=t tε ()23101.3107212--⨯=⨯+⨯=V根据楞次定律,R 上的电流从左向右。
17-4如图所示,两个半径分别为R 和r 的同轴圆形线圈,相距x ,且,R >>r ,x >>R 。
若大线圈有电流I 而小线圈沿x 轴方向以速度v 运动。
试求x =NR 时(N >0),小线圈中产生的感应电动势的大小。
[解] 因R>>r 可将通过小线圈的B 视为相等,等于在轴线上的B()2322202xR IR B +=μ由于x >>R ,有 3202x IR B μ=所以 t xxIS R t d d 32d d 420μ=Φ-=ε 而v t x=d d 因此 x =NR 时, 242023R N v r I πμ=ε17-5 如图所示,半径为R 的导体圆盘,它的轴线与外磁场平行,并以角速度ω转动(称为法拉第发电机)。
求盘边缘与中心之间的电势差,何处电势高?当R =0.15m ,B =0.60T ,rad 30=ω时,U 等于多大?[解] 圆盘可看成无数由中心向外的导线构成的,每个导线切割磁力线运动且并联,因此有2021d d )(BR r rB R L ωω==⋅⨯=⎰⎰l B v 感ε因电动势大于零,且积分方向由圆心至边缘,所以边缘处电位高(或由右手定则判断)代入数据得201506030212...=⨯⨯⨯==εU V 17-6 一长直导线载有电流强度I =5.0A 的直流电,在近旁有一与它共面的矩形线圈,线圈长l =20cm ,宽a =10cm ,共1000匝,如图所示。
大学物理习题17电磁感应

班级______________学号____________姓名________________练习 十七一、选择题1、 如图所示,有一边长为1m 的立方体,处于沿y 轴指向的强度为0。
2T 的均匀磁场中,导线a、b 、c 都以50cm/s的速度沿图中所示方向运动,则 ( )(A)导线a 内等效非静电性场强的大小为0。
1V/m;(B)导线b 内等效非静电性场强的大小为零;(C)导线c内等效非静电性场强的大小为0。
2V/m;(D)导线c 内等效非静电性场强的大小为0。
1V/m。
2、 如图所示,导线AB 在均匀磁场中作下列四种运动,(1)垂直于磁场作平动;(2)绕固定端A 作垂直于磁场转动;(3)绕其中心点O 作垂直于磁场转动;(4)绕通过中心点O的水平轴作平行于磁场的转动。
关于导线AB的感应电动势哪个结论是错误的? ( )(A)(1)有感应电动势,A端为高电势;(B)(2)有感应电动势,B端为高电势;(C)(3)无感应电动势; (D)(4)无感应电动势。
3、 一“探测线圈”由50匝导线组成,截面积S =4cm 2,电阻R =25∧。
若把探测线圈在磁场中迅速翻转,测得通过线圈的电荷量为,则磁感应强度B 的大小为( )(A)0。
01T; (B)0、05T; (C)0。
1T; (D)0、5T 。
4。
如图所示,一根长为1m 的细直棒ab ,绕垂直于棒且过其一端a的轴以每秒2转的角速度旋转,棒的旋转平面垂直于0、5T 的均匀磁场,则在棒的中点,等效非静电性场强的大小和方向为( )(A)314V/m,方向由a 指向b ;(B)6。
28 V/m,方向由a指向b;(C)3。
14 V/m,方向由b 指向a ;(D)628 V/m,方向由b 指向a。
二、填空题1。
电阻R=2Ω的闭合导体回路置于变化磁场中,通过回路包围面的磁通量与时间的关系为,则在t =2s 至t =3s的时间内,流过回路导体横截面的感应电荷 C 。
大学物理习题集

大学物理习题集上册物理教研室2004年元月目录部分物理常量练习一描述运动的物理量练习二刚体定轴转动的描述相对运动练习三牛顿运动定律非惯性系中的力学练习四动量角动量练习五功和能碰撞练习六刚体定轴转动的转动定律转动惯量练习七刚体定轴转动中的动能及角动量练习八力学习题课练习九状态方程压强公式练习十理想气体的内能分布律练习十一分布律(续) 自由程碰撞频率练习十二热力学第一定律等值过程练习十三循环过程练习十四热力学第二定律熵练习十五热学习题课练习十六谐振动练习十七谐振动能量谐振动合成练习十八阻尼受迫共振波动方程练习十九波的能量波的干涉练习二十驻波多普勒效应练习二十一振动和波习题课练习二十二光的相干性双缝干涉光程练习二十三薄膜干涉劈尖练习二十四牛顿环迈克耳逊干涉仪衍射现象练习二十五单缝圆孔光学仪器的分辨率练习二十六光栅X射线的衍射练习二十七光的偏振练习二十八光学习题课23h3456789101112131415图9.1 161718192021232425(A)图15.12627图17.24. 一平面简谐波沿x 轴负方向传播,已知x=x 0处质点的振动方程为y=A cos(ω t+ϕ0). 若(B)v (m/s)O1 x (m)ωA(A)·图18.3图18.54041距离 (从地上一点看两星的视线间夹角)是(A) 5.3×10-7 rad.(B) 1.8×10-4 rad .(C) 5.3×10-5 rad .(D) 3.2×10-3 rad二.填空题1. 惠更斯引入的概念提出了惠更斯原理,菲涅耳再用的思想补充了惠更斯原理,发展成了惠更斯-菲涅耳原理.2. 如果单缝夫琅和费衍射的第一级暗纹发生在衍射角为30 的方位上,所用单色光波长λ =5×103 Å, 则单缝宽度为m .3. 平行单色光垂直入射于单缝上,观察夫琅和费衍射. 若屏上P点处为第二级暗纹,则单缝处波面相应地可划分为个半波带,若将单缝宽度减小一半, P点将是级纹.三.计算题1. 用波长λ =6328Å 的平行光垂直照射单缝, 缝宽a= 0.15mm , 缝后用凸透镜把衍射光会聚在焦平面上, 测得第二级与第三级暗条纹之间的距离为1.7mm , 求此透镜的焦距.四.问答题1. 在单缝衍射实验中, 当缝的宽度a远大于单色光的波长时, 通常观察不到衍射条纹, 试由单缝衍射暗条纹条件的公式说明这是为什么.练习二十六光栅X射线的衍射一.选择题1. 一束平行单色光垂直入射到光栅上,当光栅常数(a+b) 为下列哪种情况时(a代表每条缝为宽度) ,k =3、6、9等级次的主极大均不出现?(A) a+b=3a.(B) a+b=2a .(C) a+b=4a .(D) a+b=6a .2. 若用衍射光栅准确测定一单色可见光的波长,在下列各种光栅常数的光栅中选用哪一种最好?(A) 1.0×10-1 mm .(B) 5.0×10-1 mm .(C) 1.0×10-2 mm .(D) 1.0×10-3 mm .3. 在双缝衍射实验中,若保持双缝s1和s2的中心之间的距离d不变,而把两条缝的宽度a 42略微加宽,则(A) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目变少.(B) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目变多.(C) 单缝衍射的中央主极大变窄,其中所包含的干涉条纹数目变少.(D) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目不变.(E) 单缝衍射的中央主极大变窄,其中所包含的干涉条纹数目变多.4. 某元素的特征光谱中含有波长分别为 1 = 450 n m 和 2 = 750 n m (1 n m = 10-9 m)的光谱线. 在光栅光谱中,这两种波长的谱线有重叠现象,重叠处 2的谱线的级次数将是(A) 2、3、4、5 …….(B) 2、5、8、11 …….(C) 2、4、6、8 …….(D) 3、6、9、12 …….5. 设光栅平面、透镜均与屏幕平行,则当入射的平行单色光从垂直于光栅平面入射变为斜入射时,能观察到的光谱线的最高级数k(A) 变小.(B) 变大.(C) 不变.(D) 的改变无法确定.二.填空题1. 用波长为5461 Å的平行单色光垂直照射到一透射光栅上,在分光计上测得第一级光谱线的衍射角 = 30 ,则该光栅每一毫米上有条刻痕.2. 可见光的波长范围是400 n m—760 n m,用平行的白光垂直入射到平面透射光栅上时,它产生的不与另一级光谱重叠的完整的可见光光谱是第级光谱.3. 一束平行单色光垂直入射到一光栅上,若光栅的透明缝宽度a与不透明部分宽度b相等,则可能看到的衍射光谱的级次为.三.计算题1. 一块每毫米500条缝的光栅,用钠黄光正入射,观察衍射光谱, 钠黄光包含两条谱线,其波长分别为5896 Å和5890 Å, 求在第二级光谱中这两条谱线互相分离的角度.2. 一衍射光栅,每厘米有200条透光缝,每条透光缝宽为a =2×10-3 c m ,在光栅后放一焦距f =1m 的凸透镜,现以 = 6000 Å的平行单色光垂直照射光栅,求: (1) 透光镜a的单缝衍射中央明条纹宽度为多少?(2) 在该宽度内, 有几个光栅衍射主极大?练习二十七光的偏振一.选择题1. 一束光强为I0的自然光垂直穿过两个偏振片,且此两偏振片的偏振化方向成45 角,若不考虑偏振片的反射和吸收,则穿过两个偏振片后的光强I为4344454647。
大学物理习题及解答(打印版)
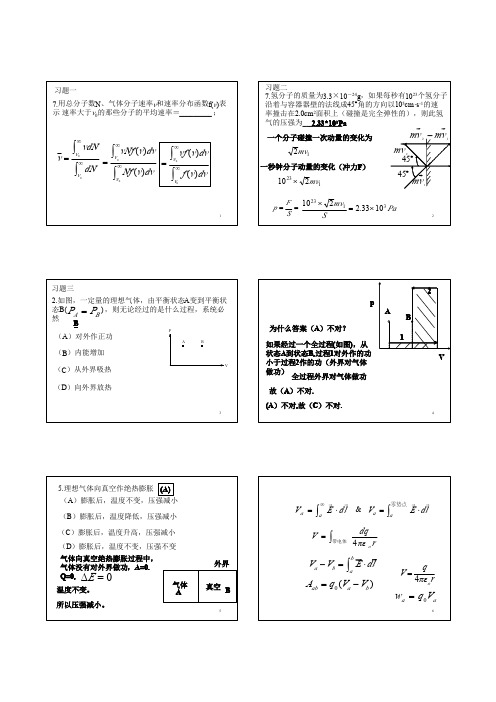
q V = 4πε o r
9
q .o V = o 4πε o R
q
.o
x
r
R dq
10
圆弧圆心、圆环轴线上的电场?
例题 均匀带电圆盘,半径为R,电荷面密度为 σ,求轴线上离盘心距离为x的P点的电势。(取无穷远 为电势零点) 解 将圆盘分为若干个圆环, 利用圆环公式积分。 P
例题 求半径为R、总电量为q的均匀带电球面的电 势分布。 q 解 由高斯定理求出其场强分布:
习题一 7.用总分子数N、气体分子速率v和速率分布函数f(v)表 示 速率大于v0的那些分子的平均速率=_________ ;
习题二 7. 氢分子的质量为3.3×10-24g,如果每秒有1023个氢分子 沿着与容器器壁的法线成45°角的方向以105cm·s-1的速 率撞击在2.0cm2面积上(碰撞是完全弹性的),则此氢 气的压强为___________ *103 Pa 2.33 2.33* 一个分子碰撞一次动量的变化为
-q
a
R
+q
R o
c
R
将Vo代入功的式子,得
A∞ o = −
q πε o a
q 6 πεo R qqo 6πεo R
8
∴ Aac = −
7
例题 一均匀带电直线段,长为L,电量为q;求直 线延长线上离一端距离为d的P点的电势。(取无穷远 为电势零点) 解 将带电直线分 为许多电荷元dq(点电 荷),利用点电荷电势公 式积分:
∂V ∂V = 0, E z = − =0 ∂y ∂z
17
18
3
例题7.1 两平行金属板A、B,面积S, 相距d, 带电:QA,QB,求两板各表面上的 电荷面密度及两板间的电势差(忽略金属板的 边缘效应)。 解 (σ1+ σ2)S=QA (σ3+ σ4)S=QB P1点: P2点:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理练习题十七P231.17.117.217.宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于3K黑体辐射.求:此辐射的单色辐射强度在什么波长下有极大值?地球表面接收此辐射的功率是多少?[解答]根据公式λmT = b,可得辐射的极值波长为λm = b/T =.897×10/=.66×10.地球的半径约为R =.371×106m,表面积为S =πR2.根据公式:黑体表面在单位时间,单位面积上辐射的能量为M = σT4,因此地球表面接收此辐射的功率是P = MS =.67×10×3×4π=.34×10.-19-717.铝表面电子的逸出功为 6.72×10J,今有波长为λ =.0×10m的光投射到铝表面上.试求:由此产生的光电子的最大初动能;遏止电势差;铝的红限波长. [解答]光子的能量为E = hν = hc/λ,根据爱因斯坦光电效应方程hν = Ek + A,产生的光电子的最大初动能为Ek = hν – A =.63×10-34×3×108/2.0×10-7-6.72×10-1=.23×10-19.遏止电势差的公式为eUs = Ek,遏止电势差为Us = Ek/e =.23×10-19/1.6×10-19=2.0.铝的红限频率为ν0 = A/h,红限波长为λ0 = c/ν0 = hc/A =.63×10-34×3×108/6.72×10-1=.96×10-7.-1017.康普顿散射中入射X射线的波长是λ = 0.70×10m,散射的X射线与入射的X射线垂直.求:反冲电子的动能EK;散射X射线的波长;反冲电子的运动方向与入射X射线间的夹角θ. [解答]根据康普顿散射公式得波长变化为-84629-3-42?sin2?2?2?2.426?10?12sin2π4=.426×10-12,散射线的波长为λ’ = λ + Δλ = 0.72426×10.反冲电子的动能为Ek?hc?hc-10?6.63?10?34?3?10?1080.7?10?6.63?10?34?3?10?1080.72426?10=.52×10-17.由于tan??hc/??hc/???0.70.72426?0.9665,所以夹角为θ =4°1’.17.求波长分别为λ1 =.0×10-7m的红光;λ=0.25×10-10m的X射线的能量、动量和质量. [解答]X射线的能量为E = hν = hc/λ,动量为p = h/λ;由E = hc/λ = mc,得其质量为m = h/cλ.对于红光来说,能量为E1?6.63?10?342?3?10?787?10=.84×10-19,动量为p1?6.63?107?10?34?7=.47×10-25,质量为m1?6.63?108?34?73?10?7?10=.16×10-36.对于X射线来说,能量为 E2?6.63?10?34?3?10?1080.25?10=.956×10-15,动量为p2?6.63?100.25?10?34?10=.652×10,-23-1质量为m2?6.63?108?34?103?10?0.25?10=.84×10-32.17.处于第四激发态上的大量氢原子,最多可发射几个线系,共几条谱线?那一条波长最长.[解答]第四激发态的氢原子处于第5个能级,最多可发射四个线系.能级5到4,1条谱线;能级5和4到3,2条谱线;能级5、4和3到2,3条谱线;能级5、4、3和2到1,4条谱线.共10条谱线.从能级5跃迁到4发射的光谱频率最小,波长最长.17.设氢原子中电子从n =的状态被电离出去,需要多少能量. [解答]氢原子能级公式为En??me20421n28?h,当n=1时,基态能级的能量为E1??me20428?h≈-2.18×10-18 = -13.6,因此En?E1n2.当电子从n能级跃迁到m能级时放出或吸收光子的能量为?E?En?Em?E1.电离时,m趋于无穷大.当电子从n =的能级电离时要吸收能量?E??13.6= -3.4,因此需要3.4eV的能量.17.917.10 质量为m的卫星,在半径为r的轨道上环绕地球运动,线速度为v.假定玻尔氢原子理论中关于轨道角动量的条件对于地球卫星同样成立.证明地球卫星的轨道半径与量子数的平方成正比,即r = Kn2,;应用的结果求卫星轨道和下一个“容许”轨道间的距离,由此进一步说明在宏观问题中轨道半径实验上可认为是连续变化的卫星绕地球运动的向心力是万有引力GMmr2-34243?mvr2;根据玻尔理论,角动量为mvr = nh/2π.将前式乘以mr得GMmr??2234π22,所以r?hn22222?Kn,4πGMm即:卫星的轨道半径与量子数的平方成正比.假设卫星质量m = 100kg,比例系数为K?h2224πGMm?224?6?10?2=.77×10.-87可见:比例系数很小.当r = R时,地球表面的量子数为n0??4.8?1046.可见:地球表面处的量子数很大.地面以上的量子数设为n’,,则总量子数可表示为两个量子数之和:n =n0 + n’.轨道间的距离为Δr = K[ - ] = K[2 + 1].由于n0>>1,所以Δr =Kn0 +Kn’.设n’ = kn0,即:取地面以上的量子数为地球表面量子数的倍数,有n = n0,则r = Kn022,Δr =Kn0 =.66×10-40.这说明:当地面以上的量子数按k + 1成倍地增加时,半径将按k + 1的平方的规律增加,而轨道之间的距离只按k + 1的一次方的规律增加;由于Δr的系数很小,所以轨道间距是非常非常小的,因此可认为轨道半径是连续变化的.-1017.11 电子和光子各具有波长 2.0×10m,它们的动量和总能量各是多少? [解答]它们的动量都为p?h?6.63?102?10?3422??10=.315×10-24.根据公式E= p2c+ m02c4,电子的总能量为E?10×[+ ]=8.19×10.8-248-24-31821/2-14光子的静止质量为零,总能量为E = cp=×10×3.315×10 =.945×10.17.1室温下的中子称为热中子T =00K,试计算热中子的平均德布罗意波长.[解答]中子热运动的平均速度为?-23-1-27其中k为玻尔兹曼常数k = 1.38×10J·K,mn是中子的质量mn = 1.675×10kg,可得平均速度为10,=.509×平均动量为10.?mn=.2×平均德布罗意波长为-1010 = 0.158.??h/= 1.58×-27-1417.1假定对某个粒子动量的测定可精确到千分之一,试确定这个粒子位置的最小不确定量.该粒子质量为5×10-3kg,以2m·s-1的速度运动;该粒子是速度为1.8×10m·s的电子. [解答]粒子的动量为p = mv,动量的不确定量为Δp = p/1000,根据动量和位置的不确定关系Δp·Δx ≥ ?/2,位置的不确定量为Δx = ?/2Δp.?x?h2?ph2?p?1000h4πmv1000h4πmv?1000?6.63?103?348-14??5?10?21000?6.63?104??9.1?10?31?34=.276×10-30.?x????1.8?108=.22×10-10.17.1一束动量是p的电子,通过缝宽为a的狭缝,在距离狭缝为R处放置一屏,屏上电子衍射图样中央最大的宽度是多少?[解答]根据动量和位置的不确定关系Δpx·Δx ≥ h,其中位置不确定量为Δx = a,动量的不确定量为Δpx = psinθ.设电子衍射图样的中央最大半宽度为w,则sinθ = w/R,可得pwR?a?h,宽度为2w?2hRpa.第十一章静电场例题答案:11—1. B; 11—2. B; 11—3. B 11—4.qdqd;从O点指向缺口中心点 ?4??0R22?R?d8?2?0R3?d/?0 ; ??04R?d11—5.11—6. D 11—7.?d22;沿矢径OP?3?向右 ; 向右2?02?011—8.11—9. D; 11—10. C; 11—11. C 11—12. V—1V 11—13-14. 11—15. 无答案练习题答案:11—1. 证明:设杆的左端为坐标原点O,x轴沿直杆方向.带电直杆的电荷线密度为?=q/L,在x处取一电荷元dq =?dx = qdx/L,它在P点的场强: dE?dq4??0L?d?x2?qdx4??0LL?d?x2qdxq总场强为:E? ?24??0L?4??0dL?d011—2. Q / ?0, 011—3. -? / ,3? / 11—4.B11—5. 解:在任意位置x处取长度元dx,其上带有电荷dq=?0 dxL它在O点产生的电势 dU??0?x?a?dx4??0xO点总电势:U??dU?a?ldx??0?0?a?ldx?aax?4??0??a?4??0a?l??l?aln??a??11—6. 解:在圆盘上取一半径为r→r+dr范围的同心圆环.其面积为 dS=2?rdr其上电荷为dq=2??rdr它在O点产生的电势为 dU?dq?dr?4??0r2?0总电势 U?dU?S??2?0?Rdr??R2?011—7. 解:设导线上的电荷线密度为?,与导线同轴作单位长度的、半径为r的高斯圆柱面,则按高斯定理有 ?rE =? / ?0得到 E = ? / 方向沿半径指向圆筒.导线与圆筒之间的电势差 U12??R2R1??E?dr??2??0?R2R1R?dr?ln r2??0R1则E?U12代入数值,则:rlnR2/R1 导线表面处 E1?U12=2.5×10V/mR1lnR2/R1 圆筒内表面处 E2?U12=1.70×10V/mR2lnR2/R111—8. 解:设小球滑到B点时相对地的速度为v,槽相对地的速度为V.小球从A→B过程中球、槽组成的系统水平方向动量守恒mv+MV=0 ①对该系统,由动能定理 mgR-EqR=121mv+MV②22①、②两式联立解出 v?2MRmg?qE 方向水平向右.mM?mmv2mRmg?qE 方向水平向左. ??MMM?m V??11—9. 解:设无穷远处为电势零点,则A、B两点电势分别为UA??R2?0R2?3R2???R? UB??224?06?2?0R?8R0q由A点运动到B点电场力作功q??? A?q?UA?UB??q12?4?6?0?0?0注:也可以先求轴线上一点场强,用场强线积分计算. 11—10. 解:球心处的电势为两个同心带电球面各自在球心处产生的电势的叠加,即1U0?4??0?q1q2?1r??1r2?4??0?4?r12?4?r22r?r2?1r10U0?0-=8.85×10C / m r1?r2?? 设外球面上放电后电荷面密度为??,则应有 U0 即1?0??r1r2?= 0r1? r2外球面上应变成带负电,共应放掉电荷q??4?r224?r22???1???r1???r2??4??r2?r1?r2??4??0U0r2=6.67×10C-第十二章导体电学例题答案: 12—1. D 12—2. C 12—3. 没答案 12—4. –q,球壳外的整个空间 12—5.1d12—6. 12-7. C2Fd/C,2FdC12-8-9.练习题答案:12—1. C=712Uf12—解:三块无限大平行导体板,作高斯面如图,知:E1=?1 ? ?0,E2=?2? ?0∴左边两极板电势差U1=?1d1 ? ?0,右边两极板电势差U2=E2d2=?2d? ?0,而U1=U2,则?1 ? ?2= d? d1。
