数学思维导引-六年级-方程解应用题 (3)
北师版数学六年级下册-小升初专题:列方程解应用题专项解析

小升初专题:列方程解应用题专项解析知识要点:1 .列方程解应用题的意义★用方程式去解答应用题求得应用题的未知量的方法。
2 .列方程解答应用题的步骤★弄清题意,确定未知数并用x表示;★找出题中的数量之间的相等关系;★列方程,解方程;★检查或验算,写出答案。
3.列方程解应用题的方法★综合法:先把应用题中已知数(量)和所设未知数(量)列成有关的代数式,再找出它们之间的等量关系,进而列出方程。
这是从部分到整体的一种思维过程,其思考方向是从已知到未知。
★分析法:先找出等量关系,再根据具体建立等量关系的需要,把应用题中已知数(量)和所设的未知数(量)列成有关的代数式进而列出方程。
这是从整体到部分的一种思维过程,其思考方向是从未知到已知。
4.列方程解应用题的范围a.一般应用题;b.和倍、差倍问题;c.几何形体的周长、面积、体积计算;d.分数、百分数应用题;e.比和比例应用题。
5.常见的一般应用题一、以总量为等量关系建立方程例题两列火车同时从距离536千米的两地相向而行,4小时相遇,慢车每小时行60千米,快车每小时行多少小时?解法一:快车 4小时行的+慢车4小时行的=总路程解:设快车小时行X千米4X+60×4=5364X+240=5364X=296X=74解法二:(X+60)×4=536X+60=536÷4X=134一60X=74答:快车每小时行驶74千米。
练一练①降落伞以每秒10米的速度从18000米高空下落,与此同时有一热汽球从地面升起,20分钟后伞、球在空中相遇,热汽球每秒上升多少米?②甲、乙两个进水管往一个可装8吨水的池里注水,甲管每分钟注水400千克,要想在8分钟注满水池,乙管每分钟注水多少千克?③两城相距600千米,客货两车同时从两地相向而行,客车每小时行70千米,货车每小时行80千米,几小时两车相遇?④两地相距249千米,一列火车从甲地开往乙地,每小时行55.5千米,行了多少小时还离乙地有27千米?⑤电机厂计划生产1980台电动机,已经生产了4天,每天生产45台,由于改进了技术,以后每天比原来增产15台,实际完成任务需几天?二、以总量为等量关系建立方程例题甲、乙两个粮仓一共有粮6800包,甲是乙的3倍,两仓各有多少包?解设:乙仓有粮X包,那么甲仓有粮3X包。
高思奥数导引小学六年级含详解答案第03讲 方程解应用题

第
兴趣篇
1.图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米。已知 厘米, 厘米, 厘米,求图形的面积。
【分析】
2. 如图所示, 等于多少度?
【分析】将这六个角用中心六边形的六个内角代换,利用六边形内角和为 ,列方程得
,
所以
3. 如图,平行四边形 的周长为75厘米。以 为底时高是14厘米,以 为底时高是16厘米。求平行四边形 的面积。
【分析】 ,根据面积相等,底的比与高的比成反比例,所以 ,因此 ,平行四边形 的面积是 平方厘米
4. 如图所示,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是 平方米、 平方米、 平方米和 平方米。已知图中的阴影部分是正方形,那么它的面积是多少平方米?
【分析】 ,因此 , , ,所以 , ,因此 ,那么它的面积是 平方米
【分析】
从A点向BC做垂线交BC于F点,交BD于H点。
三角形ABH面积等于三角形CDE的面积,又四边形AEDH为平行四边形。
所以三角形AED的面积=75-45=30。
7. 在长方形 中, 、 、 、 分别是边 、 、 、 上的点,将长方形的四个角分别沿着 、 、 、 对折后, 点与 点重合, 点与 点重合。已知 =3, =4,求线段 与 的长度比。
2. 如图, 是正五边形, 是正三角形, 等于多少度?
【分析】 ,因为 ,所以 ,因此
3. 一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图所示。问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?
【分析】设 ,有 ,解得 ,所以 平方厘米
4. 图中大长方形被分成四个小长方形,面积分别为12、24、36、48。请问:图中阴影部分的面积是多少?
苏教版六年级数学——列方程解应用题.doc

苏教版六年级数学——列方程解应用题教学内容:教材第24页练一练,练习十四6-10题教学要求:1、使学生进一步掌握列方程解应用题的步骤,明确其中的关键,是找出数量之间的相等关系,能根据题意正确地列出方程解答,两三步计算的应用题。
2、使学生能根据应用题的特点,选择恰当的方法来解答。
进一步培养学生分析数量关系的能力,发展学生的思维。
教学过程:一、揭示课题1、根据题意列出方程比一个数的2倍多5是70。
一个数加上它的1.2倍是13,220乘以4的积减去一个数得11一个数的2.5倍加上3个0.6是6.8口答:板书,说一说列方程时是怎样想的。
3、引入新课。
我们已经学会根据几个数之间的等量关系列出议程,今天这节课着重复习根据应用题数量之间的相等关系,列方程解答,通过复习,要能根据题意正确地列方程来解答应用题,同时还要能根据数量关系的特点,灵活地选择算术方法或用方程来解答应用题。
二、复习列方程解应用题的思路。
1、复习解题步骤。
提问:我们学过的列议程解应用题的步骤怎样?审题用X表示未知数;找等量关系列方程;解方程检验写答案)你认为其中最关键的是哪一步?为什么?指出:列方程解应用题要按照解题步步骤进行,其中最关键的一步是找等量关系列方程。
2、什么练一练三人报演,各练集体订正,说说对照什么关系式列方程的三、综合练习1、练习十四第6题先讨论后口答。
2、练习十四第7题。
学生读题,说一说每道题里数量之间的相等关系,并说出根据什么,找出等量关系的。
让学生列出方程,口答方程,老师板书。
3、做练习十四第8题。
两人板演,齐练,集体订正。
4、讨论第9题用什么方法解答比较合适。
5、做练习十四第10题。
让学生列出每题的方程。
四、课堂小结你通过列方程解应用题,进一步明确了哪些内容?五、作业。
课堂作业,练习十四9、10外业:第7题。
小学六年级列方程解应用PPT课件

02
列方程解应用题的步骤
审题
仔细阅读题目,理解题意,明确问题的要求和条件。 确定问题的类型和所涉及的数学概念。 确定需要解决的问题和未知数。
设未知数
根据题意,选择适当的未知数 表示问题中的数量关系。
02
01
设未知数时,尽量选择简单的字 母表示,以便于计算和简化方程
。
建立方程
01
根据题意,利用已知条件和未知 数之间的关系,建立方程。
解出方程后,对答案进行检验, 确保其符合实际情况和题目的要
求。
根据问题背景和常识,判断答案 是否合理。
如果答案不合理,需要重新审视 方程和解题过程,找出错误并修
正。
05
列方程解应用题的实例分 析
例题一:追及问题
题目
甲、乙两车同时从A地出发,在相距60千米的A、B两地之间不断往返行驶,已知甲车 的速度是每小时30千米,乙车的速度是每小时20千米,则多长时间后甲乙两车第五次
列方程解应用题的重要性
01
实际应用
列方程解应用题在实际生活中 有着广泛的应用,如工程、经
济、金融等领域。
02
培养能力
通过列方程解应用题,可以培 养学生的逻辑思维、抽象思维
和问题解决能力。
03
数学建模
列方程解应用题是数学建模的 基础,有助于学生理解数学与
实际问题的联系。
列方程解应用题的历史与发展
03
追及问题
追及问题的特点是两个物体在同一直线上运动,一个在前, 一个在后,后者要追上前者。解决这类问题时,我们需要找 出两者之间的速度差和距离差,然后根据时间=路程差÷速度 差来求解。
例如:甲、乙两辆汽车同时从A、B两地相向而行,甲车的速 度为60千米/小时,乙车的速度为40千米/小时,两车相遇后 继续前行,求两车到达各自出发地所需的时间。
列方程解应用题奥数思维拓展(试题)-小学数学六年级上册人教版(含答案)

列方程解应用题奥数思维拓展-小学数学六年级上册人教版一.选择题(共6小题)1.一个学生投篮,没投进去的比投进去的多6个,投进去的比总数的多3个,这个学生一共投篮()次.A.12B.21C.27D.362.甲、乙两班学生的平均人数是43人,甲班比乙班多4人,甲、乙两班各有多少人?设乙班有x人,列出的方程是()A.43×2﹣x=4B.43×2+4=2xC.x+(x+4)=43×23.有2只桶装油44千克,如第一桶倒出,第二桶里倒进2.8千克,则2只桶内油相等,原来第二桶装油多少千克.()A.18千克B.15千克C.8千克D.28千克4.动物园的门票售价:成人票每张50元,儿童票每张30元.某日动物园售出门票700张,收入29000元.设儿童票售出x张,根据题意可列出方程为()A.30x+50(700﹣x)=29000B.50x+30(700﹣x)=29000C.30x+50(700+x)=29000D.50x+30(700+x)=290005.甲乙两条绳子共长20米,如果甲减去2米,乙增加米,则两条绳子相等,求乙绳的长度?设乙绳的长为x米,可列方程()A.B.x+=20﹣x﹣2C.x+x=20﹣x﹣2D.x+﹣2=20﹣x6.和平小学共有教师120人,其中男教师是女教师的,求女教师的人数.解:设女教师有x人.下列所列方程中正确的是()A.x+x=120B.x+3x=120C.x+2x=120D.x+x=120二.填空题(共6小题)7.老王体重的等于小李体重的,老王体重的比小李体重的轻1.5千克.求老王的体重是千克,小李的体重是千克.8.两袋粮食共重81千克,第一袋吃去了,第二袋吃去了,共余下29千克,原来第一袋粮食重千克.9.甲、乙两数的和是42.14,甲数的小数点向左移动一位就恰好等于乙数的,则甲数是.10.甲、乙两个数的和是136,甲数的小数点向左移动一位等于乙数的,甲数是.11.两个书架共有372本书,甲书架本数的与乙书架本数的相等,甲书架有书本.12.由于浮力的作用,金放在水里称,重量减轻,银放在水里称,重量减轻.有一块重500克的金银合金,放在水里称减轻了32克,这块合金含金克.三.应用题(共9小题)13.“6•26”禁毒日当天,学校组织甲、乙两组学生参观禁毒教育基地,甲组人数是乙组的,如果从乙组调整40人到甲组,这时甲组人数是乙组人数的2倍,那么甲、乙两组原来各有多少人?(用方程解答)。
【机构秘籍思维导引】数学六年级第03讲方程解应用题(教师版+学生版,含详细解析)全国通用

第3讲 方程解应用题兴趣篇1、解下列方程:(1)x x x -+-=-12225; (2)()x x ⨯-=1251356;(3)x x -=+111233.[分析](1)()()x x x --=-+10512022 x x x x x -+=--==10552024711117;(2)x x ⎛⎫-= ⎪⎝⎭22155x x x x -===425529251029; (3)()x x -=+31123x x x x -=+==33323256282、在一次选举中,有甲、乙丙三位候选人,乙的选票比甲的2倍还多5张,丙的选票比甲的一半还少4张.如果甲、乙、丙三人的选票一共有36张.请问:甲得了多少张选票?[分析]设甲有选票x 票,那么乙有25x +票,丙有142x -票.依题意有1254362x x x +++-=解得,10x =答:甲得了5票.3、有若干名学生上体育课,体育老师规定每两人合用一个排球,每三人合用一个足球,每四人合用一个篮球,已知排球、足球、篮球共用了26个.问:有多少名学生上体育课? [分析]设一共有x 名学生上课.那么有112634x x x ++= 解得,26x =答:一共有26名学生上体育课.4、唐老师给幼儿园大班的小朋友每人发17张画片,小班每人发13张画片.已知大班人数是小班的35,小班比大班总共多发126张画片,求小班的人数.[分析]设小班有x 人,那么大班有35x 人.依题意有317131265x x ⨯+=解得,45x =答:小班有45人.5、明知小学六年级一班男生的人数占全班总人数的70%,六年级二班的男生比一班男生少2名,而女生人数为一班女生的2倍.如果两班合在一起,则男生所占的比例为60%.请问:二班有多少名女生? [分析]设一班男生有7x 人,那么一班女生有3x 人,二班男生72x -人,二班女生326x x ⨯=人.依题意有: 7723664x x x x+-+=解得,4x =,那么二班女生有4624⨯=(人)答:二班有24名女生.6、甲、乙两车同时从A 、B 两地出发,相向而行,在A 、B 之间不断往返行驶.甲车到达B 地后,在B 地停留了2个小时,然后返回A 地;乙车到达A 地后,马上返回B 地;两车在返回的途中又相遇了,相遇的地点距离B 地288千米.已知甲车的速度是每小时60千米,乙车的速度是每小时40千米.请问:A 、B 两地相距多少千米? [分析]设A 、B 两地相距x 千米.那么相遇时甲走了288x +千米,乙走了2288x -千米.根据题意列方程 288228826040x x +-+=解得,420x =答:A 、B 两地相距420千米7、解下面的方程组:(1),;x y x y +=⎧⎨+=⎩422217780 (2),.x y x y +=⎧⎨-=⎩4714412824[分析](1)1x =,9y =;(2)15x =,12y =8、冬冬与小悦一起在水果店买水果,冬冬买了3千克苹果和2千克梨,共花了18.8元,小悦买了2千克苹果和3千克梨,共花了18.2元.你能算出1千克苹果多少元,1千克梨多少元吗? [分析]设1千克苹果x 元,1千克梨y 元,由题意 3218.842318.2 3.4x y x x y y +==⎧⎧⇒⎨⎨+==⎩⎩答:苹果4元,梨3.4元.9、2个蟹将和4个虾兵能打扫龙宫的310,8个蟹将和10个虾兵就能把龙宫全部打扫完.如果只让蟹将打扫龙宫,需要多少个?只让虾兵打扫龙宫,需要多少个?[分析]设只让蟹将打扫龙宫,需要x 个;只让虾兵打扫龙宫,需要y 个.2431210810301x x y y x y⎧+=⎪=⎧⎪⇒⎨⎨=⎩⎪+=⎪⎩ 答:只让蟹将打扫龙宫,需要12个;只让虾兵打扫龙宫,需要30个.10、如图,小玲有两种不同形状的纸板,一种是正方形的,一种是长方形的.正方形纸板的总数与长方形纸板的总数之比是1:2.她用这些纸板做成一些竖式和横式的无盖纸盒,正好将纸板用完.那么在小玲所做纸盒中,竖式纸盒的总数与横式纸盒的总数之比是多少?[分析]设做了竖式纸盒x 个,横式纸盒y 个.那么共用正方形纸板2x y +个,长方形纸板43x y +个. 21432x y x y +=+解得,:1:2x y =答:竖式纸盒的总数与横式纸盒的总数之比是1:2.拓展篇1、解下列方程:(1)x x xx +-++=+31714612;(2)()x x ⎡⎤⨯⨯++-=⎢⎥⎣⎦321721223423;(3)x x +=+355412;(4)(x +1)(x +7)()x =++225.[分析](1)()()123321712x x x x +++-=+ (2)17213423x x ++-=12392271210512x x x x x x +++-=+== x x ==5112265(3)()()235541x x +=+ (4)2287445x x x x ++=+++610205514x x x +=+=;4212x x ==2、一个分数,分子与分母的和是122.如果分子、分母都减去19,得到的分数约分后是15,那么原来的分数是多少?[分析]设原分数是122xx-,那么191122195x x -=--,解得33x =,原来的分数是3389.3、130克含盐5%的盐水,与若干含盐9%的盐水混合,配成含盐6.4%的盐水.请问:最后配成的盐水有多少克? [分析]设9%的盐水有x 克,依题意 ()5%1309% 6.4%130x x ⨯+=⨯+解得,70x =,因此最有有盐水200克.答:最后配成的盐水有200克.4、如图1中的短除式所示,一个自然数被8除余1,所得的商被8除也余1,再把第二次所得的商被8除后余7,最后得到的商是a .如图2中的短除式表明:这个自然数被17除余4,所得的商被17除余15,最后得到的商是a 的2倍.求这个自然数.图2图117余4……所求的自然数第二次商……余15172a a 8余7……第二次商第一次商……余188余1……所求的自然数[分析]原数可以表示成()328711878181512457a a a =⨯+⨯+⨯+=+ 也可表示成()()()217215421715174578259a a a =⨯+⨯+=+ 那么512457578259a a +=+,解得3a =那么原数为51234571993⨯+=5、给六年级五班的同学分苹果,第一组每人3个,第二组每人4个,第三组每人5个,第四组每人6个.已知第二组和第三组共有22人,第一组人数是第二组的2倍,第三组和第四组人数相等,总共分出去230个苹果.问:该班一共有多少名学生? [分析]设第二组有x 名学生,那么,第三组、第四组有22x -名,第一组有2x 名. 依题意:()()234225226230x x x x ⨯+⨯+-⨯+-⨯=,解得12x = 那么一共有:()122122221256⨯++⨯-=(名)学生.答:该班一共有56名学生.6、解下面的方程组:(1),;x y x y +=⎧⎨-=⎩1194913317 (2),;y x x y -=⎧⎨-=⎩2113859 (3),.x y x y +=⎧⎨+=⎩18293071628284[分析](1)2x =,3y =;(2)7x =,4y =;(3)9x =,5y =7、商店里有大盒、中盒、小盒共27盒筷子,其中大盒中装有18双筷子,中盒中装有12双筷子,小盒中装有8双筷子,一共装有330双筷子,其中小盒数是中盒数的2倍.问:三种包装的筷子各有多少盒? [分析]设有x 个中盒,那么有2x 个小盒,273x -个大盒. ()182731282330x x x ⨯-++⨯=,解得,6x =那么,大盒数9,中盒数6,小盒数12答:共有大盒9个,中盒6个,小盒12个.8、甲、乙两人从相距36千米的两地相向而行.如果甲比乙先出发2小时,那么他们在乙出发2.5小时候相遇;如果乙比甲先出发2小时,那么他们在甲出发3小时候后相遇.问:甲、乙两人每小时各走多少千米?[分析]设甲速每小时x 千米,乙速每小时y 千米.那么依据题意列方程组: 4.5 2.53663536 3.6x y x x y y +==⎧⎧⇒⎨⎨+==⎩⎩答:甲每小时走6千米,乙每小时走3.6千米.9、一台天平,右盘上有若干重量相等的白球,左盘上有若干重量相等的黑球,这时两边平衡.如果从右盘中取走一个白球置于左盘上,再把左盘的两个黑球置于右盘上,同时给左盘加20克砝码,这时两边也平衡.如果从右盘两个白球到左盘上,从左盘移一个黑球到右盘上,那么需要再给右盘加50克砝码,两边才能平衡.问:白球、黑球每个各重多少克? [分析]设白球重xg ,黑球重yg ,因为,原来天平是平衡的,在进行调整后天平重新达到平衡,但总重量增加了一个砝码的重量.对于第一次调整,增加了20g ,对于第二次调整,增加了50g .那么实际上,第一次调整,天平两边各重了10g ,第二次调整各重了25g . 通过天平一侧的重量变化建立方程:2102022515y x x x y y -==⎧⎧⇒⎨⎨-==⎩⎩所以,白球重20g ,黑球重15g .[分析]白球20克,黑球15克10、奥运指定商品零售店里的福娃有大号、中号和小号三种.小悦买了一个大号的、三个中号的和两个小号的,共花了360元;冬冬买了两个大号的、一个中号的和一个小号的, 共花了270元;阿奇买了一个大号的、两个中号的和两个小号的,共花了300元.请问:商店里的大号、中号和小号福娃的单价各是多少? [分析]设大、中、小3种型号的福娃单价分别是,,x y z .那么有 32360802270602230050x y z x x y z y x y z z ++==⎧⎧⎪⎪++=⇒=⎨⎨⎪⎪++==⎩⎩答:大号80元,中号60元,小号50元11、如图,墙边放着一块木块,一只猫淘气,爬了上去,使得木块向下滑动了一段距离,现在已知图中的三段长度(单位:厘米),你能求出这块木板的长度吗?[分析]设下滑后,木块低端距离地面x 厘米.那么根据勾股定理可以列式:()22222007090x x +=++,解得150x = 222200150250+=,因此木块长250厘米.答:木块的长度为250厘米12、甲、乙、丙、丁四人,每三个人的平均年龄加上余下一人的年龄分别为29,23,21和17.这四人中最大年龄与最小年龄的差是多少? [分析]设四个人的年龄分别为,,,a b c d ,那么有293233213173a b cd a b d c a c d b b c d a ++⎧+=⎪⎪++⎪+=⎪⎨++⎪+=⎪⎪++⎪+=⎩四试相加,得()29045a b c d a b c d +++=⇒+++= 把上式代入方程组,有22915143212231581232921156332171523d a c b c b d a ⎧=-=⎪⎪=⎧⎪=-=⎪⎪=⎪⇒⎨⎨=⎪⎪=-=⎪⎪=⎩⎪⎪=-=⎩,因此,最大与最小之差为18另解:四个人的年龄分别为a b c d >>>,那么29,1733b c d a b ca d +++++=+=,两式相减得:()2121218333b c d a b c a d a d a d +++++--=⇒-=⇒-= 即最大年龄与最小年龄的差是18岁超越篇1、丙看到甲、乙两人正在解下面这个方程组:x y x y +=⎧⎨+=⎩2536704 其中未知数前面的系数被甲和乙遮住了.甲计算得出方程的解是x =7,y =3;而乙误把“2536”看作“1536”,得到的解是x =4,y =4.试问:方程组四个被遮住的系数中最小的一个是多少?[分析]把x ,y 的值代入方程,以方框为未知数,重新建立方程,得:73253634673704384415364444704132a b a c d b a b c c d d +==⎧⎧⎪⎪+==⎪⎪⇒⎨⎨+==⎪⎪⎪⎪+==⎩⎩ 最小的是38.2、幼儿园有三个班,甲班比乙班多4人,乙班比丙班多4人.老师给小孩分枣,甲班每个小孩比乙班每个小孩少分3个枣;乙班每个小孩比丙班每个小孩少分5个枣.结果甲班比乙班总共多分3个枣,乙班比丙班总共多分5个枣.问:三个班总共分了多少个枣? [分析]设丙班有x 人,则乙班x +4人,甲班x +8人.丙班每个小孩共分了y 个枣,则乙班分了y -5个枣,甲班分了y -8个枣.则:(8)(8)(4)(5)3434711(4)(5)5452520x y x y y x x x y xy y x y +--+-=-==⎧⎧⎧⇒⇒⎨⎨⎨+--=-==⎩⎩⎩则三班总共分了(8)(8)(4)(5)191215151120673x y x y xy +-++-+=⨯+⨯+⨯=个枣 答:三个半总共分了673个枣3②钓到3条或3条以上的选手平均每人钓到了6条鱼; ③钓到12条或者12条以下的选手平均每人钓到了5条鱼.请问:一共有多少名选手参赛?这些选手一共钓到了多少条鱼?[分析]设共有x 人参加比赛,则钓到3条及以上的人数为95721x x ---=-,掉到12条及以下的人数为5218x x ---=-.依题意列方程:(21)61527(8)5135142151x x -⨯+⨯+⨯=-⨯+⨯+⨯+⨯ 解得175x =.则共钓鱼:(17521)61527943-⨯+⨯+⨯=条.答:一共有175名选手;一共钓上943条鱼.4、A 、B 两地相距2400米.甲、乙两人分别从A 、B 两地同时出发,相向而行.两人在途中某处相遇后,甲又继续行进18分钟到达B 地,乙又继续行进50分钟到达A 地.请问:甲比乙每分钟多走多少米? [分析]设甲速为x ,乙速为y .那么,甲走乙50分钟的路程和乙走甲18分钟的路程需要的时间相同(都为两者相遇时对方走的路程).那么可以建立方程: 1850240050501830x y x y xy x y +=⎧=⎧⎪⇒⎨⎨==⎩⎪⎩,甲比乙每分钟多走20米.答:甲比乙每分钟 多走20米.5、甲、乙两车运一堆货物,甲车单独运比乙车单独运要少运5次;如果一起运,各运6次就刚好运完.问:甲车单独运要几次运完? [分析]设甲效x ,乙效y ,建立方程 11151011156x y x y x y ⎧⎧-==⎪⎪⎪⎪⇒⎨⎨⎪⎪=+=⎪⎪⎩⎩,甲单独运要10次. 答:驾车单独运要10次运完.6、一个从小到大排列的等差数列,如果把这个数列的首项除以2,末项乘以2,这些数的平均数就增加了7;如果把首项乘以2,末项除以2,平均数就少了2.已知这个等差数列中所有数的和等于245,求这个数列的末项. [分析]题目出错7、一个水池,顶部有一个进水管,底部有一个出水管.如果只打开进水管,50分钟可以把水池灌满;如果只打开出水管,60分钟可以把一池水放完.现在水池在中间的某个位置出现了一条与池底平行的裂缝,如果只打开进水管,需要80分钟才能放满一池水,而只打开出水管只需46.5分钟即可放完一池水.请问:裂缝出现在离池底几分之几高度的地方?[分析]设裂缝出现在离池底x 处,裂缝漏水的效率为1y.那么可以建立方程:1180(8050)125051110046.5(46.560)160x y x y x y ⎧⨯--⨯=⎧⎪=⎪⎪⇒⎨⎨⎪⎪=⨯+-⨯=⎩⎪⎩. 答:裂缝出现在离池底25高的地方. 8、“太平洋号”和“北冰洋号”两艘潜艇在海下沿直线同向潜航,“北冰洋号”在前,“太平洋号”在后.在某个时刻,“太平洋号”发出声波,间隔2秒后,再次发出声波.当声波传到“北冰洋号”时,“北冰洋号”会反射声波.已知“太平洋号”的速度是每小时54千米,第一次和第二次探测到“北冰洋号”反射的回波的间隔时间是2.01秒,声波传播的速度是每秒1185米.请问:“北冰洋号”的速度是每小时多少千米?ONQPME DCB [分析]用上图示意太平洋号、北冰洋号和声波运动的情况:A 、D 分别是第一次发出声波时太平洋号和北冰洋号的位置,M 和Q 分别是第二次发出声波时太平洋好和北冰洋号的位置;C 和E 分别是太平洋好接收到北冰洋号第一次反射声波时太平洋好和北冰洋号的位置,P 和O 分别是太平洋好接收到北冰洋号第二次反射声波是太平洋好和北冰洋号的位置;B 是北冰洋号收到第一次声波时的位置,N 是北冰洋号收到第二次声波时的位置. 太平洋好的速度是54千米/小时,相当于15米/秒.声波的速度是1185米/秒,设北冰洋号的速度为x 米/秒.设0t 为太平洋好第一次发出声波的时刻,02t +为太平洋好第二次发出声波的时刻,设0t t +为太平洋号收到第一次发出声波返回的时刻,0 2.01t t ++是太平洋号收到第二次发出声波返回的时刻.(1)如图,AC 是太平洋号第一次发出声波到接收反射回的声波潜航的距离,15AC t =,AB BC +是第一次声波传导的距离,1185AB BC t +=,他们的和等于21200AC AB BC AB t ++==;(2)类似的,()150.01,MP t MN NP =++是第二次声波传导的距离,()11850.01MN NP t +=+,他们的和等于()212000.01MP MN NP MN t ++==+;(3)由(1),(2)得:6,11850.01MN AB MN AB NP BC -=-+-=⨯,也有611850.01BC NP -=-⨯(4)由于DB 是北冰洋号从太平洋好第一次发出声波到北冰洋号接收到声波时潜航的距离,1185BCDB tv v =-;QN 是北冰洋号从太平洋好第二次发出声波到北冰洋号接收到声波时的潜航距离,()0.011185NPQN t v v =+-;(5)由(3),(4)得到:()0.01611850.011185vQN DB v -=+-⨯⨯.(6)AD 是太平洋好第一次发出声波时两艘潜艇之间的距离,是太平洋好第二次发出声波时两艘潜艇之间的距离,()215MD AD v -=-.因为,AD AB DB MQ MN QN =-=-,所以,()()()660.01611850.01611851185MQ AD MN AB QN DB v v v -=---=---⨯⨯=-于是:()662151185vv -=- 解得211722v =因此北冰洋号潜航的速度是每小时21717642211=千米. 答:北冰洋号潜航的速度是每小时76411千米.。
小学六年级列方程解应用题方法归纳

小学六年级列方程解应用题方法归纳小学六年级列方程解应用题专项复习解决1系列方程应用问题的意义★正向思维,把未知量当已知量。
2.方法总结用方程式解决应用问题的步骤如下:(1)审题:弄清题意,确定已知量、未知量及它们的关系;(2)设元:选择适当未知数,用字母表示;(3)列代数公式:根据条件,用包含集合未知数的代数公式表示其他未知数;(4)列方程:用列代数公式中未使用的等价关系列出方程;(5)解方程:正确利用方程的性质求方程的解;(6)检查并回答问题。
3列方程解应用题的方法★ 综合方法:首先将应用问题中的已知数(量)和设定的未知数(量)列成相应的代数表达式,然后找出它们之间的等价关系,然后列出方程式。
这是一个从局部到整体的思维过程,其思维方向是从已知到未知。
★分析法:先找出等量关系,再根据具体建立等量关系的需要,把应用题中已知数(量)和所设的未知数(量)列成有关的代数式进而列出方程。
这是从整体到部分的一种思维过程,其思考方向是从未知到已知。
4列方程解应用题的范围一般应用问题;B)和差时间;C计算几何体的周长、面积和体积;D.分数和百分比的应用问题;E比例和比例应用问题。
5.常见的一般应用问题一、以总量为等量关系建立方程例如,两列火车同时从536公里外的两个地方出发。
他们四小时后见面。
这列慢车时速60公里。
特快列车每小时运行多少小时?解法一:快车4小时行的+慢车4小时行的=总路程解设:快车小时行x千米4x+60×4=5364x+240=5364x=296x=74溶液二:解设:快车小时行x千米(x+60)×4=536x+60=536÷4x=134-60x=74答:快车每小时行驶74千米。
练一练① 降落伞以每秒10米的速度从18000米的高度降落。
与此同时,一个热蒸汽球从地面上升20分钟分钟后伞球在空中相遇,热汽球每秒上升多少米?② 两条进水管a和B将水注入一个可容纳8吨水的水池。
六年级小升初奥数列方程解方程列方程解决问题
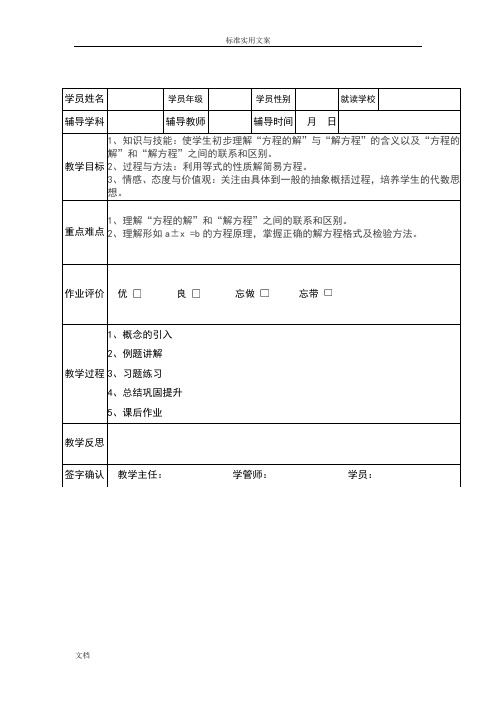
作业评价优良忘做忘带六年级第4讲解方程列方程知识要点:一、解方程步骤:1.去分母,(通过最小公倍数约掉),2.移项,把带有X的都到等号的一边,要变负号:原来是+移项就变成-;原来是-移项就变成+3.合并同类项(把带X的放到等号的一边,数字的放到等好的另一边)4.把X的前面的数字,变为1,(两边同时除以X前面的数字)2.移项、7x+10x=35+33×353.合并同类项:(10+7)x=11904.把X的前面的数字,变为1.两边同时除17:x=1190÷7=70练习1:(1)X-0.8X=6(2)200=450+5X+X16×5+5X=90 6.8X-4.4=0.4×6(3)25000+x=6x(4)2(X+X+0.5)=9.8二、根据条件写出相应的数量关系。
例2:六(五)班有男生30人,比女生的2倍少10人?相等关系:1.男生人数加上10等于2乘以女生的人数2.男生人数等于2乘以女生的人数减去10练习2:1、甲数比乙数的2倍少1 。
相等关系:()。
2、甲数与乙数的和是180。
相等关系:()。
3、东西两仓共存粮230吨。
相等关系:()4、甲数的一半比乙数大25。
相等关系:()。
三、经典例题:例3、一个数的3.7倍加上这个数的1.3倍,和是120,求这个数? 【解析】:1.设未知数:设这个数是X2.找出等量关系:这个数的3.7倍加上这个数的1.3倍等于1203.列方程、解方程:3.7x+1.3x=1205x=120x=24练习3:1、 3.4比x的3倍少5.6,求x。
2、一个数的8倍比它的5倍多24,求这个数?例4、学校买来40跟跳绳和30服羽毛球拍,共用去1020元.每副羽毛球拍30元,每跟跳绳的售价是多少元?【解析】设每根跳绳售价x元40x+30×30=1020得x=3元练习4:1、小亚带10元钱为家里养的金鱼买鱼食,她买的是1.3元一包的鱼食,找回7.4元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3讲方程解应用题兴趣篇1、解下列方程:(1)x x x -+-=-12225;(2)()x x ⨯-=1251356;(3)x x -=+111233.[分析](1)()()x x x --=-+10512022x x x x x -+=--==10552024711117;(2)x x⎛⎫-= ⎪⎝⎭22155x xx x -===425529251029;(3)()x x -=+31123x x x x -=+==33323256282、在一次选举中,有甲、乙丙三位候选人,乙的选票比甲的2倍还多5张,丙的选票比甲的一半还少4张.如果甲、乙、丙三人的选票一共有36张.请问:甲得了多少张选票?[分析]设甲有选票x 票,那么乙有25x +票,丙有142x -票.依题意有1254362x x x +++-=解得,10x =答:甲得了5票.3、有若干名学生上体育课,体育老师规定每两人合用一个排球,每三人合用一个足球,每四人合用一个篮球,已知排球、足球、篮球共用了26个.问:有多少名学生上体育课?[分析]设一共有x 名学生上课.那么有112634x x x ++=解得,26x =答:一共有26名学生上体育课.4、唐老师给幼儿园大班的小朋友每人发17张画片,小班每人发13张画片.已知大班人数是小班的35,小班比大班总共多发126张画片,求小班的人数.[分析]设小班有x 人,那么大班有35x 人.依题意有317131265x x ⨯+=解得,45x =答:小班有45人.5、明知小学六年级一班男生的人数占全班总人数的70%,六年级二班的男生比一班男生少2名,而女生人数为一班女生的2倍.如果两班合在一起,则男生所占的比例为60%.请问:二班有多少名女生?[分析]设一班男生有7x 人,那么一班女生有3x 人,二班男生72x -人,二班女生326x x ⨯=人.依题意有:7723664x x x x+-+=解得,4x =,那么二班女生有4624⨯=(人)答:二班有24名女生.6、甲、乙两车同时从A 、B 两地出发,相向而行,在A 、B 之间不断往返行驶.甲车到达B 地后,在B 地停留了2个小时,然后返回A 地;乙车到达A 地后,马上返回B 地;两车在返回的途中又相遇了,相遇的地点距离B 地288千米.已知甲车的速度是每小时60千米,乙车的速度是每小时40千米.请问:A 、B 两地相距多少千米?[分析]设A 、B 两地相距x 千米.那么相遇时甲走了288x +千米,乙走了2288x -千米.根据题意列方程288228826040x x +-+=解得,420x =答:A 、B 两地相距420千米7、解下面的方程组:(1),;x y x y +=⎧⎨+=⎩422217780(2),.x y x y +=⎧⎨-=⎩4714412824[分析](1)1x =,9y =;(2)15x =,12y =8、冬冬与小悦一起在水果店买水果,冬冬买了3千克苹果和2千克梨,共花了18.8元,小悦买了2千克苹果和3千克梨,共花了18.2元.你能算出1千克苹果多少元,1千克梨多少元吗?[分析]设1千克苹果x 元,1千克梨y 元,由题意3218.842318.2 3.4x y x x y y +==⎧⎧⇒⎨⎨+==⎩⎩答:苹果4元,梨3.4元.9、2个蟹将和4个虾兵能打扫龙宫的310,8个蟹将和10个虾兵就能把龙宫全部打扫完.如果只让蟹将打扫龙宫,需要多少个?只让虾兵打扫龙宫,需要多少个?[分析]设只让蟹将打扫龙宫,需要x 个;只让虾兵打扫龙宫,需要y 个.2431210810301x x y y x y ⎧+=⎪=⎧⎪⇒⎨⎨=⎩⎪+=⎪⎩答:只让蟹将打扫龙宫,需要12个;只让虾兵打扫龙宫,需要30个.10、如图,小玲有两种不同形状的纸板,一种是正方形的,一种是长方形的.正方形纸板的总数与长方形纸板的总数之比是1:2.她用这些纸板做成一些竖式和横式的无盖纸盒,正好将纸板用完.那么在小玲所做纸盒中,竖式纸盒的总数与横式纸盒的总数之比是多少?[分析]设做了竖式纸盒x 个,横式纸盒y 个.那么共用正方形纸板2x y +个,长方形纸板43x y +个.21432x y x y +=+解得,:1:2x y =答:竖式纸盒的总数与横式纸盒的总数之比是1:2.拓展篇1、解下列方程:(1)x x xx +-++=+31714612;(2)()x x ⎡⎤⨯⨯++-=⎢⎥⎣⎦321721223423;(3)x x +=+355412;(4)(x +1)(x +7)()x =++225.[分析](1)()()123321712x x x x +++-=+(2)17213423x x++-=12392271210512x x x x x x +++-=+==x x ==5112265(3)()()235541x x +=+(4)2287445x x x x ++=+++610205514x x x +=+=;4212x x ==2、一个分数,分子与分母的和是122.如果分子、分母都减去19,得到的分数约分后是15,那么原来的分数是多少?[分析]设原分数是122xx-,那么191122195x x -=--,解得33x =,原来的分数是3389.3、130克含盐5%的盐水,与若干含盐9%的盐水混合,配成含盐6.4%的盐水.请问:最后配成的盐水有多少克?[分析]设9%的盐水有x 克,依题意()5%1309% 6.4%130x x ⨯+=⨯+解得,70x =,因此最有有盐水200克.答:最后配成的盐水有200克.4、如图1中的短除式所示,一个自然数被8除余1,所得的商被8除也余1,再把第二次所得的商被8除后余7,最后得到的商是a .如图2中的短除式表明:这个自然数被17除余4,所得的商被17除余15,最后得到的商是a 的2倍.求这个自然数.图2图117余4……所求的自然数第二次商……余15172a 8余7……第二次商第一次商……余188余1……所求的自然数[分析]原数可以表示成()328711878181512457a a a =⨯+⨯+⨯+=+也可表示成()()()217215421715174578259a a a =⨯+⨯+=+那么512457578259a a +=+,解得3a =那么原数为51234571993⨯+=5、给六年级五班的同学分苹果,第一组每人3个,第二组每人4个,第三组每人5个,第四组每人6个.已知第二组和第三组共有22人,第一组人数是第二组的2倍,第三组和第四组人数相等,总共分出去230个苹果.问:该班一共有多少名学生?[分析]设第二组有x 名学生,那么,第三组、第四组有22x -名,第一组有2x 名.依题意:()()234225226230x x x x ⨯+⨯+-⨯+-⨯=,解得12x =那么一共有:()122122221256⨯++⨯-=(名)学生.答:该班一共有56名学生.6、解下面的方程组:(1),;x y x y +=⎧⎨-=⎩1194913317(2),;y x x y -=⎧⎨-=⎩2113859(3),.x y x y +=⎧⎨+=⎩18293071628284[分析](1)2x =,3y =;(2)7x =,4y =;(3)9x =,5y =7、商店里有大盒、中盒、小盒共27盒筷子,其中大盒中装有18双筷子,中盒中装有12双筷子,小盒中装有8双筷子,一共装有330双筷子,其中小盒数是中盒数的2倍.问:三种包装的筷子各有多少盒?[分析]设有x 个中盒,那么有2x 个小盒,273x -个大盒.()182731282330x x x ⨯-++⨯=,解得,6x =那么,大盒数9,中盒数6,小盒数12答:共有大盒9个,中盒6个,小盒12个.8、甲、乙两人从相距36千米的两地相向而行.如果甲比乙先出发2小时,那么他们在乙出发2.5小时候相遇;如果乙比甲先出发2小时,那么他们在甲出发3小时候后相遇.问:甲、乙两人每小时各走多少千米?[分析]设甲速每小时x 千米,乙速每小时y 千米.那么依据题意列方程组:4.5 2.53663536 3.6x y x x y y +==⎧⎧⇒⎨⎨+==⎩⎩答:甲每小时走6千米,乙每小时走3.6千米.9、一台天平,右盘上有若干重量相等的白球,左盘上有若干重量相等的黑球,这时两边平衡.如果从右盘中取走一个白球置于左盘上,再把左盘的两个黑球置于右盘上,同时给左盘加20克砝码,这时两边也平衡.如果从右盘两个白球到左盘上,从左盘移一个黑球到右盘上,那么需要再给右盘加50克砝码,两边才能平衡.问:白球、黑球每个各重多少克?[分析]设白球重xg ,黑球重yg ,因为,原来天平是平衡的,在进行调整后天平重新达到平衡,但总重量增加了一个砝码的重量.对于第一次调整,增加了20g ,对于第二次调整,增加了50g .那么实际上,第一次调整,天平两边各重了10g ,第二次调整各重了25g .通过天平一侧的重量变化建立方程:2102022515y x x x y y -==⎧⎧⇒⎨⎨-==⎩⎩所以,白球重20g ,黑球重15g .[分析]白球20克,黑球15克10、奥运指定商品零售店里的福娃有大号、中号和小号三种.小悦买了一个大号的、三个中号的和两个小号的,共花了360元;冬冬买了两个大号的、一个中号的和一个小号的,共花了270元;阿奇买了一个大号的、两个中号的和两个小号的,共花了300元.请问:商店里的大号、中号和小号福娃的单价各是多少?[分析]设大、中、小3种型号的福娃单价分别是,,x y z .那么有32360802270602230050x y z x x y z y x y z z ++==⎧⎧⎪⎪++=⇒=⎨⎨⎪⎪++==⎩⎩答:大号80元,中号60元,小号50元11、如图,墙边放着一块木块,一只猫淘气,爬了上去,使得木块向下滑动了一段距离,现在已知图中的三段长度(单位:厘米),你能求出这块木板的长度吗?[分析]设下滑后,木块低端距离地面x 厘米.那么根据勾股定理可以列式:()22222007090x x +=++,解得150x =222200150250+=,因此木块长250厘米.答:木块的长度为250厘米12、甲、乙、丙、丁四人,每三个人的平均年龄加上余下一人的年龄分别为29,23,21和17.这四人中最大年龄与最小年龄的差是多少?[分析]设四个人的年龄分别为,,,a b c d ,那么有293233213173a b c d a b d c a c d b b c d a ++⎧+=⎪⎪++⎪+=⎪⎨++⎪+=⎪⎪++⎪+=⎩四试相加,得()29045a b c d a b c d +++=⇒+++=把上式代入方程组,有22915143212231581232921156332171523d a c b c b d a ⎧=-=⎪⎪=⎧⎪=-=⎪⎪=⎪⇒⎨⎨=⎪⎪=-=⎪⎪=⎩⎪⎪=-=⎩,因此,最大与最小之差为18另解:四个人的年龄分别为a b c d >>>,那么29,1733b c d a b ca d +++++=+=,两式相减得:()2121218333b c d a b c a d a d a d +++++--=⇒-=⇒-=即最大年龄与最小年龄的差是18岁超越篇1、丙看到甲、乙两人正在解下面这个方程组:x y x y +=⎧⎨+=⎩2536704 其中未知数前面的系数被甲和乙遮住了.甲计算得出方程的解是x =7,y =3;而乙误把“2536”看作“1536”,得到的解是x =4,y =4.试问:方程组四个被遮住的系数中最小的一个是多少?[分析]把x ,y 的值代入方程,以方框为未知数,重新建立方程,得:73253634673704384415364444704132a b a c d b a b c c d d +==⎧⎧⎪⎪+==⎪⎪⇒⎨⎨+==⎪⎪⎪⎪+==⎩⎩最小的是38.2、幼儿园有三个班,甲班比乙班多4人,乙班比丙班多4人.老师给小孩分枣,甲班每个小孩比乙班每个小孩少分3个枣;乙班每个小孩比丙班每个小孩少分5个枣.结果甲班比乙班总共多分3个枣,乙班比丙班总共多分5个枣.问:三个班总共分了多少个枣?[分析]设丙班有x 人,则乙班x +4人,甲班x +8人.丙班每个小孩共分了y 个枣,则乙班分了y -5个枣,甲班分了y -8个枣.则:(8)(8)(4)(5)3434711(4)(5)5452520x y x y y x x x y xy y x y +--+-=-==⎧⎧⎧⇒⇒⎨⎨⎨+--=-==⎩⎩⎩则三班总共分了(8)(8)(4)(5)191215151120673x y x y xy +-++-+=⨯+⨯+⨯=个枣答:三个半总共分了673个枣3、下表显示了一次钓鱼比赛的结果:n 0123…131415钓了n 条鱼的人数95723…521已知:①冠军钓到15条鱼;②钓到3条或3条以上的选手平均每人钓到了6条鱼;③钓到12条或者12条以下的选手平均每人钓到了5条鱼.请问:一共有多少名选手参赛?这些选手一共钓到了多少条鱼?[分析]设共有x 人参加比赛,则钓到3条及以上的人数为95721x x ---=-,掉到12条及以下的人数为5218x x ---=-.依题意列方程:(21)61527(8)5135142151x x -⨯+⨯+⨯=-⨯+⨯+⨯+⨯解得175x =.则共钓鱼:(17521)61527943-⨯+⨯+⨯=条.答:一共有175名选手;一共钓上943条鱼.4、A 、B 两地相距2400米.甲、乙两人分别从A 、B 两地同时出发,相向而行.两人在途中某处相遇后,甲又继续行进18分钟到达B 地,乙又继续行进50分钟到达A 地.请问:甲比乙每分钟多走多少米?[分析]设甲速为x ,乙速为y .那么,甲走乙50分钟的路程和乙走甲18分钟的路程需要的时间相同(都为两者相遇时对方走的路程).那么可以建立方程:1850240050501830x y x y x y x y +=⎧=⎧⎪⇒⎨⎨==⎩⎪⎩,甲比乙每分钟多走20米.答:甲比乙每分钟多走20米.5、甲、乙两车运一堆货物,甲车单独运比乙车单独运要少运5次;如果一起运,各运6次就刚好运完.问:甲车单独运要几次运完?[分析]设甲效x ,乙效y ,建立方程11151011156x y x y x y ⎧⎧-==⎪⎪⎪⎪⇒⎨⎨⎪⎪=+=⎪⎪⎩⎩,甲单独运要10次.答:驾车单独运要10次运完.6、一个从小到大排列的等差数列,如果把这个数列的首项除以2,末项乘以2,这些数的平均数就增加了7;如果把首项乘以2,末项除以2,平均数就少了2.已知这个等差数列中所有数的和等于245,求这个数列的末项.[分析]题目出错7、一个水池,顶部有一个进水管,底部有一个出水管.如果只打开进水管,50分钟可以把水池灌满;如果只打开出水管,60分钟可以把一池水放完.现在水池在中间的某个位置出现了一条与池底平行的裂缝,如果只打开进水管,需要80分钟才能放满一池水,而只打开出水管只需46.5分钟即可放完一池水.请问:裂缝出现在离池底几分之几高度的地方?[分析]设裂缝出现在离池底x 处,裂缝漏水的效率为1y.那么可以建立方程:1180(8050)125051110046.5(46.560)160x y x y x y ⎧⨯--⨯=⎧⎪=⎪⎪⇒⎨⎨⎪⎪=⨯+-⨯=⎩⎪⎩.答:裂缝出现在离池底25高的地方.8、“太平洋号”和“北冰洋号”两艘潜艇在海下沿直线同向潜航,“北冰洋号”在前,“太平洋号”在后.在某个时刻,“太平洋号”发出声波,间隔2秒后,再次发出声波.当声波传到“北冰洋号”时,“北冰洋号”会反射声波.已知“太平洋号”的速度是每小时54千米,第一次和第二次探测到“北冰洋号”反射的回波的间隔时间是2.01秒,声波传播的速度是每秒1185米.请问:“北冰洋号”的速度是每小时多少千米?ONQPME DCB [分析]用上图示意太平洋号、北冰洋号和声波运动的情况:A 、D 分别是第一次发出声波时太平洋号和北冰洋号的位置,M 和Q 分别是第二次发出声波时太平洋好和北冰洋号的位置;C 和E 分别是太平洋好接收到北冰洋号第一次反射声波时太平洋好和北冰洋号的位置,P 和O 分别是太平洋好接收到北冰洋号第二次反射声波是太平洋好和北冰洋号的位置;B 是北冰洋号收到第一次声波时的位置,N 是北冰洋号收到第二次声波时的位置.太平洋好的速度是54千米/小时,相当于15米/秒.声波的速度是1185米/秒,设北冰洋号的速度为x 米/秒.设0t 为太平洋好第一次发出声波的时刻,02t +为太平洋好第二次发出声波的时刻,设0t t +为太平洋号收到第一次发出声波返回的时刻,0 2.01t t ++是太平洋号收到第二次发出声波返回的时刻.(1)如图,AC 是太平洋号第一次发出声波到接收反射回的声波潜航的距离,15AC t =,AB BC +是第一次声波传导的距离,1185AB BC t +=,他们的和等于21200AC AB BC AB t ++==;(2)类似的,()150.01,MP t MN NP =++是第二次声波传导的距离,()11850.01MN NP t +=+,他们的和等于()212000.01MP MN NP MN t ++==+;(3)由(1),(2)得:6,11850.01MN AB MN AB NP BC -=-+-=⨯,也有611850.01BC NP -=-⨯(4)由于DB 是北冰洋号从太平洋好第一次发出声波到北冰洋号接收到声波时潜航的距离,1185BCDB tv v =-;QN 是北冰洋号从太平洋好第二次发出声波到北冰洋号接收到声波时的潜航距离,()0.011185NPQN t v v =+-;(5)由(3),(4)得到:()0.01611850.011185vQN DB v -=+-⨯⨯.(6)AD 是太平洋好第一次发出声波时两艘潜艇之间的距离,是太平洋好第二次发出声波时两艘潜艇之间的距离,()215MD AD v -=-.因为,AD AB DB MQ MN QN =-=-,所以,()()()660.01611850.01611851185MQ AD MN AB QN DB v vv -=---=---⨯⨯=-于是:()662151185vv -=-解得211722v =因此北冰洋号潜航的速度是每小时21717642211=千米.答:北冰洋号潜航的速度是每小时76411千米.第4讲浓度问题与经济问题典型问题◇◇兴趣篇◇◇1.200克浓度为15%的盐水中加入50克盐,这时盐水浓度变为多少?然后再加上150克水,浓度变为多少?最后又加入200克浓度为8%的盐水,浓度变为多少?答案:32%;20%;16%2.(1)在120克浓度为20%的盐水中加入多少克水,才能把它稀释成浓度为10%的盐水?(2)在900克浓度为20%的糖水中加入多少克糖,才能将其配成浓度为40%的糖水?答案:(1)120克;(2)300克【分析】(1)十字交叉法:(2)十字交叉法:3.现有浓度为20%的盐水100克,加入相同质量的盐和水后,变成了浓度为30%的盐水。
