2011江苏南通中考数学
南通数学中考卷.docx

南通市2011年初中毕业、升学考试试卷数学—— --------------- 注重事项考生在答HttWU*阅读*注重事项:】.本试卷共6萸.椅分为150分,考■试时间为,2。
分的.与试结电后,请捋奉试卷和答瞠卡一, 并交回.2.答题前,请务必将自己的姓名,考试证号用°-5*米黑色字卷的签字笔填写在试卷及答题 卡上指定的位置・ 〔3.答案必须按妾京填涂•书写在答矍卡上,在试卷、草暗我上芬题-律无数.一、选择题(本大题共10小题.每小鹿3分.共30分.在每小睑治出的四个逸项中,检有一项是符合噎目要求的.谓将正嘛小的字2代号坟涂在巷鼠飞学区您里上)1. 如果60 m 表示"向北走60 m".W 么"向南走40 m”可以&小为4. 下列长度的三条线段,不能组成三角形的是• ・ 3.计算国的结果.足A, 120,C. 100,A. ±3^3B. 3V35. 巳知:如图,AB 〃CD.,DCE-80",JH/BEF 的度救为B. 110*A. — 20 mB. — 40 tn C, 20 m2. 下面的图形中.既是轴对称图形又是中心对林图形的矩A. 3,8,4B. 4・9,6C. 15.20.86.下列水平放置的几何体中.俯视(8压蛆彪的是D. 68.如ffi.OO 的弦AB-8.M 是AB 的中点,且OM-3.R3O 的半径等于A. 8B. 4D. 59.甲、乙购人沿相同的路线由A 地到B 地勾速前进.A.J3两地间的路程为20千米.他们耕史 的路程为式单位:千米).甲出发后的时间为可单位:小时),甲、乙前进的路程与时闻的词数 图象如图所示.根据国象信息,F 列说法正确的是A.C. 甲的速度第4千米/小时 乙的速度是10千米/小时乙比甲晚出发1小时 甲比乙晚到B 地3小时10.设 m>n>0.E : + ”:=4,e.SM 竺二^的ff!等于 ranB. V3 Q 76二、填空通(本大题共8小48.每小慝3分,共24分.不需写出解答过程.请把答案直接填写在 旨革专单度但星上)11. 巳知匕『・20•.则/<,的余角等于 ▲ 度.12. 计算:而一搪=▲.*+213.函数岩中,自变量N 的取值范圈是 A.14.七位女生的体直(单位:kg )分别是36.42,38.42.35.45.40,则这七位女生体直的中位二▲ kg.7-巳如3是关于工的方fBx l -5x+c-0的一个机.财这个方fg 的另一个根是A. —2B. 215. 如图,矩形旋片ABCD 中,AB-2 cm,点E 在BC 上.且 AAE-EC.若将蛾片沿AE 折建.点B 恰好与AC 上的威8'重合.则 AC- A erm16. 分解珥式;3m(2x —y)T —3mn : =-▲ 17.如图.测量河竟AB (假设河的两岸平行),在C^MWZACB = 3O\D AMftZADB-60..又CD-60 m.J«河宛AB 为 ▲ m 《结果保留根号).18.巳知;如图,三个半06依次相外切•它们的08心都在X 袖的正半轴上.并与直蟆y-yx 相 切.设牛08 G 、半跚C :,半IM C,的半径分别是r.r.r ,购当r = 1时,,=.▲ •rt /三、解答题(本大题共10小题.共96分.靖在内作答.解答时应写出必要的文字说明、证明过程或演算步骤)19. (本小厩滴分10分)(1)计算 2,+(-1)4 +('/?-2)0-|-3| I(2〉先化简.再求值:。
2011年南通数学中考卷

专业课原理概述部分一、选择题(每题1分,共5分)1. 若a是实数,且(a1)²=0,则a的值为()A. 0B. 1C. 1D. 22. 下列函数中,既是奇函数又是偶函数的是()A. y=x³B. y=x²C. y=|x|D. y=cos(x)3. 已知等差数列{an}的公差为3,且a3=7,则a1的值为()A. 1B. 4C. 7D. 104. 在直角坐标系中,点P(2, 2)关于原点的对称点是()A. (2, 2)B. (2, 2)C. (2, 2)D. (2, 2)5. 下列命题中,正确的是()A. 任何两个实数的和都是一个实数B. 任何两个实数的乘积都是一个实数C. 任何两个实数的商都是一个实数D. 任何两个实数的差都是一个实数二、判断题(每题1分,共5分)1. 若函数f(x)在区间(a,b)上单调递增,则f'(x)>0。
()2. 两个平行线的斜率相等。
()3. 等差数列的通项公式为an=a1+(n1)d。
()4. 向量a与向量b垂直的充分必要条件是a·b=0。
()5. 任何两个复数都可以进行四则运算。
()三、填空题(每题1分,共5分)1. 已知函数f(x)=x²2x+1,则f(x)的零点为______。
2. 若向量a=(3,4),则向量a的模长是______。
3. 已知等差数列{an}的公差为2,a1=1,则a5的值为______。
4. 设复数z=2+3i,则z的共轭复数为______。
5. 若函数f(x)=|x1|,则f(x)在x=1处的导数为______。
四、简答题(每题2分,共10分)1. 简述实数与虚数的关系。
2. 解释等差数列与等比数列的区别。
3. 如何判断一个函数的单调性?4. 什么是向量的数量积(点积)?5. 简述复数乘法的运算规律。
五、应用题(每题2分,共10分)1. 已知函数f(x)=x²4x+3,求f(x)在区间[0, 3]上的最大值和最小值。
2011年南通中考数学试卷
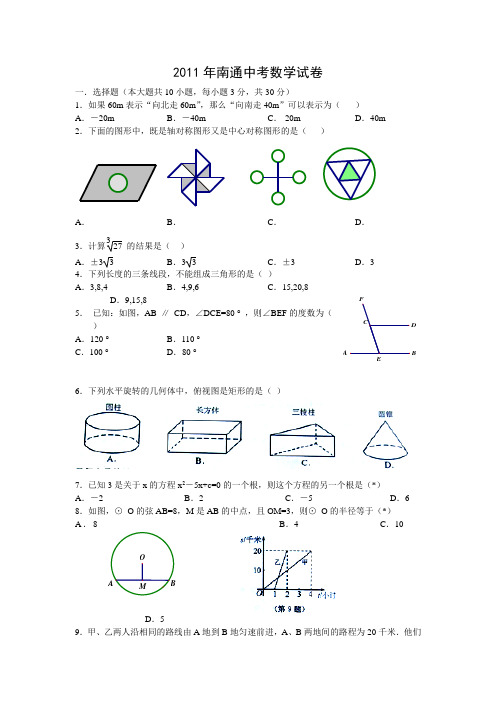
ABCDEF OABM2011年南通中考数学试卷一.选择题(本大题共10小题,每小题3分,共30分) 1.如果60m 表示“向北走60m ”,那么“向南走40m ”可以表示为( )A .-20mB .-40mC . 20mD .40m2.下面的图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .3.计算327 的结果是( )A .±3 3B .3 3C .±3D .34.下列长度的三条线段,不能组成三角形的是( ) A .3,8,4 B .4,9,6 C .15,20,8 D .9,15,85. 已知:如图,AB ∥ CD ,∠DCE=80 ° ,则∠BEF 的度数为( ) A .120 ° B .110 ° C .100 ° D .80 °6.下列水平旋转的几何体中,俯视图是矩形的是( )7.已知3是关于x 的方程x 2-5x+c=0的一个根,则这个方程的另一个根是(*) A .-2 B .2 C .-5 D .6 8.如图,⊙ O 的弦AB=8,M 是AB 的中点,且OM=3,则⊙ O 的半径等于(*) A .8 B .4 C .10D .59.甲、乙两人沿相同的路线由A 地到B 地匀速前进,A 、B 两地间的路程为20千米.他们ABC DEB'前进的路程为s (单位:千米),甲出发后的时间为t (单位:小时),甲、乙前进的路程与时间的函数图像如图所示,根据图像信息,下列说法正确的是(*) A .甲的速度 4千米/小时 B .乙的速度 10千米/小时 C .乙比甲晚出发1小时 D .甲比乙晚到B 地3小时10.设m > n > 0, m 2+n 2=4mn,则m 2-n 2mn的值等于(*)A .2 3B . 3C . 6D .3二.填空题(本大题共8小题,每小题3分,共24分) 11.已知∠α ° ,则∠α的余角等于 度. 12.计算:8 - 2 = .13.函数y=x+2x -1中,自变量x 的取值范围是 .14.七位女生的体重(单位:Kg )分别是36、42、38、42、35、45、40,则这七位女生的体重的中位数为 Kg .15.如图,矩形纸片A BCD ,AB=2cm ,点E 在BC 上,且AE=EC ,若将纸片折叠,点B 恰好与AC 上的点B ′重合,则AC= cm . 16.分解因式:3m(2x -y)2-3mn 2= . 17.如图,测量河宽AB (假设河的两岸平行),在C 点测得∠ ACB=30 ° ,点D 测得∠ ADB=60 ° ,又CD=60m ,则河宽AB 为 m (结果保留根号).18.已知:如图,三个半圆依次相外切,它们的圆心都在x 轴的正半轴上,并与直线y=33x 相切,设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3,则当r 1=1时,r 3=三.解答题(本大题共10小题,共96分) 19.(本小题满分10分) (1)计算:22+(-1)4+( 5 -2)0-︱-3︱(2)先化简,再求值: (4ab 3-8a 2b 2)÷ 4ab+(2a+b)(2a -b),其中a=2,b=1.20.(本小题满分8分) ABD C求不等式组⎩⎨⎧3x -6≥x -42x+1>3(x -1)的解集,并写出它的整数解.21.(本小题满分9分)某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类)并将调查的结果绘制成如下的两幅不完整的统计图.请根据图中提供的信息,解答下面的问题: (1)参加调查的学生共有 人;在扇形图中,表示“其他球类”的扇形的圆心角为 度 (2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有 人. 22.(本小题满分8分)如图,AM 为⊙ O 的切线,A 为切点,BD ⊥ AM 于点D ,BD 交⊙ O 于点C ,OC 平分∠ AOB .求∠ B 的度数.23.(本小题满分8分)列方程解应用题:在社区全民健身活动中,父子俩参加跳绳比赛,相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个? 24.(本小题满分8分)比较正五边形与正六边形,可以发现它们的相同点与不同点. 例如 它们的一个相同点:正五边形的各边相等,正六边形的各边也相等. 它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形. 请你再写出它们的两个相同点和两个不同点. 3060120其他球类足球乒乓球篮球12090600项目人数30CO A M B DAD 其他球类篮球中球乒乓球篮球 乒乓球 足球相同点:(1) (2) 不同点:(1) (2) 25.(本小题满分9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测,某次检测设有A 、B 两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力. (1) 求甲、乙、丙三名学生在同一处检测视力的概率;(2) 求甲、乙、丙三名学生中至少有两人在B 处检测视力的概率. 26.(本小题满分10分)已知:如图1,O 为正方形ABCD 的中心,分别延长OA 到点F ,OD 到点E ,使OF=2OA ,OE=2OD ,连接EF ,将△ FOE 绕点O 逆时针旋转α角得到△ F ′OE ′(如图2). (1) 探究AE ′与BF ′的数量关系,并给予证明;(2) 当α=30 ° 时,求证:△AOE ′为直角三角形.27.(本小题满分12分)已知A (1,0),B (0,-1),C (-1,2),D (2,-1),E (4,2)五个点,抛物线y=a(x -1)2+k(a > 0),经过其中三个点.(1) 求证:C 、E 两点不可能同时在抛物线y=a(x -1)2+k(a > 0)上. (2) 点A 抛物线y=a(x -1)2+k(a > 0)上吗?为什么? (3) 求a 与k 的值. 28.(本小题满分14分) 如图,直线l 经过点A (1,0),且与曲线y=m x (x > 0)交于点B (2,1),过点P (p ,p -1)(p > 1)作x 轴的平行线分别交曲线y=m x (x > 0)和y=-mx (x < 0)于M 、N 两点.(1) 求m 的值及直线l 的解析式;(2) 若点P 在直线y=2上,求证:△PMB ∽ △PNA ;(3) 是否存在实数p ,使得S △AMN =4S △APM ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.a E'F'O C D E F OC D ABB A xylOBA2011年南通中考数学试题参考答案1-10:B.C.D.A.C.B.B.D.C.A.11.7012. 213.x≠114. 4015.416.3m(2x-y+n)(2x-y-n)17.30 318.9.19.(1)3 (2)4a²-2ab, 12.20.1≤x<4, 整数解为:1、2、321.(1)300 36 (2)略(3)80022.60度23.父亲每分钟跳120个,儿子每分钟跳140个24.正五边形的各内角相等,正六边形各内角相等;正五边形是轴对称图形,正六边形也是轴对称图形.正五边形不能密铺,正六边形可以密铺;正五边形的各边不平行,正六边形的对边平行.25.1/4, 1/226.(1)用边角边证明△AOE’和△BOF’全等,即可证得AE’=BF’(2)取OE ’的中点G,得到等边△AOG ,等到∠AGO=60°,又由AG=E ’G 得到∠AE ’O =30°,从而得到∠OAE ’是90°,即为直角三角形。
江苏省2011年中考数学试题(13份含有解析)-7

盐城市二○一一年高中阶段教育招生统一考试数 学 试 题注意事项:1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上) 1.-2的绝对值是 A .-2 B .- 12C .2D .12【答案】C 。
【考点】绝对值。
【分析】根据绝对值的定义,直接得出结果。
2.下列运算正确的是A .x 2+ x 3= x 5B .x 4·x 2= x 6 C .x 6÷x 2 = x 3D .( x 2)3 = x 8【答案】B 。
【考点】同底幂的乘法。
【分析】42426x x x x +⋅==3.下面四个几何体中,俯视图为四边形的是【答案】D 。
【考点】几何体的三视图。
【分析】根据几何体的三视图,直接得出结果。
4.已知a -b =1,则代数式2a -2b -3的值是A .-1B .1C .-5D .5【答案】A 。
【考点】代数式代换。
【分析】()22323231a b a b --=--=-=-5.若⊙O 1、⊙O 2的半径分别为4和6,圆心距O 1O 2=8,则⊙O 1与⊙O 2的位置关系是 A .内切 B .相交 C .外切 D .外离A B CD【答案】B 。
【考点】圆心距。
【分析】126464<O O <-+∴ 两圆相交。
6.对于反比例函数y = 1x,下列说法正确的是A .图象经过点(1,-1)B .图象位于第二、四象限C .图象是中心对称图形D .当x <0时,y 随x 的增大而增大 【答案】C 。
【考点】反比例函数。
【分析】根据反比例函数性质,直接得出结果。
11--13南通中考数学

11--13年南通中考数学试题一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)1.下列各数中,小于﹣3的数是()A.2B.1C.﹣2 D.﹣42.计算(-x)2·x3的结果是()A.x5B.-x5C.x6D.-x63.下面的图形中,既是轴对称图形又是中心对称图形的是【】4.有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为()A.1B.2C.3D.45.已知x2+16x+k是完全平方式,则常数k等于【】A.64 B.48 C.32 D.166.下列水平放置的几何体中,俯视图是矩形的为【】7.如图,在△ABC中,∠C=70º,沿图中虚线截去∠C,则∠1+∠2=【】A.360ºB.250ºC.180ºD.140º8.若3是关于方程x2-5x+c=的一个根,则这个方程的另一个根是【】A.-2 B.2 C.-5 D.59.已知点A(-1,y1)、B(2,y2)都在双曲线y=3+2mx上,且y1>y2,则m的取值范围是【】A.D.圆柱长方体三棱柱圆锥A.m<0 B.m>0 C.m>-3 2D.m<-3210.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于【】A.8 B.4 C.10 D.5二、填空题(本大题共8小题,每小题3分,共24分.)11.单项式3x2y的系数为.12.计算:8-2=.13.某校9名同学的身高(单位:cm)分别是:163、165、167、164、165、166、165、164、166,则这组数据的众数为14.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是.15.如图,在矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=cm.16.如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),则不等式4x+2<kx+b<0的解集为.17.设m、n是一元二次方程x2+3x-7=0的两个根,则m2+4m+n=.18.如图,在▱ABCD中,AB=6cm,AD=9cm,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4cm,则EF+CF的长为cm.A BOMABB1CD三、解答题(本大题共8小题,共96分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤) 19.(11分)(1)计算:;(2)先化简,再求代数式的值:,其中m =1.20.(8分)求不等式组⎩⎨⎧3x -6≥x -42x +1>3(x -1)的解集,并写出它的整数解21.某水果批发市场将一批苹果分为A ,B ,C ,D 四个等级,统计后将结果制成条形图,已知A 等级苹果的重量占这批苹果总重量的30%. 回答下列问题:(1)这批苹果总重量为 kg ; (2)请将条形图补充完整;(3)若用扇形图表示统计结果,则C 等级苹果所对应扇形的圆心角为 度.22、在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?23、光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某次检测设有A 、B 两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.(1)求甲、乙、丙三名学生在同一处检测视力的概率;(2)求甲、乙、丙三名学生中至少有两人在B 处检测视力的概率.24、如图,△ABC 内接于⊙O ,AB 是⊙O 的直径,∠BAC =2∠B ,⊙O 的切线AP 与OC 的延长线相交于点P ,若P A =cm ,求AC 的长.25、如图,某测量船位于海岛P 的北偏西60º方向,距离海岛100海里的A 处,它沿正南方向航行一段时间后,到达位于海岛P 的西南方向上的B 处.求测量船从A 处航行到B 处的路程(结果保留根号).26、如图,已知直线l 经过点A (1,0),与双曲线y =m x(x >0)交于点B (2,1).过点P (p ,p -1)(p >1)作x 轴的平 行线分别交双曲线y =m x (x >0)和y =-mx(x <0)于点M 、N .(1)求m 的值和直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;OABlxy。
江苏省13市2011年中考数学试题分类解析汇编(12份)

江苏13市2011年中考数学试题分类解析汇编专题5:数量和位置变化一、选择题1. (常州、镇江2分)若2-x 在实数范围内有意义,则x 的取值范围A .x ≥2 B.x ≤2 C.x >2 D .x <2【答案】A.【考点】函数自变量的取值范围,二次根式有意义的条件。
【分析】根据二次根式被开方数必须是非负数的条件,要使2x -在实数范围内有意义,必须202x x -≥⇒≥,故选A 。
2.(常州、镇江2分)在平面直角坐标系中,正方形ABCD 的顶点分别为A ()1,1、B ()1,1-、C ()1,1--、D ()1,1-,y 轴上有一点P ()2,0。
作点P 关于点A 的对称点1P ,作1P 关于点B 的对称点2P ,作点2P 关于点C 的对称点3P ,作3P 关于点D 的对称点4P ,作点4P 关于点A 的对称点5P ,作5P 关于点B 的对称点6P ┅,按如此操作下去,则点2011P 的坐标为A .()2,0B .()0,2C .()2,0-D . ()0,2-21世纪教育网 【答案】D 。
【考点】分类归纳,点对称。
【分析】找出规律,P 1(2,0),P 2(0,-2),P 3(-2,0),P 4(0,2},……,P 4n (0,2},P 4n+1(2,0),P 4n+2(0,-2),P 4n+3(-2,0)。
而2011除以4余3,所以点P 2011的坐标与P 3坐标相同,为(-2,0)。
故选D 。
21世纪教育网3.(宿迁3分)在平面直角坐标中,点M(-2,3)在A .第一象限B .第二象限C .第三象限D .第四象限【答案】B 。
[来源:21世纪教育网]【考点】点的坐标。
【分析】利用平面直角坐标系中各象限符号特征进行判断:点M(-2,3)横坐标小于0,纵坐标大于0,则这点在第二象限。
故选B 。
4.(徐州2分)若式子1x -在实数范围内有意义,则x 的取什范围是A .1x ≥B ..1x >C ..1x <D .1x ≤【答案】A 。
江苏南通中考数学试题解析版.doc

江苏省南通市2011年中考数学试题一、选择题(本大题共10小题,每小题3分,满分30分)1.如果60m 表示“向北走60m”,那么“向南走40m”可以表示为【 】A .-20mB .-40mC .20mD .40m【答案】B .【考点】相反数。
【分析】向北与向南是相反方向两个概念,向北为+,向南则为负。
故根据相反数的定义,可直接得出结果2.下面的图形中,既是轴对称图形又是中心对称图形的是【 】错误!未指定书签。
【答案】C .【考点】轴对称图形,中心对称图形。
【分析】根据轴对称图形和中心对称图形的定义,可知A 是中心对称图形而不是轴对称图形;B 也是中心对称图形而不是轴对称图形;C 既是轴对称图形又是中心对称图形,它有四条对称轴,分别是连接三个小圆线段所在的水平和竖直直线,这水平和竖直直线之间的两条角平分线;D 既不是轴对称图形也不是中心对称图形。
3.计算327的结果是【 】A .±3 3B .3 3C .±3D .3【答案】D .【考点】立方根。
【分析】根据立方根的定义,因为33=273。
4.下列长度的三条线段,不能组成三角形的是【 】A .3,8,4B .4,9,6C .15,20,8D .9,15,8【答案】A .【考点】三角形的构成条件。
【分析】根据三角形任两边之和大于第三边的构成条件,A 中3+4<8,故A 的三条线段不能组成三角形。
5.如图,AB ∥CD ,∠DCE =80°,则∠BEF =【 】 A .120° B .110° C .100° D .80° 【答案】C .【考点】平行线的性质。
【分析】根据同旁内角互补的平行线性质,由于AB ∥CD ,∠DCE 和∠BEF 是同旁内角,从而∠BEF =00018080100-=。
6.下列水平放置的几何体中,俯视图是矩形的为【 】错误!未指定书签。
【答案】B .【考点】几何体的三视图。
2011年江苏南通中考数学试题(含答案)
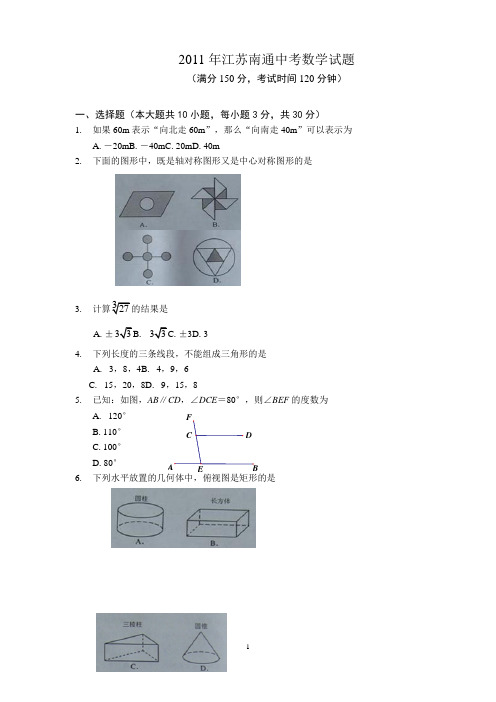
EA BC DF一、选择题(本大题共10小题,每小题3分,共30分)1.如果60m表示“向北走60m”,那么“向南走40m”可以表示为A.-20mB.-40mC.20mD.40m2.下面的图形中,既是轴对称图形又是中心对称图形的是3.计算327的结果是A.±33B. 33C.±3D.34.下列长度的三条线段,不能组成三角形的是A. 3,8,4B. 4,9,6C. 15,20,8D. 9,15,85.已知:如图,AB∥CD,∠DCE=80°,则∠BEF的度数为A. 120°B.110°C.100°D.80°6.下列水平放置的几何体中,俯视图是矩形的是2011年江苏南通中考数学试题(满分150分,考试时间120分钟)MOABt /小时s /千米乙甲2010432A1DA7. 已知3是关于x 的方程250x x c -+=的一个根,则这个方程的另一个根是A .-2B .2C . -5D .68. 如图,⊙O 的弦AB =8,M 是AB 的中点,且OM =3,则⊙O 的半径等于A . 8B . 4C . 10D .59. 甲、乙两人沿相同的路线由A 地到B 地匀速前进,A 、B 两地间的路程为20千米.他们前进的路s (单位:千米),甲出发后的时间为t (单位:小时),甲、乙前进的路程与时间的函数图像如图所示,根据图象信息,下列说法正确的是A .甲的速度是4千米/小时B .乙的速度是10千米/小时C .乙比甲晚出发1小时D .甲比乙晚到B 地3小时10. 设m n 0>>,+=m n mn 224,则-m n mn22的值等于 A .23B .3C .6D .3二、填空题(本题有8个小题,每小题3分,共24分)11. 已知∠α=20°,则∠α的余角等于_______度. 12. 计算-82=_________. 13. 函数+=-x y x 21中,自变量x 的取值范围是_____ 14. 七位女生的体重(单位:kg )分别是36,42,38,42,35,45,40,则这七位女生体重的中位数为________kg .15. 如图,矩形纸片ABCD 中,AB =2cm ,点E 在BC 上,且AE =EC .若将纸片沿AE 折AC 上的点重合,则叠,点B 恰好与xyOC 1C 2C 3AC =_____cm .16. 分解因式:()--m x y mn 22323=__________.17. 如图,测量河宽AB (假设河的两岸平行),在C 点测得∠ACB =30°,D 点测得∠ADB =60°,又CD =60m ,则河宽AB 为____m (结果保留根号).18. 已知:如图,三个半圆依次相外切,它们的圆心都在x 轴的正半轴上,并与直线=y x 3相切.设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1,r 2,r 3,则当r 1=1时,r 3=______.三、解答题(本大题有10个小题,共96分)19. (本小题满分10分)(1)计算()()+-+--04221523;(2)先化简,再求值:()()()--32248422÷++ab a b ab a b a b ,其中=a 2,=b 1.20. (本小题满分8分)求不等式组()3642131x x x x --⎧⎨+-⎩≥>的解集,并写出它的整数解.21. (本小题满分9分)某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.18题图DBCOAM根据图中提供跟信息,解答下面的问题:(1)参加调查的学生共有人;在扇形图中,表示“其他球类”的扇形的圆心角为度;(2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有人.22. (本小题满分8分)如图,AM 为⊙O 的切线,A 为切点.BD ⊥AM 于点D ,BD 交⊙O 于点C ,OC 平分∠AOB .求∠B 的度数.23. (本小题满分8分)列方程解应用题:在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?24. (本小题满分8分)正六边形正五边形F比较正五边形和正六边形,可以发现它们的相同点与不同点.例如 它们的一个相同点:正五边形的各边相等,正六边形的各边也相等. 它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.请你再写出它们的两个相同点和两个不同点. 相同点:(1); (2). 不同点:(1);(2).25. (本小题满分9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某此检测设有A ,B 两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力. (1)求甲、乙、丙三名学生在同一处检测视力的概率;(2)求甲、乙、丙三名学生中至少有两人在B 处检测视力的概率.26. (本小题满分10分)已知:如图1,O 为正方形ABCD 的中心,分别延长OA 到点F ,OD 到点E ,使OF =2OA ,OE =2OD ,连接EF .将△FOE 绕点O 逆时针旋转α角得到△''F OE ’(如图2).(1)探究'AE 与'BF 的数量关系,并给予证明; (2)当α=30°时,求证:△'AOE 为直角三角形.27. (本小题满分12分)已知A (1,0),B (0,-1),C (-1,2),D (2,-1),E (4,2)五个点,抛物线()()=-+y a x k a 210>经过其中三个点.(1)求证:C ,E 两点不可能同时在抛物线()()=-+y a x k a 210>上; (2)点A 在抛物线()()=-+y a x k a 210>上吗?为什么? (3)求a 与k 的值.xylBOA28. (本小题满分12分)如图,直线l 经过点A (1,0),且与曲线()=my x x0>交于点B (2,1).过点P (p ,p -1)(p >1)作x 轴的平行线分别交曲线()=my x x0>和()=-my x x0<于M 、N 两点. (1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ; (3)是否存在实数p ,使得=?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.参考答案江苏南通一、选择题二、填空题11.70;12;13. x ≠1;14.40;15.4;16.3m (2x -y +n )(2x -y -n );17.18.9.三、解答题19.(1)3; (2)12. 20.1、2、3. 21.(1)300、36;(2)足球:300×30%=90(人); (3)800. 22. ∠B =60°.23.父亲:120个;儿子:140个.24.相同点:(1)轴对称图形;(2)正五边形各角都相等.不同点:(1)对称轴条数不同;(2)边角数量不同,内角大小不同. 25.(1)14;(2)14. 26.(1)AE ′=BF ′证明:由∠E ′OA =∠BOF ′,OB =OA ,OF ′=OE ′ 可得△OAE ′≌△OBF ′ (2)证明略 27.(1)略 (2)不在(3)12a k =,=-或31188a k =,=- 28.(1)m =2,1y x =- (2)略(3)i)当P>2时,pii)当p=2时不成立iii)当1<p<2时,12 p=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南通市2011年初中毕业、升学考试试卷数学注意事项考生在答题前请认真阅读注意事项:1.本试卷共6页,满分为150分,考试时间为120分钟,考试结束后,请将本试卷和答题卡一并交回。
2.答题前,请务必将自己的姓名、考试证号用0.5毫米黑色字迹的签字笔填写在试卷及答题卡上指定的位置。
3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效。
一、选择题(本大题共10小题,每小题2分,共30分,在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置.......上)1. 如果60m表示“向北走60m”,那么“向南走40m”可以表示为A.-20mB.-40mC. 20mD. 40m【答案】B2.下面的图形中,既是轴对称图形又是中心对称图形的是【答案】C3.A.±B.C.±3D. 3【答案】D.4.下列长度的三条线段,不能组成三角形的是A.3,8,4B. 4,9,6C. 15,20,8D. 9,15,8【答案】A5.已知:如图AB∥CD,∠DCE=80°,则∠BEF的度数为A.120°B. 110°C. 100°D. 80°【答案】C6.下列水平放置的几何体中,俯视图是矩形的是【答案】B7. 已知3是关于x 的方程x 2-5x +c =0的一个根,则这个方程的另一个根是A. -2 B . 2 C . 5 D . 6【答案】B8. 如图,⊙O 的弦AB =8,M 是AB 的中点,且OM =3,则⊙O 的半径等于A. 8 B . 2 C . 10 D . 5 【答案】D9. 甲、乙两人沿相同的路线由A 地到B 地匀速前进,A ,B 两地间的路程为20千米,他们前进的路程为s (单位:千米),甲出发后的时间为t (单位:小时),甲、乙前进的路程与时间的函数图像如图所示.根据图像信息,下列说法正确的是 A. 甲的速度是4千米/小时B. 乙的速度是10千米/小时C. 乙比甲晚出发1小时D. 甲比乙晚到B 地3小时 【答案】C10. 设m >n >0,m 2+n 2=4mn ,则22m n mn-的值等于A. B .C .D . 3【答案】A二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置.......上) 11. 已知∠α=20°,则∠α的余角等于 ▲ 度. 【答案】70.12. 计算:= ▲ .13. 函数y =21x x +-中,自变量x 的取值范围是 ▲ . 【答案】x ≠1.14. 七位女生的体重(单位:kg )分别是36,42,38,42,35,45,40,则这七位女生体重的中位数为 ▲ kg . 【答案】4215.如同,矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点'B重合,则AC=▲cm.【答案】416.分解因式:3m(2x-y)2-3mn2=▲【答案】3m(2x-y+n)(2x—y-n)17.如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为▲m(结果保留根号).【答案】18.已知:如图,三个半圆以此相外切,它们的圆心都在x轴的正半轴上并与直线y x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3=▲【答案】9.三、解答题(本大题共10小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或盐酸步骤)19.(本小题满分10分)(1)计算:22+(-1)4+-2)0-3-;【答案】3.(2)先化简,再求值:(4ab3-8a2b2)÷4ab+(2a+b) (2a-b),其中a=2,b=1.【答案】化简原式=2a(2a-b),将a=2,b=1代入得12.20.(本小题满分8分)求不等式组364213(1)x xx x-≥-⎧⎨+>-⎩的解集,并写出它的整数解.【答案】不等式组的解集为1≤x<4,其整数解为x=1,2,321.(本小题满分9分)某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.请根据途中提供的信息,解答下列问题:(1)参加调查的人数共有▲人;在扇形图中,表示“其它球类”的扇形的圆心角为▲度;(2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有▲人.【答案】(1)300,36;(2)见下图:.(3)∵2000×120300=800(人)∴喜欢篮球的学生估计共有800人,填800.22.(本小题满分8分)如图,AM为⊙O的切线,A为切点,BD⊥AM于点D,BD交⊙O于C,OC平分∠AOB.求∠B的度数.【答案】60°.23.(本小题满分8分)列方程解应用题:在社区全民活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个,已知儿子每分钟比父亲多跳20个,问父亲、儿子每分钟各跳多少个?【答案】设父亲每分钟跳x个,依题意得,180 x =21020x,解得x=120,经检验x=120是原题的解.答:父亲、儿子每分钟各跳绳120和140个.24.(本小题满分8分)比较正五边形与正六边形,可以发现它们的相同点与不同点.例如它们的一个相同点:正五边形的各边相等,正六边形的各边也相等.它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.请你再写出它们的两个相同点和不同点.相同点:(1)▲(2)▲不同点:(1)▲(2)▲【答案】相同点(1)每个内角都相等(或每个外角都相等或对角线都相等…);(2)都是轴对称图形(或都有外接圆和内切圆…);.不同点(1)正五边形的每个内角是108°,正六边形的每个内角是120°(或…);(2)正五边形的对称轴是5条,正六边形的对称轴是6条(或…).25.(本小题满分9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某次检测设有A、B两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.(1)求甲、乙、丙三名学生在同一处检测视力的概率;(2)求甲、乙、丙三名学生中至少有两人在B处检测视力的概率.【答案】∵甲、乙、丙的检测情况,有如下8种可能:∴(1)P(甲、乙、丙在同一处检测)=28=14;(2)P(至少有两人在B处检测)=48=12.26.(本体满分10分)已知:如图1,O为正方形ABCD的中心,分别延长OA到点F,OD到点E,使OF=2OA ,OE =2OD ,连结EF ,将△FOE 绕点O 逆时针旋转α角得到△''F OE (如图2). (1) 探究AE ′与BF'的数量关系,并给予证明; (2) 当α=30°时,求证:△AOE ′为直角三角形.【答案】(1)AE ′=BF 证明:如图2,∵在正方形ABCD 中, AC ⊥BD ∴∠''F OE =∠AOD =∠AOB =90°即∠AO E ′+∠AOF ′=∠BOF ′+∠AOF ′ ∴∠AOE ′=∠BOF ′又∵OA =OB =OD ,OE ′=2OD ,OF ′=2OA ∴OE ′=OF ′∴△OAE ′≌△OBF ′ ∴AE ′=BF(2)作△AOE ′的中线AM ,如图3.则OE ′=2OM =2OD =2OA ∴OA =OM ∵α=30° ∴∠AOM =60° ∴△AOM 为等边三角形∴ MA =MO =ME ′,∠'AE M =∠'E AM 又∵∠'AE M +∠'E AM =∠AMO 即2∠'AE M =60° ∴∠'AE M =30°∴∠'AE M +∠AOE ′=30°+60°=90° ∴△AOE ′为直角三角形. 27. (本小题满分12分) 已知A (1,0), B (0,-1),C (-1,2),D (2,-1),E (4,2)五个点,抛物线y =a (x -1)2+k (a >0),经过其中三个点.(1) 求证:C ,E 两点不可能同时在抛物线y =a (x -1)2+k (a >0)上; (2) 点A 在抛物线y =a (x -1)2+k (a >0)上吗?为什么? (3) 求a 和k 的 值. 【答案】(1)证明:将C ,E 两点的坐标代入y =a (x -1)2+k (a >0)得,4292a k a k +=⎧⎨+=⎩,解得a =0,这与条件a >0不符, ∴C ,E 两点不可能同时在抛物线y =a (x -1)2+k (a >0)上.(2)【法一】∵A 、C 、D 三点共线(如下图),∴A 、C 、D 三点也不可能同时在抛物线y =a (x -1)2+k (a >0)上. ∴同时在抛物线上的三点有如下六种可能: ①A 、B 、C ; ②A 、B 、E ; ③A 、B 、D ; ④A 、D 、E ; ⑤B 、C 、D ; ⑥B 、D 、E .将①、②、③、④四种情况(都含A 点)的三点坐标分别代入y =a (x -1)2+k (a >0),解得:①无解;②无解;③a =-1,与条件不符,舍去;④无解. 所以A 点不可能在抛物线y =a (x -1)2+k (a >0)上.【法二】∵抛物线y =a (x -1)2+k (a >0)的顶点为(1,k )假设抛物线过A (1,0),则点A 必为抛物线y =a (x -1)2+k (a >0)的顶点,由于抛物线的开口向上且必过五点A 、B 、C 、D 、E 中的三点,所以必过x 轴上方的另外两点C 、E ,这与(1)矛盾,所以A 点不可能在抛物线y =a (x -1)2+k (a >0)上. (3)Ⅰ.当抛物线经过(2)中⑤B 、C 、D 三点时,则142a k a k +=-⎧⎨+=⎩,解得12a k =⎧⎨=-⎩ Ⅱ. 当抛物线经过(2)中⑥B 、D 、E 三点时,同法可求:38118a k ⎧=⎪⎪⎨⎪=-⎪⎩.∴12a k =⎧⎨=-⎩或38118a k ⎧=⎪⎪⎨⎪=-⎪⎩.28.(本小题满分14分)如图,直线l 经过点A (1,0),且与双曲线y =mx(x >0)交于点B (2,1),过点P (p ,p -1)(p >1)作x 轴的平行线分别交曲线y =m x (x >0)和y =-mx(x <0)于M ,N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ; (3)是否存在实数p ,使得S △AMN =4S △APM ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由. 【答案】(1)∵点B (2,1)在双曲线y =mx上, ∴12m=,得m=2. 设直线l 的解析式为y =kx +b∵直线l 过A (1,0)和B (2,1) ∴021k b k b +=⎧⎨+=⎩,解得11k b =⎧⎨=-⎩∴直线l 的解析式为y =x -1.(2) 证明:当x =p 时,y =p -1,点P (p ,p -1)(p >1)在直线l 上,如右图.∵P (p ,p -1)(p >1)在直线y =2上,∴p -1=2,解得p =3 ∴P (3,2)∵PN ∥x 轴,∴P 、M 、N 的纵坐标都等于2把y =2分别代入双曲线y =2x 和y =2x -,得M (1,2),N (-1,2)∴3111(1)PM MN -==--,即M 是PN 的中点, 同理:B 是P A 的中点, ∴BM ∥AN ∴△PMB ∽△PNA .(3)由于PN ∥x 轴,P (p ,p -1)(p >1), ∴M 、N 、P 的纵坐标都是p -1(p >1)把y =p -1分别代入双曲线y =2x (x >0)和y =-2x(x <0),得M 的横坐标x =21p -和N 的横坐标x =-21p -(其中p >1)∵S △AMN =4S △APM 且P 、M 、N 在同一直线上,∴4AMN APM S MNS PM∆∆==,得MN =4PM 即41p -=421p p --(见(3)两幅图) 整理得:p 2-p -3=0或p2-p -1=0 解得:pp由于p >1,∴负值舍去 ∴p经检验p∴存在实数p ,使得S △AMN =4S △APM ,p。
