2013第三章、第四章作业答案 (1)
至作业答案噪声

第二章作业答案:1.答:声波不能在真空中传播。
因为:在真空中不存在能够产生振动的弹性媒质。
2. 根据:/c f λ= 340/c m s =当500/0.68()f Hz c f m λ==340时, ==5005000/0.068()f Hz c f m λ==340时, ==500010000/0.034()f Hz c f m λ==340时, ==100003.根据/c fλ=在空气中时,/0.68()c f m λ=340==500在水中时, / 2.97()c f m λ=1483==500在钢中时, /12.20()c f m λ=6100==5004.根据声速331.450.61c t =+在夏天40℃时的声速为:40331.450.6140355.85(/)c x m s =+= 对于1000H z声波,其波长为:40355.85/0.356()1000c f m λ===在冬天为0℃时的声速为:0331.450.610331.45(/)c x m s =+=对于1000H z声波,其波长为:0331.45/0.331()1000c f m λ===40℃时的声速比0℃时的声速快:400355.85331.4524.4(/)c c c m s ∆=-=-=5.质点振动速度:300.61.4610/1.21340P U x m s c x ρ-=== 声强:224200.68.7610/1.21340e P I x W m c x ρ-===声能密度:22632200.6 2.57810/1.21340eP D x J m c x ρ-=== 声功率:点声源发出的声波球面声波,其波阵面面积为:222443.14250.24S r x x m π===声功率428.761050.24 4.4010W IS x x x W --===9. 由题可知:ρAir =1.21kg/m 3, c Air =340m/s, ρH2O =998kg/m 3, c H2O =1483m/s 垂直入射时:反射声的声强透射系数:112222211324()4 1.2134099814831.1110(9981483 1.21340)t I i I c c I c c x x x x x x x ρρτρρ-==+==+斜入射时:根据Snell 定律12sin sin it c c θθ=,得:0sin sin 103401483t θ=则折射角为010sin101483arcsin 49.26340t x θ-==根据112arcsin ()iec c θ-=, 则11012340arcsin ()arcsin ()13.261483iec c θ--===即当入射临界角为13.260时会产生全反射。
自动检测与转换技术课后作业参考答案

第一章作业答案2-3何谓真空度?某点的真空度为0.4×105Pa ,其绝对压力和相对压力分别是多少? 答:绝对压力比大气压小的那部分数值为真空度。
绝对压力=大气压力—真空度=0.6×105Pa 相对压力=—真空度=—0.4×105Pa2-5在图2-12中,液压缸直径150D mm =,活塞直径100d mm =,负载50000F N =。
若不计油液自重及活塞或缸体重量,求a) 、b)两种情况下的液压缸内部的油液压力。
解:a)列活塞受力平衡式:柱pA F =,则MPa d F A F p 66221037.6101004500004⨯=⨯⨯===-ππ柱b) 列缸体受力平衡式:缸环pA pA F =+,则MPa d F A F p 66221037.6101004500004A -⨯=⨯⨯===-ππ环缸2-6如图2-13所示的液压装置中,已知120d mm =,250d mm =,180D mm =,2130D mm =,130/min q L =。
求1υ、2υ和2q 各是多少?解:s m A qv /106.0)2080(4601030223111=-⨯⨯⨯==-π在大小缸活塞之间,根据连续性方程可知:22221144D v D v ππ= 则有:s m v /04.0106.013080222=⨯=s m d D v q /105.410)50130(404.0)(434622222222--⨯=⨯-⨯⨯=-⨯⨯=ππ第三章作业答案3-9 图3-20中,若不计管路压力损失,试确定如图所示各工况下,泵的工作压力p (压力表的读数)各为多少?(已知图c 中节流阀的压差为Δp )答:0=p ;AFp =;p p ∆=;0=p 3-11 某液压泵的工作压力为5MPa ,转速为1450r/min ,排量为40mL/r ,容积效率为0.93,总效率为0.88,求泵的实际输出功率和驱动该泵所用电动机的功率。
水力学课后答案

答案说明以下答案就是由老师自己做出来的,其中的每一题的画图都省略了,希望同学们自己在做题过程中补充上完整的图形。
在答案电子话过程中可能会有一些错误,希望同学们可多提宝贵意见。
第二章作业答案2-9 10(1.5 1.0)53.9a p p g p kpa ρ=+--=11151.9abs a p p p kpa =+= 20(1.50.5)58.8a p p g p kpa ρ=+--=22156.8abs a p p p kpa =+=1212 6.5p pZ Z m g gρρ+=+= 2-11 略2-120(2.50.9)(2.00.9)(2.00.7)(1.80.7)0Hg Hg p g g g g ρρρρ+---+---=0265p kpa =2-14 受压面为矩形平面 76.38c P gh kN ρω==34112c b a J m ⋅==289c D c c J y y y ω=+= 所以,作用点至A 点的距离 10'29D y y '=-= 根据合力矩守恒2cos 60'84.9o T P y T kN⋅=⋅=2-18 c P gh ρω=(sin 60)2146.5o ag H abkNρ=-⋅= sin 60(cos 60)o o T G G P f =⋅++⋅45.9T kN =闸门的静水压强分布图为梯形,根据梯形的压力中心距底部距离的计算公式12122()3h h a e h h +=+ 21sin h H h H a θ==-1.13e m =2-21 仅考虑左侧水:11144.1x c x P gh kN ρω== (→) 1134.6z P gV kN ρ== (↑)仅考虑右侧水22211.03x c x P gh kN ρω== (←)2217.32z P gV kN ρ== (↓)综合两侧水1233.08x x x P P P kN =-= (→)1217.32z z z P P P kN =-= (↑) 总压力37.34P kN ==tan ZxP P θ=2-23 分析上半球0x P =232[()]3ZP gVT n n g R H R R n ρρππ===+- 第三章作业答案3-32max 000.0342max max 00[(1())]1/20.212/r rQ ud u d r u u r r L s ωωωωπ==-=-⋅⋅=⎰⎰0.075/Qv m s ω==3-6 根据连续性方程123Q Q Q =+ 34/v m s =3-7根据连续性方程123Q Q Q =+234ωω= 22231482.3370.58m mωω==3-11建立能量方程22111222121222122122()2.252hg p p v p v z z g g g gz z p p v v h m g g ααρρρρρρ++=++=---===油油油油油51.1/Q L s μ==3-15在图上12d d 和断面建立能量方程2211122212122220p v p v z z g g g gz z p ααρρ++=++==联立连续性方程 1122v v ωω= 2 4.9/v m s = 在图自由液面与2d 断面建立能量方程221.232v H m g== 3-18 建立能量方程22111222121212221.8 1.680p v p v z z g g g gz m z mp p ααρρ++=++====连续性方程12211.8(1.80.30.12)1.3v v v v ⋅=--⋅=⋅13111.23/5.98/v m s Q v m sω===3-20建立的坐标系比较特别,X 轴沿着1Q 方向,Y 轴与X 轴垂直 根据能量方程可知1268.1/v v v m s ===建立动量方程,沿X 轴方向:11221212cos 600cos 60o oQ v Q v Q v Q Q Q Q Q Qρρρ--=-=+=连续性方程12(1cos 60)2(1cos 60)2o o QQ QQ =+=-313225.05/8.35/Q m s Q m s==建立动量方程,沿Y 轴方向:0(sin60)1969o y R Q v N ρ=--=3-23 在A-A,B-B 断面间建立能量方程2.4/3.8/A b v m s v m s==221112221212222175.7p v p v z z g g g gz z p kNααρρ++=++==在A-A,B-B 断面间建立动量方程沿X 轴方向:1cos 60(cos 60)sin 60sin 60o o A A B B x B ooB B y B p v p v R Q v v p v R Qv ρρ--=-+=-54555984y x R N R N==3-24 (1)建立能量方程2212120022v v h h g g++=++连续性方程1122h v h v =3228.9215)998(v v +⨯⨯=+ 0294107232=+-v v s m v /512.82= m h v v h 762.15512.831212=⨯==(2)以1-1断面与2-2断面之间的水体为控制体,并假设整个坝面对水体的水平反力为F '。
过程控制技术课后作业答案详解

过程控制与自动化仪表课后作业详解第一章P152-1. (1)简述图1-6所示系统的工作原理,画出控制系统的方框图并写明每一方框图的输入/输出变量名称和所用仪表的名称。
答:1)图为液位控制系统,由储水箱(被控过程X液位检测器(测量变送器)、液位控制器、调节阀组成的反馈控制系统,为了达到对水箱液位进行控制的目的,对液位进行检测,经过液位控制器来控制调节阀,从而调节Q 1 (流量)来实现液位控制的作用。
2)框图如图1-7所示:图1-7控制系统框图3)控制器输入输出分别为:设定值与反馈值之差e (t )、控制量u(t );执行器输入输出分别为:控制量u(t)、操作变量Q 1(t);被控对象的输入输出为:操作变量Q 1(t)、扰动量Q2 (t),被控量h;所用仪表为:控制器(例如PID控制器)、调节阀、液位测量变送器。
2-3某化学反应过程规定操作温度为800℃,最大超调量小于或等于5%,要求设计的定值控制系统,在设定值作最大阶跃干扰时的过渡过程曲线如图所示。
要求:1)计算该系统的稳态误差、衰减比、最大超调量和过渡过程时间;2)说明该系统是否满足工艺要求。
答:1)稳态误差:e(8)=810-800=10衰减比:n=B1/B2=(850-810)/(820-810)=4最大超调量:。
=(850-810)/810=4.9%假设以系统输出稳定值的2%为标准,则810*2%=16.2,则过渡过程时间:ts=17min2)由于规定操作温度为800 °C,而系统稳态值为810 ℃所以不满足工艺要求。
第二章P711-3某台测温仪表测量的上下限为500℃~1000℃,它的最大绝对误差为±2℃,试确定该仪 表的精度等级;答:根据题意可知:最大绝对误差为±2℃ 则精度等级5 =±烹义100% = ±0.4% 所以仪表精度等级为0.4级1-4某台测温仪表测量的上下限为100℃~1000℃,工艺要求该仪表指示值的误差不得超过土 2℃,应选精度等级为多少的仪表才能满足工艺要求?答: 由题可得:5=± ——2—— x 100% = ±0.22%1000 -100仪表精度等级至少0.2以上。
2013年版有机化学作业答案(1)
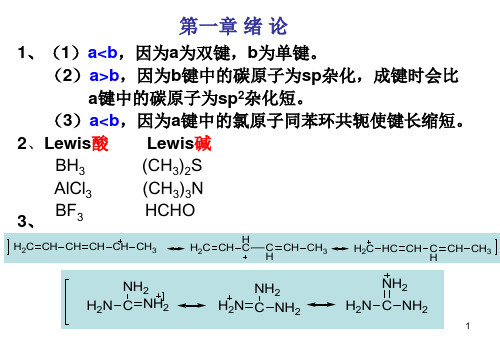
NH2 H2N C NH2
NH2 H2N C NH2
NH2 H2N C NH2
1
第二章 饱和烃
1. 用系统命名法命名下列化合物。 (CH3)2CHCH(CH3)CH2CH3 2,3-二甲基戊烷
2.下图为1,1,2-三氯乙烷的1H NMR图(300 MHz)。试指出图中质子的 归属,并说明其原因。
Ha:受邻近2个Cl的影响,其向低场位移的比较多,δ=5.75 ppm, 且积分面积为1H,另外,该峰受到Hb的偶合,裂分为三重峰; Hb:受邻近1个Cl的影响,其稍向低场位移,δ=3.95 ppm,且积分 面积为2H,另外,该峰受到Hb的偶合,裂分为双峰;
H2SO4,H2O,Hg2+
CH3CH2COCH3
AgNO3 氨溶液 H2/Pd-BaSO4
CH3CH2C≡CAg
(2)
(3)
CHO
(4) CH2 CHCH CH2 + CH2 CHCHO
1
14
3. 以丙炔为原料并选用必要的无机试剂合成下列化合物。 (1)正丙醇
喹啉
林德拉(Lindlar)催化剂: Pd-CaCO3/Pb(OAc)2或Pd-BaSO4/喹啉 (2)正己烷
B. CHBrCH3
>
CH2Br
>
CH2CH2Br
(3) ①>③>② CH3CH2CH2CH2Br >(CH3)2CHCH2Br >(CH3)3CCH2Br (4) ①>③>② CH3CH2CH2CH2Br >CH3CH2CHBrCH3 >(CH3)3CBr
第四章常微分方程参考答案(1)

爱启航在线考研第四章常微分方程4.1答案:应选(C )解析:原方程写成23e 0+'+=yxyy ,分离变量有23e d =e d y x y y x --,积分得232e 3e --=x y C ,其中C 为任意常数.4.2答案:应填sin e=C xy ,其中C 为任意常数.解析:原方程分离变量,有d cos d ln sin =y xx y y x,积分得1ln |ln |ln |sin |ln =+y x C ,通解为ln sin =y C x 或sin e=C x y ,其中C 为任意常数.4.3答案:应填()2112e-=x y x 解析:原方程化为d 1d ⎛⎫=- ⎪⎝⎭y x x y x .积分得通解211ln ||ln ||2y C x x =-,即122ex y Cx -=.由初值(1)1=y 解出12e C =得特解.故答案为:()2112e-=x y x .4.4答案:应选(B )解析:原方程求导得()2()'=f x f x ,即()2()'=f x f x ,积分得2()e =x f x C ,又(0)ln 2=f ,故ln 2=C ,从而2()e ln 2=x f x .故应选(B ).4.5解:曲线()=y f x 在点(,)x y 处的切线方程为()'-=-Y y y X x ,令0=X ,得到切线在y 轴截距为'=-xy y xy ,即(1)'=-xy y x .此为一阶可分离变量的方程,于是d 11d ⎛⎫=- ⎪⎝⎭y x y x ,两边积分有1ln ||ln =-y C x x ,得爱启航线考研到e =x Cx y .又()11e y -=,故1=C ,于是曲线方程为e =xx y .4.6解:22d d 11+y y y x x x x =∆=+,得2d d 1=+y y x x ,变量分离2d 1d 1=+y x y x.两边积分得1ln arctan y x C =+.可得arctan exy C =又()0y =π,则C =π.所以arctan πexy =,()πarctan141πeπe y ==.4.7解:令=yu x,即=y ux ,则y u x u ''=+,又由题给表达式可得2y u u '=,即有u x u '+2u u =-d 1d 22=-x xu u ,两边积分得1ln 1ln ln u x C -=+,即ln(1ln ln 1=-+⇒-=⇒-=y Cu x C x xy C x x.4.8答案:应填2(ln ||)=+x y y C 解析:将x 看成未知函数,原方程改写为2d 1d 222+==+x x y x y xy y x这是一个伯努利方程,令2=z x ,有d 1d -=z z y y ,得11d d 2e ed (ln ||)-⎛⎫⎰⎰==+=+ ⎪ ⎪⎝⎭⎰y y y y x z y C y y C .故答案为:2(ln ||)=+x y y C ,其中C 为任意常数.4.9答案:应填()cos +x C x解析:属于一阶非齐次线性方程,直接根据一阶非齐次线性微分方程的通解公式即可得出答案.故答案为:()cos +x C x ,其中C 为任意常数.4.10答案:应填1爱启航在线考研解析:()2d 2d 22e 4e d e4ed x x xxy x x C x x C--⎛⎫⎰⎰=+=+ ⎪⎝⎭⎰⎰222e (21)e (21)e x x xx C x C --⎡⎤=-+=-+⎣⎦.当0=x 时,1=-y ,则0=C .可得21=-y x ,则()11=y .故答案为1.4.11答案:应填1解析:由11()()'+=y P x y Q x 及22()()'+=y P x y Q x 得()()1212()()()αββαβ'+++=+y y P x ay y Q x .又因12αβ+y y 满足原方程,故应有()()()β+=a Q x Q x ,即1αβ+=.故答案为1.4.12解:()sin d sin d e cos e d -⎛⎫⎰⎰=+ ⎪⎝⎭⎰x xx x gx x x C ()cos cos e cos ed -=+⎰xxx x C又()00g =,故()()cos cos cos 0e cos ed cos ed limlime lim xxxx x x x x Cx x Cg x xxx--→→→++==⋅=⎰⎰cos 0e lim cos e 1x x x -→⋅=.4.13解:2d 1d 2y x x y =-,则2d 2d x x y y =-,即2d 2d x x yy-=-()()2d 2d 222222111e e d e e d e 224yy y y y x y y C y y C y y C --⎛⎫⎰⎰⎡⎤=-+=-+=+++ ⎪⎣⎦⎝⎭⎰⎰.4.14解:令=tx u ,则u t x d d =,则代入到题给表达式101()d ()d xf tx t f u u x =⎰⎰,可得20()d 2()xf u u xf x x =+⎰.两边求导得()2()2()2f x f x xf x x '=++,则()2()2f x xf x x '+=-.从而11131d d 2222222()e (1)ed 33x x x x f x x C x x C x Cx ---⎛⎫⎛⎫⎰⎰=-+-+=-+ ⎪⎝ ⎝⎭=⎪⎭⎰.爱启航在线考研4.15解:将原方程改写成211cos sin y x x yy '+=-,并令1z y =,则21z y y ''=-,且原方程化为sin cos z z x x '-=-.d de (sin cos )e d x x z x x x C -⎡⎤⎰⎰=-+⎢⎥⎣⎦⎰e (sin cos )e d x x x x x C -⎡⎤=-+⎣⎦⎰()e sin ed cose d xxx x x x x C --=-+⎰⎰,其中()sin e d sin d e sin e e cos d x x x x x x x x x x ----=-=-+⎰⎰⎰,故()e sin e e sin x x x z x C C x -=-+=-,即1e sin x C x y=-为所求通解.4.16答案:应选(C )解析:因原方程阶数为2,通解中应包含两个任意常数(可求出通解为3126++x C C x );特解中不含有任意常数(3*6=x y 为特解);36+x Cx 满足原方程,为原方程的解,故选项(A ),(B ),(C )都不对,应选(C ).4.17解:(1)令y p '=,则d d p y x ''=,从而2d 1d pp x=+,则2d d 1p x p =+积分得p arctan 1arctan p x C =+,故()1d tan d yp x C x=+=,则两边对x 积分1d tan()d y x C x =+⎰⎰,得()1121sin()d ln cos cos()x C y x x C C x C +==-+++⎰.(2)()10xy xy C '''=⇒=,即1y xC '=,故12ln y C x C =+.4.18解:由21e x y =,得212e x y x '=,()22124e x y x ''=+;由22e x y x =,得222(12)e x y x '=+,()22364e x y x x ''=+.因爱启航在线考研()()()22222211144224e 42e 42e 0x x x y xy x y x x x x '''-+-=+-⋅+-=.()()()()222232222244264e 412e 42e 0x x x y xy x y x x x x x x '''-+-=+-++-=.故1y 与2y 都是方程的解.又因21y x y =不等于常数,故1y 与2y 线性无关.于是方程的通解为()2112212e x y C y C y C C x =+=+.4.19答案:应选(A )解析:根据高阶线性微分方程根的形式可知,选(A ).4.20答案:应选(B )解析:由题意可知,-1是特征方程二重特征根,1是特征方程的特征根,故特征方程为()()2110+-=r r ,即3210+--=r r r .故三阶常系数齐次线性方程为0y y y y ''''''+--=.故选(B ).4.21答案:应选(C )解析::特征方程为2220++=r r 即2(1)1+=-r ,解得特征根为1,21i r =-±.而()e sin x f x x -=,i 1i w ±=-±λ是特征根,故特解的形式为*e (cos sin )x y x a x b x -=+.4.22答案:应填()*22e xy x ax bx c dx =+++解析:特征方程为220-=r r ,特征根10r =,22r =.对21()1=+f x x ,10λ=是特征根,所以()*21y x ax bx c =++.对22()exf x =,22λ=也是特征根,故有*22e =x y dx .从而***12=+y y y 就是特解.故答案为()*22e x y x ax bx c dx =+++.4.23解:所给微分方程的特征方程为256(2)(3)0++=++=r r r r ,特征根为12=-r ,23=-r .于是,对应齐次微分方程的通解为2312)e e xx y x C C --=+.爱启航在线考研设所给非齐次方程的特解为*e xy A -=.将*()y x 代入原方程,可得1A =.由此得所给非齐次方程得特解*e xy -=.从而,所给微分方程得通解为2312()e e e xx x y x C C ---=++,其中1C ,2C 为任意常数.4.24答案:应选(C )解析:将()()000y y '==代入3e xy py qy '''++=,得()01''=y .()()()()()22000ln 122limlimlimlim 2x x x x x x x y x y x y x y x →→→→+===='''.故选C.4.25答案:应填12e(cos sin )e xxC x C x ++解析:所给微分方程的特征方程为22201i -+=⇒=±r r r ,从而齐次通解为12e (cos sin )x C x C x +,设特解为e x A ,代入方程得e 2e 2e e 1x x x x A A A A -+=⇒=,即得特解为e x .非齐次通解为12e(cos sin )e xx C x C x ++.。
国科大应用光学作业答案_1-7_

1、根据费马原理证明反射定律。
答案:略2、某国产玻璃的n C=1.51389, n d=1.5163, n F=1.52195,计算其阿贝数,并查出该玻璃的牌号。
答案:V=64.06、K93、求图1-5的入射角i1。
答案:25.81︒4、已知入射光线A的三个方向余弦为cosα、cosβ、cosγ,反射光线A'的三个方向余弦为cosα'、cosβ'、cosγ',求法线方向。
答案:cosα'-cosα、cosβ'-cosβ、cosγ'-cosγ5、有一光线o o=+A i j入射于n=1和n'=1.5的平面分界面上,平面cos60cos30的法线为o oN i j,求反射光线A'和折射光线A''。
cos30cos60=+答案:略6、有一光线以60︒的入射角入射于n=点反射和折射的光线间的夹角。
答案:90︒7、在水中深度为y处有一发光点Q,作QO面垂直于水面,求射出水面折射线的延长线与QO交点Q '的深度y'与入射角i的关系。
答案:'y=1、一个玻璃球直径为400mm,玻璃折射率为1.5。
球中有两个小气泡,一个在球心,一个在1/2半径处。
沿两气泡连线方向,在球的两侧观察这两个气泡,它们应在什么位置?如在水中观察(水的折射率为1.33)时,它们又应在什么位置?答案:空气中:80mm、200mm;400mm、200mm水中:93.99mm、200mm;320.48mm、200mm2、一个折射面r=150mm, n=1, n'=1.5,当物距l=∞, -1000mm, -100mm, 0, 100mm, 150mm, 1000mm时,横向放大率各为多少?答案:0、-3/7、3/2、1、3/4、2/3、3/133、一个玻璃球直径为60mm,玻璃折射率为1.5,一束平行光射到玻璃球上,其汇聚点在何处?答案:l'=15mm4、一玻璃棒(n=1.5),长500mm,两端面为凸的半球面,半径分别为r1=50mm, r2= -100mm,两球心位于玻璃棒的中心轴线上。
第三章第四章课后题答案

第三章课后练习答案1.通过本章学习,分析自己的成长过程,提出自己对生命的理解。
答案:略。
2.怎样能让自己的生命更有价值?答案:(1)首先了解生命的意义和价值,不自伤自残,不伤害他人,遇到心理危机时主动寻找途径解决危机。
(2)生命的价值在于了解自我,实现自我,了解自己的兴趣爱好,在大学期间努力学习,为自我实现奠定基础。
(3)生命的价值还在于为社会的贡献,爱自己的同时也爱他人,爱这个世界,用爱的眼光去看待问题,用爱的心去对待他人。
3.当我遇到心理危机的时候,我可以寻找哪些帮助?答案:(1)首先,自己可以帮助自己,心理学家认为每个人都有解决自己心理问题的潜力。
通过读书、旅行等途径,让自己慢慢走出心理危机。
(2)其次,可以通过自我的社会支持系统帮助自己,包括身边的同学、朋友、父母等,他们都是无条件支持者,所以可以充分信任他们,将自己遇到的问题告诉他们,寻求帮助。
(3)最后,可以通过专业机构帮助自己,比如学校的心理咨询室,那里有专业的心理咨询师,可以从专业的角度帮助大家分析解决问题。
第四章课后练习答案1.通过本章学习,分析自己的优势与劣势,提出完善我的打算。
答案:略。
2.试结合自己分析,幼师生自我意识的发展具有怎样的特征?答案:(1)强烈关心自己的发展;(2)较高的自我评价能力;(3)自我体验丰富复杂;(4)自我控制的能力提高;(5)自我意识水平有年级差异。
3.请结合实际,谈谈自我意识与心理健康的关系。
答案:(1)良好的自我意识可以维护个体人格完整独立;(2)良好的自我意识可以促进大学生的社会适应,比如学习适应和环境适应;(3)良好的自我意识可以促进自我调节功能的完善;(4)良好的自我意识可以促进心理健康的发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章消费税纳税筹划作业
3-2:某卷烟厂2010年某月购入一批价值150万元的烟叶,并委托其他卷烟厂加工成烟丝,协议规定加工费为100万元,收回烟丝后继续加工为甲类卷烟,加工成本费用共计100万元,共生产出750标准箱甲类卷烟,每箱250标准条,售价400元/条,且全部实现销售。
另一方案:如果该卷烟厂直接委托其他卷烟厂将委托加工的烟丝加工成甲类卷烟,加工费用共计200万元,共生产出750标准箱甲类卷烟,每箱250标准条,收回卷烟成品后直接对外销售,售价400元/条,且全部实现销售。
分析要求:该卷烟厂采用哪个方案有利?(卷烟消费税比例税率56%,烟丝消费税税率30%,城市维护建设税与教育费附加暂不计,所得税税率25%,比较两个方案的消费税和税后利润)
解题思路:
方案一:受托方代收代缴消费税税额为:
(1500000+1000000)/(1-30%)×30%=1071429(元)
或(150+100)/(1-30%)×30%=107.14万元
销售完卷烟后,应纳消费税税额为:
750×150+750×250×400×56%-1071429=41 041 071(元)
或750×150÷100000+750×250×400÷10000×56%-107.14=4104.11万元
税后利润为:
(750×250×400-1500000-1000000-1000000-41 041 071-1071429)×(1-25%)=22040625元或(750×250×400÷100000-150-100-100-107.14-4104.11)×(1-25%)=2204.06万元
方案二:如果该卷烟厂直接委托其他卷烟厂将委托加工的烟丝加工成甲类卷烟,加工费用共计200万元,共生产出750标准箱甲类卷烟,每箱250标准条,收回卷烟成品后直接对外销售,售价400元/条,且全部实现销售。
受托方代收代缴消费税税额为:
750×150+(1500000+2000000+750×150)/(1-56%)×56%=4710227.2(元)
或750×150÷100000+(150+200+750×150÷100000)/(1-56%)×56%=471.02万元
对外销售不必再缴纳消费税,税后利润为:
(750×250×400-1500000-2000000-4710227.2)×(1-25%)=50092350(元)
或(750×250×400÷100000-150-200-471.02)×(1-25%)=5009.24万元
应选择方案二
3-1:某日化企业,除了自己外购原材料生产化妆品销售以外,还可以通过外购化妆品继续生产化妆品销售。
方案一:2008年8月,企业将外购的化妆品80 000元(不含增值税)继续生产化妆品销售,继续生产加工的成本费用为20 000元(不含增值税),全部销售收入120 000元。
假设当期期初、期末的外购化妆品库存为零。
方案二:如果该企业自己用外购的原材料76 000元,继续生产化妆品出售,同样取得销售收入120 000元。
解题思路:
方案一:当期应交消费税=120 000×30%一80 000×30%=12 000(元)
方案二,则当期应交消费税:120 000×30%=36 000(元)
应选择方案一。
第四章营业税纳税筹划作业
4-1:某超市销售空调器1000台,不含税销售额250万元,当月可抵扣进项税额40万元;同时为客户提供上门安装业务,收取安装费23.4万元。
计算该超市交纳的税额,并做出筹划方案。
解题思路:
按税法规定,销售空调器属于增值税的范围,取得的安装费属于营业税中建筑业税目的纳税范围,即该项销售行为涉及增值税和营业税两个税种。
但该项销售行为所销售的空调器和收取的安装费又是因同一项销售业务而发生的。
因此该连锁超市商业公司的这种销售行为实际上是一种混合销售行为。
由于该连锁超市商业公司是从事货物的批发、零售企业,故该连锁超市商业公司取得的安装费收入20万元,应并入空调器的价款一并缴纳增值税,不再缴纳营业税。
其应纳税额=〔250+23.4÷(1+17%)〕×17%-40=5.9万元;
纳税筹划做法:该连锁超市商业公司把安装空调器的部门独立出来,并实行独立核算,这样,空调器的安装费就不再交纳增值税,改为交纳营业税。
其应纳税款计算如下:应纳税额,
增值税=250×17%-40 = 2.5(万元)营业税=23.4×3%=0.7(万元),合计为3.2万元与不进行纳税筹划相比可少交税款2.7万元
4-2:教材P148页案例7-3
解题思路:
Dt=( St-Pt)/ St×100%=(3000-2250)/3000×100%=25%>20.65%,
所以,该混合销售缴纳营业税可以节税。
(1)该混合销售如果缴纳增值税,则应缴纳的增值税为:
(3000-2250)/(1+17%)×17%=108.97(万元)
(2)该混合销售如果缴纳营业税,则应缴纳的营业税为
3000×3%=90万元)
所以选择缴纳营业税可以节税18.97万元。
