华东理工大学多元统计分析与SPSS应用实验-(2)
多元统计分析(聚类分析,判别分析,对应分析)

操判作步别骤分析
输入数据,选择分析→分类→判别,然后把“概 况”选入分组变量中,再点击“定义范围…”来定义 范围为1(最小数值)到4(最大数值),然后将 “语文”、“数学”、“外语”、“体育”选入自 变量中,然后点击“Statistics…”,在出现的对话框 中勾选平均值与Fisher’s,其余选项为默认,点击 继续,确定运行。
Wilks' Lambda (λ)
Wilks' Lambda
函數的檢定 (λ)
卡方
df
1 至3
.083
87.142 12
2 至3
.936
2.302
6
3
.990
.352
2
顯著性 .000 .890 .839
是对三个判别函数的显著性检验, 看出第一判别函数在0.05的显著 性水平上是显著的,第二与第三 判别函数不显著。
目录
定聚义类分析
聚类分析是统计学中研究“物以类聚”问题的多 元统计分析方法。聚类分析又称群分析,它是研究对 样品或指标进行分类的一种多元统计方法。所谓的 “类”,通俗地说就是相似元素的集合。
基聚本步类骤 分析
(1)计算n个样品两两间的距离,得样品间的距离矩阵 。 类与类之间的距离本文应用的是类平均法。所谓类平均法 就是:两类样品两两之间平方距离的平均作为类之间的距 离,即: 采用这种类间距离的聚 类方法,称为类平 均法。 (2) 初始(第一步:i=1)n个样本各自构成一类,类的 个数k=n,第t类 (t=1,2···,n)。此时类间的距离就是样 品间的距离(即 )。 (3)对步骤i得到的距离矩阵 ,合并类间距离最小的两类 为一新类。此时类的总个数k减少1类,即k=n-i+1. (4)计算新类与其他类的距离,得新的距离矩阵 。若合 并后类的总个数k扔大于1,重新步骤(3)和(4);直到 类的总个数为1时转到步骤(5)。 (5)画谱系聚类图; (6)决定总类的个数及各类的成员。
(整理)多元统计分析上机实验.

多元统计分析上机实验指导第一部分 SPSS软件基本操作当用户安装SPSS软件后,点击快捷图标,将会出现以下界面:图1.1 启动SPSS后出现的对话框对话框包括一个六选一单选对话框和一个复选对话框,其内容为:●Run the tutorial 运行操作指南;●Type in data 输入数据选项,建立新的数据集时可选择此项;●Run an existing query 运行一个已经存在的数据文件选项;●Create new query using Database Wizard 用数据库处理工具建立新文件;●Open an existing date source 打开一个已经存在的数据文件;●Open another type of file 打开其他类型的文件。
●Don’t show this dialog in the future 是一复选对话框,选中该复选项后,下次启动SPSS时将不会显示对话框,直接显示数据编辑窗口。
如果只是利用该软件做一般性的统计分析,不做高级开发工作,可以在“Don’t show this dialog in the future”左方的小方块里打钩,以后启动SPSS时将不会显示对话框,直接显示数据编辑窗口。
§1.1 数据文件的建立SPSS 软件包的数据编辑主窗口类似于EXCEL ,数据文件的建立就是在数据编辑窗口中完成的。
数据编辑窗口可以显示两张表,分别是Data View (见图1.2)和Variable View (见图1.3),通过点击下端的2个同名窗口标签按钮实现相互切换。
数据编辑区是SPSS 的主要操作窗口,是一个二维平面表格,用于对数据进行各种编辑;标尺栏由纵向标尺栏和横向标尺栏,横向标尺栏显示数据变量,纵向标尺栏显示数据顺序(如时间顺序)。
Data View 表可以直接输入观测数据值或存放数据,表的左端列边框显示观测个体的序号,最上端行边框显示变量名。
多元分析与spss 应用
多元统计分析习题(二)
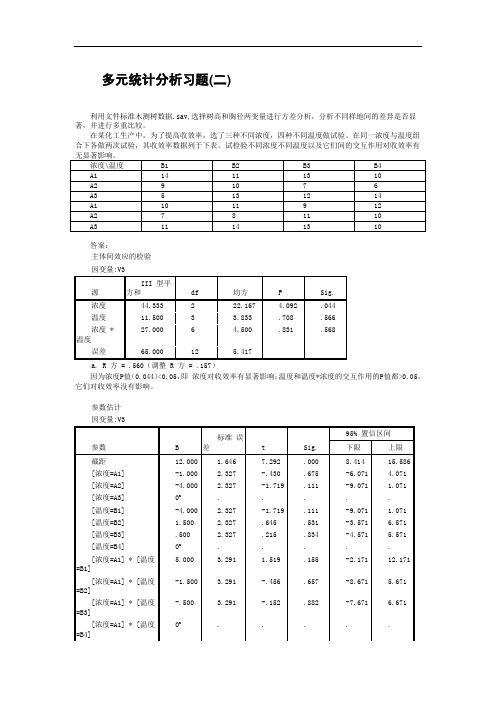
利用文件标准木测树数据.sav,选择树高和胸径两变量进行方差分析,分析不同样地间的差异是否显著,并进行多重比较。
在某化工生产中,为了提高收效率,选了三种不同浓度,四种不同温度做试验。
在同一浓度与温度组合下各做两次试验,其收效率数据列于下表。
试检验不同浓度不同温度以及它们间的交互作用对收效率有
P值都>0.05,它们对收效率没有影响。
A3因素对收效率最好。
通过比较A, B因素的交互作用发现A3对B2组合的均值最大,说明A3对B2组合对收效率最好,因此说A3对B2是最优组合。
根据实验结果,进行多元方差分析SPSS操作步骤

根据实验结果,进行多元方差分析SPSS操作步骤多元方差分析(MANOVA)是一种统计方法,用于比较两个以上组之间在多个连续因变量上的差异。
SPSS是一款功能强大的统计分析软件,可以用于进行多元方差分析。
下面是进行多元方差分析的SPSS操作步骤:1. 打开SPSS软件,并导入实验数据。
2. 在菜单栏选择“分析”(Analyze),然后选择“一元方差分析”(General Linear Model)。
3. 在弹出的对话框中,将多个连续因变量添加到“因变量”(Dependent Variables)框中。
点击“添加”按钮,然后选择需要分析的连续因变量。
4. 将一个或多个离散自变量添加到“因子”(Factors)框中。
点击“添加”按钮,然后选择需要分析的离散自变量。
5. 点击“选项”(Options)按钮,可以进行一些附加的设置。
例如,可以选择是否计算效应大小、调整误差项或进行共同协方差矩阵的检验等。
6. 点击“确定”按钮,开始进行多元方差分析。
7. 分析结果会显示在SPSS的输出窗口中。
可以查看因变量之间的差异是否显著,以及不同组之间是否存在显著差异。
8. 为了更好地理解结果,可以进一步进行后续分析。
例如,可以进行事后比较(Post hoc tests)来确定具体哪些组之间存在显著差异。
请注意,进行多元方差分析前,需要确保数据满足一些假设条件,如正态性、方差齐性和无多重共线性等。
另外,为了减少假阳性结果,应谨慎解释显著性水平。
以上是根据实验结果进行多元方差分析SPSS操作的步骤。
希望对您有所帮助!如有需要,请随时与我联系。
多元统计分析及SPSS应用课件

03
详细描述
SPSS的对应分析功能可以将分类变量 转换为数量型变量,通过降维技术展 示变量间的关系。
SPSS的对应分析功能简单易用,能够 处理大型数据集,并且可以清晰地展 示变量间的关系和类别间的比较。
SPSS的对应分析功能支持多种距离度 量方式,允许用户自定义类别间的比 较方式,并且可以结合图形界面直观 地展示结果,如散点图和气泡图。
03
生物医学
分析生物标志物和疾 病之间的关系,发现 潜在的治疗方法和药 物。
04
金融
分析多个经济指标和 股票价格,进行投资 决策和风险管理。
02
SPSS软件介绍
Chapter
SPSS软件的特点与优势
强大的统计分析功能
SPSS提供了广泛的统计分析方法,包括描述性统计、推论性统计、 多元统计分析等,可满足各种数据分析和科学研究的需求。
多维尺度分析
01
用于研究数据之间的相似性或差异性。
02
多维尺度分析是一种用于研究数据之间的相似性或差异性的方法。它通过建立一 个低维空间来表示高维数据,使得相似的数据点在空间中距离较近,差异较大的 数据点距离较远。多维尺度分析广泛应用于市场研究、心理学等领域。
判别分析
基于已知分类的数据建立判别函数, 对新的观测值进行分类。
用户可以从SPSS官网或其他授权渠道获取 SPSS软件的安装包。
安装过程
按照安装向导的指引,逐步完成软件的安装过程, 包括选择安装路径、配置软件组件等。
启动SPSS软件
安装完成后,双击桌面快捷方式或从开始菜 单启动SPSS软件。
SPSS软件的基本操作界面
主界面概览
SPSS的主界面包括菜单栏、工具栏、 数据编辑窗口、结果输出窗口等部分 。
应用多元统计分析课后答案 (2)

(1)解:随机变量 X1 和 X 2 的边缘密度函数、均值和方差;
'.
.
fx1 (x1)
d c
2[(d
c)( x1
a)
(b a)(x2 (b a)2 (d
c) c)2
2( x1
a)( x2
c)]
dx
d
2(d c)(x1 (b a)2 (d
a)x2 c)2
d c
2[(b
a)( x2 (b
差阵。)
2.6 渐近无偏性、有效性和一致性;
2.7 设总体服从正态分布, X ~ N p (μ, Σ) ,有样本 X1, X2 ,..., Xn 。由于 X 是相互独立的正
态分布随机向量之和,所以 X 也服从正态分布。又
E(X)
E
n
Xi
n
n
E Xi
n
n μ
nμ
i1
i1
i1
D(X) D n Xi i1
μ j
nj i1
Σ1 ( Xij
μj)
0(
j
1, 2,..., k)
解之,得
μˆ j
xj
1 nj
nj
xij , Σˆ
i 1
k nj
xij x j
j1 i1
xij x j
n1 n2 ... nk
第三章
3.1 试述多元统计分析中的各种均值向量和协差阵检验的基本思想和步骤。 其基本思想和步骤均可归纳为: 答:
i 1
i 1
n
(Xi - μ)(Xi - μ) 2n(X μ)(X μ) n(X μ)(X μ) i 1
n
(Xi - μ)(Xi - μ) n(X μ)(X μ) i 1
SPSS统计分析实用教程(第2版)

探索性分析
03
均值比较与t检验
总结词
单样本t检验用于检验单个样本的均值是否与已知的某个值或参考值存在显著差异。
详细描述
在单样本t检验中,我们将已知的某个值或参考值作为检验标准,然后比较单个样本的均值与此标准之间的差异。通过计算t统计量和对应的p值,我们可以判断样本均值与标准值是否存在显著差异。
单样本t检验
通过图形方式展示两个变量之间的关系,可以直观地观察到它们之间的模式和趋势。
相关分析
散点图
相关系数
预测模型
通过一个或多个自变量预测因变量的值,建立预测模型,并评估模型的拟合优度和预测能力。
回归系数
描述自变量对因变量的影响程度,通过回归系数可以了解各个自变量对因变量的贡献。
线性回归分析
非线性关系
协方差分析是在考虑一个或多个协变量的影响后,比较两个或多个分类变量对数值型变量的影响。通过控制协变量的影响,可以更准确地评估各组之间的差异,并确定分类变量对数值型变量的真实效应。
总结词
详细描述
协方差分析
05
非参数检验
适用范围
01
卡方检验主要用于比较实际观测频数与期望频数之间的差异。
计算方法
02
通过卡方统计量,即实际观测频数与期望频数的差的平方与期望频数的比值,来评估两者之间的差异程度。
聚类分析
聚类分析基于观测数据之间的相似性或距离将它们分组,使得同一聚类中的数据尽可能相似,不同聚类中的数据尽可能不同。
聚类分析在市场细分、生物信息学和社交网络等领域有广泛应用。
THANKS FOR
WATCHING
感谢您的观看
详细描述
探索性分析
总结词
探索性分析还可以用于预测和分类,例如决策树、逻辑回归等。
华东理工大学《多元统计分析与SPSS应用实验》实验报告2

华东理工大学《多元统计分析与SPSS应用实验》实验报告2 班级学号姓名开课学院商学院任课教师任飞成绩实验报告:实验2.1 熟悉One---Sample T Test 功能(1)选用Employee data.sav 文件中的变量,Analyze→Compare Means→One---Sample T Test,将salary作为Test因变量,test值分别取34000、35000、34419、24000,作均值检验。
如图实验结果:1.Test Value=34000:双尾概率P=0.593>α=0.05,故接受原假设,说明样本salary均值与假设值34000无显著性差异;2.Test Value=35000:双尾概率P=0.460>α=0.05,故接受原假设,说明样本salary均值与假设值35000无显著性差异;3.Test Value=34419:双尾概率P=0.999>>α=0.05,故接受原假设,说明样本salary均值与假设值35000不仅无显著性差异,而且接近样本均值。
4.Test Value=24000:双尾概率P=0.00<<α=0.05,故接受原假设,说明样本salary均值与假设值24000显著性差异。
(2). 仍选用Employee data.sav 文件中的变量,先作10%的随机抽样,然后将salary作为Test因变量,test 值取34419,作均值检验。
随机抽样:data→select cases→random sample of cases→sample→approximately 10%→Continue→OK实验结果(部分原始数据序号被划掉):再均值检验过程:Analyze →Compare Means →One---Sample T Test,将salary作为Test因变量,test 值取34419,所得实验数据结果如下图所示:双尾概率P=0.284>α=0.05,故接受原假设,说明随机抽样样本的salary均值与假设值34419无显著性差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华东理工大学多元统计分析与SPSS应用实验-(2)
华东理工大学2013—2014 学年第二学期
《多元统计分析与SPSS应用》实验报告2
班级学号姓名
开课学院商学院任课教师任飞成绩
实验内容:实验 2 方差分析
2.1.熟悉One---Sample T Test 功能
Analyze
Compare Means
One---Sample T Test
( t检验)
(1). 选用Employee data.sav 文件中的
变量,将salary作为Test因变量,test
值分别取34000、35000、34419、24000,
作均值检验。
(2). 仍选用Employee data.sav 文件中
的变量,先作10%的随机抽样,然后将
salary作为Test因变量,test值取34419,
作均值检验。
2.2.熟悉
Independent--Samples T Test 功能Analyze
Compare Means
Independent--Samples T test…选用Employee data.sav 文件中的变量,将Current Salary作为Test Variables, gender作Grouping Variable,作两样本比较T检验。
2.3.熟悉Paired--Samples T Test 功能Analyze
Compare Means
Paired--Samples T test…
选用Trends chapter 12. sav文件中的变量,将connect, dsconect作为paired variables作配对样本统计分析。
2.4.熟悉One—Way ANOV A 功能运用Analyze
Compare Means
One—Way ANOV A…
选用Tomato.sav 文件中的变量,将height作为dependent variable, fert作为
factor,作单因素方差分析
2.5.熟悉General Factorial功能
Analyze
General Linear Model
GLM---Univariate …
选用Plastic.sav 文件中的变量,将
tear_res作为dependent variable,
extrusn,
additive作为factor,作双因素方差分析实验要求:
根据实验内容撰写分析报告。
教师评语:
教师签名:
年月日
实验报告:
实验2.1 熟悉One---Sample T Test 功能
(1)选用Employee data.sav 文件中的变量,Analyze →Compare Means→One---Sample T Test,
将salary作为Test因变量,test值分别取34000、35000、
34419、24000,作均值检验。
如图
实验结果:
1.Test Value=34000:
双尾概率P=0.593>α=0.05,故接受原假设,说明样本salary均值与假设值34000无显著性差异;
2.Test Value=35000:
双尾概率P=0.460>α=0.05,故接受原假设,说明样本salary均值与假设值35000无显著性差异;
3.Test Value=34419:
双尾概率P=0.999>>α=0.05,故接受原假设,说明样本salary均值与假设值35000不仅无显著性差异,而且接近样本均值。
4.Test Value=24000:
双尾概率P=0.00<<α=0.05,故接受原假设,说明样本salary均值与假设值24000显著性差异。
(2). 仍选用Employee data.sav 文件中的变量,先作10%的随机抽样,然后将salary作为Test因变量,test 值取34419,作均值检验。
随机抽样:data→select cases→random sample of cases →sample→approximately 10%→Continue→OK
实验结果(部分原始数据序号被划掉):
再均值检验过程:Analyze →Compare Means →One---Sample T Test,将salary作为Test因变量,test 值取34419,所得实验数据结果如下图所示:
双尾概率P=0.284>α=0.05,故接受原假设,说明随机抽样样本的salary均值与假设值34419无显著性差异。
实验 2.2 熟悉Independent--Samples T Test 功能
选用Employee data.sav 文件中的变量,选择Analyze →Compare Means→Independent--Samples T test,将Current Salary作为Test Variables, gender作Grouping Variable,作两样本比较T检验,选择define groups,两个group分别定义为0、1,如下图
实验结果如下图
表中双尾概率P都为0.000<<α=0.05,故不接受原假设,说明样本salary与gender有显著性差异。
实验 2.3 熟悉Paired--Samples T Test 功能
选用Trends chapter 12. sav 文件中的变量,选择
Analyze→Compare Means→Paired--Samples T test,将connect, dsconect作为paired variables作配对样本统计分析,如下图
实验结果如下图
双尾概率P=0.000<α=0.05,故拒绝原假设,说明connect 和dsconect变量间有显著性差异。
实验 2.4 熟悉One—Way ANOV A 功能运用
选用Tomato.sav 文件中的变量,选择Analyze →Compare Means→One—Way ANOV A,将height作为dependent variable, fert作为factor,作单因素方差分析,如下图
实验结果如下图:
概率值P=0.025<α=0.05,说明肥料的不同造成的最终高度之间有显著性差异,即肥料与高度存在因果关系。
实验 2.5 熟悉General Factorial 功能
选用Plastic.sav 文件中的变量,Analyze →General Linear Model→Univariate,将tear_res选入到“dependengt variable”框里,extrusn, additive选入到“fixed factor”框中,作双因素方差分析。
单击“model”按钮,弹出“univariate mode”对话框,选择“custom”。
在效应选项中选择主效应选项“main effects”,将extrusn ,additive两个因子选入“model”框中,如下图
实验结果如下图
由上述实验结果可知,extrusn因子的α=0.001<α=0.05,additive的P=0.015<α=0.05,则知extrusn,和additive 都高度显著,即不同的extrusn,不同的additive都会对tear_res有显著影响。
