SPSS实验报告
spss分析实验报告

spss分析实验报告SPSS分析实验报告引言在社会科学研究领域,SPSS(Statistical Package for the Social Sciences)作为一种数据分析工具,被广泛应用于统计分析和数据挖掘。
本实验报告旨在通过SPSS软件对某项研究进行数据分析,探索其背后的数据模式和相关关系。
一、研究背景与目的本次研究旨在探究大学生的学习成绩与睡眠时间之间的关系。
学习成绩和睡眠时间是大学生日常生活中两个重要的方面,通过分析两者之间的关联,可以为学生提供科学的学习指导,提高学习效果。
二、研究设计与数据收集本研究采用问卷调查的方式,通过随机抽样的方法选取了500名大学生作为研究对象。
问卷内容包括学生的学习成绩和每日平均睡眠时间。
收集到的数据以Excel表格的形式整理并导入SPSS软件进行分析。
三、数据预处理在进行数据分析之前,需要对数据进行预处理。
首先,检查数据是否存在缺失值或异常值。
通过SPSS软件的数据清洗功能,将缺失值进行填补或删除,确保数据的完整性和准确性。
其次,对数据进行标准化处理,以消除不同变量之间的量纲差异。
四、描述性统计分析描述性统计分析是对数据的基本特征进行总结和描述。
通过SPSS软件的统计功能,可以计算出学生的学习成绩和睡眠时间的平均值、标准差、最大值、最小值等统计指标。
同时,可以绘制直方图、箱线图等图表来展示数据的分布情况。
五、相关性分析相关性分析是研究不同变量之间相关关系的一种方法。
本研究中,我们使用Pearson相关系数来衡量学习成绩和睡眠时间之间的线性相关性。
通过SPSS软件的相关性分析功能,可以得到相关系数的数值和显著性水平。
如果相关系数接近于1或-1,并且显著性水平小于0.05,则说明学习成绩和睡眠时间之间存在显著的相关关系。
六、回归分析回归分析是研究自变量对因变量影响程度的一种方法。
在本研究中,我们使用线性回归模型来探究睡眠时间对学习成绩的影响。
通过SPSS软件的回归分析功能,可以得到回归方程的系数、显著性水平和模型的拟合优度。
spss实验报告,心得体会

spss实验报告,心得体会篇一:SPSS实验报告SPSS应用——实验报告班级:统计0801班学号:1304080116 姓名: 宋磊指导老师:胡朝明2010.9.8一、实验目的:1、熟悉SPSS操作系统,掌握数据管理界面的简单的操作;2、熟悉SPSS结果窗口的常用操作方法,掌握输出结果在文字处理软件中的使用方法。
掌握常用统计图(线图、条图、饼图、散点、直方图等)的绘制方法;3、熟悉描述性统计图的绘制方法;4、熟悉描述性统计图的一般编辑方法。
掌握相关分析的操作,对显著性水平的基本简单判断。
二、实验要求:1、数据的录入,保存,读取,转化,增加,删除;数据集的合并,拆分,排序。
2、了解描述性统计的作用,并1掌握其SPSS的实现(频数,均值,标准差,中位数,众数,极差)。
3、应用SPSS生成表格和图形,并对表格和图形进行简单的编辑和分析。
4、应用SPSS做一些探索性分析(如方差分析,相关分析)。
三、实验内容:1、使用SPSS进行数据的录入,并保存: 职工基本情况数据:操作步骤如下:打开SPSS软件,然后在数据编辑窗口(Data View)中录入数据,此时变量名默认为var00001,var00002,…,var00007,然后在Variable View窗口中将变量名称更改即可。
具体结果如下图所示:输入后的数据为:将上述的数据进行保存:单击保存即可。
2、读取上述保存文件:选择菜单File--Open—Data;选择数据文件的类型,并输入文件名进行读取,出现如下窗口:选定职工基本情况.sav文件单击打开即可读取数据。
3、对上述数据新增一个变量工龄,其操作步骤为将当前数据单元确定在某变量上,选择菜单Data—Insert Variable,SPSS自动在当前数据单元所在列的前一列插入一2个空列,该列的变量名默认为var00016,数据类型为标准数值型,变量值均是系统缺失值,然后将数据填入修改。
结果如下图所示:篇二:SPSS相关分析实验报告本科教学实验报告(实验)课程名称:数据分析技术系列实验实验报告学生姓名:一、实验室名称:二、实验项目名称:相关分析三、实验原理相关关系是不完全确定的随机关系。
SPSS上机实验报告一
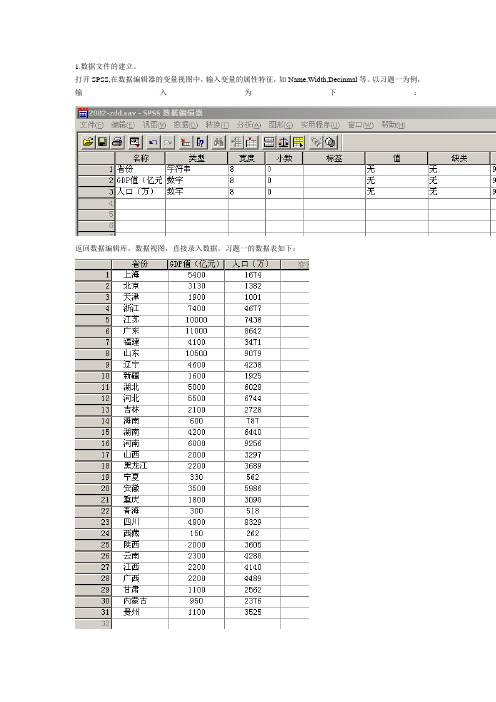
1.数据文件的建立。
打开SPSS,在数据编辑器的变量视图中,输入变量的属性特征,如Name,Width,Decinmal等。
以习题一为例,输入为下:返回数据编辑库,数据视图,直接录入数据。
习题一的数据表如下:点击Save,输入文件名将文件保存。
2.数据的整理数据编辑窗口的Date可提供数据整理功能。
其主要功能包括定义和编辑变量、观测量的命令,变量数据变换的命令,观测量数据整理的命令。
以习题一为例,将上图中的数据进行整理,以GDP值为参照,升序排列。
数据整理后的数据表为:整理后的数据,可以直观看出GDP值的排列。
3、频数分析。
以习题一为例(1).单击“分析→描述统计→频率”(2)打开“频率”对话框,选择GDP为变量(3)单击“统计量”按钮,打开“统计量”对话框.选择中值及中位数。
得到如下结果:(4)单击“分析→描述统计→探索”,打开“探索”对话框,选择GDP(亿元),输出为统计量。
结果如下:4、探索分析以习题2为例子:(1)单击“分析→统计描述→频率”,打开“频率”对话框,选择“身高”变量。
(2)选择统计量,分别选择百分数,均值,标准差,单击图标。
的如下结果:(3)单击“分析→统计描述→探索”,选择相应变量变量,单击“绘制”,选择如下图表,的如下结果:从上述图标可以看出,除了个别极端点以外,数据都围绕直线上下波动,可以看出,该组数据,在因子水平下符合正态分布。
4.交叉列联表分析:以习题3,原假设是吸烟与患病无关备择假设是吸烟与患病有关操作如下:单击“分析→统计描述→交叉表”,打开“交叉表”对话框,选择相应变量变量,单击精确,并选择“统计量”按钮,选择“卡方”作为统计量检验,然后单击“单元格”按钮,选择“观测值”和“期望值”进行计数。
得出分析结果如下:分析得出卡方值为7.469,,自由度是1,P值为0.004<0.05拒绝原假设,故有大于95%的把握认为吸烟和换慢性气管炎有关。
习题4:原假设是性别与安全性能的偏好无关备择假设是性别与安全性能的偏好有关操作如下:单击“分析→统计描述→交叉表”,打开“交叉表”对话框,选择相应行列变量然后选择“统计量”按钮,以“卡方”作为统计量检验.单击“单元格”按钮,选择“观测值”和“期望值”进行计数单击“确定”,得出分析结果如下:分析得出卡方值为19自由度是4,P值为0.001<0.05拒绝原假设,故有99.9%的把握认为性别与安全性能的偏好有关5实验作业补充。
SPSS实验报告完整版
SPSS实验实验课程专业统计软件应用上课时间学年学期周(年月日—日)学生姓名学号所在学院指导教师第五章第一题通过样本分析,结果如下图One-Sample StatisticsN Mean Std. Deviation Std. Error Mean 成绩27 77.9312.111 2.331One-Sample TestTest Value = 70t df Sig. (2-tailed)Mean Difference 95% Confidence Interval of theDifferenceLower Upper成绩 3.400 26.0027.926 3.13 12.72从图看出,sig=0.002,小于0.05,因此本班平均成绩与全国平均成绩70分有显著性差异。
第五章第二题通过独立样本分析,结果如下图Group Statistics成绩N Mean Std. Deviation Std. Error Mean成绩1=男10 84.0011.528 3.6450=女10 62.9018.454 5.836Independent Samples TestLevene's Test forEquality of Variances t-test for Equality of MeansF Sig. t dfSig.(2-tailed)MeanDifferenceStd. ErrorDifference95% Confidence Interval of theDifferenceLower Upper成绩Equalvariancesassumed1.607.221 3.06718.007 21.100 6.881 6.64435.556Independent Samples TestLevene's Test forEquality of Variances t-test for Equality of MeansF Sig. t dfSig.(2-tailed)MeanDifferenceStd. ErrorDifference95% Confidence Interval of theDifferenceLower Upper成绩Equalvariancesassumed1.607.221 3.06718.007 21.100 6.881 6.64435.556Equalvariancesnotassumed3.06715.096.008 21.100 6.881 6.44235.758在显著性水平为0.05的情况下,t统计量的概率p为0.007,故拒绝零假设,既两样本的均值不相等,既男女生成绩有显著性差异。
SPSS聚类分析实验报告

SPSS聚类分析实验报告一、实验目的本实验旨在通过SPSS软件对样本数据进行聚类分析,找出样本数据中的相似性,并将样本划分为不同的群体。
二、实验步骤1.数据准备:在SPSS软件中导入样本数据,并对数据进行处理,包括数据清洗、异常值处理等。
2.聚类分析设置:在SPSS软件中选择聚类分析方法,并设置分析参数,如距离度量方法、聚类方法、群体数量等。
3.聚类分析结果:根据分析结果,对样本数据进行聚类,并生成聚类结果。
4.结果解释:分析聚类结果,确定每个群体的特征,观察不同群体之间的差异性。
三、实验数据本实验使用了一个包含1000个样本的数据集,每个样本包含了5个变量,分别为年龄、性别、收入、教育水平和消费偏好。
下表展示了部分样本数据:样本编号,年龄,性别,收入,教育水平,消费偏好---------,------,------,------,---------,---------1,30,男,5000,大专,电子产品2,25,女,3000,本科,服装鞋包3,35,男,7000,硕士,食品饮料...,...,...,...,...,...四、实验结果1. 聚类分析设置:在SPSS软件中,我们选择了K-means聚类方法,并设置群体数量为3,距离度量方法为欧氏距离。
2.聚类结果:经过聚类分析后,我们将样本分为了3个群体,分别为群体1、群体2和群体3、每个群体的特征如下:-群体1:年龄偏年轻,女性居多,收入较低,教育水平集中在本科,消费偏好为服装鞋包。
-群体2:年龄跨度较大,男女比例均衡,收入中等,教育水平较高,消费偏好为电子产品。
-群体3:年龄偏高,男性居多,收入较高,教育水平较高,消费偏好为食品饮料。
3.结果解释:根据聚类结果,我们可以看到不同群体之间的差异性较大,每个群体都有明显的特征。
这些结果可以帮助企业更好地了解不同群体的消费习惯,为市场营销活动提供参考。
五、实验结论通过本次实验,我们成功地对样本数据进行了聚类分析,并得出了3个不同的群体。
spss实验报告---方差分析

实验报告——(方差分析)一、实验目的熟练使用SPSS软件进行方差分析。
学会通过方差分析分析不同水平的控制变量是否对结果产生显著影响。
二、实验内容1、某职业病防治院对31名石棉矿工中的石棉肺患者、可疑患者及非患者进行了用力肺活量(L)测定,问三组石棉矿工的用力肺活量有无差别?(自建数据集)石棉肺患者可疑患者非患者1.82.3 2.91.42.13.21.52.1 2.72.1 2.1 2.81.92.6 2.71.72.53.01.82.33.41.92.43.01.82.43.41.8 3.32.03.5SPSS计算结果:在建立数据集时定义group1为石棉肺患者,group2为可疑患者,group3为非患者。
零假设:各水平下总体方差没有显著差异。
相伴概率为0.075,大于0.05,可以认为各个组的方差是相等的,可以进行方差检验。
从上表可以看出3个组之间的相伴概率都小于显著性水平0.05,拒绝零假设,说明3个组之间都存在显著差别。
2、某汽车经销商在不同城市进行调查汽车的销售量数据分析工作,每个城市分别处于不同的区域:东部、西部和中部,而且汽车经销商在不同城市投放不同类型的广告,调查数据放置于附件中数据文件“汽车销量调查.sav”。
(1)试分析不同区域与不同广告类型是否对汽车的销量产生显著性的影响?(2)如果考虑到不同城市人均收入具有差异度时,再思考不同区域和不同广告类型对汽车销量产生的影响差异是否改变,这说明什么问题?SPSS计算结果:(1)此为多因素方差分析相伴概率为0.054大于0.05,可以认为各个组总体方差相等可以进行方差检验。
不同地区贡献的离差平方和为7149.781,均方为3574.891;不同广告贡献的离差平方和为7625.708,均方为3812.854。
说明不同广告和不同地区对汽车销量都有显著性影响。
广告对于销量的影响略大于地区对销量的影响。
从地区这个变量比较:第一组和第三组的相伴概率为0.000,低于显著性水平,一、三组均值差异显著;第二组和第三组的相伴概率为0.028,低于显著性水平,二、三组均值差异显著。
主成分分析、因子分析实验报告--SPSS

主成分分析、因子分析实验报告--SPSS主成分分析、因子分析实验报告SPSS一、实验目的主成分分析(Principal Component Analysis,PCA)和因子分析(Factor Analysis,FA)是多元统计分析中常用的两种方法,旨在简化数据结构、提取主要信息和解释变量之间的关系。
本次实验的目的是通过使用 SPSS 软件对给定的数据集进行主成分分析和因子分析,深入理解这两种方法的原理和应用,并比较它们的结果和差异。
二、实验原理(一)主成分分析主成分分析是一种通过线性变换将多个相关变量转换为一组较少的不相关综合变量(即主成分)的方法。
这些主成分是原始变量的线性组合,且按照方差递减的顺序排列。
主成分分析的主要目标是在保留尽可能多的数据信息的前提下,减少变量的数量,从而简化数据分析和解释。
(二)因子分析因子分析则是一种探索潜在结构的方法,它假设观测变量是由少数几个不可观测的公共因子和特殊因子线性组合而成。
公共因子解释了变量之间的相关性,而特殊因子则代表了每个变量特有的部分。
因子分析的目的是找出这些公共因子,并估计它们对观测变量的影响程度。
三、实验数据本次实验使用了一份包含多个变量的数据集,这些变量涵盖了不同的领域和特征。
数据集中的变量包括具体变量 1、具体变量 2、具体变量 3等,共X个观测样本。
四、实验步骤(一)主成分分析1、打开 SPSS 软件,导入数据集。
2、选择“分析”>“降维”>“主成分分析”。
3、将需要分析的变量选入“变量”框。
4、在“抽取”选项中,选择主成分的提取方法,如基于特征值大于1 或指定提取的主成分个数。
5、点击“确定”,运行主成分分析。
(二)因子分析1、同样在 SPSS 中,选择“分析”>“降维”>“因子分析”。
2、选入变量。
3、在“描述”选项中,选择相关统计量,如 KMO 检验和巴特利特球形检验。
4、在“抽取”选项中,选择因子提取方法,如主成分法或主轴因子法。
实验报告四.spss一元线性相关回归分析预测

实验报告四.spss一元线性相关回归分析预测
本实验使用spss 17.0软件,针对50个被试者,使用一元线性相关回归分析预测变
量X和Y的关系。
一、实验目的
通过一元线性相关回归分析,预测50个被试者的被试变量X(会计实操次数)和被试变量Y(综合评价分)之间的关系,来检验变量X是否能够预测变量Y的值。
二、实验流程
(2)数据收集:通过收集50个被试者的实际实操次数与综合评价分,建立反映这两
者之间关系的一元线性回归方程。
(3)数据分析:通过SPSS软件的一元线性相关回归分析预测变量X和Y的关系,使
用R方值进行检验研究结果的显著性。
以分析变量X对于变量Y的影响程度。
三、实验结果及分析
1.回归分析结果如下所示:变量X的系数b = 0.6755,t = 7.561,p = 0.000,说
明变量X和被试变量Y之间存在着显著的相关关系;R方值为0.941,说明变量X可以较
好地预测变量Y。
2.可以得出一元线性回归方程为:Y=0.67×X+5.293,其中,b为系数,X是自变量,Y是因变量。
四、结论
(1)50个被试者实际实操次数与综合评价分之间存在着显著的相关性;
(2)变量X可以较好地预测变量Y,R方值较高;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章描述性统计分析一、实验目的通过计算诸如样本均值、中位数、样本方差等重要基本统计量,并辅助于SPSS提供的图形功能,能够使分析者把握数据的基本特征和数据的整体分布形态,对进一步的统计推断和数据建模工作起到重要作用。
并且,通过例子学习描述性统计分析及其在SPSS中的实现,包括统计量的定义及计算、频率分析、描述性分析、探索性分析、交叉表分析和多重响应分析,能够使分析者更好的掌握基本的统计分析,即单变量频数分布的编制、基本统计量的计算以及数据的探索性分析等。
二、实验内容1.打开数据文件data4-8.sav,完成以下统计分析。
(1)计算各科成绩的描述统计量:平均成绩、中位数、众数、标准差、方差、极差、最大值和最小值;①解决问题的原理:描述性分析②实验步骤:通过“分析-描述统计-描述”,打开“描述性”对话框,根据题目所需要的统计量进行设置。
③结果及分析:表中分析变量“成绩”的个案数、所有个案中的极大值、极小值、均值、标准差及方差。
(2)使用Recode命令生成一个新变量“成绩段”,其值为各科成绩的分段:90~100为1,80~89为2,70~79为3,60~69为4,60分以下为5,其值标签:1—优,2—良,3—中,4—及格,5—不及格。
分段以后进行频数分析,统计各分数段的人数,最后生成条形图和饼图。
①解决问题的原理:频率分析。
②实验步骤:通过“分析-描述统计-频率”,打开“频率”对话框,根据题目所需要的统计量进行设置。
③结果及分析:成绩频率百分比有效百分比累积百分比有效15 1 2.2 2.2 2.219 1 2.2 2.2 4.424 1 2.2 2.2 6.728 1 2.2 2.2 8.930 1 2.2 2.2 11.132 2 4.4 4.4 15.633 1 2.2 2.2 17.834 1 2.2 2.2 20.036 1 2.2 2.2 22.237 2 4.4 4.4 26.743 1 2.2 2.2 28.949 1 2.2 2.2 31.150 1 2.2 2.2 33.355 1 2.2 2.2 35.656 4 8.9 8.9 44.460 3 6.7 6.7 51.162 1 2.2 2.2 53.363 1 2.2 2.2 55.669 1 2.2 2.2 57.870 1 2.2 2.2 60.073 3 6.7 6.7 66.774 1 2.2 2.2 68.975 1 2.2 2.2 71.176 1 2.2 2.2 73.378 1 2.2 2.2 75.681 1 2.2 2.2 77.883 1 2.2 2.2 80.085 2 4.4 4.4 84.486 1 2.2 2.2 86.790 2 4.4 4.4 91.191 1 2.2 2.2 93.395 2 4.4 4.4 97.898 1 2.2 2.2 100.0合计45 100.0 100.0表中显示了变量“成绩段”在各个取值上出现的次数(频率)、其频率占所有个案中的百分比、有效百分比及累积百分比。
表中显示了变量“成绩段”的直方图,从图上可以看出不具备明显的正态分布。
表中显示了变量“成绩段”的饼图,从图上可以更好的看出“成绩段”的分布。
2.打开数据文件data4-9.sav ,完成以下统计分析。
(1)对身高进行考察,分析四分位数,计算上奇异值、上极端值、下奇异值和下极端值,并生成茎叶图和箱图; ①解决问题的原理:探索性分析②实验步骤:通过“分析-描述统计-探索”,打开“绘制”对话框,根据题目所需要的统计量进行设置。
③结果及分析:身高 Stem-and-Leaf PlotFrequency Stem & Leaf2.00 9 . 9916.00 10 . 000000122233334439.00 10 . 555555556666677778888888999999999999999 18.00 11 . 000000112222233344 13.00 11 . 5556667788999 7.00 12 . 0000002000 1.00 12 . 5Stem width: 10.0 Ea00ch leaf: 1 case(s)从上的茎叶图可以更加详细地分析身高数据。
表4.22 吸烟人群健康状况调查表 是 患病 43 是 健康 162 否 患病 13 否健康121从上的箱图可以分析变量“身高”的四分位数。
(2)考察身高、体重和胸围的正态性。
①解决问题的原理:运用频率分析、描述性分析、探索性分析。
②实验步骤:通过“分析-描述统计-交叉表”,打开“交叉表”对话框,根据题目所需要的统计量进行设置。
③结果及分析:从上的Q-Q图中可以看出,身高、体重、胸围三个变量都很好的服从正态分布。
3.表4.22是对吸烟与患气管炎的调查表,试分析吸烟与患气管炎之间的关系。
(用交叉列联表分析,参见数据文件:data4-10.sav。
)①解决问题的原理:运用交叉表分析。
②实验步骤:通过“分析-描述统计-交叉表”,打开“交叉表”对话框,根据题目所需要的统计量进行设置。
③结果及分析:表给出了数据基本信息,表中给出了参与分析的个案数、缺失信息等。
本例中,每个变量有4个个案参与分析,无缺失值。
是否患气管炎* 是否吸烟交叉制表计数是否吸烟是否合计是否患气管炎患病 1 1 2健康 1 1 2合计 2 2 4表给出了了数据的交叉表,与原始数据在形式上基本一致。
各组状况条形图相当于交叉表的直观表示,用图形表示可直观地得出各种情况的比较。
4.为分析某中学学生填报志愿的倾向,设计了一道问卷调查题,每位同学可填报3个志愿,请按顺序依次选择打算报考的大学:第一志愿第二志愿第三志愿①北京大学②清华大学③复旦大学④中国人民大学⑤北京交通大学⑥四川大学问卷调查的结果存放在SPSS数据文件data4-11.sav中,按如下要求进行统计分析。
(1)对第一、二、三志愿填报情况进行统计分析;(2)对各学校填报志愿的情况进行统计分析,包括人数、百分比等。
①解决问题的原理:运用频率分析、描述性分析、交叉表分析。
②实验步骤:通过“分析-描述统计-频率”,打开“频率”对话框,根据题目所需要的统计量进行设置。
通过“分析-描述统计-交叉表”,打开“交叉表”对话框,根据题目所需要的统计量进行设置。
③结果及分析:统计量志愿1 志愿2 志愿3N 有效100 100 100缺失0 0 0中值 3.00 3.00 3.00众数 3 3 4标准差 1.578 1.429 1.642方差 2.491 2.041 2.695极小值 1 1 1极大值 6 6 6百分位数25 2.00 2.00 2.0050 3.00 3.00 3.0075 4.00 4.00 5.00频率表志愿1频率百分比有效百分比累积百分比有效 1 20 20.0 20.0 20.02 17 17.0 17.0 37.03 26 26.0 26.0 63.04 14 14.0 14.0 77.05 14 14.0 14.0 91.06 9 9.0 9.0 100.0合计100 100.0 100.0志愿2频率百分比有效百分比累积百分比有效 1 20 20.0 20.0 20.02 24 24.0 24.0 44.03 26 26.0 26.0 70.04 15 15.0 15.0 85.05 10 10.0 10.0 95.06 5 5.0 5.0 100.0合计100 100.0 100.0志愿3频率百分比有效百分比累积百分比有效 1 14 14.0 14.0 14.02 19 19.0 19.0 33.03 18 18.0 18.0 51.04 21 21.0 21.0 72.05 12 12.0 12.0 84.06 16 16.0 16.0 100.0合计100 100.0 100.0表中显示了变量“志愿”在各个取值上出现的次数(频率)、其频率占所有个案中的百分比、有效百分比及累积百分比。
三、实验心得与体会通过本章例子学习描述性统计分析及其在SPSS中的实现,学会了基本描述性统计量的定义及计算、频率分析、描述性分析、探索性分析、交叉表分析。
深刻体会到了如何计算诸如样本均值等重要的基本统计量,并辅助于SPSS提供的图形功能来分析把握数据的基本特征和数据的整体分布形态。
同时加强了自己的操作能力。
第五章参数估计与假设检验一、实验目的如果掌握了所研究总体的全部数据,那么只需做一些简单的统计描述,就可得到有关总体的数据特征,如方差、总体均值等,但在现实情况中,很多时候不可能或者不必对总体中的每个单位进行测定,就需要从总体抽取一部分单位进行测定,通过样本提供的信息来对总体信息进行估计和推断。
而参数估计和假设检验就是通过样本分析总体,从样本的观察或试验结果的特征对总体的特征进行估计和推断。
表5.20 某班学生数学成绩单个样本统计量N 均值标准差均值的标准误成绩27 77.93 12.111 2.331表给出了单样本T检验的描述性统计量,包括样本数(N) 、均值、标准差、均值的标准差。
表是单样本T检验结果表,当置信区间为95%时,显著水平为0.05,从表中可以看出,双尾检测概率P值为0.02,小于0.05,故原假设不成立,也就是说,数学成绩与全国的平均成绩70分之间有显著性差异。
4.在某次测试中,随机抽取男女学生的成绩各10名,数据如下:男:99 79 59 89 79 89 99 82 80 85女:88 54 56 23 75 65 73 50 80 65假设样本总体服从正态分布,比较置信度为95%的情况下男女得分是否有显著性差异。
(参见数据文件:data5-17.sav。
)①解决问题的原理:独立样本T检验②实验步骤:通过“分析-比较均值-独立样本T检验(T)”, 打开“独立样本T检验”对话框,根据题目所需要的统计量进行设置。
③结果及分析:上表中是独立样本T检验的均值检验结果。
显著水平为0.05,从表中可以看出T统计量的概率P小于0.05,故拒绝原假设,所以男女得分有显著性差异。
5.某医疗机构为研究某种减肥药的疗效,对16位肥胖者进行为期半年的观察测试,测试指标为使用该药之前和之后的体重,数据如表5.21所示。
假设体重近似服从正态分布,试分析服药前后,体重是否有显著变化。
(参见数据文件:data5-18.sav。
)表①解决问题的原理:配对样本T检验②实验步骤:通过“分析-比较均值-配对样本T检验(P)”, 打开“配对样本T检验”对话框,根据题目所需要的统计量进行设置。
③结果及分析:从上表一及表二中可以看出,在显著水平为0.05时,概率P值明显小于0.05,拒绝原假设,可以认为减肥药前后的体重有明显的线性关系。
