激光原理及应用(第2版)(陈家璧)课后答案(全)
陈家璧版-光学信息技术原理及应用习题解答(4-7章)

第四章习题4.1若光波的波长宽度为λΔ,频率宽度为νΔ,试证明:λλννΔΔ=。
设光波波长为nm 8632=.λ,nm 8-10⨯2=λΔ,试计算它的频宽νΔ。
若把光谱分布看成是矩形线型,那么相干长度?=c l 证明:参阅苏显渝,李继陶《信息光学》P349,第4.1题答案。
421.510c λνλ∆∆==⨯赫,32010()c c cl ct m ν===⨯∆4.2设迈克尔逊干涉仪所用的光源为nm 0589=1.λ,nm 6589=.2λ的钠双线,每一谱线的宽度为nm 010.。
(1)试求光场的复自相干度的模。
(2)当移动一臂时,可见到的条纹总数大约为多少?(3)可见度有几个变化周期?每个周期有多少条纹?答:参阅苏显渝,李继陶《信息光学》P349,第4.2题答案。
假设每一根谱线的线型为矩形,光源的归一化功率谱为()^1212rect rect νννννδνδνδν⎡--⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦G (1)光场的复相干度为^1()()exp(2)1sin ()exp(2)[1exp(2)]2r j d c j j τνπντνδντπντπντ∞==+∆⎰G 式中12ννν-=∆,复相干度的模为ντπδνττ∆=cos )(sin )(c r 由于νδν∆ ,故第一个因子是τ的慢变化非周期函数,第二个因子是τ的快变化周期函数。
相干时间由第一个因子决定,它的第一个零点出现在δντ1=c 的地方,c τ为相干时间,故相干长度δλλδλλδντ22≈===cc l c c 。
(2)可见到的条纹总数589301.05893====δλλλcl N (3)复相干度的模中第二个因子的变化周期ντ∆=1,故可见度的变化周期数601.06==∆=∆==δλλδννττc n 每个周期内的条纹数9826058930===n N 4.3假定气体激光器以N 个等强度的纵模振荡,其归一化功率谱密度可表示为()()()()∑21-21--=+-1=N N n n NνννδνΔgˆ式中,νΔ是纵模间隔,ν为中心频率并假定N 为奇数。
激光原理与应用答案(陈家壁主编)

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
光学信息技术原理及技术陈家壁第二版课后习题答案

第一章 习题解答1.1 已知不变线性系统的输入为()()x x g comb = 系统的传递函数⎪⎭⎫⎝⎛bfΛ。
若b 取(1)50=.b (2)51=.b ,求系统的输出()x g '。
并画出输出函数及其频谱的图形。
答:(1)()(){}1==x x g δF 图形从略, (2)()()()()()x s co f f δf δx g x x x πδ232+1=⎭⎬⎫⎩⎨⎧1+31+1-31+=F 图形从略。
1.2若限带函数()y x,f 的傅里叶变换在长度L 为宽度W 的矩形之外恒为零, (1)如果L a 1<,Wb 1<,试证明()()y x f y x f b x a x ab ,,sinc sinc =*⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛1 证明:(){}(){}(){}()()(){}(){}()y x,f sinc sinc 1,,y x,f ∴,,,,y x,f ====bxa x ab bf af rect y x f bf af rect y x f Wf L f rect y x f y x yx yx F F F F F 1-(2)如果L a 1>, Wb 1>,还能得出以上结论吗? 答:不能。
因为这时(){}(){}()y x yx bf af rect y x f Wf L f rect y x f ,,F ,,F ≠⎪⎪⎭⎫ ⎝⎛。
1.3 对一个空间不变线性系统,脉冲响应为 ()()()y x y x h δ77=sinc ,试用频域方法对下面每一个输入()y x f i ,,求其输出()y x g i ,。
(必要时,可取合理近似)(1)()x y x f π4=1cos ,答:()(){}(){}{}{}()(){}{}{}{}{}xcos x cos f rect x cos y 7x sin x cos y x h y x f y x g x πππδπ4=4=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛74=74==1-1-1-11-1F F F F F F F ,F ,F F ,(2)()()⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754=2y rect x rect x cos y x f π, 答:()(){}(){}{}()()(){}{}()()()()⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛77575⋅75*4=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754==1-1-11-2y rect x rect x cos f rect f sinc 75f sinc x cos y 7x sin y rect x rect x cos y x h y x f y x g x y x ππδπF F F F F ,F ,F F ,(3)()()[]⎪⎭⎫⎝⎛758+1=3x rect x cos y x f π,答:()()[]()(){}(){}()()()()()()()()()()()(){}⎪⎭⎫ ⎝⎛75=75≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛7⎪⎭⎫ ⎝⎛75*⎪⎭⎫ ⎝⎛4+81+4-81+=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775*8+1=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛758+1=1-1-1-1-1-3x rect f 75f sinc f rect f 75f sinc f rect f δ75f sinc f f x f rect f δ75f sinc x cos y 7x sin x rect x cos y x g y x x y x x y x x x x y x δδδδδπδπF F F F F F F F ,(4)()()()()()y rect x rect x comby x f 22*=4, 答:()()()()(){}()(){}{}()()()()()()()()()()()()(){}()()x π6cos x π2cos f f f f f f f f f f f rect f f δf f δf f δf f δf rect f sinc 2f sinc f f com b y 7x sin y rect x rect x com by x g y x y x y x y x y x x yx y x y x y x x y x y x 1060-3180+250=3+0530-3-0530-1+1590+1-1590+=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛7⎪⎭⎫ ⎝⎛-3-2120-1+6370+1-6370+41=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛7⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛2⎪⎭⎫ ⎝⎛41=722*=1-1-1-1-2...,.,.,.,.,F ,.,.,.,F F F F F ,δδδδ0.25δδδ1.4 给定一个不变线性系统,输入函数为有限延伸的三角波()()x x rect x comb x g i Λ*⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛50⎪⎭⎫ ⎝⎛331=对下述传递函数利用图解方法确定系统的输出。
激光技术原理及应用的答案

激光技术原理及应用的答案激光技术原理激光(Laser)是指在受激辐射作用下产生的,具有高度一致性、单色性和方向性的光线。
它的原理基于激活物质(如气体、固体或液体)的原子或分子通过受激辐射释放出光子。
具体来说,激光技术原理包括以下几个方面:1.受激辐射:激光的原理是基于受激辐射过程。
当外界光或电子束等能量激发到激光介质中的原子或分子时,它们会处于高能级态,然后通过跃迁回到低能级态,同时发射出与入射能量一致的光子。
2.光放大:在激光器中,激光介质中的光子会与待激发的原子或分子作用,导致原子或分子处于高能级态。
通过引入一个辐射源,其能量很容易被激光介质吸收并转化为更多的光子,从而达到放大激光的效果。
3.光反馈:在激光器中,光放大过程可以被反馈回来,形成一个光学谐振腔。
这个腔体包含一个完全或部分反射镜和一个输出镜。
放大的光通过反射镜反射回来,然后经过多次反射和放大,在腔中形成更多的激光。
4.单色性:激光的光子是高度一致的,它们具有非常狭窄而单一的频率。
这是因为激光器中的光放大过程只允许某个特定的模式在腔中持续放大,其他模式的能量会很快耗散掉。
激光技术应用激光技术由于其独特的特性,在许多领域都有着广泛的应用。
以下是一些常见的激光技术应用:1.激光切割和焊接:激光切割和焊接技术在工业生产中得到了广泛应用。
激光切割可以实现高精度、高速度和无接触的材料切割,适用于金属、塑料和木材等材料。
激光焊接则可以实现高强度的焊接连接,适用于汽车制造和电子设备制造等领域。
2.激光医学:激光在医学领域具有重要应用。
例如,激光手术可以实现无创伤、高精度和快速的手术操作,适用于眼科、皮肤美容和神经外科等领域。
激光也可以用于医学成像,如激光扫描显微镜和激光共聚焦显微镜。
3.激光测距和测量:激光测距和测量技术广泛应用于工程和地理测量领域。
例如,激光测距仪可以测量远距离和高精度的距离,适用于建筑测量和地形测绘。
激光测量仪也可以测量物体的尺寸、形状和表面特征。
激光原理及应用(第2版)(陈家璧)课后答案(全)

5 10 4
7.6 109
5.在红宝石 Q 调制激光器中, 有可能将全部 Cr3+ (铬离子 )激发到激光上能级并产生巨脉冲。
设红宝石直径 0. 8cm,长 8cm,铬离子浓度为 2× 1018cm-3,巨脉冲宽度为 10ns。求: (1)
输出 0. 6943 m 激光的最大能量和脉冲平均功率;
(2) 如上能级的寿命
3.已知氢原子第一激发态
(E2)与基态 (E1)之间能量差为
- 18
1. 64× l0 J,设火焰 (T = 2700K) 中
含有 1020 个氢原子。设原子按玻尔兹曼分布,且
4g1= g2。求: (1)能级 E2 上的原子数 n2 为
多少? (2)设火焰中每秒发射的光子数为 l08 n2,求光的功率为多少瓦?
1 /c 1 / c 0 ,在一级近似下为:
0(1 ) c
c ,证明接收器接收到的频率
证明: 即证
1 1
c c
0
21
(1
)(1 c
c2 ) 2
0
12
(1
)(1 c
2 c2 )
0
(1 ) c
0
11.静止氖原子的 3S2 2P4 谱线的中心波长为 0. 6328 m,设氖原子分别以
的速度向着接收器运动,问接收到的频率各为多少?
答:( 1) nm / gm nn / gn
( Em En)
e n kT 则有: 2 n1
h
e kT
6.63 10 34 3 109
exp[
]1 1.38 10 23 300
( 2) n2 n1
h
e kT
6.63 10 34 3 108
exp[ 1.38 10 23
《激光原理及应用》陈家璧第二版 - 第七章

图7-2 等离子云变化的过程
7.2.1 激光淬火技术的原理与应用
1.激光淬火技术,又称激光相变硬化,它利用聚焦后的激光束照射到钢铁材料表 面,使其温度迅速升到相变点以上。当激光移开后,由于仍处于低温的内层材料 的快速导热作用,使表层快速冷却到马氏体相变点以下,获得淬硬层。 2.图7-3 为一台柔性激光加工系统的示意图。它通过五维运动的工作头把激光照 射到被加工的表面,在计算机控制下直接扫描被加工表面完成激光淬火 3. 激光淬火可以使工件表层0.1到1.0mm范围内的组 织结构和性能发生明显变化。图7-4所示为45钢表 面激光淬火区横截面金相组织图
图7-5该淬火区显微硬度沿深度方向的分布曲线图
图7-6 基材含碳量与激光淬火层显微 Nhomakorabea度的关系
7.2.1 激光淬火技术的原理与应用
5.依据激光器的特点不同,激光淬火可分为CO2激光淬火和因素YAG激光淬火。 但两者中影响淬硬性能的主要基本相同 2) 激光工艺参数:激光淬火层的宽度主要决定于光斑直径;淬硬层深度由激光功 率、光斑直径和扫描速度共同决定;描述激光淬火的另一个重要工艺参数为功率 密度,即单位面积注入工件表面的激光功率。为了使材料表面不熔化,激光淬火 的功率密度通常低于104W/cm2,一般为1000-6000W/cm2。 3)表面预处理状态:一是表面组织淮备,即通过调质处理等手段使钢铁材料表面 具有较细的表面组织,以便保证激光淬火时组织与性能的均匀、稳定。如图7-7 为原始组织及扫描速度对激光淬硬层深度的影响;二是表面“黑化”处理,以便 提高钢铁表面对激光束的吸收率。
(2) 材料的加热 设入射激光束的光功率密度为qi,材料表面吸收的光功率密度为q0 ,则有 q0 Aqi qi 1 R az 激光从表面入射到材料内部深度为处的光强 qz q0 e 一般将激光在材料内的穿透深度定义为光强降至I0/e时的深度,因而穿透深 度为1/a
激光原理及应用1-6章部分课后答案

激光原理及应用部分课后答案1-4为使He-Ne 激光器的相干长度达到1KM ,它的单色性0λλ∆应是多少?2-2当每个模式内的平均光子数(光子简并数)大于1时,以受激辐射为主。
2-3如果激光器和微波激射器分别在um 10=λm 500n =λ和z 3000MH =ν输出1W 连续功率,问美秒从激光上能级向下能级跃迁的粒子数是多少?2-4当一对激光能级为E2和E1(f1=f2),相应的频率为v (波长为λ),能级上的粒子数密度分别为n2和n1,q 求:(1)当v=3000MHZ ,T=3000K 时,n2/n1=?(2)当λ=1um ,T=3000K 时,n2/n1=?(3)当λ=1um ,n2/n1=0时,温度T=?解:2-5激发态的原子从能级E2跃迁到E1时,释放出λ=5um的光子,求这个两个能级的能量差。
若能级E1和E2上的原子数分别为N1和N2,试计算室温T=300K的N2/N值。
2-7如果工作物质的某一跃迁是波长为100nm的远紫外光,自发辐射跃迁概率1621s10-=A,试问:(1)改跃迁的受激辐射爱因斯坦系数B21是多少?(2)为使受激辐射跃迁概率比自发辐射跃迁概率大三倍,腔内的单色能量密度νρ应为多少?2-9某一物质受光照射,沿物质传播1mm的距离时被吸收了1%,如果该物质的厚度是0.1m,那么入射光中有百分之几能通过该物质?并计算该物质的吸收系数α。
2-10激光在0.2m 长的增益介质中往复运动过程中,其增强了30%。
求该介质的小信号增益系数0G 。
假设激光在往复运动中没有损耗。
3-2CO2激光器的腔长L=100cm,反射镜直径D=1.5cm,两镜的光强反射系数分别为r1=0.985,r2=0.8.求由衍射损耗及输出损耗所分别引起的δ,τ。
3-4,分别按下图中的往返顺序,推导近轴光线往返一周的光学变换矩阵⎪⎪⎭⎫ ⎝⎛D C B A ,并证明这两种情况下的)(D A +21相等。
《激光原理及应用》陈家璧第二版-第七章课件
T0,0,AqS0r
232t
Ø激光功率密度过高,材料在外表汽化,不在深层熔化;激光功率密度过低, 则能量会集中到较大的体积内,使焦点处熔化的深度很小
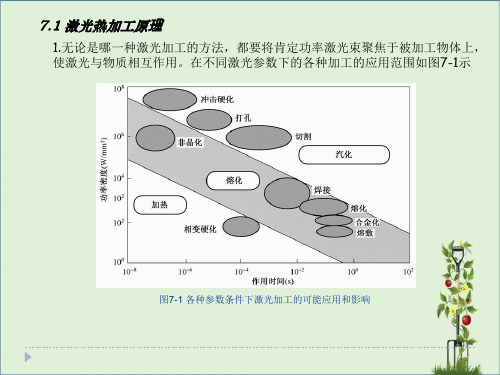
7.1 激光热加工原理
(4) 激光等离子体屏蔽现象 Ø激光作用于靶外表,引发蒸汽,蒸汽连续吸取激光能量,使温度上升,最终 在靶外表产生高温高密度的等离子体。等离子体快速向外膨胀,在此过程中连 续吸取入射激光,阻挡激光到达靶面,切断了激光与靶的能量耦合。 如图7-2所示,为等离子云变化的过程
Ø简化:假设半无限大〔即物体厚度无限大〕物体外表受到均匀的激光垂直照 射加热,被材料外表吸取的光功率密度不随时间转变,而且光照时间足够长, 以至被吸取的能量、所产生的温度、导热和热辐射之间到达动平衡,此时圆形 激光光斑中心的温度可以由下式确定
T0, AP
r0t
7.1 激光热加工原理
(2) 材料的加热 假设光照时间为有限长(s),考察点离开外表的距离(cm)也不为零,此时圆形激 光光斑中心轴线上考察点的温度为
图7-14离焦量对打孔质量的影响
7.3.1 激光打孔
3. 激光打孔工艺参数的影响 ※ 脉冲激光的重复频率对打孔的影响
用调Q方法取得巨脉冲时,脉冲的平均功率根本不变,脉宽也不变,重复频率越高 ,脉冲的峰值功率越小,单脉冲的能量也越小。这样打出的孔深度要减小。
※ 被加工材料对打孔的影响 材料对激光的吸取率直接影响到打孔的效率。由于不同材料对不同激光波长有不同 的吸取率,必需依据所加工的材料性质选择激光器。
7.3.1 激光打孔
1.激光打孔原理:激光打孔机的根本构造包括激光器、加工头、冷却系统、数控 装置和操作面盘〔图7-13〕。加工头将激光束聚焦在材料上需加工孔的位置,适 中选择各加工参数,激光器发出光脉冲就可以加工出需要的孔。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激 光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
设红宝石直径0.8cm ,长8cm ,铬离子浓度为2×1018cm -3,巨脉冲宽度为10ns 。
求:(1)输出0.6943μm 激光的最大能量和脉冲平均功率;(2)如上能级的寿命τ=10-2s ,问自发辐射功率为多少瓦? 答:(1)最大能量J ch d r h N W 3.2106943.01031063.61010208.0004.0683461822=⨯⨯⋅⨯⋅⨯⨯⋅⋅⨯=⋅⋅⋅⋅=⋅=--πλρπν脉冲平均功率=瓦8961030.21010103.2⨯=⨯⨯=--t W (2)瓦自自自145113.2112002021=⎪⎭⎫⎝⎛-⨯==⎪⎭⎫⎝⎛-==⎰-e h N P e n dt e n N t A τνττ6.试证单色能量密度公式,用波长λ来表示应为5811hc kThc eλλπρλ=-证明:11811852322-⨯=⋅-⨯=⋅=⋅==kT h kT h e hc c e h c c dVd dw dVd dw νννλλπλλπλρλνλρ 7. 试证明,黑体辐射能量密度()ρν为极大值的频率m ν由关系112.82m T kh ν--=给出,并求出辐射能量密度为极大值的波长m λ与m ν的关系。
答:(1)由 33811hv kTh c eνπνρ=-可得:0))1(113(82323=⋅⋅--⋅+-=∂∂kT he e e ch kT h kT h kT h ννννννπνρ 令kTh x ν=,则上式可简化为:xx xe e =-)1(3解上面的方程可得:82.2≈x即:1182.282.2--=⇒≈kh T kTh m mνν(2)辐射能量密度为极大值的波长m λ与m ν的关系仍为mm c λν=8.由归一化条化证明(1-65a)式中的比例常数1A τ=证明: 2202)2/1()(4)(τννπν+-=Af N ,由归一化条件且0ν是极大的正数可得: ⇒=+-⎰∞1)2/1()(402202ντννπd A ⇒=+-⎰∞1)2/1()(4202202ντννπνd A⇒='+'⎰∞1)41(120222νπτνπd A τπτνπτπ11]'4[4202=⇒=⋅⋅∞A arctg A9.试证明:自发辐射的平均寿命211A =τ,21A 为自发辐射系数。
证明:自发辐射时在上能级上的粒子数按(1-26)式变化:t A e n t n 21202)(-=自发辐射的平均寿命可定义为 ()dt t n n ⎰∞=2201τ式中()dt t n 2为t 时刻跃迁的原子已在上能级上停留时间间隔dt 产生的总时间,因此上述广义积分为所有原子在激发态能级停留总时间,再按照激发态能级上原子总数平均,就得到自发辐射的平均寿命。
将(1-26)式代入积分即可得出 21121A dt e t A ==⎰∞-τ10.光的多普勒效应中,若光源相对接收器的速度为c υ<<,证明接收器接收到的频率01/1/ccυννυ+=-,在一级近似下为:0(1)c υνν≈+证明:0022021220)1()211)(1()1)(1(11υυυυυυυυυυυν⋅+≈⋅⋅++≈⋅-+=⋅-+=-c c c cc c c 即证11.静止氖原子的3S 2→2P 4谱线的中心波长为0.6328μm ,设氖原子分别以±0.1c ,±0.5c 的速度向着接收器运动,问接收到的频率各为多少? 答:Hz cc cc 146801.010241.5106328.01039.01.19.01.111⨯=⨯⨯⋅=⋅=-+=-+λυυνν 同理可求:Hz c 141.010288.4⨯=-ν;Hz c 145.010211.8⨯=+ν;Hz c 145.010737.2⨯=-ν12.设氖原子静止时发出0.6328μm 红光的中心频率为4.74×1014Hz ,室温下氖原子的平均速率设为560m/s 。
求此时接收器接收频率与中心频率相差若干?答:Hzc 81460680010848.81074.4108667.1)108667.11()1035601()1(⨯=⨯⨯⨯=∆⇒⨯+=⨯+=+=--νννυνν13.(1) 一质地均匀的材料对光的吸收为0.01mm -1、光通过10cm 长的该材料后,出射光强为入射光强的百分之几? (2) —光束通过长度为1m 的均匀激活的工作物质,如果出射光强是入射光强的两倍,试求该物质的增益系数。
答;(1)368.01)0()()0()(10001.0===⇒=⋅--ee I z I eI z I Az(2)11693.02ln 2)0()()0()(-⋅==⇒==⇒=m G e I z I eI z I G Gz思考练习题21. 利用下列数据,估算红宝石的光增益系数n 2-n 1=5⨯1018cm -3,1/f (ν)=2×1011 s -1,t 自发=211A -≈3⨯10-3s ,λ=0.6943μm ,μ=l.5,g 1=g 2。
答:)(8)(8)(8)()(222133321333212121νπμλννμνπμννπμννμνf A n f h c h c A n G c h B A f h c nB G ⋅⋅∆=⋅⋅∆=⇒⎪⎪⎭⎪⎪⎬⎫=∆=11122431871.010215.18)106943.0(1031105)(---=⨯⨯⨯⋅⨯⋅⨯=cm G πν 2. He-Ne 激光器中,Ne 原子数密度n 0=n 1+n 2=l012 cm -3,1/f (ν)=15×109 s -1,λ=0.6328μm ,t 自发=211A -=10-17s ,g 3=3,g 2=5,11μ≈,又知E 2、E 1能级数密度之比为4,求此介质的增益系数G 值。
答:11112211211112312210103141081021410⨯=-=∆⇒⎪⎩⎪⎨⎧⨯=⨯=⇒⎭⎬⎫=+=-n g g n n n n E E cm n n n 比能级数密度之比为和 332121333332121888νπνπνπμh c A B c h c h B A =⇒== 192617112212172.0105.118)106328.0(1010314)(8)()(--=⨯⨯⨯⨯⨯=∆=∆=cmf A n f h c nB G πνπλννμν3. (a)要制作一个腔长L =60cm 的对称稳定腔,反射镜的曲率半径取值范围如何?(b)稳定腔的一块反射镜的曲率半径R 1=4L ,求另一面镜的曲率半径取值范围。
答:(a )R R R ==21;cm R RLR L 301)1)(1(0≥⇒≤--≤ (b )L R L R R LR L R L 31)1(4301)1)(1(022221-≤≥⇒≤-⋅≤⇒≤--≤或 4. 稳定谐振腔的两块反射镜,其曲率半径分别为R 1=40cm ,R 2=100cm ,求腔长L 的取值范围。
答:cm L cm L L L R L R L 1401004001)1001)(401(01)1)(1(021≤≤≤≤⇒≤--≤⇒≤--≤或5. 试证非均匀增宽型介质中心频率处的小讯号增益系数的表达式(2-28)。
证明:2102100021000210002100)ln2( 2)()2ln (2)()( )()( )(πννμνπννννμνννμνh c B n G f f h c B n G f h cB n G D D DD D D D D ∆∆=⇒⎪⎪⎭⎪⎪⎬⎫∆=∆=⇒∆= 即证。
6. 推导均匀增宽型介质,在光强I ,频率为ν的光波作用下,增益系数的表达式(2-19)。
证明:220022000)2)(1()()(])2()[()()(1 )()(ννννννννννν∆++-∆+-=+=s s I I G f f I I G G 而:())()(2)2()(12)()()(2)()( )()( )(0022000000002100002100ννπνννπννννννπνννμνννμνG G f f G f f h c B n G f h cB n G ∆∆+-∆==⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫∆=∆=∆≈依据上面两式可得:220002)2)(1()()()2()(νννννν∆++-∆=s I I G G ;即证。
