2011北京初三数学一模-昌平

合集下载

6.初三一模题答案-昌平.doc

昌平区2011—2012学年第二学期初三年级第一次统一练习数学试卷参考答案及评分标准 2012．1一、选择题（共8个小题，每小题4分，共32分）二、填空题（共4个小题，每小题4分，共16分）三、解答题（共6道小题，每小题5分，共30分） 13．解：原式=3212-⨯+ ……………………… 4分 =4+． ……………………… 5分 14．解：1?2(2)3.x x x -⎧⎨+⎩≥0， ①＞②由①得x ≥1． ……………………… 2分由②得x ＜4． ……………………… 4分所以原不等式组的解集为1≤x ＜4． ……………………… 5分 15．解：原式=22142m m m --- ……………………… 1分 =22(2)(2)(2)(2)m m m m m m +-+-+-=22(2)(2)m m m m --+-=2(2)(2)m m m -+-． ……………………… 4分=12m + ． ……………………… 5分 16．证明：∵ △ABC 和△ADE 都是等边三角形，∴ AB =AC ，AE =AD ，∠DAE =∠CAB ， ∵ ∠DAE -∠CAE =∠CAB -∠CAE ， ∴ ∠DAC =∠EAB ，ED CBA∴ △ADC ≌△AEB ． ……………………… 4分 ∴ CD =BE ． ……………………… 5分17．解：22(1)(1)10x x x x ---+ 原式=x (x 2-2x +1)-x 3+x 2+10=x 3-2x 2+x -x 3+x 2+10 =-x 2+x +10=-(x 2-x )+10． ……………………… 3分∵ 260x x --=， ∴ 26x x -=，∴ 原式=4． ……………………… 5分 18．解：延长DC ，FE 相交于点H ．∵ 四边形ABCD 是平行四边形，∴ AB ∥DC ，AB =CD ，AD =BC ． ……………………… 1分 ∴ ∠B ＝∠ECH ，∠BFE ＝∠H ． ∵ AB ＝5，AD ＝10， ∴ BC =10，CD =5． ∵ E 是BC 的中点，∴ BE =EC =152BC =． ∴ △BF E ≌△CHE ． ……………………… 3分 ∴ CH =BF ，EF=EH ． ∵ EF ⊥AB ，∴∠BFE ＝∠H =90°．在Rt △BFE 中， ∵ cos B =BF BE ＝35， ∴ BF =CH =3．∴ EF4=，DH =8．在Rt △FHD 中，∠H =90°，∴ 222DF FH DH =+=28+28=2×28．∴ DF． ……………………… 5分四、解答题（共4道小题，每小题5分，共20分） 19．（1）证明：连结OC ．∵ OC =OA ，∴ ∠OAC = ∠OCA ． ∵ AC 平分∠P AE ， ∴ ∠DAC = ∠OAC ， ∴ ∠DAC = ∠OCA ，HABC D EF∴ AD ∥OC ． ∵ CD ⊥P A ，∴ ∠ADC = ∠OCD =90°，即 CD ⊥OC ，点C 在⊙O 上，∴ CD 是⊙O 的切线． ……………………… 2分（2）解：过O 作OE ⊥AB 于E ． ∴ ∠OEA =90．° ∵ AB =8，∴ AE =4． ……………………… 3分在Rt △AEO 中，∠AEO =90°，∴ AO 2=42+OE 2．∵ ∠EDC = ∠OEA =∠DCO =90°， ∴ 四边形DEOC 是矩形， ∴ OC =DE ，OE =CD ． ∵ AD:DC =1:3，∴ 设AD =x ，则DC =OE =3x ，OA =OC =DE =DA +AE =x +4，∴ (x +4)2=42+(3x )2，解得 x 1=0(不合题意，舍去)，x 2=1．则 OA =5． ∴ ⊙O 的半径是5． ……………………… 5分 20．解：(1)30，56 ； ……………………… 2分 (2)y =-56x +235．2(3．7≤x≤4．2) ……………………… 4分(3)不能．小明从家出发到回家一共需要时间：1+2．2+2÷4×2=4．2（小时），从8:00经过4．2小时已经过了12:00，∴ 不能再12:00前回家，此时离家的距离：56×0．2=11．2（千米）． ………………… 5分 21．解：（1）80÷40％=200（名）答：该校对200名学生进行了抽样调查． ………………… 1分（2）………30图2 其它10% 踢毽子20%跳绳40%抖空竹各运动项目的最喜欢人数占抽样总人数百分比统%抽样调查学生最喜欢的运动项目的人数统图1人好2468………… 3分（3）120+180+200=500（名） 500×20％=100（名）答：全校学生中最喜欢踢毽子活动的人数约为100名． ………………… 5分22．解：（1）如图1，画出对角线AC 与BD 的交点即为点P ． ………………… 1分注：以BC 为直径作上半圆（不含点B 、C ），则该半圆上的任意一点即可．（2）如图2，以BC 为一边作等边△QBC ，作△QBC 的外接圆⊙O 分别与AB ，DC 交于点 M 、N ，弧MN 即为点P 的集合． ………………… 3分（3）如图3，以BC 为一边作等边△QBC ，作△QBC 的外接圆⊙O 与AD 交于点 P 1、P 2 ，点P 1、P 2即为所求． ………………… 5分五、解答题（共3道小题，第23小题6分，第24，25小题各8分，共22分） 23．解：（1）当1k =-时，方程44x --=0为一元一次方程，此方程有一个实数根；当1k ≠-时，方程2(1)(31)22k x k x k ++-+-=0是一元二次方程，△=（3k -1）2-4(k +1)(2k -2)=（k -3）2．∵（k -3）2≥0，即△≥0，∴ k为除-1外的任意实数时，此方程总有两个实数根． ……………………… 2分综上，无论k 取任意实数，方程总有实数根．（2）13(3)2(1)k k x k -±-=+，x 1=-1，x 2=421k -+． ∵ 方程的两个根是整数根，且k 为正整数，∴ 当k =1时，方程的两根为-1，0；当k =3时，方程的两根为-1，-1． ∴k =1，A B B3． ……………………… 4分（3）∵ 抛物线y =（k +1）x 2+(3k -1)x +2k -2与x 轴的两个交点之间的距离为3，∴，12x x -=3，或21x x -=3．当12x x -=3时，k =-3；当21x x -=3时，k =0．综上，k =0，-3． ……………………… 6分24．解：（1）∵ 抛物线2y ax bx c =++（0a ≠）A （-1，0）、B （3，0）C （0，3）三点，∴ 933030a b a b ++=⎧⎨-+=⎩，解得 12a b =-⎧⎨=⎩．∴ 抛物线的解析式为223y x x =-++，顶点M 为（1，4）． ……………… 2分（2）∵ 点A 、B 关于抛物线的对称轴对称，∴ 连结BC 与抛物线对称轴交于一点，即为所求点P ．设对称轴与x 轴交于点H ，∵ PH ∥y 轴，∴ △PH B ∽△CBO ．∴ PH BH CO BO=．由题意得BH =2，CO =3，BO =3，∴ PH =2．∴ P （1，2）． ……………………… 5分（3）∵ A （-1，0）B （3，0），C (0，3)，M (1，4)， ∴ S 四边形ABMC =9．∵ S 四边形ABMC =9S △PDE ， ∴PDE S ∆=1． ∵ OC =OD ，∴∠OCB =∠OBC = 45°．∵ DE ∥PC ，∴∠ODE =∠OED = 45°． ∴ OD =OE =3-m ．∵ S 四边形PDOE =9322m -， ∴ S △PDE = S 四边形PDOE - S △DOE =21322m m -+（0<m <3）． ∴213122m m -+=．解得，m 1=1， m 2=2． ……………………… 8分25．解：图3图2图1D CBANC'OMPD'D CBAN C'O MPD'D'PM OC'N A BCD（1） A D ’=B C ’，∠APB =∠α． …………………… 2分（2） A D ’=B C ’ 仍然成立，∠APB =∠α不一定成立． …………………… 3分（3）∠APB =180°-∠α． …………………… 4分证明：如图3，设OC ’，PD ’交于点E ．∵ 将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’， ∴ △DOC ≌△D ’OC ’，∴ OD =OD ’， OC =OC ’，∠DOC =∠D ’OC ’． ∵ 四边形ABCD 是等腰梯形，∴ AC =BD ，AB =CD, ∠ABC = ∠DCB ． ∵ BC =CB ，∴ △ABC ≌△DCB ． ∴ ∠DBC =∠ACB ． ∴ OB =OC ，OA =OD ． ∵ ∠AOB = ∠COD =∠C ’O D ’， ∴ ∠BOC ’ = ∠D ’O A ． ∵ OD ’=OA ，OC ’=OB ， ∴ △D ’OC ’≌△AOB ， ∴ ∠OD ’C ’= ∠OAB ．∵ OD ’=OA ，OC ’=OB ，∠BOC ’ = ∠D ’O A ， ∴ ∠OD ’A = ∠OAD ’=∠OBC ’=∠OC ’ B ． ∵ ∠C ’EP = ∠D ’EO ，∴ ∠C ’PE = ∠C ’OD ’=∠COD =∠α． ∵∠C ’PE +∠APB =180°，∴∠APB =180°-∠α． …………………… 8分E。

北京市各区2011年中考一模数学试题分类汇编专题六统计

市各区2011年中考一模数学试题分类汇编专题六统计（昌平区一模）2．据昌平交通局网上公布，地铁昌平线（一期）2011年1月4日出现上班运营高峰，各站进出站约47600人次. 将47 600用科学记数法表示为 A ．50.47610⨯ B ．247610⨯ C ．44.7610⨯ D ．54.7610⨯ 答案：C6．在“爱的奉献”为地震灾区捐款活动中，某班以小组为单位的捐款额（单位：元）分别为10，20，15，15，21，15，在这组数据中，众数及中位数分别是A ．15，10B ．15，15C ．15，20D ．15，16 答案：B（大兴区一模）2．截止到2011年4月9日0时，小客车指标申请累计收到个人申请491671个，第四轮摇号中签率接近28比1. 将491671用科学记数法表示应为 A ．4101671.49⨯ B ．51091671.4⨯ C ．61091671.4⨯ D ．710491671.0⨯ 答案：B4．某校对1200名女生的身高进行了测量，身高在1.58～1.63（单位：M ）这一小组的频率为0.25，则该组的人数为A ．150人B ．300人C ．600人D ．900人答案：B（某某区一模）2．2011年3月11日，里氏9.0级的日本大地震导致当天地球的自转时间减少了0.000 001 6 秒，将0.000 001 6用科学记数法表示为A ．16×10-7B ．1.6×10-6C ．1.6×10-5D ．0.16×10-5答案：B5．在某次射击训练中，甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表：答案：D（东城区一模）2.根据国家统计局的公布数据，2010年我国GDP 的总量约为398000亿元人民币. 将398000用科学记数法表示应为A. 398×103B. 0.398×106C . 3.98×105D. 3.98×106答案：C5.甲、乙、丙、丁四名学生10次小测验成绩的平均数(单位：分)和方差如下表：市各区2011年中考一模数学试题分类汇编专题六统计市各区2011年中考一模数学试题分类汇编专题六统计选手甲乙丙丁平均数方差0.270.15选手甲乙丙丁则这四人中成绩最稳定的是 A.甲 B 答案：B（房山区一模）2． 2010年某某世博会共有园区志愿者79965名。

中考数学阅读理解题型含答案

2011 年阅读理解试题汇编：（ 2011 年昌平区一模） 22．现场学习题问题背景：在△ ABC 中， AB 、 BC 、AC 三边的长分别为 2、 13、 17 ，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为 1），再在网格中画出格点△ ABC （即△ABC 三个顶点都在小正方形的顶点处），如图 1 所示．这样不需求△ ABC 的高，而借用网格就能计算出它的面积．（1） _________________________________________ 请你将△ ABC 的面积直接填写在横线上．思维拓展：（2）我们把上述求△ ABC 面积的方法叫做构图法．若△ ABC 三边的长分别为 2a 、2 5a 、 26a （a 0），请利用图 2 的正方形网格（每个小正方形的边长为 a ）画出相应的 △ ABC ，并求出它的面积是：．探索创新：(3)若△ ABC 三边的长分别为 4m 2 n 2 、 16m 2 n 2 、 2 m 2 n 2(m 0,n o,m n) ，请运用构图法在图 3 指定区域内画出示意图，并求出△ ABC 的面积为：5 答案：（ 1） 5．2（ 2）面积： 3a 2 ．图33）面积： 3mn ．（通州区一模）图2图3图1图23 22．问题背景S ABC 2 8 8 182011 年房山区一模） 22．（本小题满分 5 分）小明想把一个三角形拼接成面积与它相等的矩形．他先进行了如下部分操作，如图（1）如图 22（1），△ABC 中， DE ∥BC 分别交 AB ，AC 于 D ，E 两点，过点 E 作EF ∥AB交 BC 于点 F ．请按图示数据填空：四边形 DBFE △ ADE 的面积探究发现（ 2）在（ 1）中，若拓展迁移的面积 S S2， △EFC 的面积 S 1BF a ， FC b ，DE 与 BC 间的距离为 h ．请证明 S 2 4S 1S 2．（3）如图 22（2），□DEFG 的四个顶点在 △ABC 的三边上，若 △ADG 、△DBE 、△GFC 5、3，试利．用．（2．）中．的．结．论．求△ABC 的面积．答案： (1)四边形 DBFE 的面积 S 2 3 6 ，1△EFC 的面积 S 16 3 9 ，12△ ADE 的面积 S 2 1．(2)根据题意可知：1 S ah ， S 1bh ，2DE ∥BC ， EF ∥AB四边形 DEFB 是平行四边形， ADE EFC , AED CDE=aADE ∽ EFC ,a 2 S 2b S 12aa S 22S1 b 22b4S 1S 24 bh a 2h a 2h 22 2bS 2 4S 1S 2(3) 过点 G 作 GH//AB由题意可知：四边形 DGFE 和四边形 DGHB 都是平行四边形DG=BH=EFBE=HFSDBE SGHFSGHCS 2四边形 DGHB 4S ADG S GHC 4 2 8 642hS 四边形 DGHB 81 所示：A2S 16 C A的面积B 分别为E2、 22（1）3①取△ ABC 的边 AB 、AC 的中点 D 、E ，联结 DE ；②过点 A 作 AF ⊥DE 于点 F ；1）请你帮小明完成图 1 的操作，把△ ABC 拼接成面积与它相等的矩形．2）若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形，那么原三角形的一边与这边上的高之间的数量关系是 ________________ ．3）在下面所给的网格中画出符合（ 2）中条件的三角形，并将其拼接成面积与它相等的答案：解：（ 1）2）若要拼接成正方形，原三角形的一边与这一边上的高之间的数量关系是 1：2或 2：13）画对一种情况的一个图给 1 分（2011 年海淀一模）22．如图 1，已知等边△ ABC 的边长为 1，D 、E 、F 分别是 AB 、BC 、AC 边上的点（均不与点 A 、B 、C 重合），记△ DEF 的周长为 p .（1）若 D 、E 、F 分别是 AB 、BC 、AC 边上的中点，则 p = _______ ；（2）若 D 、E 、F 分别是 AB 、BC 、AC 边上任意点，则 p 的取值范围是.①②点上（网格图中每个小正方形边长都为 1）.小亮和小明对第（ 2）问中的最小值进行了讨论，小亮先提出了自己的想法：将翻折一次得 △AB 1C ，再将△ AB 1C 以B 1C 为轴翻折一次得 △A 1B 1C ，如图2所示. 则由轴对称的性质可知，DF FE 1 E 1D 2 p ，根据两点之间线段最短，可得 p DD 2. 老师听了后说： “你的想法很好，但 DD 2的长度会因点 D 的位置变化而变化，所以还得不出我们想要的结果 . ”小明接过老师的话说： “那我们继续再翻折3 次就可以了 ”请.参考他们的想法，写出你的答案 .3答案解：（1） p 3 ;232) 3 ≤ p 3.22011 年顺义一模）22．如图，将正方形沿图中虚线（其 x y ）剪成①形（非正方形）．（1）画出拼成的矩形的简图；x（ 2）求的值． y答案．（1）如图② ③ ④ 四块图形，用这四块图形恰好能拼成一个矩2 2 2 x 2xy y xy 2y22x xy y 0拼接成新的图形（如图③ ）.拼接时不重叠、无空隙，并且拼接后新图形的顶点在所给正方形网格图中的格2 2)面积可得(x y)2(x 2y)y--------------------- 3 分△ABC 以 AC 边为轴2分 5分xy( x )2 x1 0 yyx 5 1 y2（舍去）2011 年朝阳区一模） 22．阅读并操作：如图①，这是由十个边长为 1 的小正方形组成的一个图形， x 5 1 y2对这个图形进行适当分割（如图② ），然后图1图2请你参照上述操作过程，将由图①所得到的符合要求的新图形画在下边的正方形网格图中（2011 年丰台一模） 22．认真阅读下列问题，并加以解决：问题 1：如图 1，△ ABC 是直角三角形，∠ C =90o ．现将△ ABC 补成一个矩形．要求：使△ ABC 的两个顶点成为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上．请将符合条件的所有矩形在答案：解： 2）图②1）新图形为平行四边形； 2）新图形为等腰梯形图1 图 2问题 2：如图 2，△ABC 是锐角三角形，且满足 BC >AC >AB ，按问题 1 中的要求把它补成矩形．请问符合要求的矩形最多可以画出个，并猜想它们面积之间的数量关系是（填写“相等”或“不相等” ）；问题 3：如果△ ABC 是钝角三角形，且三边仍然满足 BC >AC > AB ，现将它补成矩形．要求：△ ABC 有两个顶点成为矩形的两个顶点，第三个顶点落在矩形的一边上 , 那么这几个矩形面积之间的数量关系是（填写“相等”或“不相等” ）．2）符合要求的矩形最多可以画出 3 个，它们面积之间的数量关系是相等；（3）不相等． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯答案：第 2 次划分，共有 9 个正方形；第 100 次划分后，共有 401 个正方形；依题意，第 n 次划分后，图中共有 4n+1 个正方形，而方程 4n+1=2011 没有整数解，所以，不能得到 2011个正方形 .（2011 年西城一模）22.我们约定，若一个三角形（记为 A 1）是由另一个三角形（记为 A ）通过一次平移，或绕其任一边中点旋转180 得到的，称 A 1 是由 A 复制的。

北京市2011年中考数学一模试题精选汇编：方程与不等式

北京市各区2011年中考一模数学试题分类汇编专题二方程与不等式（2011年昌平区一摸）14．解不等式：512x -≤2(43)x -，并把它的解集在数轴上表示出来．答案：解：512x -≤86x - 58x x -≤126- 3x -≤6x ≥2-012-1-2（2011年昌平区一摸） 15．解分式方程：2111xx x =-+-．答案：解：去分母，得：2（x-1）=x （x+1）-（x+1）（x-1）2x-2=x 2+x- x 2+1x=3经检验x=3是原方程的解（2011年昌平区一摸） 19．已知关于x 的方程 (m -1) x 2- 2x + 1=0有两个不相等的实数根．（1）求m 的取值范围；（2）若m 为非负整数，求抛物线y =(m -1) x 2- 2x + 1的顶点坐标．答案：解：（1）∵方程 (m-1) x 2- 2x + 1=0有两个不相等的实数根，∴()()01422>---=∆m .解得m<2.∴m 的取值范围是m ＜2且m≠1. （2）由（1）且m 为非负整数, ∴m=0.∴抛物线为y= -x 2- 2x + 1= -(x+1)2+2. ∴顶点(-1,2).（2011年朝阳区一摸） 14. 求不等式组46,1(3)22x x +≤⎧⎪⎨->-⎪⎩ 的整数解．-4-3-2-104321-4-3-2-104321答案：解：由①得：x ≤2. 由②得：x-3＞-4,x ＞-1.∴原不等式组的解集为 -1＜x ≤2. ∴原不等式组的整数解为 0,1,2.（2011年大兴区一摸） 7．若2(2)30x y ++-=，则xy 的值为A ．5B ．6C ．6-D ．8-答案：C（2011年大兴区一摸） 14．（本小题满分5分）解方程： xx x --=--31132 答案：解：去分母：231x x -=-+ 移项：231x x +-=+合并同类项：24x = 系数化为1：2x = 经检验验2x =是原方程的解 ∴原方程的解是2x =（2011年东城区一摸） 6. 已知关于x 的一元二次方程22x m x -= 有两个不相等的实数根，则m 的取值范围是A ． m ＞－1B ． m ＜－2C ．m ≥-1D ．m ＜1 答案：A（2011年东城区一摸） 16.解不等式4-5x ≥3(2x+5),并把它的解集在数轴上表示出来答案：解：4-5x ≥6x+15 -5x-6x ≥15-4 -11x ≥11 x ≤-1（2011年房山区一摸） 14．解不等式 232x 4125x ->-，并把它的解集在数轴上表示出来.答案： 5x-12>8x-6，-121-3x>6，x<-2.∴ 不等式的解集是x<-2. 数轴上正确表示解集（2011年丰台区一摸） 14．解不等式组： )1(42121+<-≤-x x x 并写出不等式组的整数解.答案：解：由不等式①，得到 x ≤3由不等式②，得到 x>-2 所以这个不等式组的解集是3x 2-≤< 将这个解集在数轴上略所以这个不等式组的整数解集是-1,0 1，2,3（2011年燕山区一摸） 3．以方程组21y x y x =-+⎧⎨=-⎩的解为坐标的点(,)x y 在（）.A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案：A（2011年燕山区一摸） 14．解不等式组 302(1)33,x x x +>⎧⎨-+⎩，≥ 并判断3=x 是否为该不等式组的解．答案：由①得3x >-．由②得x ≤1．∴ 原不等式组的解集是3-＜x ≤1． ∵ 31>，∴ 3x =不是该不等式组的解．（2011年燕山区一摸） 17. 已知关于x 的一元二次方程)0(0212≠=++a bx ax 有两个相等的实数根，求()()()11122-++-b b a ab 的值．答案：解：由题意，2214202b a b a ∆=-⨯=-=． ∴ 22b a =． ∴ 原式222211ab a a b =-++-①②2222ab a b a =+- 2222222a a a a a a a⋅==+-． ∵ 0a ≠， ∴ 原式2222a a==．四、解答题（本题共20分，每小题5分）（2011年延庆区一摸） 14．解方程：542332x x x +=-- 答案：解：去分母得：()3245-=-x x解之得：1=x . 检验：把1=x 代入32-x0132≠-=-x∴1=x 是原方程的解.（2011年西城区一摸） 14. 解不等式 2151132x x -+-≥,并把它的解集在数轴上表示出来.答案：14. 解：去分母，得 2(21)3(51)6x x --+≥去括号，得 421536x x ---≥移项合并同类项，得 1111x -≥系数化为1，得 1x ≤-所以，此不等式的解集为1x ≤- ，在数轴上表示如图所示（2011年西城区一摸） 15. 已知a 是一元二次方程2320x x +-=的实数根，求代数式2352362a a a a a -⎛⎫÷+- ⎪--⎝⎭的值. 答案：解：原式=3(2)(2)53(2)22a a a a a a a -+-⎡⎤÷-⎢⎥---⎣⎦=2393(2)2a a a a a --÷--=323(2)(3)(3)a a a a a a --⨯-+- =13(3)a a +=2139a a+∵ a 是方程2320x x +-=的实数根，∴ 232a a += ∴ 原式=21113(3)326a a ==+⨯（2011年西城区一摸） 23．已知：关于x 的一元二次方程23(1)230mx m x m --+-=()m 为实数(1) 若方程有两个不相等的实数根，求m 的取值范围；（2）求证：无论m 为何值，方程总有一个固定的根；（3）若m 为整数，且方程的两个根均为正整数，求m 的值.答案：（1）解： []22243(1)4(23)(3)b ac m m m m ∆=-=----=-∵方程有两个不相等的实数根，∴ 2(3)0m -> 且 0m ≠∴ 3m ≠且 0m ≠∴m 的取值范围是3m ≠且 0m ≠（2）证明：由求根公式243(1)(3)22b b ac m m x a m-±--±-==∴ 133323322m m m x m m m -+--===-233312m m x m--+==∴无论m 为何值，方程总有一个固定的根是1（3）∵m 为整数，且方程的两个根均为正整数∴132x m=-必为整数 ∴ 1m =± 或 3m =±当1m =时，11x =- ；当1m =-时，15x =；当3m =时， 11x = ；当3m =-时，13x =.∴ 1m =- 或3m =±（2011年通州区一摸） 14．解不等式组⎪⎩⎪⎨⎧⋅-≥++->-②)1(517,①4113x x x x 并把解集在数轴上表示出来．答案：解：解不等式① 3<x解不等式② 3-≥x 原不等式组的解集为33＜x ≤-（2011年顺义区一摸） 14．求不等式组⎪⎩⎪⎨⎧-≤--x x x x 22158)2(3＞的整数解. 答案：解：由3(2)8x x --≤ 得，1x -≥由1522x x -> 得，2x < 12x -<∴≤.∴ 不等式组的整数解是.1,0,1- .（2011年石景山区一摸） 14．解不等式1315>--x x ，并将解集在数轴上表示出来．答案：解：3315>--x x 42>x2>x （2011年平谷区一摸） 14．解分式方程 6133xx x +=+-．答案： 14．解分式方程6133x x x +=+-．解：去分母，6(3)(3)(3)(3)x x x x x -++=+-．整理，得 99x =．解得 1x =．经检验，1x =是原方程的解．所以原方程的解是1x =．1-12-3-23212- 1-（2011年平谷区一摸） 20．解法一：求两个班人均捐款各多少元？设1班人均捐款x 元，则2班人均捐款（x+4）元，根据题意得 1800x ·90%=1800x+4………………………………………………………（3分）解得x=36 经检验x=36是原方程的根，且符合实际意义………………………（4分） ∴x+4=40 ……………………………………………（5分）答：1班人均捐36元，2班人均捐40元解法二：求两个班人数各多少人？设1班有x 人，则根据题意得1800x +4=180090x% …………（3分）解得x=50 ，经检验x=50是原方程的根，且符合实际意义…（4分）∴90x % =45 ……………（5分）答：1班有50人，2班有45人.（2011年密云区一摸） 14．解不等式组：48011.32x x x -<⎧⎪+⎨-<⎪⎩，答案：解：解不等式480x -<，得 2x <,解不等式1132x x+-<，得 2263x x +-<, 即 4x >-, 所以，这个不等式组的解集是42x -<<.（2011年密云区一摸） 16．已知m 是方程220x x --=的一个实数根，求代数式22()(1)m m m m --+的值.答案：16．解：∵ m 是方程220x x --=的一个根，∴ 220m m --=.∴ 22m m -=，22m m -=.∴ 原式=222()(1)m m m m--+=2(1)mm⨯+ =22⨯=4.（2011年密云区一摸） 18．列方程（组）解应用题国家的“家电下乡”政策激活了农民购买能力，提高了农民的生活水平。

北京市各区2011年中考一模数学试题分类汇编专题八综合与实践

市各区2011年中考一模数学试题分类汇编专题八综合与实践（昌平区一模） 22．现场学习题问题背景：在△ABC 中，AB 、BC 、AC小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC （即△ABC 三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC 的高，而借用网格就能计算出它的面积．AB C图3图2图1(1)请你将△ABC 的面积直接填写在横线上．________ 思维拓展：(2)我们把上述求△ABC 面积的方法叫做构图法．若△ABC 、、(0)a >，请利用图2的正方形网格(每个小正方形的边长为a )画出相应的△ABC ，并求出它的面积是：．探索创新：(3)若△ABC三边的长分别为、、(0,,)m n o m n >>≠，请运用构图法在图3指定区域内画出示意图，并求出△ABC 的面积为：答案：（1） 25．（2）面积：23a ．（3）图2ABCA C 4m n n 2n面积：3mn ．25.已知：如图，在平面直角坐标系xOy 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA =2，OC =3．过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D 作DE ⊥DC ，交OA 于点E ．（1）求过点E 、D 、C 的抛物线的解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ．如果EF =2OG ，求点Ｇ的坐标．（3）对于（2）中的点G ，在位于第一象限内的该抛物线上是否存在点Q ，使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．答案：解：（1）∵OD 平分∠AOC , ∠AOC =90°∴∠AOD =∠DOC =45° ∵在矩形ABCD 中，∠BAO =∠B =∠BOC =90°,OA =BC =2,AB =OC =3 ∴△AOD 是等腰Rt △∵∠AOE +∠BDC =∠BCD +∠BDC =90° ∴∠AOE =∠BCD ∴△AED ≌△BDC ∴AE =DB =1∴D (2,2),E (0,1),C (3,0)则过D 、E 、C 三点的抛物线解析式为：1613652++-=x x y（2）DH ⊥OC 于点H ,∴∠DHO =90° ∵矩形 ABCD 中, ∠BAO =∠AOC =90° ∴四边形AOHD 是矩形 ∴∠ADH =90°. ∴∠1+∠2=∠2+∠3=90° ∴∠1=∠3∵AD =OA =2，∴四边形AOHD 是正方形. ∴△FAD ≌△GHD ∴FA =GH∴设点 G （x ，0）， ∴OG =x ，GH =2-x∵EF =2OG=2x ，AE=1， ∴2-x =2x -1， ∴x=1.∴G (1,0)(3)由题意可知点P 若存在，则必在AB 上，假设存在点P 使△PCG 是等腰三角形 1）当点P 为顶点，既 CP =GP 时，易求得P 1（2,2），既为点D 时，此时点Q 、与点P 1、点D 重合，O C BA Dxy EG H F312O C B A D xyE∴点Q 1(2,2)2) 当点C 为顶点，既 CP =CG =2时, 易求得P 2(3,2)∴直线GP 2的解析式：1-=x y求交点Q :⎪⎩⎪⎨⎧++-=-=16136512x x y x y 可求的交点（57,512）和（-1，-2）∵点Q 在第一象限∴Q 2（57,512）3)当点G 为顶点，既 GP =CG =2时, 易求得P 3(1,2) ∴直线GP 3的解析式：1=x求交点Q :⎪⎩⎪⎨⎧++-==16136512x x y x 可求的交点（37,1）∴Q 3（37,1）所以，所求Q 点的坐标为Q 1(2,2)、Q 2（57,512）、Q 3（37,1）．（某某区一模）12．如图，P 为△ABC 的边BC 上的任意一点，设BC=a ，当B 1、C 1分别为AB 、AC 的中点时，B 1C 1=a 21，当B 2、C 2分别为BB 1、CC 1的中点时，B 2C 2=a 43，当B 3、C 3分别为BB 2、CC 2的中点时，B 3C 3=a 87，当B 4、C 4分别为BB 3、CC 3的中点时，B 4C 4=a 1615，当B 5、C 5分别为BB 4、CC 4的中点时，B 5C 5=______， ……当B n 、分别为BB n-1、C -1的中点时，则B n =；设△ABC 中BC 边上的高为h ，则△PB n 的面积为______(用含a 、h 的式子表示)．答案：a 3231, a n n 212-, ah n n 12212+-25．已知：△ABC 和△ADE 都是等腰直角三角形，∠ABC =∠ADE =90°，点M 是CE 的中点，连接BM .（1）如图①，点D 在AB 上，连接DM ，并延长DM 交BC 于点N ，可探究得出BD 与BM 的数量关系为；（2）如图②，点D 不在AB 上，（1）中的结论还成立吗？如果成立，请证明；如果不成立，说明理由.B (第12题图)NMD ECABMEC BAD1分析：由题意知，B 5C 5∥BC ，555212AB AB -=，根据相似的性质，可得到B 5C 5=3132a ，同理可得到B n =a n n 212-.因为△ABC 中BC 边上的高为h ，所以△PB n 中B n 边上的高为h n21，△PB n 的面积为ah h a n n n nn 122122121221+-=⨯-⨯.答案：(1)BD=2BM. (2)结论成立.证明:连接DM ，过点C 作CF ∥ED ，与DM 的延长线交于点F ，连接BF ，可证得△MDE≌△MFC ∴DM=FM, DE=FC. ∴AD=ED=FC. 作AN⊥EC 于点N.由已知∠ADE =90°，∠ABC =90°，可证得∠1=∠2, ∠3=∠4. ∵CF ∥ED ，∴∠1=∠FCM.∴∠BCF=∠4+∠FCM =∠3+∠1=∠3+∠2=∠BAD. ∴△BCF≌△BAD. ∴BF=BD，∠5=∠6.∴∠DBF=∠5+∠ABF=∠6+∠ABF=∠ABC=90°. ∴△DBF 是等腰直角三角形. ∵点M 是DF 的中点，则△BMD 是等腰直角三角形.654321NMECABD图①图②∴BD=2BM.22．阅读并操作：如图①，这是由十个边长为1的小正方形组成的一个图形，对这个图形进行适当分割(如图②)，然后拼接成新的图形(如图③).拼接时不重叠、无空隙，并且拼接后新图形的顶点在所给正方形网格图中的格点上(网格图中每个小正方形边长都为1).图① 图② 图③请你参照上述操作过程，将由图①所得到的符合要求的新图形画在下边的正方形网格图中.（1）新图形为平行四边形；（2）新图形为等腰梯形.答案：解：（1）（2）（注：每图2分）（东城区一模） 12. 如图，直线x y 33=，点1A 坐标为（1，0），过点1A 作x 轴的垂线交直线于点1B ，以原点O 为圆心，1OB 长为半径画弧交x 轴于点2A ；再过点2A 作x 轴的垂线交直线于点2B ，以原点O 为圆心，2OB 长为半径画弧交x 轴于点3A ，…，按此做法进行下去，点4A 的坐标为（，）；点n A （，）．答案：938，01)332(-n ，024. 等边△ABC 边长为6，P 为BC 边上一点，∠MPN =60°，且PM 、PN 分别于边AB 、AC 交于点E 、F .（1）如图1，当点P 为BC 的三等分点，且PE ⊥AB 时，判断△EPF 的形状；（2）如图2，若点P 在BC 边上运动，且保持PE ⊥AB ，设BP =x ，四边形AEPF 面积的y ，求y 与x 的函数关系式，并写出自变量x 的取值X 围；（3）如图3，若点P 在BC 边上运动，且∠MPN 绕点P 旋转，当CF =AE =2时，求PE 的长.图1 图2 图3答案：（1）△EPF 为等边三角形. （2）设BP=x ，则CP ＝6－x.由题意可 △BEP 的面积为238x . △CFP 的面积为23(6)2x -. △ABC 的面积为93.设四边形AEPF 的面积为y. ∴93y =-238x 23(6)2x --=25363938x x -+-. 自变量x 的取值X 围为3＜x ＜6.（3）可证△EBP ∽△PCF.∴BP BECF CP=. 设BP=x ，则 (6)8x x -=. 解得 124,2x x ==. ∴ PE 的长为4或23.（房山区一模）12．如图，以边长为1的正方形的四边中点为顶点作四边形，再以所得四边形四边中点为顶点作四边形，．．．．．．依次作下去，图中所作的第三个四边形的周长为________；所作的第n 个四边形的周长为_________________．答案：2,42()2n（12题图）22．（本小题满分5分）小明想把一个三角形拼接成面积与它相等的矩形．他先进行了如下部分操作，如图1所示： ①取△ABC 的边AB 、AC 的中点D 、E ，联结DE ； ②过点A 作AF ⊥DE 于点F ；（1）请你帮小明完成图1的操作，把△ABC 拼接成面积与它相等的矩形．（2）若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形，那么原三角形的一边与这边上的高之间的数量关系是________________．（3）在下面所给的网格中画出符合（2）中条件的三角形，并将其拼接成面积与它相等的正方形．答案：解：（1）（2）若要拼接成正方形，原三角形的一边与这一边上的高之间的数量关系是1：2或2：1 （3）画对一种情况的一个图给1分NM ②①②①F E D C B ADC B A A B C DA B C D 图3图2图12n-1B 2C 2A BCB1C 1C 1B 1CBA或∴正方形ABCD 为所求（丰台区一模） 12．已知在△ABC 中，BC=a.如图1，点B 1 、C 1分别是AB 、AC 的中点，则线段B 1C 1的长是_______；如图2，点B 1 、B 2，C 1、C 2分别是AB 、AC 的三等分点，则线段B 1C 1 + B 2C 2的值是__________；如图3, 点12......、、、n B B B ，12......、、、n C C C 分别是AB 、AC 的（n+1）等分点，则线段B 1C 1 + B 2C 2+……+ B n 的值是 ______.答案：1,2a a ,12na25.已知:在△ABC 中，BC=a ，AC=b ，以AB 为边作等边三角形ABD. 探究下列问题:（1）如图1，当点D 与点C 位于直线AB 的两侧时，a=b=3，且∠ACB=60°，则CD=；（2）如图2，当点D 与点C 位于直线AB 的同侧时，a=b=6，且∠ACB=90°，则CD=；（3）如图3，当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时，求 CD 的最大值及相应的∠ACB 的度数.图1 图2 图3E D CB A DABCE 答案：解：（1）33；（2）2363 ；（3）以点D 为中心，将△DBC 逆时针旋转60°，则点B 落在点A ，点C 落在点E.联结AE,CE ，∴CD=ED ，∠CDE=60°，AE=CB= a ， ∴△CDE 为等边三角形， ∴CE=CD.当点E 、A 、C 不在一条直线上时，有CD=CE<AE+AC=a +b ；当点E 、A 、C 在一条直线上时， CD 有最大值，CD=CE=a +b ；此时∠CED=∠BCD=∠ECD=60°，∴∠ACB=120°，因此当∠ACB=120°时，CD 有最大值是a +b .（燕山区一模）12．已知：点F 在正方形纸片ABCD 的边CD 上，AB=2，∠FBC=30°（如图1）；沿BF 折叠纸片，使点C 落在纸片内点C ＇处（如图2）；再继续以BC ＇为轴折叠纸片，把点A 落在纸A D A D D C ＇F F F A ＇B C B B图1 图2 图3…答案：2-622．将正方形ABCD （如图1）作如下划分：第1次划分：分别联结正方形ABCD 对边的中点（如图2），得线段HF 和EG ，它们交于点M ，此时图2中共有5个正方形；第2次划分：将图2左上角正方形AEMH 按上述方法再作划分，得图3，则图3中共有_______个正方形；若每次都把左上角的正方形依次划分下去，则第100次划分后，图中共有_______个正方形；继续划分下去，能否将正方形ABCD 划分成有2011个正方形的图形？需说明理由.答案：第2次划分，共有9个正方形；第100次划分后，共有401个正方形；依题意，第n 次划分后，图中共有4n+1个正方形，而方程4n+1=2011没有整数解，所以，不能得到2011个正方形.（延庆区一模）12．如图，图①是一块边长为1，周长记为1P 的正三角形纸板，沿图①的底边剪去一块边长为12的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的21）后，得图③，④，…，记第)3(≥n n 块纸板的周长为n P ，则=-34P P ；1--n n P P =．A D A H D A H DE M G E M GB C B F C B F C 图1 图2 图3第22题图1第22题图 3DCBA 第22题图2CBA第12题图答案：81 , 121-⎪⎭⎫ ⎝⎛n22．阅读下列材料：根据所给的图形解答下列问题：（1）如图1，ABC ∆中，AC AB =，90=∠BAC ，D BC AD 于⊥，把ABD ∆绕点A 旋转，并拼接成一个正方形,请你在图1中完成这个作图；（2）如图2，ABC ∆中，AC AB =，90=∠BAC ，请你设计一种与(1)不同方法，将这个三角形拆分并拼接成一个与其面积相等的正方形,画出利用这个三角形得到的正方形；（3）设计一种方法把图3中的矩形ABCD 拆分并拼接为一个与其面积相等的正方形,请你依据此矩形画出正方形.25. 在Rt ABC △中，902BAC AB AC ∠===，，点D 在BC 所在的直线上运动，作45ADE ∠=（A D E ，，按逆时针方向）．（1）如图1，若点D 在线段BC 上运动，DE 交AC 于E ．①求证：ABD DCE △∽△；②当ADE △是等腰三角形时，求AE 的长．（2）①如图2，若点D 在BC 的延长线上运动，DE 的反向延长线与AC 的延长线相交于点E '，是否存在点D ，使ADE '△是等腰三角形？若存在，写出所有点D 的位置；若不存在，请简要说明理由；②如图3，若点D 在BC 的反向延长线上运动，是否存在点D ，使ADE △是等腰三角形？若存在，写出所有点D 的位置；若不存在，请简要说明理由．4545DAECABD 45ABDCE第25题图1答案： ①证明：在Rt ABC △中，∵902BAC AB AC ∠===， ∴∠B=∠C=45°又 ∠ADE=45° ∴∠ADB+∠EBC=∠EBC+∠DEC=135° ∴∠ADB=∠DEC ∴ABD DCE △∽△② 当ADE △是等腰三角形时,分以下三种情况讨论第一种情况：DE=AE∵DE=AE∴∠ADE=∠DAE=45°∴∠AED=90°, 此时，E 为AC 的中点，∴AE=12AC=1.第二种情况：AD=AE （D 与B 重合） AE=2第三种情况：AD=AE如果AD=DE ，由于ABD DCE △∽△， ∴△ABD ≌△DCE,∴BD=CE,AB=DC,设BD=CE=x在Rt ABC △中，∵902BAC AB AC ∠===，， ∴ BC=22, DC=22－x∴22－x =2 ,解得，x =22－2 ， ∴ AE= 4 －22综上所述：AE 的值是1，2，4 －2 (2)①存在。

11年北京昌平区初三数学一模试题及答案

昌平区2008—2009学年第二学期初三年级第一次统一练习数学试卷 2009．5考生须知1．本试卷共5页，共九道大题，25个小题，满分120分。

考试时间120分钟。

2．在试卷和答题卡上认真填写学校名称、姓名和考试编号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．考试结束，请将本试卷和答题卡一并交回。

一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个．．是符合题意的． 1．3-的相反数是 A ．13-B ．13C ．3-D ．32．今年两会期间，新华网、人民网、央视网等各大网站都推出了“向总理提问”的网上互动话题，上百万网民给总理提出了内容广泛的问题．在新华网推出的“总理，请听我说”栏目中，网民所提出的问题就达200 000多条. 将200 000用科学记数法表示应为 A ．60.210⨯B ．42010⨯C ．4210⨯D ．5210⨯3．如图，在Rt ABC ∆中, 90C ∠=︒，D 是AC 上一点，直线DE ∥CB 交AB 于点E ，若30A ∠=︒，则AED ∠的度数为 A ．30︒ B ．60︒ C ．120︒ D ．150︒4．把代数式222a ab b -+分解因式，下列结果中正确的是 A ．()2a b -B ．()2a b +C ．()()a b a b +-D ．22a b -5．在下列所表示的不等式的解集中，不包括．．．5-的是A ．4x ≤-B ．5x ≥-C ．6x ≤-D ．7x ≥-6．某校初三学生为备战5月份中考体育测试，分小组进行训练. 其中一个小组7名同学的一次训练的成绩（单位：分）为：18，27，30，27，24，28，25. 这组数据的众数和中位数分别是A ．27，30B ．27，25C ．27，27D ．25，30 7．把点()1,2A 、()1,2B -、()1,2C -、()1,2D --分别写在四张卡片上，随机抽取一张，该点在函数2y x =-的图象上的概率是 A ．13B ．12C ．23D ．348．将左图中的正方体纸盒沿所示的粗．线．剪开，其平面展开图的示意图为纸盒裁剪线A B C DDEC BABCADE二、填空题（共4道小题，每小题4分，共16分） 9．在函数11y x=-中，自变量x 的取值范围是． 10．若()240x -=，则x y +的值为．11．如图所示，把一个直角三角尺ACB 绕着30°角的顶点B 顺时针旋转，使得点A 落在CB 的延长线上的点E 处，则∠BDC 的度数为．12．一组按规律排列的式子：3579234,,,,x x x x y y y y-- （0≠xy ），其中第6个式子是，第n 个式子是（n 为正整数）．三、解答题（共5道小题，每小题5分，共25分） 130(1)2sin 602-π++- ．14．已知310x -=，求代数式22()(31)4x x x x x -+++的值．15．解分式方程：26111x x x -=+-．16．已知：如图，在矩形ABCD 中，点E 、F 在 AD 上，AE DF =，连接BE 、CF ．求证：BE CF =．17．已知方程组24,5x y x y +=⎧⎨-=⎩的解为,.x m y n =⎧⎨=⎩又知点(),A m n 在双曲线()0ky k x =≠上，求该双曲线的解析式．四、解答题（共2道小题，每小题5分，共10分）18．如图，在梯形ABCD 中，AD BC ∥，90A ∠=︒，︒=∠45C ，E 是CD 的中点，24AB AD ==，求BE 的长．AB FDCE19．如图，点A B F 、、在O 上，30AFB ∠=︒，OB 的延长线交直线AD 于点D ，过点B 作BC AD ⊥于C ，60CBD ∠=︒，连接AB . （1）求证：AD 是O 的切线；（2）若6AB =，求阴影部分的面积.五、解答题（本题满分6分）20．某校欲从甲、乙、丙三名候选人中挑选一名作为学生会主席，根据设定的录用程序，首先，随机抽取校内200名学生对三名候选人进行投票选举，要求每名学生最多推荐一人. 投票结果统计如下：200名学生投票结果统计图三名候选人得票情况统计图其次，对三名候选人进行了笔试和面试两项测试，成绩如下表所示：测试项目测试成绩（分）甲乙丙笔试 75 80 90 面试937068请你根据以上信息解答下列问题：（1）补全图1和图2；（2）若每名候选人得一票记1分，根据投票、笔试、面试三项得分按3:4:3的比例确定个人综合成绩，综合成绩高的被录用，请你分析谁将被录用.六、解答题（共2道小题，21题5分，22题4分，共9分） 21．列方程或方程组解应用题：为保证学生有足够的睡眠，政协委员于今年两会向大会提出一个议案，即“推迟中小学生早晨上课时间”，这个议案当即得到不少人大代表的支持. 根据北京市教委的要求，学生小强所在学校将学生到校时间推迟半小时. 小强原来7点从家出发乘坐公共汽车，7点20分到校；现在小强若由父母开车送其上学，7点45分出发，7点50分就到学校了. 已知小强乘自家车比乘公交车平均每小时快36千米，求从小强家到学校的路程是多少千米？22．请阅读下列材料：弃权2%乙38% 丙 %甲25%图1 图2乙图3lC ABP A 'D问题：如图1，点,A B 在直线l 的同侧，在直线l 上找一点P ，使得AP BP +的值最小. 小明的思路是：如图2，作点A 关于直线l 的对称点A '，连接A B '，则A B '与直线l 的交点P 即为所求.All图2图1AB请你参考小明同学的思路，探究并解决下列问题：（1）如图3，在图2的基础上，设AA '与直线l 的交点为C ，过点B 作BD ⊥l ，垂足为D . 若1CP =，2PD =，1AC =，写出AP BP +的值；（2）将（1）中的条件“1AC =”去掉，换成“4BD AC =-”，其它条件不变，写出此时AP BP +的值；（3）请结合图形，直接写出.七、解答题（本题满分7分）23．已知：关于x 的一元二次方程2220kx x k ++-=．（1）若原方程有实数根，求k 的取值范围；（2）设原方程的两个实数根分别为1x ，2x ． ①当k 取哪些整数时，1x ，2x 均为整数；②利用图象，估算关于k 的方程1210x x k ++-=八、解答题（本题满分7分）24．在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴交于A B 、两点（点A 在点B 的左侧），过点A 的直线1y kx =+交抛物线于点（1）求直线AC 及抛物线的解析式；（2）若直线1y kx =+与抛物线的对称轴交于点E ，以点E 为中心将直线1y kx =+顺时针旋转90︒得到直线l ，设直线l 与y 轴的交点为P ，求APE ∆的面积；（3）若G 为抛物线上一点，是否存在x 轴上的点F ，使以B E F G 、、、为顶点的四边形为平行四边形，若存在，直接写出点F 的坐标；若不存在，请说明理由．九、解答题（本题满分8分）25.已知90AOB ∠=︒，OM 是AOB ∠的平分线．将一个直角RPS 的直角顶点P 在射线OM 上移动，点P 不与点O 重合.（1）如图，当直角RPS 的两边分别与射线OA 、OB 交于点C 、D 时，请判断PC 与PD 的数量关系，并证明你的结论；（2）如图，在（1）的条件下，设CD 与OP 的交点为点G ，且PG =，求GD OD 的值；（3）若直角RPS 的一边与射线OB 交于点D ，另一边与直线OA 、直线OB 分别交于点C 、E ，且以P 、D 、E 为顶点的三角形与OCD ∆相似，请画出示意图；当1OD =时，直接写出OP 的长.RB PCADOG SM昌平区2008—2009学年第二学期初三年级第一次统一练习数学试卷答案及评分参考一、选择题（共8道小题，每小题4分，共32分）题号 1 2 3 4 5 6 7 8 答案DDBACCBC二、填空题（共4道小题，每小题4分，共16分）题号9101112答案1x ≠ 215°136x y-,211(1)n n n x y++- 三、解答题（共5道小题，每小题5分，共25分） 130(1)2sin 602-π++-1222=+⨯+··········································································································· 4分1=． ···························································································································· 5分 14．解：22()(31)4x x x x x -+++=323234x x x x -+++ ·········································································································· 2分 =344x +． ······························································································································ 3分当310x -=时，3x =1． ······································································································ 4分原式4148=⨯+=． ·············································································································· 5分 15．解：分母因式分解，得()()61111x x x x -=++-·························································· 1分方程两边同乘()()11x x +-，得()()()1611x x x x --=+- ············································ 3分解得 5x =-． ······················································································································· 4分经检验，5x =-是原分式方程的解． ··················································································· 5分 16．证明：∵四边形ABCD 是矩形， 90A D ∴∠=∠=︒，AB DC =．………………………………………2分在AEB △和DFC △中，A BF DCE,AB DC A D AE DF =⎧⎪∠=∠⎨⎪=⎩，，AEB DFC ∴△≌△． ·········································································································· 4分 BE CF ∴=． ························································································································ 5分17．解：解方程组24,5x y x y +=⎧⎨-=⎩得3,2.x y =⎧⎨=-⎩…………………………………………2分∴点A 的坐标为()3,2-． ··································································································· 3分 ∵点(3,2)A -在双曲线ky x=上， 2.3k ∴-=解得6k =-． ························································································································· 4分∴该双曲线的解析式为6y x=-． ························································································· 5分四、解答题（共2道小题，每小题5分，共10分）18．解：如图，分别过点D E 、作DF BC ⊥于点F ，EH BC ⊥于点H ． ∴EH DF ∥，90DFB DFC EHB EHC ∠=∠=∠=∠=︒．又90A ∠=︒，AD BC ∥，90ABC ∴∠=︒ .∴四边形ABFD 是矩形． ∵24AB AD ==,2AD ∴=．2BF AD ∴==，4DF AB ==． ······················ 1分在Rt DFC △中，45C ∠=，4FC DF ∴==． ················································································································· 2分又∵E 是CD 的中点，122EH DF ∴==． ············································································································· 3分2HC EH ∴==． 2FH ∴=．4BH ∴=． ··························································································································· 4分在Rt EBH △中，BE ∴== ······································································· 5分 19．（1）证明：如图，连结OA ． 30AFB ∠=︒ , 点F 在⊙O 上，ABCD EHF60AOB ∴∠=︒． 60CBD ∠=︒ , CBD AOB ∴∠=∠．OA ∴∥BC ．…………………1分又BC AD ⊥ , OA AD ∴⊥ ． ∵点A 在O 上，∴AD 是O 的切线． ·········································································································· 2分（2）解：∵60AOB ∠=︒，OA OB =， OAB ∴∆是等边三角形． ∵6AB =，6OA AB ∴==．在Rt OAD △中，90OAD ∠=，tan ADAOD OA∴∠=，6tan60AD ∴=︒= ．162OAD S ∆∴=⨯=． ·························································································· 3分26066360AOBS ππ⨯⨯== 扇形， ··························································································· 4分6S π∴=阴影． ··········································································································· 5分五、解答题（本题满分6分）20．解：（1）图1中，丙得票所占的百分比为35%． ························································· 1分补全图2见下图． ················································································································· 2分三名候选人得票情况统计图（2）∵5030%7540%9330%72.930%40%30%x ⨯+⨯+⨯==++甲，7630%8040%7030%75.830%40%30%x ⨯+⨯+⨯==++乙，7030%9040%6830%77.430%40%30%x ⨯+⨯+⨯==++丙． ································································ 5分∴丙被录用． ·························································································································· 6分六、解答题（共2道小题，21题5分，22题4分，共9分）21．解：设小强乘公交车的平均速度是每小时x 千米，则小强乘自家车的平均速度是每小时(36)x +千米． ······················································································································· 1分依题意，得205(36)6060x x =+． ·························································································· 2分解得12x =．·························································································································· 3分2012460∴⨯=．······················································································································ 4分答：从小强家到学校的路程是4千米． ················································································ 5分 22．解：（1）AP BP +的值为·················································································· 2分（2）AP BP +的值为5． ····································································································· 3分（3················································ 4分七、解答题（本题满分7分）23．解：（1）∵一元二次方程2220kx x k ++-=有实数根，()2k 0,2420.k k ≠⎧⎪∴⎨-⨯⨯-≥⎪⎩ ··································································································· 1分 ()2k 0,410.k ≠⎧⎪∴⎨-≥⎪⎩ ∴当0k ≠时，一元二次方程2220kx x k ++-=有实数根． ············································ 2分（2）①由求根公式，得1(1)k x k-±-=．1221k x k k-∴==-，21x =-．…………………3分要使1x ，2x 均为整数，2k必为整数，所以，当k 取12±±、时，1x ，2x 均为整数． ……………………………………5分 ②将121x k=-，21x =-代入方程 1210x x k ++-=中，得21k k=-．设12y k =，21y k =-，并在同一平面直角坐标系中分别画出12y k=与21y k =-的图象（如。

北京市各区2011年中考一模数学试题分类汇编专题五图形与证明

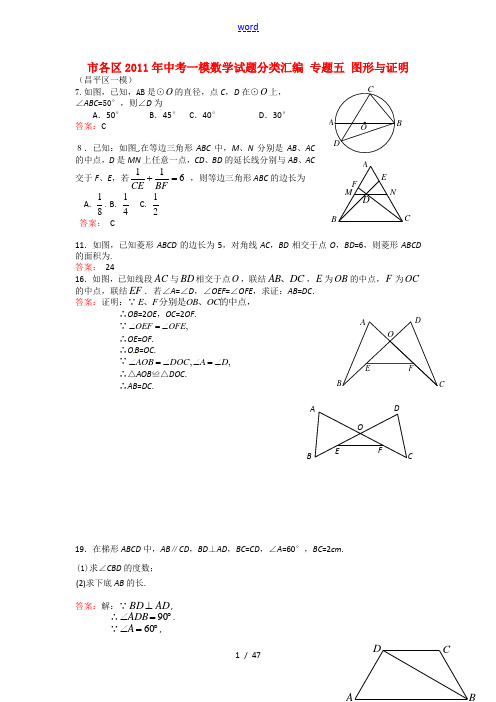
ODCBA 市各区2011年中考一模数学试题分类汇编专题五图形与证明（昌平区一模）7.如图，已知，AB 是⊙O 的直径，点C ，D 在⊙O 上， ∠ABC =50°，则∠D 为A ．50°B ．45°C ．40°D ．30° 答案：C８．已知：如图,在等边三角形ABC 中，M 、N 分别是AB 、AC 的中点，D 是MN 上任意一点，CD 、BD 的延长线分别与AB 、AC交于F 、E ，若116CE BF+= ，则等边三角形ABC 的边长为A. 81B. 14C. 21答案： C11．如图，已知菱形ABCD 的边长为5，对角线AC ，BD 相交于点O ，BD =6，则菱形ABCD 的面积为. 答案： 2416．如图，已知线段AC 与BD 相交于点O ，联结AB DC 、，E 为OB 的中点，F 为OC 的中点，联结EF ．若∠A =∠D ，∠OEF =∠OFE ，求证：AB =DC ．答案：证明：∵E F OB OC 、分别是、的中点，∴OB =2OE ，OC =2OF .∵,OEF OFE ∠=∠∴OE =OF . ∴O B =OC .∵,,AOB DOC A D ∠=∠∠=∠∴△AOB ≌△DOC .∴AB =DC .19．在梯形ABCD 中，AB ∥CD ，BD ⊥AD ，BC =CD ，∠A =60°，BC =2cm . (1)求∠CBD 的度数； (2)求下底AB 的长.答案：解：∵AD BD ⊥,∴︒=∠90ADB . ∵︒=∠60A ,OD CABEFNMC B A E DFOFA B CD E∴︒=∠30ABD ∵AB ∥CD ,∴︒=∠=∠30CBD ABD ∵BC=CD,∴︒=∠=∠30CBD CDB ∴︒=∠60ABC . ∴ABC A ∠=∠.∴梯形ABCD 是等腰梯形. ∴AD=BC =2.在中，︒=∠90ADB ，︒=∠30ABD ， ∴AB=2AD=4.20．如图所示，AB 是⊙O 的直径，OD ⊥弦BC 于点F ，且交⊙O 于点E ，若∠AEC =∠ODB ．（1）判断直线BD 和⊙O 的位置关系，并给出证明；（2）当AB =10，BC =8时，求BD 的长．答案：1）答：BD 和⊙O 相切.证明：∵OD ⊥BC ,∴∠OFB =∠BFD =90°, ∴∠D +∠3=90°.∵∠4=∠D =∠2, ∴∠2+∠3=90°, ∴∠OBD =90°,即OB ⊥BD . ∵点B 在⊙O 上， ∴BD 和⊙O 相切.(2) ∵OD ⊥BC ,BC =8,∴BF =FC =4.∵AB =10,∴OB =OA =5.在R t △OFB 中, ∠OFB =90°, ∵OB =5,BF =4,∴OF =3.∴tan ∠1=34=OF BF . 在R t △OBD 中, ∠OBD =90°,∵tan ∠1=34=OB BD , OB =5, ∴320=BD24．已知，点P 是∠MON 的平分线上的一动点，射线PA 交射线OM 于点A ，将射线PA 绕点P 逆时针旋转交射线ON 于点B ，且使∠APB + ∠MON =180°.（1）利用图1，求证：PA =PB ；（2）如图2，若点C 是AB 与OP 的交点，当 3POB PCB S S ∆∆=时，求PB 与PC 的比值；（3）若∠MON =60°，OB =2，射线AP交ON 于点D ，且满足且PBD ABO ∠=∠，请借助图3补全图形，并求OP 的长.3214FODBCE APMT图1TNBPOA答案：解：（1）在OB 上截取OD =OA ，连接PD ，∵OP 平分∠MON ， ∴∠MOP =∠NOP ．又∵OA =OD ，OP =OP ， ∴△AO P ≌△DO P ．∴PA =PD ，∠1=∠2．∵∠APB +∠MON =180°， ∴∠1+∠3=180°． ∵∠2+∠4=180°，∴∠3=∠4． ∴PD =PB ．∴PA =PB ．（2）∵PA =PB ，∴∠3=∠4．∵∠1+∠2+∠APB =180°，且∠3+∠4+∠APB =180°，∴∠1+∠2=∠3+∠4．∴∠2=∠4． ∵∠5=∠5， ∴△PBC ∽△POB ． ∴33P S =∆∆=POB S BC PB PC ．（3）作BE ⊥OP 交OP 于E ，∵∠AOB =600，且OP 平分∠MON ， ∴∠1=∠2=30°．∵∠AOB +∠APB =180°， ∴∠APB =120°． ∵PA =PB ，∴∠5=∠6=30°． ∵∠3+∠4=∠7，∴∠3+∠4=∠7=(180°-30°)÷2=75°． ∵在Rt △OBE 中，∠3=600，OB =2D 1234AO P M N T51243T NMP OA C7612435ECAOPBM NT图2图3TN B P A C∴∠4=150，OE =3，BE =1 ∴∠4+∠5=450，∴在Rt △BPE 中，EP =BE =1 ∴OP =13+（某某区一模）11．如图，△ABC 内接于⊙O ，AC 是⊙O 的直径，∠ACB =40°，点D 是弧BAC 上一点，则∠D 的度数是______．答案：50°18．如图，在矩形ABCD 中，AB =5，BC =4，将矩形ABCD 翻折，使得点B 落在CD 边上的点E 处，折痕AF 交BC 于点F ，求FC 的长．FEDABC答案：解：由题意，得AE=AB=5,AD=BC=4,EF=BF.在Rt △ADE 中，由勾股定理，得DE=3. 在矩形ABCD 中，DC=AB=5. ∴CE=DC-DE=2. 设FC=x ，则EF=4-x.在Rt △CEF 中，()22242x x -=+.解得23=x . 即FC=23.21．已知：如图，⊙O 的半径OC 垂直弦AB 于点H ，连接BC ，过点A 作弦AE ∥BC ，过点C作CD ∥BA 交EA 延长线于点D ，延长CO 交AE 于点F ．（1）求证：CD 为⊙O 的切线；（2）若BC ＝5，AB ＝8，求OF 的长．答案：（1）证明：∵OC ⊥AB ，CD ∥BA ，∴∠DCF=∠AHF=90°.∴CD 为⊙O 的切线.（2）解：∵OC ⊥AB ，AB ＝8，∴AH=BH=2AB =4.在Rt △BCH 中，∵BH=4，BC=5， ∴CH=3.E O B HC AD F EO BHC ADF40︒OAB C∵AE ∥BC ，∴∠B=∠HAF. ∴△HAF ≌△HBC. ∴FH=CH=3，CF=6.连接BO ，设BO=x ，则OC=x ，OH=x-3.在Rt △BHO 中，由()22234x x =-+，解得625=x ∴611=-=OC CF OF .23．如图，在直角梯形ABC D 中，AD ∥BC ，∠B =90°，AB =8，34tan =∠CAD ，CA =CD ，E 、F分别是线段AD 、AC 上的动点（点E 与点A 、D 不重合），且∠FEC =∠ACB ，设DE=x ，CF=y . （1）求AC 和AD 的长；（2）求y 与x 的函数关系式；（3）当△EFC 为等腰三角形时，求x 的值.答案：解：（1）∵AD ∥BC ，∠B=90°， ∴∠ACB=∠CAD. ∴tan ∠ACB =tan ∠CAD=34. ∴34=BC AB . ∵AB=8，∴BC=6. 则AC=10过点C 作CH ⊥AD 于点H ，∴CH=AB=8,则AH=6. ∵CA=CD, ∴AD=2AH=12.（2）∵CA=CD, ∴∠CAD=∠D. ∵∠FEC=∠ACB ，∠ACB=∠CAD ， ∴∠FEC=∠D.∵∠AEC=∠1+∠FEC=∠2+∠D ， ∴∠1=∠2.∴△AEF ∽△DCE. ∴AECDAF DE =，即x -1210y -10x =. F CBDAE∴1056101y 2+-=x x . （3）若△EFC 为等腰三角形.①当EC=EF 时，此时△AEF ≌△DCE ，∴AE=CD. 由12-x=10，得x=2.②当FC=FE 时，有∠FCE=∠FEC=∠CAE ， ∴CE=AE=12-x.在Rt △CHE 中，由()()2228612+-=-x x ，解得311=x ③当CE=CF 时，有∠CFE=∠CEF=∠CAE ，此时点F 与点A 重合，故点E 与点D 也重合，不合题意，舍去综上，当△EFC 为等腰三角形时，x=2或311=x .7．一元钱硬币的直径约为24mm ，则用它能完全覆盖住的正六边形的边长最大不能超过 A ．12 mm B ．123mm C ．6mm D ．63mm 答案：A答案：（1）证明：∵AD ∥BC ， ∴∠1 =∠F ． ∵点E 是AB 的中点， ∴BE=AE.在△BCE 和△AFE 中， ∠1=∠F ，∠3=∠2， BE=AE ，∴△BCE ≌△AFE. （2）相等，平行.（大兴区一模）3．如图，△ABC 中，D 、E 分别为AC 、BC 边上的点，AB ∥DE ，若AD ＝5，CD ＝3，DE ＝4，则AB 的长为 A ．332B ．316C ．310D ．38答案：A321FE BCA D7．如图3，四边形OABC 为菱形，点A 、B 在以点O 为圆心的弧DE 上，若OA=3，∠1=∠2,则扇形ODE 的面积为A.3π2B. 2πC.5π2D. 3π 答案：D11．如图，AB 是⊙O 的直径，C 、D 、E 都是⊙O 上的点，则∠ACE ＋∠BDE ＝．答案： 90º .15．已知，在△ABC 中，D E ∥AB ，F G ∥AC ，BE=GC. 求证：DE=FB.答案：证明：∵DE ∥AB ∴∠B=∠DEC又∵FG ∥AC ∴∠FGB=∠C ∵BE=GC∴BE+EG=GC+EG 即BG=EC在△FBG 和△DEC 中⎪⎩⎪⎨⎧∠=∠=∠=∠C FGB ECBG DEC B ∴△FBG ≌△DEC∴DE=FB19．已知：如图，在直角梯形ABCD 中，AD ∥BC,∠A=90°,∠C=45°，上底AD = 8，AB=12,CD 边的垂直平分线交BC 边于点G ，且交AB 的延长线于点E ，求AE 的长. 答案：解：联结DG∵EF 是CD 的垂直平分线 ∴DG =CG∴∠GDC =∠C , 且∠C =45° ∴∠DGC=90°∵AD ∥BC,∠A=90° ∴∠ABC=90°∴四边形ABGD 是矩形 ∴BG=AD=8∴∠FGC =∠BGE =∠E= 45° ∴BE=BG=8 ∴AE=AB+BE=12+8=20∠x+∠y 的度数，并加以证明.答案：∠x +∠y =45°.证明：如图，以AG 所在直线为对称轴，作AC 的轴对称图形AF ，连结BF ，∵网格中的小正方形边长为1，且A 、B 、F 均在格点处， ∴AB=BF =13，AF =26.∴222BF AB AF +=∴△ABF 为等腰直角三角形，且∠ABF =90°G FE DCB A 21E DCB AOEGFEDCBA∴∠BAF=∠BFA =45°.∵AF 与AC 关于直线AG 轴对称， ∴∠FAG =∠CAG. 又∵AG ∥EC ， ∴∠x =∠CAG . ∴∠x =∠FAG. ∵DB ∥AG ， ∴∠y =∠BAG.∴∠x +∠y=∠FAG+∠BAG =45°.23．在平面直角坐标系xOy 中，矩形ABCO 的面积为15，边OA 比OC 大2，E 为BC 的中点，以OE 为直径的⊙O ′交x 轴于D 点，过点D 作DF ⊥AE 于F. （1）求OA ，OC 的长；（2）求证：DF 为⊙O ′的切线；（3）由已知可得，△AOE 是等腰三角形.那么在直线BC 上是否存在除点E 以外的点P ，使△AOP 也是等腰三角形？如果存在，请你证明点P 与⊙O ′的位置关系，如果不存在，请说明理由. 答案：（1）解：在矩形ABCO 中，设OC=x ，则OA=x +2，依题意得，x(x+2)=15.解得.5,321-==x x （不合题意，舍去） ∴OC=3 ，OA =5 .（2）证明：连结O ′D ，在矩形OABC 中， ∵ OC=AB ，∠OCB =∠ABC ，E 为BC 的中点，∴△OCE ≌△ABE . ∴EO=EA .∴∠EOA =∠EAO . 又∵O ′O = O ′D ，∴∠O ′DO =∠EOA =∠EAO . ∴ O ′D ∥EA . ∵DF ⊥AE ， ∴DF ⊥O ′D .又∵点D 在⊙O ′上，O ′D 为⊙O ′的半径， ∴DF 为⊙O ′的切线. （3）答：存在 .① 当OA=AP 时，以点A 为圆心，以AO 为半径画弧，交BC 于点1P 和4P 两点，则△AO 1P 、△AO 4P 均为等腰三角形.证明：过1P 点作1P H ⊥OA 于点H ，则1P H =OC=3， ∵A 1P =OA=5，∴AH =4，OH=1.y x O 'F EDCBAO∴1P （1,3）.∵1P （1,3）在⊙O ′的弦CE 上，且不与C 、E 重合， ∴ 点1P 在⊙O ′内. 类似可求4P （9,3）. 显然，点4P 在点E 的右侧， ∴点4P 在⊙O ′外.② 当OA=OP 时，同①可求得，2P （4,3），3P （-4,3）. 显然，点2P 在点E 的右侧，点3P 在点C 的左侧因此，在直线BC 上，除了E 点外，还存在点1P ，2P ，3P ，4P ，它们分别使△AOP 为等腰三角形，且点1P 在⊙O ′内，点2P 、3P 、4P 在⊙O ′外.24．已知：如图，在四边形ABCD 中，AD =B C ,∠A 、∠B 均为锐角． (1) 当∠A=∠B 时，则C D 与A B 的位置关系是CDAB ，大小关系是CDAB ； (2) 当∠A>∠B 时，（1）中C D 与A B 的大小关系是否还成立，证明你的结论．答案：解：（1）答：如图1，CD ∥AB ，C D <A B ．（2）答：C D <A B 还成立．证法1：如图2，分别过点D 、B 作BC 、C D 的平行线，两线交于F 点．∴ 四边形DCBF 为平行四边形． ∴.,FB DC BC FD == ∵AD =B C ， ∴AD =FD ．作∠ADF 的平分线交A B 于G 点，连结GF ． ∴ ∠ADG =∠FDG ．在△ADG 和△FDG 中⎪⎩⎪⎨⎧=∠=∠=,,,DG DG FDG ADG FD AD ∴△ADG ≌△FDG ． ∴AG =FG ．∵在△BFG 中，BF BG FG >+． ∴.DC BG AG >+ ∴DC <A B ．证法2：如图3，分别过点D 、B 作A B 、AD 的平行线，两线交于F 点．∴ 四边形DABF 为平行四边形． ∴.,BF AD AB DF == ∵A D =B C ， ∴B C =BF ．作∠CBF 的平分线交DF 于G 点，连结C G ．D CBA以下同证法 112．.将一个面积为1的等边三角形挖去连接三边中点所组成的三角形（如第①图）后，继续挖去连接剩余各个三角形三边中点所成的三角形（如第②图、第③图）…如此进行挖下去，第④个图中，剩余图形的面积为，那么第n(n 为正整数)个图中，挖去的所有三角形形的面积和为（用含n 的代数式表示）.(3)若该公司购买全部门票共花了36000元，试求每X 田径门票的价格．答案：⎪⎭⎫ ⎝⎛25681)43(4或， n）（431-.22．一块矩形纸片，利用割补的办法可以拼成一块与它面积相等的平行四边形（如图1所示）：请你根据图1作法的提示，利用图2画出一个平行四边形，使该平行四边形的面积等于所给的矩形面积.要求：（1）画出的平行四边形有且只有一个顶点与B 点重合；（2）写出画图步骤；（3）写出所画的平行四边形的名称.答案：解：（1）过点C 作射线CE （不过A 、D 点）；（2）过点B 作射线BF ∥CE ，且交DA 的延长线于点F ；（3）在CE 上任取一点G ，连结BG ；（4）过点F 作FE ∥BG ，交射线CE 于点E .则四边形BGEF 为所画的平行四边形.（东城区一模）3．如图，直线AB ∥CD ，∠A ＝70︒，∠C ＝40︒，则∠E 等于A. 30°B.40°C.60° D .70° 答案：A4．如图，在△ABC 中，D 、E 分别是BC 、AC 边的中点．若DE =2，则AB 的长度是图1D'D CBA图2DCBAA．6 B．5C．4 D．3答案：C6．已知圆锥的母线长为4，底面半径为2，则圆锥的侧面积等于A．11πB．10πC．9πD．8π答案：D8. 如图，在矩形ABCD中，AB=5，BC=4，E、F分别是AB、AD的中点.动点R从点B出发，沿B→C→D →F方向运动至点F处停止．设点R运动的路程为x，EFR△的面积为y，当y取到最大值时，点R应运动到A．BC的中点处B．C点处C．CD的中点处D．D点处答案：B16. 如图，在四边形ABCD中，AC是∠DAE的平分线，DA∥CE，∠AEB=∠CEB.求证：AB=CB.答案：证明：∵AC 是∠DAE的平分线，∴∠1=∠2.又∵AD∥EC，∴∠2=∠3.∴∠1=∠3.∴AE=CE.在△ABE和△CBE中，，∠AEB=∠CEB，，∴△ABE≌△CBE.∴AB=CB.18．如图，在平行四边形ABCD中，过点A分别作AE⊥BC于点E，AF⊥CD于点F．（1）求证：∠BAE=∠DAF；（2）若AE=4，AF=245，3sin5BAE∠=，求CF的长．答案：证明：（1）∵四边形ABCD是平行四边形，A BCDE231D∴∠B=∠D. 又AE ⊥BC ，AF ⊥CD ，∴∠AEB=∠AFD. ∴∠BAE=∠DAF.（2）在Rt △ABE 中，sin ∠BAE=53，AE=4,可求 AB=5. 又∵∠BAE=∠DAF ， ∴ sin ∠DAF=sin ∠BAE=53. 在Rt △ADF 中，AF=524, sin ∠DAF =53,可求DF=518∵ CD=AB=5. ∴CF=5-518=57．20.已知：AB 是⊙O 的弦，OD ⊥AB 于M 交⊙O 于点D ，CB ⊥AB 交AD 的延长线于C ．（1）求证：AD ＝DC ；（2）过D 作⊙O 的切线交BC 于E ，若DE ＝2，CE=1，求⊙O 的半径．答案：（1）证明：在⊙O 中，OD ⊥AB ，CB ⊥AB ，∴AM ＝MB ，OD ∥BC . ∴AD ＝DC .（2）∵DE 为⊙O 切线，∴OD ⊥DE∴四边形MBED 为矩形. ∴DE ∥AB. ∴MB=DE =2，M D=BE ＝EC =1. 连接OB.在R t △OBM 中，OB 2=OM 2+BM 2.解得 OB=25.22. 如图1，在△ABC 中，已知∠BAC ＝45°，AD ⊥BC 于D ，BD ＝2，DC ＝3，求AD 的长. 小萍同学灵活运用轴对称知识，将图形进行翻折变换如图1.她分别以AB 、AC 为对称轴，画出△ABD 、△ACD 的轴对称图形，D 点的对称点为E 、F ，延长EB 、FC 相交于G 点，得到四边形AEGFAD =x ，利用勾股定理，建立关于x 的方程模型，求出x 的值. （1）请你帮小萍求出x 的值.M O A B C D E(2) 参考小萍的思路，探究并解答新问题：如图2，在△ABC 中，∠BAC ＝30°，AD ⊥BC 于D ，AD ＝4.请你按照小萍的方法画图,得到四边形AEGF ，求△BGC 的周长.（画图所用字母与图1中的字母对应）图1 图2答案：解：（1）设AD =x ，由题意得，BG=x －2，CG=x-3. 在Rt △BCG 中，由勾股定理可得 222(2)(3)5x x -+-=. 解得 6x =.（2）参考小萍的做法得到四边形AEGF ，∠EAF=60°，∠EGF=120°，∠AEG=∠AFG= 90°，AE=AF=AD=4. 连结EF ，可得 △AEF 为等边三角形. ∴ EF=4.∴∠FEG=∠EFG= 30°. ∴ EG=FG.在△EFG 中，可求，433EG =. ∴△EFG 的周长＝BG+CG+BC=BG+CG+EB+FC=2EG=833（房山区一模）GF ED CBAABA4．如图，AB 为圆O 的直径，弦CD AB ，垂足为点E ，联结OC ，若OC=5，AE=2，则CD 等于A ．3B ．4C ．6D ．8 答案：D11．如图，在△ABC 中，点D 、E 分别在AB 、AC 边上， DE//BC ，若AD ：AB=3：4，DE=6，则BC=________．答案： 8；15．（本小题满分5分）如图，A 、B 、C 三点在同一条直线上，AB=2BC ，分别以AB ，BC为边做正方形ABEF 和正方形BCMN ，联结FN ，EC ．求证：FN=EC答案：在正方形ABEF 和正方形BCMN 中 AB=BE=EF,BC=BN, FEN=EBC=90° AB=2BC EN=BC FNEEBC FN=EC 19．（本小题满分5分）在△ABC 中，AC=BC ，∠ACB=90°，AB=6，过点C 作射线CP ∥AB ，在射线CP 上截取CD=2，联结AD ，求AD 的长．答案：解：过点D 作DE ⊥AB 于E ，过点C 作CF ⊥AB 于F ，则DE ∥CF ∵CP ∥AB ，∴四边形DEFC 是矩形∵在△ABC 中，AC=BC ，∠ACB=90°，AB=6，CD=2∴AF=CF=12AB=3 ∴EF=CD=2,DE=CF=3 ∴AE=1在△ADE 中，∠AED=90°,DE =3,AE=1 ∴20．（本小题满分5分）已知：如图，在△ABC 中，AB=AC ，以AB 为直径的⊙O 分别交BC 、AC 于点D 、E ，联结EB 交OD 于点F ．（1）求证：OD ⊥BE ；（2）若AB=5，求AE 的长．答案：解：（1）联结AD∵AB 是⊙O 的直径，∴∠ADB=∠AEB=90°--- 1分FE P D CBA∵AB=AC ，∴CD=BD ∵OA=OB ，∴OD//AC ∴OD ⊥BE（2）方法一：∵∠CEB=∠AEB=90°，∴,在△ABE 、△BCE 中，∠CEB=∠AEB=90°，则有2222AB AE BC EC -=- 设AE=x,则(()222255x x -=--解得：x=3 ∴AE=3方法二：∵OD ⊥BE ，∴BD=DE ，BF=EF 设AE=x,∴OF=12x ，在△OBF 、△BDF 中，∠OFB=∠BFD=90° ∴2222BD DF OB OF -=-∵AB=5，∴22225151()()()2222x x --=- 解得：x=3，∴AE=3 方法三：∵BE ⊥AC AD ⊥BC, ∴S △ABC =21BC ·AD=21AC ·BE, ∴BC ·AD=AC ·BE∵AC=AB=5∴BE=4 , ∴AE=325．（本小题满分7分）已知：等边三角形ABC（1）如图1，P 为等边△ABC 外一点，且∠BPC=120°．试猜想线段BP 、PC 、AP 之间的数量关系,并证明你的猜想；（2）如图2，P 为等边△ABC 内一点，且∠APD=120°．CABPEC PB A B’C A B PD O D C BA 求证：PA+PD+PC ＞BD答案：猜想：AP=BP+PC（1）证明：延长BP 至E ，使PE=PC ，联结CE ∵∠BPC=120°∴∠CPE=60°，又PE=PC∴△CPE 为等边三角形∴CP=PE=CE ，∠PCE=60° ∵△ABC 为等边三角形 ∴AC=BC ，∠BCA=60°∴∠ACB=∠PCE ，∴∠ACB+∠BCP=∠PCE+∠BCP 即：∠ACP=∠BCE∴△ACP ≌△BCE ∴AP=BE ∵BE=BP+PE∴AP=BP+PC（2）方法一：在AD 外侧作等边△AB ′D 则点P 在三角形ADB ′外∵∠APD=120°∴由（1）得PB ′=AP+PD 在△PB ′C 中，有PB ′+PC ＞CB ′，∴PA+PD+PC ＞CB ′∵△AB ′D 、△ABC 是等边三角形∴AC=AB ，AB ′=AD ，∠BAC=∠DA B ′=60° ∴∠BAC+∠CAD=∠DAB ′+∠CAD即：∠BAD=∠CAB ′∴△AB ′C ≌△ADB∴C B ′=BD∴PA+PD+PC ＞BD方法二：延长DP 到M 使PM=PA ，联结AM 、BM ∵∠APD=120°，∴△APM 是等边三角形， ∴AM=AP ，∠PAM=60°∴DM=PD+PA∵△ABC 是等边三角形∴AB=AC ，∠BAC=60° ∴△AMB ≌△APC∴BM=PC在△BDM 中，有DM + BM ＞BD ， ∴PA+PD+PC ＞BD（丰台区一模）11．如图，AB 为⊙O 的弦，⊙O 的半径为5，OC ⊥AB 于点D ，交⊙O 于点C ，且CD ＝l ，则弦AB 的长是．答案：6 19.已知:如图，在四边形ABFC 中，ACB =90°,BC 的垂直平分线EF 交BC 于点D,交ABM P D C B AA BCAB CABCDEFO F E DCB A 321AB CDEF于点E,且CF=AE.(1) 求证：四边形BECF 是菱形；(2) 当A ∠的大小为多少度时,四边形BECF 是正方形？答案：解：⑴∵EF 垂直平分BC, ∴CF=BF,BE=CE ，∠BDE=90°又∵∠ACB=90°∴EF ∥AC∴E 为AB 中点，即BE=AE ∵CF=AE ∴CF=BE ∴CF=FB=BE=CE ∴四边形是BECF 菱形.⑵当∠A= 45°时，四边形是BECF 是正方形.20．在Rt △AFD 中，∠F =90°，点B 、C 分别在AD 、FD 上，以AB 为直径的半圆O 过点C ，联结AC ，将△AFC 沿AC 翻折得△AEC ，且点E 恰好落在直径AB 上.（1）判断：直线FC 与半圆O 的位置关系是_______________；并证明你的结论. （2）若OB =BD =2,求CE 的长．答案：（1）直线FC 与⊙O 的位置关系是_相切_；证明：联结OC ∵OA=OC ，∴∠1=∠2，由翻折得，∠1=∠3，∠F=∠AEC=90° ∴∠3=∠2∴OC ∥AF ，∴∠F=∠OCD=90°，∴FC 与⊙O 相切（2）在Rt △OCD 中，cos ∠COD=OC 1OD 2=∴∠COD=60°在R t △OCD 中，CE=OC ·sin ∠322．认真阅读下列问题，并加以解决：问题1：如图1，△ABC 是直角三角形，∠C =90º．现将△ABC 补成一个矩形．要求：使△ABC 的两个顶点成为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上．请将符合条件的所有矩形在图1中画出来；图1 图2问题2：如图2，△ABC 是锐角三角形，且满足BC ＞AC ＞AB ，按问题1中的要求把它补成矩形．请问符合要求的矩形最多可以画出个，并猜想它们面积之间的数量关系是（填写“相等”或“不相等”）；问题3：如果△ABC 是钝角三角形，且三边仍然满足BC ＞AC ＞AB ，现将它补成矩形．要求：△ABC 有两个E DCB A 顶点成为矩形的两个顶点，第三个顶点落在矩形的一边上,那么这几个矩形面积之间的数量关系是（填写“相等”或“不相等”）．答案：解：（1）（2）符合要求的矩形最多可以画出3个，它们面积之间的数量关系是相等；………4’ (3) 不相等．15. 已知：如图，∠B =∠D ，∠DAB=∠EAC ，AB=AD ．求证：BC=DE ．答案：证明：∵∠DAB=∠EAC∴∠DAB+∠BAE =∠EAC+∠BAE∵即∠DAE=∠BAC在△DAE 和△BAC 中B DAB ADBAC DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BC=DE（燕山区一模）3．已知一个等腰三角形有两边的长分别为2和5，则它的周长为A ．7B ．9C ．12D ．9或12 答案：C10．已知⊙O 1、⊙O 2的半径分别是2cm 、3cm ，当它们相切时，圆心距O 1 O 2= ．答案：1cm 或5cm11．已知△ABC 中，D 、E 分别是两边AB 和AC 的中点，若△ABC 的面积是8cm 2，则四边形BCED 的面积是cm 2．答案：615．已知：如图，点D 在AB 的延长线上，AB ＝DE ，∠A ＝∠CBE ＝∠E. 判断△ABC 和△BDE 是否全等？并证明你的结论.答案：全等证明：∵∠CBE =∠E ， ∴ BC ∥DE.又∵点D 在AB 的延长线上，∴∠CBA=∠D.在△ABC 和△EDB 中, 又∵∠A=∠E, AB=DE, ∴△ABC ≌△EDB.21．如图，等腰△ABC 中，AE 是底边BC 上的高，点O 在AE 上，⊙O 与AB 和BC 分别相切. （1）⊙O 是否为△ABC 的内切圆？请说明理由. （2）若AB=5， BC=4，求⊙O 的半径. 答案：⑴是理由是：∵⊙O 与AB 相切，把切点记作D.联结OD ，则OD ⊥AB 于D. 作OF ⊥AC 于F ， ∵AE 是底边BC 上的高，∴AE 也是顶角∠BAC 的平分线. ∴OF=OD=r 为⊙O 的半径. ∴⊙O 与AC 相切于F.又∵⊙O 与BC 相切， ∴⊙O 是△ABC 的内切圆. ⑵∵OE ⊥BC 于E ，∴点E 是切点，即OE=r. 由题意，AB=5，BE=21AB=2， ∴ AE=222-5=21.∵Rt △AOD ∽Rt △ABE ，∴BEODAB OA =，即2r5r -21=.解得，r=7212.∴⊙O 的半径是7212.24．已知：如图，等边△ABC 中，AB=1，P 是AB 边上一动点，作PE ⊥BC ，垂足为E ；作EF ⊥AC ，垂足为F ；作FQ ⊥AB ，垂足为Q. （1）设BP=x ，AQ=y ，求y 与x 之间的函数关系式；（2）当点P 和点Q 重合时，求线段EF 的长；（3）当点P 和点Q 不重合，但线段PE 、FQ 相交时，求它们与线段EF 围成的三角形周长的取值X 围. 24.答案：⑴∵△ABC 是等边三角形，AB=1. ∴∠A=∠B=∠C=60°, BC=CA=AB=1. 又∵∠BEP=∠CFE=∠FQA=90°, BP=x.∴BE=21x, CE=1-21x, CF=21-41x, AF=1-(21-41x)=21+41x.∴AQ=21AF=21(21+41x),∴ y=81x+41. D F⑵由方程组⎪⎩⎪⎨⎧+==+.41x 81y 1,y x得x =32.∴当点P 和点Q 重合时，x =32，∴EF=3CF=3(21-41x)=33.⑶设线段PE 、FQ 相交于点M ，易证△MEF 是等边三角形，且当点P 和点A 重合时，EF 最短为43.∴433≤ m ＜3.25．已知：如图，在梯形ABCD 中，∠BCD=90°，tan ∠ADC=2，点E 在梯形内，点F 在梯形外，0.5CDABCE BE ==，∠EDC=∠FBC ，且DE=BF ．（1）判断△ECF 的形状特点，并证明你的结论；（2）若∠BEC=135°，求∠BFE 的正弦值．答案：答案：⑴ 是等腰直角三角形. …………………………………………1分证明：作AH ⊥CD 于H ，∵梯形ABCD 中，∠BCD=90°，tan ∠ADC=2，即∠ADC ≠90°. ∴ AB ∥CD ，AH=BC ，AB=CH.又∵0.5CDAB=，即CH+DH=2AB=2CH ∴ DH=CH ，CD=2DH. ∵ tan ∠ADC=DHAH=2， ∴ AH=2DH=CD=BC. 在△EDC 和△FBC 中，又∵∠EDC=∠FBC ，DE=BF ， ∴△EDC ≌△FBC. ∴CE=CF, ∠ECD=∠FCB. ∵∠ECD+∠ECB=∠BCD=90°, ∴∠FCB+∠ECB=90°，即∠ECF=90°.∴△ECF 是等腰直角三角形. …………… ⑵∵ 在等腰Rt △ECF 中，∠ECF=90°，∴∠CEF=45°，CE=22EF. 又∵∠BEC=135°，CEBE=0.5 ，H第19题图第5题图∴∠BEF=90°，EF BE =42. 不妨设BE=2，EF= 4，则BF=18.∴sin ∠BFE=BF BE =182=31.（延庆县一模）5．如图是一X 矩形纸片ABCD ，cm 10AD =，若将纸片沿DE 折叠，使DC 落在DA 上，点C 的对应点为点F ，若cm BE 6=，则DC 的长是A ．cm 4B ．cm 6C ．cm 8D ．cm 10 答案：A11．如图,⊙O 是等边三角形ABC 的外接圆,点P 在劣弧AB 上,ABP ∠ 22=,则BCP ∠的度数为_____________.、答案：3819. 已知如图：直角梯形ABCD 中，BC AD //，90=∠BAD ，26CD ==BC ，1312sin =C , 求：梯形ABCD 的面积；答案：解：过点D 做E BC DE 于点⊥，CD=26 在DCE Rt ∆中，26DECD DE 1312sin ===C ∴DE=24∴由勾股定理得：CE=10∴BE=CD-CE=16∵90=∠BAD ，E BC DE 于点⊥ ∴DE//B C ∵BC AD //∴四边形ABED 是平行四边形 ∴AD=BE=16 ∴5042DEBC AD S ABCD =+=）（20．如图，ABC ∆是等腰三角形，AC AB =，以AC 为直径的⊙O 与BC 交于点D ，AB DE ⊥，垂足为E ，ED 的延长线与AC 的延长线交于点F ．（1）求证：DE 是⊙O 的切线；（2）若⊙O 的半径为2，1=BE ，求A cos 的值．FEDBAC答案：证明：（1）连结AD ，OD ∵AC 是直径 ∴BC AD ⊥ ∵AB=AC∴D 是BC 的中点 ∵O 是AC 的中点 ∴AB //OD ∵AB DE ⊥ ∴DE OD ⊥∴DE 是⊙O 的切线（2）由（1）可知，AE OD //∴AE ODFA FO =∴BE AB OD AC FC OC FC -=++ ∴14242-=++FC FC ∴FC=2 ∴AF=6 ∴21cos ==AF AE A15．如图，AE AB =,AC AD =,EAC BAD ∠=∠, DE BC ，交于点O . 求证：AED AB C ∠=∠. 答案：证明: ∵EAC BAD ∠=∠∴DAC EAC DAC BAD ∠+∠=∠+∠ 即:EAD BAC ∠=∠ 在EAD BAC ∆∆和 AE AB =EAD BAC ∠=∠ AC AD =∴EAD BAC ∆≅∆ ∴AED AB C ∠=∠（西城区一模）7．如图，在梯形ABCD 中，AB ∥CD ，∠A =60°，∠B =30°，若AD =CD =6，则AB 的长等于（）．A ．9B ．12C ．633+D ．18答案：D8．如图，点A 在半径为3的⊙O 内，3，P 为⊙O 上一点，当∠OPA 取最大值时，PA 的长等于（）.A ．32B ．6C ．32D ．23答案：B10．如图，甲、乙两盏路灯相距20米. 一天晚上，当小明从路灯甲走到距路灯乙底部4米处时，发现自己的身影顶部正好接触到路灯乙的底部．已知小明的身高为，那么路灯甲的高为米．答案: 816. 如图，在四边形ABCD 中，AB =BC ，BF 平分∠ABC ，AF ∥DC ，连接AC ，CF . 求证：（1）AF =CF ；（2）CA 平分∠DCF . 答案：证明：如图2.（1）∵BF 平分ABC ∠，∴ABF CBF ∠=∠．在△ABF 与△CBF 中，,,,AB CB ABF CBF BF BF =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△CBF ． ∴AF CF =．（2）∵AF CF =，∴FCA FAC ∠=∠． ∵AF ∥DC ，∴FAC DCA ∠=∠．∴FCA DCA ∠=∠，即CA 平分DCF ∠．20．如图，四边形ABCD 是边长为9的正方形纸片，B '为CD 边上的点，C B '=3．将纸片沿某条直线折叠，使点B 落在点B '处，点A 的对应点为A '，折痕分别与A D ，BC 边交于点M ，N ．（1）求BN 的长；（2）求四边形ABNM 的面积. 答案：解：如图3．（1）由题意，点A 与点A '，点B 与点B '分别关于直线MN 对称， ∴AM A M '=，BN B N '=．设BN B N x '==，则9CN x =-． ∵ 正方形ABCD ， ∴o 90C ∠=．∴222CN B C B N ''+=．∵C B '=3，∴222(9)3x x -+=．图2解得5x =．∴5BN =．（2）∵ 正方形ABCD ，∴AD ∥BC ，o 90A ∠=．∵ 点M ，N 分别在AD ，BC 边上， ∴四边形ABNM 是直角梯形． ∵'5BN B N ==，9BC =，∴4NC =．∴4sin 15∠=，4tan 13∠=． ∵1290∠+∠=︒，2390∠+∠=︒， ∴31∠=∠．∴4sin 3sin 15∠=∠=．在Rt △ DB P '中，∵90 D ∠=︒，6DB DC B C ''=-=，4sin 35DB PB '∠=='， ∴152PB '=． ∵9A B AB ''==，∴32A P AB PB ''''=-=． ∵43∠=∠， ∴4tan 4tan 33∠=∠=．在Rt △ A MP '中，∵90 A A '∠=∠=︒，32A P '=，4tan 43A M A P '∠=='， ∴2A M '=．…………………………………………………………………4分 ∴1163()(25)9222ABNM S AM BN AB =+⨯=⨯+⨯=梯形．…………………5分21．如图，D 是⊙O 的直径CA 延长线上一点，点 B 在⊙O 上，且AB ＝AD ＝AO ．（1）求证：BD 是⊙O 的切线；（2）若E 是劣弧BC 上一点，AE 与BC 相交于点F ， △BEF 的面积为8，且cos ∠BFA ＝32，求△ACF 的面积．答案：（1）证明：连接BO ．（如图4） ∵AB ＝AD ，∴∠D ＝∠ABD ．∵AB ＝AO ，∴∠ABO ＝∠AOB ．图4又∵在△OBD 中，∠D +∠DOB +∠ABO +∠ABD ＝180°， ∴∠OBD ＝90°．∴BD ⊥BO ．∵点B 在⊙O 上， ∴BD 是⊙O 的切线．（2）解：∵∠C ＝∠E ，∠CAF ＝∠EBF ， ∴△ACF ∽△BEF ．∵AC 是⊙O 的直径，点B 在⊙O 上， ∴∠ABC ＝90°．∵在Rt △BFA 中，∠ABF ＝90°，cos ∠BFA ＝32=AF BF ， ∴24()9BEF ACF S BF S AF ∆∆==．又∵BEF S ∆＝8 ， ∴ACF S ∆＝18 ．25．在Rt △ABC 中，∠C =90°，D ，E 分别为CB ，CA 延长线上的点，BE 与AD 的交点为P . （1）若BD=AC ，AE=CD ，在图1中画出符合题意的图形，并直接写出∠APE 的度数；（2）若3AC BD =，3CD AE =，求∠APE 的度数.答案：解：（1）如图9，∠APE=45°. 2）解法一：如图10，将AE 平移到DF ，连接BF ，EF ．则四边形AEFD 是平行四边形． ∴AD ∥EF ，AD=EF ．∵3AC BD ，3CD AE ，∴3=BD AC ，3==DFCDAE CD ． ∴AC CDBD DF =． ∵∠C =90°，∴18090BDF C ∠=︒-∠=︒． ∴∠C=∠BDF ． ∴△ACD ∽△BDF ．∴3AD ACBF BD==1=∠2．图9∴3EF ADBF BF=． ∵∠1+∠3=90°，∴∠2+∠3=90°． ∴BF ⊥AD ． ∴BF ⊥EF ．∴ 在Rt △BEF 中，3tan BF BEF EF ∠=． ∴∠APE =∠BEF =30°．解法二：如图11，将CA 平移到DF ，连接AF ，BF ，EF ．则四边形ACDF 是平行四边形． ∵∠C =90°，∴四边形ACDF 是矩形，∠AFD =∠CAF = 90°，∠1+∠2=90°．∵ 在Rt △AEF 中，3tan 33AE AE AF CD ∠===，在Rt △BDF 中，3tan 13BD BD DF AC ∠==， ∴3130∠=∠=︒．∴∠3+∠2=∠1+∠2=90°，即∠EFB =90°． ∴∠AFD =∠EFB ．又∵32DF AF BF EF ==∴△ADF ∽△EBF ． ∴∠4=∠5．∵∠APE+∠4=∠3+∠5， ∴∠APE =∠3=30°．（通州区一模）6．如图，⊙O 的半径为2，直线PA 、PB 为⊙O 的切线， A 、B 为切点，若PA ⊥PB ，则OP 的长为（） A ．42．4 C ．22 D ．2 答案：C16．已知：如图，90ACB ∠=︒，AC BC =，CD 是经过点C 的一条直线，过点A 、B 分别作AE CD ⊥、BF CD ⊥，垂足为E 、F ，求证：CE BF =. 答案：证明：CD AE ⊥，CD BF ⊥∴︒=∠=∠90BFC AEC图10图11F DA∴︒=∠+∠90B BCF,90︒=∠ACB∴︒=∠+∠90ACF BCF ∴B ACF ∠=∠在BCF ∆和CAE ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠BC AC B ACE BFC AEC . ∴BCF ∆≌CAE ∆（AAS ）. ∴BF CE =（3）按要求应该由哪位同学担任学生会干部职务，请你计算出他的最后得分.20．已知，如图，矩形ABCD 绕着它的对称中心O 按照顺时针方向旋转60°后得到矩形DFBE ，连接AF ，CE .请你判断四边形AFED 是我们学习过的哪种特殊四边形，并加以证明. 答案：解：判断：等腰梯形证明：连结AO 、DO依题意可知：︒=∠=∠60DOE AOD , AO=OD=OE=OFEF 是矩形的对角线∴点F O E 、、在一条直线上， ∴︒=∠60AOF∴DOE AOD AOF ∆∆∆、、都是等边三角形，且AOF ∆≌AOD ∆≌DOE ∆()SAS∴DE AF =ADO ∠=DOE ∠=︒60∴EF AD //,且EF AD ≠∴四边形AFED 是等腰梯形21．如图在平面直角坐标系xOy 中，点A 的坐标为(2，0)，以点A 为圆心，2为半径的圆与x 轴交于O ，B 两点，C 为⊙A 上一点，P 是x 轴上的一点，连结CP ，将⊙A 向上平移1个单位长度，⊙A 与x 轴交于M 、N ，与y 轴相切于点G ，且CP 与⊙A 相切于点C ，60CAP ∠=︒. 请你求出平移后MN 和PO 的长.答案：解：（1）过点A 作x AH ⊥轴，垂足为H ，连结AMAM =2,AH =1,根据勾股定理得：MH=3,∴MN=32B A O yxODCB AOEDCBA（2）CP 是⊙A 切线，且︒=∠60CAP ∴满足要求的C 有两个：C 1、C 2如图，︒=∠6011AP C 或︒=∠6022AP C当︒=∠6011AP C 时，CP 是⊙A 切线， ∴11P AC ∠=︒90,21=AC∴41=AP在H AP Rt 1∆中，AH =1,41=AP∴151=H P ∴2151-=OP同理可求152=H P∴2152+=OP∴OP 的长是215-或215+（顺义区一模）7．如图，ABC △内接于圆O ，50A =∠，60ABC =∠，BD 是圆O 的直径，BD 交AC 于点E ，连结DC ，则BEC ∠等于 A ．50︒ B ．60︒ C ．70︒ D ．110︒答案：C16 已知：如图，ABC △中，45ABC ∠=°，CD AB ⊥于D ，BE AC ⊥于E ，BE 与CD 相交于点F ．求证：BF AC =；答案：证明： ∵CD AB ⊥∴90BDC CDA ∠=∠=︒ ∵45ABC ∠=︒∴45DCB ABC ∠=∠=︒ ∴DB DC = ∵BE AC ⊥ ∴90AEB ∠=︒∴90A ABE ∠+∠=︒ ∵90CDA ∠=︒∴90A ACD ∠+∠=︒ ∴ABE ACD ∠=∠ 在BDF ∆和CDA ∆中BDC CDA DB DCABE ACD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BDF ∆≌CDA ∆ ∴BF AC =19．已知：如图，梯形ABCD 中，AD ∥BC ，90B ∠=︒，4AD AB ==，7BC =，点E 在BC 边上，将△CDE 沿DE 折叠，点C 恰好落在AB 边上的点'C 处．HP 1P 2C 1G yxO NMC 2B A E A BCDO（1）求'C DE ∠的度数；（2）求△'C DE 的面积．答案：解：(1) 过点D 作DF BC ⊥于F . ∵AD BC , 90B ∠=︒, AD AB =, ∴ 四边形ABFD 是正方形.∴4DF BF AB === , 3FC = 在Rt DFC ∆中，2222435CD DF FC =+=+=∴'5C D =∵AD FD =,90A DFC ∠=∠=︒, 'C D CD =∴'AC D FCD ∆≅∆∴'ADC FDC ∠=∠ , '3AC FC ==∴''''90ADF ADC C DF FDC C DF C DC ∠=∠+∠=∠+∠=∠=︒ ∵'C DE CDE ∠=∠ ∴'45C DE ∠=︒(2) 设 EC x = ，则7BE x =- ，'C E x = ∵'3AC = ∴'1BC =在Rt 'BEC ∆中22(7)1x x -+= 解方程，得 257x =∴'11255014722777C DE CDES S EC DF ∆∆==⋅=⨯⨯==20. 已知：如图，AB 是O 的直径，BC 切O 于B ，AC 交O 于P ，D 为BC 边的中点，连结DP ．(1) DP 是O 的切线； (2) 若3cos 5A =，O 的半径为5，求DP 的长.答案：（1）证明：连结OP 和BP∵AB 是O 的直径，BC 切O 于B ，∴90APB ∠=︒ , AB BC ⊥ , ∴90ABC ABP PBC ∠=∠+∠=︒ 在Rt BPC ∆中，D 为BC 边的中点C'E D CBA OPCD BOP∴BD PD =∴BPD PBD ∠=∠ ∵OB OP =∴OPB OBP ∠=∠∴90OPD OPB BPD OBP PBD ABC ∠=∠+∠=∠+∠=∠=︒ 即 PD OP ⊥∴DP 是O 的切线(2) 连结OD 在Rt ABC ∆中∵3cos 5A =，O 的半径为5 ∴50cos 3AB AC A ==∵OA OB =, DC DB =∴12523OD AC ==在Rt OPD ∆中222225202()56333PD OD OP =-=-==24．已知：如图，等边△ABC 中，点D 为BC 边的中点，点F 是AB 边上一点，点E 在线段DF 的延长线上，∠BAE ＝∠BDF ，点M 在线段DF 上，∠ABE ＝∠DBM ．（1）猜想：线段AE 、MD 之间有怎样的数量关系，并加以证明；（2）在（1）的条件下延长BM 到P ，使MP ＝BM ，连接CP ，若AB ＝7，AE ＝72，求tan ∠BCP 的值．答案：（1）猜想：2AE MD =证明：∵△ABC 是等边三角形，点D 为BC 边的中点， ∴2AB BC BD ==∵∠BAE ＝∠BDF , ∠ABE ＝∠DBM∴ABE ∆∽DBM ∆∴2AE ABDM DB== 即 2AE MD =（2）解：如图，连接EP由（1）ABE ∆∽DBM ∆BPO∴2BE ABBM DB== ∴2BE BM =∵MP BM = ∴2BP BM =∴BE BP =∵60EBP ABE ABP PBC ABP ABC ∠=∠+∠=∠+∠=∠=︒ ∴EBP ∆为等边三角形 ∴EM BP ⊥∴90BMD ∠=︒ ∴90AEB ∠=︒在Rt △AEB 中，AB ＝7，AE ＝72 ∴BE =21=22AE -AB∴3tan 2BAE ∠=∵AB CB = ，BE BP = ，∠ABE ＝∠DBM ∴ABE CBP ∆≅∆ ∴BCP BAE ∠=∠∴tan BCP ∠=3tan 2BAE ∠=（石景山区一模）3．已知：如图，m l ∥，等边ABC △的顶点B 在直线m 上，边BC 与直线m 所夹锐角为︒20，则α∠的度数为A ．︒60B ．︒45C ．︒40D ．︒30 答案：C6．已知：⊙O 的半径为2cm ，圆心到直线l 的距离为1cm ，将直线l 沿垂直于l 的方向平移，使l 与⊙O 相切，则平移的距离是 A ．1 cmB ．2 cmC ．3cmD ．1 cm 或3cm 答案：D8．已知：如图，无盖无底的正方体纸盒ABCD EFGH -，P ，Q 分别为棱FB ，GC 上QPHG FED C BA的点，且12,2FP PB GQ QC ==，若将这个正方体纸盒沿折第3题图l 20︒mBAαC线AP PQ QH --裁剪并展开，得到的平面图形是A ．一个六边形B ．一个平行四边形C ．两个直角三角形D ．一个直角三角形和一个直角梯形答案：B11．已知：如图，AB ，BC 为⊙O 的弦，点D 在AB 上，若4=OD ，10=BC ，︒=∠=∠60B ODB ，则DB 的长为．答案：615．如图，在△ABC 中，BC AB ⊥，AC BE ⊥于E ，点F 在线段BE 上，21∠=∠，点D 在线段EC 上，请你从以下两个条件中选择一个作为条件，证明△AFD ≌△AFB ．（1）DF ∥BC ；（2）DF BF =．答案：情况一、添加条件：DF //BC证明: ∵DF ∥BC ∴C FDE ∠=∠∵BC AB ⊥,AC BE ⊥∴︒=∠+∠=∠+∠90EBC C EBC ABF ∴C ABF ∠=∠ ∴ADF ABF ∠=∠在ABF ∆和ADF ∆中 ⎪⎩⎪⎨⎧=∠=∠∠=∠AF AF ADF ABF 21 ∴AFD ∆≌AFB ∆情况二、添加条件：DF BF = 证明：过点F 作AB FG ⊥于G ∵AC BE ⊥,21∠=∠ ∴EF FG =在BGF Rt ∆和DEF Rt ∆中 ︒=∠=∠90DEF BGF ∵⎩⎨⎧==DFBF EF FG ∴BGF Rt ∆≌()HL DEF Rt ∆第11题图D A O B C 21FA B CDEG 21F ABCDE∴EDF GBF ∠=∠ 在ABF ∆和ADF ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠AF AF ADF ABF 21 ∴AFD ∆≌AFB ∆19．已知：如图，直角梯形ABCD 中，AD AB CDA BCD =︒=∠︒=∠，，6090，4,2AB DF ==，求BF 的长．答案：解：如图，过A 作AH ⊥FC 于H则四边形ABCH 为矩形AB CH AH BC ==,∵60,4CDA AD AB ===∠∴AH ==︒60sin AD 23，HD ==︒60cos AD 2 ∴CF =CH +HD +DF =4+2+2=8， ∴BF =22219BC CF +=20．已知：如图，在矩形ABCD 中，点O 在对角线BD 上，以OD 的长为半径的⊙O 与AD ，BD 分别交于点E 、点F ，且∠ABE =∠DBC ．（1）判断直线BE 与⊙O 的位置关系，并证明你的结论；（2）若33sin =∠ABE ，2=CD ，求⊙O 的半径．答案：解：(1)直线BE 与⊙O 相切证明：联结OE在矩形ABCD 中,AD ∥BC ∴∠ADB =∠DBC ∵OE OD =∴∠OED =∠ODE 又∵∠ABE =∠DBC ∴∠ABE =∠OED∵矩形ABDC ,∠︒=90A ∴︒=∠+∠90AEB ABE ∴︒=∠+∠90AEB OED ∴︒=∠90BEO∴直线BE 与⊙O 相切 (2) 联结EF 方法1：∵四边形ABCD 是矩形,2=CD ∴︒=∠=∠90C A ,2==CD AB ∵∠ABE =∠DBC∴=∠CBD sin 33sin =∠ABE ∴32sin =∠=CBDDCBD在AEB Rt ∆中,可求2=AEO FEDC BA∴勾股定理求得6=BE在BEO Rt ∆中，︒=∠90BEO222OB EB EO =+ 设⊙O 的半径为r则()()222326r r -=+∴r =23 方法2：∵DF 是⊙O 的直径 ∴︒=∠90DEF∵四边形ABCD 是矩形∴︒=∠=∠90C A ,2==CD AB ∵∠ABE =∠DBC∴=∠CBD sin 33sin =∠ABE 设x BD x DC 3,==，则x BC 2= ∵2=CD ∴22=BC∵ABE CBD ∠=∠tan tan ∴AB AE BC DC = ∴2222AE = ∴2=AE∴E 为AD 中点．∵DF 为直径，∠︒=90FED ∴AB EF // ∴321==BD DF ∴⊙O 的半径为2322．在边长为1的正方形网格中，正方形ABFE 与正方形EFCD 的位置如图所示．（1）请你按下列要求画图： ① 联结BD 交EF 于点M ；②在AE 上取一点P ，联结BP ，MP ，使△PEM 与△PMB 相似；（2）若Q 是线段BD 上一点，连结FQ 并延长交四边形ABCD 的一边于点R ，且满足BD FR 21=，则QR FQ 的值为_____________．答案：（1）如图所示PMF EDCBA O FEDC（2）1、32或2（平谷区一模）3．如图，已知AB ∥CD ，∠C =35°，BC 平分∠ABE ，则∠ABE 的度数是 A ．° B ．35°C ．70° D ．105° 答案：C8．如图，AB 是O ⊙的直径，弦2cm BC =，F 是弦BC 的中点， 60ABC ∠=°．若动点E 以2cm/s 的速度从A 点出发沿着A B A →→方向运动，设运动时间为()(03)t s t <≤，连结EF ，当BEF △是直角三角形时，t （s ）的值为 A ．47 B ．1 C ．47或1 D ．47或1 或49 答案D ：11．如图，⊙O 是△ABC 的外接圆，OD ⊥AB 于点D 、交⊙O 于点E ，∠C =60°，如果⊙O 的半径为2，那么OD =．答案：115．已知：如图，C F 、在BE 上，A D AC DF BF EC ∠=∠=，∥，．求证：△ABC ≌DEF ．答案：证明：AC DF ∥，ACE DFB ∴∠=∠ ∴ACB DFE ∠=∠．又BF EC =，BF CF EC CF ∴-=-，即BC EF =．在△ABC 与△DEF 中，⎪⎩⎪⎨⎧=∠=∠∠=∠,,,EF BC DFE ACB D A ABC DEF ∴△≌△．19．已知，如图，梯形ABCD 中，AD ∥BC ,∠A =90°，∠C =45°， BE ⊥DC 于E ，BC =5，AD :BC =2:5. 求ED 的长.答案：解：作DF ⊥BC 于F,EG ⊥BC 于G. ∵∠A =90°，AD ∥BC ∴四边形ABFD 是矩形. ∵BC =5,AD :BC =2:5. ∴ AD=BF=2.OBG E C M AFEB CDAABO D CEA BC FEDB C FED。

北京中考昌平一模数学(含答案)

昌平区2011—2012学年第二学期初三年级第一次统一练习数学2012．5一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个．．是符合题意的． 1．15的相反数是 A ．5B ．5-C ．15D ． 15-2．方程组⎩⎨⎧=+=-422y x y x 的解是A ．⎩⎨⎧==21y xB ．⎩⎨⎧==13y xC ．⎩⎨⎧-==2y xD ．⎩⎨⎧==02y x3．2012年伦敦奥运会体育场位于伦敦东部的斯特拉特福，因外形上阔下窄，又被称为“伦敦碗”，预计可容纳8万人，分为两层，上层是55000个临时座位．将55000用科学记数法表示为A ． 55×103B ． 0．55×105C ． 5．5×104D ． 5．5×1034．如图，AB ∥CD ，点E 在BC 上，且CD =CE ，∠B =32°，则∠D 的度数为A ．32°错误！未找到引用源。

B ．68°错误！未找到引用源。

C ．74°错误！未找到引用源。

D ．84°5．一名警察在高速公路上随机观察了6辆汽车的车速，记录如下：则这6辆车车速的众数和中位数是 A ．84，90B ．85，82C ．82，86D ．82，836．三张卡片上分别画有等腰直角三角形、等边三角形和菱形，从这三张卡片中随机抽取一张，则取到的卡片上的图形是中心对称图形的概率是E DC BAＡ．13Ｂ．23Ｃ．12Ｄ．17．若关于x 的一元二次方程(a －1)x 2－2x +1=0有两个不相等的实数根,则a 的取值范围是A ．a ＜2且a ≠0 Ｂ．a ＞2 Ｃ．a ＜2且a ≠1 Ｄ．a ＜－2 ８．如图，已知□ABCD 中，AB =4,AD =2,E 是AB 边上的一动点（与点A 、B 不重合），设AE =x ,DE 的延长线交CB 的延长线于点F ，设BF =y ，则下列图象能正确反映y 与x 的函数关系的是DC B AFEDC BA二、填空题（共4道小题，每小题4分，共16分）9有意义，则x 的取值范围为． 10．分解因式： 244x y xy y -+= ． 11．符号f 表示一种运算，它对一些数的运算结果如下：（1）0)1(=f ，1)2(=f ，2)3(=f ，3)4(=f ，… （2）2)21(=f ，3)31(=f ，4)41(=f ，5)51(=f ，… 利用以上规律计算：1()(2012)2012f f -= ． 12．己知□ABCD 中，AD =6，点E 在直线AD 上，且DE ＝3，连结BE 与对角线AC 相交于点M ，则MCAM= ．三、解答题（共6道小题，每小题5分，共30分）13．计算：101()2cos30(1)3π--︒-．14．解不等式组：12(2)3.x x x -⎧⎨+⎩≥0，＞15．计算：22142m m m+--．16．如图，已知△ABC 和△ADE 都是等边三角形，连结CD 、BE ．求证：CD =BE ．ED CBA17．已知260x x --=，求代数式22(1)(1)10x x x x ---+的值．18．如图，在□ABCD 中，AB ＝5，AD ＝10，cos B ＝35，过BC 的中点E 作EF ⊥AB ，垂足为点F ，连结DF ，求DF 的长．F ED CBA四、解答题（共4道小题，每小题5分，共20分）19．如图，已知直线P A 交⊙O 于A 、B 两点，AE 是⊙O 的直径，C 为⊙O 上一点，且AC 平分∠P AE ，过点C 作CD ⊥P A 于D ．（1）求证：CD 是⊙O 的切线；（2）若AD ：DC =1：3，AB =8，求⊙O 的半径．20．某周六上午8：O0小明从家出发，乘车1小时到郊外某基地参加社会实践活动．在基地活动2．2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回，同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇．接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x 小时，小明离家的路程y (千米)与x (小时)之间的函数图象如图所示． (1)小明去基地乘车的平均速度是千米/时，爸爸开车的平均速度是千米/时； (2)求线段CD 所表示的函数关系式，不用写出自变量x 的取值范围；(3)问小明能否在中午12：00前回到家？若能，请说明理由；若不能，请算出中午12：00时他离家的路程．)21．为了更好地利用“大课间”加强学生的体育锻炼，调动学生运动的积极性，某校围绕着“你最喜欢的体育活动项目是什么（只写一项）？”的问题，对在校学生进行了随机抽样调查，得到一组数据，绘制如下的统计图表：各年级学生人数统计表:（1）该校对多少名学生进行了抽样调查?（2）请分别在图1和图2中将“抖空竹”部分的图形补充完整；（3）已知该校九年级学生比八年级学生多20人，请你补全上表，并利用样本数据估计全校学生中最喜欢踢毽子运动的人数约为多少？图1抽样调查学生最喜欢的运动项目的人数统计图%各运动项目的喜欢人数占抽样总人数百分比统计图抖空竹跳绳40%踢毽子 20%其它 10%图222．问题探究：（1）如图1，在边长为3的正方形ABCD 内（含边）画出使∠BPC =90°的一个点P ，保留作图痕迹；（2）如图2，在边长为3的正方形ABCD 内（含边）画出使∠BPC =60°的所有的点P ，保留作图痕迹并简要说明作法；（3）如图3，已知矩形ABCD ，AB =3，BC =4，在矩形ABCD 内（含边）画出使∠BPC =60°，且使△BPC 的面积最大的所有点P ，保留作图痕迹．图3图2图1A DCBABCDD CBA五、解答题（共3道小题，第23小题6分，第24，25小题各8分，共22分） 23．已知关于x 的方程（k +1）x 2+(3k -1)x +2k -2=0．（1）讨论此方程根的情况；（2）若方程有两个整数根，求正整数k 的值；（3）若抛物线y =（k +1）x 2+(3k -1)x +2k -2与x 轴的两个交点之间的距离为3，求k 的值．24．如图，已知抛物线2y ax bx c =++与x 轴交于A （-1，0）、B （3，0）两点，与y 轴交于点C （0，3）．（1）求抛物线的解析式及顶点M 坐标；（2）在抛物线的对称轴上找到点P ，使得△P AC 的周长最小，并求出点P 的坐标；（3）若点D 是线段OC 上的一个动点（不与点O 、C 重合）．过点D 作DE ∥PC 交x 轴于点E ．设CD 的长为m ，问当m 取何值时，S △PDE =19S 四边形ABMC ．25．如图，在四边形ABCD 中，对角线AC 、BD 相交于点O ，直线MN 经过点O ，设锐角∠DOC =∠ ，将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’，直线A D ’、B C ’相交于点P ．（1）当四边形ABCD 是矩形时，如图1，请猜想A D ’、B C ’的数量关系以及∠APB 与∠α的大小关系；（2）当四边形ABCD 是平行四边形时，如图2，（1）中的结论还成立吗？（3）当四边形ABCD 是等腰梯形时，如图3，∠APB 与∠α有怎样的等量关系？请证明．图3图2图1D BANC'OMPD'D CBAN C'O MPD'D'PMOC'NA BCD昌平区2011—2012学年第二学期初三年级第一次统一练习数学试卷参考答案及评分标准 2012．1一、选择题（共8个小题，每小题4分，共32分）二、填空题（共4个小题，每小题4分，共16分）三、解答题（共6道小题，每小题5分，共30分） 13．解：原式=3212-⨯+ ……………………… 4分 =4+ ……………………… 5分 14．解：1?2(2)3.x x x -⎧⎨+⎩≥0， ①＞②由①得x ≥1． ……………………… 2分由②得x ＜4． ……………………… 4分所以原不等式组的解集为1≤x ＜4． ……………………… 5分 15．解：原式=22142m m m --- ……………………… 1分 =22(2)(2)(2)(2)m m m m m m +-+-+-=22(2)(2)m m m m --+-=2(2)(2)m m m -+-． ……………………… 4分=12m + ． ……………………… 5分 16．证明：∵ △ABC 和△ADE 都是等边三角形，∴ AB =AC ，AE =AD ，∠DAE =∠CAB ， ∵ ∠DAE -∠CAE =∠CAB -∠CAE ， ∴ ∠DAC =∠EAB ，ED CBA∴ △ADC ≌△AEB ． ……………………… 4分 ∴ CD =BE ． ……………………… 5分17．解：22(1)(1)10x x x x ---+ 原式=x (x 2-2x +1)-x 3+x 2+10=x 3-2x 2+x -x 3+x 2+10 =-x 2+x +10=-(x 2-x )+10． ……………………… 3分∵ 260x x --=， ∴ 26x x -=，∴ 原式=4． ……………………… 5分 18．解：延长DC ，FE 相交于点H ．∵ 四边形ABCD 是平行四边形，∴ AB ∥DC ，AB =CD ，AD =BC ． ……………………… 1分 ∴ ∠B ＝∠ECH ，∠BFE ＝∠H ． ∵ AB ＝5，AD ＝10， ∴ BC =10，CD =5． ∵ E 是BC 的中点，∴ BE =EC =152BC =． ∴ △BF E ≌△CHE ． ……………………… 3分 ∴ CH =BF ，EF=EH ． ∵ EF ⊥AB ，∴∠BFE ＝∠H =90°．在Rt △BFE 中， ∵ cos B =BF BE ＝35， ∴ BF =CH =3．∴ EF4，DH =8．在Rt △FHD 中，∠H =90°，∴ 222DF FH DH =+=28+28=2×28．∴ DF． ……………………… 5分四、解答题（共4道小题，每小题5分，共20分） 19．（1）证明：连结OC ．∵ OC =OA ，∴ ∠OAC = ∠OCA ． ∵ AC 平分∠P AE ， ∴ ∠DAC = ∠OAC ， ∴ ∠DAC = ∠OCA ， ∴ AD ∥OC ．HABC D EF∵ CD ⊥P A ，∴ ∠ADC = ∠OCD =90°，即 CD ⊥OC ，点C 在⊙O 上，∴ CD 是⊙O 的切线． ……………………… 2分（2）解：过O 作OE ⊥AB 于E ． ∴ ∠OEA =90．° ∵ AB =8，∴ AE =4． ……………………… 3分在Rt △AEO 中，∠AEO =90°，∴ AO 2=42+OE 2．∵ ∠EDC = ∠OEA =∠DCO =90°， ∴ 四边形DEOC 是矩形， ∴ OC =DE ，OE =CD ． ∵ AD:DC =1:3，∴ 设AD =x ，则DC =OE =3x ，OA =OC =DE =DA +AE =x +4，∴ (x +4)2=42+(3x )2，解得 x 1=0(不合题意，舍去)，x 2=1．则 OA =5．∴ ⊙O 的半径是5． ……………………… 5分 20．解：(1) 30 ， 56 ； ……………………… 2分 (2) y =-56x +235．2 (3．7≤x ≤4．2) ……………………… 4分 (3)不能．小明从家出发到回家一共需要时间：1+2．2+2÷4×2=4．2（小时），从8:00经过4．2小时已经过了12:00，∴ 不能再12:00前回家，此时离家的距离：56×0．2=11．2（千米）． ………………… 5分 21．解：（1）80÷40％=200（名）答：该校对200名学生进行了抽样调查． ………………… 1分（2）………………… 3分（3）120+180+200=500（名） 500×20％=100（名）答：全校学生中最喜欢踢毽子活动的人数约为100名． ………………… 5分30图2 其它10% 踢毽子20%跳绳40%抖空竹各运动项目的最喜欢人数占抽样总人数百分比统计图%抽样调查学生最喜欢的运动项目的人数统计图图122．解：（1）如图1，画出对角线AC 与BD 的交点即为点P ． ………………… 1分注：以BC 为直径作上半圆（不含点B 、C ），则该半圆上的任意一点即可．（2）如图2，以BC 为一边作等边△QBC ，作△QBC 的外接圆⊙O 分别与AB ，DC 交于点 M 、N ，弧MN 即为点P 的集合． ………………… 3分（3）如图3，以BC 为一边作等边△QBC ，作△QBC 的外接圆⊙O 与AD 交于点 P 1、P 2 ，点P 1、P 2即为所求． ………………… 5分五、解答题（共3道小题，第23小题6分，第24，25小题各8分，共22分） 23．解：（1）当1k =-时，方程44x --=0为一元一次方程，此方程有一个实数根；当1k ≠-时，方程2(1)(31)22k x k x k ++-+-=0是一元二次方程，△=（3k -1）2-4(k +1)(2k -2)=（k -3）2．∵（k -3）2≥0，即△≥0，∴ k 为除-1外的任意实数时，此方程总有两个实数根． ……………………… 2分综上，无论k 取任意实数，方程总有实数根．（2）13(3)2(1)k k x k -±-=+，x 1=-1，x 2=421k -+．∵ 方程的两个根是整数根，且k 为正整数，∴ 当k =1时，方程的两根为-1，0；当k =3时，方程的两根为-1，-1．∴ k =1，3． ……………………… 4分（3）∵ 抛物线y =（k +1）x 2+(3k -1)x +2k -2与x 轴的两个交点之间的距离为3，∴，12x x -=3，或21x x -=3．当12x x -=3时，k =-3；当21x x -=3时，k =0．综上，k =0，-3． ……………………… 6分24．解：（1）∵ 抛物线2y ax bx c =++（0a ≠）A （-1，0）、B （3，0）C （0，3）三点，∴ 933030a b a b ++=⎧⎨-+=⎩，解得 12a b =-⎧⎨=⎩．∴ 抛物线的解析式为223y x x =-++，顶点M 为（1，4）． ……………… 2分B B A（2）∵ 点A 、B 关于抛物线的对称轴对称，∴ 连结BC 与抛物线对称轴交于一点，即为所求点P ．设对称轴与x 轴交于点H ，∵ PH ∥y 轴，∴ △PH B ∽△CBO ．∴ PH BH CO BO=．由题意得BH =2，CO =3，BO =3，∴ PH =2．∴ P （1，2）． ……………………… 5分（3）∵ A （-1，0）B （3，0），C (0，3)，M (1，4)， ∴ S 四边形ABMC =9．∵ S 四边形ABMC =9S △PDE ， ∴PDE S ∆=1． ∵ OC =OD ，∴∠OCB =∠OBC = 45°．∵ DE ∥PC ，∴∠ODE =∠OED = 45°． ∴ OD =OE =3-m ．∵ S 四边形PDOE =9322m -， ∴ S △PDE = S 四边形PDOE - S △DOE =21322m m -+（0<m <3）． ∴213122m m -+=．解得，m 1=1， m 2=2． ……………………… 8分25．解：图3图2图1D CBANC'OMPD'D CBAN C'O MPD'D'PM OC'NA BCD（1） A D ’=B C ’，∠APB =∠α． …………………… 2分（2） A D ’=B C ’ 仍然成立，∠APB =∠α不一定成立． …………………… 3分（3）∠APB =180°-∠α． …………………… 4分证明：如图3，设OC ’，PD ’交于点E ．∵ 将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’， ∴ △DOC ≌△D ’OC ’，∴ OD =OD ’， OC =OC ’，∠DOC =∠D ’OC ’． ∵ 四边形ABCD 是等腰梯形，∴ AC =BD ，AB =CD, ∠ABC = ∠DCB ． ∵ BC =CB ，∴ △ABC ≌△DCB ．E∴∠DBC=∠ACB．∴OB=OC，OA=OD．∵∠AOB=∠COD=∠C’O D’，∴∠BOC’ =∠D’O A．∵OD’=OA，OC’=OB，∴△D’OC’≌△AOB，∴∠OD’C’=∠OAB．∵OD’=OA，OC’=OB，∠BOC’ =∠D’O A，∴∠OD’A =∠OAD’=∠OBC’=∠OC’ B．∵∠C’EP=∠D’EO，∴∠C’PE=∠C’OD’=∠COD=∠α．∵∠C’PE+∠APB=180°，∴∠APB=180°-∠α．……………………8分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B
昌平区2010—2011学年第二学期初
三年级第一次统一练习
数
学
2011．4
一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个．．是符合题意的． 1． -4的相反数是
A ．-4
B ．4
C ．-
14
D ．
14
2．据昌平交通局网上公布，地铁昌平线（一期）2011年1月4日出现上班运营高峰，各站进出站约47600人次. 将47 600用科学记数法表示为 A ．5
0.47610⨯
B ．2
47610⨯
C ．4
4.7610⨯
D ．5
4.7610⨯
3．在一个不透明的笔袋中装有两支黑色笔和一支红色笔，除颜色不同外其他都相同，随机从其中摸出一支黑色笔的概率是 A ．12
B ．
13
C ．
2
3
D ．1
426y += 0，则x y -的值为
A ．5-
B ．1-
C ．1
D ．5 5．函数y x 的取值范围是
A ．1x ≥
B ．1x ≤
C ．1x >
D ．1x ≠
6．在“爱的奉献”为地震灾区捐款活动中，某班以小组为单位的捐款额（单位：元）分别为10，20，15，15，21，15，在这组数据中，众数及中位数分别是
A ．15，10
B ．15，15
C ．15，20
D ．15，16 7.如图，已知，AB 是⊙O 的直径，点C ，D 在⊙O 上， ∠ABC =50°，则∠D 为
A ．50°
B ．45°
C ．40°
D ． 30°
８．已知：如图,在等边三角形ABC 中，M 、N 分别是AB 、AC 的中点，D 是MN 上任意一点，CD 、BD 的延长线分别与AB 、AC 交于F 、E ，若116CE BF
+= ，则等边三角形ABC 的边长为
N
M C
B
A E D
F
A.
81 B. 14 C. 2
1
D.1 二、填空题（共4道小题，每小题4分，共16分）
9．若分式
4
2
x x -+的值为0，则x 的值为． 10．分解因式：2
4ax a -= ．
11．如图，已知菱形ABCD 的边长为5，对角线AC ，BD 相交于点O ，BD =6，则菱形ABCD 的面积为 .
12．如图，在函数12
y x
=
（x ＞0）的图象上，有点1P
2P ，3P ，…，n P ，1n P +，若1P 的横坐标为a 每点的横坐标与它前面一个点的横坐标的差都为2，过点1P ，2P ，3P ，…，n P ，1n P +分别作x 轴、 y 部分的面积从左到右依次记为1S ，2S ，3S ，…，n S 则1S = ， 1S +2S +3S +…+n S = ．（用n 的代数式表示）
三、解答题（共6道小题，每小题5分，共30分） 13．计算：0
4sin 30(3.14)--︒+-π
14．解不等式：512x -≤2(43)x -，并把它的解集在数轴上表示出来．
15．解分式方程：
2111x
x x =-+-．
16．如图，已知线段AC 与BD 相交于点O ，联结AB DC 、，E 为OB 的中点，F 为OC 的中点，联结EF ．若∠A =∠D ，∠OEF =∠OFE ，求证：AB =DC ．
17．当2
2310x x ++=时，求2
(2)(5)28x x x x -+++-的值.
18．列方程（组）解应用题
国家的“家电下乡”政策激活了农民购买能力，提高了农民的生活水平。

“家电下乡”的补贴标准是：农户每购买一件家电，国家将按每件家电售价的13%补贴给农户．李大叔购买
O
D
C A
B
E
F
O B
D
C
A
了一台彩电和一台洗衣机，从乡政府领到了390元补贴款．若彩电的售价比洗衣机的售价高1000元，求彩电和洗衣机的售价各是多少元．
四、解答题（共4道小题，每小题均5分，共20分）
19．在梯形ABCD 中，AB ∥CD ，BD ⊥AD ，BC =CD ，∠A =60°，BC =2cm . (1)求∠CBD 的度数； (2)求下底AB 的长.
20．如图所示，AB 是⊙O 的直径，OD ⊥弦BC 于点F ，且交⊙O 于点E ，若∠AEC =∠ODB ．
（1）判断直线BD 和⊙O 的位置关系，并给出证明；（2）当AB =10，BC =8时，求BD 的长．
21．某班同学积极响应“阳光体育工程”的号召，利用课外活动时间积极参加体育锻炼，每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练，训练前后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表．
项目选择情况统计图: 训练前定时定点投篮测试进球数统计图:
训练后篮球定时定点投篮测试进球数统计表:
请你根据图表中的信息回答下列问题：
（1）选择长跑训练的人数占全班人数的百分比是，该班共有同学人；（2）补全“训练前篮球定时定点投篮测试进球数统计图；（3）训练后篮球定时定点投篮人均进球数 .
立定跳远
20％
长跑铅球
10％篮球60％4
5673进球数(个)
1
20
A B C
D
22．现场学习题
问题背景：在△ABC 中，AB 、BC 、AC
小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC （即△ABC 三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC 的高，而借用网格就能计算出它的面积．
A
B C
图3
图2
图1
(1)请你将△ABC 的面积直接填写在横线上．________ 思维拓展：
(2)我们把上述求△ABC 面积的方法叫做构图法．若△ABC
、
(0)a >，请利用图2的正方形网格(每个小正方形的边长为a )画出相应的△
ABC ，并求出它的面积是：．探索创新：
(3)若△ABC 三边的长分别
为
、
、
(0,,)m n o m n >>≠ ，请运用构图法在图3指定区域内画出示意图，并求出△ABC 的
面积为：．
五、解答题（共3道小题，第23小题6分，第24，25小题各8分，共22分） 23．已知二次函数2
2
(1)(31)2y k x k x =---+．
（1）二次函数的顶点在x 轴上，求k 的值；
（2）若二次函数与x 轴的两个交点A 、B 均为整数点（坐标为整数的点），当k 为整数时，求A 、B 两点的坐标.
24．已知，点P 是∠MON 的平分线上的一动点，射线P A 交射线OM 于点A ，将射线P A 绕点P 逆时
针旋转交射线ON 于点B ，且使∠APB + ∠MON =180°.
（1）利用图1，求证：P A =PB ；
（2）如图2，若点C 是AB 与OP 的交点，当
3POB PCB S S ∆∆=时，求PB 与PC 的比值；
（3）若∠MON =60°，OB =2，射线AP
交ON 于点D ，且满足且PBD ABO ∠=∠，请借助图3补全图形，并求OP 的长.
C
A
O
P
B
M
N
T
图1
图2
图3
T
N
M B
P O
A
C
T
N
M
B
P
O
A
25.已知：如图，在平面直角坐标系xOy中，
矩形OABC的边OA在y轴的正半轴上，OC Array在x轴的正半轴上，OA=2，OC=3．过原点
O作∠AOC的平分线交AB于点D，连接DC，
过点D作DE⊥DC，交OA于点E．
（1）求过点E、D、C的抛物线的解析式；
（2）将∠EDC绕点D按顺时针方向旋转
后，角的一边与y轴的正半轴交于点F，
另一边与线段OC交于点G．如果
EF=2OG，求点Ｇ的坐标．
（3）对于（2）中的点G，在位于第一象限
内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG
是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．。